Estimation and imaging of breast lesions using a two-layer tissue structure by ultrasound-guided optical tomography

Abstract.

A new two-step estimation and imaging method is developed for a two-layer breast tissue structure consisting of a breast tissue layer and a chest wall underneath. First, a smaller probe with shorter distance source-detector pairs was used to collect the reflected light mainly from the breast tissue layer. Then, a larger probe with $9\times 14$ source-detector pairs and a centrally located ultrasound transducer was used to collect reflected light from the two-layer tissue structure. The data collected from the smaller probe were used to estimate breast tissue optical properties. With more accurate estimation of the average breast tissue properties, the second layer properties can be assessed from data obtained from the larger probe. Using this approach, the unknown variables have been reduced from four to two and the estimated bulk tissue optical properties are more accurate and robust. In addition, a two-step reconstruction using a genetic algorithm and conjugate gradient method is implemented to simultaneously reconstruct the absorption and reduced scattering maps of targets inside a two-layer tissue structure. Simulations and phantom experiments have been performed to validate the new reconstruction method, and a clinical example is given to demonstrate the feasibility of this approach.

1. Introduction

Diffuse optical tomography (DOT) in the near-infrared (NIR) spectrum is a promising noninvasive approach for functional breast imaging.^1–15 However, the resolution and lesion localization are poor due to intense light scattering in tissue. Additionally, the inverse problem of DOT is ill-posed and the solution is not unique. To improve the target quantification accuracy of DOT, several research groups have explored the use of a priori information provided by MRI, x-ray, and ultrasound (US).^4,7–12 Our group has pioneered the use of US-guided DOT by deploying many source and detection fibers around a US transducer located in the middle of a hand-held probe. In general, a semi-infinite model is used as a reasonable approximation for calibration and weight matrix calculation when the patient is in a supine position. However, when the breast tissue thickness is $<2\mathrm{cm}$, the chest wall underneath the tissue layer needs to be accounted for. In this case, a two-layer tissue structure is a more precise model for more accurate imaging reconstruction.^16–19

In the past, we have introduced several approaches to account for chest wall effects. For example, we have implemented an analytical solution for a two-layer tissue structure with and without a tilted interface²⁰ and developed a finite-element method to handle the reference mismatch problem due to the presence of the chest wall.²¹ However, these approaches require the fitting of amplitude and phase profiles of reflected light to estimate four parameters of background tissue absorption and reduced scattering coefficients of both layers. The errors of the estimated second layer absorption and reduced scattering coefficients are much larger than that of the first layer. In this paper, we introduce a new approach by utilizing a small probe with several short distance source-detector pairs to estimate the first layer absorption and reduced scattering coefficients. The estimated first layer properties are used to fit the amplitude and phase profiles of reflected light measured from a larger probe with both short and longer source-detection separations and to estimate the second layer properties. Using this approach, the unknown variables have been reduced from four to two and the results are more accurate and robust. In addition, we have implemented a two-step reconstruction using a genetic algorithm (GA) and conjugate gradient (CG) method²² to simultaneously reconstruct the absorption and reduced scattering maps of a target inside a two-layer tissue structure. Simulations and phantom experiments have been performed to validate the new reconstruction method, and a clinical example is given to demonstrate the feasibility of this approach.

2. Methods

2.1. Two-Layer Tissue Model

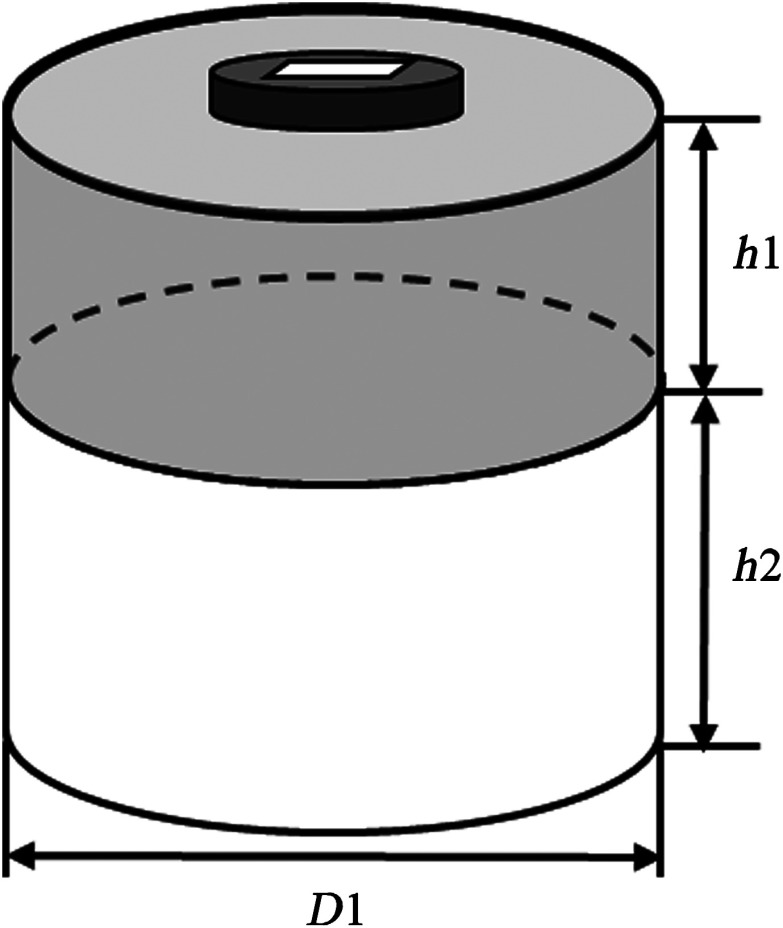
Figure 1 illustrates the structure of the two-layer tissue model. A cylinder with a 10-cm diameter was used to model a homogeneous medium, which had two layers of different absorption and reduced scattering coefficients. The first layer simulates the breast tissue layer with $<2.5\mathrm{cm}$ thickness and the second layer represents the chest wall of 7 cm depth. To estimate the optical properties of the two-layer medium, a four-parameter analytical fitting method was developed in our previous work.¹⁷ Briefly, by solving the two-layer diffusion equation, the measured fluence rate at the tissue surface is related to the absorption and reduced scattering coefficients of the two tissue layers.

$$\varphi (r,\omega )=f({\mu }_{a1},{\mu }_{s1}^{\prime },{\mu }_{a2},{\mu }_{s2}^{\prime }),$$ (1)

where $\varphi (r,\omega )$ is the fluence rate and ${\mu }_{a1}$, ${\mu }_{s1}^{\prime }$, ${\mu }_{a2}$, and ${\mu }_{s2}^{\prime }$ are absorption and reduced scattering coefficients of the two tissue layers. A nonlinear optimization method based on Nelder-Mead simplex algorithm^20,23 was used to simultaneously fit the amplitude and phase and estimate the background properties of the two layers. To improve the accuracy of the estimation, this method was modified to two-parameter fitting by taking the first layer ${\mu }_{a1}$ and ${\mu }_{s1}^{\prime }$ fitted from a smaller probe as known background values. The smaller probe consists of three sources and five detectors with source-detector separations ranging from 1.5 to 3.5 cm as shown in Fig. 2(a). The number of sources and detectors of the smaller probe was optimized based on the accuracy of the estimated optical properties of intralipid solution with different concentrations.

Fig. 1.

A two-layer tissue model. $h1$ is the first layer thickness, $h2$ is the second layer thickness, and $D1$ is the diameter of the medium. $D1$ is typically $\ge 10\mathrm{cm}$.

Fig. 2.

Probes used in simulations and experiments. (a) Smaller probe with short distance source-detector pairs (1.5 to 3.5 cm) for estimation of first layer optical properties. (b) Larger probe with a central slot used for ultrasound (US) transducer.

2.2. Two-Step Reconstruction with GA

Recently, we have developed a two-step reconstruction method using GA followed by the CG method for simultaneous image reconstruction of absorption and scattering maps of targets inside a semi-infinite medium.²² Briefly, GA was used to obtain an initial estimate of the optical properties of a lesion. Because coregistered US images were used to locate the target approximately in the middle of the probe, the target center and its radius in the $z$ direction were estimated from US images, and its radius in spatial $x$ and $y$ dimensions ($r_x$ $r_y$) was iteratively estimated by GA. First, an initial population is generated, formed by certain individuals while each member is a possible solution of the optimization problem and can be represented by a vector of real numbers, for example, [${\mu }_{\mathrm{am}}$ ${\mu }_{\mathrm{sm}}^{\prime }$ $r_x{r}_y$], where ${\mu }_{\mathrm{am}}$ and ${\mu }_{\mathrm{sm}}^{\prime }$ are unknown maximum target absorption and reduced scattering coefficients. These individuals then undergo a set of genetic operations—selection, crossover, and mutation—in order to promote the population evolution. The error of each individual is defined as

$$\mathrm{Er}={\Vert U_{\mathrm{sc}}-WX\Vert }^2,$$ (2)

$$W=[W_A,W_S],$$ (3)

$$X=\left[\begin{array}{c}{\int }_v\delta {\mu }_a\mathrm{d}v\\ {\int }_v\delta D\mathrm{d}v\end{array}\right]=\left[\begin{array}{c}{\int }_v({\mu }_a-{\mu }_{a0})\mathrm{d}v\\ {\int }_v({\mu }_s^{\prime -1}-{\mu }_{s0}^{\prime -1})/3\mathrm{d}v\end{array}\right],$$ (4)

where $U_{\mathrm{sc}}$ is the measurement, $W_A$ and $W_S$ are weight matrices for the absorption and reduced scattering coefficients, respectively, and (${\mu }_a$, ${\mu }_s^{\prime }$) and (${\mu }_{a0}$, ${\mu }_{s0}^{\prime }$) are the lesion and background absorption and reduced scattering coefficients, respectively. The fitness of each individual is defined as $1/\mathrm{Er}$. When the improvement in the fitness of members is $<{10}^{-6}$, or the generation number exceeds 100, the generation of the populations is stopped and the selected values for the unknown parameters of the model are obtained. After that, the CG reconstruction method with the initial guess obtained from GA is applied to obtain the absorption and scattering distributions. The GA method is modified for use in the two-layer structure; the weight matrix $W$ in Eq. (3) is calculated as

$$W_A=G(r_{vj},r_{di}){\mathrm{\Phi }}_0(r_{si},r_{vj})/D_l\mathrm{and}{W}_S=-\nabla G(r_{vk},r_{di})\nabla {\mathrm{\Phi }}_0(r_{si},r_{vk})/D_l,$$

where $D_l$ is the diffusion coefficient and equals $D_1$ or $D_2$, depending on the voxel location in the layered medium; $r_v$ represents the voxel location, $r_s$ is the source position, and $r_d$ is the detector position. In Eq. (4), ${\mu }_{a0}$, ${\mu }_{s0}^{\prime }$ are modified to ${\mu }_{a01}$, ${\mu }_{s01}^{\prime }$ and ${\mu }_{a02}$, ${\mu }_{s02}^{\prime }$, which are the background optical properties of the first and the second layer obtained from the two-parameter fitting, respectively. After the initial values were obtained from GA, they were applied to the CG reconstruction algorithm, which computes the final distribution of the lesion.

2.3. Simulation and Experiments

In simulations, a commercial finite-element package COMSOL was employed to solve the forward diffusion equation in the frequency domain.^21,24 A modulation frequency of 140 MHz was used in all simulations. A cylinder of 10 cm diameter consisting of two layers was used to model the two-layer tissue medium (Fig. 1), and 9 sources and 14 detectors were distributed on the surface in reflection geometry as shown in Fig. 2(b). The first layer thickness varied from 1.0 to 2.5 cm, and the second layer thickness was fixed to 7 cm.

In imaging reconstruction, a target of a 1.0-cm diameter sphere was embedded in the first layer. The corresponding reference data were generated from the same two-layer structure without the target inside and the perturbation was the difference between the target and the reference data sets.

In phantom experiments, a frequency domain system consisting of 14 parallel detectors and 4 laser diodes of wavelengths 740, 780, 808, and 830 nm was used to acquire data. Each laser diode was sequentially switched to nine positions on the probe. The central slot on the probe shown in Fig. 2(b) was used for the US transducer, and the source and detector fibers were distributed on both sides. Figure 2(a) shows the small probe with three central sources and five detectors to estimate the first layer background optical properties. The small probe was designed by starting a populated probe of 9 sources and 14 detectors with source and detector distances ranging from 1.5 to 4.5 cm. Then different combinations of sources and detectors were tested with an intralipid solution to select the minimal number of sources and detectors to obtain the same estimated properties as the populated probe.

The first layer of the phantom was made of an intralipid solution with drops of Indian ink. The absorption and reduced scattering coefficients were calibrated with the frequency domain system. Soft phantoms made of polyvinyl chloride-plastisol (PVCP) solution were placed underneath the solution as the second layer. To validate the simulations, experiments were made at similar optical properties and layer thicknesses. To control the properties of the first layer, the smaller probe was used to calibrate and adjust the amount of Indian ink and intralipid until reaching the required absorption and reduced scattering coefficients. Phantoms of the second layer were made of PVCP solution, which was a white opaque solution and became translucent when it was heated.²⁵ When the solution was gradually heated, the Indian ink and titanium dioxide powder were added to control the optical absorption and reduced scattering coefficients of the phantom. The heated solution was poured into a 10-cm-diameter bowl and solidified after cooling for several hours.

In imaging experiments, a target of a 1.0-cm diameter sphere made of PVCP was embedded in the first layer. The corresponding reference data were generated from the same two-layer structure without a target inside and the perturbation was the difference between the target and the reference data sets.

Clinical experiments were performed with a system of similar electronic and optical design as that used for phantom experiments. The study protocol was approved by the UConn Health Center institution review board. All patients who participated in our study signed the informed consent. The patients’ data were taken at the lesion area and the contralateral breast of the same quadrant as the lesion. Contralateral data set was used to estimate background optical properties for weight matrix computation. The perturbations computed between lesion data and contralateral data were used for imaging reconstruction.

3. Results

3.1. Estimation of Optical Properties of the Two-Layer Structure

3.1.1. Simulations

Simulations were performed using the two-layer model shown in Fig. 1. In simulations, optical properties of the first layer were assumed as known values, and the second layer properties were estimated from the two-parameter fitting described in Sec. 2.1. Three sets of typical breast tissue optical properties were used as the first layer properties of (1) ${\mu }_a=0.02{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=4{\mathrm{cm}}^{-1}$; (2) ${\mu }_a=0.05{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=6{\mathrm{cm}}^{-1}$; and (3) ${\mu }_a=0.05{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=9{\mathrm{cm}}^{-1}$. Two sets of second layer optical properties of (1) ${\mu }_a=0.1{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=6{\mathrm{cm}}^{-1}$ and (2) ${\mu }_a=0.2{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=6{\mathrm{cm}}^{-1}$ were used as the estimate of chest wall properties (see Table 1). These values were obtained from our clinical studies of several hundred patients.^8,11 Simulations were performed for first layer thicknesses of 1.0, 1.5, 2.0, and 2.5 cm, respectively. Figure 3 shows one example of estimated second layer ${\mu }_a$ and ${\mu }_s^{\prime }$ versus iterations. The first layer properties used in simulations were true values given in set #1 (Table 1), and the fitted results of the second layer were converged to ${\mu }_a=0.12{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=6.7{\mathrm{cm}}^{-1}$. The true values of the second layer were ${\mu }_a=0.1{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=6{\mathrm{cm}}^{-1}$. The average accuracy of the fitted second layer properties for each set of first layer properties is given in Table 1. The average was obtained from results of different first layer thicknesses, however, with the same first layer optical properties. On average, the fitting errors of ${\mu }_a$ and ${\mu }_s^{\prime }$ are $<5$ and 23%, respectively, for the first set of second layer properties and the corresponding errors are $<17$ and 42% for the second set of second layer properties (see Fig. 4). In general, the error is larger when the second layer ${\mu }_a$ is higher and the mismatch of ${\mu }_s^{\prime }$ between two layers is larger.

Table 1.

Simulation results of accuracy of fitted second layer properties. The first layer properties are the true values given in the first column.

First layer (${\mathrm{cm}}^{-1}$)	Second layer (${\mathrm{cm}}^{-1}$)
		1. ${\mu }_a=0.1$, ${\mu }_s^{\prime }=6.0$	2. ${\mu }_a=0.2$, ${\mu }_s^{\prime }=6.0$
1. ${\mu }_a=0.02$, ${\mu }_s^{\prime }=4.0$	${\mu }_a$${\mu }_s^{\prime }$	97.9% 76.3%	85.0% 63.2%
2. ${\mu }_a=0.05$, ${\mu }_s^{\prime }=6.0$	${\mu }_a$${\mu }_s^{\prime }$	97.5% 93.4%	86.3% 66.1%
3. ${\mu }_a=0.05$, ${\mu }_s^{\prime }=9.0$	${\mu }_a$${\mu }_s^{\prime }$	90.0% 61.3%	77.7% 43.4%

Fig. 3.

Simulation results of the fitted second layer optical properties versus iterations. (a) Fitted second layer absorption coefficient versus iterations and (b) fitted reduced scattering coefficient versus iterations. The dashed lines are the calibrated values. The first layer optical properties of ${\mu }_a=0.02{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=4.0{\mathrm{cm}}^{-1}$ were used as the initial values. The layer thickness was 1.5 cm. The fitted second layer properties were ${\mu }_a=0.12{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=6.7{\mathrm{cm}}^{-1}$ .

Fig. 4.

Simulation results of the estimated second layer properties versus different thickness of the first layer. Data estimated from three sets of first layer properties and the first set of second layer properties (Table 1) were plotted in black and those from the second set of second layer properties were plotted in gray. (a) The fitted second layer absorption coefficients and (b) the fitted second layer reduced scattering coefficients. The dashed lines are the true values.

3.1.2. Phantom experiments

To validate the simulation results, experiments were conducted. Optical properties of the first layer were measured from the smaller probe, and the second layer properties were estimated from the two-parameter fitting approach. The calibrated intralipid solution was used as the first layer and the soft phantom was placed underneath. The thickness of the first layer was defined by the coregistered US image. The first layer had the same calibrated optical properties as the simulation, and the two phantoms used for the second layer had similar values as simulations of ${\mu }_a=0.1{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=9.0{\mathrm{cm}}^{-1}$ and ${\mu }_a=0.2{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=8.0{\mathrm{cm}}^{-1}$, respectively. We varied the first layer depths from 1.0 to 2.5 cm, and the results have shown that the estimation of the first layer was more accurate when the first layer was thicker (Fig. 5). For example, for the same combination of the first layer of ${\mu }_a=0.02{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=4.0{\mathrm{cm}}^{-1}$ and the second layer of ${\mu }_a=0.1{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=9.0{\mathrm{cm}}^{-1}$, the estimated ${\mu }_a$ for the first layer were 0.06, 0.05, 0.03, and $0.023{\mathrm{cm}}^{-1}$ for the layer thicknesses of 1.0, 1.5, 2.0, and 2.5 cm, respectively. After the estimation of the first layer, the large probe with the US transducer located in the central slot was used to collect the data of the homogenous layers. The estimation from the smaller probe was used as the initial values for the first layer, and the properties of the second layer were fitted by the two-parameter fitting method. Figure 6 shows an example of one fitting result of the second layer ${\mu }_a$ and ${\mu }_s\text{'}$ when the first layer of calibrated ${\mu }_a=0.02{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=4.0{\mathrm{cm}}^{-1}$ and the second layer of ${\mu }_a=0.1{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=9.0{\mathrm{cm}}^{-1}$ were used. The thickness of the first layer was 1.5 cm. The initial values of the first layer estimated from the smaller probe were ${\mu }_a=0.025{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=5.0{\mathrm{cm}}^{-1}$, and the fitted results of the second layer were ${\mu }_a=0.103{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=8.9{\mathrm{cm}}^{-1}$. The accuracy of the fitted optical properties of the second layer for each set of the experiments is given in Table 2. For each set of calibrated first layer optical properties, eight experiments of different first layer thickness and second layer properties were conducted, and the ranges of fitted optical properties obtained from the smaller probe are given in the first column. On average, the fitting error of the second layer was $<15.6\%$ for ${\mu }_a$ and 35.3% for ${\mu }_s^{\prime }$ when the first set of the second layer properties was used, and the error was $<18.1\%$ for ${\mu }_a$ and 37.2% for ${\mu }_s^{\prime }$ when the second set of the second layer properties was used (see Fig. 7). The 15.7% fitting error for the first set of lower second layer ${\mu }_a$ compared with 18.1% error of the second set of higher second layer ${\mu }_a$ is in the same trend as that observed in simulations. A much smaller difference was obtained for the fitted second layer ${\mu }_s^{\prime }$ 35.3% compared with 37.2%.

Fig. 5.

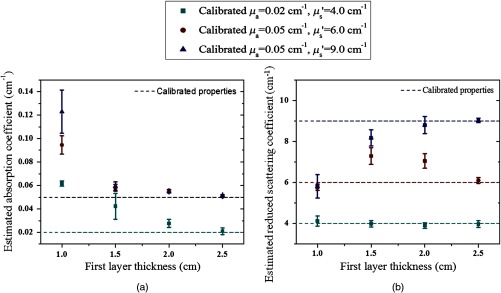
Experimental results of estimated properties of the first layer versus layer thickness. (a) The estimated absorption coefficient and (b) the estimated reduced scattering coefficient versus the layer thickness of 1.0, 1.5, 2.0, and 2.5 cm, respectively. The dashed lines are the calibrated values of the first layer optical properties.

Fig. 6.

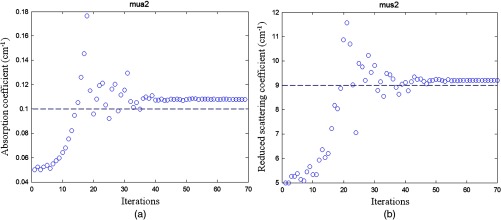
Phantom experiment of fitted second layer properties versus iterations. (a) Fitted absorption coefficient versus iterations and (b) fitted reduced scattering coefficient versus iterations. The dashed lines are the true values. First layer properties estimated from the smaller probe were ${\mu }_a=0.025{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=5.0{\mathrm{cm}}^{-1}$, and the layer thickness is 1.5 cm. The second layer of ${\mu }_a=0.1{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=9.0{\mathrm{cm}}^{-1}$ was used. The fitted results of the second layer were ${\mu }_a=0.103{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=8.9{\mathrm{cm}}^{-1}$ .

Table 2.

Phantom results of accuracy of fitted second layer properties. The first layer properties are calibrated or true values given in the first column. The ranges of fitted properties from the smaller probe were given in the first column as well.

First layer (unit: ${\mathrm{cm}}^{-1}$)	Second layer (unit: ${\mathrm{cm}}^{-1}$)
		1. ${\mu }_a=0.1$, ${\mu }_s^{\prime }=9.0$	2. ${\mu }_a=0.2$, ${\mu }_s^{\prime }=8.0$
1. ${\mu }_a=0.02$, ${\mu }_s^{\prime }=4.0$ Fitted ${\mu }_a$ (range: 0.018 to $0.035{\mathrm{cm}}^{-1}$) Fitted ${\mu }_s^{\prime }$ (range: 3.2 to $5.0{\mathrm{cm}}^{-1}$)	${\mu }_a$${\mu }_s^{\prime }$	88.3% 75.3%	80.0% 70.0%
2. ${\mu }_a=0.05$, ${\mu }_s^{\prime }=6.0$ Fitted ${\mu }_a$ (range: 0.045 to $0.058{\mathrm{cm}}^{-1}$) Fitted ${\mu }_s^{\prime }$ (range: 5.3 to $8.2{\mathrm{cm}}^{-1}$)	${\mu }_a$${\mu }_s\text{'}$	85.0% 56.9%	83.3% 53.8%
3. ${\mu }_a=0.05$, ${\mu }_s^{\prime }=9.0$ Fitted ${\mu }_a$ (range: 0.048 to $0.060{\mathrm{cm}}^{-1}$) Fitted ${\mu }_s^{\prime }$ (range: 7.7 to $11.0{\mathrm{cm}}^{-1}$)	${\mu }_a$${\mu }_s\text{'}$	80.0% 61.9%	82.5% 64.6%

Fig. 7.

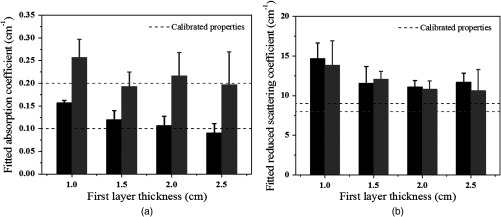
Fitted second layer properties versus different thickness of the first layer obtained from all sets of phantom experiments. (a) Fitted absorption coefficients and (b) fitted reduced scattering coefficients as functions of first layer thickness of 1.0, 1.5, 2.0, and 2.5 cm. Black bars were fitted optical properties corresponding to the first set of second layer properties given in Table 2, and gray bars represent fitted optical properties corresponding to the second set of second layer properties given in the same table. The dashed lines are the calibrated values.

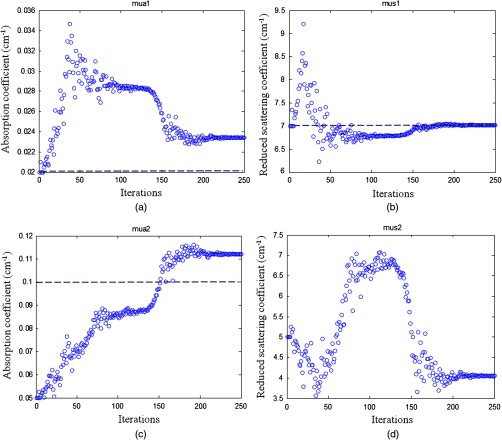
To compare with the previous four-parameter fitting method reported in Ref. 17, four parameters (${\mu }_a$ and ${\mu }_s^{\prime }$ of the two layers) were fitted from the data acquired from the large probe. The calibrated two-layer phantom optical properties were ${\mu }_a=0.02{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=7.0{\mathrm{cm}}^{-1}$ for the first layer and ${\mu }_a=0.1{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=9.0{\mathrm{cm}}^{-1}$ for the second layer. As shown in Fig. 8, the fitted results using the four parameters converge to first layer properties of ${\mu }_a=0.023{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=6.9{\mathrm{cm}}^{-1}$, and second layer properties of ${\mu }_a=0.11{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=4.1{\mathrm{cm}}^{-1}$. The absorption coefficient of the second layer is reasonable, but the scattering coefficient is far lower than the true value. When the new method was used, the first layer properties were first estimated by the smaller probe, which were ${\mu }_a=0.025{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=7.2{\mathrm{cm}}^{-1}$. Using this result as the known parameters, the second layer properties were estimated as ${\mu }_a=0.11{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=9.1{\mathrm{cm}}^{-1}$ (Fig. 9). One can see that the new method can obtain a much higher fitting accuracy for the second layer reduced scattering coefficient than that of the four-parameter fitting. Additionally, the new method converges within 70 iterations, which is $\sim 3.5$ times faster than that of the four-parameter fitting method.

Fig. 8.

Phantom results of fitted properties of both layers versus iterations using the four-parameter fitting. (a) and (c) fitted absorption coefficient versus iterations of the first layer and the second layer, respectively. (b) and (d) fitted reduced scattering coefficient versus iterations of the first layer and the second layer, respectively. The dashed lines are the calibrated values. The first layer thickness is 1.5 cm. The calibrated values for first layer were ${\mu }_a=0.02{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=7{\mathrm{cm}}^{-1}$, and those for the second layer were ${\mu }_a=0.1{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=9{\mathrm{cm}}^{-1}$ .

Fig. 9.

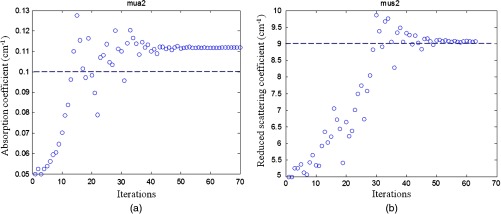
Phantom results of fitted properties of the second layer versus iterations using the calibrated values of the first layer. (a) Fitted absorption coefficient versus iterations and (b) fitted reduced scattering coefficient versus iterations. The dashed lines are the calibrated values. The first layer properties of ${\mu }_a=0.02{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=7.0{\mathrm{cm}}^{-1}$ and layer thickness of 1.5 cm were used. The estimated first layer properties by the smaller probe were ${\mu }_a=0.025{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=7.2{\mathrm{cm}}^{-1}$. The fitted second layer properties were ${\mu }_a=0.11{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=9.1{\mathrm{cm}}^{-1}$.

3.2. Target Imaging Using Two-Step Reconstruction Method

3.2.1. Simulations

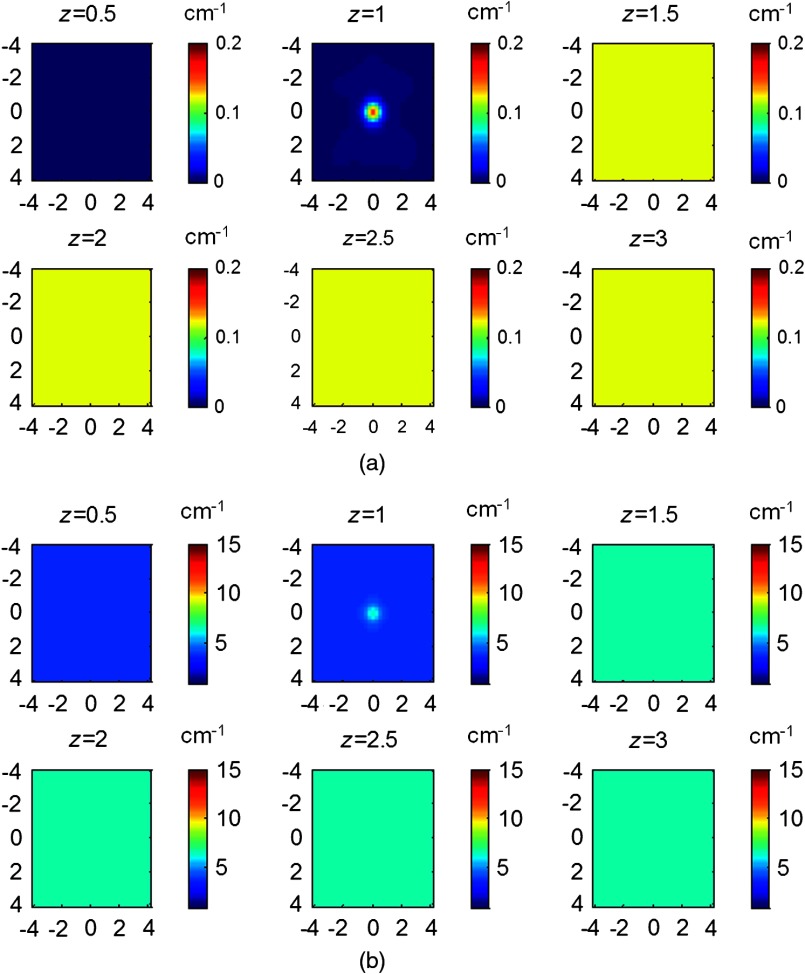
In simulations, targets of 1.0 cm diameter were located at 1.0 cm depth (center location) in the first layer of thicknesses 1.5 and 2.0 cm. Because the 1.0 cm first layer thickness was too shallow to embed the 1 cm target and 2.5 cm thickness was deep enough to neglect the chest wall effect, we did not include them in the simulation and phantom experiments. In this data set, we simulated targets of absorption coefficient ${\mu }_a=0.16{\mathrm{cm}}^{-1}$ and different scattering coefficients of ${\mu }_s^{\prime }=6.0{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=15.0{\mathrm{cm}}^{-1}$. The two-layer structures with optical properties used are given in Table 1. The GA fitted and the GA fitted and CG reconstructed maximum absorption and reduced scattering coefficients of the targets obtained from all sets of simulations were plotted in Fig. 10. The GA fitted parameters were applied as the initial values to the CG-based reconstruction method. The target with ${\mu }_a=0.16{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=6.0{\mathrm{cm}}^{-1}$ embedded in the two-layer structure with the first layer properties of ${\mu }_a=0.02{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=4.0{\mathrm{cm}}^{-1}$ and the second layer properties of ${\mu }_a=0.1{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=6.0{\mathrm{cm}}^{-1}$ was taken as an example. The target center depth was 1.0 cm and the thickness of the first layer was 1.5 cm. The GA fitted initial parameters were ${\mu }_a=0.147{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=4.86{\mathrm{cm}}^{-1}$, and the CG reconstructed values were ${\mu }_a=0.154{\mathrm{cm}}^{-1}$ (96%) and ${\mu }_s^{\prime }=6.5{\mathrm{cm}}^{-1}$ (108.3%). The absorption and scattering distributions are shown in Fig. 11. On average, the accuracy of the reconstructed ${\mu }_a$ for the targets was $>88.3\%$. The accuracy of reconstructed ${\mu }_s^{\prime }$ was 106% using calibrated ${\mu }_s^{\prime }=6.0{\mathrm{cm}}^{-1}$ and 76.7% using calibrated ${\mu }_s^{\prime }=15.0{\mathrm{cm}}^{-1}$, respectively.

Fig. 10.

Genetic algorithm (GA) fitted (black) and GA fitted and conjugate gradient (CG) reconstructed (gray) maximum (a) absorption coefficient and (b) reduced scattering coefficient of the simulated targets located in 1.0 cm center depth obtained from all sets of optical properties of the two-layer structure with 1.5 and 2.0 cm first layer thickness.

Fig. 11.

Simulated (a) absorption and (b) reduced scattering coefficient maps of a target with ${\mu }_a=0.1{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=6.0{\mathrm{cm}}^{-1}$ located in the 1.0 cm center depth of the first layer. The first layer thickness was 1.5 cm and properties were ${\mu }_a=0.02{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=4.0{\mathrm{cm}}^{-1}$. The second layer properties were ${\mu }_a=0.1{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=6.0{\mathrm{cm}}^{-1}$. Tomography images are shown in six slices at different depths from 0.5 to 3 cm with 0.5 cm increment in depth.

3.2.2. Phantom experiments

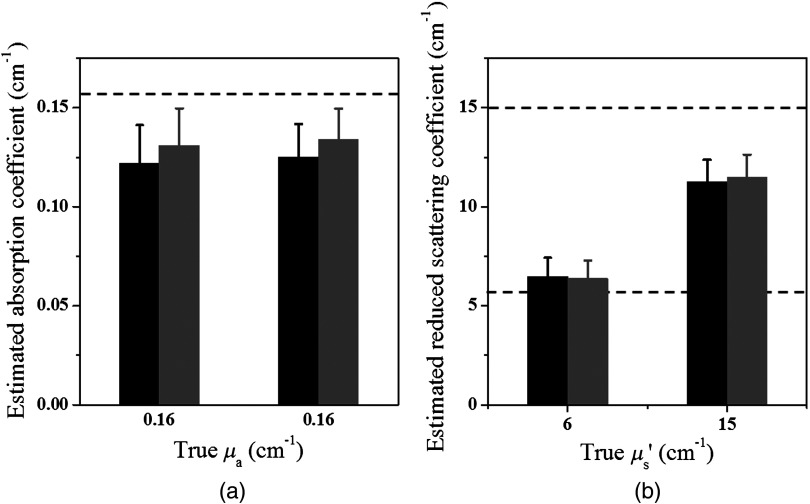
Phantom experiments were performed to validate the simulations. Two targets, one with ${\mu }_a=0.18{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=11{\mathrm{cm}}^{-1}$ and another one with ${\mu }_a=0.14{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=15{\mathrm{cm}}^{-1}$, were tested in the two-layer turbid medium. Just as with the simulations, the initial values of ${\mu }_a$ and ${\mu }_s^{\prime }$ of the targets were fitted by GA algorithm, and these values were applied to the two-layer CG-based reconstruction method. Figure 12 shows the GA fitted initial and GA fitted and CG reconstructed properties. On average, the accuracy of the reconstructed ${\mu }_a$ for the target of ${\mu }_a=0.18{\mathrm{cm}}^{-1}$ was 105.7%, and for ${\mu }_a=0.14{\mathrm{cm}}^{-1}$, it was 95.6%, and that of the reconstructed ${\mu }_s^{\prime }$ was 101.5% using calibrated ${\mu }_s^{\prime }=11{\mathrm{cm}}^{-1}$ and 108.6% using calibrated ${\mu }_s^{\prime }=15{\mathrm{cm}}^{-1}$. Thus, the average error of reconstructed target ${\mu }_a$ is $<6\%$ and ${\mu }_s^{\prime }$ is $<9\%$ under various first layer thicknesses and first layer and second layer properties.

Fig. 12.

GA fitted (black) and GA fitted and CG reconstructed (gray) maximum (a) absorption coefficient and (b) reduced scattering coefficient of the phantom targets located in 1.0 cm depth obtained from all sets of optical properties of the two-layer structure with 1.5 and 2.0 cm first layer thickness.

Figure 13 shows the reconstructed images of an example with the target ${\mu }_a=0.18{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=11{\mathrm{cm}}^{-1}$ embedded in a 1.5-cm-thick intralipid solution of ${\mu }_a=0.02{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=4.0{\mathrm{cm}}^{-1}$ using a phantom of ${\mu }_a=0.2{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=8.0{\mathrm{cm}}^{-1}$ as the second layer underneath. The fitted first layer properties from the smaller probe were ${\mu }_a=0.029{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=3.87{\mathrm{cm}}^{-1}$. The GA fitted initial parameters were ${\mu }_a=0.21{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=10.07{\mathrm{cm}}^{-1}$, and the CG reconstructed values were ${\mu }_a=0.204{\mathrm{cm}}^{-1}$ (113%) and ${\mu }_s^{\prime }=10.38{\mathrm{cm}}^{-1}$ (94.4%). Figure 13(a) is the coregistered US image, Fig. 13(b) is the target absorption map, and Fig. 13(c) is the scattering map.

Fig. 13.

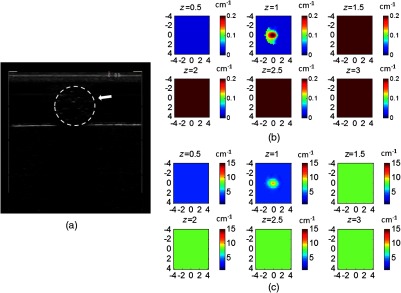
(a) Coregistered US image and CG reconstructed (b) absorption and (c) reduced scattering coefficient maps of a target with ${\mu }_a=0.18{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=11.0{\mathrm{cm}}^{-1}$ located at the 1.0 cm depth of the first layer. The fitted first layer properties estimated from the smaller probe were ${\mu }_a=0.029{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=3.87{\mathrm{cm}}^{-1}$. The first layer thickness was 1.5 cm with optical properties of ${\mu }_a=0.02{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=4.0{\mathrm{cm}}^{-1}$, and the second layer properties were ${\mu }_a=0.2{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=8.0{\mathrm{cm}}^{-1}$.

3.3. Clinical Example

A 37-year-old patient who had an advanced cancer with mixed ductal and lobular features was imaged with an NIR system of 9 sources and 14 detectors.²⁶ A smaller probe was constructed by using a hard sponge with a center source to replace the US transducer slot and four detectors on the imaging probe to estimate the first layer properties on the contralateral normal breast. As shown in Fig. 14(a) US image, the malignant lesion was located on top of the chest wall marked by the white arrows. The center of the lesion is $\sim 1.0\mathrm{cm}$ and the chest wall is $\sim 1.5\mathrm{cm}$ in depth. First, the breast tissue background properties of contralateral side were estimated as ${\mu }_a=0.04{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=4.8{\mathrm{cm}}^{-1}$ using the center source and the four detectors as an equivalent smaller probe. Then the properties of the chest wall (second layer) were fitted as ${\mu }_a=0.15{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=11.0{\mathrm{cm}}^{-1}$ using the data acquired from the entire probe at the contralateral side. After that, using the two-layer structure and the estimated layer properties as the background, the GA fitted initial values of the lesion were ${\mu }_a=0.19{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }=8.6{\mathrm{cm}}^{-1}$ at 780 nm. These initial values were applied to the CG-based reconstruction method to obtain the absorption and scattering maps of the lesion at 780 nm, as shown in Figs. 14(b) and 14(c). The maximum reconstructed ${\mu }_a$ is $0.197{\mathrm{cm}}^{-1}$ and ${\mu }_s^{\prime }$ is $7.9{\mathrm{cm}}^{-1}$. Absorption and scattering maps of the other three wavelengths were similarly reconstructed with maximum ${\mu }_a$ and ${\mu }_s^{\prime }$ of 0.157 and $7.4{\mathrm{cm}}^{-1}$, 0.198 and $9.2{\mathrm{cm}}^{-1}$, and 0.233 and $9.2{\mathrm{cm}}^{-1}$, at 740, 808, and 830 nm, respectively. Figures 14(d)–14(f) show the total hemoglobin, oxyhemoglobin, and deoxyhemoglobin maps calculated from the absorption maps of four wavelengths. The maximum concentrations of total hemoglobin and oxyhemoglobin were 100.3 and $81.0\mu \mathrm{mol}/l$, which were at the level of the malignant category based on the threshold obtained from $>200$ patients.^8,11

Fig. 14.

A clinical example of an advanced carcinoma. (a) Coregistered US image of the cancer located at $\sim 1.0\mathrm{cm}$ depth. The chest wall is marked by the white arrows. CG reconstructed (b) absorption and (c) reduced scattering coefficient maps at 780 nm. (d) Total hemoglobin, (e) oxyhemoglobin, and (f) deoxyhemoglobin maps calculated from the absorption maps of four wavelengths of 740, 780, 808, and 830 nm.

4. Discussion and Summary

In this paper, we have introduced a new estimation and imaging procedure suitable for imaging breast lesions presented inside a two-layer tissue structure. As validated by simulations and phantom experiments, the new procedure is more accurate and robust in recovering lesion optical properties. A clinical example is given to demonstrate the feasibility of this approach. In clinical studies, the chest wall presented in $<2.0$ to 2.5 cm deep, causes a fitted average breast tissue absorption higher than it should be if a semi-infinite tissue structure is used. As a result, the weight matrix computed from the estimated background properties is smaller, and the reconstructed lesion absorption is higher as compared with using accurate background properties. This could lead to false positives for cancer diagnosis if the chest wall is not accounted for.

Our new estimation and imaging procedure does not account for the errors introduced by chest-wall depth and position mismatch between lesion and reference sites. In practice, we have used real-time coregistered US to guide the probe position by matching the chest-wall depths at both lesion and reference sites. This effort minimizes the difference in chest-wall positions at both sites and produces the best imaging results.²¹ Therefore, the operators’ knowledge and skills are important. For the reported in vivo experiment using the new procedure, an extra step was needed to unplug the US probe and place its replacement probe with one central source when imaging normal contralateral side of the breast. This procedure adds complexity and time to the overall imaging protocol. In future clinical studies, a dual probe system is ideal for clinical operation and will be investigated in the near future.

A two-layer tissue structure is a simple approximation to model and estimate the influence of the chest wall upon the measured photon-density waves when patients are studied in reflection geometry. The interface between the breast tissue and the chest wall is not always flat and can be more complex, which may need additional effort on modeling. In Ref. 27, the possible distortion and mismatch were discussed extensively. Here, we have focused on the new estimation and imaging method for the two-layer tissue structure. However, our method can be extended to two-layer models with complex boundaries.

In summary, a new estimation and imaging procedure is investigated and it provides more accurate estimation and reconstruction of lesions presented in the layered structure. Simulations and phantom experiments have been performed to validate the new reconstruction method, and a clinical example is given to demonstrate the feasibility of this approach. A dual probe system will be investigated for easy and robust clinical operation in the near future.

Biographies

Yan Xu obtained her PhD from the Electrical Engineering Department of the University of Connecticut. She has been working on ultrasound-guided diffuse wave optical tomography for breast cancer detection and diagnosis during her PhD study at UConn. Currently, she is working as a development engineer at IBM.

Quing Zhu obtained her PhD from the University of Pennsylvania and is currently a professor in the Departments of Electrical and Biomedical Engineering at the University of Connecticut. She is a leading researcher in combining ultrasound and NIR diffuse light tomography for breast cancer diagnosis. She has also extended the technology to predict and monitor patients’ neoadjuvant chemotherapy response. In addition, she and her team have developed several multimodality techniques for ovarian cancer detection and diagnosis. She is a fellow of SPIE.