Distinct Functional Roles of Cardiac Mitochondrial Subpopulations Revealed by a 3D Simulation Model

Abstract

Experimental characterization of two cardiac mitochondrial subpopulations, namely, subsarcolemmal mitochondria (SSM) and interfibrillar mitochondria (IFM), has been hampered by technical difficulties, and an alternative approach is eagerly awaited. We previously developed a three-dimensional computational cardiomyocyte model that integrates electrophysiology, metabolism, and mechanics with subcellular structure. In this study, we further developed our model to include intracellular oxygen diffusion, and determined whether mitochondrial localization or intrinsic properties cause functional variations. For this purpose, we created two models: one with equal SSM and IFM properties and one with IFM having higher activity levels. Using these two models to compare the SSM and IFM responses of [Ca²⁺], tricarboxylic acid cycle activity, [NADH], and mitochondrial inner membrane potential to abrupt changes in pacing frequency (0.25–2 Hz), we found that the reported functional differences between these subpopulations appear to be mostly related to local [Ca²⁺] heterogeneity, and variations in intrinsic properties only serve to augment these differences. We also examined the effect of hypoxia on mitochondrial function. Under normoxic conditions, intracellular oxygen is much higher throughout the cell than the half-saturation concentration for oxidative phosphorylation. However, under limited oxygen supply, oxygen is mostly exhausted in SSM, leaving the core region in an anoxic condition. Reflecting this heterogeneous oxygen environment, the inner membrane potential continues to decrease in IFM, whereas it is maintained to nearly normal levels in SSM, thereby ensuring ATP supply to this region. Our simulation results provide clues to understanding the origin of functional variations in two cardiac mitochondrial subpopulations and their differential roles in maintaining cardiomyocyte function as a whole.

Introduction

Mitochondria located in specific cell regions are reported to have different morphological and biochemical properties (1). In cardiomyocytes, Palmer et al. (2) first demonstrated the presence of two mitochondrial subpopulations, specifically, subsarcolemmal mitochondria (SSM) and interfibrillar mitochondria (IFM). Subsequent studies revealed that IFM located in the core region have higher oxidative phosphorylation and tricarboxylic acid (TCA) cycle enzymatic activities, and higher Ca²⁺ accumulation (2–5). It has also been shown that IFM and SSM are differentially affected under pathological conditions such as diabetes mellitus (6,7), cardiac volume (8) and pressure (9) overload, and cardiomyopathy (10). However, it remains to be determined whether these mitochondrial subpopulations are functionally different, as the differences can be explained by variations in the isolation procedures or assessment techniques used (11).

We hypothesize that numerical simulations can help resolve this issue by enabling in silico experiments to be performed under controlled conditions. In particular, detailed three-dimensional (3D) cell models of subcellular organelles and functional molecules are a powerful tool. Using the finite-element method (FEM), we previously developed a 3D model of cardiomyocytes (12–14). In that model, detailed cardiac electrophysiology, Ca²⁺ dynamics, ATP metabolism localized to specific loci, Ca²⁺ and energy metabolite diffusion, and deformation by sarcomere force generation were simulated along with subcellular structures. Here, we extended that model to assess local environmental influences surrounding SSM and IFM, including oxygen diffusion, myoglobin buffering, and oxidative phosphorylation dependent on local oxygen concentration.

First, we validated these modifications by comparing the calculated subcellular distributions of oxygen and NADH with experimental observations (15,16). Next, to determine whether differences in subcellular location or intrinsic properties are responsible for the observed variations in the functional properties of these two mitochondrial subpopulations, we compared two models: 1) equal membrane permeability and enzymatic activity in SSM and IFM, and 2) IFM augmented. Finally, we examined the functional implications of SSM and IFM by simulating cellular responses under hypoxic conditions.

Materials and Methods

3D cardiomyocyte model

The 3D cardiomyocyte model has been previously reported and validated (12,13). Briefly, a segment containing three myofibrils of one sarcomere length, together with the adjacent cell membrane and organelles, was modeled using the FEM (Fig. 1 A). To validate newly introduced functions (oxygen diffusion, myoglobin buffering, and oxidative phosphorylation dependence on local oxygen concentration), we compared simulated oxygen and NADH distributions with the experimental results of Takahashi et al. (15,16), but using a larger model, as Takahashi et al. selected relatively large myocytes to obtain clear visualization. Therefore, our model has six myofibrils arranged from the cell surface to the core (double the number of myofibrils in the normal model), resulting in a larger diameter (18 μm) but without changing the size, relative position, or volume ratio of subcellular structures (Fig. 1 B). To reproduce anatomical structure, subcellular components, including mitochondria, myofibrils, junctional sarcoplasmic reticulum (SR), network SR, and surface and transverse (t)-tubular sarcolemma, are located at the appropriate FEM nodes. Each subcellular component exchanges ions and/or metabolites according to mathematical formulations expressed as functions of the molecular concentrations in the surrounding cytosol (17,18). These molecules diffuse freely through the cytosolic space, and processes are calculated by solving reaction-diffusion equations. Further details of the model are given in the Supporting Material of the previously published article (12).

Figure 1.

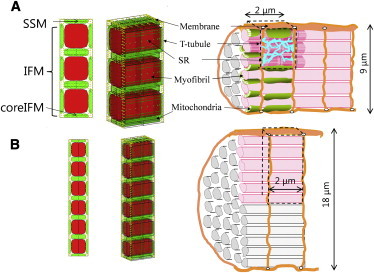
Three-dimensional (3D) cardiomyocyte model. (A and B) Transverse views (left), 3D presentations (middle), and schematics (right) of a cardiomyocyte are shown for the regular (A) and larger (B) models. In both models, mitochondria are colored green and myofibrils are red. Other subcellular components (channels and pumps) were assigned to nodes representing sarcolemma (yellow) or SR (blue). To see this figure in color, go online.

Modeling SSM and IFM

Mitochondria facing the surface sarcolemma were taken to be SSM and others were taken to be IFM (Fig. 1). For analysis, SSM and IFM located in the cell core region (core IFM) were compared. Because most molecules included in the model can freely enter the space between the outer and inner membranes (intermembrane space), 10% of the mitochondrial node volume was treated as cytosolic space (corresponding to intermembrane space), but with a diffusion coefficient 1/100th that of cytosolic space. The remaining 90% corresponds to the mitochondrial matrix, wherein Ca²⁺ diffusivity is limited by buffers and dense structures. Details on the mitochondrial model can also be found in the Supporting Material of our previously published article (12). According to Palmer et al. (2,3) and Schwarzer et al. (9), IFM have ∼50% higher oxidative capacity and TCA activity than SSM. To examine the effect of these differences on activity, we prepared two models: one with equal enzymatic activities in SSM and IFM (equal model) and one with 50% higher enzymatic activity in IFM (hetero model). In our model, the volume of SSM accounts for 14% of the total; therefore, to maintain the total activity of each model as a whole, we modulated the oxidative capacity and TCA cycle activity by reducing the rate constants (ρ_res, k^CS_cat, k^ACO_f, k^IDH_cat, k^KGDH_cat, k^SL_f, k^SDH_cat, k^FH_f, and k^MDH_cat) by 30% in SSM and increasing them by 5% in IFM (0.14 × 70% + 0.86 × 105% ≈ 100%). Table 1 summarizes the parameter values for SSM and IFM in the equal and hetero models.

Table 1.

Modified parameter values for SSM and IFM in the hetero model

Parameter (unit)	Equal Model	Hetero SSM	Hetero IFM	Description
(%)	100	14	86	relative volume
ρres (mM)	0.1	0.07	0.105	concentration of electric carriers of respiratory complexes
kCScat (ms−1)	0.1	0.07	0.105	catalytic constant of citrate synthase
kACOf (ms−1)	2.22	1.55	2.33	catalytic constant of aconitase
kIDHcat (ms−1)	0.05	0.035	0.0525	catalytic constant of isocitrate dehydrogenase
kKGDHcat (ms−1)	0.1	0.07	0.105	catalytic constant of α-ketoglutarate dehydrogenase
kSLf (M−1 ms−1)	7.5	5.25	7.875	forward rate constant of succinate lyase
kSDHcat (s−1)	7.5	5.25	7.875	catalytic constant of succinate dehydrogenase
kFHf (s−1)	5.0	3.5	5.25	forward rate constant for fumarate hydratase
kMDHcat (ms−1)	0.1665	0.1166	0.1748	catalytic constant of malate dehydrogenase

Oxygen diffusion and oxidative phosphorylation

To examine the influence of oxygen diffusion on oxidative phosphorylation, we introduced the effects of oxygen diffusion, subsequent myoglobin buffering, and oxidative phosphorylation dependence on local oxygen concentration. Because the myoglobin diffusion coefficient is ∼70 times smaller than that of oxygen, we treated myoglobin as an immobile oxygen buffer and adopted a fast equilibrium assumption; thus, the myoglobin diffusion effect is small enough to be ignored. Accordingly, myoglobin saturation (S_Mb) was calculated as S_Mb = $\left[{\text{O}}_2\right]/\left(\frac{k^{-}}{k^{+}}+\left[{\text{O}}_2\right]\right)$, and partial oxygen pressure (PO₂) was calculated as PO₂ = $\left[{\text{O}}_2\right]/\alpha$, with α = 1.5 μM/mmHg (19).

Rates of oxygen consumption and proton pumping (complex IV activity) were multiplied by the factor $1/\left(1+k_{\text{O}2}/\left[{\text{O}}_2\right]\right)$ to account for the observed dependence on oxygen concentration (20–22). In simulating isolated myocytes, we set the oxygen membrane permeability (λ_O2) at 0.14 m/s, based on the oxygen diffusion coefficient and membrane thickness, whereas in the simulated in situ ischemic protocol, we decreased it to 3 × 10⁻⁵ m/s according to Dash and Bassingthwaighte (23) to include the diffusion resistance of capillaries and interstitial fluid. The governing equations are shown in the Appendix with rate constants obtained from the literature.

Simulation protocols

To validate the oxygen diffusion and mitochondrial response to oxygen concentration, we compared our simulation with the published experiment by Takahashi et al. (15,16), which measured intracellular oxygen and intramitochondrial NADH gradients. In that experiment, they measured isolated, relatively large rat cardiomyocytes in a 15.2–22.8 mmHg oxygen suspension with 1 μM carbonyl cyanide m-chlorophenylhydrazone (an oxidative phosphorylation uncoupler). For comparison, they performed a simulation using the large model under 20 mmHg oxygen (λ_O2 = 0.14 m/s) with a 15-fold increase in V_Hu (the proton gradient consumption rate of the mitochondrial inner membrane) to raise the oxygen consumption to the level observed experimentally (15,16).

To simulate electrical pacing, we applied a current pulse (100 μA/cm², duration 0.5 ms) to sarcolemma. We examined the responses in the equal and hetero models while switching the contraction frequency between 0.25 Hz (low frequency) and 2 Hz (high frequency). Simulations were performed under normoxic in situ conditions (40 mmHg oxygen, λ_O2 = 3 × 10⁻⁵ m/s). We also examined the response to acute and moderate ischemia by decreasing PO₂ in the extracellular space from 40 to 1 mmHg or 10 mmHg, respectively.

Calculations

All program codes were written in house using the Fortran programming language. Computation was performed using an Intel (Santa Clara, CA) Xeon CPU (3.2 GHz).

Results

Validation of the oxygen diffusion model

Fig. 2 shows the simulated distributions of myoglobin oxygen saturation (S_Mb; Fig. 2 A, solid line), intracellular PO₂ (Fig. 2 A, dotted line), and intramitochondrial NADH (Fig. 2 B) in a radial direction, together with experimental results (Fig. 2, C (15) and D (16)). Since we set a symmetry boundary condition at the center of the cell, the simulated results (Fig. 2, A and B) were obtained by mirroring. For comparison, the proton gradient consumption rate was increased to simulate the effect of the uncoupler in the published experiments (15,16). We found that the simulated rate of oxygen consumption was 0.23 μM/ms, which is comparable to the rates observed experimentally (0.15 μM/ms in Fig. 2 C and 0.24 μM/ms in Fig. 2 D; units were converted using a cell volume of 25 pl (24)).

Figure 2.

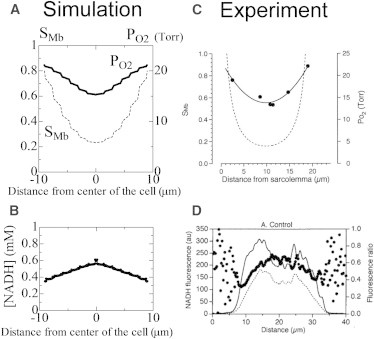
(C and D) Comparison of simulated (C (15)) and experimental (D (16)) results. (A–D) Radial distribution of myoglobin oxygen saturation (S_Mb) (solid line) and intracellular PO₂ (broken line) (A versus C), and intramitochondrial NADH concentration (B versus D) using the large model under uncoupled conditions. Experimental result C from Takahashi et al. (15) is provided with permission from the American Physiological Society, and result D from Takahashi et al. (16) is provided with permission from Elsevier.

The simulated submembrane PO₂ was just below the extracellular PO₂ (20 mmHg), reaching ∼15 mmHg in the core region, and thus was similar to experimental results. We observed significant S_Mb gradients from the membrane toward the cell center (0.8–0.2), which again were similar to experimental results (15). Zigzag patterns observed in the PO₂ and S_Mb profiles reflect changes in local mitochondrial density. The NADH concentration was slightly higher in the cell center, as shown experimentally, but upon a detailed examination of the profile, we noted minute fluctuations superimposed on the smooth profile. These fluctuations were due to intramitochondrial variations in TCA activity, which was upregulated near the boundary owing to the high Ca²⁺ concentration in this region.

SSM and IFM responses to changes in contraction frequency

We compared the responses to stepwise frequency changes between SSM and IFM under normoxic (PO₂ = 40 mmHg) conditions. First, we examined changes in mitochondrial [Ca²⁺], [NADH], [ADP], and inner membrane potential (ΔΨ_m) of core IFM (black) and SSM (red) using the equal model (Fig. 3, A–D). Under steady-state conditions with low-frequency stimulation, SSM and IFM behaved similarly, but functional differences became apparent when the frequency was changed. With an increase in pacing frequency, [Ca²⁺] increased in both types of mitochondria, albeit to much lower levels in SSM (Fig. 3 A). In contrast, in IFM, [NADH] reductions were smaller, followed by a strong recovery toward initial levels (Fig. 3 B). This strong recovery is consistent with the fluorescence measurements of Brandes and Bers (25). Although NADH decreased in both IFM and SSM, [ADP] increased only in SSM during high-frequency stimulation (Fig. 3 C). This phenomenon may indicate that the TCA cycle activity in SSM cannot match the higher energy demands during rapid pacing.

Figure 3.

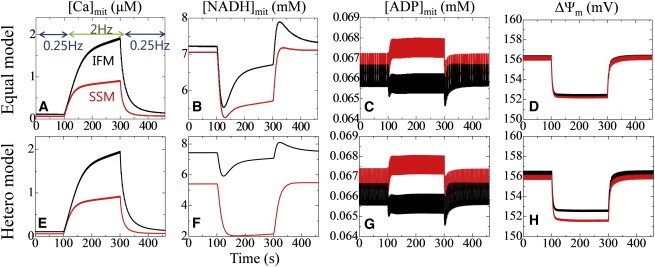
Transient response to abrupt changes in the pacing rate between 0.25 and 2 Hz. (A–H) Core IFM (black) and SSM (red) responses are compared using the same (equal model; A–D, upper panels) and different (hetero model; E–H, lower panels) enzymatic activities. From left to right: mitochondrial Ca²⁺, NADH, ADP, and inner membrane potential. In each panel, data averaged over the mitochondrion are shown. To see this figure in color, go online.

Despite the higher NADH and inner membrane potential levels, IFM synthesized ATP at nearly the same rate as SSM (0.25 Hz: IFM, 7.55 μM/s; SSM, 7.89 μM/s; 2 Hz: IFM, 33.6 μM/s; SSM, 34.7 μM/s). This apparent discrepancy is likely due to membrane potential exhaustion because of Ca²⁺ uptake by mitochondrial Ca²⁺ uniporters. These results strongly indicate a dominant effect of the local environment on the apparent functional differences between IFM and SSM.

We repeated the protocol using the hetero model (Fig. 3, E–H). Compared with the equal model simulation, there were greater differences in [NADH] levels between SSM and IFM during low-frequency pacing at 0.25 Hz, and increasing frequency further accentuated these differences by reducing the NADH levels in SSM. Differences in the mitochondrial inner membrane potential also became apparent during rapid pacing (Fig. 3 H), probably reflecting low NADH levels. Conversely, [Ca²⁺] and [ADP] were less sensitive to changes in rate constants introduced in the hetero model.

Response to hypoxia

Fig. 4 summarizes the responses to abrupt change in extracellular PO₂ from 40 to 1 mmHg. Intracellular oxygen levels initially dropped from steady-state values, reaching varied levels depending on the location. Immediately below the sarcolemma, PO₂ decreased to 0.042 mmHg because of the transportation barrier created by the sarcolemma, whereas in the core region, PO₂ dropped to <10⁻⁵ mmHg (Figs. 4 A and 5 A). Reflecting this PO₂ environment, proton pump activity in core IFM dropped to nearly zero, resulting in mitochondrial membrane potential deprivation, whereas SSM continued to function (Fig. 4, B and C). ATPase activity dropped to minus values in core IFM, indicating consumption of ATP reserves rather than production (Fig. 4 D). When averaged over the entire cell, creatine phosphate (CrP) decreased fairly rapidly, and after depletion ATP started to drop (Fig. 4 E). Following the course of ATP levels, peak Ca²⁺ transient levels decreased after a latent period, and after 120 s, Ca²⁺ transients with small peaks and slow decay were observed (Fig. 4 F and inset). Such changes in Ca²⁺ transients result from depletion of SR Ca²⁺ content caused by depressed SR Ca²⁺-ATPase (SERCA) activity (Fig. 4 G, red). Force development started to decline from ischemia onset (Fig. 4 H), caused mainly by increased [Pi] coinciding with decreased [CrP] and [ATP]. These changes are shown in Movie S1 in the Supporting Material. In comparison with SERCA activity, sarcolemmal ATPase activity was maintained for a longer period (Fig. 4 G, black).

Figure 4.

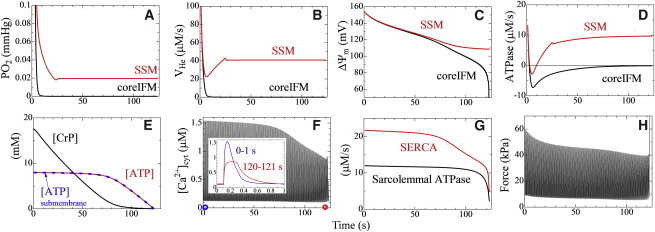
Response to step decreases in extracellular PO₂ from 40 to 1 mmHg. (A–D) In the upper panels, core IFM and SSM responses are shown in black and red, respectively: (A) local PO₂, (B) proton pump activity, (C) mitochondrial inner membrane potential, and (D) mitochondrial ATPase activity. (E–H) Lower panels show the response averaged over the entire cell: (E) CrP concentration (black), ATP concentration (red), and ATP concentration in submembrane space (blue); (F) Ca²⁺ transient (inset, single transient at 0 (blue) and 120 s (red) after ischemia onset); (G) activity of sarcolemmal ATPase (black) and SERCA (red); and (H) developed force. To see this figure in color, go online.

Figure 5.

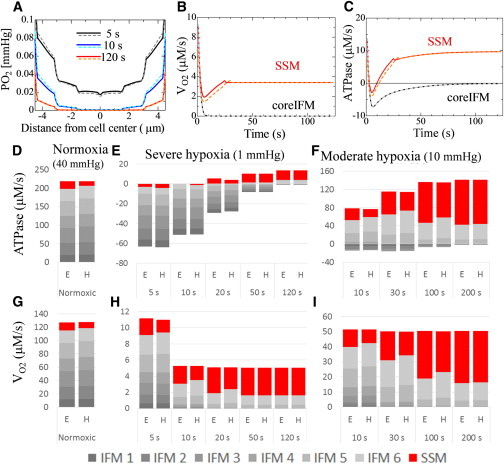
Response to step decreases in extracellular PO₂ from 40 to 1 mmHg (severe hypoxia) or 10 mmHg (moderate hypoxia). (A–C) Upper panels compare responses to severe hypoxia between the equal (solid line) and hetero (dotted line) models: (A) radial distribution of oxygen at 5, 10, and 120 s after onset; (B) oxygen consumption; and (C) mitochondrial ATPase activity. (D–I) Lower panels show the contributions of IFM and SSM to ATP production (D–F) and oxygen consumption (G–I) under normoxic (D and G), severely hypoxic (E and H), and moderately hypoxic (F and I) conditions. In graphs D–I, cumulative bar charts are used to show changes in the total amount and contribution of each subpopulation. E, equal model; H, hetero model. IFMs are numbered by their locations from the core to the cell surface. To see this figure in color, go online.

Comparing the hypoxic response of the hetero and equal models

We repeated the hypoxia protocol using the hetero model. Fig. 5 A compares the radial distribution of oxygen tension between the hetero (dotted line) and equal (solid line) models. In the early phase of hypoxia (5–10 s), oxygen tension in the outer region of the hetero model was higher than the equal model (reflecting reduced oxygen consumption of SSM), but lower in the core region (due to increased oxygen consumption of IFM). These differences disappeared in the later phase of hypoxia (120 s) because the severely limited oxygen supply overwhelmed this small difference in oxygen consumption and became the dominant factor.

Oxygen consumption changes in SSM and core IFM (Fig. 5 B) are consistent with the above reasoning, yet the difference between the equal and hetero models is minimal in core IFM. Conversely, changes in ATPase activity are of interest because they dropped to negative values, suggesting consumption rather than synthesis of ATP (Fig. 5 C). Accordingly, we examined the relative contributions of SSM and IFM at six locations (numbered from the core to the cell surface) to oxygen consumption and ATP synthesis under normoxic and hypoxic conditions (Fig. 5, D–I). Under normoxic conditions, the contribution of SSM to ATP production was relatively small, only ∼9.5% in the equal model and 5.8% in the hetero model (Fig. 5 D). However, under hypoxic conditions, the role of SSM dramatically increased in both models, with >70% of ATP being produced in SSM in the later stage of hypoxia (Fig. 5, E and F). Major differences between the models were observed during the early phase of hypoxia, during which oxygen consumption by IFM was greater in the hetero model, despite the smaller amount of total oxygen consumption (Fig. 5 H, 5–20 s). Regarding ATPase activity, IFM (especially outer IFM) showed less negative activity in the hetero model. We also examined the relative contributions of IFM and SSM under moderate (10 mmHg) hypoxia and identified distinct differences between the equal and hetero models during the early phase (Fig. 5, F and I). Downregulation of SSM in the hetero model may serve to maintain IFM activities by balancing oxygen consumption.

Discussion

In this study, we have extended our guinea-pig cardiomyocyte model by incorporating oxygen diffusion, myoglobin buffering, and oxidative phosphorylation to examine functional cross talk between mitochondrial location, heterogeneity in enzyme activity, and the surrounding environment, including oxygen, Ca²⁺, and metabolite concentrations.

Validation of the model

The validity of our previous model has already been determined with regard to a number of phenomena, i.e., an averaged and local [Ca²⁺] time course consistent with experimental observations (12), the mitochondrial response to changing contraction frequency (14), and Ca²⁺ propagation with deletion of t-tubules (13). Accordingly, here we examined newly added functional components, specifically, oxygen diffusion, myoglobin buffering, and oxidative phosphorylation dependence on local oxygen concentration. We compared our simulated results with those obtained experimentally and obtained good agreement with reports by Takahashi et al. (15,16).

Effect of subcellular location on mitochondrial Ca²⁺ handling

Even when tested using the equal model, SSM showed lower Ca²⁺ levels, weaker NADH recovery, and higher ADP levels, indicating a dominant effect of the local environment (Fig. 3). We propose that these functional variations are primarily caused by differences in local cytosolic Ca²⁺ concentrations, introduced by Ca²⁺ extrusion owing to sarcolemmal Na⁺-Ca²⁺ exchangers. Based on the findings of Pásek et al. (26), L-type Ca²⁺ channels are mostly located in t-tubules in our model, whereas Na⁺-Ca²⁺ exchangers are distributed evenly between t-tubules and sarcolemma. As a consequence, net Ca²⁺ flux entering the cell tends to be small in subsarcolemmal regions and thus the SSM have a relatively low-Ca²⁺ environment. In support of this, Palmer et al. (3) reported that IFM show higher Ca²⁺ accumulation. There is also corroboratory evidence from several experiments showing higher Ca²⁺ accumulation activity (27) and greater V_max of Na⁺-Ca²⁺ exchangers (28) in IFM. However, in contrast, Kuznetsov et al. (29) reported that SSM have higher Ca²⁺. There are several possible explanations for this discrepancy. For example, we distributed Na⁺-Ca²⁺ exchangers evenly throughout guinea pig myocytes, yet a higher density in t-tubules has been reported for other animals (30). Similarly, sarcolemmal Na⁺-Ca²⁺ exchanger distribution between the surface and t-tubules would change the mitochondrial Ca²⁺ environment. Although further experimental evidence should be considered, our results show that the local Ca²⁺ environment plays a significant role in causing differences in the mitochondrial response to changing contraction frequency.

Response to hypoxia

The results obtained under hypoxic conditions clearly demonstrate the heterogeneous impact of this pathological insult. Because of induced steep oxygen gradients, core IFM stopped functioning and even started to consume ATP reserves, whereas in SSM function was upregulated. Thus, IFM are particularly vulnerable to ischemic insult, which would explain differences in ischemic damage between IFM and SSM reported under pathological conditions. It was recently shown in pressure-overload-induced heart failure that IFM show a greater degree of depression in respiratory capacity than SSM (9). Cardiac pressure overload requires increased ATP consumption to meet demand, but in myocardium, insufficient capillary growth increases the distance for oxygen diffusion, thereby rendering it susceptible to hypoxia (31). Our finding is also pertinent to the selective oxidative defect induced in IFM by cardiomyopathy (10). However, there is also the contradictory experimental finding that ischemia in rabbit heart selectively depletes cardiolipin in SSM and decreases oxidative phosphorylation (32). Further studies are needed before a comprehensive view of the mitochondrial response in various pathological conditions can be obtained (6–8).

According to our previous studies, ATP and CrP diffusion is fast enough to keep [ATP] constant throughout the cell under normoxic conditions (12). Under extremely low [ATP] conditions, ATP is consumed locally before it diffuses to remote sites; therefore, ATP produced in SSM may preferentially serve to maintain the reactions of neighboring organelles and molecules, and sustain them for longer periods of time. Such a mechanism may account for a phenomenon known as the ischemic cascade (33), in which, after an acute ischemic insult, contractile activity supported by IFM deteriorates quickly, but electrical activity in sarcolemmal ion channels and pumps supported by SSM can maintain integrity for longer durations.

Possible differences in intrinsic properties between IFM and SSM

IFM have been reported to have higher levels of enzymatic activity in cardiomyocytes (2,3,6,9). We incorporated this difference by upregulating the TCA cycle and oxidative phosphorylation enzymatic activities in IFM compared with SSM. Regarding pacing frequency, IFM showed a higher NADH, inner membrane potential, and faster recovery after a change in the pacing frequency in the hetero model compared with the equal model. This is reflected in the larger IFM ratio of ATP production: 90% in the equal model compared with 94% in the hetero model. We speculate that if such differences in activity were present, they would be adaptive and lead to improvements in total capacity, efficiency, and cell responsiveness as a whole regarding the [CrP], [NADH], and ATP synthase/oxygen consumption ratio, as well as faster upregulation of ATP synthase with a change in the pacing frequencies. However, we did not find notable improvements in these functional parameters: at 0.25 Hz, cytosolic ADP and Pi were observed at similar levels, whereas at 2Hz, Pi was lower by only 0.3%. Moreover, differences in the response rate were not appreciable. Conversely, with hypoxia simulation, the hetero model showed slightly reduced oxygen consumption and ATP production in the early stage. However, a close examination of the relative contribution of each mitochondrion revealed that IFM consumed more oxygen and produced more ATP in the hetero model than in the equal model. These results indicate that under hypoxic conditions, SSM (with a relatively conserved oxygen supply) suppress consumption to compensate for the loss of oxygen supply to IFM, although the amount is small. We also observed that the role of SSM in ATP production increased significantly under hypoxic conditions. ATP production in SSM was upregulated by >5-fold with moderate hypoxia, whereas approximately half of the IFM showed negative ATPase activity, indicating that ATP consumption rather than production had increased in this mitochondrial population. Thus, during hypoxia, SSM exert a dampening effect by acting as an energy source for IFM behaving as an energy sink.

Our in silico study provides insight into the controversy of whether two mitochondrial populations differ in terms of their physiological makeup or location. Simulations using the equal model revealed that two aspects of a location effect are apparent. Well-developed t-tubule structures with abundant L-type Ca²⁺ channels supply a high Ca²⁺ environment to IFM, leading to clearly distinct behaviors by the IFM and SSM (see also the Supporting Material for the response of each IFM). Under hypoxic conditions, the oxygen supply determined by the distance from the cell surface contributes to functional differences among IFM (Fig. 5, E and F). Conversely, a comparison of the equal and hetero models under hypoxic conditions revealed an important role for the intrinsic differences between IFM and SSM in balancing oxygen consumption. Altogether, the results of our in silico experiments suggest that both location and intrinsic properties play significant roles in fine-tuning mitochondrial function to various conditions.

Study limitations

To further examine the hypoxic condition, one must include functional components while working under low-[ATP] conditions, i.e., glycolysis, adenylate kinase, acidosis, and ADP- and AMP-dependent reactions, including KATP channels and myosin ATPase. However, implementation of these factors requires additional tuning and validation of complex chemical systems, even though comprehensive knowledge about the control mechanisms may be lacking. Therefore, we left incorporation of these factors for future studies, and in this work focused on the impact of the mitochondrial local environment and heterogeneity.

In summary, our simulation results show that differences in the local environment can have a significant influence on apparent functional variations between SSM and IFM. Differences in intrinsic properties between these two mitochondrial subpopulations, if present, would accentuate such functional variations, but would not contribute significantly to functional adaptation of the myocyte as a whole. Although we need to further validate and improve the model by integrating advanced knowledge in this field, current computer simulations of subcellular events within a detailed 3D structure can enhance our understanding of complex physiological systems.

Author Contributions

A.H. performed the simulations, analyzed data, and wrote the article. J.O., T.W., and T.H. contributed to the development of analytic tools and discussion. S.S. analyzed data and wrote the article.

Appendix

The reaction-diffusion equation for oxygen is

$$\frac{\partial \left[{\text{O}}_2\right]}{\partial t}={\text{D}}_{\text{app}}^{{\text{O}}_2}\nabla \cdot \left(\nabla \left[{\text{O}}_2\right]\right)+f^{{\text{O}}_2}$$

$${\text{D}}_{\text{app}}^{{\text{O}}_2}={\left(1+\frac{{\text{K}}_{{\text{O}}_2}{\left[\text{Mb}\right]}_{\text{tot}}}{{\left({\text{K}}_{{\text{O}}_2}+\left[{\text{O}}_2\right]\right)}^2}\right)}^{-1}{\text{D}}^{{\text{O}}_2},$$

where ${\text{D}}_{\text{app}}^{{\text{O}}_2}$ is the apparent oxygen diffusion coefficient, assuming that myoglobin is a stationary buffer (34); ${\text{D}}^{{\text{O}}_2}$ is the cytosolic oxygen diffusion coefficient; ${\text{K}}_{{\text{O}}_2}$ is the half-saturation constant of myoglobin; ${\left[\text{Mb}\right]}_{\text{tot}}$ is the total myoglobin concentration; and $f^{{\text{O}}_2}$ is the functional myoglobin form representing oxygen reactions. The oxygen consumption rate, V_O2 (12), multiplied by the oxygen dependence factor, $\left[{\text{O}}_2\right]/\left(\frac{k^{-}}{k^{+}}+\left[{\text{O}}_2\right]\right)$, corresponds to $f^{{\text{O}}_2}$ in mitochondria, and the permeation flux of oxygen, λ_O2 ([O₂]_{extracellular −} [O₂]_cyt), corresponds to $f^{{\text{O}}_2}$ at membrane nodes and to $f^{{\text{O}}_2}$ = 0 in other areas. Parameter values are shown in Table A1

Table A1.

Myoglobin oxygen buffering and mitochondrial reaction constants

Parameter	Value	Unit	Description	Refs.
${\text{K}}_{{\text{O}}_2}$	3.9	μM	half-saturation constant of myoglobin	(19)
${\left[\text{Mb}\right]}_{\text{tot}}$	0.2	mM	total concentration of myoglobin	(19)
${\text{D}}^{{\text{O}}_2}$	1.4 × 10−9	m2/s	oxygen diffusion coefficient	(19)

.

Supporting Material

Movie S1. Ca²⁺ changes under normoxic and hypoxic conditions

Comparison of Ca²⁺ dynamics and contraction under normoxic (left) and hypoxic (right) conditions, 120 s after decreasing the extracellular oxygen concentration to 122 mmHg.