Retrograde NGF Axonal Transport—Motor Coordination in the Unidirectional Motility Regime

Abstract

We present a detailed motion analysis of retrograde nerve growth factor (NGF) endosomes in axons to show that mechanical tugs-of-war and intracellular motor regulation are complimentary features of the near-unidirectional endosome directionality. We used quantum dots to fluorescently label NGF and acquired trajectories of retrograde quantum-dot-NGF-endosomes with <20-nm accuracy at 32 Hz in microfluidic neuron cultures. Using a combination of transient motion analysis and Bayesian parsing, we partitioned the trajectories into sustained periods of retrograde (dynein-driven) motion, constrained pauses, and brief anterograde (kinesin-driven) reversals. The data shows many aspects of mechanical tugs-of-war and multiple-motor mechanics in NGF-endosome transport. However, we found that stochastic mechanical models based on in vitro parameters cannot simulate the experimental data, unless the microtubule-binding affinity of kinesins on the endosome is tuned down by 10 times. Specifically, the simulations suggest that the NGF-endosomes are driven on average by 5–6 active dyneins and 1–2 downregulated kinesins. This is also supported by the dynamics of endosomes detaching under load in axons, showcasing the cooperativity of multiple dyneins and the subdued activity of kinesins. We discuss the possible motor coordination mechanism consistent with motor regulation and tugs-of-war for future investigations.

Introduction

The long-distance retrograde axonal transport of neurotrophins (nerve growth factor (NGF), brain-derived neurotrophic factor (BDNF), etc.), from the axon terminals to cell bodies, is fundamental for the structure, function, and survival of neurons (1,2). Briefly, the binding of NGF to its membrane TrkA receptor at the axon terminals triggers the internalization of NGF-TrkA into early endosomes of 50–150 nm in diameter (3). These NGF-endosomes are retrogradely transported by dyneins all the way to the cell body for initiating prosurvival gene expression (2). However, the retrograde motion of NGF-endosomes (∼90% of the motion) is interspersed by frequent pauses and sporadic transient direction reversals indicating the activity of kinesins (3,4). Further, biochemical studies have confirmed the simultaneous presence of kinesins and dyneins on many retrograde cargoes: e.g., purified neuronal vesicles (5), retrograde autophagosomes (6,7), and retrograde prion protein vesicles (8) in axons. The functional relevance of kinesins and their coordination with dyneins in the long-distance retrograde transport are yet to be understood.

Specifically, what determines the directionality of NGF-endosome transport in axons? How do retrograde moving dyneins and anterograde moving kinesins work cooperatively on the NGF-endosomes? Two mechanisms that feature prominently in this context are the tug-of-war and the coordinated-motor-switching models. The tug-of-war model posits that the cargo directionality results from stochastic tugs-of-war between dyneins and kinesins. Tuning the composition of opposite polarity motors and their mechanochemical properties is shown to result in a wide range of unidirectional to bidirectional cargo motility states (9–12). On the other hand, the motor-switching model suggests that some regulator proteins enforce the exclusive activity of either kinesins or dyneins, thereby avoiding tugs-of-war between motors in coordinating the cargo direction (8,12,13). Recent studies reveal potential regulators like Huntingtin and JIP1 that switch between kinesins and dyneins on unidirectional autophagosomes (14) and APP vesicles (15) in neurons. For instance, the phosphorylation state of JIP1 in a kinesin-JIP1-dynein complex determines the exclusive activity of either kinesin or dynein, thereby avoiding tugs-of-war within the complex. However, it is still not clear how (and if) the collective activity of multiple such dual-motor complexes on a cargo can be coordinated with no instances of tug-of-war at all.

In this article, we undertook a detailed motion analysis of the retrograde NGF-endosomes in the axons of dorsal root ganglion (DRG) neurons, to dissect the mechanical and regulatory aspects of this near-unidirectional transport. The main objectives of this study are 1) to quantify the relative activity of opposing motors on NGF-endosomes and analyze the data for potential tugs-of-war, and 2) to analyze whether stochastic tug-of-war models, based on parameters reported in Kunwar et al. (13), can explain the biased-directionality and dynamics of NGF-endosome transport. To this end, we developed processing methods to accurately quantify the forward (retrograde) and highly subdued reverse (anterograde) motion characteristics of retrograde NGF-endosomes. Our results reveal several aspects of tug-of-war and multiple-motor mechanics in axonal NGF-endosome transport. However, mechanical model simulations show that the motion statistics can only be simulated reasonably by assuming that the microtubule-binding affinity of kinesins on the endosomes is 10 times lower than seen in vitro. Cellular regulation of kinesin motors on NGF-endosomes therefore seems vital to limit the tug-of-war frequency and establish the retrograde directionality.

Materials and Methods

In this section, we present 1) an experimental method that allowed us to image the cargo position with sufficient spatiotemporal resolution to capture the transient direction reversals, and 2) data analysis methods that accurately extract the subdued reversal statistics of NGF-endosome transport for quantitative modeling.

Oblique illumination imaging of axonal transport in microfluidic DRG neuron cultures

The use of microfluidic devices for primary neuron culture and imaging axonal transport had been documented by us elsewhere (2,4). In this article, we used mature DRG neuron cultures (7–9 days old) for the NGF transport studies. NGF was purified from mouse submaxillary glands, biotinylated and coupled to quantum-dot (QD) QD605 via biotin-streptavidin linkage (3).

An inverted microscope (Eclipse Ti-U; Nikon, Melville, NY), customized with 561-nm laser excitation, was set for oblique illumination (Fig. S1 in the Supporting Material). Briefly, the laser beam was expanded to 3-cm diameter and focused at the back-focal plane of the microscope objective (CFI Plan Apo TIRF, 100×/1.49 NA; Nikon). Starting from total internal reflection geometry, the incident angle was gradually lowered below the critical angle until the QD-endosomes within the axons are made visible by the oblique angle illumination. Because the microfluidic channels in our device are 3-μm high, a penetration depth of 1–3 μm is sufficient to illuminate the axonal fluorophores in multiple focal planes. The fluorescence collected by the objective was relayed and focused onto an electron-multiplying charge-coupled device sensor (Ixon DU-897; Andor Technology, South Windsor, CT).

The axon terminals in the microfluidic culture are incubated with 1 nM QD-NGF for 45 min, which was then washed off by the culture medium. Shortly before imaging, the culture medium was replaced by CO₂-independent medium and the culture was imaged on a water-heated custom microscope stage set to maintain the culture at 24°C or 37°C. Imaging was started typically 2 h after the incubation start and restricted to a <45-min session. Time-lapse movies of QD-NGF transport were acquired at 32 frames/s.

Single-particle tracking

Semiautomated custom MATLAB software (The MathWorks, Natick, MA) is used to extract QD-NGF endosome trajectories. Briefly, we used two-dimensional Gaussian fitting adapted to detect the locations of QD-NGF in each movie frame. Intensity and signal/noise cutoffs were adjusted to achieve localization accuracy <20 nm. We then used a particle-tracking algorithm, adapted from Jaqaman et al. (16), to link these detected locations into QD-NGF trajectories. The flux of QD-NGF transport, kept sparse by controlled incubation conditions, lead to minimal tracking errors. Occasional errors associated with crossing trajectories are corrected by manual inspection in the final step of processing.

Bayesian parsing of endosome trajectories—transient and point noise analysis

Petrov et al. (17) have validated an excellent approach, based on experimental noise, for parsing cargo trajectories into linear constant velocity segments. However, accurate description of the noise for general intracellular cargo trajectories is complicated by 1) noise variation from trajectory to trajectory due to heterogeneity of the cargo size and local environment, 2) Brownian noise variation within a trajectory from different transient behaviors and the dynamics of cargo-motor-microtubule connectivity, and 3) noise variation from fluorescence imaging accuracy. We developed a parsing algorithm based on Petrov et al. (17) to account for such noise variations and make it generally applicable to heterogeneous cargo transport in cells (Fig. S3). Briefly, the optimal segmentation of an N_T point trajectory with M_L segments is obtained by maximizing the likelihood function modified to include local thermal and position uncertainties. Starting with an over-fit number of segments we gradually reduced the segments, with intermediate optimization, until the error statistic matched the calibrated error from stationary endosome trajectories (Fig. S3).

Transient motion analysis

Cellular cargos often exhibit different transient behaviors like linear motion interspersed by constrained or diffusive pauses ranging from milliseconds to seconds. Huet et al. (18) had outlined a versatile approach to classify such transient behaviors based on local analysis of mean-square displacement and asymmetry in motion. Recently, Zajac et al. (19) presented a complimentary method for analyzing endosome trafficking and diffusion in cells. We combined these approaches with the parsed segmental properties (from above), to accurately classify the endosome trajectories into linear motion and pauses. Briefly, we use a sliding window (fixed 1-s window moved along the trajectory with one frame displacement) analysis to compute the local diffusion constant, mean-square displacement scaling, and asymmetry of trajectories. Based on these parameters, we segregated the trajectories into periods of linear motion and periods of pauses (Fig. S4).

Computer simulations using stochastic one-dimensional models for multimotor cargo transport

We adapted the stochastic one-dimensional mechanical model, elaborated by Kunwar et al. (13), to simulate the motility of NGF-endosomes in axons. The stochastic models and Monte Carlo simulation of cargo trajectories have been discussed in various references earlier (20–23). Briefly, our model comprises endosomes, with a stable number of kinesins and dyneins, moving on a one-dimensional microtubule. Dynamics of the individual motors, which determine the course of endosome trajectory, are governed by their microtubule-binding, unbinding, forward, and backward-stepping rates that include the load dependence of velocities and detachment kinetics. We used specific parameter sets reported in literature from in vitro measurements as well as in vivo data fitting (13). These parameters are summarized in Table S1 in the Supporting Material. Simulated trajectories are parsed to extract statistical distributions of various dynamic variables in forward and reverse directions, and are compared to experimental statistics. A complete description of the model and Monte Carlo simulation is given in the Supporting Material.

Results

Experimental measurement of QD-NGF transport in DRG neurons

Axonal transport of QD-labeled NGF-endosomes was tracked in real-time using oblique illumination imaging in microfluidic DRG neuron cultures (Fig. S1) (2–4). The imaging was carried out in axonal segments far from (hundreds of microns) the terminals and cell bodies, after distal incubation of QD-NGF. The endosome motion is almost unidirectional (retrograde direction) and highly processive at both 24°C and 37°C (Fig. S1 and Movie S1 in the Supporting Material). Most endosomes traverse the imaging field of view (∼90 μm) with no indication of detachment from the microtubules and diffusion within axons. Notably, the retrograde endosome motion is interrupted by frequent pauses and transient direction reversals. We imaged the NGF-endosome motility at both 24°C and 37°C for two reasons. First, the endosome motility at 24°C is more amenable for quantitative modeling because the in vitro characterization of motors under load and their detachment kinetics is mostly done at 24°C. Second, in order to establish that the transient reversals of NGF-endosomes are motor-driven (and not just Brownian movements) we needed to analyze the temperature dependence of reversals (discussed in a later section).

From the time-lapse movies, we extracted the NGF-endosome trajectories (x(t),y(t)) with ∼20-nm accuracy using single-particle tracking (16). In order to convert the endosome trajectories from the (x,y) camera coordinates to (Q^||,Q^⊥) microtubule coordinates (parallel and perpendicular to microtubules), we first obtained the underlying microtubular track (Q^x,Q^y) for each (x,y) trajectory using an edge-tracing based algorithm (Fig. S2 B). Then we decomposed the endosome trajectories from (x,y) units to (Q^||,Q^⊥) based on the microtubular track (Fig. S2 C). While Q^⊥ (mean = 0, σ ∼ 20 nm) is dominated by the thermal fluctuation of endosomes and instrument noise, Q^|| represented the forward/reverse motor-driven endosome motion along the microtubule. Fig. 1 shows a few retrograde trajectories Q^||(t) acquired at 24°C. The endosomes exhibit sustained periods of dynein-driven retrograde motion interspersed with pauses and direction reversals. The reversals, which can run up to 4 μm (Fig. S1), highlight the sporadic activity of kinesins on the endosomes. The nature of coordination between kinesins and dyneins can be gleaned from the functional forms of dynamic features like endosome pauses, velocities, and run lengths.

Figure 1.

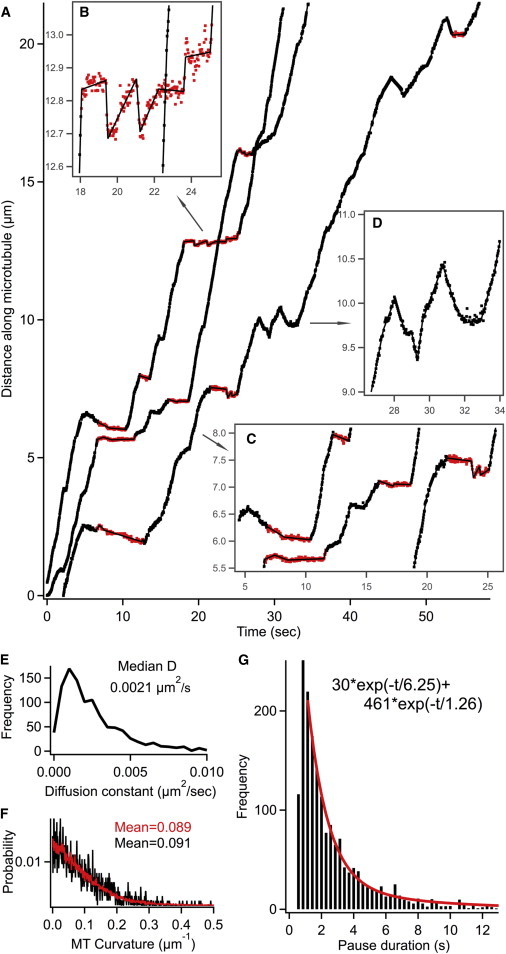
(A) Retrograde QD-NGF endosome trajectories at 24°C, shown as the motion along microtubules, Q^||(t). (Black) Parsed constant velocity segments are also shown superimposed. (Red/gray) The periods (B and C, insets) are pauses identified by transient motion analysis with a 1-s sliding window. (D, inset) Anterograde direction reversals. (E) Distribution of diffusion constant for endosome pauses >1.5 s. (F) Distributions of microtubule curvature obtained from endosome tracks using sliding window quadratic fitting (red/gray, N = 22,399) and the curvature at pause locations (black, N = 1566). See Fig. S2. (G) Distribution of pause duration at 24°C fits to a double-exponential (χ² = 1.01). We fit the bins with pause duration >1.1 s and counts >5. To see this figure in color, go online.

Pause analysis indicates two different mechanistic origins

We analyzed pause properties to distinguish pauses caused by tugs-of-war between opposing molecular motors from those caused by other cellular mechanisms such as endosome interactions with local cellular structural features. Most of the NGF-endosome pauses are essentially motionless periods with velocities <0.1 μm/s. However, there are quite a few long pauses with small to-and-fro displacements resulting in net zero linear motion (Fig. 1 B). To capture both types of pauses, we used transient motion analysis (see Materials and Methods) with a 1-s sliding window and found that NGF-endosomes paused ∼35% of the time at 24°C. These pauses are highly constrained in nature. The effective diffusion constant obtained by transient motion analysis (0.0021 μm²/s, for pauses >1.5 s) is 30 times lower than that of diffusing endosomes (0.069 μm²/s) in axons (Figs. 1 E and S5). Comparing this with the effective diffusion constant of surface-immobilized quantum dots (∼0.0002 μm²/s from localization errors) highlights the constrained nature of endosome pauses. Further, Fig. 1 F shows that the local microtubule curvature at pause locations is comparable to the overall distribution, and shows no increased curvature expected of microtubule switching (24). The constrained mobility during pauses and linearity of microtubular tracks at pause locations suggest that 1) the endosomes are anchored within axons during pauses and 2) the primary cause of pauses is not due to switching between microtubules.

The distribution of pause duration at 24°C is a monotonically decaying function, which could not be fit to a single-exponential (reduced χ² = 2.3 with probability, P < 0.01%). We found a good fit with a double-exponential (reduced χ² = 1.01 with P = 45%) shown in Fig. 1 G. The fits are weighted with variances obtained by bootstrapping the endosome trajectories, which are close to Poisson statistics. The long time component (24%, 6.3 ± 2.6 s) is comparable to the pause duration caused by steric interactions and collisions between endosomes and other organelles/cytoskeletal structures (19,25). The short time component (76%, 1.26 ± 0.16 s) is higher than the pause timescale expected from tugs-of-war between opposing motors (0.3–0.8 s) (13). However, the width (1 s) of sliding window limits the detection of very short pauses, thus overestimating the timescale of short pause duration in a fit. A more accurate analysis of the short pauses using a parsing approach is presented in the next section. At 37°C, the pause duration decreased significantly but still fits reasonably to a double-exponential (reduced χ² = 1.22 with P = 24%). Both the long-pause component (19%, 2.5 ± 1.1s) and the short-pause component (81%, 0.71 ± 0.15 s) are shortened significantly at 37°C, indicating that the paused states are connected to temperature-dependent mechanisms.

The distinction of short and long pauses suggests that the NGF-endosome pauses in axons have multiple mechanistic origins. The short pause component is consistent with tugs-of-war and is comparable to the pause timescales reported for other cellular cargo (26). The long pauses on the other hand are consistent with local structural interactions, as mentioned above (19,25). It is also plausible that the long pauses could result from specific dynein-regulators on endosomes and/or microtubules (27–29). Regardless of the actual mechanism, the long pauses cannot be explained by tugs-of-war between opposite polarity motors on NGF-endosomes. So we asked if stochastic tug-of-war models could accurately describe the endosome motion devoid of the long pauses, which are presumably from structural or regulatory interactions. To this end, we classified each NGF-endosome trajectory into periods of directed motion (including short pauses) and long pauses (pauses with time duration >2 times the short-pause component). We then analyzed the relative activity of opposite polarity motors during the directed motion, as elaborated in the next section.

Directed motion analysis by Bayesian parsing

We used a Bayesian parsing approach to quantify the forward (retrograde) and reverse (anterograde) motion statistics within the directed motion of NGF-endosomes. First, we parsed each endosome trajectory into a series of constant velocity segments (Figs. 1 A and S3). We then clubbed consecutive segments in the same direction to obtain retrograde and anterograde runs. A run is a sustained period of motion in the same direction that ends with a pause or a direction reversal. A pause is defined as a motionless segment >0.15 s (i.e., five frames) with <0.1 μm/s velocity. A direction reversal is counted when the reversed motion lasts >0.13 s (i.e., four frames). The definitions and thresholds used in characterizing segments and runs are given in the Supporting Material and are consistent with those generally adopted in literature.

Temperature dependence of endosome velocities

Fig. 2 shows the distributions of NGF-endosome transport in axons at 24°C and 37°C. The average velocity of directed motion (i.e., excluding long pauses) increases from 0.64 μm/s at 24°C to 1.49 μm/s at 37°C (Fig. 2 A). We also note a pronounced increase in the width of the speed distribution with temperature, consistent with earlier measurements (4). The forward (retrograde) and reverse (anterograde) run velocities are shown in Fig. 2 B. Going from 24°C to 37°C, the mean retrograde run velocity increases from 0.74 to 1.5 μm/s, and the mean anterograde velocity increases from 0.61 to 1.13 μm/s. This further confirms that the short anterograde reversals correspond to motor-driven motion as opposed to diffusion, which can only have a weak (∼5%) temperature dependence. The mean retrograde run velocity is comparable to the unloaded dynein velocity (∼0.6–1 μm/s) at 24°C and saturating ATP (30,31). The mean anterograde run velocity (0.61 μm/s) is within the range of unloaded velocities (0.4–1.5 μm/s) reported for different kinesins (32–35). Interestingly, we observe a clear distinction between the retrograde (peaked) and anterograde (decaying) run velocity distributions. Further, anterograde runs are rather short-lived, with average duration of 0.3 s compared to 1.1 s average duration of retrograde runs.

Figure 2.

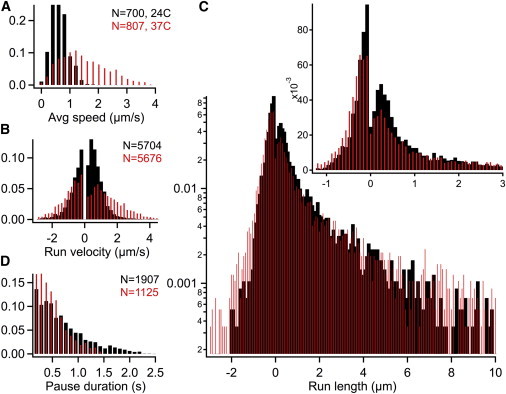
Probability distributions of transport metrics for retrograde NGF-endosomes at 24°C (black) and 37°C (red/gray). (A) Average speed of directed motion. (B) Retrograde (+) and anterograde (−) run velocities. (C) Retrograde (+) and anterograde (−) run lengths shown on a log-linear scale. (Inset) Same figure on linear scale. (D) Duration of parsed pauses. To see this figure in color, go online.

Retrograde and anterograde run lengths

The disparity between retrograde and anterograde run velocities/durations is reflected in the run lengths shown in Fig. 2 C. The retrograde run lengths exhibit a peak at ∼240 nm and a long plateau that extends beyond 10 μm. The peak arises from thresholding the run duration (>0.13 s) and run velocity (> 0.1 μm/s). The decay from the peak fit well to a double-exponential (reduced χ² = 0.99, P = 50%) with a short component (59%, 0.44 ± 0.03 μm) and a long component (41%, 3.1 ± 0.35 μm) that exceeds the processivity of a single dynein at 24°C. At 37°C, the retrograde run lengths still fit to a double-exponential (reduced χ² = 1.08, P = 29%) with a similar pattern of short (49%, 0.51 ± 0.04 μm) and long (51%, 4.44 ± 0.45 μm) components. Indeed, these are generic features of bidirectional transport reported for other cellular cargos like lipid droplets (26) and pigment granules (36).

The anterograde run lengths could not be fit satisfactorily either with a single- or a double-exponential (reduced χ² ∼ 1.7, P < 2%). For the purpose of analysis, we fit the distribution with a single-exponential, which gave a mean anterograde run length of 0.24 ± 0.01 μm at 24°C and 0.34 ± 0.01 μm at 37°C. The 7:1 ratio of retrograde (mean = 1.55 μm) to anterograde run lengths (mean = 0.24 μm) determines the dominant (90%) retrograde directionality of NGF-endosome transport. The processivity of retrograde runs can be attributed to the cooperativity of multiple dyneins, which decreases the rate of endosome detachment from microtubules (37,38). The run lengths are very likely limited by opposite motor interactions (pauses and reversals) as opposed to endosome detachments. Inferring the number of motors from run lengths is therefore complicated, and entails a multimotor modeling approach.

Analysis of short pauses and their correlation with direction reversals

Fig. 2 D shows the duration of parsed pauses within the directed motion of NGF-endosomes (not including long-pauses that are identified during the initial pausing analysis). The average duration of 0.69 s at 24°C is much lower than the short time component (1.26 s) identified by transient motion analysis with a 1-s window. Because our parsing analysis ignores pauses <0.15 s, this represents an upper limit for the timescale of parsed pauses. Nearly 84% of the parsed pauses resume motion in the retrograde direction. This suggests that most pauses are terminated by the detachment of kinesins if the pauses are indeed the result of tugs-of-war. The parsed pause duration (<0.69 s) is comparable to the pause timescales expected from the detachment rate of kinesins at stall force (0.3–0.8 s). We also see a 28% decrease in the average pause duration from 24°C to 37°C (0.5 s).

Within the assumption that the short-pauses and directional reversals result from tugs-of-war between dyneins and kinesins, we expect a variation of these motility features among different endosomes because the relative number of motors can vary from one endosome to another. To this end, we defined several dynamic variables like pause propensity (number of pauses per s) and reversal propensity (number of reversals per s) for each trajectory based on its run/pause properties. Indeed, the endosomes exhibited a varying degree of pauses and reversals and a smooth dispersion in net directionality ranging from 60 to 100% of retrograde motion (mean = 90%, Fig. 3). The data indicates that some endosomes inherently tended to pause and/or reverse more than the others. Further, we found that endosomes that paused more also tended to reverse more and moved at a slower speed on average. The pause and reversal propensities showed a positive correlation with Pearson’s r = 0.31 and p-value < 0.01% (Fig. 3 D).

Figure 3.

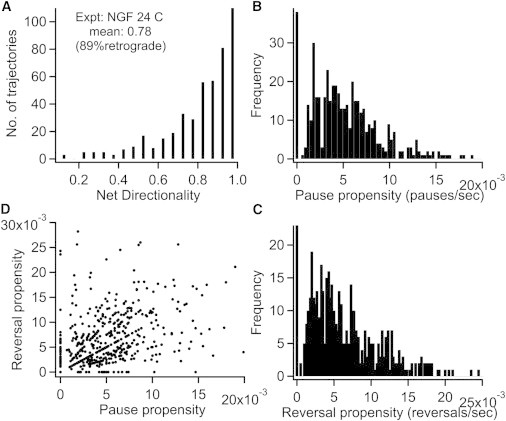
Distributions of net-directionality (A), pause propensity (B), and reversal propensity (C) from the experimental trajectories at 24°C. (D) Scatter plot demonstrating the correlation between reversal and pause propensities.

Simulation of NGF-endosome transport by stochastic mechanical models

We then asked if mechanical tug-of-war models could rationalize the experimental statistics of NGF-endosome transport that were detailed above. To address this question, we simulated the endosome motility in axons using stochastic one-dimensional models for multimotor transport (13). The key model parameters are the number/type of motors on endosomes, their unitary stall forces, microtubule-binding rates, unbinding rates, forward and backward stepping rates, and the load dependence of these rates (Table S1). Simulated trajectories were parsed and compared with experimental distributions of NGF-transport at 24°C. The number of dyneins and kinesins on endosomes, and their mechanochemical properties, directly impact the distributions of forward and reverse run length, average velocity, and pause distributions, which are compared with the experimental distributions to evaluate the model performance (Table 1).

Table 1.

In vitro model simulation of the average speed, pause duration, and run lengths of NGF-endosomes

	Model Parameters	Average Speed μm/s (±SD)	Pause Duration (s)	Retrograde Run Length μm (±SE)	Anterograde Run Length μm (±SE)
	NGF 24°C EXPT	0.64 (0.30)	0.69	0.44 (0.03) 59%	0.24 (0.01)
				3.10 (0.35) 41%
A	1 kinesin, 8 dyneins, πk = 5	0.30 (0.10)	0.58	0.36 (.004)	0.107 (.001)
B	1 kinesin, 12 dyneins, πk = 5	0.40 (0.03)	0.68	0.58 (.007)	0.057 (.001)
C	2 kinesins, 5 dyneins, πk = 0.5	0.53 (0.12)	0.34	1.15 (.02)	0.187 (.002)
D	2 kinesins, 6 dyneins, πk = 0.5	0.55 (0.12)	0.44	1.26 (0.02)	0.180 (.003)
E	2 kinesins, 7 dyneins, πk = 0.5	0.58 (0.09)	0.48	1.32 (0.02)	0.148 (.003)
F	Poisson distribution, 〈D〉 = 5, 〈K〉 = 2, πk = 0.5	0.57 (0.22)	0.42	0.54 (0.03) 42%	0.201 (0.002)
				1.62 (0.06) 58%
G	Poisson distribution, 〈D〉 = 5, 〈K〉 = 1.5, πk = 0.5	0.63 (0.20)	0.43	0.49 (0.05) 34%	0.196 (0.002)
				1.69 (0.06) 66%
	NGF 37°C EXPT	1.49 (0.8)	0.50	0.49 (0.04) 49%	0.34 (0.01)
				4.41 (0.30) 51%
I	Poisson distribution, 37°C 〈D〉 = 5, 〈K〉 = 1.5, πk = 0.5, 2 velocity, 2ε	1.56 (0.33)	0.34	0.94 (0.15) 20%	0.193 (0.002)
				3.61 (0.13) 80%

Anterograde run lengths are fit to a single-exponential. Retrograde run lengths are fit to a single-or a double-exponential (% of two components given). The SD and SE in fit parameters are given in parentheses. The value π_k is the microtubule binding rate of kinesin, and ε is the unbinding rate of motors in the model. The rest of the model parameters are listed in Table S1. (Rows A and B) Full kinesin activity at π_k = 5. (Rows C–E) Reduced kinesin activity at π_k = 0.5 for fixed motor numbers. (Rows F–G) Poisson-distributed motors and reduced kinesin activity. (Row I) In vitro model at 37°C, with velocities and ε increased by two times from 24°C.

Fast retrograde transport cannot be simulated using in vitro properties of dyneins and kinesins

We tried to simulate the average properties of NGF-transport by constraining the model parameters to the experimental values measured in vitro. The unitary stall forces of motors in this model are 1.25 pN for dynein and 5 pN for kinesin (13,39,40). The motor velocity and detachment rates depend on the load as reported in vitro (13). The only parameters we varied were the number of dyneins and kinesins on endosomes. Earlier studies on isolated neuronal vesicles (5) as well as immunostaining of prion protein vesicles in axons (8) revealed 1–4 kinesins and 1–5 dyneins stably associated with the vesicles.

We could not simulate the experimental metrics for any ratio of dynein/kinesin by varying the number of motors alone (Table 1, A and B). We note that the number of dyneins on the endosome should at least be five times the number of kinesins in order to achieve the retrograde directionality, considering the 1:5 disparity in their stall forces. In the case of dynein/kinesin of 8:1, the simulated trajectories show frequent tugs-of-war and pauses that result in the average velocity ∼60% lower than experiment (Fig. S6). The simulated retrograde run lengths are also an order-of-magnitude shorter than the experiment values. On the other hand, the simulated average anterograde run velocity (0.2 μm/s) is less than half the experimental value, suggesting that the load on kinesin is too high. When we increase the dynein/kinesin ratio to 12:1, the average velocity and the retrograde run length are closer to the experimental values. However, the anterograde run velocity and run lengths are much worse, at <20% of the experimental values. An endosome with two kinesins would necessitate an unrealistic number of 12 dyneins just to attain net retrograde motion, and the overall fitting is even worse than a single kinesin. From these results, we conclude that it is not possible to simulate fast retrograde transport using a tug-of-war model with unmodulated kinesin activity.

Downregulation of kinesin activity results in qualitative agreement with experiment

We then asked if turning-down the kinesin activity in our model, and thereby limiting the frequency of tugs-of-war, could simulate the experimental statistics. To this end, we tested the microtubule-binding rate of kinesins within the range 0.2–5/s in our model. With a binding rate of 0.5/s (10 times lower than in vitro activity of kinesins at 5/s), we see qualitative agreement with experiments over a range of 1–2 kinesins and 4–7 dyneins (Table 1, C–E). In this range of motors, the simulated parameters are consistent with experiment (Fig. S6). The ratio of retrograde/anterograde run lengths is smoothly varying based on the relative number of dyneins and kinesins (6.15:1 for 2 kinesins and 5 dyneins, 7:1 for 2 kinesins and 6 dyneins, and 8.9:1 for 2 kinesins and 7 dyneins) and agrees with the experimental value of 7:1. The simulated average velocity (0.53–0.58 μm/s) is also very close to the experimental measurement of 0.64 μm/s. More importantly, the simulated distribution of the anterograde run velocity is a decaying functional form, while the simulated distribution of the retrograde run velocity is a peaked functional form, which agrees with the experimental data. The low binding rate of kinesins limits the tugs-of-war in our model and results in retrograde run velocities (and run lengths) comparable to unloaded estimates. On the other hand, because the effective binding rate of dyneins is much higher than that of kinesins, more often the kinesins have to work against the dyneins in tugs-of-war. The load exerted by dyneins results in smaller anterograde velocities (causing a decaying distribution) and short-lived anterograde runs (20,37), both of which lead to shorter anterograde run lengths.

There are a few discrepancies between the simulations and experiment. First, the spread in average velocity of endosomes is significantly underestimated by simulation (Fig. S6). Second, a single-exponential can reasonably fit the simulated retrograde run length while the experiment is a double-exponential. Third, the values of both anterograde and retrograde run lengths are shorter in simulation than in experiments (Table 1, C–E). We note that experiments are composed of trajectories of ∼700 endosomes, each of which could be associated with different numbers of dyneins and kinesins. As seen above, the variation in the relative number of dyneins and kinesins can lead to dispersion in the endosome directionality as well as average velocity (Table 1, C–E). The distribution of motor numbers could therefore stretch the experimental run-length distribution both in retrograde and anterograde directions.

Simulations with Poisson-distributed motor numbers and down-tuned kinesin activity

We then simulated the endosome transport with Poisson-distributed dyneins and kinesins over the range of [3,8] for dynein and [0,4] for kinesin, respectively. Indeed, these simulations are in better agreement with experiment (Table 1, F and G, and Fig. 4). The spread in the average velocity of endosomes is well accounted for by the distribution of motors. We fit the retrograde run-length distribution with a double-exponential and the anterograde run lengths to single-exponentials for comparison with experiment. The mean anterograde run length is within 20% and the mean retrograde run length (from both short and long components) is within 24% of the experimental run lengths.

Figure 4.

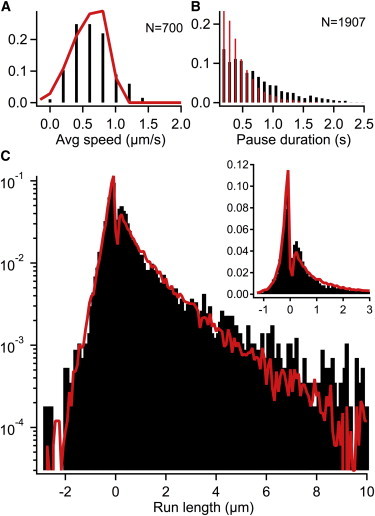
(A–C) In vitro model simulation (red/gray) with Poisson-distributed dyneins (mean = 5) and kinesins (mean = 1.5) on endosomes. The kinesin binding rate is reduced by 10 times to 0.5/s. Experiments (black) at 24°C. The parameter set is summarized in Table S1 and the model performance is quantified in Table 1G. To see this figure in color, go online.

The net directionality of endosomes simulated with Poisson-distributed motors (Table 1 G) varies from 60 to 100% retrograde motion that is comparable with experiment (Fig. S7). The downregulated kinesin activity is vital for the retrograde directionality seen in simulations over this range of dynein/kinesin ratios. Further, the simulations (Table 1 G) reveal many correlations borne out by experiment. The pause and reversal propensities (simulated) show a positive correlation (r = 0.42, p < 0.01%) and exhibit right-skewed multimodal distributions as seen in the experiments (Fig. S7). The multimodal pattern, obvious in simulated distributions, is due to the variation in the relative number of dyneins and kinesins on endosomes.

We emphasize that the only model parameters varied here are the number of motors and the microtubule-binding rate of kinesin. Despite the simplicity of the one-dimensional model and constrained parameters, the model provides reasonable accuracy (60–95%) in fitting our data, assuming that NGF-endosomes are driven by Poisson-distributed dyneins (mean = 5–6) and kinesins (mean = 1–2). While the presence of kinesins on the retrograde endosomes is imperative to explain the reversed runs seen in experiments, our model does not require all retrograde endosomes to have kinesins. The simulation in Fig. 4 is based on a Poisson distribution with 22% of endosomes having no kinesins (Fig. S7). Earlier cytofluorimetric studies suggest that only a little amount (<12%) of kinesin is recycled by retrograde transport (41). The exact stoichiometry of kinesins on NGF-endosomes therefore needs further substantiation, considering the simplicity of stochastic models. Notably, the simulations reveal that the downregulation of kinesin activity on the endosomes is imperative for their fast retrograde transport. We also reached similar conclusions by adopting a model with identical stall forces for dynein and kinesin, based on the lipid droplet transport in Drosophila embryos (Fig. S8).

Simulations predict the temperature-dependence of pause duration

The trends in endosome transport between 24°C and 37°C are also simulated well (Table 1 I). The temperature dependence of model parameters is either adopted from literature (33,42,43) or estimated from the velocities of NGF-endosomes (Table S1). Most of the changes in simulated transport statistics at 37°C are due to the increased velocities and increased unbinding rates of motors. Subtle changes in microtubule-binding rates of motors, expected of barrier-free reactions, did not affect the simulated statistics significantly. The stochastic models predict a ∼40–45% reduction in the mean pause duration, which is borne out experimentally (∼28%). This reduction of simulated pause duration comes from two factors increasing the detachment rate of kinesins in a tug-of-war. First, the unloaded detachment rate of motors is 2–3 times higher at 37°C than at 24°C (42,43). Second, the load on kinesins stalled in a tug-of-war is ramped up higher by faster moving dyneins at 37°C, thus increasing the detachment rate of kinesins (13). We note that the stochastic model simulations only account for ∼73% of the width in the average speed distribution at 24°C (and 40% at 37°C). It is plausible that there is some heterogeneity in endosome speeds not explicit in the models. For instance, intracellular motor velocities can be modulated by biochemical interactions (44), which may vary in temperature dependence.

NGF-endosomes under load: stalls and detachments

The cooperative mechanics of multiple dyneins and the subdued activity of kinesins on endosomes are further corroborated by the dynamics of endosomes under load. Occasionally, NGF-endosomes (<3%) come under load in axons, which results in the endosomes gradually stalling (like beads held by an optical trap) and the leading motors detaching from the microtubule (Fig. 5 and Movie S2). Similar dynamics have been reported for melanosomes running into cargo obstacles (45) and EGF-endosomes (19) in cells. The motion leading to the stalls and endosome recoil after lead-motor(s) detachment contains information about the cooperativity and detachment kinetics of dyneins.

Figure 5.

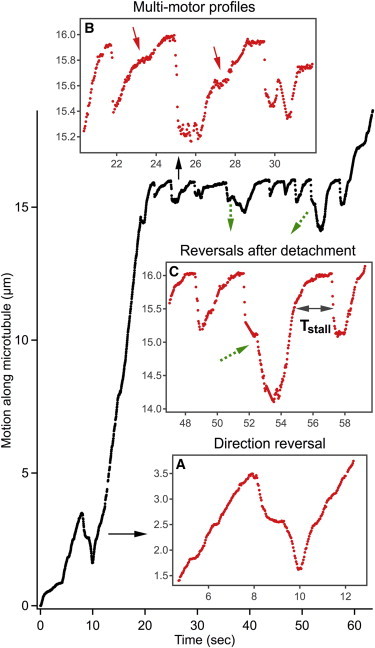
Dynamics of QD-NGF-endosomes under load in axons. (A, Inset) The 2-μm reversal confirming the activity of opposite polarity motors on the endosome. (B, Inset) Repeated stalling, detachment, and relaunch of the endosomal motors working against load. (B, Arrows) The shoulders that are typical of stochastic load sharing and multimotor stall profiles. Two of the nine detachments result in direction reversals of the endosome (green/dashed arrows). (C, Inset) Zoomed-in view of one such reversal showing T_Stall, the stall duration before detachment. To see this figure in color, go online.

Fig. 5 shows an endosome repeatedly stalling and detaching under load, with notable features including: 1) memory of retrograde direction, 2) multimotor stall profiles and stability under load, and 3) sudden detachment profile. The long runs in both retrograde and anterograde directions (Fig. 5 A) before stalling confirm the activity of both kinesins and dyneins on the endosome. After the stalling and sudden detachment, the endosome direction is predominantly retrograde but anterograde reversals are also observed in rare cases (green/dashed arrows in Fig. 5). The mechanical advantage (dynein/kinesin) and downregulated activity of kinesins within stochastic tug-of-war models can explain the retrograde bias seen here. Fig. 5 B highlights the shoulders, typical of stochastic load sharing and multimotor force profiles, in the motion leading to the stall (20,40,46). Recent intracellular studies reveal that the cooperativity of multiple dyneins improves their stability under load, which can be gleaned from the stall duration before detachment (40). We found the mean stall duration (T_stall in Fig. 5 C) of NGF-endosomes at 37°C to be 0.94 ± 0.48 s (N = 25), which corresponds to a multidynein stall force in the range 4–5 pN (40). This suggests that ∼4 dyneins (stall force = 1.25 pN) can be involved in driving the NGF-endosomes cooperatively.

Discussion

The dichotomy of classical tug-of-war and coordination models, which are often viewed as exclusive from one another, is evidently becoming obsolete in recent years. The axon itself is a conduit for a diverse range of unidirectional to bidirectional cargoes (47). Substantial evidence indicates that the classical unregulated tug-of-war model is untenable for a variety of axonal cargoes like mitochondria (48–51), autophagosomes (6,7,14,52,53), APP (15), and prion protein (8) vesicles with several regulatory scaffolding proteins (54). However, even for regulated cargoes, there is no conclusive proof yet for discarding occasional tugs-of-war due to the simultaneous activity of opposite polarity motors. It is more instructive to analyze how the mechanical and regulatory interactions are mixed and matched depending on the cellular context of the cargo motility. For instance, the bidirectional transport of mitochondria caters to its functional relevance within axons by maintaining a stable population along axons. On the other hand, the near-unidirectional axonal transport of signaling endosomes ensures their fast delivery to cell bodies, thus maintaining the balance between survival and apoptotic signaling pathways. Analyzing a diverse range of motility regimes is therefore essential for a better understanding of motor coordination mechanisms in intracellular transport.

The retrograde transport of NGF-endosomes in axons is a unique model system to study the mechanical and regulatory aspects of motor coordination in near-unidirectional motility regime. Our analyses show that stochastic tug-of-war models, constrained by known parameters, can qualitatively simulate the biased directionality and dynamics of NGF-endosomes. However, the kinesin activity on the endosomes had to be reduced substantially to fit our data with reasonable accuracy. Within the framework of the simple stochastic models, our results suggest that NGF-endosomes are driven on average by 5–6 active dyneins and 1–2 downregulated kinesins. These observations are also corroborated by the dynamics of endosomes detaching under load in axons; showcasing the cooperativity of multiple dyneins and the subdued activity of kinesins on the endosomes. The exact stoichiometry and the heterogeneous distribution of motors on endosomes, however, need further substantiation from experiments. In what follows, we discuss the scenarios of kinesin regulation and tugs-of-war that are consistent with our data analyses as well as recent studies on other vesicular cargos in axons.

Regulatory interactions and tugs-of-war on NGF-endosomes

The long pauses (∼4–10 s) of NGF-endosomes cannot be rationalized by tugs-of-war, based on the detachment kinetics of motors. Besides the trivial interruptions caused by local structural features in axons, these pauses could also result from regulatory interactions. Dynactin (28,29,55,56) and LIS1 (22,27) are known dynein regulators that are essential in the activation or sustenance of dynein-mediated transport. Acute inhibition of LIS1 resulted in distinct patterns of long pauses and oscillatory transport of lysosomes and large vesicles in axons (27). It is plausible that the dynein-regulator interactions can undergo sporadic lapses, resulting in long pauses.

Our simulations suggest that the kinesin activity is drastically reduced on NGF-endosomes in axons. A similar feature was reported for the axonal transport of autophagosomes. Maday et al. (6,7) showed that the autophagosomes exhibit bidirectional motility within ∼200 μm from growth cones before becoming retrograde, despite the presence of both kinesins and dyneins. The switch in motility is attributed to the inhibition of kinesins, involving regulatory roles for Huntingtin and HAP1 proteins (14,52). We could not confirm whether such spatially localized regulation is also involved in NGF-endosome transport because the QD-fluorescence background precluded the possibility of imaging near growth cones (site of QD incubation). We believe that the downregulation of kinesins within our model is not fundamentally different from the inhibition of kinesins noted with autophagosomes. Even with a time resolution of 3 s, retrograde autophagosomes were seen to exhibit anterograde direction reversals in axons (7). With improved time resolution of ∼30 ms, our experiments reveal the anterograde reversals of NGF-endosomes more quantitatively. In both cases the kinesins seem to be nearly inhibited with sporadic activity. It remains to be established whether this regulation of kinesins on NGF-endosomes is due to specific interactions on kinesin alone, or to biased-adaptors between kinesins and dyneins, like JIP1 (15) or Huntingtin (14).

Despite the reduced activity of kinesins, many features in our data are qualitatively consistent with tugs-of-war between opposite polarity motors on NGF-endosomes. These include the asymmetry of forward and reverse run velocities, timescale of short pauses, nonnormal multimodal distributions of pauses and reversals, and the positive correlation between pauses and reversals. Further, these features are simulated with reasonable quantitative accuracy by stochastic mechanical models constrained by experimental parameters. We can make two important inferences from our data analysis. First, tugs-of-war between opposite polarity motors are integral features of retrograde endosome transport. However, the apparent agreement between the simulations and our data does not necessarily mean that tug-of-war model is the mechanism by design. It is likely that the tugs-of-war are incidental events within the framework of a coordination mechanism that is discussed below. Second, the motility of each endosome reflects the composition of opposite polarity motors on the endosome and their mechanochemical properties. Indeed, an earlier report showed that the decreased processivity of a single-dynein mutant was reflected by the cargo run lengths in cells (23). The molecular mechanism behind the apparent kinesin binding rate in our model (∼0.5/s, 10× downregulated) is, however, not clear.

Possible scenarios for kinesin-regulation on NGF-endosomes

While the kinesins not associated with cargo can be autoinhibited by specific intramolecular interactions, there is no reported evidence for cargo-bound kinesins with reduced microtubule binding affinity in cells. However, intermolecular interactions with other cargo-bound adaptors have been implicated in the modulation of kinesin autoinhibition. As mentioned above, adaptors like JIP1 and (15) and Huntingtin (57,58) have been proposed to modulate the relative activity of kinesins and dyneins on axonal vesicular cargo. Further, analogous adaptors have been suggested for motor coordination on other cellular cargo (59–61). Here, we discuss the specific interactions relevant for NGF-endosomes that would need future studies for corroboration.

It has been shown that hetero-tetrameric kinesin-1 (kinesin heavy chain (KHC) dimer bound to kinesin light chain (KLC) dimer) has a reduced microtubule binding affinity than the homodimeric kinesin-1 (2 KHC dimers) (62,63). KLC is a known adaptor for recruiting KHC to vesicular cargoes and had also been colocalized with retrograde prion protein vesicles in axons (8). Further, KLC binds to adaptors like JIP1 and Huntingtin, which can interact with dynein and kinesin in a mutually exclusive fashion. So, the reduced kinesin activity could result from the mode of KHC recruitment on endosomes and the role of modulators like JIP1 and/or Huntingtin. For instance, JIP1 interacts with a KHC binding protein that is required to activate KHC in the presence of KLC (64). Huntingtin is a scaffolding protein involved in the retrograde transport of the vesicles of brain growth factor (BDNF, a neurotrophin-like NGF) (58). Huntingtin directly binds to dynein, and the huntingtin-associated protein 1 (HAP1) can modulate the inhibition of kinesin (14). Phosphorylation of JIP1 and Huntingtin at S421 is shown to enhance the anterograde axonal transport of APP (15) and BDNF (58) vesicles, respectively. Therefore, we hypothesize that the kinesins on NGF-endosomes are in an inhibited configuration and the transient reversals result from sporadic fluctuations in the state of adaptors.

Considering these scenarios of kinesin regulation, we put forward a coordination model that combines motor switching by intracellular adaptors with potential tugs-of-war. This model proposes that the kinesins are recruited onto endosomes as kinesin-adaptor-dynein complexes. The state of the adaptor determines the exclusive activity of either kinesin or dynein within a complex. However, multiple such complexes on the same endosome can still lead to occasional tugs-of-war depending on the specific states of the adaptors. The apparent binding rate of kinesin (∼0.5/s) could result from the switching rate of the adaptor from dynein-active to kinesin-active state. Modulating the switching kinetics can lead to a wide range of motility regimes (retrograde to bidirectional to anterograde) with a complex pattern of tugs-of-war. Characterizing the adaptors and their kinetics involved in the regulation of kinesin/dynein activity is an important step forward in this regard.

Unidirectional motility in axons: prospects for motion analyses and modeling

The retrograde motility of NGF-endosomes is a generic transport pathway shared by other neurotrophins (BDNF, etc.) as well as endocytic cargos like tetanus toxin, lectins, etc. (65). Our emphasis in this article was on the coordination of motors on dynein-driven retrograde NGF-endosomes in axons. However, our methodology and approach are also applicable for the study of kinesin-driven anterograde endosomes in axons. Several ligands like lectins and viruses are also known to be endocytosed at cell bodies and transported anterogradely to the axon terminals (65). Microfluidic compartmentalization of neurons affords the selectivity to study anterograde or retrograde endosomes in axons. Fitting the motion statistics of anterograde and retrograde endosomes simultaneously would be a more rigorous test for mechanical models and could help distinguish between in vitro and intracellular mechanochemical properties of motors.

Author Contributions

P.D.C., D.L.C., and B.C. designed the research; P.D.C. and D.L.C. performed the research; and all authors contributed to the data analysis. P.D.C., D.L.C., and B.C. wrote the article.

Supporting Material

Movie S1. Retrograde transport of NGF-endosomes recorded at 37°C

The motion is nearly unidirectional with frequent pauses. The movie lasts 15 s and is played at 2× the original speed. Scale bar on the first movie frame is 7 μm.

Movie S2. Retrograde NGF-endosome repeatedly stalling and detaching under load

The endosome trajectory is shown in Fig. 5. The movie lasts 60 s and is played at 3× the original speed. Scale bar on the first movie frame is 3 μm.

Supporting Citations

References (66–69) appear in the Supporting Material.