Exploring the Dynamics of Cell Processes through Simulations of Fluorescence Microscopy Experiments

Abstract

Fluorescence correlation spectroscopy (FCS) methods are powerful tools for unveiling the dynamical organization of cells. For simple cases, such as molecules passively moving in a homogeneous media, FCS analysis yields analytical functions that can be fitted to the experimental data to recover the phenomenological rate parameters. Unfortunately, many dynamical processes in cells do not follow these simple models, and in many instances it is not possible to obtain an analytical function through a theoretical analysis of a more complex model. In such cases, experimental analysis can be combined with Monte Carlo simulations to aid in interpretation of the data. In response to this need, we developed a method called FERNET (Fluorescence Emission Recipes and Numerical routines Toolkit) based on Monte Carlo simulations and the MCell-Blender platform, which was designed to treat the reaction-diffusion problem under realistic scenarios. This method enables us to set complex geometries of the simulation space, distribute molecules among different compartments, and define interspecies reactions with selected kinetic constants, diffusion coefficients, and species brightness. We apply this method to simulate single- and multiple-point FCS, photon-counting histogram analysis, raster image correlation spectroscopy, and two-color fluorescence cross-correlation spectroscopy. We believe that this new program could be very useful for predicting and understanding the output of fluorescence microscopy experiments.

Introduction

Fluorescence correlation spectroscopy (FCS) methods (1–7) are widely used to explore the dynamics of biological processes (8). FCS consists of the analysis of intensity fluctuations caused by fluorescently labeled molecules moving through the small observation volume of a confocal or two-photon excitation microscope. Since the temporal window of these fluctuations is given by the processes that determine the mobility of the molecules and their photophysics, this technique has been extensively applied to study diffusion, transport, chemical reactions, etc. (reviewed in Elson (9)). Analysis of fluorescence intensity fluctuations also provides the local concentration of fluorescent molecules and their brightness, which can be used to detect the formation of molecular complexes (10,11). The great innovations made in fluorescence fluctuation measurements will probably produce new and useful approaches to be applied to an increasingly wide range of subjects (8).

For simple cases, such as molecules following Brownian motion, FCS analysis yields analytical functions that can be fitted to the experimental data to recover the phenomenological parameters (e.g., diffusion coefficients and chemical rate constants). Unfortunately, many dynamical processes in cells do not follow these simple models, and in many instances it is not possible to obtain an analytical function through a theoretical analysis of a more complex model (9). In such cases, the analysis can be combined with Monte Carlo simulations (for example, see Dix et al. (12) and the SimFCS program from the Laboratory for Fluorescence Dynamics, University of California, Irvine (UCI), Irvine, CA; http://www.lfd.uci.edu/globals/). A comparison of experimental data and the predictions of a reduced, simulated model could provide important clues about the dynamical processes hidden in the FCS data.

Most of the Monte Carlo methods used to simulate FCS experiments consist of ad hoc tools designed for specific scenarios, which makes it difficult for an inexperienced user to adapt the routine to a different situation. Moreover, these routines usually assume homogeneous systems and do not allow inclusion of a user-defined geometry (12,13), which is necessary to describe, for example, the complex architecture of cells.

In this work, we present FERNET (Fluorescence Emission Recipes and Numerical routines Toolkit), a new, to our knowledge, toolkit we designed to simulate the output of a variety of FCS-based techniques in user-defined scenarios. This program works in combination with the MCell-Blender platform (14–16), which was designed to treat the reaction-diffusion problem under realistic scenarios. The program can be used on standard desktop computers with no special hardware requirements, and allows the user to define the architecture of the space and reactions among species, opening up a wide range of possible simulation scenarios. We believe that this new program will be useful for predicting and interpreting the output of fluorescence fluctuation experiments.

Materials and Methods

Simulation of dynamical processes

MCell is a tool that was designed to capture the complexity involved in biological processes such as signaling and metabolic pathways, which include interactions between various components in solution and/or in structures. This program has several advantages with respect to other simulation tools because the standard approximation for reaction-diffusion systems ignores the discrete nature of the reactants and the stochastic character of their interactions, whereas techniques based on the chemical master equation, such as the Gillespie algorithm (17), assume that at each instant the particles are uniformly distributed in space.

The MCell package (http://mcell.org) includes optimized routines to support Brownian dynamics to model the diffusion of individual molecules in volumes or surfaces, ray tracing of random walk motion vectors to detect collisions among molecules, ray marching to propagate rays after collisions, and Monte Carlo probabilities to decide which collisions lead to reaction events (14–16). The particles move diffusively and it is assumed that if a reaction exists, it follows a Poisson process and happens instantaneously. This allows one to decouple the reaction event from the diffusive motion of the particle. The time step of the algorithm is determined such that only single particles or pairs of particles have to be considered, avoiding complex reaction rules.

To deal with the definition of the complex environment for the simulation, MCell is combined with CAD program Blender (http://www.blender.org) using the CellBlender plugin. Blender provides a broad spectrum of modeling, texturing, lighting, animation, and video postprocessing functionalities in one package. The combination of these tools allows one to create realistic 3D scenarios that can be used to simulate the complexity of the underlying biological processes.

Obtaining fluorescence intensity traces with FERNET

FERNET generates fluorescence intensity traces and images from MCell simulations according to the algorithm schematized in Fig. 1. For the simulations presented in this work, we considered a Gaussian confocal volume; however, the size of the observation volume can be easily modified, as indicated in File S1 in the Supporting Material. At every simulation time step, the program evaluates the position of each particle and calculates the probability of emission (g) as follows (5):

$$g\left(x,y,z\right)=\text{exp}\left(\frac{-2\left({\left(x-x_0\right)}^2+{\left(y-y_0\right)}^2\right)}{{\omega }_{xy}^2}+\frac{-2{\left(z-z_0\right)}^2}{{\omega }_z^2}\right),$$ (1)

where ω_xy and ω_z are the radial and axial waists of the point spread function (PSF), respectively, and (x₀, y₀, z₀) is the center of the confocal volume.

Figure 1.

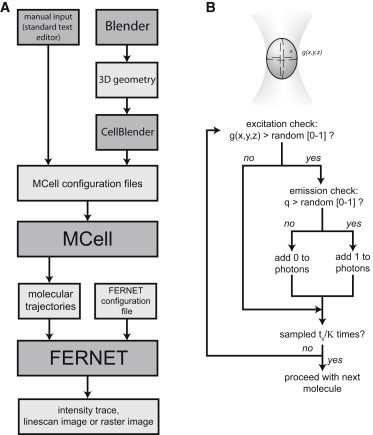
(A and B) Schematic representation of the MCell-FERNET workflow (A) and FERNET routine (B).

To determine whether the molecule is excited, the value of g is compared with a random number between 0 and 1; if the former is greater, the molecule is considered to be promoted to an excited state. To determine whether the excited molecule emits photons, a random number between 0 and 1 is compared with the value of q, defined as q = ε′⋅ κ, where ε′ is the molecular brightness (in counts per second per molecule) and κ is the dwell time between emission events. The molecule emits if the random number is higher than q. The user can set the values of ε and κ as desired; we included as default parameters ε′ = 10⁵ cpsm and κ = 200 ns (12).

To determine the number of photons emitted by the molecule during the sampling time set by the user (t_s), the program repeats this last step t_s/κ times, assuming that the position of the simulated molecule is approximately constant during t_s. This statement may not be true for fast-moving molecules; therefore, the program compares t_s with the mean residency time for the fastest molecule (τ_D): if τ_D < 10 t_s, the program suggests that t_s be modified to correctly sample the simulated system.

This procedure is repeated with all of the molecules at every simulation time step, and the intensity trace is then calculated by adding up the photons emitted by the molecules at each time step.

To ensure that the fluorescence experiments were simulated in the equilibrium condition, we first ran MCell, let the system evolve to equilibrium, and set the obtained concentration of the species as initial parameters for the MCell-FERNET routine.

Correlation functions and photon-counting histogram analysis

Correlation functions and photon-counting histograms (PCHs) were calculated from the simulated intensity traces using specific correlation software (SimFCS; Laboratory for Fluorescence Dynamics, UCI) or custom-made MATLAB (The MathWorks, Natick, MA) routines.

The correlation function was calculated as

$$G_{ij}\left(\tau \right)=\frac{\langle \delta I_i\left(t\right)\cdot \delta I_j\left(t+\tau \right)\rangle }{\langle I_i\left(t\right)I_j\left(t\right)\rangle },$$ (2)

where δI(t) = I(t) − <I(t)> represents the fluctuation of the intensity (I), the brackets indicate the time average, and τ is the lag time. The subscripts i and j refer to the detection channels. If i = j, then G_ii represents the autocorrelation function (ACF), whereas i ≠ j corresponds to the cross-correlation function (CCF).

Results and Discussion

We first ran simulations of molecules passively diffusing in a 3D homogeneous medium and calculated the ACF and PCH from the intensity trace recovered in this simple simulation condition (Fig. 2). The continuous lines in the figure represent the best fit of the PCH obtained by using the theoretical PCH function (11) and the fitting of the ACF data to the equation expected for 3D Brownian diffusion (18):

$$G\left(\tau \right)=\frac{\gamma }{N}\frac{1}{\left(1+\frac{4D\tau }{{\varpi }_o^2}\right)\sqrt{\left(1+\frac{4D\tau }{z_o^2}\right)}},$$ (3)

where D is the diffusion coefficient of the molecules, τ is the lag time, N is the mean number of molecules in the confocal volume, γ is a geometric factor that depends on the detection profile for a Gaussian volume γ = 0.35 (18), and ω_o and z_o are the radial and axial waists of the PSF, respectively.

Figure 2.

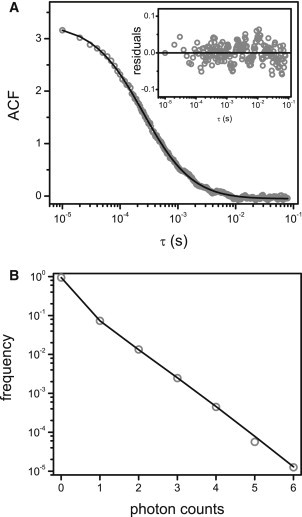
Simulation of FCS routines. (A and B) Single-point FCS: a simulation of 300 molecules (ε = 10⁵ cpsm) passively moving with D = 40 μm²/s in a cube (side length = 6 μm) was run with t_s = 10 μs during 100 s. The ACF (A) and PCH (B) data calculated from the intensity trace obtained with the FERNET routine were fitted as described in the text (continuous lines), resulting in the parameters detailed in Table 1.

Table 1 shows that both the diffusion coefficient (D) and brightness of molecules (ε) are correctly recovered, illustrating the robustness of the routine presented in this work for single-point FCS measurements.

Table 1.

Simulated and recovered parameters of PCH and RICS analyses

Experiment	Parameter	Simulation	Correlation Analysis	PCH Analysis
Single-point FCS	D (μm2/s)	40.00	39.79 ± 0.35	–
	N	0.31	0.29 ± 0.01	0.31 ± 0.01
	ε (cpm)	1.00	–	0.92 ± 0.02
RICS	D (μm2/s)	40	40.72 ± 0.56	–
	N	0.27	0.28 ± 0.01	–

Values are expressed as mean ± standard error from 10 independent simulations.

To show the extra possibilities provided by the ability of MCell to create spatial features, we defined two compartments separated by a permeable barrier (Fig. S1 A in the Supporting Material) and considered different diffusion coefficients and brightness levels for molecules in each compartment. Thus, whenever a molecule moves from one compartment to the other (e.g., when moving between cellular compartments with different rheological properties), the diffusion coefficient changes. This process was simulated as a reaction occurring on the membrane: every time a molecule hit the membrane, there was a probability of destroying this molecule and creating a second one with different D and ε values at the same position on the other side of the membrane.

We then calculated the ACF and PCH curves at different positions of the sample as could be done using different multifocal FCS techniques (2,19,20). Fig. S1 shows pseudocolor images of the D, N, and ε values recovered at every analyzed position either by fitting Eq. 3 to the ACFs or by PCH analysis. These maps closely resemble the simulated data, with the exception of the positions intersecting the barrier, which presented intermediate values as expected.

FERNET also includes the possibility of moving the observation volume, allowing simulations of both the image acquisition (Movie S1) and different scanning-FCS routines (1,5–7). Fig. S2 shows the results obtained in a simulated raster-image correlation spectroscopy (RICS) experiment (12). We fitted the correlation matrix as shown in Digman et al. (6) and obtained the expected values of D and N (Table 1).

Two-color cross-correlation FCS (FCCS) is powerful extension of FCS that allows one to detect interactions between molecules (reviewed in Bacia et al. (4)). Thus, we included in the program the possibility of simulating multicolor measurements (see configuration details in Document S2).

To illustrate how this tool could be used to explore interactions, we considered different scenarios involving the binding of molecules to fixed targets. Previous works showed that such simulations are extremely helpful for exploring the interaction of transcription factors (TFs) with chromatin in living cells (13,21). First, we analyzed simple cases in which two molecules (e.g., different TFs labeled with spectrally well-separated fluorophores) interacted with different binding sites (Fig. 3 A) or competed for the same targets (Fig. 3 B). While the ACFs of the two molecules were very similar and showed the diffusion (τ_diff ∼0.2–0.5 ms) and binding (τ_binding ∼10 ms) components expected according to Michelman-Ribeiro et al. (13), these different scenarios could be clearly distinguished through the cross-correlation analysis.

Figure 3.

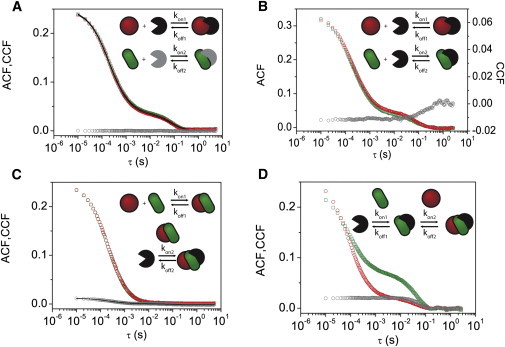
Detecting interactions with two-color FCS. Simulations of two-color FCS experiments were run considering two populations of molecules tagged with spectrally separated fluorescent probes (depicted as red circles and green rectangles). The fluorescence intensity of these molecules was assumed to be collected in independent channels (red and green symbols, respectively). (A–D) The ACFs of the intensity obtained for the red (○) and green (□) channels, and the CCFs (gray symbols) were calculated for the following scenarios: (A) noncompetitive binding, (B) competitive binding, (C) complex formation and binding, and (D) sequential binding. The diffusion and binding model proposed by Michelman-Ribeiro et al. (13) was fitted to the ACF and CCF curves in those scenarios in which the assumptions of the model were fulfilled (continuous lines). The simulated and recovered parameters are summarized in Table S1. To see this figure in color, go online.

To show how the versatility of MCell allows one to include user-defined reactions, we considered other interactions that may affect the binding of molecules with targets. In the first case, molecule A (red circle in Fig. 3 C) interacts with molecule B (green rectangle in Fig. 3 C), and the A-B complex binds to the target. This case is similar to a TF whose DNA-binding efficiency is influenced by its interaction with other proteins (e.g., the estrogen receptor requires calmodulin to bind DNA (22,23). Fig. 3 C shows that the CCF presents two components that are compatible with the free diffusion of complexes and their binding to the targets. Also, we simulated a sequential recruitment of A and B to the binding site (e.g., the glucocorticoid receptor bound to chromatin recruits co-regulators involved in receptor-mediated promoter activation (24). The ACFs obtained for the green and red channels were different due to the sequential binding of molecules (Fig. 3 D). In addition, there was a clear, positive cross correlation in a timescale compatible with the binding process.

Recent improvements in microscopy cameras have resulted in more efficient detection and higher acquisition speeds, allowing the simultaneous and parallel collection of intensity traces with a millisecond time resolution. This development constitutes the basis of imaging-FCS, in which microscopy techniques such as total internal reflection fluorescence microscopy and selective plane illumination microscopy, which confines the excitation to a thin z section of the sample, are combined with FCS (25–27). Given the relevance of these new techniques, we also included in the program the possibility of simulating FCS experiments with camera detection (Fig. S3).

The above examples illustrate how the program can help the user to predict the results of FCS experiments, to rationalize how relevant information can be extracted from experiments, and to understand how different parameters of either the system or the data acquisition could influence the output of the experiments.

For a correct interpretation of the experimental data, these analyses should be combined with an adequate selection of the model based on a strict statistical study that also considers the influence of noise in fluorescence fluctuation measurements and cell-to-cell variability. In recent years, the Bathe group (25,26,28) has developed a Bayesian inference procedure for testing multiple competing models to describe temporal ACFs. This procedure enables the systematic and objective evaluation of different models for FCS data, appropriately penalizing model complexity as the signal/noise ratio decreases.

This group also proposed a statistical blocking procedure (25) that can be easily applied to experimental data to properly estimate the correlated noise present in ACF curves. This step is essential for an unbiased model selection and parameter estimation.

Conclusion

In this work, we have presented, to our knowledge, a new simulation platform based on MCell that allows one to simulate advanced fluorescence microscopy experiments. Because of the easy-to-program options provided by MCell, the MCell-FERNET platform could also be adapted to include a wide variety of photochemical and photophysical processes such as photobleaching and/or photoswitching reactions (12,29), binding to uniform or asymmetrically organized targets (Movie S1), and complex interactions among molecules. We believe that this program could be extremely useful for predicting and understanding the output of fluorescence microscopy experiments.

FERNET and the customized version of MCell can be downloaded from our website (http://www.dc.uba.ar/FERNET).

Author Contributions

E.M., N.P., and V.L. designed research. J.A. and E.M. programmed the custom version of MCell and FERNET. J.A., V.L., and E.M. performed the simulations and data analysis. J.A., E.M., N.P., and V.L. wrote the manuscript.

Supporting Material

Movie S1. Simulating confocal imaging

MCell-Blender was programmed to simulate a complex geometrical model in which green fluorescent molecules are covalently bound to a filamentous structure (e.g., a microtubule), and red fluorescent molecules diffuse freely on the simulated space and can attach to the filamentous structure and diffuse over it (e.g., microtubule-associated proteins). FERNET was set to perform the raster-scan image acquisition in dual-channel mode to simulate images acquired for this scenario in a confocal microscope.