Abstract
Current-displacement (I-X) and the force-displacement (F-X) relationships characterize hair-cell mechano-transduction in the inner ear. A common technique for measuring these relationships is to deliver mechanical stimulations to individual hair bundles with microprobes and measure whole cell transduction currents through patch pipette electrodes at the basolateral membrane. The sensitivity of hair-cell mechano-transduction is determined by two fundamental biophysical properties of the mechano-transduction channel, the stiffness of the putative gating spring and the gating swing, which are derived from the I-X and F-X relationships. Although the hair-cell stereocilia in vivo deflect <100 nm even at high sound pressure levels, often it takes >500 nm of stereocilia displacement to saturate hair-cell mechano-transduction in experiments with individual hair cells in vitro. Despite such discrepancy between in vivo and in vitro data, key biophysical properties of hair-cell mechano-transduction to define the transduction sensitivity have been estimated from in vitro experiments. Using three-dimensional finite-element methods, we modeled an inner hair-cell and an outer hair-cell stereocilia bundle and simulated the effect of probe stimulation. Unlike the natural situation where the tectorial membrane stimulates hair-cell stereocilia evenly, probes deflect stereocilia unevenly. Because of uneven stimulation, 1) the operating range (the 10–90% width of the I-X relationship) increases by a factor of 2–8 depending on probe shapes, 2) the I-X relationship changes from a symmetric to an asymmetric function, and 3) the bundle stiffness is underestimated. Our results indicate that the generally accepted assumption of parallel stimulation leads to an overestimation of the gating swing and underestimation of the gating spring stiffness by an order of magnitude.
Introduction
The cochlea detects sounds and encodes them into neural signals. The transduction from mechanical energy to electrical energy happens at specialized microvilli on hair cells, termed stereocilia. The hair-cell stereocilia bundle (hair bundle) is a sophisticated structure that effectively transfers mechanical energy to mechano-sensitive ion channels (1,2). In mammalian auditory hair cells, stereocilia are arranged in 2–5 rows according to their height. Numerous filamentous links bind the stereocilia (3,4). Two types of filamentous links exist in fully developed auditory hair bundles: tip links and horizontal top connectors (Fig. 1). The tip links run obliquely along the bundle’s primary axis of bilateral symmetry. The horizontal top connectors run along all three axes of the pseudo-hexagonal-array of stereocilia. Functional mechano-sensitive channels localize to the tops of stereocilia, near to the lower end of the tip link (5). The tips of the first (tallest) row of outer hair-cell (OHC) stereocilia are attached to the overlying tectorial membrane so that all the stereocilia columns move together (6). The inner hair-cell (IHC) stereocilia are not attached to the tectorial membrane (7), and are subjected to the viscous fluid flow between the tectorial membrane and the reticular lamina (8,9). Because the tectorial membrane displacement is considered uniform over the span of an IHC (10), the IHC stereocilia are also subjected to uniform stimulation. This uniform stimulation together with the tight binding of the stereocilia bundle may ensure maximal sensitivity and the fastest response.
Figure 1.
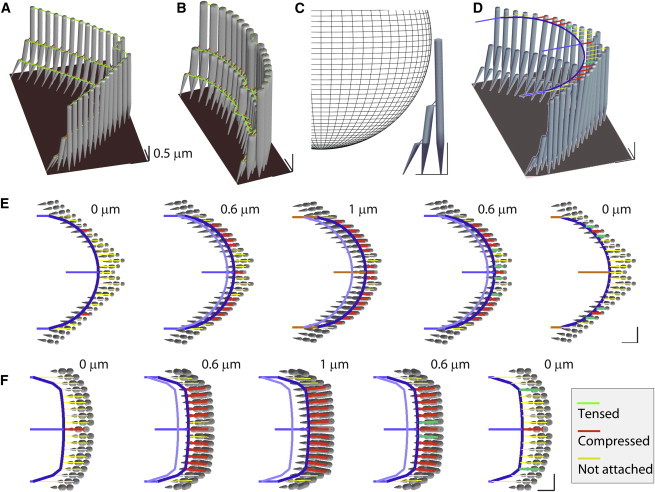
Probe tip contacts the stereocilia unevenly (simulation). (A) The modeled OHC stereocilia bundle has 29 columns and three rows of stereocilia. Two types of horizontal connectors. Different mechanical properties were assigned for the horizontal connectors along the primary axis (kHC1 = 10 mN/m) and nonprimary axes (kHC2 = 1 and 5 mN/m for OHC and IHC, respectively). (B) The modeled IHC stereocilia bundle has 19 columns and three rows of stereocilia. (C) Vertical view of a probe with 3.5-μm radius contacting the OHC stereocilia. (D) It was assumed that the probe contacts the stereocilia at their tips. (E) Sequential plots of probe attachment to the OHC stereocilia. The probe with a spherical tip (r = 3.5 μm) was represented by a rigid beam elements (dark-blue curve). Contact links connect the probe surface and the stereocilia tips (see Materials and Methods for details). As the probe moves from 0 to 1 μm and back to 0 μm, the number of contacting stereocilia (red and green contact links) varies. An established contacting point holds up to 100 pN of tension. (F) Probe attachment to the IHC stereocilia. The IHC probe tip has a greater radius of curvature (r = 15 μm) than the OHC probe to fit well into the IHC stereocilia bundle. The scale bars in hair bundle plots indicate 0.5 μm. To see this figure in color, go online.
In many experiments, the overlying tectorial membrane is removed to get access to individual hair cells. Usually, the hair bundle is deflected by a microprobe and whole cell transduction currents are measured using a patch-clamp electrode at the basolateral membrane of the cell during deflections. Current-displacement (I-X) and the force-displacement (F-X) relationships are obtained from these experiments to characterize hair-cell mechano-transduction. These probe measurement data provide key biophysical information for the gating spring theory of hair-cell mechano-transduction (11). The gating spring theory implies that the hair bundle not only translates mechanical stimulations into electrical signals but also returns mechanical feedback to the external system. Although it remains unclear whether the mechanical feedback from the hair bundle contributes to cochlear function (12), the mechanical force from the hair bundle has been measured in low-frequency hair cells (11) and auditory hair cells (13,14).
Mammalian auditory hair cells are highly sensitive. According to measurements of cochlear partition mechanics (15), auditory hair cells detect vibrations as small as an Ångstrom (0.1 nm). The operating range (OR) of the hair cell’s mechano-transduction (the 10–90% width of the I-X relationship) is an indicator of the cell’s sensitivity. Inconsistent with the notion of auditory hair cell’s high sensitivity, the measured OR of OHC ranges between 200 and 1000 nm in many in vitro experiments (e.g., (16–19)). This value is greater than the 100–500 nm OR of the turtle auditory hair cells (20–23). Recently, by fabricating probes that better match the hair bundle profile, efforts were made to acquire more-consistent I-X relationships for OHCs (18).
In this study, we investigate how the use of microprobes affects the nominal sensitivity of the hair cell through computational model analyses and in vitro experiments. For computational analyses, custom-written three-dimensional (3-D) finite-element (FE) models of the OHC and the IHC hair bundles were used. For experiments, the hair bundles of the rat cochlear OHCs and IHCs were stimulated with various microprobes and fluid-jets. We demonstrate that microprobe stimulations splay hair bundles, which results in 1) broader OR 2) asymmetric I-X relationship, and 3) underestimated hair bundle stiffness. In turn, these artifacts are responsible for an incorrect estimation of two key biophysical properties of hair-cell mechano-transduction—gating swing and gating spring stiffness.
Materials and Methods
Structural model of mammalian cochlear hair-cell bundle
The 3-D FE models of the hair-cell bundle were constructed as described previously (24–28). An OHC and an IHC bundle were modeled based on the geometry of fully developed rat cochlear hair bundles (29) in the apical turn. The OHC stereocilia bundle consists of 87 stereocilia in 27 columns and three rows of decreasing heights (4.3-, 2.2-, and 1.1-μm tall, respectively; Fig. 1 A). The IHC bundle has 57 stereocilia arranged in 19 columns and 3 rows of varying heights (5.0-, 2.5-, and 1.2-μm tall, respectively; Fig. 1 B). Detailed geometric and mechanical properties are listed in Table 1.
Table 1.
Model parameters
| Parameter | Value | Description of Parameter |
|---|---|---|
| kP (10−15 N·m·rad−1) | 0.6, 1.9 | rotational stiffness of stereociliary rootlet (OHC, IHC)a |
| kGS (mN·m−1) | 4 | stiffness of tip link complex (gating spring) |
| kHC1 (mN·m−1) | 10 | stiffness of horizontal connectors along the primary axis |
| kHC2 (mN·m−1) | 1–25 | stiffness of horizontal connectors along the nonprimary axis |
| cHC1 (nN·s·m−1) | 100 | friction coefficient between stereocilia along the primary axis |
| cHC2 (nN·s·m−1) | 1 | friction coefficient between stereocilia along the nonprimary axes |
| f0 (pN) | 40 | setting point of the resting open probability |
| A (ms−1) | 100 | mechano-transduction channel activation rate constant |
| b (nm) | 0.6 | gating swing |
| kES (mN·m−1) | 0.5 | stiffness of the extent spring |
| fM (pN) | 15 | stalling force of the adaptation motor |
| kA (nm·ms−1 pN−1) | 1.5, 0.5 | adaptation rate constant (OHC, IHC) |
Rootlet insertion diameter of 0.04 and 0.05 μm for the OHC and IHC bundle, respectively. The tapering region of the stereocilia is 1 μm long. The Young’s modulus is 0.2 GPa, and shear modulus is 1.0 MPa.
Each stereocilium is shaped like a sharpened pencil consisting of a straight upper shaft and a 1-μm-long root tapered into the rigid cuticular plate of the hair cell. The stereocilium was discretized into 10–20 Timoshenko beam elements to represent the varying diameter along the height and to place nodes connecting interciliary links (28). The stereocilia were bound by link elements representing tip links and horizontal top connectors. The tip links run along the axis of the bundle’s bilateral symmetry to connect the stereocilia tips and the shafts of their nearest tall stereocilium. The stereocilia in the tallest and the shortest rows were tilted toward the second row so that the length and the rising angle of the tip link became ∼200 nm and 45°. The horizontal top connectors bind the tips of stereocilia and their neighboring stereocilia.
Probe attached to the hair bundle
In experiments, probe tips were chosen/fabricated for a better contact with the stereocilia (18,28). I.e., for the V-shaped OHC hair bundle, probes with a round tip are used (Fig. 1 C), while for the flatter IHC hair bundle, flat-tipped probes are used. A freshly fabricated probe adheres to the cell membrane presumably because of electrostatic adhesion between the glycocalyx of the cell membrane and the probe tip, particularly after acid cleaning (30–32).
To simulate such experimental procedures, a round tip probe (radius of 3.5 μm) for the OHC bundle and a blunt tip probe for the IHC bundle (tip surface radius of curvature 15 μm) were modeled. Although it is intended and assumed that the probe tips contract the tips of the tallest row stereocilia, in experiments, the 3-D probe can contact the lower row stereocilia, too (33). We limited our scope to two-dimensional contact, assuming that the probe is optimally positioned at the level of bundle height (Fig. 1 D). The probe surface contacting the stereocilia bundle was represented by a rigid frame (thick blue curves in Fig. 1, E and F). The contact elements were installed along the primary axis connecting the probe surface and stereocilia tips. The contact elements were links that carry only axial force. Due to the bilateral symmetry of the modeled hair bundle, at initial contact, only one or two stereocilia tips contact the probe. At each time step of computational analysis, the distances between the probe tip and the stereocilia were computed. A new attachment was established when the distance between the probe surface and a stereocilia tip became equal or smaller than a predetermined length of contacting elements (0.65 and 1.3 μm for the OHC and IHC bundle, respectively). Once the two surfaces make contact, a stereocilium remains attached to the probe tip until the contact tension exceeds 100 pN. Because of this adhesion between the stereocilia membrane and the probe, the contact elements can carry either tensile or compressive force (i.e., the probe can pull the stereocilia to some extent). The contact elements in red and green (Fig. 1) are under compression and tension, respectively. Whenever there is an event of attachment or detachment between the probe surface and the stereocilia, the stiffness matrix was updated to include or exclude the stiffness contributed by the newly established or lost contract element. Throughout this work, only the stiff probe condition was simulated, i.e., the hair bundle’s probe-contacting points were displacement-clamped.
It was assumed that contact regions with the glass probe are limited to the tallest row of stereocilia. In real experimental situations, the problem is more complicated because of the 3-D geometry of the glass probes and the hair bundle. For example, the probe can contact the middle or the shortest row before it contacts the tallest row, as was considered by others as a potential experimental artifact (33). The 3-D contact issue should be more problematic in IHC stimulations because the probe tip is flat and thick to fit with the flat bundle geometry (Fig. 1). Depending on the approaching angle, the probe tip can contact the lower row stereocilia or even the apical surface of the cell, which may partly explain why IHC experimental results are often less consistent than OHC results. Due to uncertainties in the 3-D contact region and approaching angle, we excluded 3-D contact effects from this study. Silicon probes help to prevent the 3-D contact issue because they can be fabricated as a thin plate (<2-μm thick (18)).
Bundle mechanics
The flexural rigidity of the stereocilia is determined by the rootlet geometry and elastic modulus. There are numerous combinations of rootlet geometry and elastic modulus that result in the same angular stiffness of the stereocilium. The rotational stiffness of the stereocilia rootlet and the specific model parameters are presented in Table 1. The tip link stiffness of this work reflects the stiffness of the putative gating spring rather than the tip link itself, which consists of Cdh23 and Pcdh15 (34). The stiffness of the tip link element was set to 4 mN/m. The horizontal top connectors were assigned a stiffness depending on their direction (10 mN/m along the primary axis, and 1–25 mN/m along the nonprimary axes). Note that the stiffness of both the tip link and the horizontal top connector represents the effective stiffness of the elastic complex between the actin cores of two stereocilia (not just the extracellular filaments). The stiffness of the tip link was determined to match the experimentally measured hair bundle stiffness and stiffness reduction after tip link removal (28).
The viscous friction of the hair bundle was represented by the damping coefficient of the stereocilia elements. The level of stereocilia damping was chosen so that the equivalent viscous friction coefficient of the whole hair bundle became 50 nN·s/m. In order to consider the viscous coupling between the stereocilia, a damping coefficient of 100 nN·s/m was given to the horizontal top connectors along the primary axis (the axis of bilateral symmetry) and 1 nN·s/m was given for the horizontal top connectors along the nonprimary axes to account for different separation along the two directions. Increasing the viscous damping coefficient between the stereocilia by a factor of 100 had minimal effects on the bundle mechanics because the coupling between the stereocilia is dominated by the elastic coupling (see Results). The mass density of the bundle structures was assumed to be the same as water. Because inertial force is negligible compared to elastic or viscous force in the micromechanics of hair bundle, the mass density does not affect the results.
Mechano-transduction channel kinetics
The mechano-transduction channels were considered connected in series with the tip links and interactions between the mechano-transduction channel and the hair bundle occurred via the tip links. Because of the staircase-like structure of the stereocilia and the rising angle of the tip links along the staircase shape, hair bundle deflection toward its taller edge increases the tip link tension and thus activates mechano-transduction channels. Conversely, a configuration change or adaptation of the channel alters tip link tension, which results in bundle deflection.
The channel status (either open or closed configuration) were determined stochastically according to close-to-open (kCO) or open-to-close (kOC) rate coefficients as
| (1) |
| (2) |
where kB is the Boltzmann constant, T is the absolute temperature, and A is a rate constant. ΔE is defined by the tension in the tip link assembly (f) and the gating swing (b),
| (3) |
where f0 is a constant that sets the resting open probability. In the model, the unstrained length of the tip link assembly changes according to the channel state and adaptation,
| (4) |
where n is the channel state (0 when closed, 1 when open) and xA is the equivalent length change of the tip link due to adaptation. Note that the upper/lower insertion node of the tip link does not physically move in the model. Instead, the length of the tip link changes to cause the same mechanical effect.
Unlike low-frequency hair cells, it is being debated whether the adaptation of mammalian cochlear hair cell is affected by intracellular Ca2+ (18,35). Instead of presuming a specific Ca2+-dependent adaptation mechanism (such as myosin-driven adaptation, fast channel release, etc.), the speed of adaptation was assumed proportional to the tip link tension,
| (5) |
where fM is the stalling force of the adaptation motor, kES is the stiffness of an imaginary spring that limits the extent of adaptation (36), and kA is the adaptation rate coefficient. The value of kA was chosen to match experimentally observed adaptation time constants (18,28).
At any moment of time t, the probability of any closed channel remains closed is
| (6) |
where tC is the time when the channel was closed. Likewise, the probability of any open channel remaining open is
| (7) |
where tO is the time when the channel was open. The probability obtained by Eqs. 6 or 7 decreases from 1 right after the state change toward 0 along the time. A random number between 0 and 1 is generated whenever the channel state changes using the RAND function of the software MATLAB (The MathWorks, Natick, MA). Because the probability of a channel becomes lower than the random number associated with the channel, the channel state changes. Because of this stochastic nature, there are no static initial conditions—the channel and the hair bundle are in dynamic balance around the resting open probability of 5% and the resting position (by definition, zero displacement). The dynamic equilibrium is achieved within 2 ms. All the simulations were done with the hair bundle in dynamic equilibrium.
Simulations and postprocessing
The programs were written with MATLAB, Ver. 8.1, and run on a PC (IBM, Armonk, NY; running a model No. i7-3770, 3.40-GHz processor; Intel, Santa Clara, CA). With the time-step size of 1 μs, it took ∼60 and 35 s to simulate 1 ms of OHC and IHC bundle response, respectively. Because of the noise due to stochastic channel kinetics, 5–20 simulations were averaged. Approximately two-thirds of the CPU time was used to solve the linear system of equations (∼6300 and 4400 degrees of freedom for the OHC and IHC bundles, respectively) with the MATLAB-default sparse matrix solver. No MATLAB toolbox was used. We will provide the source code upon request.
Electrophysiological recordings
Preparation and recordings
Animals were euthanized by decapitation using methods approved by the Stanford University Administrative Panel on Laboratory Animal Care. Organs of Corti were dissected from postnatal day (P) 6–10 Sprague-Dawley rats and placed in recording chambers as previously described in Beurg et al. (5). Tissue was viewed using a 60× (1.0 NA; Olympus, Melville, NY) or 100× (1.0 NA, Olympus) water-immersion objective through a 2× magnifier onto a digital Rolera XR camera (Qimaging, Surrey, BC, Canada) on a BX51 microscope (Olympus). Tissue was dissected and perfused with external solution containing 140 mM NaCl, 2 mM KCl, 2 mM CaCl2, 2 mM MgCl2, 10 mM HEPES, 2 mM creatine monohydrate, 2 mM Na-pyruvate, and 6 mM dextrose, pH = 7.4, 300–310 mOsm. In all preparations, the tectorial membrane was peeled off the tissue using forceps.
Electrophysiological recordings
Whole-cell patch-clamp was achieved on IHCs or first- and second-row OHCs from middle to apical cochlea turns using an Axon 200B amplifier (Molecular Devices, Eugene, OR) with thick-walled borosilicate patch pipettes (2–6 MΩ) filled with an intracellular solution containing 125 mM CsCl, 3.5 mM MgCl2, 5 mM ATP, 5 mM creatine phosphate, 10 mM HEPES, 1 mM cesium BAPTA, and 3 mM ascorbate, pH = 7.2, 280–290 mOsm. For Ca2+ imaging, 0.5 mM Fluo-4 or Fluo-4FF (Invitrogen, Carlsbad, CA) and 0.08 mM Alexa 594 hydrazide (Invitrogen) was added to an internal mixture containing 85 mM CsCl, 3 mM MgCl2, 3 mM ATP, 5 mM creatine phosphate, 10 mM HEPES, 40 mM ascorbate, and 1 mM EGTA, pH = 7.2, 280–290 mOsm. Experiments were performed at 18–22°C. Whole cell currents were filtered at 10 kHz and sampled at 0.05–1 MHz using a model No. USB-6356 (National Instruments, Austin, TX) or a Personal DAQ3000 (IOtech, National Instruments) controlled by the software jClamp (SciSoft, http://www.scisoftco.com/jclamp.html). Cells were voltage-clamped at −80 mV, not accounting for liquid junction potentials.
Stiff probe hair bundle stimulation
Borosilicate pipettes were fire-polished to various shapes to test the effect of probe shape. These glass probes were mounted in an aluminum holder attached to a piezoelectric stack (AE0505D08F; Thorlabs, Newton, NJ or PSt 150/7x7/7; APC International, Mackeyville, PA) driven by a custom high-voltage/high-current amplifier. Silicon probes, manufactured to fit the shape of the hair bundle, had a cantilever thickness of 1–2 μm. The silicon devices were mounted to a macroscale piezoelectric stack (AE0505D08F; Thorlabs) via an aluminum holder. Step stimuli were filtered with an 8-pole Bessel filter (L8L 90PF; Frequency Devices, Ottawa, IL) at 200–15 kHz and variably attenuated (PA5; Tucker-Davis Technologies, Alachua, FL) before reaching the piezo amplifier. Probe rise times were measured using a dual photodiode system (18) for the stimulator.
Ca2+ imaging
Organs of Corti from Sprague-Dawley rats, ages P7–P9, were harvested. High-speed swept field confocal Ca2+ imaging (Prairie Technologies/Bruker, Billerica, MA) (5) used a 35-μm slit at 500 frames/s, where the Ca2+ indicator was excited using a 488-nm laser and the Alexa 594 was excited using a 594-nm laser. Hair bundles were stimulated using a Picospritzer III (Parker Hannifin, Cleveland, OH; (5)). Data were collected and analyzed using a Neuroplex (RedShirtImaging, Decatur, GA). Currents were sampled at 8 kHz.
Data analysis
I-X plots were generated by subtracting leak current and normalizing to the peak current. I-X plots with different probe shapes and probe speeds were generated as above, and fit to a double-Boltzmann equation as
| (8) |
where Z1 and Z2 are the slope factors, and x0 represents the operating point. Data were analyzed using jClamp (SciSoft), and EXCEL (Microsoft, Redmond, WA). Graphs were created using the softwares MATLAB, ORIGIN 8.6 (OriginLab, Northampton, MA), and Adobe Illustrator (Adobe, San Jose, CA).
Results
Hair bundle deflection due to stimulation with a microprobe
Under artificial conditions without the tectorial membrane, it is nontrivial to substitute the role of the tectorial membrane—to deliver uniformly coordinated mechanical stimulations to hair bundles at the frequency of mammalian hearing. A popular means of stimulating individual hair cells is to use microprobes. In these experiments, a probe is driven toward the hair bundle before it is withdrawn to an approximate zero-displacement position. Because of the unique shape of the hair bundle of the OHC and the IHC, a probe tip is chosen to fit the hair bundle profile.
We modeled and simulated such a probe positioning (Fig. 1, F and G). A simple probe with a circular contact surface was chosen (tip radius of curvature of 3.5 and 15 μm for the OHC and the IHC bundle, respectively). Due to the bilateral symmetry of the modeled hair bundles, initially two (OHC) or one (IHC) stereocilia tip(s) was in contact with the probe (State 1). As the probe moves in the excitatory direction, the probe contacts more stereocilia (State 2).At the largest displacement, the stereocilia bundle deformed to conform to the probe profile (State 3). As the probe was pulled back to the initial position, most newly established contacts were lost (State 4), but several points remained attached because of the adhesion between the cell membrane and the probe (State 5). The number of contacting stereocilia after the withdrawal is determined by the static equilibrium between the bending moment of the stereocilia and the adhesion force. For example, compliant stereocilia and strong adhesion will leave more stereocilia in contact with the probe. Similarly, the same stereocilia stiffness and more compliant horizontal connectors will result in more stereocilia in contact with the probe (data not shown).
The stereocilia of our simulated hair cells do not deflect uniformly—they splay. The splaying of the hair bundle is important because when the stereocilia deflect nonuniformly, the transduction channels do not respond in parallel. There are two possible modes of hair bundle splaying that lead to nonuniform mechano-transduction responses: First, the splay between rows, in which the stereocilia in a column can splay, as was noted in previous studies (37–39), although it was not observed experimentally (40,41); and second, the splay between columns, in which the stereocilia in some columns can deflect more than other columns. This intercolumn splay of the stereocilia was observed previously in OHCs (42) and IHCs (43).
Splaying between different columns of stereocilia
The hair bundle splayed more prominently between columns than between rows. To ascertain the two modes of bundle splay and to correlate the bundle’s coherence with mechano-transduction, the states of individual transduction channels were simulated when hair bundles were stimulated either with a probe or through an imaginary tectorial membrane (Fig. 2). We assumed that, in the natural situation, the tips of the tallest row stereocilia are displaced evenly by the tectorial membrane so that there is no splay between columns. Unlike the natural (ideal) situation, when the hair bundle was stimulated with a probe, the stereocilia that contact the probe surface deflect more (Fig. 2, A and C, top contour plots; hotter colors correspond to greater displacement toward the excitatory direction) as compared to the uniform deflection in the ideal case (Fig. 2, B and D). In the hair bundle, there are the upper and the lower row of the transduction channels located at the tips of the second- and the third-row stereocilia. The upper-row transduction channels near the contacting stereocilia (Fig. 2, A and C, second-row panels, channel states in red) tended to open more often and stay open longer as compared to channels distant from the probe (channel states in black). The lower-row transduction channels in the same column of the contacting stereocilia (channel states in green) responded nearly the same as the upper-row channels, indicating there was minimal splay between different rows of stereocilia. When the bundle was stimulated evenly (Fig. 2, B and D), the mechano-transduction channels in the hair bundle responded uniformly.
Figure 2.
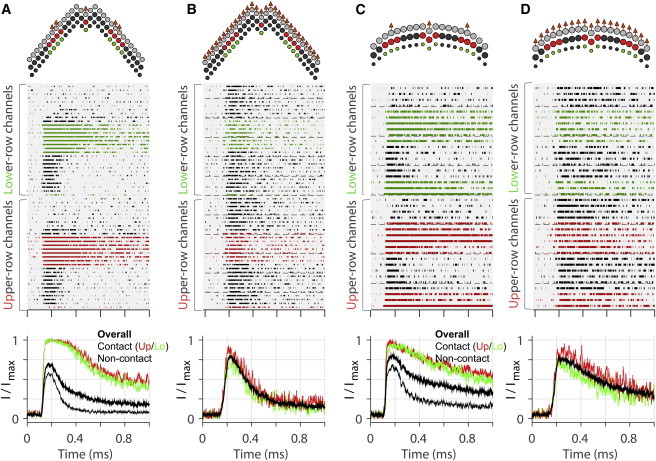
Probe stimulation versus ideal stimulation (simulation). (Top plots) Top-down view of the hair bundle. Arrows indicate the stimulated stereocilia either by the probe-contact (A and C) or the tectorial membrane. (Middle plots) States of individual transduction channels along the time (filled spans indicate the open state); channel colors correspond to the stereocilia colors in the top plots. (Bottom plots) Normalized whole cell transduction current. Ten-to-twenty trials were averaged to reduce the stochastic noise of the Monte Carlo simulation. (Thick black line) Overall normalized transduction current. (Red, green, and thin black lines) Sum of channel activities in middle plots. (A) OHC stereocilia subjected to 0.2-μm probe-displacement. (B) OHC stereocilia tips subjected to 0.1 μm of uniform displacement along stereocilia columns. (C) IHC stereocilia subjected to 0.25-μm probe-displacement. (D) IHC stereocilia subjected to 0.1 μm of uniform displacement along stereocilia columns. The stimulation is considered a step displacement because it is ramped faster (τ = 20 μs) than the adaptation of mechano-transduction. To see this figure in color, go online.
There are two explanations for why the stereocilia splay between columns, but not between rows: First, the angle between the applied force/displacement and the direction of the horizontal connectors contributes to the difference. If a pair of stereocilia bound by links between their shafts is considered, they splay most easily by a shear force orthogonal to the direction of the links and least by an axial force parallel to the direction of the links (result not shown). Second, there are only three rows in the OHC and the IHC hair bundle. If the elastic horizontal connectors are the primary means to bind the stereocilia, as the number of stereociliary rows increases, the splay between the tallest and the shortest stereocilia becomes more prominent as was shown by Cotton and Grant (37).
To confirm stereocilia splaying, we visualized local activation of mechano-transduction. We stimulated hair bundles and monitored mechano-transduction channel opening through high-speed calcium imaging (5). We stimulated hair bundles locally using a low-pressure stimulus on one side of the hair bundle, where the stimulus to the hair bundle was barely optically detectable. Here, only local activation of mechano-transduction channels near the stimulus pipette (Fig. 3 A) was observed, indicating splay between stereocilia columns. There was a clear dropoff of the stimulus intensity to stereocilia moving from the site of stimulation as seen by the size of the calcium signal in stereocilia moving from left to right (Fig. 3 A, bottom; black, red, green, and blue traces). To ensure that the local activation of channels was not due to the absence of functional channels in neighboring stereocilia caused by damage during the experiment, we stimulated the whole bundle with the same pipette positioned further back with higher pressure to demonstrate functional channels in nearly all stereocilia (Fig. 3 A, right). The relative stimulus size was also seen in the whole-cell mechano-transduction currents (Fig. 3 C, black and red traces). We also tested the recruitment of stereocilia with increasing stimulus size at a given location (Fig. 3, B and C). With a small stimulus we found low-level activation of mechano-transduction channels for part of the hair bundle (Fig. 3 B, left top Ca2+ traces), but channel activation decreased, moving toward the right side of the hair bundle (Fig. 3 B, left bottom Ca2+ traces). Increasing stimulus pressure recruited activation of more stereocilia (Fig. 3 B, right). Again, there was a decrease in the channel activation further from the stimulus site (Fig. 3 B, right top Ca2+ traces). In some instances, we even observed a delay in activation of the mechano-transduction channels located further from the stimulus site (Fig. 3 B, right bottom Ca2+ traces). These data confirm the modeling results that stereocilia splay across columns.
Figure 3.
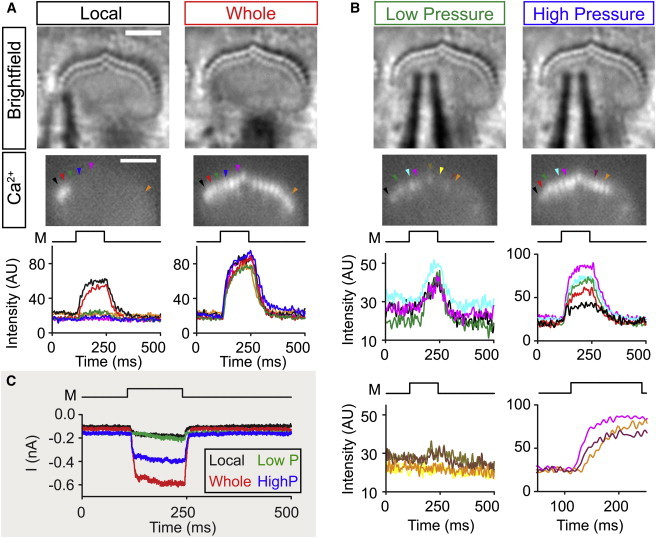
Local stimulation leads to local recruitment (Experiment). (A) Using high-speed calcium imaging (500 frames/s) we applied a low pressure local stimulus to the left side of the hair bundle (left). Local stimulation led to channel opening and calcium influx near the stimulating pipette leading to fluorescence of the calcium dye Fluo-4ff (black and red arrows). Ca2+ images are taken as an average of 25 frames at the end of the mechanical stimulus (M). Fluorescence traces (bottom graphs) are taken from cilia indicated (arrowheads) in the Ca2+ image. Ca2+ signals decrease moving away from the stimulating pipette (red, green, and blue traces) and eventually are undetectable (magenta and orange traces). The lack of signal in the remaining parts of the bundle is not due to damaged mechano-transduction, because when the pipette is moved back and the pressure increased, functional stereocilia can be seen throughout the whole hair bundle (right panels). All stereocilia where the calcium level was followed for the local stimulation show strong Ca2+ signals when the whole bundle is stimulated. (B) To further illustrate the process of recruitment, we stimulated the hair bundle in (A) at one position with a low pressure and high pressure stimulus. In the low-pressure stimulus (left), Ca2+ signals are low, rise slowly, and get smaller moving more distant to the right of the hair bundle (left bottom traces). When stimulating with higher pressure (right), Ca2+ signals increase in other stereocilia, indicating recruitment of more stereocilia with larger stimulation. Recruitment of stereocilia sometimes entails a delayed activation of channels as seen by Ca2+ signals in stereocilia traces in the right bottom. (C) Current traces for the different stimulations: local (black), whole bundle (red), low pressure (green), and higher pressure (blue). M indicates the time of the drive signal for the mechanical stimulus. To see this figure in color, go online.
Stimulation artifacts affect the I-X relationship
The artificial stimulation using an uneven probe attachment affects the I-X relationship in two ways: First, the artificial stimulation broadens the I-X curve, because it takes more displacement for nonuniform stimulation to saturate the transduction current. Second, the artificial stimulation results in an asymmetric I-X curve. If the mechano-transduction channel has two conformational states, its kinetics are described by the first-order Boltzmann equation, and the I-X curve is symmetric with respect to the half-activation point. Even if individual mechano-transduction channels follow the first-order kinetics, the whole cell I-X curve can appear asymmetric when artificially stimulated.
Our computational model simulated the effect of different probe shapes (Fig. 4). The model applied a family of step displacements using probes with two different widths (equivalent to one-third and one-times the bundle width) in addition to the standard probe in Fig. 1. Because the thin and thick probes do not fit with the bundle’s profile, the probes contact either the center or the peripheral stereocilia columns. The stereocilia in contact with the probe deflected more than non-contact stereocilia. In Fig. 4, A–C, colored circles indicate displaced stereocilia tips and black circles indicate their locations at rest (for illustrative purposes, stereocilia tips in the second and the third rows were projected to the plane of the first row tips). These simulations show that the bundle splays (Fig. 4 B) or squeezes (Fig. 4 C) depending on the probe shape. The geometrical conformity of the probe with the hair bundle affected the mechano-transduction process. It took more than 0.5 μm to saturate the transduction current (Fig. 4 D). The OR of the simulated OHC mechano-transduction was 0.09, 0.2, 0.5, and >0.5 μm for the ideal, standard, thin, and thick probe cases, respectively. In other words, our simulation results indicate that the probe stimulation overestimates the OR by a factor of 2 or more.
Figure 4.
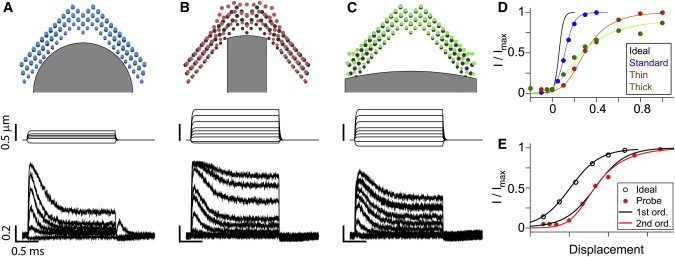
Stimulation with different probes (simulation). (A) Standard probe in Fig. 1. (Top) The hair bundle and the probe geometry. (Middle) Probe displacement along time. (Bottom) Normalized transduction current along time. (B) Thin probe. (C) Thick probe. (D) I-X curves. Line colors correspond to the probe types. (E) Ideally stimulated I-X curve fits perfectly with the first-order Boltzmann equation, while probe-stimulated I-X curves do not (thick probe case shown). For comparison, the displacement of the ideal case was expanded five times and shifted horizontally. To see this figure in color, go online.
The stimulation method affected not only the slope of the I-X curve, but the shape (symmetry) of the I-X curve (Fig. 4 E). When the bundle was ideally stimulated, the first-order Boltzmann equation fits the simulated I-X data perfectly. Conversely, when the bundle was stimulated with probes, the slope of the curve was steeper at small deflection and flatter at large deflection, which required a higher-order Boltzmann equation to fit. This trend became more obvious when the probe did not fit well with the hair bundle. The fit curves in Fig. 4 E were the second-order Boltzmann equation except for the ideal case. This result implies that the second-order Boltzmann fit of the I-X relationship may be an artifact of the uneven stimulation of the hair bundle, and the channel itself may have only two states.
To confirm the broadening of the I-X curve experimentally, we made glass probes that were purposely misshapen to compare to the glass probes normally used (Fig. 5). With normal probes, adaptation was fast and robust, and I-X curves were the narrowest (Fig. 5, black traces). With a flat probe shape (fat probe, red traces), I-X curves broadened, suggesting that it took greater probe displacement to deflect the stereocilia in the middle of the bundle. Similarly, probes that were very thin increased the width of the activation curve (green traces). Thin probes were poor at closing channels in the negative direction, suggesting insufficient probe adhesion to the bundle. Finally, with a silicon probe that is only 1–2 μm in thickness, adaptation was robust and I-X curves were narrow like the normal probe (blue traces).
Figure 5.
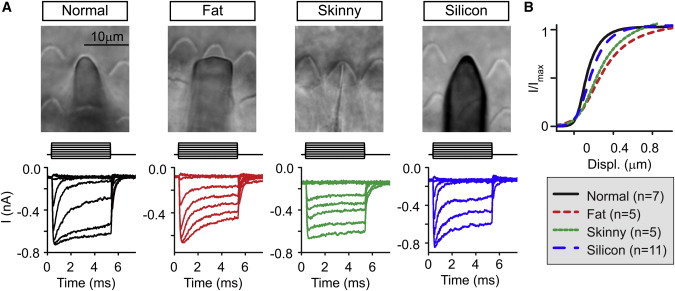
Misshapen probes increase the width of the I-X curve (Experiment). (A) Using different shaped probes, a family of step displacement responses was generated. Bright-field images of the probes used on the outer hair-cell bundles. M represents the mechanical stimulus used. (B) Average I-X curves were generated for double Boltzmann fits of the I-X curves. Probes that are too fat or too thin lead to wider activation curves than probes shaped like the hair bundle. Each double Boltzmann fit calculated and averaged to get a mean Boltzmann fit curve. The n-values are given in parentheses in the legend. To see this figure in color, go online.
The speed of stimulation is also important for the width of the I-X relationship. The OR increased as the stimulation became slower (Fig. 6, C and D). As the time constant of the displacement increased from 0.01 to 0.32 ms, the ORs of the standard probe cases increased from 0.19 to 0.43 μm (OHC) and from 0.31 to 0.39 μm (IHC), and the ORs of the ideal cases increased to 0.23 μm (OHC) and 0.18 μm (IHC). This increase in the OR is due to adaptation, and when adaptation is removed, the OR does not change with activation time constant (kA = 0, broken lines in Fig. 6, also see Fig. S1 in the Supporting Material). The IHC’s OR changed less than the OHC’s because adaptation of the OHC was set faster (adaptation time constant τA = 0.16 ms for the OHC and 0.32 ms for the IHC). For all simulations in this study, the displacement time constant was made sufficiently small (τ = 20 μs) to exclude the effect of adaptation.
Figure 6.
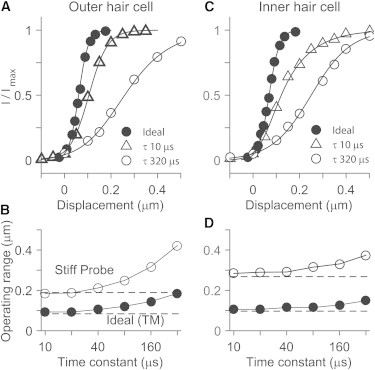
Effect of stimulating speed (simulation). (A) OHC’s I-X curves when ideally stimulated and stimulated with the standard probe in Fig. 1. The time constant (τ) of the displacement ramp affects the I-X curve. The time constant was 10 μs for the ideal case and 10 and 320 μs for the probe case. (B) IHC’s I-X curves. (C) OR versus stimulating speed, OHC. (D) OR versus stimulating speed, IHC. (Horizontal lines in C and D indicate the OR when there was no adaptation.) To see this figure in color, go online.
To confirm the effects of probe speed on the width of the I-X curve, we stimulated hair bundles with different filter settings to control the rise time of the probe. We found that faster probes filtered at 15 kHz have the narrowest I-X curve. Interestingly, even at 1 kHz, the width of the I-X curve is similar, but the curve itself was shifted to the right. When slowing the probe even further with 200-Hz filtering, the I-X curve widened significantly and shifted further to the right (Fig. 7, B and C).
Figure 7.
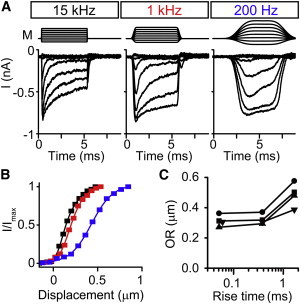
Slowed activation speed of the probe can also widen the I-X curve (Experiment). (A) In a single cell using a normal probe, the filtering of the stimulating step response was changed to 15, 1, and 200 Hz. Families of step responses were done at each filter setting keeping the position of the probe the same. (B) Corresponding I-X curves for the traces in (A) for 15 (black), 1 (red), and 200 Hz (blue) showing the broadening of the I-X curve at the slowest stimulating speed. (C) Summary of the OR of the I-X curve calculated from the double Boltzmann fit for the different stimulating speeds for four different cells represented with different symbols. The probe rise time was measured for the stimulator. To see this figure in color, go online.
Parameters that affect the I-X relationship
In these models of hair bundle mechanics, the stereocilia are bound by two mechanical forces: elastic coupling provided by tip links and horizontal top connectors, and viscous coupling according to the damping coefficients assigned to horizontal top connectors. The elastic links apply binding forces proportional to the distance change between the stereocilia. The viscous coupling applies resistive forces proportional to the relative velocity between the stereocilia. We found that the elastic coupling between stereocilia columns is most relevant to the I-X relationship.
The stiffness of horizontal top connectors along the nonprimary axes (kHC2) was identified by comparing simulation results with two previous experimental results (Fig. 8). Langer et al. (42) used an AFM tip to displace a single column of stereocilia to estimate the force transmission between stereocilia columns. The horizontal top connector stiffness between kHC2 = 1 mN/m and 5 mN/m resulted in similar spatial decay of stereociliary displacement that indicates the force transmission between stereociliary columns. This comparison, however, should be taken with caution. In their experiment, 4-day-old rats were used and the interciliary links at that stage are not fully developed (6). When simulated similarly, even 2–3 orders of magnitude greater value of kHC2 (1000 mN/m) than the reasonable value (1–5 mN/m) could not prevent the splay between stereocilia columns (Fig. 8 A). This indicates that the trend of our finding (expanded I-X curve due to intercolumnar splay) holds, despite the choice of the model parameter (kHC2). More recently, Karavitaki et al. (43) measured the splay between stereocilia columns of the gerbil cochlear IHC. The space constant of displacement decay along the stereocilia columns of 0.6 μm was also comparable to our simulated IHC hair bundle with kHC2 = 5 mN/m (Fig. 8 B).
Figure 8.
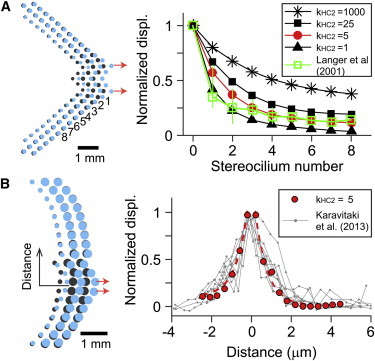
Identification of horizontal connector stiffness (simulation). The hair bundle was pulled locally and the decaying of the displacement along the stereocilia columns was measured. (Dark circles) In each bundle plot, the dark circles indicate the undeformed configuration. The pulled stereocilia are indicated with arrows. (A) OHC bundle. The displacement decay along different columns is dependent on kHC2. The result was compared with an OHC experimental result from the rat cochlea (42). (B) IHC bundle. The result was compared with an IHC experimental result from the gerbil cochlea (43). Note that the x axes of the two panels are found different from the respective experimental data. To see this figure in color, go online.
The stiffness of the horizontal top connectors affects the OR of hair-cell mechano-transduction when stimulated with probes (Fig. 9). In this work, considering their different lengths, the horizontal top connectors along the primary axis and the nonprimary axes were given different stiffness values: standard values were 10 mN/m along the primary axis (kHC1) and 5 mN/m along the nonprimary axes (kHC2) for both the OHC and the IHC. Because the splay between stereocilia columns was prominent (Fig. 2), we investigated the effect of different stiffness values of the horizontal top connectors along the nonprimary axes. The OHC bundle was subjected to a family of step displacements using the standard probe shown in Fig. 1. Four cases were simulated: an ideal case with the first-row stereocilia deflected evenly, and three cases with the standard probe (Fig. 4 A). In the probe stimulation cases, we used hair bundles with three different stiffness values of the intercolumn horizontal connectors (kHC2 = 25, 5, and 1 mN/m). Note that the ideal condition is equivalent to an infinite coupling stiffness between stereocilia columns. The stiffness of the horizontal connectors strongly affects the bundle coherence (Fig. 9 C). As the kHC2 increased from 1 mN/m to 25 mN/m, the steady-state value of the normalized splay decreased from 0.9 to 0.2. This difference in the intercolumn splay affected the nominal sensitivity of the hair cell: the OR values for the four cases were 90, 120, 200 and 360 nm for the ideal, 25, 5, and 1 mN/m cases, respectively. The effect of different kHC2 values becomes greater when unfit probes were used (such as those in Fig. 4, B and C, data not shown).
Figure 9.
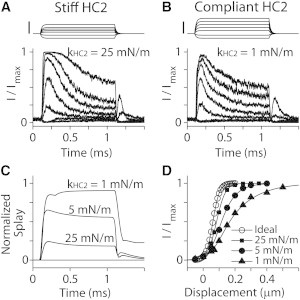
Effect of horizontal connector stiffness (simulation). OHC stereocilia bundle with different levels of horizontal connector stiffness (kHC2) was stimulated with the standard probe in Fig. 1. (A) When kHC2 = 25 mN/m. Scale bar, 0.4 μm. (B) When kHC2 = 1 mN/m. Scale bar, 0.4 μm. (C) Normalized splay of the OHC hair bundles with different horizontal connector stiffnesses (0 = no splay, or complete coherence; 1 = no coherence at all). (D) Normalized transduction current versus hair bundle displacement. The ideal case is when the tallest row stereocilia are evenly deflected.
Unlike elastic coupling, viscous coupling has little influence in hair bundle coherence and the nominal sensitivity of the hair cell (Fig. S2). In the computational model, the interstereociliary viscous coupling was simulated by assigning a viscous friction coefficient to the horizontal connectors. For example, with the standard cHC1 = 100 nNs/m, when a pair of stereocilia separate with a velocity of 1 μm/ms, the pair is subjected to 100 pN of resisting force against the separation. It has been shown that the viscous friction coefficient can be as large as 10,000 nNs/m (44). Because there should be much less viscous friction in shear separation (i.e., between columns) as compared to normal separation (i.e., between rows), the friction coefficient between the columns (cHC2) was given one-hundredth of cHC1.
The OHC hair bundle was stimulated with the standard probe. One-tenth (Fig. S2 A), and 100 times (Fig. S2 B) the standard viscous friction were simulated. Despite the three orders-of-magnitude change in the viscous coupling, there was little difference in the transduction current responses. The I-X curve was nearly identical in those two cases. The magnitudes of the elastic coupling force compared to the viscous coupling force (bottom two rows in Fig. S2) explains this result. Even with the large viscous coupling case, the viscous coupling forces were transient and at most 30 pN. Of course, as the displacement is ramped faster, the viscous coupling force will increase proportionally. The simulated displacement ramping time constant of 20 μs is comparable to an 8-kHz sinusoidal stimulation. The viscous coupling force may increase in the hair bundles vibrating at higher frequencies. However, at the high-frequency location, the viscous coupling will be less efficient because shorter stereocilia (<1.5 μm) are separated by a significant gap between tapered stereocilia rootlets (∼0.5 μm, see microscopic images in Verpy et al. (6) and Furness et al. (45)). I.e., long parallel stereocilia with a minimal separation are more efficient for viscous coupling. Therefore, the elastic coupling is also expected to dominate in the high-frequency location.
Uneven contact of stimulating probe results in underestimation of hair-cell bundle stiffness
Hair bundle stiffness measurements depend on how the stimulation is delivered. Under natural conditions, the first row of the stereocilia will be evenly deflected. Under experimental conditions using microprobes, the stereocilia are not stimulated uniformly, resulting in an underestimation of the bundle stiffness. Hereafter, we will call the stiffness measured by artificial stimulation the nominal stiffness, to distinguish it from the intrinsic hair bundle stiffness felt by the tectorial membrane.
In this work, the linear stiffness of a single stereocilium (kS) in the tallest row is 0.033 and 0.077 mN/m for the OHC and the IHC, respectively. This property is determined by the elastic modulus of the stereocilia and the stereocilia dimension (primarily the diameter at the root). If every stereocilium contributes equally to the whole bundle stiffness, these values correspond to 2.9 mN/m (OHC) and 4.4 mN/m (IHC) for the whole bundle. When the tips of the first-row stereocilia are evenly deflected, the passive bundle stiffness is 4.7 mN/m (OHC) and 4.4 mN/m (IHC). According to Cotton and Grant (37), in a column of stereocilia, if the stiffness of horizontal top connectors is more than one order-of-magnitude greater than the linear stiffness of a stereocilium (kHC1/kS > 10), the sum of individual stereocilia stiffness approximates the stiffness of the bundle (stereociliary column). The oblique tip links add further stiffness to the bundle. In this work, the stiffness of the horizontal top connectors between rows is 10 mN/m, and the linear stiffness of a stereocilium in the third (shortest and stiffest) row is 0.50 mN/m (OHC) and 1.3 mN/m (IHC). Therefore, our chosen value of kHC1 = 10 mN/m was sufficient to bind the OHC stereocilia, but not sufficient to bind the IHC stereocilia. When the bundles are stimulated with probes shown in Fig. 1, F and G, the nominal stiffness of the bundle (applied force divided by probe tip displacement) was 2.6 mN/m (OHC) and 0.73 mN/m (IHC). These values were reduced by 52% (OHC) and 12% (IHC) when the tip links were removed and by 79% (OHC) and 52% (IHC) when all the horizontal top connectors were removed. Active adaptation of channels reduced the steady-state stiffness by 27% (OHC) and 8% (IHC). Note that these nominal stiffness values are dependent on the probe shape (the number of contacting stereocilia and the locations of contact). Our simulation results indicate that the stiffness measurement by microprobes tend to underestimate the true bundle stiffness. In the simulated cases, the nominal stiffness obtained from the stimulation with the standard probe resulted in 44% (OHC) and 83% (IHC) lower values than the true bundle stiffness. See Figs. S3 and S4 for the F-X plots in different cases.
Discussion
The contemporary theory of hair-cell mechano-transduction is established on the assumption that the mechano-transduction channels respond in parallel. Our results, however, show that such an assumption does not hold, at least, in the popular experiments using microprobes in mammalian cochlear hair cells. Different stereociliary columns did not deflect evenly when the hair bundle was stimulated unevenly with a probe or a fluid-jet. Neglecting the effect of uneven stimulation has fundamental consequences in hair-cell biophysics such as: 1) underestimation of the true sensitivity of the hair-cell mechano-transduction, 2) misinterpretation of mechano-transduction channel kinetics such as the number of channel states, 3) underestimation of the hair bundle stiffness, and 4) overestimation of the gating swing.
True operating range of hair-cell mechano-transduction
One of the key biophysical parameters to characterize hair-cell mechano-transduction is the sensitivity. The sensitivity of a hair cell is represented by the slope of the I-X curve. According to the gating spring theory (11) and two-state channel kinetics model (46), the single channel gating force (z = γ kGSb, where γ is the geometric gain; kGS is the gating spring stiffness; and b is the gating swing) determines the sensitivity of mechano-transduction. The geometric gain may be the most straightforward parameter of the three because it is determined by the hair bundle geometry (kinematics). The gating spring stiffness can be estimated from the stiffness reduction due to the removal of the tip links or from gating compliance (nonlinear F-X relationship). With the geometric gain and gating spring stiffness fixed, the gating swing is uniquely determined from the measured I-X curve.
In the majority of experiments, individual hair cells were stimulated with microprobes. The operating range (OR) of mammalian auditory hair cells obtained from microprobe experiments is between 0.2 and 1.0 μm (e.g., Lelli et al. (47) and Kennedy et al. (48)). Compared to the amphibian saccule hair-cell bundle (one of the most investigated types of hair cell), the rodent auditory hair-cell bundle in the apical turn is shorter by a factor of 2. The OR of the amphibian hair cells was measured to be 0.1–0.4 μm (11,49–52). In theories to explain the spontaneous motions of the bullfrog sacculus hair bundle, the OR is even narrower than 0.05 μm (53,54). From these, it seems like the mammalian auditory hair cells are less sensitive than the amphibian vestibular hair cells. However, there are other data indicating that the OR of cochlear hair cells may be narrower than 0.1 μm.
First, the basilar membrane displacements have not been observed to exceed 100 nm even at the 80-dB sound pressure level or above. For example, the basilar membrane displacement in the apical turn of the mouse cochlea is ∼10 nm at the 80-dB sound pressure level (55). Considering that the hair bundle displacement is comparable to the basilar membrane displacement (56–59), the OR of hair-cell mechano-transduction at the apical turn is likely <100 nm. Second, in hemicochlear preparations where the tectorial membrane remained on top of the hair bundles, the OR of the IHC and OHC in the apical turn of the gerbil cochlea was ∼100 nm (60,61). Third, hair bundle stimulations with a fluid-jet, using sinusoidal stimulation, resulted in an OR < 200 nm (1,35), despite the slower application speed of fluid-jet. Our results, together with these results, suggest that the OR of hair-cell mechano-transduction is considerably overestimated in most experiments using microprobes. However, the microprobe technique has an irreplaceable advantage over other methods—it can deliver controlled force to measure the F-X relationships of hair bundle. Correct estimation of the hair bundle’s mechanical properties is mandatory to define the mechano-transduction channel kinetics.
Gating spring stiffness and the gating swing after considering stimulation artifact
Our model follows the gating spring theory (11). Different from most other models, our model replaced the single degree of freedom (DOF) hair bundle mechanics with fully deformable 3-D FE models. The single DOF mechanical model assumes that all mechano-transduction units in a hair bundle respond in parallel (62). In our simulation performed under natural (ideal) conditions, the transduction channels in the bundle behave in parallel from a functional point of view (Fig. 2, B and D). However, in mammalian auditory hair cells, the channels do not respond uniformly when the hair bundle is stimulated by a nonconforming probe.
Because of the nonuniform deflection of hair bundles when stimulated with probes, using the single DOF hair bundle mechanical model to analyze experimental results leads to skewed estimates of key biophysical properties of hair-cell mechano-transduction. First, the hair bundle stiffness is underestimated. To date, the use of compliant microprobes is the only practical method to measure the F-X relationship of the hair bundle. From our results, uneven contact with the probe will result in underestimation of the physiological stiffness of the hair bundle (Figs. S3 and S4). In our simulated cases in Fig. 1, the nominal stiffness of hair bundle obtained from the probe simulations was smaller than the true stiffness by 45% (OHC) and by 83% (IHC). Unfortunately, this estimation depends highly on the congruence of the probe to the hair bundle, which may partly explain the wide variation in experimental measurements (e.g., Beurg et al. (28)). Second, the gating spring stiffness is underestimated. Our simulated OHC has the nominal stiffness of 2.6 mN/m when stimulated with the probe shown in Fig. 1, and it is reduced by 52% after the removal of tip links. If we apply single DOF bundle mechanics to this stiffness reduction, the gating spring stiffness is estimated to be 0.16 mN/m (kGS = 0.52∗kHB/γ/NTL, where NTL is the number of tip links and kHB is the nominal stiffness of hair bundle) as compared to the actual 4-mN/m value used by the model. Third, the gating swing is overestimated because of the underestimated gating spring stiffness and overestimated OR. The OR of our probe-stimulated OHC was ∼200 nm, which corresponds to the single channel gating force z = 4.4∗kBT/OR = 0.088 pN. From z = γkGSb, the estimated gating swing is 3.8 nm, which is approximately six times greater than the actual model value of 0.6 nm. The gating swing of our model is in agreement with the measured pore size of the mechano-transduction channel (63). Fourth, with uneven stimulations, the I-X relationship does not fit to a first-order Boltzmann equation. Because the modeled transducer channels have two configuration states, the I-X relationship should follow a first-order Boltzmann equation (Fig. 4 E). Our results suggest that the higher-order I-X relationship can be an artifact of imperfect stimulation and/or bundle splay, as was hypothesized in a recent review (1). To summarize, our results warn that analyzing the hair bundle mechano-transduction experimental results obtained from uneven stimulation using a single DOF hair bundle mechanical model can lead to incorrect biophysical property values.
Conditions for functional coherence
The FE model analyses showed that the stereocilia bundle can splay due to finite stiffness of the horizontal connectors (37), which results in graded tip link tension along the line of bilateral symmetry (38). According to the model analysis (37), the splay aggravates as the number of stereocilia rows increases. In contrast to the model analysis, experimental measurements with the bullfrog saccule hair bundles showed little splay between stereocilia rows (40,41). The discrepancy between the model analysis and the observation is not irreconcilable. As Cotton and Grant (37) showed, if the horizontal connector is at least one order-of-magnitude stiffer than the linear stiffness of a stereocilium, it can bind a pair of stereocilia tight enough to minimize the splay. Notably, instead of overengineering the horizontal connectors or inventing a remarkable binding mechanism, the mammalian cochlear hair cells seem to come up with a simple solution to achieve their high sensitivity—mechano-transduction channels arranged in parallel by minimizing the number of stereocilia rows.
In this work and in the previous works with similar FE models (27,28), functional coherence of the mechano-transduction channels (Figs. 3 and 4) were investigated in addition to mechanical coherence (Figs. 4 and 9). Mechanically, the stiffness of the horizontal connectors (kHC1 = 10 mN/m) in our FE models is sufficient (OHC) or marginal (IHC) to bind the three rows of stereocilia because a single IHC stereocilium was given greater stiffness than OHC stereocilium. This mechanical difference between the two hair bundle models resulted in different levels of functional coherence—the upper-row and the lower-row transduction channels are more strictly coherent in the OHC than in the IHC (the red and green curves in the bottom panel of Fig. 2, B and D). If a smaller kHC1 value is used, the OR increases, but a greater kHC1 value than this work hardly affects the OR (data not shown).
Our computational models and experiments with the cochlear hair cells do not provide an explicit explanation on how low-frequency hair cells’ stereocilia bundle achieves its mechanical coherence. Yet, we can speculate about those hair bundles’ coherence based on previous theoretical works (25,26,39). Stereocilia tightly packed in a hexagonal array with stronger horizontal connectors than those used in previous studies should be able to bind the bundle tight enough to secure the functional coherence. When we used a greater value of horizontal connectors for the hair-cell stereocilia bundle of the turtle utricle (kHC1 = kHC2 > 2 mN/m), the hair bundle could show spontaneous oscillations, which is evidence of the functional coherence (result not shown). A fundamental question ensues, however: Is the high sensitivity a universal virtue for all types of hair cells? For example, some type-II hair cells’ hair bundle in the turtle utricle (38,64) contrasts the mammalian cochlear hair-cell bundles in their stereocilia arrangement—their hair bundles have less than 5 columns and more than 10 rows of short stereocilia (<4 μm) attached to a lengthy kinocilium (>10 μm). It is likely that those hair cells are specialized for encoding a wide OR at the cost of low sensitivity, while type-I hair cells of the same organ are dedicated to high sensitivity (65).
Limitations of this study
The hair bundle stiffness of this work might be lower than the true value. The mechanical properties of these models were mostly from a previous study (28) with the exception of the stiffness and viscous damping values of horizontal connectors. In that study, the mechanical properties were estimated after assuming the ideal stimulating condition. Unless the probe tip shapes and their contacting condition with hair bundles are known, it is difficult to estimate the true stiffness. To better estimate the hair bundle stiffness, custom-fabricated probes can be used to assure even contact with the tallest row of stereocilia (18).
This computational study did not analyze another popular method of hair bundle stimulation—fluid-jet. A recent work (35) speculated that the modes of stimulation (probe or fluid-jet) can cause differences in hair-cell adaptation. Fluid-jet methods have the merit of stimulating the hair bundle more evenly, an important feature described by this work. While the probe method is intuitive and straightforward for calculating the force delivered to the hair bundle, in order to estimate the amplitude of applied force/pressure, the fluid-jet method will require a careful calibration of fluid velocity and analysis of fluid dynamics. This study does not include such fluid dynamics analysis. Instead, the viscous drag of the hair bundle due to fluid was represented by the viscous damping of the stereocilia. Therefore, with these results, we cannot compare the two methods. That said, two general statements can be made on the fluid-jet stimulation based on our experimental results (Fig. 3). 1) If the fluid-jet mouth size is comparable to or smaller than the hair bundle width, the stimulation will be localized; and 2) the flow pattern of the fluid-jet (a plug flow) will be different from the natural shear flow developing linearly along the hair bundle height.
Author Contributions
J.-H.N. and A.J.R. designed the research; J.-H.N. performed computational simulations; A.W.P. and A.J.R. performed the experiments; J.-H.N., A.W.P., and A.J.R. analyzed the data; and J.-H.N., A.W.P., and A.J.R. wrote the article.
Acknowledgments
We thank the students of the 2014 Stanford Intensive Neuroscience class for help collecting some of the imaging data.
This work was supported by National Science Foundation grant No. CMMI 1233595 (to J.-H.N.), and National Institutes of Health grants No. NIDCD K99 DC013299 (to A.W.P.), and No. NIDCD DC003896 (to A.J.R.).
Editor: Markus Deserno.
Footnotes
This is an open access article under the CC BY-NC-ND license (http://creativecommons.org/licenses/by-nc-nd/4.0/).
Supporting Material
References
- 1.Fettiplace R., Kim K.X. The physiology of mechanoelectrical transduction channels in hearing. Physiol. Rev. 2014;94:951–986. doi: 10.1152/physrev.00038.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Hudspeth A.J. Integrating the active process of hair cells with cochlear function. Nat. Rev. Neurosci. 2014;15:600–614. doi: 10.1038/nrn3786. [DOI] [PubMed] [Google Scholar]
- 3.Goodyear R.J., Marcotti W., Richardson G.P. Development and properties of stereociliary link types in hair cells of the mouse cochlea. J. Comp. Neurol. 2005;485:75–85. doi: 10.1002/cne.20513. [DOI] [PubMed] [Google Scholar]
- 4.Hackney C.M., Furness D.N. The composition and role of cross links in mechanoelectrical transduction in vertebrate sensory hair cells. J. Cell Sci. 2013;126:1721–1731. doi: 10.1242/jcs.106120. [DOI] [PubMed] [Google Scholar]
- 5.Beurg M., Fettiplace R., Ricci A.J. Localization of inner hair cell mechanotransducer channels using high-speed calcium imaging. Nat. Neurosci. 2009;12:553–558. doi: 10.1038/nn.2295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Verpy E., Leibovici M., Petit C. Stereocilin connects outer hair cell stereocilia to one another and to the tectorial membrane. J. Comp. Neurol. 2011;519:194–210. doi: 10.1002/cne.22509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Lim D.J. Cochlear anatomy related to cochlear micromechanics. A review. J. Acoust. Soc. Am. 1980;67:1686–1695. doi: 10.1121/1.384295. [DOI] [PubMed] [Google Scholar]
- 8.Billone M., Raynor S. Transmission of radial shear forces to cochlear hair cells. J. Acoust. Soc. Am. 1973;54:1143–1156. doi: 10.1121/1.1914361. [DOI] [PubMed] [Google Scholar]
- 9.Freeman D.M., Weiss T.F. The role of fluid inertia in mechanical stimulation of hair cells. Hear. Res. 1988;35:201–207. doi: 10.1016/0378-5955(88)90118-9. [DOI] [PubMed] [Google Scholar]
- 10.Ghaffari R., Aranyosi A.J., Freeman D.M. Longitudinally propagating traveling waves of the mammalian tectorial membrane. Proc. Natl. Acad. Sci. USA. 2007;104:16510–16515. doi: 10.1073/pnas.0703665104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Howard J., Hudspeth A.J. Compliance of the hair bundle associated with gating of mechanoelectrical transduction channels in the bullfrog’s saccular hair cell. Neuron. 1988;1:189–199. doi: 10.1016/0896-6273(88)90139-0. [DOI] [PubMed] [Google Scholar]
- 12.Ashmore J., Avan P., Canlon B. The remarkable cochlear amplifier. Hear. Res. 2010;266:1–17. doi: 10.1016/j.heares.2010.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ricci A.J., Crawford A.C., Fettiplace R. Active hair bundle motion linked to fast transducer adaptation in auditory hair cells. J. Neurosci. 2000;20:7131–7142. doi: 10.1523/JNEUROSCI.20-19-07131.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kennedy H.J., Crawford A.C., Fettiplace R. Force generation by mammalian hair bundles supports a role in cochlear amplification. Nature. 2005;433:880–883. doi: 10.1038/nature03367. [DOI] [PubMed] [Google Scholar]
- 15.Robles L., Ruggero M.A. Mechanics of the mammalian cochlea. Physiol. Rev. 2001;81:1305–1352. doi: 10.1152/physrev.2001.81.3.1305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Stauffer E.A., Holt J.R. Sensory transduction and adaptation in inner and outer hair cells of the mouse auditory system. J. Neurophysiol. 2007;98:3360–3369. doi: 10.1152/jn.00914.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lelli A., Asai Y., Géléoc G.S. Tonotopic gradient in the developmental acquisition of sensory transduction in outer hair cells of the mouse cochlea. J. Neurophysiol. 2009;101:2961–2973. doi: 10.1152/jn.00136.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Peng A.W., Effertz T., Ricci A.J. Adaptation of mammalian auditory hair cell mechanotransduction is independent of calcium entry. Neuron. 2013;80:960–972. doi: 10.1016/j.neuron.2013.08.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Johnson S.L., Beurg M., Fettiplace R. Prestin-driven cochlear amplification is not limited by the outer hair cell time constant. Neuron. 2011;70:1143–1154. doi: 10.1016/j.neuron.2011.04.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Crawford A.C., Fettiplace R. The mechanical properties of ciliary bundles of turtle cochlear hair cells. J. Physiol. 1985;364:359–379. doi: 10.1113/jphysiol.1985.sp015750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ricci A.J., Fettiplace R. The effects of calcium buffering and cyclic AMP on mechano-electrical transduction in turtle auditory hair cells. J. Physiol. 1997;501:111–124. doi: 10.1111/j.1469-7793.1997.111bo.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ricci A.J., Fettiplace R. Calcium permeation of the turtle hair cell mechanotransducer channel and its relation to the composition of endolymph. J. Physiol. 1998;506:159–173. doi: 10.1111/j.1469-7793.1998.159bx.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ricci A.J., Crawford A.C., Fettiplace R. Tonotopic variation in the conductance of the hair cell mechanotransducer channel. Neuron. 2003;40:983–990. doi: 10.1016/s0896-6273(03)00721-9. [DOI] [PubMed] [Google Scholar]
- 24.Cotton J.R., Grant J.W. A finite element method for mechanical response of hair cell ciliary bundles. J. Biomech. Eng. 2000;122:44–50. doi: 10.1115/1.429626. [DOI] [PubMed] [Google Scholar]
- 25.Nam J.H., Cotton J.R., Grant W. A virtual hair cell, I: addition of gating spring theory into a 3-D bundle mechanical model. Biophys. J. 2007;92:1918–1928. doi: 10.1529/biophysj.106.085076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Nam J.H., Cotton J.R., Grant W. A virtual hair cell, II: evaluation of mechanoelectric transduction parameters. Biophys. J. 2007;92:1929–1937. doi: 10.1529/biophysj.106.085092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Nam J.H., Fettiplace R. Theoretical conditions for high-frequency hair bundle oscillations in auditory hair cells. Biophys. J. 2008;95:4948–4962. doi: 10.1529/biophysj.108.138560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Beurg M., Nam J.H., Fettiplace R. The actions of calcium on hair bundle mechanics in mammalian cochlear hair cells. Biophys. J. 2008;94:2639–2653. doi: 10.1529/biophysj.107.123257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Roth B., Bruns V. Postnatal development of the rat organ of Corti. II. Hair cell receptors and their supporting elements. Anat. Embryol. (Berl.) 1992;185:571–581. doi: 10.1007/BF00185616. [DOI] [PubMed] [Google Scholar]
- 30.Santi P.A., Anderson C.B. A newly identified surface coat on cochlear hair cells. Hear. Res. 1987;27:47–65. doi: 10.1016/0378-5955(87)90025-6. [DOI] [PubMed] [Google Scholar]
- 31.Dolgobrodov S.G., Lukashkin A.N., Russell I.J. Electrostatic interaction between stereocilia: II. Influence on the mechanical properties of the hair bundle. Hear. Res. 2000;150:94–103. doi: 10.1016/s0378-5955(00)00196-9. [DOI] [PubMed] [Google Scholar]
- 32.Sun M., Graham J.S., Grandbois M. Multiple membrane tethers probed by atomic force microscopy. Biophys. J. 2005;89:4320–4329. doi: 10.1529/biophysj.104.058180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Indzhykulian A.A., Stepanyan R., Frolenkov G.I. Molecular remodeling of tip links underlies mechanosensory regeneration in auditory hair cells. PLoS Biol. 2013;11:e1001583. doi: 10.1371/journal.pbio.1001583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Söllner C., Rauch G.J., Nicolson T. Mutations in cadherin 23 affect tip links in zebrafish sensory hair cells. Nature. 2004;428:955–959. doi: 10.1038/nature02484. [DOI] [PubMed] [Google Scholar]
- 35.Corns L.F., Johnson S.L., Marcotti W. Calcium entry into stereocilia drives adaptation of the mechanoelectrical transducer current of mammalian cochlear hair cells. Proc. Natl. Acad. Sci. USA. 2014;111:14918–14923. doi: 10.1073/pnas.1409920111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Shepherd G.M., Corey D.P. The extent of adaptation in bullfrog saccular hair cells. J. Neurosci. 1994;14:6217–6229. doi: 10.1523/JNEUROSCI.14-10-06217.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Cotton J., Grant W. Computational models of hair cell bundle mechanics: II. Simplified bundle models. Hear. Res. 2004;197:105–111. doi: 10.1016/j.heares.2004.06.005. [DOI] [PubMed] [Google Scholar]
- 38.Silber J., Cotton J., Grant W. Computational models of hair cell bundle mechanics: III. 3-D utricular bundles. Hear. Res. 2004;197:112–130. doi: 10.1016/j.heares.2004.06.006. [DOI] [PubMed] [Google Scholar]
- 39.Nam J.H., Cotton J.R., Grant W. Mechanical properties and consequences of stereocilia and extracellular links in vestibular hair bundles. Biophys. J. 2006;90:2786–2795. doi: 10.1529/biophysj.105.066027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Kozlov A.S., Risler T., Hudspeth A.J. Coherent motion of stereocilia assures the concerted gating of hair-cell transduction channels. Nat. Neurosci. 2007;10:87–92. doi: 10.1038/nn1818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Karavitaki K.D., Corey D.P. Sliding adhesion confers coherent motion to hair cell stereocilia and parallel gating to transduction channels. J. Neurosci. 2010;30:9051–9063. doi: 10.1523/JNEUROSCI.4864-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Langer M.G., Fink S., Ruppersberg J.P. Lateral mechanical coupling of stereocilia in cochlear hair bundles. Biophys. J. 2001;80:2608–2621. doi: 10.1016/s0006-3495(01)76231-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Karavitaki K.D., Niksch P.D., Corey D.P. Weak lateral coupling between stereocilia of mammalian hair cells requires new stimulus methods to study the biomechanics of hearing. J. Acoust. Soc. Am. 2013;133:3509. [Google Scholar]
- 44.Kozlov A.S., Baumgart J., Hudspeth A.J. Forces between clustered stereocilia minimize friction in the ear on a subnanometer scale. Nature. 2011;474:376–379. doi: 10.1038/nature10073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Furness D.N., Mahendrasingam S., Hackney C.M. The dimensions and composition of stereociliary rootlets in mammalian cochlear hair cells: comparison between high- and low-frequency cells and evidence for a connection to the lateral membrane. J. Neurosci. 2008;28:6342–6353. doi: 10.1523/JNEUROSCI.1154-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Corey D.P., Hudspeth A.J. Kinetics of the receptor current in bullfrog saccular hair cells. J. Neurosci. 1983;3:962–976. doi: 10.1523/JNEUROSCI.03-05-00962.1983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Lelli A., Kazmierczak P., Holt J.R. Development and regeneration of sensory transduction in auditory hair cells requires functional interaction between cadherin-23 and protocadherin-15. J. Neurosci. 2010;30:11259–11269. doi: 10.1523/JNEUROSCI.1949-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Kennedy H.J., Evans M.G., Fettiplace R. Fast adaptation of mechanoelectrical transducer channels in mammalian cochlear hair cells. Nat. Neurosci. 2003;6:832–836. doi: 10.1038/nn1089. [DOI] [PubMed] [Google Scholar]
- 49.Eatock R.A., Corey D.P., Hudspeth A.J. Adaptation of mechanoelectrical transduction in hair cells of the bullfrog’s sacculus. J. Neurosci. 1987;7:2821–2836. doi: 10.1523/JNEUROSCI.07-09-02821.1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Assad J.A., Hacohen N., Corey D.P. Voltage dependence of adaptation and active bundle movement in bullfrog saccular hair cells. Proc. Natl. Acad. Sci. USA. 1989;86:2918–2922. doi: 10.1073/pnas.86.8.2918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Assad J.A., Corey D.P. An active motor model for adaptation by vertebrate hair cells. J. Neurosci. 1992;12:3291–3309. doi: 10.1523/JNEUROSCI.12-09-03291.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Stauffer E.A., Scarborough J.D., Gillespie P.G. Fast adaptation in vestibular hair cells requires myosin-1c activity. Neuron. 2005;47:541–553. doi: 10.1016/j.neuron.2005.07.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Nadrowski B., Martin P., Jülicher F. Active hair-bundle motility harnesses noise to operate near an optimum of mechanosensitivity. Proc. Natl. Acad. Sci. USA. 2004;101:12195–12200. doi: 10.1073/pnas.0403020101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Tinevez J.Y., Jülicher F., Martin P. Unifying the various incarnations of active hair-bundle motility by the vertebrate hair cell. Biophys. J. 2007;93:4053–4067. doi: 10.1529/biophysj.107.108498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Gao S.S., Wang R., Oghalai J.S. Vibration of the organ of Corti within the cochlear apex in mice. J. Neurophysiol. 2014;112:1192–1204. doi: 10.1152/jn.00306.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Rhode W.S., Geisler C.D. Model of the displacement between opposing points on the tectorial membrane and reticular lamina. J. Acoust. Soc. Am. 1967;42:185–190. doi: 10.1121/1.1910547. [DOI] [PubMed] [Google Scholar]
- 57.Dallos P. Organ of Corti kinematics. J. Assoc. Res. Otolaryngol. 2003;4:416–421. doi: 10.1007/s10162-002-3049-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Nam J.H., Fettiplace R. Force transmission in the organ of Corti micromachine. Biophys. J. 2010;98:2813–2821. doi: 10.1016/j.bpj.2010.03.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Chen F., Zha D., Nuttall A.L. A differentially amplified motion in the ear for near-threshold sound detection. Nat. Neurosci. 2011;14:770–774. doi: 10.1038/nn.2827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.He D.Z., Jia S., Dallos P. Mechanoelectrical transduction of adult outer hair cells studied in a gerbil hemicochlea. Nature. 2004;429:766–770. doi: 10.1038/nature02591. [DOI] [PubMed] [Google Scholar]
- 61.Jia S., Dallos P., He D.Z. Mechanoelectric transduction of adult inner hair cells. J. Neurosci. 2007;27:1006–1014. doi: 10.1523/JNEUROSCI.5452-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Hudspeth A.J., Choe Y., Martin P. Putting ion channels to work: mechanoelectrical transduction, adaptation, and amplification by hair cells. Proc. Natl. Acad. Sci. USA. 2000;97:11765–11772. doi: 10.1073/pnas.97.22.11765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Pan B., Waguespack J., Ricci A.J. Permeation properties of the hair cell mechanotransducer channel provide insight into its molecular structure. J. Neurophysiol. 2012;107:2408–2420. doi: 10.1152/jn.01178.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Xue J., Peterson E.H. Hair bundle heights in the utricle: differences between macular locations and hair cell types. J. Neurophysiol. 2006;95:171–186. doi: 10.1152/jn.00800.2005. [DOI] [PubMed] [Google Scholar]
- 65.Spoon C., Moravec W.J., Peterson E.H. Steady-state stiffness of utricular hair cells depends on macular location and hair bundle structure. J. Neurophysiol. 2011;106:2950–2963. doi: 10.1152/jn.00469.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


