Patterns of Intersecting Fiber Arrays Revealed in Whole Muscle with Generalized Q-Space Imaging

Abstract

The multiscale attributes of mammalian muscle confer significant challenges for structural imaging in vivo. To achieve this, we employed a magnetic resonance method, termed “generalized Q-space imaging”, that considers the effect of spatially distributed diffusion-weighted magnetic field gradients and diffusion sensitivities on the morphology of Q-space. This approach results in a subvoxel scaled probability distribution function whose shape correlates with local fiber orientation. The principal fiber populations identified within these probability distribution functions can then be associated by streamline methods to create multivoxel tractlike constructs that depict the macroscale orientation of myofiber arrays. We performed a simulation of Q-space input parameters, including magnetic field gradient strength and direction, diffusion sensitivity, and diffusional sampling to determine the optimal achievable fiber angle separation in the minimum scan time. We applied this approach to resolve intravoxel crossing myofiber arrays in the setting of the human tongue, an organ with anatomic complexity based on the presence of hierarchical arrays of intersecting myocytes. Using parameters defined by simulation, we imaged at 3T the fanlike configuration of the human genioglossus and the laterally positioned merging fibers of the styloglossus, inferior longitudinalis, chondroglossus, and verticalis. Comparative scans of the excised mouse tongue at 7T demonstrated similar midline and lateral crossing fiber patterns, whereas histological analysis confirmed the presence and distribution of these myofiber arrays at the microscopic scale. Our results demonstrate a magnetic resonance method for acquiring and displaying diffusional data that defines highly ordered myofiber patterns in architecturally complex tissue. Such patterns suggest inherent multiscale fiber organization and provide a basis for structure-function analyses in vivo and in model tissues.

Introduction

Methods are necessary to unravel the exceedingly complex anatomical elements of human neuromuscular tissue. The development of such methods has been a long-standing problem, largely due to the fact that mammalian muscle embodies complex and hierarchical organizational features (1). Understanding how physical properties such as size, shape, and local mechanics affect muscular tissue organization (myoarchitecture) is a fundamental step in deciphering the underlying design of biological materials (2,3). Moreover, because muscular tissue is multiscale in terms of organization, imaging techniques that depict such organization must be capable of bridging the microscale of contractile myofibers to the macroscale of the functional organ.

The myoarchitecture of intact tissue may be determined in terms of spatially delimited molecular diffusivity employing a magnetic resonance (MR) imaging method that considers the random translational motion of protons under the influence of physical and chemical barriers. Restricted proton diffusion is a stochastic process at the molecular scale that may be used to probe the directionality of fibers or fiberlike structures in tissue (4,5). Such directionality reflects the heterogeneity of the diffusional milieu and is a consequence principally of physical obstacles created by membranes and myofilaments within aligned cellular compartments (6,7). During diffusion-weighted MR imaging, magnetic field gradients of varying magnitudes and orientations are applied in order to define macroscopic anisotropy (8). Methods have been proposed to derive fiber orientation from diffusivity resolved at the voxel scale, such as diffusion tensor imaging (4,9,10), or multiple compartment models (11,12), and those resolved at the subvoxel scale, such as Q-ball imaging (13) and diffusion spectrum imaging (14–18). Voxel-scale analysis, however, does not accurately portray crossing or diverging fiber geometries (15,18,19), whereas subvoxel scale analysis conventionally requires exceedingly long imaging times, and is thus impractical for in vivo imaging of muscular organs.

We present an approach, employing concepts of generalized Q-space imaging (GQI), which incorporates optimal magnetic gradient properties, diffusion times, and Q-space morphologies in order to resolve complex geometric patterns in whole organs. Such imaging employs elementary theories of molecular diffusivity to depict the highly ordered and multiscale features of muscular organization in situ. To demonstrate this capacity, we elected to study the human tongue, an organ that embodies anatomical complexity epitomized by crossing fibers at the voxel scale. The lingual musculature consists of geometrically interrelated myocytes (20,21), defined simultaneously at the microscopic (single fiber), mesoscopic (multifiber arrays), and macroscopic (tissue) scales (22,23). Moreover, the tongue falls into a class of organs known as muscular hydrostats, which possess fiber populations aligned at the macroscopic scale that are both perpendicular and parallel with the object’s longitudinal axis (24–26). The lingual musculature is comprised of intrinsic and extrinsic fibers (27,28), which intricately merge in order to modify shape, tension, and position during the course of physiological motions, such as speech or swallowing. We demonstrate the capacity of GQI to resolve complex fiber patterns through simulations of fiber-angle separation and demonstration of intersecting fiber patterns exhibited by the tongue ex vivo (mouse) and in vivo (human).

Materials and Methods

Theory underlying the use of generalized GQI to depict restricted proton diffusion

Restricted nuclear magnetic resonance (NMR) diffusion can be used to resolve anisotropy at a spatial scale considerably smaller than the conventional three-dimensional imaging unit (voxel) (4,29,30). If the voxel contains physical barriers, then restricted diffusion occurs as a measurable subvoxel phenomenon (4,7,29). Restricted diffusion in the biological realm reflects the aggregate effect of direction-specific physical and chemical impediments to translational motion. From a practical perspective, anisotropic diffusivity may be used to infer the presence of subvoxel scaled populations of oriented fibers. The methodology most commonly used in diffusion-weighted MR imaging is pulsed field gradients (PFG (31)). By this method, a pair of diffusion sensitizing PFG are employed, of magnitude and direction G and duration δ, and separated by a diffusion period Δ. In the classic diffusion experiment, the pulsed-gradient spin echo pulse sequence, a diffusion block, defined by Δ, is inserted (8,11,31). For this, an initial PFG encodes protons in a manner that results in spatially acquired phase, followed by a second PFG at 180° to the first, in order to entirely refocus the acquired phase. Protons that are entirely stationary acquire zero net phase, resulting in no MR signal attenuation, whereas diffusing, i.e., nonstationary, protons acquire net phase, leading to phase dispersion and signal attenuation. The presence of a barrier to diffusion, as might occur in the instance of a cell membrane or a nonrandomly positioned cytoskeletal element, results in an alteration of diffusion signal attenuation in a given direction. Such attenuation is determined through the effects of geometrically defined magnetic field gradients. This effect modifies the distribution of diffusivity per voxel and the resulting probability distribution function for diffusivity. The underlying assumption is that higher B values allow an evaluation of increased diffusion lengths, and thereby increased barrier discrimination, but at the price of higher signal attenuation and reduced signal/noise. Increasing the number of gradient directions enhances the detection of angular separation without the imposition of a signal attenuation factor, but requires longer scan times. The process of optimization incorporates the determination of the most appropriate number of gradient directions, the minimum B value, and Q-space morphology (segmented, shell) for a target angular separation defined by the underlying anatomy, and was obtained through the simulation process detailed below. While this process was carried out in the case of the human tongue, this approach is applicable for any muscular organ or material containing anisotropic components.

Simulation of GQI experiments

Diffusion imaging is sensitive to the environment, and can be understood by basic diffusion equations. The diffusion process is explained by the kinetic energy in molecules, as related by the Stokes-Einstein equation. The diffusion process, D, thus defined varies linearly with the temperature, and is inversely related to the viscosity and the Stokes radius, as

$$D=\frac{k_{\text{B}}T}{6\pi \ast \eta r},$$

where k_B is the Boltzmann constant, T is temperature, η is viscosity of the fluid, and r is the Stokes radius of the diffusing solute. The observed diffusion signal, S₁, is quantitatively related to the measured MR-signal magnitude without diffusion, S₀, and the impact of the diffusion sensitizing B value, as S₁ = S₀e^−bD (4,11,12). The B value is related to the MR pulse sequence as b = (γGδ)²τ by the G and δ, the strength and duration of the diffusion-encoding magnetic field gradient, respectively, where the effective diffusion time is τ = (Δ − δ/3 ) and the gyromagnetic ratio of protons is γ (11).

In physically complex biological specimens, the observed diffusion signal is explained by the presence of anisotropic diffusion-restricting elements along with isotropic elements, resulting in a bi-Gaussian diffusion signal with slow and fast components (12,31,32). Assaf et al. (32) modeled this behavior as a multiexponential curve in the setting of structurally heterogeneous tissues, i.e., tissues containing multiple diverging fiber populations. Accordingly, we implemented a GQI simulation based on a multiple Gaussian diffusion model with an isotropic element and two anisotropic fiber populations and varying degrees of imposed angular separation (30,33). Defining geometric precision in terms of the smallest angular separation achievable, these simulations generated model fibers with specific crossing angles (angular deviations at 5° increments, n = 6 for each trial) and then determined the MR imaging conditions, i.e., B value and gradient directions, necessary to resolve this degree of separation. The variations of imaging parameters included B₀ signal/noise = 40, fractional anisotropy (FA) = 0.6, gradient directions of 64, 128, 256, or 512, and B values from 750 to 3000 s/mm². Because FA is not known for tongue muscle, we selected a value that implies greater diffusional restriction compared to the skeletal muscles of young adults (34) or the developing chicken hind limbs (35), and intermediate to the range of FA values in the human brain (11). The MR diffusion signal, S(b,v) was generated as a function of the multiple elements as

$$S\left(b,\mathbf{v}\right)=S\left(0\right)\left(f_1{e}^{-b{\mathbf{v}}^{\tau }{D}_1\mathbf{v}}+f_2{e}^{-b{\mathbf{v}}^{\tau }{D}_2\mathbf{v}}+f_0{e}^{-b{\mathbf{v}}^{\tau }{D}_0\mathbf{v}}\right),$$

with b and v as the B value and the unit vector of the applied diffusion gradient, respectively.

S(0) is signal intensity without diffusion weighting, f₁ and f₂ the volume fraction of the two fiber populations, and f₀ is the volume fraction of the isotropic diffusion elements. D₀, D₁, and D₂ are the diffusion element matrices for these three diffusion components. Under these conditions, mean diffusivity is 1.0^∗10⁻³ mm²/s, with Rician noise added (33). This value is similar to those values obtained from rabbit hind limbs (36) and the anterior tibialis and soleus muscles in healthy volunteers (37), but lower than those determined previously in lingual tissue (10).

Data reconstruction and probability distribution function (PDF) generation

Datasets were reconstructed using GQI methods resulting in voxel-specific PDF generation. The PDF is derived from the diffusion-weighted image data by multiplying a three-dimensional orientation function with the spin density. The spin density is derived from the Fourier transform of the diffusion-weighted image data, theoretically consisting of a diffusion average propagator in the diffusion time Δ and a spin density function. The three-dimensional orientation function defines the shape of the PDF, and is determined from |q|^∗LΔ with the q value and the sampling length, LΔ. The q value is defined by the gyromagnetic ratio of protons, γ, gradient strength, G, and gradient direction, δ, as q = γGδ/2π. We assume a specific sampling length during reconstruction of LΔ, where LΔ = σ^∗6(Dτ)^1/2 and σ describes diffusion distribution. Diffusion length is equivalent to 6(Dτ)^1/2, assuming that the underlying diffusion follows a Gaussian distribution, where D is the diffusion coefficient and τ is the effective diffusion time (30). Given these assumptions, we can replace τ with a B value corresponding to the sampling time commonly used during diffusion-weighted MRI (33), which infers the capacity to probe subvoxel diffusional barriers and fiber direction (5,29). The diffusion time Δ was set as 80 ms (diffusion length = 32 μm), and the diffusion distribution factor, σ, was set to 1.25, in order to encompass 80% of the diffusion distribution under Gaussian conditions, with q values estimated from the B values by assuming that the diffusion gradient duration δ is 35 ms and that the MR signals are obtained using a standard pulse-gradient spin-echo pulse sequence (33).

Generation of multivoxel tractography

Tract generation was carried out for each simulation, using a subvoxel trilinear streamlining algorithm under Eulerian integration, modified to make use of multiple fiber orientations (19,33). Quantitative anisotropy-weighted maxima calculated for each PDF were displayed as a simplified two-dimensional anisotropy map, demonstrating the presence of two populations of the fibers in a voxel, where the direction of fibers is color-coded in three dimensions. Voxelwise selection of a particular PDF into a user-defined region of interest (ROI) was completed in individual slices using the anisotropy map, and in three dimensions with the EPI B = 0 images. Tracts were selectively generated that intersect a ROI through demonstrated intervoxel coherence fixed within a range of ±17.5° from PDF maxima, selected based on past studies, and as has been substantively validated with correlation to microscopic imaging methods (14,38). Tracts that intersected the ROI were displayed and generated from uniformly distributed seeding points within each voxel of the dataset.

Multiscale geometric resolution

While GQI resolution is related to the minimum achievable voxel size through its associated signal/noise, geometric resolution is defined by the smallest angular separation discernable within the structure of the diffusional PDF. The morphology of the PDF is indicative of the underlying anisotropic fibrous elements, and is a composite of diffusion signals in terms of the diffusion-sensitizing B values measured in multiple directions. Angular separation so defined forms the underlying construct of the myofiber tract (mesoscale) obtained during streamlining, linking PDF diffusional maxima from one voxel to neighboring voxels. Tract coherence is, in turn, dependent upon voxel-scale angular resolution and the allowable tract generation angle, and has been validated through histological comparison (16,17,39) and microscopic correlation (14,38).

In vivo imaging with GQI

MR scanning of the human tongue was approved by the Human Subject Research Protection Committee of Northeastern University. MR scanning was conducted on a Skyra 3T (Siemens Medical Systems, Erlangen, Germany) at Brigham and Women’s Hospital. Twenty normal subjects were scanned in supine position with an 18-channel head and neck coil for signal amplification. We employed a twice-refocused spin-echo diffusion pulse sequence to reduce eddy current distortions (10,40). The pulse sequence incorporated standard single-shot EPI spatial encoding. The overall scan time varied (4–40 min for complete scan) as a function of the explicit imaging parameters used, including gradient direction (64, 128, or 256), B value (750–3000 s/mm²), and axial slice thickness (2.5–4 mm). For example, scans utilizing 256 diffusion-sensitizing gradient directions, 1.7 × 1.7 × 4 mm voxel size, and a B value of 750 s/mm² required ∼14.2 min of scan time. Assuming that Q-space is symmetrical, i.e., perpendicular fibers enter and exit the voxel at the same angle, we tested the validity of a hemispherical Q-space morphology in order to further decrease scan time. Accordingly, the use of 128 hemispherical gradient directions provided similar angular resolution to 256 gradient directions, at half the scan time, that is, 7.1 min (albeit at lower signal, due to fewer overall scans). Image reconstruction was conducted in diffusion spectrum imaging using the software DSI STUDIO (DSI Studio; http://dsi-studio.labsolver.org) using GQI methods (33). As noted above, GQI is a mathematical reduction that combines the Fourier transform and calculation of the PDF from the spin density function, a unified reference comparing the voxelwise coordinate and diffusion displacement in order to enable quantitative comparisons. Ten echo-planar images (EPI) were also acquired at B = 0 during this time for image thresholding and utilized as an overlay during ROI analysis. Analysis of the PDF and tract generation was carried out similar to the above-noted simulations.

Muscle fiber patterns and skeletal insertion sites were compared with those obtained from the Visible Human Project dataset, a publicly accessible set of anatomic images obtained from one male and one female cadaver by the University of Colorado (Dr. Victor Spitzer) on contract from the National Library of Medicine (Bethesda, MD). Reconstruction of the axial slices from the visible human project into sagittal was performed using the Visible Human Server at the Ecole Polytechnique Fédérale de Lausanne (Lausanne, Switzerland) at the Peripheral Systems Lab under the direction of Professor R.D. Hersch.

Microscopic validation of GQI tractography in an excised mouse tongue

To define the microscopic determinants of GQI, we observed comparative fiber direction in multiple sagittal slices (38). Employing wild-type CD-1 mice, the lower jaw was excised, skinned, and immersed into low MR-signal fluorinated Krytox oil (Dupont, Wilmington, DE). Imaging experiments were conducted at 7 Tesla using the Bruker Biospec USR equipped with the CryoProbe (Bruker, Billerica, MA) and utilizing closed-cycle radio-frequency coil refrigeration. MR scanning was accomplished by a multishot echo-planar pulse sequence with the following imaging parameters: 512 gradient directions, B value of 750 s/mm², 8 k-space segments, and voxel size of 125 × 125 × 500 μm, for a total scan time of 8 h/tongue (n = 5 tongues). The resulting PDF was assessed to discern the orientation and magnitude of the dominant fiber populations, with the three-dimensional directionality of the fiber populations encoded by a red-green-blue scale. Intervoxel fiber tracts were constructed based on the alignment of the maximal diffusion vectors in the PDF in each voxel employing streamlines. To assess microscopic features, the tongue was fixed in neutral buffered formalin, embedded in paraffin, sectioned at 6 μm, and stained with hematoxylin and eosin. These techniques were used to minimize distortion that may occur during histological preparation and were performed by the Harvard Medical School Rodent Histopathology Core facility to ensure the fidelity of the anatomy imaged.

Results

GQI relates the diffusion signal to molecular displacement through the Fourier transform. Q-space is a convention for representing MR image data derived from proton diffusion in the frequency and spatial domains (9,41). Extending prior results (13,15,33,39), computational simulations of GQI depicted the local diffusional milieu, specifically demonstrating net angular resolution in Q-space in terms of the number and size of facets on the surface of a model unit sphere (Fig. 1 a), as well as a set of directionally color-coded gradient vectors, with vector-length scaled to their B value (Fig. 1 b).

Figure 1.

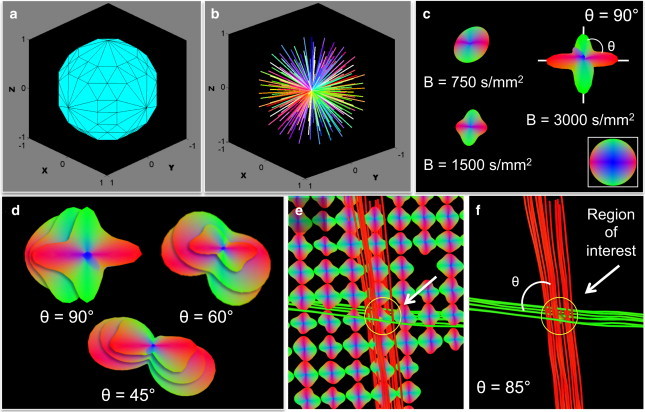
Visualization of angular separation with GQI in model Q-space. (a) Q-space shown (256 gradient directions) as a spherical coordinate system depicting facet size and field orientation. (b) Visualization of Q-space as a set of directionally color-coded gradient vectors, with vector-length scaled to B value. (c) PDF encompassing the intensities and directions of proton diffusion, displaying angular resolution as a function of increasing diffusion sensitization (B = 750, 1500, and 3000 s/mm²). Myoarchitecture resolved by crossing fibers as indicated by θ on the PDF shown where lobes correspond to principle fiber directions (θ = 90°). (d) PDF shape defined at angular separations (45°, 60°, and 90°) and increasing B values (750, 1500, and 3000 s/mm²) and B-max shell morphology. The PDF was employed as a template for tract generation employing a streamlining algorithm (e), resulting in demonstrated angular resolution of crossing tracts (f).

The multiscale attributes of myoarchitecture were demonstrated on the basis of diffusional data represented at the subvoxel, voxel, and multivoxel scales. The principal quantitative outcome of GQI is a local PDF for diffusivity, a unique descriptor of fiber organization per voxel (Fig. 1 c (33)). The shape of the PDF represents the subvoxel distribution of fiber populations and corresponds with local myoarchitecture. Resolution of the angle between two or more crossing fiber populations in a voxel was determined with a set of diffusional input parameters. The effect of increasing diffusion sensitization on the angular resolution of crossing fibers (θ = 90° in this example) is depicted in Fig. 1 c, with B value varied from 750 s/mm² to 3000 s/mm². A similar effect was observed, assuming an initial simulated angle of 45° and 60°, as shown in Fig. 1 d, through the attributes of the PDF. Multivoxel features were imaged through tractography, where principal fiber directions obtained from PDF maxima in adjacent voxels were associated via a streamlining algorithm to generate multivoxel myofiber tracts (Fig. 1, e and f). Greater B values resulted in improved angular resolution and improved discrimination of myofiber tracts at lower degrees of angular separation (i.e., θ < 90°). Modifying the representation of Q-space may refine the diffusion space sampling. Model Q-space formats are shown in Fig. 2, employing a single B value (shell format) or an array of diminishing B values from a designated maximum (segmented format). Further distinction of the Q-space sampling scheme can be made, i.e., full sphere or hemisphere, where the B vectors are assumed to be symmetrical over the Z axis. Rather than relating enhanced angular discrimination solely to diffusion sensitivity, GQI optimizes the detection of angular separation together with net scan time through the matching of the number and morphology of gradient directions and B values from a derivative set of coordinates on a model sphere.

Figure 2.

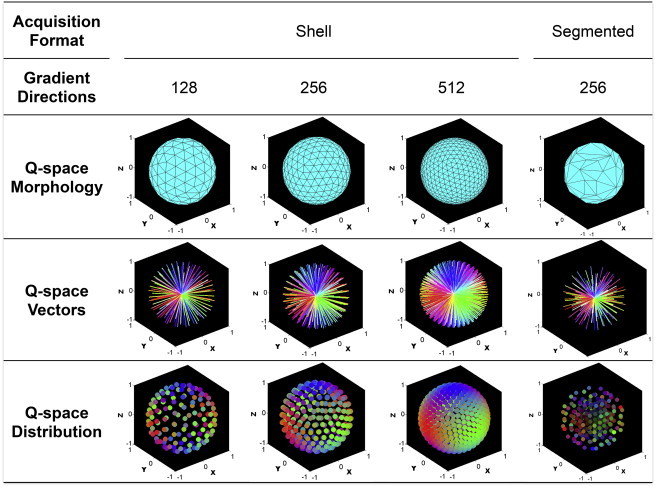
Q-space parameters applied for image optimization. Examples of four magnetic gradient schemas, created by varying the number and distribution of magnetic field gradients, method of acquisition, and morphology of Q-space (Q-space vectors are color-coded to show fiber angle distribution scaled to relative B value). Statistically uniform spacing of Q-space distributions were obtained through iterative repulsion to optimize spacing over the spherical shell, with 128, 256, and 512 gradient directions shown. The shell distribution provides the greatest angular resolution, with the tradeoff of lower signal and less versatility, compared to B values diminishing from the B-maximum (segmented format; 256 gradient directions shown).

The ability to discern architectural details in vivo with GQI was demonstrated for the human tongue (Fig. 3), an organ with a high degree of myoarchitectural complexity (15,19) that embodies merged intrinsic and extrinsic muscle fibers acting as a continuous material in order to carry out physiological deformations (39,40). MR experiments were performed in vivo at 3T, employing single-shot EPI spatial encoding, and a 1.7 × 1.7 × 4 mm voxel size.

Figure 3.

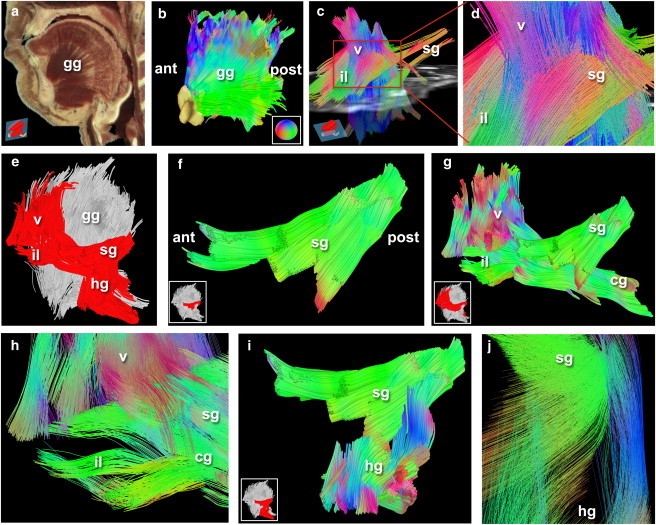
Defining myoarchitecture in vivo with GQI. (a) The midline slice reconstructed from the visible human male dataset, demonstrating anatomical orientation with the fanlike muscle fiber patterns of the genioglossus (gg) in the tongue. (a, inset, bottom left) Two-dimensional slice location, a midline sagittal through the tongue; anterior (ant) and posterior (post) indicated. (b) The human genioglossus (gg) imaged with GQI in vivo with 128 gradient directions, B-maximum of 750 s/mm², and scan time of 7.1 min, reconstructed in three dimensions. The symphysis bone is drawn for perspective (yellow-white color). (b, inset, bottom right) Tractography direction color-code. (c) Reconstructed muscle fibers of the human tongue depicting in oblique view the interface of the midline fibers of the genioglossus with the lateral fibers of the styloglossus (256 gradient directions). The EPI B = 0 image displayed in (c) is a grayscale slice from the axial plane; (inset, bottom left) middle transverse position of this slice in the tongue. Shown in (c) are reconstructed tracts of the styloglossus (sg), inferior longitudinalis (il), and verticalis (v). (d) Higher zoomed view of the insertion site of sg, il, and v with gg to display elaborate overlap of fiber populations. (e) Positional atlas of lateral muscular insertion sites including the sg, il, v, and hyoglossus (hg, in red) relative to the gg (in silver). (f) Fragment region of the sg originating from the posterior (post) styloid process, a bony protrusion of the skull, and branching in the anterior (ant) direction into superior and inferior arms. (g) Insertions of the superior branch of the sg with the chondroglossus (cg), il, and v generated from superior tracts of the fragment shown in (f) interface in a twisting pattern as shown zoomed in (h). (i) Insertions of the inferior branch of the sg interface with the hyoglossus (hg) and zoomed (j).

Inherent in architectural analysis is the ability to define a set of fibers on the basis of its orientation. As an example, select tract generation enabled computational dissection of the lingual musculature from ROIs drawn over two-dimensional EPI B = 0 images and fiber anisotropy maps. We employed 256 gradient directions in a full spherical format (or 128 gradient directions in a hemispherical format) with B values of 750 s/mm² in order to resolve the requisite angular separation. Through this analysis, we depict the fanlike genioglossus as a dominant midline structure originating at the symphysis bone (Fig. 3 b; related to the visible human in Fig. 3 a), and the lateral site at which the styloglossus, inferior longitudinalis, chondroglossus, and verticalis (Fig. 3, c and d) merge to generate a point about which the tongue pivots during rotation. Regional geometric analysis was performed by isolating the superior and inferior fragments of the styloglossus (lateral locations relative to gg shown in Fig. 3 e; sg fragments in Fig. 3 f) at its branching sites, with tracts generated from each of the sg branching regions. This demonstrated complex insertions at the interface zones (Fig. 3, g–j) with a twisting insertion pattern in the superior direction (Fig. 3, g and h) and interlocking pattern in the inferior direction (Fig. 3, i and j).

Microscopic comparison of human lingual anatomy was carried out in the setting of an intact mouse tongue using GQI at 7T with a voxel size of 125 × 125 × 500 μm (Fig. 4). The mouse genioglossus was isolated in Fig. 4 a, demonstrating similar architectural patterns to the human (Fig. 4 b). Extrinsic lingual fibers were identified in the posterior compartment (Fig. 4 c), where further isolation demonstrated a three-dimensional grid of merging fibers between the genioglossus and the chondroglossus at a lateral location (Fig. 4, d and e). GQI analysis was followed by validation through microscopic imaging of a midsagittal slice using a conventional hematoxylin and eosin histology (Fig. 4, f and g).

Figure 4.

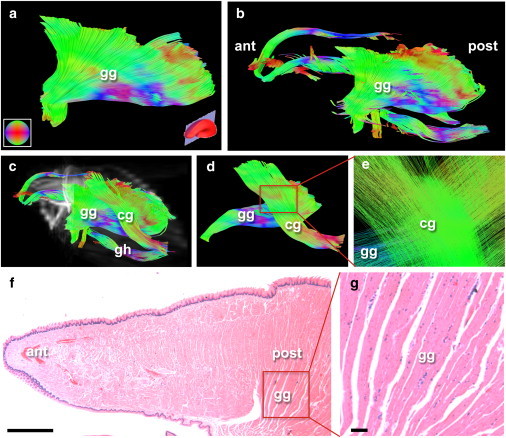
Microscopic comparison employing the excised mouse tongue. GQI was performed in an ex vivo mouse tongue in order to depict midline and lateral structures. (a) Image of isolated mouse genioglossus muscle (gg) reconstructed using GQI ex vivo with 512 gradient directions and a voxel size of 125 × 125 × 500 μm. (Inset, bottom left, a) Tractography orientation with respect to indicated color and at right the midline sagittal slice position. (b) The gg is shown relative to midline muscular structures, and in the context of (c) chondroglossus (cg), and geniohyoid (gh). (Grayscale) EPI B = 0 image slices displayed in (c) demonstrate the mouse tongue location. (d) The cg and gg point of intersection isolated from the mouse tongue. (e) Grid pattern insertion in three-dimensional space between the gg and cg from the box in (d) at closeup view. (f) Histological validation of muscle fiber orientations ex vivo in the mouse tongue obtained through hematoxylin and eosin staining of a midline sagittal slice demonstrates the fanning pattern of the mouse gg, along with relative position of muscle fibers in the anterior (ant) and posterior (post) compartments. (g) High magnification view of gg fiber bundle orientation in a midline sagittal slice of the mouse tongue. The scale bar portrayed in (f) is 1 mm and in (g) is 100 μm, whereas the relative size of the scaled box in (f) is 1 mm².

Comparison among images (GQI and microscopy) confirmed equivalent divergence and merging among lingual fibers. We illustrate in Fig. 5 the capacity of GQI to depict complex myofiber insertion patterns at the interface of various fiber populations. In particular these images demonstrate transverse fibers emanating from the midline to the periphery in an anterior axial slice (Fig. 5, a and b), in plane and continuous with superior and inferior looplike structures (Fig. 5, c–e). The modes of structural interface are shown, whereby these myofiber regions cross and insert with interwoven architecture.

Figure 5.

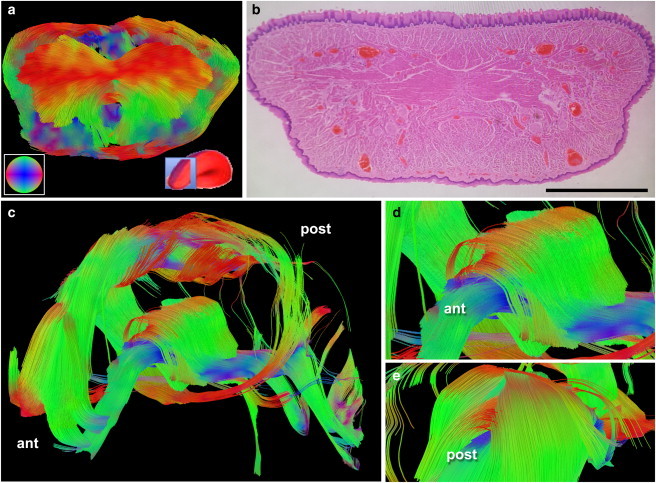
Demonstration of intersecting fiber arrays in the excised mouse tongue. (a) GQI image obtained from the mouse anterior tongue demonstrating transverse fibers branching from a central node coincident with a demonstration of the inferior and superior muscular loop structures. (Inset, bottom left, a) Color-coded orientational sphere for tractography; (bottom right) slice position location relative to the whole tongue. (b) Histological slide in an anatomically analogous region of the mouse tongue stained with H&E to demonstrate microscopic muscle fiber architecture, confirming geometric patterns noted in (a). Scale bar size is 1 mm. (c) Reconstruction of the mouse anterior tongue demonstrating the complex crossing and divergent patterns of the anterior tongue, notably the fiber insertions into the superior and inferior muscular loops. The inferior loop structure formed a reinforced core that transmitted in the anterior direction (d) and merged in the posterior direction (e) with thin muscular branches located laterally. The transverse fibers were removed in (c–e) to reveal the geometry of the loop structures in detail.

Discussion

Our results demonstrate that GQI, when parameterized through simulations of Q-space, is capable of interrogating the intravoxel and intervoxel diffusional properties of muscle in situ. This analysis provides a framework to characterize microstructural details of the constituting tissues in terms of muscle fiber orientation. Subsequent characterization of whole organs, such as the tongue, typifies an architectural phenotype and may be displayed as a set of multiscale fiber relationships. These representations emphasize the intricate and continuous nature of muscle fiber connectivity, and suggest an approach for deriving structure-based metrics in the setting of complex tissues. GQI is a method that simplifies prior diffusion techniques, enabling broad modulation of Q-space parameters. We propose that GQI comprises a method for depicting structural blueprints characteristic of mammalian muscle, which may be obtained in vivo or ex vivo, and thus opens the possibility of detailed structure-functional analysis in normal and pathological conditions.

Approaches have been employed to characterize tissue microstructure on the basis of directionally dependent variations of proton diffusivity. In the classical NMR diffusion experiment, the spinning proton is designated at two time points and the net displacement of these protons determined as a function of diffusion time (8). More recent diffusion experiments have utilized the same core concept, yet with added orientation related to the diffusion MR signal decay through the application of magnetic field gradients of varying strengths and directions (42,43). A voxel-scale degree of anisotropy may be established through the combination of multiple MR gradient-field orientations on a spherical sampling space with classic NMR diffusion experiment concepts. The microstructural properties of biological and nonbiological compartments can in this manner be determined from spatially delimited molecular diffusivity. Cory and Garroway (44) demonstrated that the Fourier relationship between the decaying MR echo intensity signal and compartment-delimited molecular displacement, employing the Q-space formalism of Callaghan (41), could be used to derive microstructural information. Displacements reflect the morphology and distribution of the compartments separating fluidic spaces (interior of the myocyte) and are delimited by physical barriers (cell membranes, myofilaments). Although the exact components responsible for diffusional anisotropy in muscle remains unknown, simulations indicate a subcellular element intermediate in scale to the thick and thin filament lattice (nanometer scale) and the sarcolemma (tens or hundreds of micrometers in scale) (45). Distributed diffusional compartmentation of protons constitutes the basis for architectural imaging in porous materials or complex biological milieus, and can be used to determine various parameters including compartment size and shape (31). The derivation of image contrast from compartmentalized diffusion may be extended to other NMR spectroscopic (46) or optical microscopic paradigms (47,48), reinforcing the capacity of diffusive transport to discern microstructure.

The use of gradient pulses of varying orientations, intensities, and sampling times enables the interrogation of complex microstructural anisotropic features at varying spatial scales (38). In particular, multiscale diffusion imaging is enabled through the linkage of the diffusion PDF maxima via tractography, enabling visualization of subvoxel phenomenon at the multivoxel scale (10,18,19). Such analysis provides a method to determine displacement probability in structurally complex milieus that are defined by crossing or diverging diffusional barriers. Such barriers are particularly important in the setting of hydrostatic muscular organs, which deform characteristically through complex patterns rather than in-line with bony surfaces (49,50). The validity of the single tensor paradigm, incorporated in the commonly used diffusion tensor imaging paradigm, is dependent on the accuracy by which the principal diffusion vector reflects the tissue’s underlying fiber arrays, i.e., linear fiber arrays at the voxel scale (15,51). Methods, such as diffusion spectrum imaging, probe the entirety of Q-space and are thus able to sample complex geometries, but at the considerable expense of scan time. The approach defined herein achieves the goal of multidirectional diffusion sampling by varying gradient direction, gradient strength, and diffusion sensitivities in the setting of a spherical simulation of Q-space. Angular separation may then be depicted at the subvoxel scale by analysis of PDF morphology and at the multivoxel scale by analysis of myofiber tract crossing and divergence patterns.

The mammalian tongue is a unique organ that achieves a vast array of forceful deformations through the contraction of complex myofiber arrays, and is thus an apt model to test the capacity of GQI. These myofiber arrays incorporate intricate structural interfaces of intrinsic and extrinsic muscles arranged in hierarchical patterns, embodying continuous material properties and precise neurological control (23,52,53). This study demonstrates that GQI identifies key muscular structures in the midline (genioglossus, chondroglossus) and the lateral complex (styloglossus, hyoglossus) of the human tongue in vivo. We confirm the presence of similar structures in the excised mouse tongue at higher MR field strength in conjunction with histology. Furthermore, through this technique, we demonstrate, to our knowledge, two novel structures in the mouse tongue, the looplike muscles located in the superior and inferior regions of the anterior tongue, approximately analogous to the superior and inferior longitudinalis in humans. The presence of complex fiber geometries, such as merging, crossing, or helicity contribute substantially to the function of various other muscular hydrostats, such as the heart (14,17) and the esophagus (14,16,17), and numerous Animalia appendages, such as the elephant trunk (25,26,54) or octopus tentacles (55,56). Acknowledging the influences of multidirectional contractions, the understanding of muscular architecture may support continuum models of force generation in the setting of such hydrostats.

GQI employs concepts of molecular diffusivity to probe the far reaches of Q-space, thereby achieving substantial levels of geometric precision in whole muscular tissue. Structural detail of this order may provide a novel basis for delineating normal and pathological architectural phenotypes in tissue types characterized by anisotropic components, principally muscle and nerve. The existence of such patterns may in turn constitute a method for evaluating treatments and interventions directed at promoting myogenesis and neuroplasticity.

Author Contributions

E.N.T. developed the MR imaging acquisition pulse sequence, performed the MR simulations and imaging experiments, assessed and represented the human MR data, and was the principal author of this article; M.P.H. performed and assessed the mouse microscopy experiments; G.E.A. performed and assessed the mouse MRI data; and R.J.G. developed the overall MR imaging technology and the application to lingual imaging, and contributed to all aspects of article development and research oversight. All authors reviewed and contributed to the writing of the article.