Creation and perturbation of planar networks of chemical oscillators

Abstract

Methods for creating custom planar networks of diffusively coupled chemical oscillators and perturbing individual oscillators within the network are presented. The oscillators consist of the Belousov-Zhabotinsky (BZ) reaction contained in an emulsion. Networks of drops of the BZ reaction are created with either Dirichlet (constant-concentration) or Neumann (no-flux) boundary conditions in a custom planar configuration using programmable illumination for the perturbations. The differences between the observed network dynamics for each boundary condition are described. Using light, we demonstrate the ability to control the initial conditions of the network and to cause individual oscillators within the network to undergo sustained period elongation or a one-time phase delay.

The spontaneous synchronization of coupled oscillators has a long history starting from Christiaan Huygens' observation of pendulum clocks^1,2 and has natural manifestations ranging from heart beats and circadian rhythms within single organisms³ to the synchronized flashing of fireflies and locking of human footsteps in groups of organisms.⁴ Numerous review articles have been written^5–9 and several textbooks have been published,^2,10–13 yet relatively few experimental systems exist to empirically test synchronization behavior. Those experimental systems that do exist, such as arrays of nickel electrodes,^14–20 transistors,²¹ metronomes,^22,23 and the Belousov-Zhabotinsky (BZ) reaction with coupled reactors,^24–26 catalyst beads,^27–29 in PDMS arrays,^30,31 or in an emulsion environment,^32–37 are either limited in their ability to control the network structure, boundary conditions, or the nature of the coupling between oscillators, or rely on electrical wiring. In this paper, we present methods of creating custom planar networks of oscillators consisting of a BZ emulsion in which interdrop coupling occurs via diffusion of an inhibitor. We demonstrate the ability to control boundary and initial conditions, and perturb individual oscillators within the network using externally applied light. Such technology enables synchronization engineering^{15,30,31,38,39} of networks of nonlinear chemical oscillators for applications in fields such as soft robotics.^40–42

I. INTRODUCTION

The aims of this paper are to present (1) methods for the creation of custom planar networks of diffusively coupled chemical oscillators based on the Belousov-Zhabotinsky (BZ) chemical reaction, (2) methods to control boundary and initial conditions, and (3) the ability to perturb individual oscillators within the network using externally applied light. The BZ reaction⁴³ has a rich history of experimental and theoretical study,^44–54 and consequently, is well understood chemically. One BZ based network involves loading the catalyst onto beads which are then immersed into a catalyst-free BZ mixture.^27–29 The BZ-beads system has recently been used to demonstrate the existence of chimera states,^29,55 but it is limited in its ability to define custom network geometries and to separate the rates of inhibitory and activation coupling. Another approach to BZ based networks consists of a periodic array of the BZ catalyst immersed in catalyst-free BZ solution, which was used to test adaptive optical coupling and therefore intentionally minimized diffusive coupling.^30,31 Under those circumstances, maintenance of dynamical attractor states required external application of light. Likewise, the BZ-bead system has been used to test adaptive optical coupling with externally applied light.⁵⁶ In contrast, coupling in our studies is entirely diffusive and dynamical attractors are autonomous.

Recently, we developed a BZ based network in an emulsion environment consisting of monodisperse drops of aqueous BZ immersed in a continuous oil phase.^32–37 The BZ solution contains polar and apolar species, but only the apolar species partition into the intervening oil. In this work, conditions are chosen such that the dominant apolar species is an inhibitor (there are other conditions in which excitatory coupling is also important³⁶), which produces two notable consequences. First, inhibitory coupling leads pairs of coupled drops to synchronize out-of-phase. Second, inhibitory coupling renders the BZ emulsion system suitable for testing Turing's theory of morphogenesis because the interdrop transport rate of the inhibitor is much greater than the activator rate.^35,57 However, our previous realizations of the emulsion system also suffered from limited abilities to define custom network geometries and control boundary conditions: two issues which are addressed here.

Section II describes the ability to create planar networks with Dirichlet (constant-concentration) boundary conditions using optical isolation, or with Neumann (no-flux) boundary conditions using physical isolation, and examines the effects of the boundary conditions on the network patterns by comparing different implementations of the same network. In Sec. III, the ability to perturb individual oscillators within the network is demonstrated by setting the initial conditions of the oscillators and by measuring the light induced period elongation and phase response curve to light of individual oscillators. Section IV concludes by describing how this work builds towards synchronization engineering of the BZ emulsion and lays out future research goals. Additional supplementary material further elucidate creating the BZ emulsion, the steps involved in creating devices that hold BZ drops with various boundary conditions, and using those functional devices in the Programmable Illumination Microscope.⁵⁸

II. NETWORK CREATION

A. Optical isolation/Dirichlet boundary conditions

Beginning with a planar, close-packed emulsion of BZ drops confined between two glass walls, networks with constant-concentration boundary conditions are created by optically isolating a subset of the drops. Optically defined networks utilize the optical inhibition properties of tris(bipyridine)ruthenium(II) (Rubpy) catalyzed BZ^52,59 and the Programmable Illumination Microscope (PIM).^34,60 The PIM is a tool developed for maskless-photolithography,^61,62 optogenetics,⁶³ and nonlinear chemical dynamics^34,35,64 including excitation via optical disinhibition.⁵⁶ Here, the PIM is used to track and illuminate individual drops for network creation using time-multiplexing with an adjustable duty cycle to collect images with and without inhibitory illumination every cycle.⁶⁰ The duty cycle is typically 3/10 (three seconds on, seven seconds off). The period of the duty cycle is short compared to the period of oscillation, ∼250–350 s, and therefore the oscillator responds to the average intensity, i.e., there is no difference between applying intensity I periodically with a duty cycle of 0.3 and applying intensity 0.3I, constantly.

In Figure 1, we show the optical inhibition and network creation properties of the PIM/BZ system for the simplest networks of 1 and 2 drops. Fig. 1(a) (Multimedia view) demonstrates a single isolated oscillator. The image shows the inhibitory light projected on all but one drop (marked in red) within the field of view. Intensity traces of the uninhibited drop and a representative inhibited drop (marked in cyan) are shown in Fig. 1(b). The uninhibited drop (red trace) clearly oscillates while the inhibited drop (cyan trace) does not. This behavior is readily reproducible for any configuration of inhibited and uninhibited drops provided the spot of light is projected into the center of the drop and the intensity of light is not too high. However, the illuminated drops do influence neighboring non-illuminated drops and we observe that non-illuminated drops stop oscillating when neighboring drops are illuminated with high intensity. Two mechanisms explain this behavior. Light increases the concentration of bromine, which diffuses to non-illuminated drops and slows their frequency. Simulations using the Vanag-Epstein model of BZ⁴⁹ demonstrate that sufficient illumination can cease oscillation in a drop that is directly illuminated. Simulations also show that when two drops are diffusively coupled and one is illuminated and the other is not illuminated, then a high enough intensity will cease the oscillation in the non-illuminated, but diffusively coupled partner drop. An additional experimental consideration is that a small fraction of the light is reflected from the glass and can illuminate neighboring drops if the glass walls containing the sample are not perpendicular to the optical axis. We typically adjust the size and intensity of the illuminated region to be the minimum required to suppress oscillations in the illuminated drops so as to minimally perturb oscillations in neighboring drops. It takes some care, of which the important considerations are elaborated below, but with practice conditions can be found in which light suppresses oscillations in the illuminated drops, while allowing non-illuminated drops to continue to oscillate. Measurements of the periods of drops as a function of the intensity of illumination are described later in this paper.

FIG. 1.

Optical isolation of single drops and pairs of drops. Typical results shown. (a) A single optically isolated drop with (b) intensity traces. (c) The schematic of a radial-phase-time plot. (d) An oscillating pair of nearest neighbor drops with (e) intensity traces color coded as in (d). (f) A radial-phase-time plot of the pair of drops shown in (d). (g) An oscillating pair of diagonally neighboring drops with (h) intensity traces color coded as in (g). (i) A radial-phase-time plot of the pair of drops shown in (g) with a dispersion ratio of 2.5%. (j) An oscillating pair of third-nearest neighbor drops with (k) intensity traces color coded as in (j). (l) A radial-phase-time plot of the pair of drops shown in (j) with a dispersion ratio of 0.9%. (Multimedia view) [URL: http://dx.doi.org/10.1063/1.4922056.1]Download video file ^{(805.7KB, mov)} DOI: 10.1063/1.4922056.1 [URL: http://dx.doi.org/10.1063/1.4922056.2]Download video file ^{(4.1MB, mov)} DOI: 10.1063/1.4922056.2 [URL: http://dx.doi.org/10.1063/1.4922056.3]Download video file ^{(4MB, mov)} DOI: 10.1063/1.4922056.3 [URL: http://dx.doi.org/10.1063/1.4922056.4]Download video file ^{(4.1MB, mov)} DOI: 10.1063/1.4922056.4

In Fig. 1(c), a schematic of a radial-phase-time plot is shown. Radial-phase-time plots are a convenient way of succinctly summarizing the synchronization behavior of an oscillatory network and are used throughout this paper. In a radial-phase-time plot, the radial axis is time and the angular axis follows phase in a right-handed direction. Plotted are the phase differences (${\varphi }_{i1}={\theta }_i-{\theta }_1$) between the phases of the color coded drops (θ_i) and the reference drop (θ₁, blue). The phase difference is plotted to highlight the occurrence of constant phase differences.

Figs. 1(d)–1(f) demonstrate the synchronization between a nearest neighbor pair of drops. Fig. 1(d) (Multimedia view) shows the locations of the two drops with all other drops inhibited. Fig. 1(e) shows intensity traces of the two drops. Fig. 1(f) is a radial-phase-time plot of the drops shown in Fig. 1(d); the two oscillatory drops start in phase and develop a constant phase difference of $\varphi =0.8\pi$. Two identical oscillators in isolation are predicted to have anti-phase synchronization with a phase difference of exactly π, whereas in experiment a range of constant phase differences near π are observed. We speculate the difference is due to some unknown heterogeneity in the boundary condition or due to the 4%–7% variation in period between the oscillators. For example, drops on the boundary may be illuminated with slightly different intensities, or the acid concentration of the drops may vary slightly.

Figs. 1(g)–1(i) demonstrate the lack of synchronization between a diagonally neighboring pair of drops. Fig. 1(g) (Multimedia view) shows the locations of the two drops with all other drops inhibited. Fig. 1(h) shows intensity traces of the two drops. Fig. 1(i) is a radial-phase-time plot of the drops shown in Fig. 1(g); the two oscillatory drops start in phase and undergo constant phase slipping, demonstrating a lack of synchronization. The dispersion ratio is calculated as Δω/ω₀, where $\Delta \omega =\left|{\omega }_i-{\omega }_0\right|$ and ω₀ is the angular frequency of the reference drop. For the pair of drops shown in Figs. 1(g)–1(i) the dispersion ratio is 2.5%. Figs. 1(j)–1(l) demonstrate the lack of synchronization between a third-nearest neighbor pair of drops. The very slow phase change between the oscillating drops indicates that they have nearly identical frequencies. For the pair of drops shown in Figs. 1(j)–1(l), the dispersion ratio is 0.9%.

The geometry of close-packed spheres in 2D dictates which ring networks can be created from a close-packed emulsion. Fig. 2(a) shows a hexagonal lattice of close-packed spheres with a dislocation defect and Fig. 2(b) demonstrates the construction of rings of 3, 4, 5, 6, 8, and 9 within that lattice. Rings of three and six occur in the ordered lattice, while rings of four and five occur at relatively mechanically stable packing defects. Rings of eight and nine can be constructed as elliptical and triangular forms in the regular lattice (rings with two or three drops inside), but rings of seven are found only at defect boundaries. We infer that such rings are mechanically highly unstable because in spite of hundreds of trials a ring of 7 has never been found for longer than a brief transient period in a packing of physically homogenous drops.

FIG. 2.

Dislocation defect in hexagonally close-packed spheres. (a) A wide field of view demonstrating the dislocation defect. (b) A zoomed in region demonstrating the ability to optically construct rings of 3, 4, 5, 6, 8, and 9 within that region. The rings of 4 and 5 would be impossible without the defect.

To create geometries not found within close-packed spheres, we developed manufacturing techniques capable of constructing custom planar geometries. A ring of seven with constant chemical concentration boundary conditions is created by manufacturing an annulus shaped cavity from a 100 μm thick polydimethylsiloxane (PDMS) layer contained between two glass sheets. We manufacture a “moat” outside the annulus that also contains drops. The drops outside of the annulus are held stationary optically, creating constant-concentration conditions for drops within the annulus. It is worth noting that as this is a closed system no chemical concentrations are truly constant but rather that the concentrations within the non-oscillatory drops change very little within the time frame of the experiment. See supplementary material for more details on the manufacturing process. Figs. 3(a) (Multimedia view) and 3(b) demonstrate a ring network of seven implemented in thin PDMS. The inner annulus of the device is sized to hold the desired number of drops in a circular network. The outer channel (moat) of the device is filled with optically inhibited drops (indicated by a white x) that provide the constant-concentration boundary conditions. The PDMS layer between the annulus and outer channel diffusively couples the two features and serves only to maintain the geometry. This diffusive coupling is evident as whenever a gas bubble is present in the outer channel the drops within the annulus cease oscillating. We explain this behavior as arising from bromine permeating through the PDMS to the gas causing a depletion of bromine within the drops in the annulus^32–34 as was measured explicitly with a partition coefficient between the PDMS and aqueous phase of ∼400.⁶⁵ One important practical consequence of bromine escaping from the BZ solution through the PDMS is that BZ solutions contained in PDMS stop oscillating if the ratio of the volumes of the BZ solution to PDMS is greater than about 1:5.

FIG. 3.

Planar networks with custom geometries. Typical results shown. (a) A polydimethylsiloxane (PDMS) device designed to create a ring network of seven with constant-concentration boundary conditions. The drops color coded as in (b). (b) A radial-phase-time plot of the ring of seven shown in (a). (c) An etched silicon device designed to create a ring network of seven with no-flux boundary conditions. The drops are color coded as in (d) and the white arrows indicate the order of oscillation. (d) A radial-phase-time plot of the ring of seven shown in (c). (e)–(h) Network patterns etched into silicon wafers imaged using an optical profilometer. (e) The ring network, (f) a six-star network, (g) a square lattice, and (h) a triangular lattice. (Multimedia view) [URL: http://dx.doi.org/10.1063/1.4922056.5]Download video file ^{(12.9MB, mov)} DOI: 10.1063/1.4922056.5 [URL: http://dx.doi.org/10.1063/1.4922056.6]Download video file ^{(10.7MB, mov)} DOI: 10.1063/1.4922056.6

The expected patterns from ring networks of BZ emulsion have been examined previously using linear stability analysis (LSA).³⁵ These results indicate that the network patterns should depend on the parity of the number of members. Networks with an even number of members should have a π phase separation between nearest neighbors resulting in two phase clusters separated by π radians. Networks with an odd number of members (N) should have a (N − 1)π/N phase separation between nearest neighbors resulting in N phase clusters evenly distributed on the phase circle with a 2π/N phase difference between clusters instead of the π phase separation found for even-membered rings. The pattern observed in the radial-phase-time plot in Fig. 3(b) qualitatively resembles the expected behavior for an inhibitorily coupled ring of seven with seven phase clusters separated at 2π/7. We speculate that deviation from the expected behavior is caused by the irregular boundary-conditions resulting from the square geometry of the outer channel and the non-uniform packing of drops in the outer channel.

B. Physical isolation/Neumann boundary conditions

Networks can be created with no-flux boundary conditions by etching containment patterns into silicon wafers and forcing the BZ emulsion into the cavities under a glass sheet. Crystalline silicon and amorphous silicon dioxide are nearly impermeable to all chemicals and gases, and thus constitute no-flux boundary conditions.^32–34 The devices are creating using Deep Reactive-Ion Etching (DRIE)^66,67 in which a process of plasma etching followed by surface treatment is repeatedly applied, allowing the plasma to etch deep into a silicon wafer with a nearly perpendicular profile, including etching entirely through the wafer.⁶⁸ The walls are slightly scalloped but this is controllable by adjusting the etch rate per cycle.⁶⁹ See supplementary material for more details. Figs. 3(e)–3(h) show profilometer images of empty DRIE etched devices.

A no-flux boundary condition device for a ring of seven drops was created by etching an annulus with an outer radius of 250 μm, inner radius of 100 μm, and depth of 70 μm into a silicon wafer (Fig. 3(e)). The devices were loaded by placing 50 μl of emulsion on top of the empty annulus and sealing with a glass sheet (Fig. 3(c)). Drops in Fig. 3(c) (Multimedia view) are color coded to coincide with the corresponding radial-phase-time plot (Fig. 3(d)), which exhibits nearly perfect seven-phase clustering with a 2π/7 separation between clusters, the expected pattern for a ring of seven. In the accompanying video, the drops labeled in Fig. 3(c) oscillate in the following sequence “blue-green-orange-pink-cyan-purple-red-blue-etc.” corresponding to every other drop as progressing clock-wise around the ring. The radial-space-time plot of Fig. 3(d) conveys the phase difference between successive oxidation transitions of the drops with the color-coded sequence of transitions proceeding in a counter-clockwise direction.

Etching devices out of a silicon wafer allows for customized planar geometries. For example, a six-star network (Fig. 3(f)) can be constructed using no-flux boundaries provided by silicon, but could not be constructed with constant-concentration boundaries using either PDMS or optical isolation because of diffusive coupling between members of the arms of the star. Additionally, coupling strength depends on drop separation. For example, drops no longer synchronize in six-star networks, when the drops are separated by more than half their diameter. Figs. 3(e)–3(h) show images from an optical profilometer of etched silicon devices used to make (e) a ring network, (f) a six-star network, (g) a square lattice, and (h) a triangular lattice. Future work will focus on the network patterns from star graphs with varying coupling strength and central node degree, and on the network patterns from various lattice structures.

C. Boundary effects

In this section, we analyze the network patterns seen in circular networks with three, four, five, and six members as a function of boundary condition. We implement constant-concentration boundaries in two ways; with optical isolation within a close-packed emulsion and with optical isolation using drops stored in wells constructed from a thin PDMS barrier. We implement no-flux boundaries by using etched silicon.

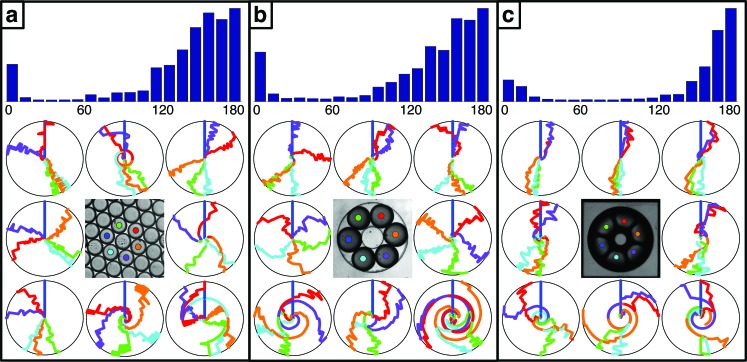
Network patterns can be observed for ring networks of up to six members with constant-concentration boundary conditions implemented with optical isolation within a close-packed emulsion. Ring networks of seven plus members can be created with constant-concentration boundary conditions implemented in thin PDMS boundaries from optically isolated drops and with no-flux boundary conditions implemented in etched silicon. Network patterns for ring networks with three, four, five, and six members from all three implementations are shown in Fig. 4 and network patterns for ring networks with seven members implemented in thin PDMS and etched silicon are shown in Figs. 3(a)–3(d).

FIG. 4.

Network patterns observed from ring networks of three (a), four (b), five (c), and six (d) members with constant-concentration and no-flux boundary conditions. Typical results shown. Top: Images of the networks with the oscillating drops color coded as below. All scale bars are 100 μm. Bottom: Radial-phase-time plots of the networks above. Left: Circular networks with constant-concentration boundary conditions implemented via optical isolation in close-packed drops. Only the color coded drops are oscillatory; the other drops are optically inhibited. Middle: Circular networks with constant-concentration boundary conditions implemented in thin PDMS with optically inhibited drops in surrounding channels. The surrounding channels are not shown. Right: Circular networks with no-flux boundary conditions implemented in etched silicon. (Multimedia view) [URL: http://dx.doi.org/10.1063/1.4922056.7]Download video file ^{(16.9MB, mov)} DOI: 10.1063/1.4922056.7 [URL: http://dx.doi.org/10.1063/1.4922056.8]Download video file ^{(3.3MB, mov)} DOI: 10.1063/1.4922056.8 [URL: http://dx.doi.org/10.1063/1.4922056.9]Download video file ^{(20.4MB, mov)} DOI: 10.1063/1.4922056.9 [URL: http://dx.doi.org/10.1063/1.4922056.10]Download video file ^{(7.3MB, mov)} DOI: 10.1063/1.4922056.10

Fig. 4(a) (Multimedia view) shows the network patterns for a ring of three implemented with optical isolation within a close-packed emulsion (left), implemented with optical isolation with thin PDMS boundaries (middle), and implemented with etched silicon (right). The 2π/3 solution is demonstrated in all three implementations with the etched silicon implementation demonstrating an initial transient and with the thin PDMS implementation temporarily demonstrating the unstable 00π state,³⁷ where the three drops form two anti-phase phase clusters. The sequence of colors in the radial-phase-time plots demonstrates the handedness of the network pattern where the close-packed implementation is right-handed and the other two implementations are left-handed. See supplementary Videos for more details.

Fig. 4(b) (Multimedia view) shows the network patterns for a ring of four implemented within a close-packed emulsion (left), with thin PDMS boundaries (middle), and with etched silicon (right). All three implementations generally demonstrate two anti-phase phase clusters with varying degrees of finer details. The etched silicon implementation most closely matches the predicted pattern and, due to the impermeable post preventing cross-network diffusion, most closely resembles the predicted LSA structure. The finer details within the close-packed emulsion and thin PDMS implementations can possibly arise from cross-network diffusion through the central region creating additional network edges with lesser weights. These additional edges may induce repulsive behavior within the phase clusters resulting in the finer structure demonstrated.

Fig. 4(c) (Multimedia view) shows the network patterns for a ring of five implemented within a close-packed emulsion (left), with thin PDMS boundaries (middle), and with etched silicon (right). The close-packed emulsion implementation demonstrates the “pseudo-triangle” state where the five drops assume the 2π/3 pattern expected from a triangular ring of three with two sets of two drops, both phase-locked together acting in unison as a single entity of the triangle. While this is not the most expected behavior for a ring of five (as determined by growth rate in the LSA), it is the second most expected state. In experiments both states are commonly found. The thin PDMS implementation is representative of the more typically expected state. The etched silicon implementation demonstrates behavior somewhere between the other two implementations, likely evidence of a superposition of states. The sequence of colors in the radial-phase-time plots demonstrates the handedness of the network pattern where the thin PDMS implementation is a left-handed pentagram, the etched silicon implementation is a right-handed pentagram, and the pseudo-triangle from the close-packed implementation is a right-handed pseudo-triangle.

Fig. 4(d) (Multimedia view) shows the network patterns for a ring of six implemented within a close-packed emulsion (left), with thin PDMS boundaries (middle), and with etched silicon (right). All three implementations generally demonstrate two anti-phase phase clusters with varying degrees of finer details. Additional examples of the network patterns for rings of six are shown in Fig. 5 with a histogram of the nearest neighbor phase differences. The histograms combine the nearest neighbor phase differences at every time point for all eight experiments shown. The phase differences are calculated using ${\varphi }_{\mathit{i}\mathit{j}}=\left|{\theta }_i-{\theta }_j\right|$ for $\left|{\theta }_i-{\theta }_j\right|\le \pi$ and as ${\varphi }_{\mathit{i}\mathit{j}}=\left|\left|{\theta }_i-{\theta }_j\right|-2\pi \right|$ for $\left|{\theta }_i-{\theta }_j\right|>\pi$ to account for the symmetry of phase differences about π. The small peaks in the histograms at $\varphi =0$ demonstrate that the drops were all started in phase and initial transients were not removed so that the rapidity of synchronization is also evident. The histograms in the etched silicon implementation are the most sharply peaked at π radians and most closely match the predicted pattern. We assume this is due to the impermeable post on the inner annulus preventing cross-network diffusion and the homogeneity of the no-flux boundary on the outer annulus. The close-packed and thin PDMS implementations demonstrate a broader range of behavior. Similar to the rings of four, the additional patterns here could possibly arise from cross-network diffusion through the central region and coupling to heterogeneities on the outer boundary.

FIG. 5.

Nearest neighbor phase differences and network patterns for ring networks of six implemented via optical isolation in close-packed drops (a), in thin PDMS with optically inhibited drops in surrounding channels (b), and in etched silicon (c). Top: Histograms of the phase differences between nearest neighbor drops demonstrating typical behavior. In all cases the drops were started in-phase. Bottom: Radial-phase-time plots demonstrating the variety of observed patterns and a color coded image representing the locations of the drops. The top left plots demonstrate the typical behavior and are the same as in Fig. 4(d).

Figs. 3(a)–3(d) show the network patterns for a ring of seven implemented with thin PDMS boundaries, Figs. 3(a) and 3(b), and with etched silicon, Figs. 3(c) and 3(d). Both implementations demonstrate the expected behavior for a ring of seven with the etched silicon implementation again most closely matching both the assumed graph structure and the expected behavior of seven evenly spaced phase clusters. For rings of seven, there are four patterns (“hands”) with the same wavelength which can be described as left-handed and right-handed cyclic heptagrams and left-handed and right-handed figure-eight heptagrams. A cyclic heptagram traces a seven sided star (similar to a five sided pentagram) as can be seen in Fig. 3(c) and the corresponding video. A figure-eight heptagram switches direction mid-cycle by skipping to the third neighbor and switches back with another third neighbor skip as is seen in the video corresponding to Fig. 3(a). The etched silicon implementation in Figs. 3(c) and 3(d) demonstrates the left-handed cyclic heptagram where the order of oscillation follows a regular left-handed {7/2} heptagram. The notation {7/2} indicates a seven sided figure with the sequence of oscillation following the 2nd neighbor. The thin PDMS implementation in Figs. 3(a) and 3(b) demonstrates the right-handed figure-eight heptagram where the order of oscillation includes four left-handed {7/2} transitions, one right-handed {7/2} transition, and two right-handed {7/3} transitions that give the pattern its reversing “figure-eight” appearance. This arrangement is referred to as the right-handed variant since the {7/3} transitions are right-handed.

III. NETWORK PERTURBATION

In addition to being able to create custom planar networks, the photo-activation of the Rubpy catalyst in BZ via the PIM allows for the perturbation of individual oscillators in networks created by any implementation. In Secs. III A–III C, we will demonstrate the ability to set the initial conditions of the oscillators within the network, elongate the period of select oscillators within a network, and perturb the phase of select oscillators within the network.

A. Initial conditions

In Fig. 6(a) (Multimedia view), a line of six drops is optically isolated from a closed packed array of drops. The initial conditions of this linear network can be set by utilizing the delay between the end of optical inhibition and the onset of oscillations. While the drops are optically inhibited, all of the drops are held in the same chemical state and thus there is no diffusive coupling between the drops. Immediately after optical inhibition is ended, the drops transition to a reduced (dark) state and after approximately one period begin to oscillate in-phase and remain in-phase for the first six oscillations, but then transition to the stable anti-phase attractor.³⁴ Fig. 6(a) also demonstrates the ability to “reset” the drops back to in-phase. Staggering the ending of optical inhibition for each drop can create other initial conditions.

FIG. 6.

A figure demonstrating setting the initial conditions, period elongation, and phase response curve. (a) A space-time plot (bottom) demonstrating setting the initial conditions of the drops (top) and resetting the phase back to zero at a later time. The blue bars indicate when the inhibitory light is on and the green dashes point out the first in-phase oscillation. (b) A demonstration of the experiments conducted to measure the period elongation curve shown in (c). Twelve drops are optically isolated and allowed to oscillate with varying levels of inhibitory light. The bottom/blue four receives no inhibition, the middle/green four receive high inhibition, and the top/red four receive middling inhibition. (c) The period elongation curve of isolated drops as a function of the inhibitory light plotted as a fraction of the inhibition threshold. (d) A schematic of the experiments conducted to measure the phase response curve shown in (e). The drop represented with the blue trace received an inhibitory pulse at a specified phase, while the red trace is from the same drop, but recorded while unperturbed. The difference in period between the blue (perturbed) trace and the red (unperturbed) trace is used to calculate the phase response. (e) The phase response curve of isolated drops. (Multimedia view) [URL: http://dx.doi.org/10.1063/1.4922056.11]Download video file ^{(1.3MB, mov)} DOI: 10.1063/1.4922056.11 [URL: http://dx.doi.org/10.1063/1.4922056.12]Download video file ^{(602.9KB, mov)} DOI: 10.1063/1.4922056.12 [URL: http://dx.doi.org/10.1063/1.4922056.13]Download video file ^{(504.1KB, mov)} DOI: 10.1063/1.4922056.13

B. Period elongation

The period of oscillators within a network can be elongated by illuminating drops with a light intensity below the inhibition threshold (I_c). Period elongated drops are continuously illuminated with subthreshold illumination. Fig. 6(c) is a plot of the ratio of the period of oscillation with light to that without light (T/T₀) of isolated drops as a function of fraction of light needed to inhibit oscillation (I/I_c). The data are fit to the function $T/T_0=\alpha {(1-I/I_c)}^{-1/2}+\beta$, consistent with behavior near a saddle-node bifurcation¹⁰ with fitting parameters α = 0.1993 and β = 0.7226. It is worth noting that an illumination of I/I_c = 0.4 results in a period of T/T₀ < 1 across numerous trials indicating that something interesting is going on, but due to low illumination experimental limitations of the current system will be the subject of future investigation.

C. Phase response curve

The Phase Response Curve (PRC) characterizes the phase shift of an oscillator in response to a single, short perturbation as a function of the phase of the perturbation. Here, we measure the PRC of a single pulse of light. Data were acquired by optically isolating 12 drops in a similar fashion as done in Figure 6(b). Then, a single pulse of light (3 s, ≤1% T₀) was applied at a specified phase to each drop and the light induced phase shift was measured by measuring the elongation of a single period as shown in Figure 6(d) (Multimedia view). Data for statistics was accumulated rapidly by using 12 drops in parallel. Figure 6(e) shows the phase response curve for optically isolated drops using the formula Δθ = −2πΔT/T₀ to calculate the phase response Δθ from the change in period ΔT. Future studies will use these results to work towards a theoretical understanding of the mechanism of optical perturbation in dual-catalyzed BZ.

IV. CONCLUSION

We have created custom planar networks of nonlinear chemical oscillators with either Dirichlet (constant-concentration) or Neumann (no-flux) boundary conditions and demonstrated the ability to perturb the phase and period of individual oscillators within the network. Constant-concentration boundary conditions were created using optical isolation in either a close-packed emulsion or in photolithographically manufactured wells containing drops in thin slabs of PDMS, a material that is highly permeable to apolar fluids and gases, but relatively impermeable to polar and charged species. No-flux boundary conditions were created by etching wells into crystalline silicon wafers, a material nearly impermeable to almost all fluids and gases. The differences in network patterns between implementations of the same graph with different boundary conditions were also examined. The ability to perturb individual oscillators by the external application of light was demonstrated by setting the initial conditions of the network, resetting the phase of the network, measuring the period elongation curve of isolated oscillators, and measuring the phase response curve of isolated oscillators.

It should be noted that this method has certain limitations such as the requirement that the network be planar. Networks with edges that cannot be constructed on a plane would require a three-dimensional device. Another limitation of the method described here is the requirement that the nodes be spaced physically near each other as the coupling strength between nodes is controlled by the physical length of the edges. This limitation renders graphs with a high degree or with edges connecting distant nodes difficult to manufacture.

Despite these limitations, the ability to create custom planar networks of nonlinear chemical oscillators with controllable boundary and initial conditions combined with the ability to perturb individual oscillators within the network is a significant advance towards the goal of synchronization engineering of reaction-diffusion systems.