Accurate and Fast Multiple-Testing Correction in eQTL Studies

Abstract

In studies of expression quantitative trait loci (eQTLs), it is of increasing interest to identify eGenes, the genes whose expression levels are associated with variation at a particular genetic variant. Detecting eGenes is important for follow-up analyses and prioritization because genes are the main entities in biological processes. To detect eGenes, one typically focuses on the genetic variant with the minimum p value among all variants in cis with a gene and corrects for multiple testing to obtain a gene-level p value. For performing multiple-testing correction, a permutation test is widely used. Because of growing sample sizes of eQTL studies, however, the permutation test has become a computational bottleneck in eQTL studies. In this paper, we propose an efficient approach for correcting for multiple testing and assess eGene p values by utilizing a multivariate normal distribution. Our approach properly takes into account the linkage-disequilibrium structure among variants, and its time complexity is independent of sample size. By applying our small-sample correction techniques, our method achieves high accuracy in both small and large studies. We have shown that our method consistently produces extremely accurate p values (accuracy > 98%) for three human eQTL datasets with different sample sizes and SNP densities: the Genotype-Tissue Expression pilot dataset, the multi-region brain dataset, and the HapMap 3 dataset.

Introduction

The advent of RNA sequencing (RNA-seq) and expression microarrays has allowed studies to accurately quantify expression levels of genes in humans and many model organisms.^1–4 With association-mapping methods, in combination with genotyping technologies that uncover individuals’ genetic states at large numbers of sites in the genome, it has become feasible to identify genomic locations where genetic variation correlates with gene-expression variation. Such variants and genomic locations are referred to as expression quantitative trait loci (eQTLs). Many studies have performed genome-wide eQTL mapping to discover eQTLs in a number of organisms, populations, cellular states, and tissues.^5–7

eQTL studies provide not only sets of genetic variants associated with gene expression but also sets of genes for which an eQTL has been identified. The term “eGenes” has been used to describe those genes whose expression levels have been associated with genetic variation at a specific genetic locus. Identifying eGenes is important because genes are the main molecular units in many biological processes, are interpretable, and allow follow-up network and pathway analyses. To detect eGenes, one typically identifies cis-variants (i.e., those located proximal to a given gene) and tests each of them for association with expression levels of the gene to assess whether any of them is an eQTL. However, since one tests multiple variants per gene, multiple-testing correction is required. Even if one observes a relatively small (significant) eQTL p value, the p value might not be sufficiently significant to overcome the multiple-testing burden for a given gene, which can require correction for up to thousands of tests.

To correct for multiple testing and obtain a p value for each gene (eGene p value), multiple different approaches are available. The Bonferroni correction is overly conservative because it fails to take into account the linkage-disequilibrium (LD) structure within a genomic region. Because the LD structure is known to vary widely across the genome, the Bonferroni correction tends to have a bias penalizing those regions that bear strongly correlated variants. Another approach is the permutation test. The permutation test properly accounts for LD but has two limitations. First, it is computationally expensive.⁸ Its time complexity increases linearly as the number of individuals increases, and recent eQTL studies have dramatically increased their sample sizes, from dozens of individuals to hundreds and even to a few thousand.^9–12 Given that we expect studies with tens of thousands of individuals in the near future, the permutation test will quickly become prohibitively inefficient for practical use. Second, significant p values are truncated to a limited level of significance determined by the number of permutations. For example, 10,000 permutations restrict the p values to a lower bound of 10⁻⁴. Typically, one will obtain a list of genes that have the same lower-bound p values, such as 10⁻⁴. However, it is desirable to know the exact significance of each eGene p value for better interpretation and prioritization of genes.

In this paper, we propose an accurate and efficient approach for assessing eGene p values in an eQTL study. We perform multiple-testing correction to obtain eGene p values by using a multivariate normal distribution (MVN). We take into account LD structure among genetic variants by incorporating genotype correlations as a covariance matrix in an MVN. Our approach samples test statistics from this MVN to create the null distribution of test statistics, which corresponds to the null distribution generated from permutations. The null distribution sampled from an MVN approximates the true null distribution well, but not exactly, because of asymptotic assumptions made in an MVN. Hence, we propose an approach that reshapes the null distribution of an MVN to account for errors induced by the asymptotic assumptions. We then assess eGene p values from this optimized null distribution in the same fashion as the permutation test.

We apply our MVN approach to three human eQTL datasets. The first dataset is the whole-blood gene-expression dataset of the Genotype-Tissue Expression (GTEx) pilot study. This dataset consists of RNA-seq data of whole blood and associated genotypes of 156 unrelated individuals. The second dataset is of a single brain region (cerebellum) from an eQTL study conducted by Gibbs et al.¹³ This study consists of microarray gene-expression data of four brain regions total (although we only used data of one brain region here) and associated genotypes of 150 individuals. The third dataset is the eQTL dataset of the HapMap 3 project.¹² This dataset consists of microarray gene-expression data of lymphoblastoid cell lines and associated genotypes of 726 individuals from eight human populations. Applying our approach to these three datasets allowed us to evaluate the performance of our approach in datasets with different sample sizes and SNP densities. We show that our method consistently yields very accurate eGene p values in all three datasets (accuracy > 98%). With regard to computational efficiency, our approach is tens of times faster than the permutation test in all these datasets. For larger eQTL datasets, the efficiency gain of our method will become even greater because the time complexity of our approach does not depend on the sample size. That is, its runtime for eQTL datasets with tens of thousands of individuals is as fast as that for datasets with dozens of individuals. Unlike the permutation test, which truncates p values to a lower bound, our method also provides an accurate eGene p value for every gene, including extremely significant genes.

Material and Methods

eQTLs and eGenes

An eQTL is a genetic variant, such as a SNP, where genotypes of the variant are associated with variation in gene expression of a given gene. An eGene is a gene that has an eQTL. Studies typically utilize the following approach to detect eGenes. First, a statistical test is performed to compute correlation and its p value between the expression of a gene and every genetic variant in cis with the gene. We consider variants within 1 Mb of a transcription start site (TSS) as cis-variants in this paper. One could also look at trans-variants (variants distant from a gene), but because of their weak effects, they require a larger sample size for detection of their effects. The minimum p value among those of all genetic variants in cis with the gene is then selected. Because many hypothesis tests are performed in this approach, the minimum p value needs to be corrected for multiple testing. This corrected p value is for the gene, and we call it a “gene-level p value” or “eGene p value.” Studies often obtain eGene p values for many genes and apply another multiple-testing correction, such as false-discovery rate, to identify eGenes.^14,15

Spearman’s Rank Correlation Coefficient

One of the widely used statistical tests for identifying eQTLs is the Spearman’s rank correlation coefficient.^{4,12,14,16–18} This is a non-parametric test, and its power and type I error are robust to the deviance of expressions from the normal distribution. The Spearman’s rank correlation is defined as the Pearson correlation of the ranks where ties are given mean values. Given the Spearman’s rank correlation, denoted as r, the test statistic

$$t=r\sqrt{\frac{n-2}{1-r^2}}$$ (Equation 1)

asymptotically follows a t distribution with n – 2 degrees of freedom, where n is the number of individuals. A p value of this t statistic can be obtained from the cumulative density function of the t distribution. In this paper, Spearman’s rank correlation test is mainly used to test for association between genetic variation and gene-expression variation unless specified otherwise.

Pearson Correlation Coefficient

Another statistical test for identifying eQTLs is the Pearson correlation coefficient. This is a parametric test that assumes that expression values follow a normal distribution. However, because the normality assumption is often violated in eQTL datasets, a rank-based inverse normal transformation is applied to make expression values follow the normal distribution.¹⁵ In this study, we used the GenABEL package¹⁹ to perform the rank-based inverse normal transformation. Once expression values are transformed, we perform a linear regression between expression values and genotypes to compute a p value of correlation between the two variables, which is equivalent to a p value of the Pearson correlation coefficient.

Traditional Approaches for Assessing eGene p Values

Bonferroni Correction

The Bonferroni correction assumes that all genetic variants in cis with a gene are independent, as if there is no LD among variants. The Bonferroni correction then corrects the minimum p value among all p values of cis-variants by multiplying the p value by the number of tests (the number of cis-variants). However, nearby genetic variants are commonly in LD with each other, which implies that the effective number of tests can be much smaller than the number of cis-variants. Hence, the Bonferroni correction is overly conservative for estimating eGene p values and could lead to a loss of power for detecting eGenes.

Permutation Test

The permutation test is the gold-standard approach for correcting for multiple testing.²⁰ It is widely used to estimate eGene p values because it takes into account LD among variants.^4,12,14 Let m be the number of variants in cis with gene y. We first compute a statistic for each variant, denoted as S_i for the i^th variant, that measures correlation strength between the i^th variant and the expression of gene y. Let S_max = max(S₁, S₂, …, S_m). We want to perform a multiple-testing correction on S_max while taking into account LD among m variants. The permutation test permutes gene-expression values of individuals and computes $S_{\text{max}}^{\text{'}}$ in each permutation. This collection of $S_{\text{max}}^{\text{'}}$ from the permutation test represents the null distribution of an eGene p value. An eGene p value of gene y is then estimated with the proportion of $S_{\text{max}}^{\text{'}}$ that is equal to or greater than S_max. Although the permutation test is the gold standard for obtaining eGene p values, it has two limitations. First, time complexity, which is O(nmp), where n is the number of individuals, m is the number of variants, and p is the number of permutations, is high. The permutation test quickly becomes infeasible as the sample size (n) of eQTL studies increases; several current eQTL studies have collected data from more than a thousand individuals.^9–11 Second, the eGene p value can be approximated only to a threshold limited by the number of permutations. If we perform 10,000 permutations, the minimum p value we can obtain is 10⁻⁴. We will have much richer information for follow-up analysis if we have the exact significant p values instead of 10⁻⁴.

eGene-MVN

eGene-MVN, the approach we propose here, consists of four steps: MVN sampling, distribution reshaping, small-sample adjustment, and extreme p value approximation.

Multivariate Normal Sampling

We first approximate the null distribution of the gold-standard permutation test by using multivariate normal sampling. Let r_ij be a genotype correlation between the i^th and j^th variants. Under the null, test statistics (S₁, S₂, …, S_m) asymptotically follow the MVN with mean 0 and variance Σ, where Σ = {r_ij} is the m × m genotype correlation matrix among m variants.^8,21 We sample m statistics from this MVN, find $S_{\text{max}}^{\text{'}}$, and compute its p value. We repeat this many times and obtain the distribution of p values of $S_{\text{max}}^{\text{'}}$ under the null hypothesis. Then, an eGene p value is the proportion of p values from this distribution that is as significant as or more significant than a p value of S_max. Note that we can use MVN under the asymptotic assumption for the Spearman’s rank correlation coefficient and the Pearson correlation coefficient, both of which give a t-distributed statistic, because a t distribution asymptotically converges to a normal distribution.

A major advantage of an MVN approach is that it is much more efficient than the permutation test for a large sample size because the time complexity of the MVN approach, O(m²p), does not depend on the number of individuals (n). Hence, an MVN approach can be used without efficiency loss for eQTL datasets with very large n. In addition to considering the runtime, an MVN approach appropriately takes into account LD among variants by incorporating LD structure as a covariance matrix in an MVN. Several MVN approaches have been developed to perform a multiple-testing correction in genome-wide association studies (GWASs) and have been shown to be very accurate and fast.^8,21,22

A drawback of the MVN approach is that it is only accurate under the asymptotic assumption. For small eQTL study sizes (dozens to hundreds of individuals), there can be discrepancy between the asymptotic distribution and the true null distribution.

Distribution Reshaping

An MVN assumes that a statistic follows a normal distribution and that the p value of a statistic follows the uniform distribution under the null hypothesis. For many statistics, including the Spearman’s rank correlation and Pearson correlation coefficients, these properties only hold asymptotically.²¹ Specifically, we discovered that a t-distribution-based p value of the Spearman’s rank correlation and Pearson correlation coefficients slightly deviates from the uniform distribution under the null. We observed a slight inflation of test statistics for common SNPs and deflation for rare SNPs. To illustrate this phenomenon, we measured the false-positive rate (FPR) of the Spearman’s rank correlation coefficients by using simulated data, including SNPs with two different minor allele frequencies (MAFs; 5% and 30%). The number of individuals was 144, and we generated their genotype data on the basis of the two MAFs. We also generated random expression data under the null hypothesis. We then computed a p value of the Spearman’s rank correlation between each SNP and gene expression by using the t distribution and measured the FPR under various thresholds. Ideally, this should have given us the exact FPR (e.g., 5%), equal to the threshold (e.g., 5%). However, we observed that a SNP with a MAF of 5% had a lower FPR than expected, whereas a SNP with a MAF of 30% had a higher FPR (Table 1). This tendency exacerbates as the threshold becomes more significant. For example, when we measured the TF ratio—the ratio between the threshold and the FPR, which should be 1 if a p value follows the uniform distribution—it was as small as 0.76 for a SNP with a MAF of 30% and as large as 4.71 for a SNP with a MAF of 5% at threshold 10⁻⁵ (Table 1).

Table 1.

FPR of Spearman’s Rank Correlation Coefficients on SNPs with Two Different MAFs, 5% and 30%

Threshold	MAF 30%		MAF 5%
	FPR	TF Ratio	FPR	TF Ratio
0.01	0.0101525	0.984981	0.0094544	1.05771
0.001	0.0010509	0.951554	0.0008058	1.24099
0.0001	0.0001108	0.902454	6.161E−5	1.62298
1E−5	1.191E−5	0.839278	3.883E−6	2.57533
1E−6	1.328E−6	0.755398	2.121E−7	4.71385

TF ratio is the ratio between the threshold and FPR, (threshold/FPR). FPR is measured from the generation of many null datasets, and a p value of Spearman’s correlation is computed from a t distribution. A sample size of 144 individuals was used.

We also found that the TF ratio of Spearman’s correlation coefficients depends on the sample size in addition to the MAF. We repeated the same simulation on the SNP with a MAF of 30% by using five different sample sizes: 70, 110, 144, 220, and 300 individuals. We measured the FPR of the SNP for each of those sample sizes and computed the TF ratio. The results showed that the TF ratio becomes closer to 1 as the sample size increases (Figure 1). This nonuniform distribution of Spearman’s rank correlation p values creates a discrepancy in the null distribution between the permutation test and an MVN. We observed a similar phenomenon with Pearson correlation coefficients.

Figure 1.

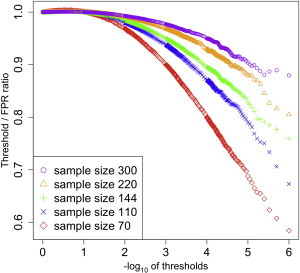
FPR of Spearman’s Correlation Coefficients on a SNP with a MAF of 30% and under Various Thresholds

The x axis is the −log₁₀ of thresholds, and the y axis is the TF ratio between the thresholds and the FPR (thresholds/FPR). The TF ratio would be 1 if the p values of Spearman’s correlation coefficients followed the uniform distribution. Five different sample sizes (n = 70, 110, 144, 220, and 300) were used.

To solve this discrepancy problem, we use the following distribution-reshaping approach.²¹ We pre-compute the FPR and the TF ratio for many different thresholds, MAFs, and sample sizes by generating a large number of datasets under the null hypothesis. Then in our MVN approach, on the basis of this pre-computed knowledge, we scale a p value of the MVN approach according to the TF ratio such that the MVN p value approximates a p value of the permutation test. This distribution-reshaping approach is applied to both Spearman’s rank correlation and the Pearson correlation coefficients.

Additional Small-Sample Adjustment

We discovered that even after we applied the distribution-reshaping approach, which approximates the correct p value at each single SNP, we still observed a residual discrepancy in the eGene p value between the permutation test and an MVN. This is possibly because the distribution-reshaping approach only adjusts for the small-sample discrepancy on each marginal distribution of MVN but not on the whole distribution with correlation structure. This residual discrepancy is observed when the sample size is small (e.g., <300).

To show an example, we created five eQTL datasets with sample sizes of 70, 110, 144, 220, and 300 individuals. Each dataset had 100 probes, and the number of cis SNPs ranged from 32 to 709. Genotype data were generated from actual genotype data from the brain eQTL dataset¹³ containing genotypes of 144 individuals. For eQTL datasets with a sample size less than 144 individuals, we used a random subset of genotypes of 144 individuals, and for eQTL datasets with a sample size larger than 144 individuals, we randomly replicated their genotypes to create genotypes of the desired number of individuals. Expression data were similarly generated with actual expression data from one brain region (cerebellum), and random noises were added to expression values when they were replicated. We estimated an eGene p value for each probe by using 1 M (million) permutations in the permutation test and 1 M samplings in an MVN. We applied the distribution-reshaping approach to correct for the discrepancy at each single-marker test statistic.

Figure 2 is a boxplot that shows the distribution of the ratio of MVN eGene p values (with distribution reshaping) to permutation-test eGene p values on the 100 probes for the different sample sizes. We excluded outliers in the boxplot because they are probes that contain a SNP with a very significant p value (e.g., 10⁻¹⁰), and hence they have a very low or very high ratio as a result of the insufficient number of permutations in the permutation test. The results show that, for eQTL datasets with small sample sizes (e.g., 70 individuals), the MVN eGene p values are overall 11% more significant than the permutation-test eGene p values. The overall discrepancy between MVN and permutation-test eGene p values, however, decreases as the sample size increases, and when the sample size is 300 individuals, the median ratio of MVN-approach eGene p values to permuation-test eGene values is 99%. Although this overall discrepancy might not be a problem for eQTL studies with large sample sizes, it could cause MVN eGene p values be more significant than the permutation test e Gene p values when the sample size is small.

Figure 2.

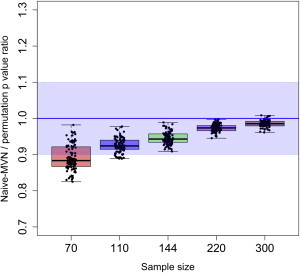
Boxplot of the Ratio of Naive-MVN eGene p Values to Permutation-Test eGene p Values

Using different sample sizes (n = 70, 110, 144, 220, and 300), we measured eGene p values of the two approaches with 1 M permutations and 1 M samplings on 100 probes and computed the ratio of eGene p values between the two methods. A distribution of the ratio on 100 probes is plotted. We excluded outliers with very significant p values to minimize sampling errors in our estimates. Blue shading denotes 90% accuracy.

To correct for this residual discrepancy, we propose the following approach. As shown in Figure 2, this residual discrepancy is only prominent when the sample size is small (e.g., <300). Thus, we can assume that this discrepancy is a characteristic of the dataset, which has a unique sample size and MAF distribution. If this is the case, we can pre-compute the dataset’s mean discrepancy value and use that for further correction. To this end, we sampled 100 genes from the dataset and performed 10,000 permutations to measure residual discrepancy between the permutation p value and MVN p value (with distribution reshaping) at each gene. After we approximated the mean value of discrepancy at this pre-computation step, we corrected for this mean value for every gene in the dataset in the main analysis. Because this pre-computation should be quick, we only used 10,000 permutations, which can only measure discrepancy for moderate p values. Thus, for this pre-computation with 100 genes, we discarded the original p values and measured discrepancy at a randomly sampled p value that was, at most, moderately significant. The assumption is that the degree of residual discrepancy is not highly dependent on the p value level, and this strategy turns out to work well. Specifically, we sampled corrected p values from the interval [0.03, 0.3] by assuming a uniform distribution. This approach is very efficient; estimating the discrepancy took 22.6 min for the brain eQTL dataset and 5.3 hr for the GTEx dataset. We recommend this algorithm when the size of an eQTL study is less than 300 individuals. This small-sample-adjustment algorithm is applied to both Spearman’s rank correlation and Pearson correlation coefficients.

Extreme p Value Approximation

To effectively approximate extremely significant p values, we use two approaches. First, we adaptively increase the number of samplings from MVN up to a very large number (default = 10 M). Note that such a large number of samplings would be impractically slow for permutations, especially with a sample size of thousands of individuals. A MVN with 10 M samplings allows us to robustly approximate very small p values, such as 10⁻⁵ (SE of estimating p = 10⁻⁵ is only ∼10⁻⁶). Second, to approximate p values even more significant than 10⁻⁵, we use the following approach. We approximate the effective number of tests (ratio between the corrected p value and the uncorrected p value) at an extreme threshold (default = 10⁻⁵ to allow accurate estimate). Then, to approximate corrected p values for extremely significant p values, we multiply any uncorrected p values beyond 10⁻⁵ by this effective number.

Speed-up for MVN

We discovered that when the number of cis-SNPs for a gene is much larger than the number of individuals, the efficiency advantage of an MVN over the permutation test diminishes. To increase the efficiency of an MVN approach in such a case, we split a gene into multiple blocks of size 500 kb. We then sampled statistics of SNPs present in each block separately and found the best p value among all blocks. This approach assumes that SNPs in different blocks are independent, and because we use a large window size (500 kb), this assumption holds for a majority of SNP pairs between blocks. We recommend this speed-up for datasets whose average number of cis-SNPs is >2,000. Of the three human datasets used in this paper, we applied this speed-up to the GTEx dataset (average number of cis-SNPs = 2,300).

Brain eQTL Dataset

Gibbs et al.¹³ quantified genome-wide gene-expression levels by using 22,184 probes in four brain regions of 150 individuals. These individuals were also genotyped at 561,466 SNPs. We removed (1) outliers based on overall probe-detection rate and (2) individuals without expression in all tissues, leaving 144 individuals in the analysis. Using the data from these same 144 individuals, we quantile normalized gene expression and performed log₂ transformation for each brain region. We removed probes if their overall detection level among all individuals was less than 95%; the Illumina detection p value of an individual had to be less than or equal to 0.01, and at least 95% of all individuals had to pass this quality control (QC). We performed the following QC for genotype data: Hardy-Weinberg equilibrium (HWE) p value of 0.0001, MAF of 5%, and genotype-missing rate of 5% for a SNP. We adjusted gene expression by using the same covariates used in Gibbs et al. We used 100 random probes that were detected in all four brain regions in our simulation, and we used the gene-expression data from a single region (cerebellum).

Dataset from the GTEx Pilot Study

The GTEx pilot study collected many tissues from multiple individuals and performed RNA-seq to quantify gene expression in those tissues. In our analysis, we used gene expression from whole blood, which had the largest sample size (n = 156) of all tissues collected. Gene-expression values were quantile normalized and corrected for 19 covariates, including three principal components estimated from genotype data, 15 PEER (probabilistic estimation of expression residuals) factors,²³ and gender. All 156 individuals were genotyped at 4.3 M SNPs and imputed with 1000 Genomes Phase I as the reference panel. After filtering out SNPs with MAF < 5% and SNPs that failed QC, we were left with about 6.8 M SNPs. For imputed SNPs, we used the best-guess genotypes. For our analysis, we focused on 3,123 genes present in chromosome 1.

HapMap 3 eQTL Dataset

We downloaded HapMap 3 normalized gene-expression data from ArrayExpress (series accession numbers E-MTAB-198 for the CEU (Utah residents with ancestry from northern and western Europe from the CEPH collection) population and E-MTAB-264 for seven additional populations).¹² For genotype data, we used the third release of HapMap phase 3, which includes data from 1,397 individuals genotyped at 1.4 M SNPs.²⁴ In our analysis, we used genotype and expression data from 716 individuals. We applied the following SNP QC: HWE p value of 0.0001, MAF of 5%, and genotype-missing rate of 1% for a SNP. We randomly selected 100 probes for which the number of cis-SNPs ranged from 265 to 1,251.

Evaluating Accuracy of p Value Approximation

In each of the genes in each dataset, we obtained an eGene p value by using our MVN approach. To evaluate the accuracy, we also obtained the gold-standard permutation p value by using up to 5 B (billion) permutations. Let pi be the MVN p value of gene i, and let qi be the permutation p value of gene i. We defined the accuracy of our method in each dataset by using the error rate of pi, which is

$$\text{error}\text{rate}=\left|1-\frac{pi}{qi}\right|.$$ (Equation 2)

We then defined the accuracy within a dataset as the average of (1 − error rate) over all genes. Obviously, the accuracy would be 100% if the MVN p values were perfectly accurate and would drop from 100% as the p values became inaccurate in either a conservative or anti-conservative direction.

Results

Comparison of Runtime between Permutation Test and MVN

We measured the runtimes of the permutation test and our MVN approach by using the brain eQTL (n = 144) and the HapMap 3 eQTL (n = 716) datasets. We used these two eQTL datasets to measure the runtime in different sample sizes (n = 70, 110, 144, 220, 300, 716, 2,000, and 10,000 individuals) by taking subsets of those individuals or by copying individual data multiple times. We randomly selected one probe from each dataset. In each selected probe, there were 245 and 1,060 cis-SNPs in the brain and HapMap 3 eQTL datasets, respectively. We measured the runtime in hours for 10 M permutations and 10 M samplings for the permutation test and an MVN, respectively. We implemented and optimized both the MVN and the permutation test by using the Intel Math Kernel Library (MKL) to make an impartial comparison between the two approaches.

Results of the runtime comparison demonstrated that our MVN approach is more than 600 times faster than the permutation test when the sample size is as large as 10,000 (Table 2). Even when the sample size is small (e.g., 70), our method is 25 times faster. As the sample size increases, the ratio of MVN runtime to permutation-test runtime also increases because the time complexity of our method does not depend on the sample size, whereas the permutation test does. This means that for recent large eQTL studies that contain data from more than 1,000 individuals,^9–11 our MVN approach would be at least 60 times faster than the permutation test while generating almost-identical eGene p values. Interestingly, the runtime of the permutation test increases slightly sub-linearly with the sample size, probably because of optimization techniques implemented in Intel MKL. We did not use the speed-up algorithm, which splits a gene into multiple windows, for our MVN approach in this comparison (Table 2).

Table 2.

Comparison of Runtime between the MVN Approach and Permutation Test on Different Sample Sizes for 10 M Permutations and 10 M Samplings

	No. of cis-SNPs
	245–247					1,060
Sample size	70	110	144	220	300	716	2,000	10,000
MVN runtime (hr)	0.09	0.09	0.1	0.09	0.09	0.68	0.69	0.77
Permutation runtime (hr)	2.41	2.71	3.12	3.71	4.49	37.56	95.08	487.49
Efficiency gain	25.78	28.77	32.77	39.33	48.09	55.6	138.35	632.65

We used the brain eQTL dataset for sample sizes of 70, 110, 144, 220, and 300 and the HapMap 3 eQTL dataset for sample sizes of 716, 2,000, and 10,000. We performed 1,000–100,000 permutations and 1,000–100,000 samplings, depending on the sample size and method, and extrapolated the runtime for 10 M permutations and 10 M samplings. Both approaches were implemented with the Intel MKL. The average runtime of ten different runs is reported.

We also measured the runtime of the two approaches for the GTEx dataset, and the MVN took 3,700 central processing unit (CPU) hr to perform 10 M samplings on 3,123 genes in chromosome 1, whereas the permutation test took 10,831 CPU hr to perform 1 M permutations. This means that the MVN is 29 times faster than the permutation test for the same number of samplings and permutations. If we applied our MVN approach to all genes in the whole genome, the runtime would be about 15 days, using a cluster with 100 CPUs and assuming 31,000 genes genome-wide, which is ten times more than the number of genes in chromosome 1 (or, 1.5 days if we chose 1 M samplings instead of 10 M). Nowadays, this can be feasibly accomplished with a computing cluster with moderate computing resources. However, the permutation test would take more than a year to perform the same number of permutations with the same number of CPUs. Note that the GTEx dataset has characteristics (relatively small sample size) that are not preferable for gaining speed over our approach. Thus, speed gain in this dataset (29 times) can be thought of as a lower bound of the gain that we can generally obtain for other datasets. We used the speed-up algorithm for an MVN approach in the GTEx dataset because its average number of cis-variants is larger than 2,000.

The Naive MVN Can Yield Inaccurate eGene p Values

We call the pure MVN approach, without our distribution-reshaping and small-sample-adjustment techniques, the “naive MVN.” Here, we show that the naive MVN can often be inaccurate, particularly in small studies. We applied the naive MVN approach and permutation test to 100 probes randomly selected from the brain eQTL dataset collected by Gibbs et al.¹³ (see Material and Methods). This dataset contains 144 individuals, and we found SNPs in cis with each probe within 1 Mb of a TSS. We performed 10 M permutations in the permutation test and 10 M samplings in the naive MVN. For significant eGene p values, we performed more permutations and samplings (e.g., up to 5 B). We estimated eGene p values of the 100 probes by using both a naive MVN approach and the permutation test, and for each probe, we computed p value ratios between the two approaches. We used the Spearman’s rank correlation coefficient for test statistics.

Results showed that there are two problems with the naive MVN approach (green dots in Figure 3). The first problem is that for significant eGene p values, p values from an MVN are more anti-conservative than those from the permutation test; in Figure 3, there are three probes whose eGene p values from the permutation test were smaller than 10⁻⁴, and the ratio between the two methods was less than 90%. The ratio decreased as the p values from the permutation test decreased, and the ratio was only 70% for the probe with the most significant p value. The second problem is that even for non-significant eGene p values between 1 and 0.1, there exists an overall p value discrepancy between the naive MVN approach and the permutation test. The overall discrepancy was about 5% in this eQTL dataset.

Figure 3.

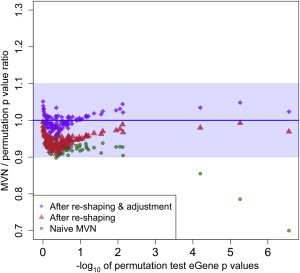
Comparison of MVN eGene p Values to Permutation-Test eGene p Values

We used the brain eQTL dataset and estimated eGene p values on the random 100 probes by using the two approaches. The x axis is the −log₁₀ of eGene p values from the permutation test, and the y axis is the ratio of naive-MVN eGene p values to permutation-test eGene p values. The dataset contains data from 144 individuals, and we performed 10 M permutations in the permutation test and 10 M samplings in an MVN to estimate eGene p values. For probes with significant p values, we performed up to 5 B permutations and 5 B samplings to accurately estimate eGene p values. Green circles denote the ratio from a naive MVN approach. Red triangles represent the ratio after application of the distribution-reshaping algorithm to an MVN. Purple diamonds represent the ratio after application of both the distribution-reshaping and small-sample-adjustment algorithms. Blue shading denotes 90% accuracy.

Our MVN Algorithm Generates Accurate eGene p Values

We propose two algorithms to scale MVN p values such that they approximate the true null distribution of the permutation test accurately. The first approach is to scale an MVN p value of a single SNP. We observed a higher discrepancy in the null distribution between an MVN and the permutation test on the single-marker test statistic for smaller sample size and more-significant p values (Figure 1). Our approach to correct for this discrepancy was to measure the discrepancy in the null distribution at various MAFs, sample sizes, and significance thresholds and to scale an MVN p value according to the discrepancy (see Material and Methods). This approach is similar to the one Han et al.²¹ used to scale MVN p values for multiple-testing correction in GWASs. After application of our distribution-reshaping algorithm, an MVN yielded more accurate eGene p values on the three probes with significant p values (red dots in Figure 3).

The second algorithm we developed attempts to correct for the overall discrepancy in eGene p values between an MVN and the permutation test when the sample size is small. For example, the overall or average discrepancy between the two methods is about 5% for the brain eQTL dataset, which contains 144 individuals. We found that this discrepancy decreases as the sample size increases (Figure 2), and when the sample size is 300, little discrepancy is present between the two methods. Our small-sample-adjustment approach pre-computes the overall discrepancy by using a subset of probes and scales the MVN eGene p values according to the discrepancy (see Figure S1).

After applying both of our algorithms, we found that eGene p values from an MVN approach were very close to those from the permutation test (purple dots in Figures 3 and 4); the average ratio of MVN eGene p values to permutation-test eGene p values was 1, the minimum was 0.96, and the maximum was 1.05. The average ratio was 1 because of the small-sample-adjustment algorithm. An average error rate, defined as the average of the absolute value of (1 − ratio) over 100 genes, was 1.56%, and accuracy, which is (1 − average error rate), was 98.44%. This shows that for the 100 probes from the brain eQTL dataset, our MVN approach yielded p values within 5% of the p values from the permutation test. It is important to note that the extreme p value approximation for the MVN approach discussed in the Material and Methods was not applied here, and we used the Spearman’s rank correlation coefficient to estimate correlation between gene expression and genotypes and to estimate the scaling factors.

Figure 4.

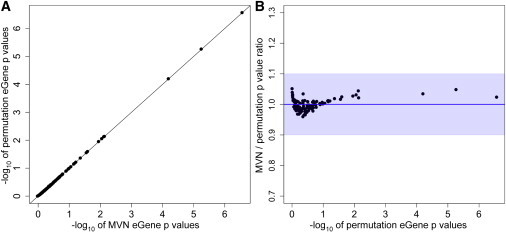
Results of Our MVN Approach Applied to 100 Probes in the Brain eQTL Dataset

We applied both distribution-reshaping and small-sample adjustment.

(A) The direct comparison of eGene p values from our MVN approach to those from the permutation test; the x axis is the −log₁₀ of MVN eGene p values, and the y axis is the −log₁₀ of the permutation-test eGene p values. A y = x line is drawn as a black line.

(B) The ratio of MVN eGene p values to permutation-test eGene p values (y axis) versus the −log₁₀ of permutation-test eGene p values (x axis). A y = 1 line is drawn as a red line. The maximum ratio is 1.05, the minimum ratio is 0.96, and the average is 1. The average error rate is 1.56%, and accuracy is 98.44%. Blue shading denotes 90% accuracy.

Next, we tested the Pearson correlation coefficient for our test statistics by using the same 100 genes after applying the rank-based inverse normal transformation. We separately estimated the Pearson-correlation scaling factors, which might be different from those for Spearman’s rank correlation. Results show that the average error rate for the Pearson correlation coefficient is 1.62%, which is very close to that for the Spearman’s rank correlation (Figure S1).

We applied our approach to the HapMap 3 eQTL study¹² to measure the performance of our approach in a larger eQTL dataset. The HapMap 3 eQTL dataset has 716 individuals, and we chose 100 random probes (see Material and Methods). We performed 100 M permutations and 100 M samplings for the permutation test and an MVN, respectively. We used the Spearman’s rank correlation coefficient for test statistics. Probes that contained SNPs with very significant p values (<10⁻⁷) were excluded from the analysis because they required many more than 100 M permutations. We then applied the distribution-reshaping algorithm. Results showed that the average ratio of MVN eGene p values to permutation-test eGene p values was 0.991, even without the small-sample-adjustment algorithm (Figure 5). The minimum and maximum ratios were 0.979 and 1.024, respectively, and the average error rate over 100 probes was 1% with 99% accuracy. Hence, our MVN approach generates eGene p values that are almost identical to those generated by the permutation test when the sample size is as large as that of the HapMap 3 eQTL study. It is also important to note that, as expected, the small-sample-adjustment algorithm is not needed for this sample size.

Figure 5.

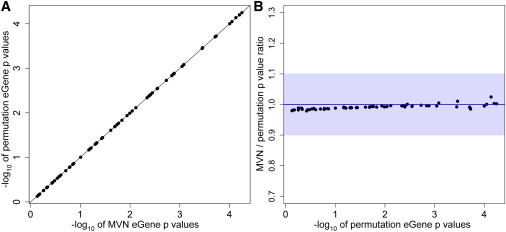
Results of the MVN Approach Applied to 100 Probes in the HapMap 3 eQTL Dataset

Because of the large sample size, we applied only the distribution-reshaping algorithm to an MVN.

(A) The direct comparison of eGene p values from our MVN approach to those from the permutation test; the x axis is the −log₁₀ of MVN eGene p values, and the y axis is the −log₁₀ of the permutation-test eGene p values.

(B) The ratio of MVN eGene p values to permutation-test eGene p values (y axis) versus the −log₁₀ of the permutation-test eGene p values (x axis). The maximum ratio is 1.024, the minimum ratio is 0.979, and the average is 0.991. The average error rate is 1.0%, and accuracy is 99.0%. Blue shading denotes 90% accuracy.

Application to the GTEx Pilot Study

We applied our MVN approach to the GTEx pilot study, which collected gene-expression data from many different tissues. We analyzed 3,123 genes in chromosome 1 from whole blood collected from 156 individuals who were genotyped and imputed at 6.8 M SNPs (see Material and Methods). We estimated eGene p values of those genes by using 10 M samplings for MVN and 10,000 permutations for the permutation test. We performed 10,000 permutations because this is the number of permutations often used in previous eQTL studies. For our MVN approach, we used both distribution-reshaping and small-sample-adjustment algorithms to scale p values, and we also applied the algorithm for approximating extreme p values to correct p values lower than 10⁻⁵. Because thousands of cis-SNPs were present for each gene, we divided each gene into 500-kb blocks and performed MVN sampling on each block to increase efficiency of the MVN (see Material and Methods). The Spearman’s rank correlation coefficient was used for test statistics.

We show the Manhattan plot of all eGene p values in Figure 6A. The plot shows that our MVN approach can estimate eGene p values, including highly significant p values up to 10⁻³⁸, of all genes because of the procedure for approximating extreme p values. By contrast, the p values of the permutation test are limited to 10⁻⁴ because of the number of permutations. The plot indicates that eGenes with permutation p values equal to 10⁻⁴ are not all the same: some p values are just below 10⁻⁴, and some p values are extremely significant, such as 10⁻³⁸. Hence, we could be ignoring important differences in p values among different genes if we use the permutation test.

Figure 6.

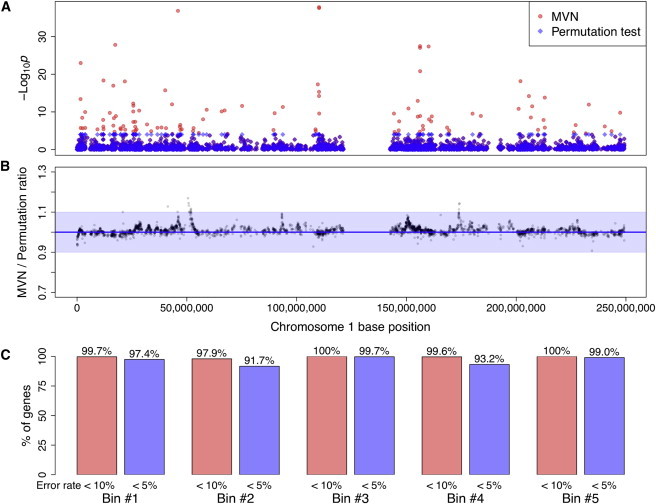
Results of GTEx Pilot Study

(A) Manhattan plot of eGene p values from our MVN approach and the permutation test on 3,123 genes in chromosome 1. We performed 10 M samplings with the algorithm for extreme p value approximation for an MVN and 10,000 permutations, which is the commonly used number of permutations in previous studies, for the permutation test.

(B) Plot showing the ratio of MVN eGene p values to permutation-test eGene p values on the 3,123 genes. We performed 1 M permutations for the permutation test and show the ratios for the genes whose corresponding permutation-test eGene p values were greater than 10⁻⁴. Blue shading denotes 90% accuracy.

(C) The proportion of genes with error rate < 10% and < 5%. Genes are divided into five bins with the same length, and the proportions are shown for each bin.

We then calculated the ratio of MVN eGene p values to permutation-test eGene p values, and to accurately measure this, we performed 1 M permutations for the permutation test and used only genes with permutation eGene p values > 10⁻⁴. Results showed that almost all genes had ratios between 0.9 and 1.1, meaning that for most genes, the error rate of the MVN approach is within 10% (Figure 6B). The average error rate over all genes was 1.57%, and accuracy was 98.43%. We also divided chromosome 1 into five bins with the same length and calculated the proportion of genes with error rates < 10% and < 5% for each bin (Figure 6C). Results demonstrated that a majority (97.9%–100%) of genes had an error rate < 10% for all bins.

Discussion

We have proposed an efficient and accurate MVN approach for performing multiple-testing correction and estimating eGene p values in eQTL studies. We developed strategies to correct for the discrepancies due to small sample sizes and achieved high accuracy regardless of study sample sizes. We applied our MVN approach to three eQTL datasets with different characteristics and demonstrated that our MVN approach yields eGene p values as accurate as those from the permutation test.

A main advantage of our approach over the permutation test is that it is considerably faster. We showed that an MVN is 55 times faster than the permutation test when the sample size is about 700. The time complexity of our approach is independent of the number of individuals, which makes it ideal for eQTL studies with large sample sizes. Recent developments in microarrays and RNA-seq technologies have enabled eQTL studies to collect data on a large number of individuals and one of the largest eQTL studies, by Wright et al.,⁹ has collected data on about 2,500 individuals. This is a similar sample size to that of GWASs, for which the permutation test is not easily feasible. As eQTL studies collect data on more individuals to uncover the genetic basis of gene expression, efficiency bottleneck will become critical in identifying eGenes, and our method can be a suitable solution. Note that even for the smallest dataset that we examined (n = 70), our method was considerably faster than the permutation test (26 times faster), which shows that our method can readily benefit current studies, as well as large future studies.

Another advantage of our approach is that our algorithm for approximating extreme p values allows an MVN to effectively estimate very significant eGene p values. Approximating eGene p values at extreme significance levels is important because it allows studies to prioritize genes for follow-up or replication studies. Using the data from the GTEx pilot study, we demonstrated that the limited number of permutations in the permutation test results in many genes with the same eGene p values (e.g., 10⁻⁴), but our approach yields very different p values such that some are as small as 10⁻³⁸. Our strategy is to use a large number of samplings (10 M) to estimate the effective number of tests at an extreme threshold (10⁻⁵) and apply the effective number to p values beyond the threshold. The limitation of this approach is that the effective number can also change beyond this threshold.²⁵ Therefore, the accuracy of multiple-testing correction for those extreme p values can be lower than the accuracy for the other p values. The creation of an even more accurate multiple-testing correction of the extreme p values can be an interesting future research direction.

Several software packages, such as Matrix eQTL,²⁶ are available for performing eQTL analysis efficiently. Although Matrix eQTL is efficient at estimating p values of SNP and gene pairs, it does not support the estimation of eGene p values explicitly. One can manually permute expression values and perform the permutation test by using Matrix eQTL. However, the time complexity of this procedure still depends on the number of individuals, and hence it will be slower than our MVN approach for large studies.

Our distribution-reshaping algorithm is inspired by an MVN approach called SLIDE,²¹ which performs multiple testing for GWASs and uses a similar distribution-reshaping algorithm. However, there are two major differences between our algorithm and the one in SLIDE. One is that our algorithm is for quantitative traits, whereas SLIDE only considers binary traits. For binary traits, it is relatively quicker and easier to estimate the TF ratio with the contingency table. However, this is not possible for quantitative traits, and we had to measure the TF ratio empirically for various sample sizes and MAFs, which is a more complicated process. Moreover, we separately built the TF-ratio information for a non-parametric test (Spearman’s rank correlation) and a parametric test (Pearson’s correlation) to support a wide range of eQTL analyses. Another difference is that our approach additionally applies a new small-sample-adjustment algorithm that scales every MVN eGene p value by a constant factor. This is not necessary for SLIDE, which considers the sample sizes of GWAS datasets, which usually involve thousands of individuals. Our finding suggests that when sample size is small, there might be a residual discrepancy in eGene p values between an MVN and the permutation test, and this needs to be corrected by direct comparison of eGene p values between the two approaches.

Our approach is based on the current practice that, to find eGenes, investigators test each cis-variant of a gene and perform multiple-testing correction. To answer the question of whether a gene is an eGene, different strategies are also possible. For example, if multiple variants near the TSS have moderate effects on expression levels, we can boost the signal by combining information from multiple variants. In that sense, eGene identification can be related to gene-based tests²⁷ or rare-variant association tests.²⁸ We expect that further research will be needed to evaluate what is the optimal strategy for eGene identification.

Recently, several eQTL studies, including the GTEx study,⁶ have collected gene-expression data from multiple tissues, and there is a growing interest in detecting eQTLs from those tissues.^7,15 One can increase statistical power to detect eQTLs and also eGenes by combining information across multiple tissues, and the permutation test is applied similarly to detect eGenes in both multi-tissue and single-tissue eQTL studies. However, approaches that attempt to identify eQTLs from multiple tissues are generally much more computationally intensive than approaches that detect eQTLs in a single tissue. Hence, the computational burden of the permutation test is considerably heavier in multi-tissue eQTL studies. Our MVN approach can be extended to detect eGenes from multiple tissues in the framework of Meta-Tissue,⁷ which we recently published. Meta-Tissue is a meta-analysis-based approach for identifying eQTLs from multiple tissues and utilizes two different meta-analysis methods: fixed effect and random effect. We can estimate correlation between two SNPs across multiple tissues by using the idea of Conneely and Boehnke,²⁹ and hence we can accurately estimate eGene p values by using our MVN framework. We tested this approach on five genes in the multi-region brain eQTL dataset and found that for the fixed-effect model of Meta-Tissue, our MVN approach yields p values very similar to those from the permutation test on those five genes (average error rate of 2.1%; Table S1). We discovered that the current multiple-testing-correction framework might perform slightly worse for the random-effect model of Meta-Tissue (average error rate of 3.6%), which is expected because Conneely and Boehnke primarily assumed the fixed-effect model. We are currently investigating the possibility of extending the framework to the random-effect model and are planning to apply it to the GTEx study.

Web Resources

The URL for data presented herein is as follows:

• eGene-MVN, http://genetics.cs.ucla.edu/egene-mvn/