Improved Ancestry Estimation for both Genotyping and Sequencing Data using Projection Procrustes Analysis and Genotype Imputation

Abstract

Accurate estimation of individual ancestry is important in genetic association studies, especially when a large number of samples are collected from multiple sources. However, existing approaches developed for genome-wide SNP data do not work well with modest amounts of genetic data, such as in targeted sequencing or exome chip genotyping experiments. We propose a statistical framework to estimate individual ancestry in a principal component ancestry map generated by a reference set of individuals. This framework extends and improves upon our previous method for estimating ancestry using low-coverage sequence reads (LASER 1.0) to analyze either genotyping or sequencing data. In particular, we introduce a projection Procrustes analysis approach that uses high-dimensional principal components to estimate ancestry in a low-dimensional reference space. Using extensive simulations and empirical data examples, we show that our new method (LASER 2.0), combined with genotype imputation on the reference individuals, can substantially outperform LASER 1.0 in estimating fine-scale genetic ancestry. Specifically, LASER 2.0 can accurately estimate fine-scale ancestry within Europe using either exome chip genotypes or targeted sequencing data with off-target coverage as low as 0.05×. Under the framework of LASER 2.0, we can estimate individual ancestry in a shared reference space for samples assayed at different loci or by different techniques. Therefore, our ancestry estimation method will accelerate discovery in disease association studies not only by helping model ancestry within individual studies but also by facilitating combined analysis of genetic data from multiple sources.

Introduction

The advent of next-generation sequencing has greatly expanded opportunities for investigation of the genetic architecture of complex diseases. Although genome-wide association studies (GWASs) have successfully identified thousands of common variants associated with human diseases and traits,¹ these association variants often explain a small proportion of the heritability and provide incomplete information about the functional mechanism of the disease.²

Many recent studies have shifted their focus to rare variants that are more likely to have direct functional impacts on gene products. Because these variants are rare, a large sample size and cost-effective approaches (such as targeted sequencing of candidate genes or the whole exome) are important to ensure sufficient statistical power.³ More recently, studies have employed the exome chip genotyping array, which includes protein-altering variants discovered by large-scale exome sequencing studies and provides a cost-effective way to assay rare variants in a large number of exomes.^4,5 Applications of targeted sequencing and exome chip genotyping have discovered several disease-associated rare coding variants, leading to important biological insights for several complex diseases.^4–9

Control of population stratification is important for large-scale genetic association studies to avoid spurious association signals caused by ancestry difference in the study sample.^10–13 Population structure can confound genetic association tests even when all study subjects are Europeans,¹⁴ highlighting the importance of estimating fine-scale ancestry. Principal-component analysis (PCA) and analogous dimension reduction techniques have been widely used to disentangle complex genetic structure and to control for population stratification in GWASs, where genome-wide genotypes are available.^15–20

Extensions of PCA-based methods have also been developed to estimate individual ancestry directly from low-coverage sequencing data when genotypes cannot be accurately estimated.^21–23 For example, using the LASER method (v.1.0) and genotypes of a set of reference individuals from the Human Genome Diversity Project (HGDP),²⁴ we can accurately estimate an individual’s continental ancestry based on off-target sequence reads generated by targeted or exome sequencing experiments.²² We have applied LASER 1.0 to facilitate identification of additional ancestry-matched controls from public resources to increase statistical power in a targeted sequencing study of age-related macular degeneration (AMD).⁸ However, estimation of fine-scale ancestry within Europe remains challenging when the sequencing depth is <0.1×.²² Estimation of fine-scale ancestry will become more challenging in the future, because fewer off-target reads will be produced when the efficiency of the capture technology in targeted sequencing experiments improves.

As more genetic data are generated by different techniques, joint analysis of data from multiple sources is becoming an attractive approach to increase sample size and statistical power for rare variant association studies. Such analysis requires estimating individual ancestry for different datasets in a consistent manner so that background ancestry can be carefully matched across datasets. For example, if we can place both exome chip genotyped samples and targeted sequenced samples into the same reference ancestry space, we might be able to use exome chip genotyped controls to boost statistical power in a targeted sequencing study. The framework of LASER 1.0 can be extended to analyze genotyping data by constructing a sample-specific PCA map for each individual using markers that overlap with the reference panel and using Procrustes analysis to transform the coordinates of the study individual into the reference ancestry space.^22,25 However, similar to the challenge in analyzing extremely low-coverage sequencing data, we show that this simple extension does not work well on exome chip genotyping data, particularly when the goal is to estimate fine-scale ancestry such as distinguishing different populations within Europe.

To overcome the limitations of LASER 1.0 when the amount of available data for each individual is small, we introduce a novel approach based on projection Procrustes analysis,²⁶ which is implemented in LASER 2.0 for analyzing either genotypes (Figure 1) or sequence reads (Figure S1). Different from the standard Procrustes analysis, which identifies optimal transformations, including scaling, translation, rotation, and reflection, between two sets of coordinates of the same dimension,^27,28 projection Procrustes analysis enables projection from a higher-dimensional space to a lower-dimensional space.²⁶ This approach can improve our ancestry estimation by integrating ancestry information from higher-order PCs of the sample-specific PCA map. We further demonstrate that genotype imputation on the ancestry reference panel, in combination with projection Procrustes analysis, can substantially improve estimation of fine-scale European ancestry for both exome chip genotyping data and low-coverage sequencing data. Using targeted sequencing data from our AMD study,⁸ we show that the improvement of ancestry estimation is more evident for samples that have extremely low coverage in the off-target regions and for which ancestry cannot be accurately estimated via LASER 1.0.²² Overall, the novel algorithm of LASER 2.0 enables us to obtain accurate genetic ancestry information in several challenging settings where LASER 1.0 doesn’t work well, including finer-scale ancestry with extremely low coverage sequencing data or with exome chip genotypes. Furthermore, LASER 2.0 can produce comparable ancestry estimates in a shared ancestry space for samples assayed at different loci or by different techniques. With these features, our estimates will be useful in facilitating integrative analysis of different data sources to increase statistical power for discovery of disease susceptibility alleles.

Figure 1.

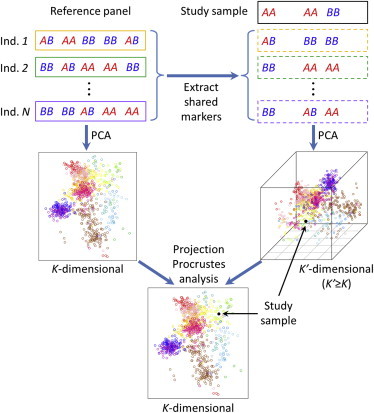
Graphical Illustration of the Algorithm for Estimating an Individual’s Genetic Ancestry using Genotype Data

This algorithm was implemented in the trace program as part of the LASER 2.0 package. A similar algorithm for analyzing sequence reads is illustrated in Figure S1.

Material and Methods

HGDP and POPRES Data

We used the Human Genome Diversity Project (HGDP) dataset²⁴ as the reference panel for analysis of worldwide ancestry and the European dataset from the Population Reference Sample (POPRES)²⁹ as the reference panel for analysis of European ancestry. Quality control (QC) procedures for these two datasets were described in Wang et al.²² After QC, the HGDP dataset includes genotypes across 632,958 autosomal SNPs for 938 unrelated individuals from 53 worldwide populations, and the POPRES dataset includes 318,682 autosomal SNPs for 1,385 unrelated individuals from 37 European populations.

Imputed POPRES Data

We imputed the PORPES data using haplotypes of 1,092 individuals sequenced in Phase 1 of the 1000 Genomes Project.³⁰ We first phased the POPRES data using MaCH³¹ with 500 hidden Markov states and 30 iterations. We then used Minimac³² to impute the POPRES data in chunks of 2,500 loci (with 500 overlapping loci between consecutive chunks). After imputation, we excluded imputed SNPs that have minor allele frequency (MAF) < 5% or estimated imputation r² < 0.8, resulting in genotypes for an additional 3,853,445 SNPs. Combining these imputed genotypes with the original POPRES genotypes, we created an expanded POPRES reference panel that includes 4,172,127 autosomal SNPs.

AMD Data

The AMD targeted sequencing data consist of 3,158 samples.⁸ These data had previously been analyzed using LASER 1.0²² and we re-analyzed the data to illustrate the improvements in LASER 2.0. We defined off-target loci as loci that have mean coverage <4× across all sequenced samples. After excluding bases with mapping quality score < 30 (Phred scale) and recalibrated base quality score < 20 (Phred scale), the average off-target coverage is 0.196× in loci overlapping with the HGDP data, 0.215× in loci overlapping with the POPRES data, and 0.305× in loci overlapping with the expanded POPRES data after imputation. The sequencing error rate at locus j of individual i, ϵ_ij, was estimated using the recalibrated base quality scores in the BAM file for bases at each locus after filtering low-quality bases. We also have GWAS data (316,475 SNPs in total, including 47,237 SNPs that overlap with the POPRES data) for 901 of these samples, enabling us to compare ancestry estimates derived using targeted sequencing data with those derived using GWAS genotypes.³³

The LASER 2.0 Method

Overview

LASER 2.0 includes two programs (named trace and laser) implementing a unified framework for estimating individual ancestry using genotypes or sequence reads as input, respectively. The algorithm for analyzing genotyped samples (trace) is illustrated in Figure 1. We first construct a K-dimensional ancestry map by applying PCA on genotypes of a set of N reference individuals. For each study sample, we perform an additional PCA on genotypes across overlapping markers between the study sample and N reference individuals to obtain a K′-dimensional map of N + 1 individuals (K′ ≥ K). We then use projection Procrustes analysis to identify an optimal set of transformations on the sample-specific PCA map to maximize its similarity to the reference ancestry map.²⁶ Using the transformations, we can place the study sample into the reference ancestry map and obtain individual ancestry information. Unlike LASER 1.0,²² which uses the standard Procrustes analysis (equivalent to K′ = K), the projection Procrustes analysis approach enables incorporation of additional information from high-dimensional PCs to increase the accuracy and robustness of our ancestry estimation. This procedure is repeated for all study samples one at a time until all samples are placed into the same reference ancestry space. The algorithm for analyzing sequenced samples (laser) follows the same framework except that in analyzing each sequenced sample, we simulate sequence reads for the reference individuals to match the quality and coverage pattern of the sequenced sample and perform PCA on the combined sequencing data to obtain the sample-specific PCA map (Figure S1). Simulation of sequence reads for the reference individuals follow a binomial model described in Wang et al.²²

Principal-Component Analysis

We use a standard PCA to construct the reference ancestry space.^15,22 Genotypes for N reference individuals across L loci are coded as an N × L matrix G, in which G_ij = 0, 1, 2, or missing for i = 1, … N and j = 1,2, … L. We impute the missing data in G with corresponding column mean μ_j, and standardize G by subtracting μ_j and dividing by standard deviation σ_j for all columns (j = 1,2, … L). Denoting the standardized genotype matrix as Q_{N × L}, we calculate PCA coordinates by applying eigenvalue decomposition (EVD) of the N × N genetic relationship matrix M₀ = QQ^T. The reference PCA coordinates are recorded as an N × K matrix Y for the top K PCs.

To compute sample-specific PCA for a genotyped sample h, we focus on loci that are in the reference panel, denoted as a 1 × L vector S_h. We standardize S_h using ${\mathit{S}}_{hj}^{\text{'}}=\left({\mathit{S}}_{hj}-{\mu }_j\right)/{\sigma }_j$ for j = 1,2, … L, where μ_j and σ_j were previously computed using the reference genotypes G. If S_hj is missing, we impute S_hj with μ_j so that ${\mathit{S}}_{hj}^{\text{'}}=0$. To account for different levels of missing data in the study samples, we compute $\mathit{M}={\mathit{M}}_0-\tilde{\mathit{Q}}{\tilde{\mathit{Q}}}^T,$ where $\tilde{\mathit{Q}}$ is a submatrix of Q for loci that are missing in S_h. The computation of $\mathit{M}={\mathit{M}}_0-\tilde{\mathit{Q}}{\tilde{\mathit{Q}}}^T$ is typically fast, because M₀ is pre-computed and the missing data rate is usually low in each study sample such that $\tilde{\mathit{Q}}$ is much smaller than Q. We then augment M to an (N + 1) × (N + 1) matrix M′ with the additional row (and column) equal to ${\mathit{S}}_h^{\text{'}}{\mathit{Q}}^T$. We apply EVD on M′ to obtain a new set of coordinates in a K′-dimensional space (K′ ≥ K), recorded as an N × K′ matrix X for N reference individuals and a 1 × K′ vector Z_h for the study sample h.

Projection Procrustes Analysis

Projection Procrustes analysis generalizes the standard Procrustes approach used in LASER 1.0 to analyze coordinate sets of different dimensions.²⁶ Given two sets of coordinates for the same N reference individuals, ${\mathit{X}}_{N\times K^{\text{'}}}$ and Y_{N × K} (K′ ≥ K), projection Procrustes analysis aims to find a set of transformations f to project X from a K′-dimensional space to a K-dimensional space and minimize the sum of squared Euclidean distances between f(X) and Y. Assuming that both X and Y have been centered to the origin (i.e., by subtracting the column mean), the objective is to find an orthonormal projection matrix ${\mathit{A}}_{K^{\text{'}}\times K}$ and an isotropic scaling factor ρ such that ${\Vert \rho \mathit{XA}-\mathit{Y}\Vert }_F^2$ is minimized. Here, we use the notation ${\Vert \mathit{X}\Vert }_F^2$ to represent the square of the Frobenius norm of matrix X, i.e., ${\Vert \mathit{X}\Vert }_F^2=\text{tr}\left(\mathit{X}{\mathit{X}}^T\right)$. When K′ = K, this optimization problem corresponds to the standard Procrustes analysis^27,28 and the solution is given by A = VU^T and ρ = tr(Λ)/tr(X^TX), where U, Λ, and V are singular value decomposition (SVD) of Y^TX = UΛV^T. When K′ > K, this optimization problem does not have a closed form solution and needs to be solved numerically.²⁶ Let’s denote the submatrix of the last K′ − K columns of matrix X as ${\left[\mathit{X}\right]}_{K^{\text{'}}-K}$. We use the following iterative algorithm to find a numerical solution (algorithm 5.1 in Gower and Dijksterjuis²⁶):

• Step 1. Augment Y to an N × K′ matrix $\tilde{\mathit{Y}}$ with K′ − K zero columns.

• Step 2. Perform SVD on ${\tilde{\mathit{Y}}}^T\mathit{X}$, i.e., ${\tilde{\mathit{Y}}}^T\mathit{X}=\mathit{U\Lambda }{\mathit{V}}^T$.

• Step 3. Calculate $\tilde{\mathit{A}}=\mathit{V}{\mathit{U}}^T$, ρ = tr(Λ)/tr(X^TX), and $f\left(\mathit{X}\right)=\rho \mathit{X}\tilde{\mathit{A}}$. Note that $\tilde{\mathit{A}}$ is a K′ × K′ rotation matrix.

• Step 4. If $\left({\Vert {\left[f\left(\mathit{X}\right)-\tilde{\mathit{Y}}\right]}_{K^{\text{'}}-K}\Vert }_F^2/{\Vert {\left[f\left(\mathit{X}\right)\right]}_{K^{\text{'}}-K}\Vert }_F^2\right)<\tau$, let A be a K′ × K submatrix of the first K columns of $\tilde{\mathit{A}}$ and exit. Here τ is a small positive number to control the convergence of the numerical solution.

• Step 5. Replace ${\left[\tilde{\mathit{Y}}\right]}_{K^{\text{'}}-K}$ by ${\left[f\left(\mathit{X}\right)\right]}_{K^{\text{'}}-K}$ and go to Step 2.

This algorithm basically translates the K′-to-K-dimensional Procrustes problem into a series of K′-to-K′-dimensional standard Procrustes problems (Steps 2 and 3) by augmenting Y with additional K′ − K columns taken from f(X) in each iteration (Step 5). We set τ = 10⁻⁶ in our analyses and the algorithm usually converges quickly after a few iterations when K′ is small. After convergence, the coordinates of sample h in the K-dimensional reference space are calculated as ${\mathit{Z}}_h^{\ast }=f\left({\mathit{Z}}_h\right)=\rho {\mathit{Z}}_h\mathit{A}$.

Choosing the Values of K and K′

The value of K defines the dimension of the reference ancestry space and is specified by users according to the features of each ancestry reference panel and their study objectives. For example, following Wang et al.,²² we chose K = 4 to construct the worldwide reference ancestry space based on the HGDP genotypes (632,958 autosomal SNPs) because major continent groups can be well separated by the top four PCs, despite the fact that higher-order PCs can further separate different populations within continents. We used the top two PCs based on the POPRES data without imputation (318,682 autosomal SNPs) to define the European reference ancestry space (K = 2), because the top two PCs reflect the geographic distribution of European populations while higher-order PCs are difficult to interpret (Figure S2). We used the same European reference ancestry map when using the imputed POPRES data as the reference panel. Our choices of K are primarily for the ease of interpretation in our examples of estimating continental ancestry and European ancestry.

We evaluated the performance of the programs laser and trace over different specified values for K′. The value of K′ can also be automatically determined by our programs as the number of significant PCs in each sample-specific PCA (p < 0.1, Tracy-Widom test¹⁵). We chose a less stringent nominal level of 0.1 instead of the typical choice of 0.05 because including more ancestry informative PCs can improve our ancestry estimation and our algorithm is not sensitive to the inclusion of a small number of non-informative PCs. Note that the number of significant PCs might vary for different study samples even when using the same reference panel. In our simulations, we found that using K′ = 20 performs substantially better than a smaller K′ and that little improvement is gained when K′ > 20 (see Results). We therefore recommend K′ = 20 in real data examples.

Measurements of Estimation Accuracy

When genome-wide SNP data are available, we used the program trace with K′ = K to derive ancestry estimates based on genome-wide SNP data. We then compared our ancestry estimates based on exome chip genotypes or low-coverage sequence reads to those based on genome-wide SNPs using a Procrustes similarity score t₀.²⁷ The Procrustes similarity score ranges from 0 to 1 and we showed that it is a weighted mean of the Pearson correlations between two sets of coordinates along different PCs (see Appendix). t₀ = 1 means two sets of coordinates are perfectly correlated with each other in all PCs after Procrustes transformations, and t₀ = 0 means two sets of coordinates have no correlation along any of the PCs. For each sample h, LASER also reports a sample-specific Procrustes similarity score t between Y and the first K columns of f(X), which measures how well the sample-specific PCA map can be matched to the reference ancestry map and which partly reflects the estimation accuracy of ${\mathit{Z}}_h^{\ast }$. Different from t₀, which is calculated by comparing two sets of estimated coordinates for the study samples, t is calculated based on coordinates of the reference individuals in the reference ancestry space and in a sample-specific PCA map. A small value of t indicates the ancestry estimates of the study sample is inaccurate; however, a high value of t does not guarantee accurate ancestry estimates of the study sample due to potential factors of overfitting and incomplete ancestry representation of the reference panel (see Discussion).

Ancestry Estimation using Exome Chip Genotypes

Because the trace program in LASER 2.0 uses only genotypes across SNPs shared with the reference panels, we designed the following experiments to test the performance of our method on exome chip genotyping data. We split the HGDP dataset into a test set of 238 randomly selected individuals and a reference set of the remaining 700 individuals. Similarly, we split the POPRES dataset and the imputed POPRES dataset into a test set of 385 randomly selected individuals and a reference set of the remaining 1,000 individuals. We extracted genotypes for the test set on SNPs that were included in the exome chip design list (see Web Resources). The exome chip design list consists of 273,468 SNPs in total, including 12,580 SNPs shared with the HGDP data, 3,983 SNPs shared with the POPRES data, and 19,123 SNPs shared with the imputed POPRES data. We then applied the trace program on the shared SNPs to estimate ancestry for the test individuals in ancestry spaces defined by the HGDP reference set and the POPRES reference set.

Ancestry Estimation using Low-Coverage Sequencing Data

Simulation

We focused on estimating fine-scale European ancestry in this simulation. We took empirical sequencing depth across loci in the POPRES data and the imputed POPRES data for 385 randomly selected samples from the National Heart, Lung, and Blood Institute (NHLBI) Exome Sequencing Project (ESP).³⁴ To mimic the off-target coverage in an efficient exome capture experiment, we set the coverage for on-target loci to 0 and reduced the off-target coverage to 5% of the original value by drawing new coverage $C_{ij}^{\text{'}}\sim \text{Binomial}\left(C_{ij},0.05\right)$ for i = 1,2, …, 385 and j = 1,2, … L, where C_ij is the original off-target coverage for locus j of the i^th selected ESP sample. Conditional on the new coverage patterns and genotypes of 385 individuals in the POPRES test set, we simulated off-target sequencing reads for 385 Europeans with sequencing error rate ϵ = 0.01 per base. We applied the laser program on the simulated sequencing data to project these samples into the ancestry space defined by the POPRES reference set.

Analysis of the AMD Targeted Sequencing Data

Because most of the AMD samples are Europeans,⁸ we first excluded non-European outliers and then focused on estimating fine-scale ancestry for the European samples in the POPRES reference space. All the analyses were based on off-target sequence reads. We used the following algorithm to identify non-European outliers: (1) use the laser program with K = 4 and K′ = 20 to place AMD samples into the HGDP worldwide ancestry space; (2) calculate the mean and standard deviation of Europeans in each of the top K PCs using the HGDP Europeans; (3) define an AMD sample as an outlier if the sample is more than 5 SDs away from the mean European coordinates in any one of the top K PCs; (4) recalculate the mean and standard deviation of Europeans in each PC using coordinates of HGDP Europeans and non-outlier AMD samples; and (5) repeat steps 3 and 4 until the outlier set does not change. In total, we excluded 92 non-European ancestry outliers. We then used the laser software to estimate fine-scale ancestry for the remaining samples using either the original POPRES reference panel with K = K′ = 2 (a setting used in LASER 1.0²²) or the imputed POPRES reference panel with K = 2 and K′ = 20 (a setting recommended in LASER 2.0).

Results

Estimation of Worldwide and European Ancestry using Exome Chip Genotypes

The exome chip was designed to include primarily nonsynonymous SNPs within protein coding regions and therefore has a small number of overlapping SNPs with GWAS arrays. We show that by using 12,580 exome chip SNPs shared with the HGDP data, we can accurately estimate worldwide ancestry in a 4-PC ancestry space defined by the HGDP genotypes (Figure S3). Using either the standard Procrustes analysis (i.e., K = K′ = 4) or the projection Procrustes analysis (K = 4 and K′ = 20), exome chip-based PC coordinates for the 238 tested samples are highly similar to those derived using all 632,958 HGDP genotyped SNPs (t₀ = 0.9985 when K′ = 4, t₀ = 0.9986 when K′ = 20). We further show that with as few as 2,000 SNPs randomly selected from the HGDP dataset, we can estimate ancestry coordinates in a worldwide scale highly similar (t₀ > 0.99) to those based on all HGDP genotyped SNPs (Figure S4A). These results confirm that exome chip genotypes are sufficient to infer an individual’s continental ancestry in the ancestry space defined by the HGDP data.

Estimation of European ancestry is more challenging because more genetic data are required to reveal fine-scale population structure^20,22 and there are only 3,983 exome chip SNPs overlapping with the POPRES data. We show that without projection from high-dimensional PCs (K = K′ = 2), ancestry estimates of 385 test samples based on 3,983 exome chip SNPs do not reflect the geographic patterns of population structure and have a low similarity score to the coordinates derived from genome-wide SNP data (t₀ = 0.5112 when comparing coordinates of the test samples in Figure 2B to those in Figure 2A). Interestingly, this estimation accuracy is much lower than the results obtained by repeating the same analysis based on a similar number of SNPs randomly selected from the POPRES data (Figure S4B). One possible explanation is that the top two PCs based on the exome chip SNPs are distorted to reflect some patterns due to the chip design, and the population structure patterns might be hidden in higher-order PCs. When we ran the trace program using standard Procrustes analysis in 20-dimensional spaces (K = K′ = 20) and focused our comparison on the top two PCs, the Procrustes similarity score between estimates based on exome chip SNPs and those based on genome-wide SNPs increases to t₀ = 0.7946, but all study samples shrink toward the center of the reference map (Figure 2C). This observation suggests that the top 20 PCs contain rich ancestry information, but the sample-specific maps cannot match well to the ancestry reference map in a 20-dimensional space, resulting in an overall shrinkage after Procrustes transformations. When we used projection Procrustes analysis to project samples from a K′-dimensional space to a two-dimensional reference ancestry space, we can see that t₀ goes up as K′ increases and reaches a plateau at about 0.8135 when K′ = 20 (Figures 2D and 3A). The shrinkage issue is much alleviated because projection Procrustes analysis maximizes the similarity between two sets of coordinates in the low-dimensional reference space without penalizing the dissimilarity in the higher dimensions (Figure 2D). It is noteworthy that the t₀ based on exome chip SNPs is close to the score based on the same number of randomly selected SNPs when we use projection Procrustes analysis (Figure S4B), confirming our hypothesis that population structure patterns are hidden in the higher-order PCs. The number of significant PCs (p < 0.1, Tracy-Widom test) in the sample-specific PCA maps is about 19.5 when averaged across 385 test samples. For estimating fine-scale European ancestry, we need more than 20,000 SNPs randomly selected from the POPRES data to obtain accurate estimates of the top two PCs with t₀ > 0.95 when compared to the estimates based on all POPRES genotyped SNPs (Figure S4B).

Figure 2.

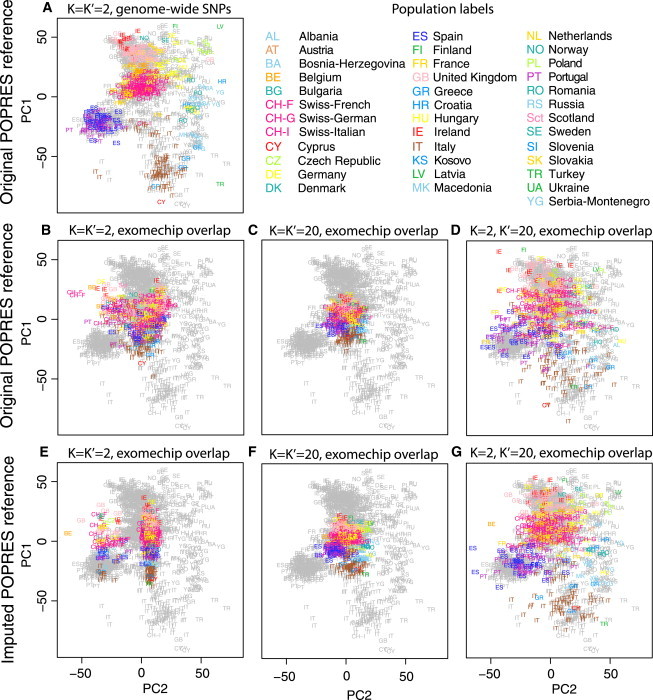
Estimation of European Ancestry using Exome Chip Genotypes

Grey symbols represent 1,000 reference individuals randomly selected from the POPRES data. Colored symbols represent the remaining 385 POPRES individuals who constitute the test set. Population abbreviations and colors follow Novembre et al.²⁹

(A) Estimated ancestry based on all 318,682 SNPs genotyped in the POPRES data with K = K′ = 2.

(B–D) Estimated ancestry based on 3,983 exome chip SNPs shared with the original POPRES data.

(B) K = K′ = 2 and t₀ = 0.5112 compared to estimates based on genome-wide SNPs in (A).

(C) K = K′ = 20 and t₀ = 0.7946 when comparing top two PCs to estimates in (A).

(D) K = 2, K′ = 20, and t₀ = 0.8135 compared to estimates based on genome-wide SNPs in (A).

(E–G) Estimated ancestry based on 19,123 exome chip SNPs shared with the imputed POPRES data.

(E) K = K′ = 2 and t₀ = 0.5594 compared to estimates based on genome-wide SNPs in (A).

(F) K = K′ = 20 and t₀ = 0.9042 when comparing top two PCs to estimates in (A).

(G) K = 2, K′ = 20, and t₀ = 0.9087 compared to estimates based on genome-wide SNPs in (A).

Figure 3.

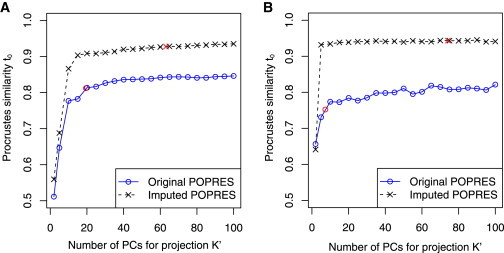
Performance of Trace and Laser Programs in Estimating Fine-Scale European Ancestry when using Different Number of PCs for Projection

The reference individuals and test individuals are the same as those used in Figure 2. K was fixed to 2 for all analyses. The x axis indicates the value of K′ = 2, 5, 10, 15 … 100. The y axis reports the Procrustes similarity t₀ between coordinates estimated from subsets of markers to estimates based on genome-wide SNPs in Figure 2A.

(A) Performance of trace program on exome chip genotypes. Two red points indicate results when K′ is chosen as the number of significant PCs (p < 0.1, Tracy-Widom test); K′ ≈ 19.5 when using the original POPRES reference panel, and K′ ≈ 63.1 when using the imputed POPRES reference panel.

(B) Performance of laser program on simulated sequence reads at depths corresponding to ∼5% of the off-target coverage from exome sequencing experiments. Two red points indicate results when K′ is chosen as the number of significant PCs (p < 0.1, Tracy-Widom test); K′ ≈ 7.4 when using original POPRES reference panel, and K′ ≈ 74.2 when using the imputed POPRES reference panel.

We then explored whether using the imputed POPRES data can further improve ancestry estimation within Europe. The number of overlapping SNPs between the exome chip and the imputed POPRES data is 19,123, which is about 5 times of the SNPs shared with the original POPRES data. Surprisingly, using the imputed reference panel with K = K′ = 2 produces two unexpected clusters along PC2 in the estimated coordinates, which have a low similarity score to the coordinates based on genome-wide SNP data (t₀ = 0.5594 when comparing coordinates of the test samples in Figure 2E to those in Figure 2A). By applying PCA on the imputed genotypes and examining the association between individual SNPs and PC2, we found that the unexpected pattern is driven by a cluster of 9,178 SNPs (8,936 of which were imputed) around the centromere of chromosome 11 (Figure S5). Due to this artifact introduced by imputation, the east-west population structure of Europe is mostly captured by PC3 (Figure S5A). When using standard Procrustes analysis in 20-dimensional spaces (K = K′ = 20), we observed a higher correlation between the top two PCs based on the exome chip SNPs and those based on the genome-wide SNPs (t₀ = 0.9042). However, similar to the analysis using the original reference panel without imputation, all study samples shrink toward the center of the reference ancestry map (Figure 2F). This undesirable shrinkage pattern is caused by the imperfect matching of the top 20 PCs in each sample-specific PCA map and in the reference PCA map. For example, PCs that reflect the imputation artifacts in the sample-specific PCA map cannot be matched in the reference PCA map. In such cases, the standard Procrustes analysis will scale all PCs toward the center in order to minimize the sum of squared Euclidean distances between two 20-PC maps. When we projected samples from a K′-dimensional space into a two-dimensional reference ancestry space using the projection Procrustes analysis, we can substantially improve our ancestry estimates because imputation artifacts can be rotated into dimensions beyond the reference ancestry space and will not be penalized in the matching procedure (Figures 2G and 3A). The Procrustes similarity score t₀ reaches a plateau at about 0.9087 when K′ = 20 and increases slightly to 0.9277 when using all significant PCs (p < 0.1, Tracy-Widom test) in the sample-specific PCA maps. The average number of significant PCs is about 63.1, much higher than 20, indicating that many PCs in the sample-specific PCA maps might reflect imputation artifacts such as strong linkage disequilibrium (LD) between imputed SNPs rather than population structure. Overall, in our exome chip example based on the POPRES data, the additional information gained by genotype imputation can be translated into an increment of ∼0.1 in t₀ (Figure 3A).

Our above analysis on estimating the fine-scale European ancestry is based on imputed genotypes at the exome chip loci rather than actual exome chip genotypes for the 385 test individuals. We performed an additional experiment using exome chip genotyping data for 152 individuals from 8 HGDP European populations (C.W., G.R.A., N.A. Rosenberg, and J.Z. Li, unpublished data) and imputed exome chip genotypes for the same set of individuals. The imputation was performed on the HGDP Illumina 650K genotyping data²⁴ following the same procedure as we imputed the POPRES data. We confirmed that our ancestry estimates derived from the imputed exome chip genotypes are highly similar to those derived from the actual exome chip genotypes. For example, when using the imputed POPRES reference panel with K = 2 and K′ = 20, we obtained a Procrustes similarity score t₀ = 0.9899 between coordinates of the 152 HGDP Europeans based on the imputed and the actual exome chip genotypes.

Estimation of European Ancestry using Simulated Low-Coverage Sequencing Data

Our simulated sequencing data have mean depth ∼0.068× across loci in the original POPRES data and ∼0.048× across loci in the imputed POPRES data (Figure S6). This off-target depth would be achieved even in a very efficient exome capture experiment where target regions are sequenced at 100× and only ∼5% of sequence reads fall off target. At this extremely low coverage level, we cannot accurately estimate fine-scale European ancestry by using the standard Procrustes analysis with K = K′ = 2 and the original POPRES reference panel (t₀ = 0.6565 when comparing coordinates of the test samples in Figure S7A to Figure 2A). When we used standard Procrustes analysis with K = K′ = 20, the Procrustes similarity score of the top two PCs increases to t₀ = 0.7677, but all samples shrink toward the center (Figure S7B versus Figure 2A). Even with improvements from projection Procrustes analysis, our ancestry estimates do not show a clear geographic pattern of population structure (t₀ = 0.7841 when K = 2 and K′ = 20, Figure S7C versus Figure 2A). When using the imputed POPRES reference panel with standard Procrustes analysis, our ancestry estimates are either distorted by imputation artifacts when K = K′ = 2 (Figure S7D) or shrink toward the center of the reference map when K = K′ = 20 (Figure S7E). In contrast, when using the imputed POPRES reference panel with high-dimensional projection, our ancestry estimates become highly similar to those based on genome-wide SNP data (for example, t₀ = 0.9388 when K = 2 and K′ = 20), revealing a clear geographic distribution of European populations (Figure S7F). In this simulated sequencing data example, the combination of using the imputed POPRES reference panel and projection Procrustes analysis leads to an increment of ∼0.28 in t₀ when K′ > 5 (Figure 3B).

Application to AMD Targeted Sequencing Data

The mean off-target coverage of our AMD targeted sequencing data is about 0.2×, a level that is sufficient for accurate estimation of European ancestry by LASER 1.0. However, there is a huge variation of the off-target coverage across samples (see Figure S3 in Wang et al.²²), which can lead to inaccurate ancestry estimates for samples with low off-target coverage. We reanalyzed this dataset to illustrate how LASER 2.0 can help increase accuracy of ancestry estimates for samples with low off-target coverage.

We first placed all AMD samples onto the HGDP worldwide ancestry map and used an iterative algorithm to detect ancestry outliers (Material and Methods). In total, we detected 92 non-European outliers, most of whom are probably African Americans (Figure S8A). We then focused on estimating fine-scale ancestry for the remaining 3,066 European samples. When using the original POPRES reference panel with standard Procrustes analysis (K = K′ = 2, a setting used in LASER 1.0), many samples have low sample-specific Procrustes similarity score, including 60 samples with t < 0.8, indicating low ancestry estimation accuracy for these samples (Figure 4A). In comparison, ancestry estimates using the imputed POPRES data with K = 2 and K′ = 20 show a less noisy fine-scale structure within Europe (Figures S8B and S8C). The improvement of ancestry estimates is more evident for samples with smaller amounts of off-target sequencing data, as suggested by the sample-specific Procrustes similarity scores (Figure 4B).

Figure 4.

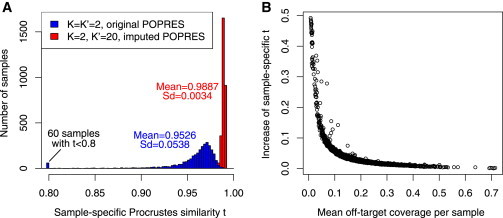
Improved Ancestry Estimation for the AMD Targeted Sequencing Data

(A) Distribution of the sample-specific Procrustes similarity score t, which compares the coordinates of the reference individuals in a sample-specific PCA map (one for each AMD sample) to the corresponding coordinates in the reference ancestry map, for 3,068 European samples when using the original POPRES reference panel with K = K′ = 2 and using the imputed POPRES reference panel with K = 2 and K′ = 20.

(B) Increase of the sample-specific Procrustes similarity score for 3,068 European samples when comparing results using the imputed reference panel with K = 2 and K′ = 20 to the results using the original POPRES reference panel with K = K′ = 2.

We further confirmed the observation that substantial improvement can be gained for samples with lower off-target sequencing depth by using 897 European samples that have both sequencing and GWAS data. We evenly split these samples into four bins based on the off-target sequencing depth across loci in the POPRES data and compared sequence-based ancestry estimates for samples in each bin to the estimates based on GWAS data using Procrustes similarity score t₀ (Table 1). For samples that have the lowest off-target coverage (<0.17×), the Procrustes similarity score (t₀) between estimated coordinates based on off-target reads and those based on 47,237 GWAS SNPs increases from 0.8680 (original POPRES, K = K′ = 2) to 0.9579 (imputed POPRES, K = 2 and K′ = 20), while for samples that have the highest off-target coverage (≥0.26×), t₀ increases from 0.9459 (original POPRES, K = K′ = 2) to 0.9666 (imputed POPRES, K = 2 and K′ = 20). In agreement with the sample-specific Procrustes similarity scores, comparisons with estimates based on GWAS data demonstrate that genotype imputation and projection Procrustes analysis can substantially improve fine-scale ancestry estimation for samples that have small amounts of sequencing data (Table 1).

Table 1.

Comparison of Sequence-Based and SNP-Based Coordinates for AMD Samples

Range of Off-Target Coverage	Number of Samples	POPRES Reference Panel	Mean Off-Target Coverage	Average Number of Covered Loci	Procrustes Similarity to SNP-Based Coordinates
					K′ = 2	K′ = 20
0.04–0.17a	225	original	0.14	32,349	0.8680	0.8878
		imputed	0.21	583,105	0.7165	0.9579
0.17–0.21a	224	original	0.19	43,723	0.9326	0.9313
		imputed	0.29	764,267	0.7111	0.9665
0.21–0.26a	224	original	0.24	52,856	0.9147	0.9248
		imputed	0.36	892,775	0.7115	0.9576
0.26–0.71	224	original	0.33	68,994	0.9459	0.9505
		imputed	0.48	1,114,473	0.7705	0.9666
Total	897	original	0.22	49,461	0.9171	0.9244
		imputed	0.33	838,370	0.7230	0.9628

The 897 AMD samples were evenly split into four bins according to their mean off-target sequencing depth across 318,682 loci in the original POPRES reference panel. For each bin, we estimated their ancestry coordinates with both original and imputed POPRES reference panels at K′ = 2 and 20, respectively. We set K = 2 in all the analyses. Note that setting K′ = 2 is equivalent to LASER 1.0. We compared each set of sequence-based coordinates to those based on 47,235 genome-wide SNPs genotyped in both the AMD GWAS data and the original POPRES data (K = K′ = 2).

^aRanges are inclusive of the low number but not the high number.

Discussion

We present a unified framework, which is implemented in the software package LASER 2.0, to estimate individual ancestry using either genotypes or sequence reads. By using a shared reference panel, we can place both genotyped and sequenced samples into the same ancestry space. Compared with LASER 1.0,²² our improved approach uses projection Procrustes analysis to incorporate ancestry information from higher-order PCs. This new technique allows us to further improve our ancestry estimates by imputing the reference panel to increase the number of loci overlapping with study samples. Through simulated and empirical data, we showed that LASER 2.0 outperforms LASER 1.0 in estimating fine-scale ancestry within Europe using small amounts of data such as genotypes on the exome chip or off-target sequence reads from targeted sequencing experiments. In our AMD example, we showed that substantial improvement could be achieved for samples that have extremely low off-target coverage and whose fine-scale ancestry cannot be accurately estimated by LASER 1.0. With more accurate ancestry estimates, we can control for population stratification at a finer scale in association studies, by either including our estimates as covariates or using our estimates to guide ancestry matching between case and control subjects.²²

Nevertheless, there are two issues regarding the usage of projection Procrustes analysis and genotype imputation. First, because projection Procrustes analysis is an optimization problem based on two sets of coordinates for N reference individuals, there is a possibility of overfitting when K′, the number of PCs used for projection, is close to N (Figure S9). In our examples based on the POPRES data, we found that our ancestry estimation accuracy, as quantified by the Procrustes similarity score t₀, usually reached a plateau at K′ ≈ 20. We therefore used K′ = 20 for estimating European ancestry when using the POPRES reference panel. In general, choosing K′ ≪ N is recommended to avoid the risk of overfitting. Another benefit of avoiding a very large value of K′ is to reduce the computational complexity of projection Procrustes analysis, which is approximately proportional to the square of K′.

A second issue arises from genotype imputation. Genotype imputation is an effective approach to increase the genotype density in our ancestry reference panel when whole-genome sequencing of a large number of reference samples is expensive. However, genotype imputation is not perfect and might introduce unexpected artifacts due to imputation errors or strong linkage disequilibrium between the imputed SNPs. To minimize the impacts of these factors, we applied stringent quality controls on the imputed SNPs, avoided imputing the study samples, and used only the original genotyped SNPs to define the reference ancestry space. In addition, we showed in our examples that projection Procrustes analysis can help remove imputation artifacts by rotating the artifact patterns out of the reference ancestry space. Our results confirm that imputing the reference panel improves fine-scale ancestry estimation within Europe. In principle, the imputation strategy can be applied to construct imputed reference panels for other continents; however, we need to be careful in evaluating the impact of imputation on the ancestry estimates, because depending on the reference haplotype set, imputation accuracy varies across populations and is often lower for non-European populations.^35,36 When whole genome sequencing data of ancestry reference panels become available, we expect that the accuracy of our method can be further improved as the number of SNPs increases and genotype error rate decreases.

Interpretation of individual ancestry estimates derived from LASER is based on comparison with the coordinates of the reference individuals in the ancestry space. The shrinkage patterns observed in some analyses can be misleading. For example, in Figures 2F and S7E, all study samples shrink toward the center of the reference map despite the fact that the coordinates are highly correlated with estimates based on genome-wide data. One might mistakenly conclude that these samples were central Europeans without a priori ancestry information. The shrinkage issue can further complicate modeling of population structure in association studies based on multiple datasets because the shrinkage magnitude might vary for samples with different sets of markers included in the analyses.

Misleading results can also arise when using an inappropriate ancestry reference panel that does not capture the ancestry of the study sample. To illustrate this point, we performed an experiment to estimate ancestry for worldwide samples from the HGDP data in a European ancestry space generated by the POPRES data (Figure S10). We see that eight HGDP European populations are well separated and are placed close to their geographic neighboring populations in the POPRES reference panel (Figure S10B). The HGDP non-Europeans, however, show misleading patterns; for example, the HGDP Oceanians cluster with the POPRES Italians and that the HGDP East Asians and Central/South Asians largely overlap with each other and with the POPRES East Europeans (Figure S10C). These results highlight the importance of selecting appropriate reference panels when using LASER. We therefore recommend users to always start with a worldwide reference panel and gradually focus on regional panels, as we previously proposed.²²

Our strategy of analyzing each study sample independently with a set of reference individuals has several advantages over the standard PCA approach,¹⁵ which analyzes all samples together. First, because we examine each sample independently, our ancestry estimates are robust to family structure or cryptic relatedness among the study samples. Second, the computational complexity of our method scales linearly to the study sample size whereas PCA scales cubically. As the sample size grows rapidly in large-scale genetic studies, our method can be more efficient than PCA in computational time and especially in memory usage (Table S1). In addition, we can easily run the analyses of different samples in parallel to further speed up the computation.

Because principal components are linear combinations of SNP genotypes, a natural way to project study samples onto a reference PCA map is to use the PC loadings (coefficients of SNPs) to compute coordinates of the study samples.^15,37 This approach, however, is likely to produce shrinkage patterns (Figure S11A). Theoretical studies have shown that the shrinkage is due to overfitting when the number of markers is much larger than the number of samples.³⁸ In a recent release of the EIGENSOFT package (v.5.02),¹⁵ a least-squares projection method lsqproject has been implemented to analyze samples that have a lot of missing data. This approach has been used to study the genetic similarity between ancient DNA samples and modern human genomes.³⁹ We caution that the lsqproject method does not address the shrinkage problem such that the results might be misleading without careful interpretation (Figure S11B). In contrast, results derived from LASER 2.0 do not show evident shrinkage patterns because the projection Procrustes analysis can rescale the coordinates based on the reference individuals.

Using LASER 2.0 with a pre-defined ancestry space, we can provide comparable ancestry estimates using either genotypes or sequence reads as input. This desirable feature can facilitate control of population stratification in disease association studies when genetic data are collected from different sources.^8,22 For example, it is possible to match the ancestry background of exome chip genotyped samples with exome sequenced samples and perform association tests at loci that have high-quality genotypes in both datasets. More broadly, our method can be applied to study population structure among samples assayed by different techniques or across different loci, including joint analysis of ancient DNA samples and modern human genomes.^23,25

Appendix A: Procrustes Similarity and Pearson Correlation

In this section, we explore the relation between the Procrustes similarity score t (or t₀) and the Pearson correlation r. Given two N × K matrices X and Y, we recall that Procrustes analysis aims to find a set of optimal transformations f on X such that $\tilde{\mathit{X}}=f\left(\mathit{X}\right)$ and Y have the minimal sum of squared Euclidean distances.^27,28 In the standard Procrustes analysis, $\tilde{\mathit{X}}=f\left(\mathit{X}\right)=\rho \mathit{XA}+\mathit{B}$, where ρ is a scaling factor, A is a K × K orthogonal matrix representing rotation and reflection, and B is a N × K translation matrix with each row equal to the same translation vector. Without loss of generality, we assume both X and Y have been centered to the origin, then B = 0 and $\tilde{\mathit{X}}=f\left(\mathit{X}\right)=\rho \mathit{XA}$. The optimal transformation identified by Procrustes analysis can be expressed as

$$\mathit{A}=\mathit{V}{\mathit{U}}^T,$$ (Equation A1)

$$\rho =\text{tr}\left(\mathit{\Lambda }\right)/\text{tr}\left({\mathit{X}}^T\mathit{X}\right),$$ (Equation A2)

where U, V, and Λ are from singular value decomposition of Y^TX as Y^TX = UΛV^T. Following Wang et al.,²⁷ the Procrustes similarity score can be expressed as

$$t\left(\mathit{X},\mathit{Y}\right)=\sqrt{1-D\left(\mathit{X},\mathit{Y}\right)}=\text{tr}\left(\mathit{\Lambda }\right)/\sqrt{\text{tr}\left({\mathit{X}}^T\mathit{X}\right)\text{tr}\left({\mathit{Y}}^T\mathit{Y}\right)},$$ (Equation A3)

where $D\left(\mathit{X},\mathit{Y}\right)=1-{\left[\mathit{tr}\left(\mathit{\Lambda }\right)\right]}^2/\left[\text{tr}\left({\mathit{X}}^T\mathit{X}\right)\text{tr}\left({\mathit{Y}}^T\mathit{Y}\right)\right]$ is the sum of squared Euclidean distances between $\tilde{\mathit{X}}$ and Y and is standardized to range from 0 to 1. We also have

$$\text{tr}\left(\mathit{\Lambda }\right)=\text{tr}\left({\mathit{U}}^T{\mathit{Y}}^T\mathit{XV}\right)=\text{tr}\left({\mathit{Y}}^T\mathit{XV}{\mathit{U}}^T\right)=\text{tr}\left({\mathit{Y}}^T\tilde{\mathit{X}}\right)/\rho ,$$ (Equation A4)

and

$$\text{tr}\left({\mathit{X}}^T\mathit{X}\right)=\text{tr}\left[{\left(\mathit{XA}\right)}^{\text{T}}\left(\mathit{XA}\right)\right]=\text{tr}\left({\tilde{\mathit{X}}}^{\mathit{T}}\tilde{\mathit{X}}\right)/{\rho }^2.$$ (Equation A5)

Substituting Equations A4 and A5 into Equation A3, we can get

$$t\left(\mathit{X},\mathit{Y}\right)=\frac{\text{tr}\left({\mathit{Y}}^T\tilde{\mathit{X}}\right)}{\sqrt{\text{tr}\left({\tilde{\mathit{X}}}^{\mathit{T}}\tilde{\mathit{X}}\right)\text{tr}\left({\mathit{Y}}^T\mathit{Y}\right)}}=\frac{{\sum }_{k=1}^K{\sum }_{i=1}^N{Y}_{ik}{\tilde{X}}_{ik}}{\sqrt{\left({\sum }_{k^{\text{'}}=1}^K{\sum }_{i=1}^N{\tilde{X}}_{i{k}^{\text{'}}}^2\right)\left({\sum }_{k^{\text{'}}=1}^K{\sum }_{i=1}^N{Y}_{i{k}^{\text{'}}}^2\right)}}.$$ (Equation A6)

Notice that both $\tilde{\mathit{X}}$ and Y are centered to the origin in the K-dimensional space. We thus have ${\sigma }_{\tilde{X},k^{\text{'}}}^2={(\text{N}-1)}^{-1}{\sum }_{i=1}^N{\tilde{X}}_{i{k}^{\text{'}}}^2$ and ${\sigma }_{Y,k^{\text{'}}}^2={(\text{N}-1)}^{-1}{\sum }_{i=1}^N{Y}_{i{k}^{\text{'}}}^2$, representing the variance of $\tilde{\mathit{X}}$ and Y along the k′^th dimension, respectively, and $r_k=\text{cor}\left({\mathit{Y}}_{\cdot k},{\tilde{\mathit{X}}}_{\cdot k}\right)={(\text{N}-1)}^{-1}{\sum }_{i=1}^N{Y}_{ik}{\tilde{X}}_{ik}/\sqrt{{\sigma }_{\tilde{X},k}^2{\sigma }_{Y,k}^2}$, representing the Pearson correlation between $\tilde{\mathit{X}}$ and Y along the k^th dimension. Equation A6 can then be written as

$$t\left(\mathit{X},\mathit{Y}\right)={\sum }_{k=1}^K{w}_k{r}_k,$$ (Equation A7)

in which

$$w_k=\sqrt{\frac{{\sigma }_{\tilde{X},k}^2}{{\sum }_{k^{\text{'}}=1}^K{\sigma }_{\tilde{X},k^{\text{'}}}^2}\times \frac{{\sigma }_{Y,k}^2}{{\sum }_{k^{\text{'}}=1}^K{\sigma }_{Y,k^{\text{'}}}^2}}.$$ (Equation A8)

Therefore, the Procrustes similarity score t(X, Y) can be interpreted as a linear combination of the Pearson correlations between the Procrustes transformed coordinates $\tilde{\mathit{X}}$ and the target coordinates Y, with the weight along each axis given by Equation A8. Although the original definition of Procrustes similarity statistic is complicated and difficult to interpret (Equation A3), our derivation shows that the Procrustes similarity score is in fact a Pearson correlation measurement in high-dimensional space. When $\tilde{\mathit{X}}$ and Y are highly similar such that ${\sigma }_{\tilde{X},k}^2\approx {\sigma }_{Y,k}^2$ for k = 1,2…,K, Equation A8 can be further simplified as

$$w_k\approx \frac{{\sigma }_{Y,k}^2}{{\sum }_{k^{\text{'}}=1}^K{\sigma }_{Y,k^{\text{'}}}^2},$$ (Equation A9)

which is the proportion of variance captured by the k^th PC among the top K PCs in Y.

Web Resources

The URLs for data presented herein are as follows:

• Exome chip design, ftp://share.sph.umich.edu/exomeChip/IlluminaDesigns/annotatedList.txt

• LASER, http://www.sph.umich.edu/csg/chaolong/LASER/

• MACH, http://www.sph.umich.edu/csg/abecasis/MACH/

• Minimac, http://genome.sph.umich.edu/wiki/Minimac/