Reciprocation and Altruism in Social Cooperation

Abstract

Altruistic behavior benefits other individuals at a cost to oneself. The purpose of the present experiment was to study altruistic behavior by players (P) in 2-person iterated prisoner's dilemma games in which reciprocation by the other player (OP) was impossible, and this impossibility was clear to P. Altruism by P could not therefore be attributed to expectation of reciprocation. The cost to P of altruistic behavior was constant throughout the study, but the benefit to OP from P's cooperation differed between groups and conditions. Rate of cooperation was higher when benefit to OP was higher. Thus altruism (not attributable to expectation of reciprocation) can be a significant factor in interpersonal relationships as studied in iterated prisoner's dilemma games, and needs to be taken into account in their analysis.

Prisoner's dilemma (PD) games abound in everyday life. Any situation where the interests of a group run counter to those of each member as an individual is a form of PD. For example, voting costs time and effort. In elections where a single vote is almost surely not going to be decisive, there is no incentive for any individual to vote. But if all of the supporters of a particular candidate do not vote, the group suffers. Giving to charity, overfishing, overhunting, driving to work instead of taking public transportation, recycling, and many other real-life situations are all forms of PD. It is therefore important to know what motivates people to cooperate in these sorts of situations. One answer is that cooperation is strategic—that people cooperate because they expect others to reciprocate in the future (“I’ll help you so that you help me”). Another answer is that people are to some extent altruistic. That is, benefit to others, in and of itself, is valuable to people. Of course, the possibility of reciprocation may motivate PD-game cooperation in the absence of altruism. But it is not clear whether altruism can motivate PD-game cooperation in the absence of the possibility of reciprocation. The present study investigates this question by eliminating the possibility of reciprocation and measuring cooperation as a function not of reward to participants themselves, but reward to another person.

Players in a 2-player prisoner's dilemma game each choose between “cooperating” and “defecting.” Both players may cooperate (in which case each receives a moderately high reward) or both may defect (in which case each receives a moderately low reward). Thus, if both choose identically, both are better off cooperating. However, if one cooperates and the other defects, the cooperator receives a very low reward, and the defector receives a very high reward. A player (P) acting purely selfishly would defect in this game since, regardless of the other player's (OP's) choice, P would earn more by defecting than cooperating. Thus (ignoring reciprocation), cooperation is costly. By cooperating, P loses what he would have obtained if he had chosen otherwise (economists call this an “opportunity cost”). On the other hand, a player acting purely altruistically (that is, with full regard for OP's earnings and none for P's) would cooperate because, regardless of OP's choice, OP would earn more if P cooperated than if P defected. In sum, ignoring reciprocation, a purely selfish P would defect and a purely altruistic P would cooperate in a PD game.

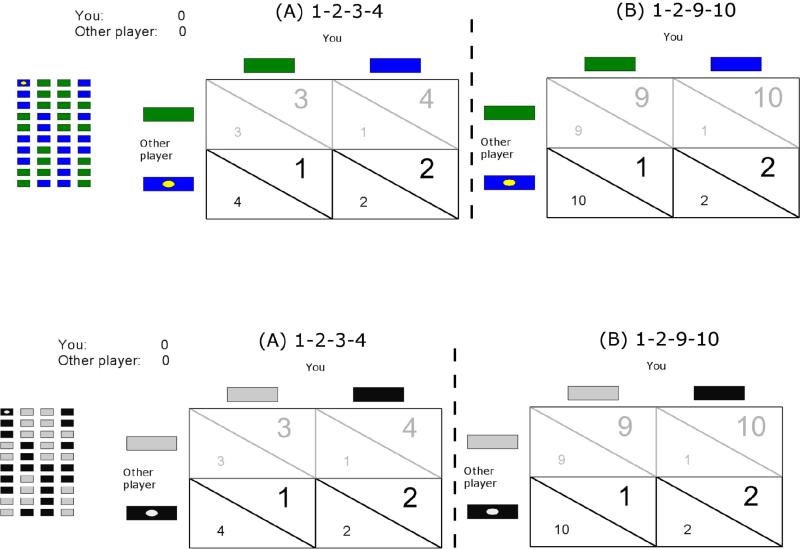
Altruistic acts have been defined, in behavioral terms, as “...costly acts that confer economic benefits on other individuals” (Fehr & Fischbacher, 2003). Cooperation in iterated prisoner's dilemma games (IPD), such as those used here and diagrammed in Figure 1, is altruistic according to this definition. With the specific outcomes shown in Figure 1 regardless of OP's choice, choice by P of cooperation (green) rather than defection (blue) cost P one unit; this was the case in both Game A (4-3 or 2-1) and Game B (10-9 or 2-1). [Screen items participants saw as green and blue appear in the figure as light gray and black, respectively.] However, again regardless of OP's choice, cooperation in Game A gave OP two units (3-1 or 4-2) while cooperation in Game B gave OP eight units (9-1 or 10-2). Note that choosing a lower gain for oneself (cooperation) was an economic loss and thus a costly act (e.g., Fehr & Fischbacher, 2003; Safin, Locey, & Rachlin, 2013). If altruism were a factor in these games, participants would be expected to cooperate more in Game B, where OP's gain was higher, than in Game A, where OP's gain was lower.

Figure 1.

Payoff matrices for the Partner-Reward groups. The two payoff schedules were presented in the form of matrices where the green (or light gray) blocks represent cooperation and the blue (or black) blocks represent defection. The 1-2-3-4 and 1-2-9-10 reward matrices for the Partner-reward group are shown, where the large font is the reward to self and the small font is the reward to other player. The No-Partner-Reward group saw a similar matrix, but the spaces for other player's outcome (small font) were left blank.

In prior experiments, Stony Brook students, playing a one-shot 1-2-9-10 PD game (B in Figure 1) with hypothetical rewards and anonymous OP, indeed cooperated at a higher rate than did those playing the 1-2-3-4 PD game (A in Figure 1) (Locey, Safin, & Rachlin, 2013); a corresponding result was found for Stony Brook students playing a face-to-face IPD game with real rewards (Safin et al., 2013). However, Safin et al. (2013) found a significant correlation in cooperation rates between partners in the IPD game, which suggests that reciprocation may have played a role in fostering cooperation or defection. The purpose of the present experiment was to eliminate the possibility of reciprocation by OP in an IPD game and to measure cooperation by P solely as a function of its benefit to OP. Because P could not influence OP's choices, strategic cooperation (i.e., to get OP to reciprocate) was removed as a motivating force in this experiment.

Social discounting (Jones & Rachlin, 2006), which proposes that people value rewards to others, but discount them based on social distance, can be measured to quantify the value of the reward to OP relative to the cost (or forgone reward) to P. Equation 1 (Jones & Rachlin, 2006) expresses the discounted value of a reward to another person (v) as a function of the reward's undiscounted value (V), the social distance to the other person (N), and a constant, k:

$$v=\frac{V}{1+kN}$$ (1)

Given a choice between receiving $1 and receiving $0, almost everyone would choose the former. If the offer is modified so the choice is between $1 to oneself and $2 to a friend, then the choice is less clear. In both situations one has the option to receive $1 or receive nothing, but in the second situation one can benefit someone else by forgoing a reward to oneself. Although people may differ vastly in social discount rate (k), given a large enough V relative to v, and a small enough N, nearly everyone will forgo a reward in favor of a greater reward to another person. These prior experiments and others (e.g., Eckel & Grossman, 1996) show clearly that pure altruism (with no possibility of reciprocation) is not uncommon. The present study examines whether this will be the case in an iterated game where reciprocation normally has a very strong effect on behavior (Baker & Rachlin, 2001).

Method

Participants

Participants were 88 undergraduate students at Stony Brook University (52 female). The sample size was based on previous studies (e.g., Safin et al., 2013). They were compensated with course credit and $5 to $7 based on performance.

Materials and Procedure

The participants arrived at the laboratory in groups of two, but after signing the consent form, they were taken to separate adjacent rooms. The experiment was administered on a personal computer with a 19” LCD screen and a standard keyboard, which were located in a small private room. Participants were randomly assigned to one of two groups, Partner-Reward and No-Partner-Reward (the control group). In random order, participants in both groups were shown a variation of the payoff matrices shown in Figure 1 and told that they would be connected online to another participant who was compelled to make predetermined choices. All participants were told that they would be paid 2 cents for every point they earned, but those in the Partner-Reward group (49 total) were also told that the other player would be paid at the same rate. In contrast, the participants in the control group (39 total) were told that the other player did not receive points and would not be paid. Thus, the participants’ choices affected the payoff of the other player only if the participant was in the Partner-Reward group, isolating reward to others as a factor in PD game cooperation. The experiment began after the participants were fully instructed on the prisoner's dilemma game task and had an opportunity to ask clarifying questions.

The task was an IPD game except that all of OP's choices were predetermined and revealed to participant as a grid of color-coded rectangles on the side of the screen (Figure 1). The oval in one rectangle indicated OP's current choice. Thus, unlike the standard IPD, this task had no strategic component: OP could not respond to P's choices. In the Partner-Reward group, both P's and OP's points were updated in real-time on the screen. In the No-Partner-Reward group, OP earned no points so only P's cumulative points were displayed.

All participants completed two conditions of the IPD game, one with the 1-2-3-4 payoff matrix; the other with the 1-2-9-10 payoff matrix. The conditions were presented in random order, and each consisted of 40 trials. The sequence of OP's choices was displayed only for the current 40-trial condition and (unlike Figure 1) only a single matrix (the currently active one) was shown. Participants were not told in advance that there would be a 40-trial condition with a different payoff matrix after the first. For each condition and participant, OP's choices were determined by shuffling together 20 decisions to cooperate and 20 decisions to defect.

After playing the PD games, participants completed a computer-based social discounting task, similar to the adjusting immediate amount method used to measure delay discounting (Holt, Green, & Myerson, 2012), with the rewards to self and other replacing immediate and delayed rewards, respectively. Preliminary instructions asked the participants to imagine a list of 100 people arranged by closeness with dearest friend or relative at #1 and a mere acquaintance at #100. Participants were then presented with a hypothetical choice between $75 to a person of social distance N (1, 2, 5, 10, 20, 50, 100 in random order) and a smaller amount to oneself. The first pair of alternatives for a given social distance was always $38 to self versus $75 to Person N and nothing to self. Subsequently, the self-amount was adjusted up (if the participant chose giving money to Person N) or down (if the participant chose giving money to herself) to find an indifference point between the two options. The last block of the social discounting task asked participants to choose between $75 to the other player from the PD game and a smaller amount to themselves, which was increased until an indifference point was determined. Upon completion, the participants were debriefed and given an opportunity for questions.

Results

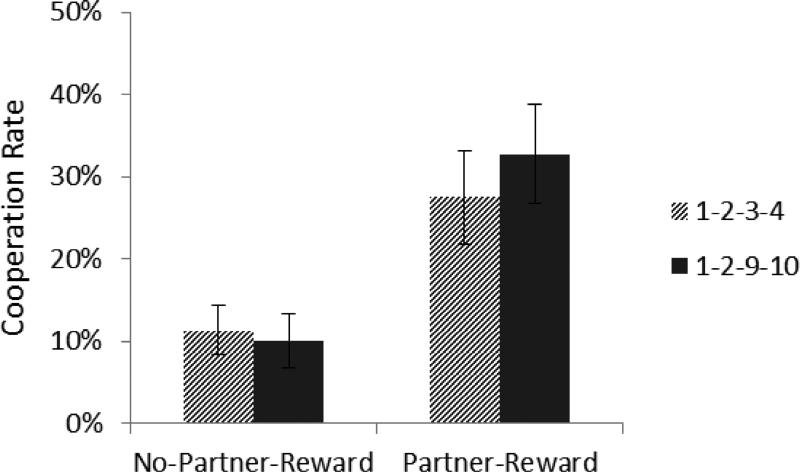
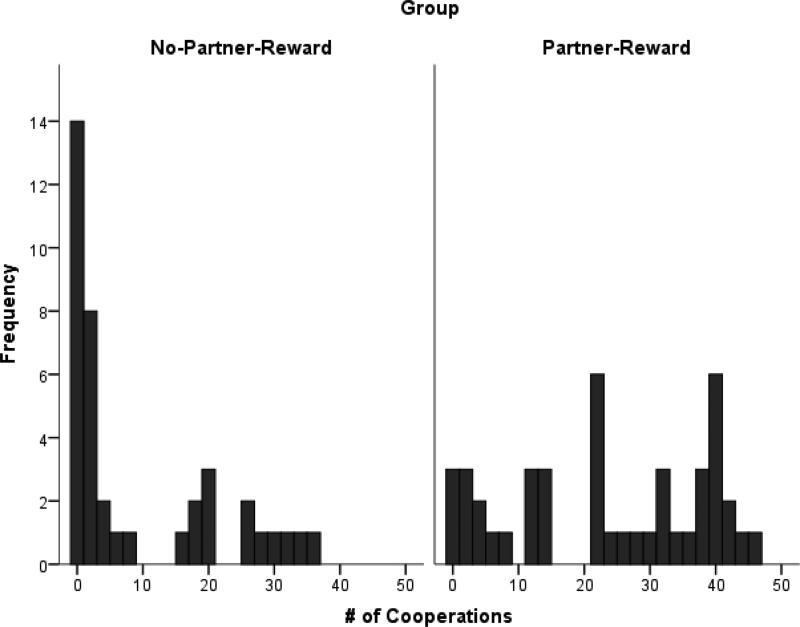
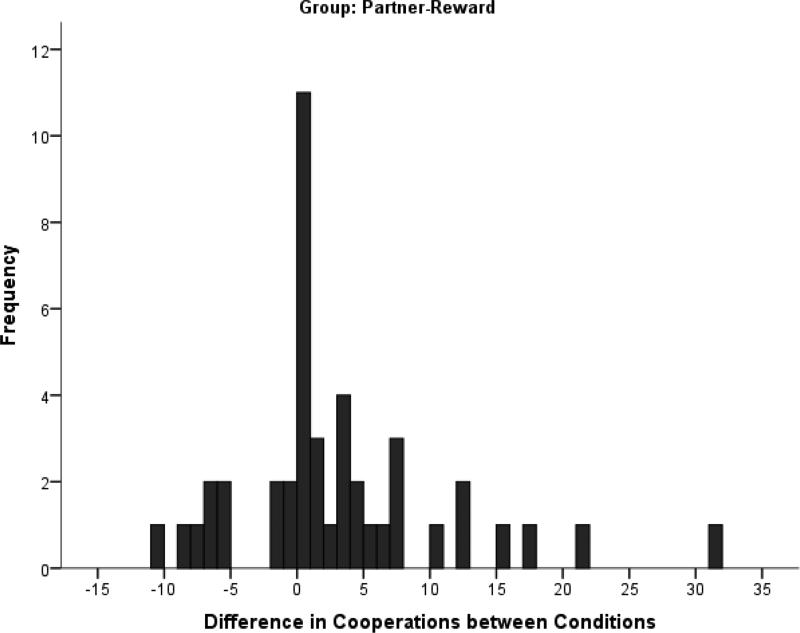
Data of 5 participants were removed from the analysis due to comprehension and technical issues during the administration of the task (e.g., a language barrier that interfered with instructions, a computer malfunction). The following analyses were performed on the remaining 39 participants in the No-Partner-Reward group and 44 participants in the Partner-Reward group. The average number of cooperations by group, condition and OP's choice, as reported in Table 1 and Figure 2, reveal an overall tendency to defect. However, while the mean cooperation rate for every group and condition was well under 50%, there were quite a few participants who cooperated at least half of the time (see Figure 3). The modal number of cooperations for the No-Partner-Reward group was 0 for both matrix conditions, regardless of OP's choice, which is reflected in the skew of 1.06 for the 1-2-3-4 condition and 1.418 for the 1-2-9-10 condition (a perfectly symmetrical distribution would have a skew of zero). However, the response distribution for the Partner-Reward condition was not positively skewed (skew = −.004), but rather bi-modal for the 1-2-3-4 condition, with peaks at 0% and 50% cooperation rate. Similarly, the distribution in the 1-2-9-10 condition had only a small positive skew of 0.096 in the Partner-Reward group, and the mode was at 50% cooperation rate, with the second largest peak at 0% (the two conditions were combined for Figure 3 due to their similarity). In other words, when participants knew their choices would affect the payoff to the other player, the two dominant strategies were to never cooperate (as in the No-Reward group) or to cooperate 50% of the time (exactly at the same rate as OP). Figures 3 and 4 show the frequency distribution of cooperations by group and the difference between a participant's cumulative cooperations in the 1-2-9-10 condition and 1-2-3-4 condition, respectively. Figure 4 illustrates that while participants were likely to cooperate more in the 1-2-9-10 condition when OP was rewarded, the plurality cooperated at the same level as in the 1-2-3-4 condition.

Table 1.

Cooperation Rates

Condition	Type	Partner-Reward	No-Partner-Reward
1-2-3-4	CC	8.09 (5.82 – 10.36)	2.74 (1.34 – 4.15)
	CD	2.18 (l.17 – 3.19)	2.10 (1.12 – 3.09)
1-2-9-10	CC	8.70 (6.49 – 10.92)	2.74 (1.13 – 4.36)
	CD	4.18 (2.50 – 5.86)	1.36 (.50 – 2.22)

Note. Average number of cooperations (out of 20 per cell) for trials when OP cooperated (CC) and trials when OP defected (CD), shown by group and condition. Numbers in parentheses are 95% confidence intervals.

Figure 2.

Average cooperation rate by group and condition (+/− SEM). Participants cooperated more when OP received higher rewards.

Figure 3.

Distribution of cumulative cooperations for each participant by group. The x-axis is the sum of cooperation responses across conditions (out of 80), and the y-value is the number of participants who cooperated that amount.

Figure 4.

Within-subject differences in cooperation rates between conditions. The frequency distribution of differences between a player's cumulative cooperation in the 1-2-9-10 condition and that player's cumulative cooperation in the 1-2-3-4 condition (the order was counterbalanced). Although the vast majority did not show a difference, the mean of 2.61 was significantly greater than 0 ( t(43) = 2.18, p < .05.), which indicated a greater cooperation in the 1-2-9-10 condition.

Choice in each trial was analyzed with a mixed-effects logistic regression model. The model had a per-subject random effect and four fixed effects: one each for the current payoff matrix, OP's choice on the same trial, and whether OP could receive rewards, as well as an interaction between the payoff matrix and whether OP could receive rewards. Participants were more likely to cooperate when OP could receive rewards (28% of choices were to cooperate when OP could receive rewards vs. 11% when she could not), when OP cooperated (28% vs. 12%), and when both of the following were true: OP was rewarded and the payoff matrix was 1-2-9-10 (32% vs. 16%; all |z|s > 4, all ps < .001). Surprisingly, participants in the No-Reward-to-Partner group were marginally less likely to cooperate when the payoff matrix was 1-2-9-10 (10% vs. 12%; z = −1.9, p = .056), whereas we expected no difference within that group.

The participants’ responses in the social discounting task were used to calculate indifference points. If, for a given social distance, the participant always preferred the reward to herself then the indifference point was set at $1. Alternatively, if the participant always preferred $75 reward to person N, then the indifference point was set at $74. For most social distances, the indifference point was somewhere between these two extremes (e.g., the indifference point is $26 when the participant prefers $75 for person N to $25 for herself, but prefers $27 for herself to $75 for person N). The combined values for the social distances 1, 2, 5, 10, 20, 50 and 100 were fit to a hyperbolic discounting function (Equation 1) to calculate the social discounting parameter k for each participant (see Jones & Rachlin, 2006). The median degree of discounting (k) for all participants was 0.0789. The median indifference point was $19. That is, the median participant was indifferent between $19 for herself and $75 for OP. As expected there was a strong negative correlation between the indifference point for which OP took the place of N, and k (log-transformed to reduce the skew of the distribution) with r = −0.55, p < .001. There were no statistically significant correlations between P's social discounting and P's cooperation in the PD game.

Discussion

Consistent with previous findings (e.g., Safin et al., 2013; Cooper, DeJong, Forsythe, & Ross, 1996), participants cooperated more when cooperation yielded a greater reward for OP (i.e., more cooperation in the Partner-Reward group than No-Partner-Reward group, and more cooperation for the 1-2-9-10 matrix within the Partner-Reward group). “Cooperation” for participants in the No-Partner-Reward group, where OP received no reward, amounted to simply choosing a smaller reward over a larger one. (Several participants remarked on this fact.) The non-zero cooperation rate of the No-Partner-Reward group participants may seem strange, as it is a costly act with no apparent benefit, but it is not uncommon for participants to vary their responses when playing against an opponent making the same choice every time. Silverstein, Cross, Brown, & Rachlin (1998) also found a cooperation rate of about 10% against OP playing an all-cooperate or all-defect strategy. The significantly higher cooperation rates found when OPs did receive rewards, and Ps were informed of these rewards, must have been due to the fact that reward to OP was positively valued by P – i.e., altruism. It is of interest that, in the Partner-Reward group, participants were more likely to cooperate on trials when OP cooperated than when OP defected (that is, the participants themselves were reciprocating). It may be that some Ps mirrored OP's responses in order to be fair—to produce an equal monetary outcome for P and OP.

In normal IPD games reciprocation clearly reinforces cooperation (Baker & Rachlin, 2001). The purpose of the present experiment was not to show that the possibility of reciprocation has no effect on choice but rather to test whether, in the absence of OP's ability to reciprocate, some degree of cooperation could be maintained solely by reward to OP. The results are evidence that this was the case, although we did not find any relationship between cooperation and the slope of the measured social discounting function. One could also argue that, although OP could not reciprocate, the participants might have believed that cooperation would eventually or generally be reinforced outside of the experiment proper. Such an expectation, coupled with a reluctance to make discriminations among particular situations (as in “casting bread upon the water”), might have led to the cooperation observed. We do not dispute the possibility of such a tendency, but we note that it would be difficult to distinguish operationally from a general altruistic tendency.

Models of altruism such as social discounting (in which the value of reward to another person is discounted hyperbolically by social distance), or inequity aversion (in which P is averse to disparities between P's and OP's point totals), may account for these results (Jones & Rachlin, 2006; Falk & Fischbacher, 2006). Both of these explanations imply that P values OP's reward. Further experiments would be required to distinguish between them in particular situations. The fact that individual degree of social discounting, which has been found to correlate negatively with altruism in public goods games (Jones & Rachlin, 2009), did not correlate with altruistic behavior in the PD game tested here, may have been due to imprecision in either or both of these measures, to the lack of wide variance in these measures among Stony Brook students, to the fact that the social-discounting rewards were both hypothetical and greater than the rewards to OP in the IPD tested here, or possibly because the kind of altruism that values reward to another person in one of these situations is different from that in another. Further experiments may tease apart these possibilities.

Highlights.

• People cooperated in a prisoner's dilemma game even when reciprocation was impossible.

• Cooperation was higher when the benefit to the other player increased.

• Pure altruism, in addition to reciprocation, plays a role in social cooperation.