An emerging trend in health sciences is the shift from a physician-centered model of care to a patient-centered model of care, and the recognition of the importance of patients’ beliefs, values, preferences, and needs in improving patient/care-provider communication, decisions about treatment options, and long-term disease management (Epstein & Street, 2011). Several different models have been developed by health psychologists to explain and predict how beliefs drive health-related behavior and decisions. For example, the health-belief model (HBM, Rosenstock, 1974; Rosenstock & Kirscht, 1979) states that a person’s perception of different aspects of a disease—susceptibility to and severity of the disease, for example—are related to the person’s specific preventive efforts. Thus, the HBM represents a rather rational view of human health activities. In the self-regulatory model of illness (Leventhal, Brissette, & Leventhal, 2003) individuals are believed to create a lay model of their illness based on their beliefs, knowledge, and experiences; variations in such beliefs, knowledge, and experiences lead to individual differences in behaviors undertaken to prevent, control, and manage the disease.
This work is motivated by the analysis of belief data collected from people with diabetes, with their beliefs about diabetes being measured under the frameworks of the Explanatory Model of Illness (Kleinman et al., 1978; Kleinman, 1980; 1988) and the Common Sense Model of Illness (Leventhal et al., 2003). The explanatory model (EM) of illness posits that individuals make sense of an illness in the context of their knowledge and experience. EMs often include ideas about etiology, symptoms, physiology, treatments and consequences. They may be only partly articulated, inconsistent and even self-contradictory. Lay EMs may overlap with those of medical professionals, but often show significant differences (Chavez et al., 1995; Baer et al., 2004; Baer et al., 2008). The idea of EM arises from anthropology and has been used to contrast the views that lay persons and professional possess for the same condition. Common sense models (CSMs) of illness are similar to EMs. They are the representation of an illness that patients develop to help them make sense of their condition and develop responses to it. With its roots in psychology, the CSM emphasizes the active cognitive process patients use to deal with an illness. That is, patients go through an active hypothesis-testing process as they deal with an illness, so their CSMs can be fluid.
The assessment of the “fluidity” of beliefs is possible in studies with a design that includes repeated measurements. For example, Brock (1984) found that persons with more stable beliefs about susceptibility to swine flu were more likely not to take flu shots in an immunization campaign. Grzywacz et al. (2011) analyzed a small sample of repeatedly measured belief items about diabetes and examined the concordance of responses at the item level. They found that lay beliefs about diabetes were not always stable across specific domains of diabetes such as causes of the disease and its medical management, as well as across different ethnic groups. Using item response theory (IRT), Ip et al. (2013c) examined the consistency of item responses on belief items about diabetes from an instrument – the Common Sense Model of Diabetes Inventory (CSMDI, Grzywacz et al., 2011) over two different occasions of measurements. An example of an item is “Feeling nervous is a sign of low blood sugar.” The items have three response categories: “Agree,” “Disagree,” and “Don’t Know (DK).” Each response was judged as congruent or incongruent to the biomedical model. In their analysis, the category “DK” was simply treated as incongruent to the biomedical model. The work confirmed the hypothesis that when patients with diabetes used the biomedical model as their belief “anchor” in their response process and displayed a higher level of consistency and less ambivalence toward the belief items.
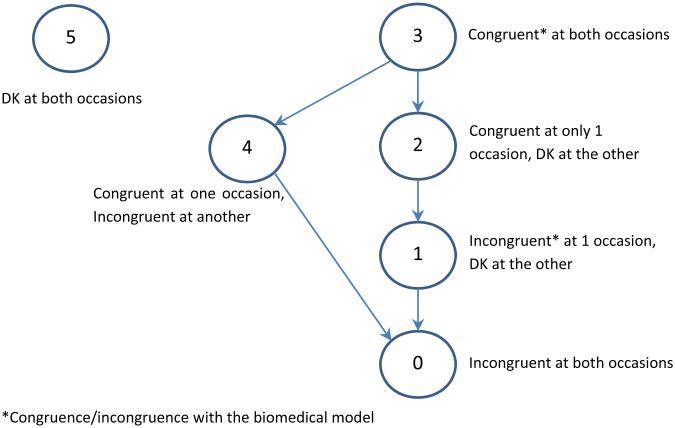
Instead of lumping DK together with other response categories and separately analyzing the repeated measurements on the belief items, the current work examines the response structure of repeated measures from belief items as a partially ordered set (poset). Figure 1 shows the partially ordered structure of an individual’s item response on the CSMDI across two consecutive measurement occasions. An arrow indicates a dominance relationship, e.g., the category of “congruent with the biomedical model on both occasions” dominates the category “congruent with the biomedical model on one and DK on the other.” The new mode of response – poset - lies somewhere between ordered data and unordered data in that some of its categories follow a rank order, while others do not. For the CSMDI data, response patterns were formed from multiple poset item responses. Thus, new item response models and methods for scaling and analyzing such data are called for.
Fig. 1.
The poset structure for congruence of beliefs with the biomedical model in individuals with diabetes.
Historically, posets have been intensively studied as a mathematical object (Birkhoff, 1940; Dushnik & Miller, 1941; Stanley, 2012). In this paper, although we present a theory for models pertaining to poset responses, our focus is not on posets’ intrinsic mathematical properties. Instead, we are interested in (1) developing a model for multiple item responses in which all or some items contain poset-response categories, (2) developing efficient methods that make use of existing tools for model estimation, and (3) applying the model to multiple belief items in the CSMDI.
The CSMDI presents data that cannot be handled using existing poset-response methods which often rely on some simplifying strategies and have their limitations. The CSMDI data in Fig. 1 are characterized by two types of poset structure – connected and disjointed. Connected poset structure, as shown in the “network” that contains categories {0,1,2,3,4} in Fig. 1, commonly occurs in many social sciences. For example, Sampson and Singh (2002) described a case of psychopathologic classification: no anxiety, mild anxiety, anxiety with depression, and severe anxiety. One solution for handling poset is to group categories into equivalent classes and impose a strict ordering on the equivalent classes (e.g., Wilson, 1992). In the anxiety example, the strategy would result in three ordered category: no anxiety, {mild anxiety, anxiety with depression}, and severe anxiety.
The CSMDI data set also features a disjointed configuration in which category 5 (DK at both occasions, see Fig.1) is separated from the other connected network. Sometimes as a tactic to reduce non-response, DK is a response category commonly used in surveys. For example, in a survey about confidence in the different levels of government, the following question was asked: “How much of the time do you think you can trust each level of government? Just about always, most of the time, some of the time, hardly ever, or don’t know?” (Konisky et al., 2008). A common approach for handling DK is to treat it as missing data or to collapse it with another category such as “Incorrect” in educational testing.
A shortcoming of the simplifying strategies such as grouping intrinsic poset categories into equivalent classes is that subtle but important information may be lost during the process. There exist alternative methods for handling posets. Conceptually, the poset model used in this paper for the targeted application is closest to the work of Meulders, Ip, and De Boeck (2005) and Ip et al. (2013a). Both of these previous works directly model posets in regression settings. The former involves the extension of the partial credit model (Masters, 1982) for ordinal responses, which can be viewed as a nonlinear mixed regression model (Rijmen et al., 2003) for poset responses. The latter extends the ordinal logistic regression framework to include outcomes that contain a poset structure and applies the method to model disablement in older adults. Neither approach, however, was designed to handle disjoint structure. Additionally, the method does not apply to multiple poset response data. Therefore these existing approaches are not suitable for analyzing the CSMDI data.
If one thinks of an individual item response in a test as part of a process of providing a share of information about a measured construct, then the development of poset models is especially important for multiple item responses such as in CSMDI because simplifying strategies applied to all multiple responses could amplify information loss. For example, in a survey of 30 items of which the item format is uniform and each item contains a DK option, a broad decision of how DK would be treated will determine if partial information from the DK category would be gleaned from not just one but all 30 items.
In this paper, we describe the poset partitioned, conditional item response theory (PPC-IRT) model and show how the model is used to analyze multiple poset responses (Fig. 1) in the CSMDI data set. The PPC-IRT does not rely on simplifying strategies such as collapsing categories, treating the resulting categories as ordered, or treating DK as missing. Guided by mathematical theory for poset, the PPC-IRT directly models multiple poset item responses under the IRT framework. While the model described in this paper is intended for analyzing the poset responses in CSMDI, of which the items all have a uniform response format, the model and the related method are rather general. For example, there is no requirement that different item responses must have the same partial order structure. The substantive questions that the current paper addresses are: (1) how to calibrate items for a scale that indicates congruence of belief to the biomedical model using poset responses, and (2) how the individual estimated scores on this scale are related to individual characteristics such as gender, educational level, and clinical variables such as length of disease and blood glucose control. The general approach for poset item calibration in PPC-IRT in (1) is an extension to the conditional poset model proposed in Zhang and Ip (2012) for handling single-response poset data.
The application of the new IRT approach to CSMDI data highlights the statistical challenges for inference about a common latent trait that drives distinct conditional poset models. A direct solution would be to develop a new estimation algorithm specific to poset IRT. In this paper we prove that the PPC-IRT can actually be implemented using existing IRT software through a scheme of recoding the response categories. As the application to CSMDI shows, the approach applies to both connected and disjointed poset structures (Fig.1). For practitioners, the recoding scheme will greatly facilitate the analysis of multiple poset responses in different applications.
The reminder of the article is organized as follows. First we provide background of the conditional approach for a single poset response and various IRT models. Next, we describe the PPC-IRT for handling multiple poset responses and prove that the model can be estimated through the standard IRT method. We describe the application of PPC-IRT to the CSMDI data set regarding biomedical beliefs in persons with diabetes. Two small simulation experiments for illustrating parameter recovery are then presented. Finally we provide a discussion of the application and the method.
Background: IRT and the single-response poset conditional model
The PPC-IRT for analyzing the CSMDI data builds upon two branches of sciences—the partially ordered set and IRT.
IRT models
The IRT (Lord, 1980; Rasch, 1960; van der Linden & Hambleton, 1996; Embretson & Reise, 2000; De Boeck & Wilson, 2004) can perhaps be best exemplified by the graded response model (GRM) (Samejima, 1969) for polytomous response and the nominal response model (Bock, 1972) for multinomial response.
Suppose that we denote the latent trait for individual i by θi and the response of individual i to item j by Yij, which could take ordered values 0,1,…, K. The GRM postulates that the conditional probability of observing a response category k or higher is given by:
| (1) |
where i = 1,…, N, j = 1,…, J, and , and θi ~ N(0,1) with the variance fixed for the purpose of identifiability. For any item j, the constraint bj1< bj2 < …bjK is imposed to enforce the proper ordering of the categories. The conditional probability of observing a response in category k is thus given by:
| (2) |
for k = 0,1,…, K −1.
Note that Eq. (1) can be rewritten as:
| (3) |
For the nominal categories item-response model (Bock, 1972), the probabilities of the response categories can be expressed in terms of the vector of logits (zjk = ajk (θi − bjk), k = 0,…, K), where k merely serves as a label for unordered category. Specifically, the item-response function is given by:
| (4) |
Because the category probabilities add to one, a constraint such as zj0 = 0 is imposed on the set of logits. Equation (4) can be rewritten so that a reference category (e.g., category 0) is selected and the other categories would be compared against the reference category:
| (5) |
Note that the parameter ajk in a nominal category model can be negative (e.g., see Bock, 1996, p. 39) because the categories are not constrained to follow a particular order and therefore its direction cannot be determined a priori, as in the case of ordered data when item-response curve for a higher category stochastically dominates a lower category. An application of the nominal response model was given in Thissen and Steinberg (1984) where DK and responses to multiple choice items were all treated as nominal categories. Bock’s nominal response model can actually be considered a GRM if the parameters ajk satisfy an ordered constraint (Samejima, 1972). For a taxonomy of item-response models including both the GRM and the nominal category model, see Thissen & Steinberg (1986).
Single-response poset conditional model
We first provide some background for the poset and set up notation. A poset (P, ≼) is reflexive (a ≼ a), anti-symmetric (if a ≼ b and b ≼ a, then a = b), and transitive (if a ≼ b and b ≼ c, then a ≼ c), where a, b, c ∈ P. When a ≼ b, we say that b dominates a. Two distinct elements, a and b in P are comparable if either a ≼ b or b ≼ a; otherwise, they are incomparable.
An element a ∈ P is maximal (minimal) if there is no other element b ∈ P such that a ≼ b (b ≼ a). In a finite poset, there is always at least one maximal element and one minimal element. A chain in a poset (P, ≼) is a totally ordered subset C of P, whereas an antichain is a set A of pairwise-incomparable elements.
To further fix notation, define a weak order between subsets S1 and S2 in P if at least one element in S2 is dominated by elements in S1 and no element in S2 dominates any element in S1.
We say that S1 weakly dominates S2. A set of subsets is called totally weakly ordered if pairwise subsets are weakly ordered. For a poset formed by three binary 0/1 variables, the set of subsets {111},{110,101,011},{100,010,001}, and {000} is totally weakly ordered.
A set of subsets {Ai, i = 1,…, n} is called a partition of a poset P if , and for i ≠ j, and if a partition is at least totally weakly ordered, we call it an ordered partition. A general mathematical treatise of poset is given in Stanley (2012, Ch. 3).
The following ordered partition theorem, proved in Zhang and Ip (2012), forms the basis of the PPC-IRT:
Theorem 1 (Ordered partition). A finite poset can always be partitioned into antichains that are totally weakly ordered.
Based on the ordered partition theorem, a simple algorithm can be used to identify partitions through the iterative removal of the maximal element. We directly describe the application of the algorithm in the PPC-IRT context in the following section.
Poset partitioned conditional IRT (PPC-IRT)
In a PPC-IRT, the poset response categories are specified by a hierarchy of both nominal and ordinal IRT models applied to the ordered partitioning antichains derived from Theorem 1; that is, elements within individual antichains follow a nominal item response model, whereas ordered antichains follow an ordinal model (e.g., the GRM). From the vintage point of modeling, such specification leverages the power of IRT for both ordered and unordered item responses and applies it to a class of data that is somewhere between completely ordered and completely unordered. By doing so, we do not have to reinvent the wheels in developing entirely new models for the new class of response type. Indeed, as we shall show, we can use all existing IRT tools including software programs for analyzing multiple poset item responses.
Operationally, the fundamental idea behind PPC-IRT is conditional modeling. Both the nominal item response models and the graded response model are tools to iteratively delineate complex poset structures through conditioning on individual weakly ordered partitions of antichains. Because a poset can have disjointed structures, in this paper we shall call each connected structure within a disjointed poset a network. For example, Fig. 1 contains two networks : {0,1,2,3,4} and {5}.
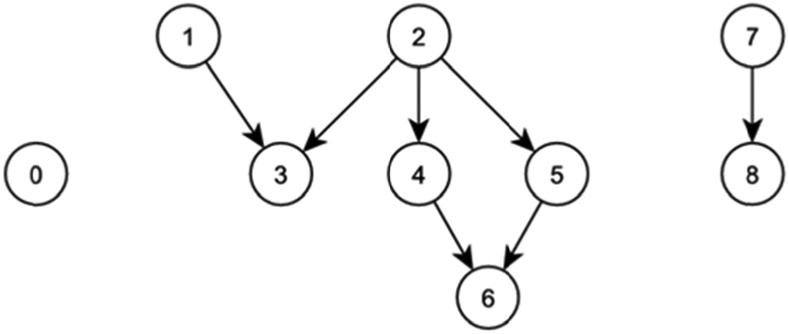
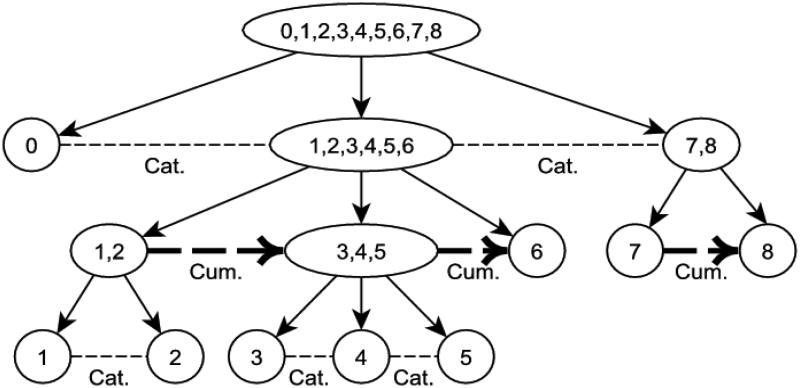
Perhaps the easiest way to explain how the PPC-IRT can be derived from the ordered partition theorem is through an example. We use a 3-network artificial example that has rich structure for illustration. A 3-network could reflect categories such as {DK}, {Refuse to respond} (such as in surveys involving sensitive subjects) or missing, and the primary response options. This poset structure example (Zhang & Ip, 2012), which is designed to illustrate the multiple layers that are present in the hierarchical and disjoint structures of poset but that are not too complex to explain, is shown in Fig. 2a. Each node in Fig. 2a represents a poset category. Assume, without loss of generality, that there are multiple items present in an instrument that share this common response structure. The algorithm for creating the PPC-IRT model for such a structure is prescribed by the following steps:
Fig. 2.
(a) A poset dominance structure including three disjoint networks; (b) A hierarchical binary-tree representation of the ordered partition process. The “Cat.” and `”Cum.” labels are respectively used to indicate a categorical (nominal) or cumulative (GRM) item-response model related to a split.
1. Partition the Hasse diagram into three disjoint networks: {0},{1,..,6}, and {7,8}. Define ≼ ijk = P(yij = k | θi) for individual i = 1,…, N and category k = 0,…,8. Use one of the partitions, say {0}, as a reference category, and specify the following nominal item-response models:
| (6a) |
| (6b) |
2. Conditional on the network {7,8}, specify the conditional two-parameter logistic (2PL) model (e.g., see Reise & Waller, 2001):
| (7) |
3. For the network {1,..,6}, partition it into a set of totally weakly ordered antichains using Theorem 1: {6} ≼ {3, 4,5} ≼ {1, 2}. Specify the following conditional GRM:
| (8a) |
| (8b) |
4. Specify two nominal models respectively for the antichains derived from the partitioned subset {1,2}:
| (9) |
and the subset {3,4,5}:
| (10a) |
| (10b) |
The procedure is graphically illustrated in Fig. 2b. The ordered partition theorem assures that for any poset structure, the kind of decomposition shown above is always valid. An appealing feature of the proposed conditional approach is that the modeling process is consistent with human cognitive processes. For example, when faced with multiple (poset) categorization of a psychiatric disorder, a psychiatrist would sort disorder categories approximately by their overall severity, and subsequently compare different disorder categories that have more or less the same level of severity. The powerful idea of conditioning has been utilized in the IRT literature - e.g., most recently in Böckenholt (2012), and De Boeck and Partchev (2012). Thus, the proposed approach can be considered as yet another application of the idea to poset responses.
Because the direction of how the logit varies with θ is not known a priori in nominal response categories, the a-parameter in a nominal model can either be positive or negative, as determined by the data. We will discuss the implication of mixed signed a-parameters later in the Discussion section. Of note, a generalized notion of GRM that does not constrain the discrimination parameter to be uniform across categories – or the heterogeneous case of GRM (Samejima, 1996; Rizopoulos, 2006; also see Ostini & Nering, 2010 for clarification of terminology) is an alternative to the GRM in Eq. (8).
Using generic IRT programs for solving PPC-IRT
We propose to use the marginal maximum likelihood (MML) method (Bock & Aitkin, 1981) for calibrating the PPC-IRT model. The procedure assumes local independence between multiple responses given a latent trait. In other words, the likelihood of the marginal model is formed by first multiplying the factorized likelihood of the conditional models and then integrating out the common latent trait θ. Formally, assume again without loss of generality that all item responses share the same poset structure, and that the response takes a value in the poset P = {1,…, K} (values not necessarily ordered). From the ordered partition theorem and the algorithm described above, denote the sequence of conditional partitions identified for response k ∈ P by , where qk +1 is the number of conditional partitions associated with response category k, and the sets to which response k belongs by , where . For example, in Fig.1, for the poset response category Y = 3, and . The conditional probability given θ for observing a poset response category k ∈ P is given by
| (11) |
For each individual i, rewrite the response pattern as a J-vector (kij). By assuming local independence between item responses given θ and independence between person, the overall likelihood can now be expressed as:
| (12) |
where g(θ ) is the density function of the latent trait.
The primary methodological challenge of the PPC-IRT is that unlike a single-response poset outcome in a regression setting, there exists an observed latent trait θ that is common to all the conditional models—some nominal and others ordinal—so the item estimation procedure cannot be separately conducted for each of the conditional components.
Surprisingly, if one is willing to recode the poset responses, inference based on the PPC-IRT can still be conducted by using IRT tools developed for estimating ordinal (including binary) and categorical responses. Using the above example to illustrate the recoding scheme, we would create 5 sub-items from this single poset item with the 3-network structure. The 5 sub-items follow Fig. 2b such that the first sub-item represents the 3-category unordered response {0}, {1,2,3,4,5,6}, and {7,8}; the second sub-item represents the 3-category ordered responses {6} ≼ {3, 4,5} ≼ {1, 2}, and so on. Table 1 shows the coding scheme for all eight response categories in the poset, with NA representing missing. As we follow our notation of using numeric labels for both ordered and unordered categories, to avoid confusion, we distinguish the two types of responses by labeling them respectively with superscript U and O. For example, response category 3 in Fig. 2 is coded into 5 sub-item responses (1U, 1O, NA, 0U, NA) in which the first coordinate 1U represents the code for the nominal (unordered) model that comprises the three categories: {0} = 0U (reference), {1,2,3,4,5,6} = 1U, and {7,8} = 2U. To facilitate future description, we shall call the coding scheme “poset conditional coding.”
The Common Sense Model of Diabetes Inventory (CSMDI)
| Domain* | Item# | Description |
|---|---|---|
| S | 1† | Feeling nervous is a sign of low blood sugar. |
| S | 2 | Blood sugar will go up if you eat too many white foods. |
| S | 3† | People with diabetes have tingling in their feet due to high blood sugar. |
| S | 4 | Falling down is a sign of diabetes. |
| S | 5† | Having to go to the bathroom often at night is caused by diabetes. |
| S | 6† | Diabetes makes people feel thirsty all the time. |
| I | 7 | Family members with diabetes are good sources of diabetes information. |
| I | 8 | People with diabetes understand their disease better than their doctors. |
| I | 9 | People could better control their diabetes if they were given the right information. |
| C | 10 | Weight does not cause diabetes because thin people also get diabetes. |
| C | 11 | Diabetes can’t be hereditary because not everyone in a family gets it. |
| C | 12 | Some people get diabetes because they ate too many sweets when they were young. |
| C | 13 | Everyone is born with diabetes but it develops at different times for different people. |
| C | 14† | Being overweight makes people get diabetes. |
| C | 15† | Diabetes runs in families. |
| Co | 16† | Diabetes causes high blood pressure. |
| Co** | It is difficult for people with diabetes when they have a full-time job. | |
| Co** | Diabetes has serious financial consequences. | |
| Co | 17† | Diabetes makes it difficult for your body to fight infection. |
| BM | 18 | Drinking lots of water helps to flush extra sugar out of the body. |
| BM | 19† | Stress makes your blood sugar go up. |
| BM | 20† | Managing the size of each meal helps control diabetes. |
| BM | 21 | The only thing people with diabetes need to know is to stay away from sweets. |
| BM | 22t | Doing household chores is enough exercise for someone who has diabetes. |
| BM | 23† | The body processes sugar in fruits and vegetables differently than sugar in sweets and starches. |
| BM | 24 | Blood sugar often goes up and down for no reason. |
| MM | 25 | Taking extra medication helps to manage high blood sugar. |
| MM | 26 | People should adjust their diabetes medication depending on how they feel. |
| MM | 27 | Low blood sugar can be managed by adjusting medication. |
| MM | 28 | Medical treatment cures diabetes. |
| MM | 29 | Taking extra medication makes it okay to eat something sweet. |
S=Symptoms, I=Information, C=Causes, Co=Consequences, BM=Behavioral Management, MM=Medical Management,
=Congruent with the Biomedical Model;
Removed from the current analysis.
The following theorem states that in general the likelihood obtained for PPC-IRT in Eq. (13) is identical to that obtained for the sub-items.
Theorem 2 (Poset conditional coding): The poset conditional coding of the response category into sub-item responses leads to the same likelihood function as evaluated by the PPC-IRT model.
The proof is given in Appendix 1.
The implication of the poset conditional coding theorem is that any IRT software that uses MML methods for estimating item parameters in dichotomous, polytomous, and nominal IRT models can be used to estimate a PPC-IRT model once the responses are preprocessed and recoded in the way described above. Because many robust IRT software programs, including but not limited to BILOG/MULTILOG/PARSCALE (Zimowski et al., 2003; Thissen, Chen, & Bock, 2003; Muraki & Bock, 2003), IRTPRO (Cai, Thissen, & Du Toit, 2011), Mplus (Muthén & Muthén, 2012), ConQuest (Wu, Adams, & Wilson, 1997), Winsteps (Bond & Fox, 2012), the R-package ltm (Rizopoulos, 2006), the Matlab-based IRTm (Braeken & Tuerlinckx, 2009), SAS-based macros (De Boeck & Wilson, 2004), and the recently released SAS program PROC IRT (SAS Inc., NC), are generally available to users of different requirements, the result implies that the poset structure can now be easily incorporated into the IRT paradigm and little initial barrier would exist for its practical implementation.
Application to common-sense belief
As part of a study of health beliefs and behavior on adults with diabetes who live in rural areas in the U.S. (Arcury et al., 2012; Quandt et al., 2012), the data used in this analysis were collected from the instrument CSMDI, which measures common-sense beliefs about their disease held by individuals with diabetes (Ip et al., 2013c). The CSMDI is composed of a battery of 31 items, which cover beliefs in six different domains—symptoms, causes, consequences, information, behavioral management of diabetes, and medical management of diabetes. All items have three response categories: “Agree,” “Disagree,” and “Don’t Know.” While the original CSMDI items were developed to capture common sense beliefs without “correct” or “incorrect” answers, for the current study, all items were coded according to the American Diabetes Association (ADA) guidelines (ADA, 2012) to reflect congruence with the current biomedical understanding of type 2 diabetes. It was determined that two study items were neither consistent nor inconsistent with the ADA guidelines and were subsequently removed after consultation with clinician investigators. As a result, responses from a total of 29 items were used in this analysis. The items and the ADA coding are provided in Appendix 2. A sample of n = 593 participants composed of rural-dwelling adults (age > 60) with diabetes were recruited to complete the CSMDI during two consecutive visits that were separated by one month. Neither treatment nor education intervention was administered between the two visits. Demographic data such as age, gender, education level, and disease related information such as years with diabetes and A1C level were collected at baseline. The study protocol was approved by the Institutional Review Board of the institution at which the study was conducted. Because of missing values, only n = 561 were used in the final sample for this study.
The latent trait of interest here is the strength of congruence of a person’s belief with the biomedical model. As described in the Introduction, Fig. 1 shows the poset structure of the responses formed from the individual responses over the two occasions of study visit. The reason we used information from both study visits is that the common sense beliefs expressed by the participants could vary substantially across different measuring occasions. The response inconsistency observed in this kind of data is sometimes above and beyond measurement error and reflects a person’s level of ambivalence about a specific belief (Ip et al., 2013c). The poset in Fig. 1 reflects a mental process in which congruence with the biomedical model on both occasions is the highest-ordered category, and incongruence with the biomedical model on both occasions is the lowest category, with one visit being congruent and the other DK, and one visit being incongruent and the other DK as middle categories. These four ordered categories reflect different levels of strength in the belief. The other response patterns—DK on both occasions and conflicting views in the two visits—cannot be linearly ranked order within the ordered categories. It is likely that these two response patterns respectively reflect indifference, and a somewhat confused state of mind in expressing contradicting and opposing views over a short period of time. Congruent at one occasion and incongruent at another is judged to be dominated by congruence at both occasions and dominates incongruence at both occasions.
An issue that was not entirely resolved was how the structure of the poset should be defined in an application—e.g., whether by prior knowledge or from the data. In this report the poset structure was user-defined. A reviewer suggested the currently defined structure instead of one that treats the category “congruent in one and incongruent at another occasion” as a disjoint category. It might also be easily argued that DK at both occasions could be dominated by congruent at both occasions. However, we determined that DK at both occasion should be treated as qualitatively different from the other response patterns because of the individual’s consistency in responding DK at both times. A separate but related issue is the use of alternative methods for analyzing the CSMDI data. For example, responses to items at two time points could be combined into a multi-component poset and dependency (interaction) parameters could be added to the model to capture the correlation between responses to the same belief response across two occasions. Another option is to treat the responses across occasions as locally dependent responses with response consistency modeled as a distinct trait (Ip et al., 2004). It is also possible that the poset structure is determined by a data-driven approach, but we do not include this kind of analysis in the current paper.
Employing the user-defined poset structure, the PPC-IRT model was applied to the CSMDI data set using the poset conditional coding scheme, which is shown in Table 2. We noted that within the data there were only two items (Item 15: “Diabetes runs in families.” and Item 22: “Doing household chores is enough exercise for someone who has diabetes.”) that contained DK responses on one or both occasions. We calibrated the 29 CSMDI items using a standard IRT software program, IRTPRO 2.1, by coding the poset responses using the poset conditional coding scheme. The calibration program in IRTPRO 2.1 is based on the marginal maximum likelihood approach. Using the recoded scheme, the likelihood of a poset item contains the product of dichotomous, polytomous, and nominal item responses to the sub-items (see Table 2), as specified by the 2-PL, the graded response model, and the nominal response model, respectively. Thus, the implementation of the PPC-IRT was achieved through a standard IRT program. Subsequently, the same standard IRT program was used to derive individual scores of congruence with the biomedical model by treating the item parameters estimated in the earlier stage as fixed.
Table 1.
Poset Conditional Coding for Poset Structure in Fig. 2.
| Response category |
Sub-item 1 | Sub-item 2 | Sub-item 3 | Sub-item 4 | Sub-item 5 |
|---|---|---|---|---|---|
| 0 | 0U | NA | NA | NA | NA |
| 1 | 1 U | 0 O | 0 | NA | NA |
| 2 | 1 U | 0 O | 1 | NA | NA |
| 3 | 1 U | 1 O | NA | 0U | NA |
| 4 | 1 U | 1 O | NA | 1 U | NA |
| 5 | 1 U | 1 O | NA | 2 U | NA |
| 6 | 1 U | 2 O | NA | NA | NA |
| 7 | 2 U | NA | NA | NA | 0 |
| 8 | 2 U | NA | NA | NA | 1 |
* sub script U represents unordered category and O represents ordered category.
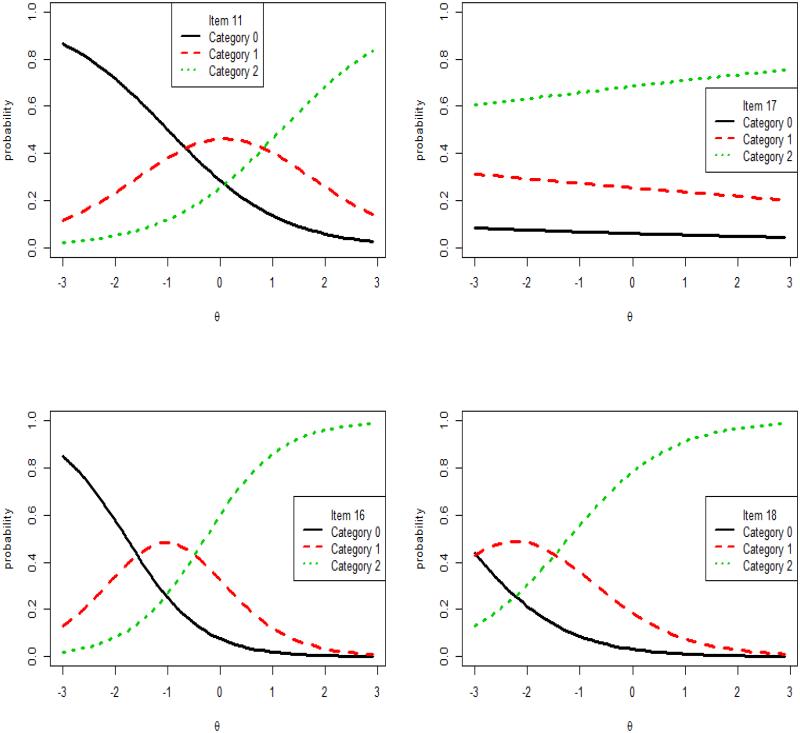
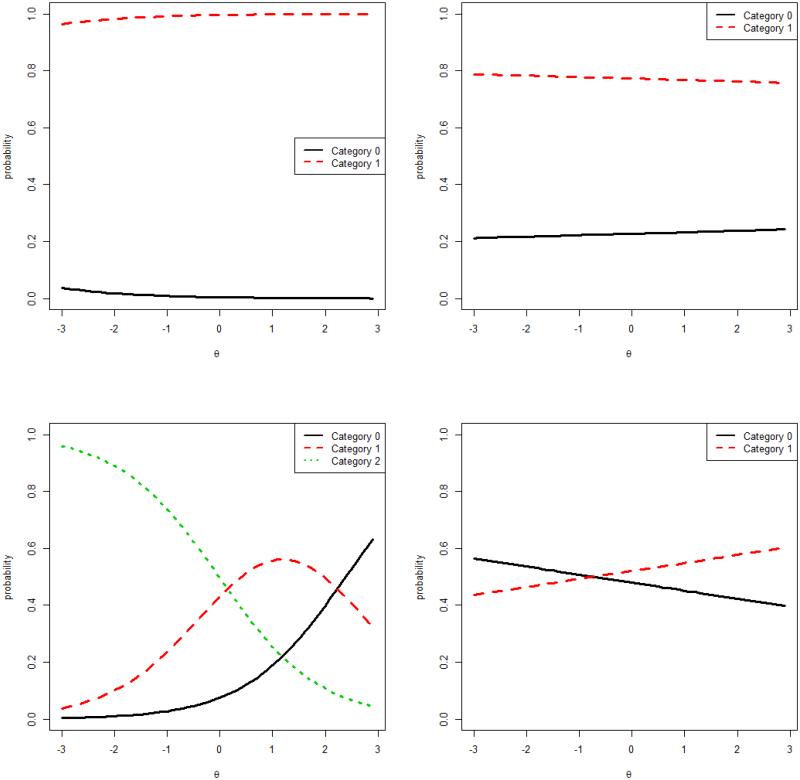
Figures 3 and 4 show selected item characteristic curves (ICCs) from the IRT calibration procedure, where a higher θ represents a higher level of consistency with the biomedical model. Figure 4 shows the ICCs of 4 items (Items 11, 16, 17, 18), all of which do not contain a DK response. In other words, the ordinal categories modeled in these items are congruent at both occasions (category 2 in Fig. 3), congruent at one and incongruent at another occasion (category 1), and incongruent at both occasions (category 0). Item 11 (“Diabetes can’t be hereditary”, not congruent with biomedical model) and Item 16 (“Diabetes causes high blood pressure”, congruent with biomedical model) has rather “normal looking” ICC, implying that the ordinal categories function properly within the normal range of θ. On the other hand, Item 17 (“Diabetes makes it difficult to fight infection”, congruent with biomedical model) has low discrimination. Item 18 (“Drinking lots of water flushes extra sugar out”, not congruent with biomedical model) behaves like a dichotomous item with the response curve for category 1 dominating that of category 0. The response of being congruence at both occasions for this item well discriminates individuals with high congruence with the biomedical model from individuals with low congruence.
Fig. 3.
Item Characteristic Curves (ICCs) of selected items that do not contain DK in the belief about diabetes application.
Fig. 4.
Item Characteristic Curves (ICCs) of Item 22, which contains the full poset structure. The ICCs are for subitem 1 (top left panel), subitem 2 (bottom left panel), subitem 3 (top right panel), and subitem 4 (bottom right panel).
Figure 4 shows the ICCs for Item 22 (“Doing household chores is enough exercise”, congruent with biomedical model), which contains a DK response and has a full poset structure as shown in Fig. 1. Following earlier notation of using superscripts O and U to respectively denote ordered and unordered sub-items, note that sub-item 2 (Table 2) in Item 22 is a graded response item (congruent at both occasions recoded as category 2O and so on). The a parameter for response category 3 (recoded as category 2, Fig. 4) was negative (−1.05). This is intriguing because it implies that individuals endorsing the item at both occasions tend to have lower overall θ. For the sub-item 3, the a parameter was negative and close to zero (a = −0.03) for the categories congruent at one occasion and incongruent at another (response category 4), as compared to the other two response categories {1,2}. This suggests that an individual with incoherent responses across the two occasions tends to be less consistent with the biomedical model, compared to congruent/incongruent and DK as a group. The information gleaned from such comparison is not strong, as evidenced by the small gradient in the ICC. Subitem 4 in Item 22 shows also that congruent/DK is indeed more consistent with the biomedical model than incongruent/DK, as evidenced by the positive slope (a = 0.11) in the ICC for the recoded category of 1 (corresponding to response category 2 in Fig. 1).
Using p<.05 and 2-sided tests to indicate significance, ANOVA tests suggested that there were significant differences in mean biomedical scores by race categories, level of education, and level of poverty. Because inference based on the mean scores could sometimes be skewed by outliers or long tails of the distribution, we also investigated the differences in distributions. The Kolmogorov–Smirnov test (Smirnov, 1944) was applied to test the equality of the subgroup-scores distributions. The results show that there were highly significant differences between the distributions by race, level of education, and level of poverty (all p < .001). An unexpected result was the suggestion that individuals with a lower level of education and a higher level of poverty tended to have higher biomedical scores. One possible explanation is that individuals with diabetes who are at a lower level of education tended to obtain their knowledge about diabetes primarily from their care providers and therefore deviate less from the biomedical beliefs. Individuals of deprived economic status may also be more sensitive to their limitations in resources and therefore pay more attention to care providers’ guidelines and recommendations in managing their disease. Additionally, those with low income may also have better access to health care by qualifying for Medicaid. Thus these individuals’ views would tend to be more aligned to the biomedical model.
Beliefs about diabetes also tend to be different by race/ethnicity. Whites tend to be less congruent with the biomedical model than blacks. America Indians are not significantly different from blacks in terms of their belief about diabetes. Finally, compared to people with less than 5 years into diabetes, people with diabetes for 10-20 years tend to be less “biomedical” (p=0.017). It is possible that this group became “hardened” in their beliefs and tended not to rely so much on using the biomedical model as their belief anchor. Table 3 shows the regression result using the same set of predictor variables and the significant results in bivariate analysis remain significant after controlling for other factors, suggesting that these findings are relatively robust.
Table 2.
Poset Conditional Coding for Poset Structure in Figure 1.
| Response category |
Sub-item 1 | Sub-item 2 | Sub-item 3 | Sub-item 4 |
|---|---|---|---|---|
| 0 | 1 | 0O | NA | NA |
| 1 | 1 | 1O | 0 | 0 |
| 2 | 1 | 1O | 0 | 1 |
| 3 | 1 | 2O | NA | NA |
| 4 | 1 | 1O | 1 | NA |
| 5 | 0 | NA | NA | NA |
Simulation experiments
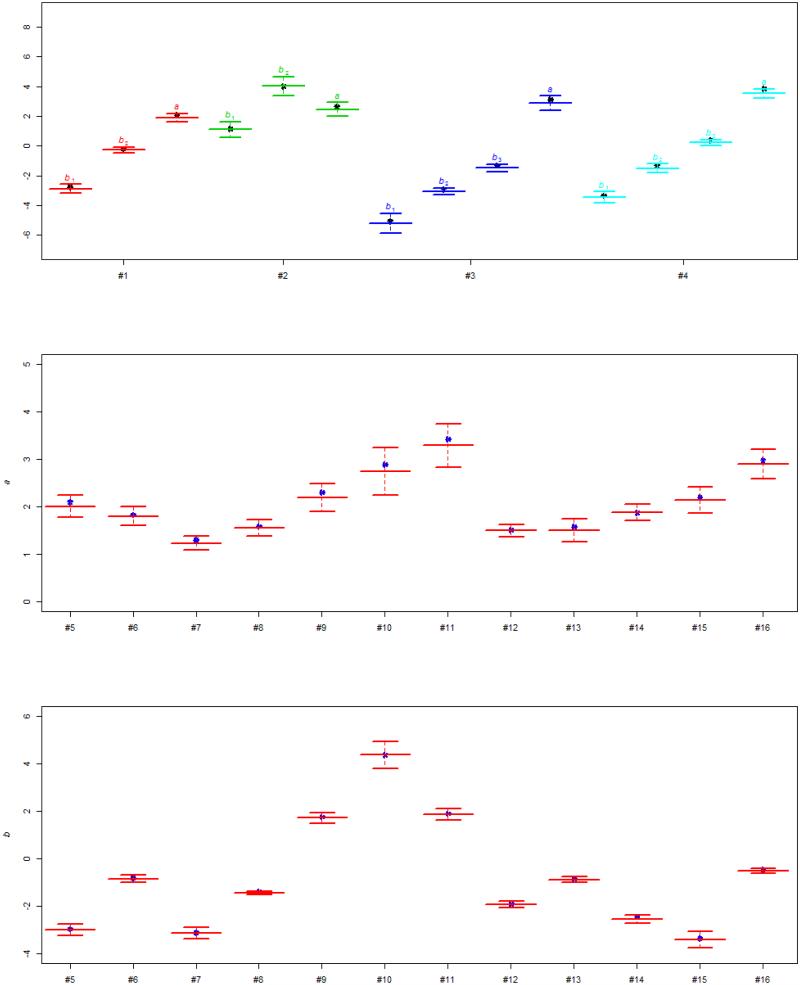
The purpose of the simulation experiments is to examine parameter recovery from PPC-IRT and to study the impact of misspecified models (treating DK as missing) on item and person estimates. We conducted two simulation experiments: simulation experiment 1 (SE1) is intended to verify the estimation results implied by Theorems 1 and 2, whereas simulation experiment 2 (SE2) aims to examine the effect of misspecification of treating DK as a missing value. For both experiments, a PPC-IRT was used to generate data. Four poset items were designated such that each has two disjoint sets of response categories: A 4-category ordered response set coded {3,2,1,0} in one; and a category of “Don’t Know” (DK) in another, following the poset structure depicted in Fig. 2b. Twelve binary items were added to the mix, thus a total of 16 items were used. Item-parameter values for the items were selected from an instrument measuring self-efficacy in physical mobility (Rejeski et al., 2006; Ip et al., 2013b). The percentages of DK in the 4 poset items ranged from 10.7% to 67%. To mimic a realistic data situation, we purposefully removed a proportion of the responses from the 4 poset items (respectively 10.6%, 15.7%, 25.7%, and 43.5%). In SE1, the poset responses were coded according to the poset conditional coding scheme. Because our purpose here is to verify the validity of the coding scheme, we chose an adequate sample size to avoid possible small sample size complications such as large variations in item parameter estimates and non-convergence. Responses from a total of 2,000 individuals were generated for a simulated data set, and twenty replications of such data sets were used to provide an estimate of the 95% confidence interval for the item parameters. To each generated data set, the MML method, which was implemented through the R package ltm (v0.9-9), was applied to calibrate the items. Our goal was to evaluate parameter recovery in terms of Type I error rates. Figure 5 shows the result of SE1. It can be seen that the true parameter values (represented by dots in Fig. 5) of all 16 items lie within their respective 95% confidence intervals, suggesting that the parameter values of a PPC-IRT model can be accurately recovered by using standard IRT software with the poset conditional coding scheme.
Fig. 5.
Estimates and 95% confidence intervals for true item parameters in simulation experiments. SE1: The first four items of the poset format (upper panel); a parameter for binary items (middle panel); b parameter for binary items (lower panel). The dots represent the true parameter value.
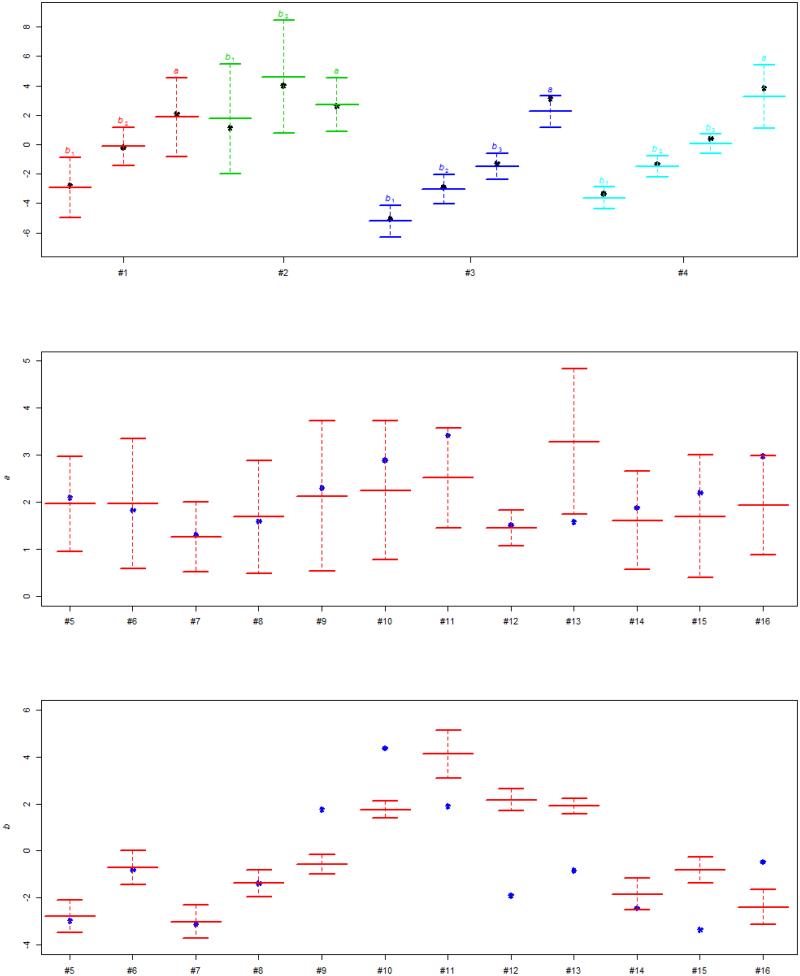
We also conducted a second small simulation experiment (SE2) to evaluate the effect of treating DK as missing on item-parameter estimates. An identical data-generation mechanism to SE1 was used for generating response data for SE2. However, instead of following the poset conditional coding scheme, the DK response was now treated as missing. In other words, a misspecified model—the GRM instead of the poset model—was used in the item parameter recovery. Figure 6 shows the item parameter estimates and confidence intervals of the GRM together with the true parameter values for all 16 items in SE2.
Fig. 6.
Estimates and 95% confidence intervals for true item parameters in simulation experiments. SE2: First four items of poset format with DK treated as missing (upper panel); a parameter for binary items (middle panel); b parameter for binary items (lower panel). The dots represent the true parameter value.
While we expect some item parameter estimates to exhibit bias, it is surprising that the true parameter values for the ordinal component of the poset in SE2 all fall within the 95% confidence limits (Fig. 6) even though their confidence intervals were substantially longer than those observed in SE1. However, the parameter estimates of the other binary items exhibit noticeably biased results. For estimates of the discrimination parameter a, Fig. 6 shows that 1 out of 12 estimates is not covered by the 95% confidence intervals, whereas for the intercept (difficulty) parameter b, 7 out of 12 are not covered, suggesting that substantial bias was introduced into the estimates of b when the underlying poset model was not correctly specified.
We also examined the recovery of the latent trait θ. Two measures – averaged (over conditions) root mean squared error (RMSE) and averaged 95% coverage rate were evaluated. The averaged RMSEs for SE1 and SE2 were respectively 0.32 (SD=0.007) and 0.40 (SD=0.06) respectively, whereas averaged 95% coverage rate were respectively 95.6% and 92.0%. We also inspected the scatterplots (not shown) for the true and estimated θ values. For some conditions (e.g., when % DK were high), the bias in the estimated θ was substantial when DK was treated as missing in SE2.
In summary, the simulation experiment offers evidence that the poset conditional coding works well in using standard IRT programs for parameter recovery, and that treating DK as missing leads to biased item parameter and ability estimates.
Discussion
We treated responses to an inventory of common sense beliefs about diabetes - the CSMDI, across two occasions as partially ordered data and applied a poset IRT to the data set. There are several unique features in this application. First, the data set is rather unique in that it comprises a relatively large sample of people with diabetes being measured at two consecutive time points, as in a test-retest study, which typically only contains small sample of twenty or so.
The current “test-retest” data set analyzed in the study is also special in that it measures beliefs about a chronic disease that is known to be fluid and exhibit diverse individual differences. Third, in this application we extended a current poset method to IRT for analyzing the data. Perhaps more importantly, we developed a poset coding scheme that allows the use of existing IRT software. From a practical perspective, this solves the key issue of implementation, which often impedes the diffusion of advanced psychometric tools.
Not only does the recoding scheme circumvent the need to rewrite software codes for poset responses, the theory underlying the result also reveals the information content of poset responses in terms of the number of sub-items that is required to recode the poset item. Consider the simple example of a 4-category poset formed from two binary items so that the category 11 is the maximal element, 00 the minimal element, and 01 and 10 are in between but not comparable to each other. The sum-score approach would turn the poset into one ordinal item with the ordered categories 00=0,{10,01}=1, and 11=2. The poset sub-item coding treats this poset structure as two items: 00=(0,NA), 10=(1,0), and 01=(1,1), and 11=(2,NA), in which (.,.) represents the recoded two sub-item responses. In terms of information, the poset is almost worth two independent items (one ordinal and one binary); “almost” because of the NA in 00 and 11 for the second sub-item. Thus, compared to the sum-score approach, the most important difference is in the treatment of the incomparable categories.
In a sense, the “additional” sub-items that arise from the PPC-IRT approach allow information from the partial ordering of responses to be gleaned from incomparable categories such that the information would contribute to the estimation of the latent trait. Using the above example again, if one uses 01 as the reference category (coded 0 in the second sub-item), and if the a parameter turns out positive, then one can argue that among the two categories 10 and 01, 10 should be the higher category with respect to the latent trait. The situation is not different if 10 is used as the reference category, because then the parameter a would be negative but retain the same magnitude. The latter specification is of course equivalent to the former. Accordingly, the PPC-IRT offers a data-driven approach in which the rank order of the incomparable poset categories need not be determined a priori, and simply “let the data determine which way to go.” In a more complex poset structure for multiple responses, it is not always immediately clear which incomparable categories need be grouped and compared. This paper provides a systemic method for processing the categories. In doing so, information is borrowed across categories as well as across items through the latent variable. Intuitively, it is the full use of the strictly and weakly ordered information present in the poset that would likely result in an increase of accuracy in the item and individual estimates. The accuracy will also increase with the number of poset items present in a test. Thus, using a proper model for poset responses is especially important when there are many poset items in a test.
As remarked previously, the PPC-IRT can accommodate both connected and disjointed response categories. Thus a possible use of the model is in educational testing. For large-scale educational assessments, not-reached responses often pose challenging analytic problems. Not-reached responses are routinely treated as “Incorrect” even though the underlying reason could be related to time constraint. The PPC-IRT would allow not-reached responses to be naturally processed as a response category analogous to the DK option in this paper. As such, the not-reached responses are included for informing the estimate of ability level.
Finally, we briefly highlight the connection between PPC-IRT and other emphases on the application of poset to data analysis, such as ranking and clustering. Because an individual score (the estimated θ ) could always be derived from the PPC-IRT, the poset item-response model could be easily used for ranking purposes. In other words, by putting each individual on a common scale of latent trait θ , all individuals could be linearly ordered: Individual i with response pattern yi would rank higher than individual j with response pattern yj if , where denotes an estimate of θ. This could serve as an alternative to existing poset ranking methods (Brüggemann & Patil, 2009; Brüggermann & Voigt, 2009). New cases that might involve a response not seen in the sample could also be scored and accordingly ranked. As for clustering, in principle the PPC component in the PPC-IRT model could be adapted and used in latent class analysis (LCA) for the purpose of clustering. The PPC-LCA approach would be similar to the latent class modeling used in Tatsuoka (2002), which describes the clustering of posets of cognitive states through LCA. It should be pointed out that existing approaches of using LCA in analyzing posets have used binary or ordered items and not poset items. For example, in Tatsuoka (2002), the test items for cognitive diagnosis are all dichotomously scored (correct/incorrect) and do not have a poset format. See also Tatsuoka, Varadi, and Jaeger (2013). Thus, if one considers both poset-format items and posets of the resulting response patterns, the approach could then be called a “poset of poset responses” analysis. In this sense, in contrast to the PPC-IRT, which derives a unidimensional summary of poset-format responses, a PPC-inspired LCA could be conceptualized as a two-level poset-poset model for clustering and subsequent classification purposes. We look forward to embarking on this line of research.
Table 3.
Regression Analysis of Scores From Poset Responses
| Estimate | SE | p-value | |
|---|---|---|---|
| Gender | |||
| Male | 0.056 | 0.934 | 0.07 |
| Age | |||
| Seventies | 0.058 | 0.080 | 0.47 |
| Eighties | −0.001 | 0.126 | 0.99 |
| Education | |||
| HSGrad | −0.362 | 0.091 | <.001 |
| Greater ThanHS | −0.703 | 0.097 | <.001 |
| Race | |||
| American Indian | −0.073 | 0.092 | 0.43 |
| White | −0.486 | 0.089 | <.001 |
| A1C | |||
| 7-7.99 | 0.000 | 0.087 | 0.99 |
| 8 and above | −0.028 | 0.094 | 0.76 |
| Years with Diabetes | |||
| >5,<=10 years | −0.158 | 0.106 | 0.14 |
| >10,<=20 years | −0.240 | 0.100 | 0.02 |
| >20 years | 0.072 | 0.108 | 0.51 |
| Poverty | |||
| At/above poverty line | −0.183 | 0.087 | 0.04 |
Acknowledgment
This work is supported by an National Science Foundation grant SES-1229549, and National Institutes of Health grants RO1-AG017587-05A1 and P30AG21332.
Appendix 1
Proof. We prove the case for two disjoint networks of dichotomous items in Fig. A1. Denote the observed response in poset structure by Y. Table A1 shows the poset conditional coding scheme for the response categories Y = a,b, c, d with the responses for the sub-items denoted by Y(1),Y(2),Y(3), each of which can take value in the set {0,1} (assume that the set {a,b} is used as a reference set, which is coded 0, and also that a and c are coded as 1 in their respective network of dichotomy).
Fig. A1.
The poset structure for an example in the proof of Theorem 2.
Table A1.
Poset Conditional Coding Scheme for the Disjoint Network in Fig. A1.
| Response Category in Poset Structure Y |
Sub-Item 1 Y(1) |
Sub-Item 2 Y(2) |
Sub-Item 3 Y(3) |
|---|---|---|---|
| a | 0 | 1 | NA |
| b | 0 | 0 | NA |
| c | 1 | NA | 1 |
| d | 1 | NA | 0 |
To derive the likelihood for PPC-IRT, we first write the following law of total probabilities:
| (A1) |
Because P(Y(2) =1|θ,Y(1) =1) = 0 by definition, the above expression simplifies to
| (A2) |
On the other hand, the MML approach under the poset conditional coding scheme would evaluate the probability of the response pattern P(Y = a |θ) as P(Y(1) = 0,Y(2) =1,Y(3) = NA |θ) (Table A1). This probability, under the local independence assumption in IRT, is evaluated as
| (A3) |
which is identical to the RHS in (A2). Note that the missing value in Y(3) in P(Y(1) = 0,Y(2) =1,Y(3) = NA |θ) is not evaluated in (A3), per the IRT assumption that administered items are sampled from a universe of items and that not-responded-to items are treated as missing-at-random. It is straightforward to verify that the same logic applies to the other response patternsY = b, c, d. Furthermore, the argument for this example can be readily extended to other disjointed or connected poset structures as Eqs. (A1–A3) do not involve a specific IRT model, and the argument can also be easily generalized to more than two responses within a network. Thus we have proved that the poset conditional coding scheme leads to the correct likelihood based on the PPC-IRT specification.
Appendix 2
Contributor Information
Edward H. Ip, PhD Department of Biostatistical Sciences, Wake Forest School of Medicine
Shyh-Huei Chen, Department of Social Science and Health Policy Wake Forest School of Medicine.
Sara A. Quandt, PhD Department of Epidemiology and Prevention, Wake Forest School of Medicine
References
- American Diabetes Association, ADA Standards of medical care in diabetes. Diabetes Care. 2012;35(Suppl. 1):S11–S63. doi: 10.2337/dc12-s011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arcury TA, Grzywacz JG, Ip EH, Saldana S, Nguyen HT, Bell RA, Kirk JK, Quandt SA. Social integration and diabetes management among rural older adults. Journal of Aging and Health. 2012;24:899–922. doi: 10.1177/0898264312449186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baer RD, Weller SC, Garcia de Alba Garcia J, Salcedo Rocha AL. A comparison of community and physician explanatory models of AIDS in Mexico and the United States. Medical Anthropology Quarterly. 2004;18:3–22. doi: 10.1525/maq.2004.18.1.3. [DOI] [PubMed] [Google Scholar]
- Baer RD, Weller SC, Garcia de Alba Garcia J, Salcedo Rocha AL. Cross-cultural perspectives on physician and lay models of the common cold. Medical Anthropology Quarterly. 2008;22:148–66. doi: 10.1111/j.1548-1387.2008.00012.x. [DOI] [PubMed] [Google Scholar]
- Birkhoff G. Lattice Theory. American Mathematical Society, Colloquium Publication; Providence, RI: 1940. [Google Scholar]
- Bock R. Estimating item parameters and latent ability when responses are scored in two or more latent categories. Psychometrika. 1972;57:29–51. [Google Scholar]
- Bock R, Aitkin M. Marginal maximum likelihood estimation of item parameters: Application of an EM algorithm. Psychometrika. 1981;46:443–459. [Google Scholar]
- Bock RD. The nominal categories model. In: van der Linder WJ, Hambleton RK, editors. Handbook of item response theory. Springer; New York: 1996. pp. 33–50. [Google Scholar]
- Böckenholt U. Modeling multiple response processes in judgment and choice. Psychological Methods. 2012;17:665–678. doi: 10.1037/a0028111. [DOI] [PubMed] [Google Scholar]
- Bond TG, Fox JC. Applying the Rasch Model: Fundamental Measurement in the Human Sciences. 2nd Routledge; New York: 2012. [Google Scholar]
- Braeken J, Tuerlinckx F. Investigating latent constructs with item response models: A MATLAB IRTm toolbox. Behavior Research Methods. 2009;41:1127–1137. doi: 10.3758/BRM.41.4.1127. [DOI] [PubMed] [Google Scholar]
- Brock B. Factors influencing intentions and behaviors toward swine flu vaccine. 1984 Doctoral dissertation, University of Michigan, Ann Arbor, MI. [Google Scholar]
- Brüggemann R, Patil GP. Ranking and prioritization for multi-indicator systems. New York; Springer: 2009. [Google Scholar]
- Brüggermann R, Voigt K. Analysis of partial orders in environmental systems applying the new software PyHasse. In: Jochen W, Michael F, editors. Simulation in Umwel-ad Geowissenchaften, Workshop Potsdam 2009. Shaker Verlag; Aachen: 2009. pp. 43–55. [Google Scholar]
- Cai L, Thissen D, du Toit SHC. IRTPRO for Windows [Computer software] Scientific Software International; Lincolnwood, IL: 2011. [Google Scholar]
- Chavez LR, Hubbell FA, McMullin JM, Martinez RG, Mishra SI. Structure and Meaning in Models of Breast and Cervical Cancer Risk Factors: A Comparison of Perceptions among Latinas, Anglo Women, and Physicians. Medical Anthropology Quarterly. 1995;9:40–74. doi: 10.1525/maq.1995.9.1.02a00030. [DOI] [PubMed] [Google Scholar]
- De Boeck P, Wilson M. Explanatory item response models: A generalized linear and nonlinear approach. Springer; New York: 2004. [Google Scholar]
- De Boeck P, Partchev I. IRTrees: Tree-based item response models of the GLMM family. Journal of Statistical Software. 2012;48:1–28. [Google Scholar]
- de Jong M, Steenkamp J, Fox J, Baumgartner H. Using item response theory to measure extreme response style in marketing research: A global investigation. Journal of Marketing Research. 2008;45:104–115. [Google Scholar]
- Dushnik B, Miller EW. Partially ordered sets. American Journal of Mathematics. 1941;63:600–610. [Google Scholar]
- Embretson S, Reise S. Item response theory for psychologists. Erlbaum; Mahwah, NJ: 2000. [Google Scholar]
- Epstein RM, Street RL. The values and value of patient-centered care. Annals of Family Medicine. 2011;9:100–103. doi: 10.1370/afm.1239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grzywacz J, Arcury TA, Ip EH, Chapman C, Kirk JC, Bell RA, Quandt S. Older adults’ common-sense models of diabetes: a multi-method approach illustrating the importance of viewing health beliefs holistically. American Journal of Health Behavior. 2011;35:318–333. doi: 10.5993/ajhb.35.3.6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ip EH, Wang Y, de Boeck P, Meulders M. Locally dependent latent trait model for polytomous responses with application to inventory of hostility. Psychometrika. 2004;62:191–216. [Google Scholar]
- Ip E, Zhang Q, Rejeski J, Harris T, Kritchevsky S. Partially ordered mixed hidden Markov model for the disablement process of older adults. Journal of the American Statistical Association. 2013a;108:370–384. doi: 10.1080/01621459.2013.770307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ip EH, Molenberghs G, Chen S, Goegebeur Y, De Boeck P. Functional unidimensional item response models for multivariate binary data. Multivariate Behavioral Research. 2013b;48:534–562. doi: 10.1080/00273171.2013.796281. [DOI] [PubMed] [Google Scholar]
- Ip EH, Saldana S, Chen S-H, Kirk JK, Bell RA, Nguyen H, Grzywacz JG, Arcury TA, Quandt SA. Unreliable Item or Inconsistent Person? A study of variation in health beliefs and belief- anchors to biomedical models. Journal of Health Psychology. 2013c doi: 10.1177/1359105313506761. Advance online publication. doi: 10.1177/1359105313506761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kleinman A. Patients and healers in the context of culture. University of California Press; Berkeley, CA: 1980. [Google Scholar]
- Kleinman A. Illness narratives: Suffering, healing and the human condition. Basic Press; New York: 1988. [DOI] [PubMed] [Google Scholar]
- Kleinman A, Eisenberg L, Good B. Culture, illness, and care: Clinical lessons from anthropological and cross-cultural research. Annals of Internal Medicine. 1978;88:251–88. doi: 10.7326/0003-4819-88-2-251. [DOI] [PubMed] [Google Scholar]
- Konisky DM, Milyo J, Richardson LE., Jr. Environmental Policy Attitudes: Issues, Geographical Scale, and Political Trust. Social Science Quarterly. 2008;89:1066–1085. [Google Scholar]
- Leventhal H, Brissette I, Leventhal EA. The common-ense model of self- regulation of health and illness. In: Cameron LD, Levethal H, editors. The self-regulation of health and illness behavior. Routledge; London: 2003. pp. 42–65. [Google Scholar]
- Lord F. Applications of item response theory to practical testing problems. Erlbaum; Mahwah, NJ: 1980. [Google Scholar]
- Masters G. A Rasch model for partial credit scoring. Psychometrika. 1982;47:149–174. [Google Scholar]
- Meulders M, Ip E, De Boeck P. Latent variable models for partially ordered responses and trajectory analysis of anger-related feelings. British Journal of Mathematical and Statistical Psychology. 2005;58:117–143. doi: 10.1348/000711005X38555. [DOI] [PubMed] [Google Scholar]
- Muraki E, Bock RD. PARSCALE 4 for Windows: IRT based test scoring and item analysis for graded items and rating scales [Computer software] Scientific Software International, Inc; Skokie, IL: 2003. [Google Scholar]
- Muthén LK, Muthén BO. Mplus User’s Guide. 7th Muthén & Muthén; Los Angeles, CA: 2012. [Google Scholar]
- Ostini R, Nering ML. New perspective and applications. In: Nering ML, Osini R, editors. Handbook of polytomous item response theory models. Taylor & Francis; New York: 2010. pp. 3–20. [Google Scholar]
- Quandt SA, Ip EH, Saldana S, Arcury TA. Comparing two questionnaires for eliciting CAM use in a multi-ethnic US population of older adults. European Journal of Integrative Medicine. 2012;4:e205–e211. doi: 10.1016/j.eujim.2011.12.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rasch G. Probabilistic models for some intelligence and attainment tests. Denmarks Paedagogiske Institut; Copenhagen: 1960. [Google Scholar]
- Reise SP, Waller NG. Dichotomous IRT models. In: Drasgow F, Schmitt N, editors. Advances in measurement and data analysis. Jossey-Bass; Williamsburg, VA: 2001. pp. 88–122. [Google Scholar]
- Rejeski J, Ip EH, Katula J, White L. Older adults’ desire for physical competence. Medicine and Science in Sports and Exercise. 2006;38:100–105. doi: 10.1249/01.mss.0000183231.61022.18. [DOI] [PubMed] [Google Scholar]
- Rijmen F, Tuerlinckx F, De Boeck P, Kuppens P. A nonlinear mixed modelframework for item response theory. Psychological Methods. 2003;8:185–205. doi: 10.1037/1082-989x.8.2.185. [DOI] [PubMed] [Google Scholar]
- Rizopoulos D. ltm: An R package for latent variable modelling and item response theory analyses. Journal of Statistical Software. 2006;17:125. [Google Scholar]
- Rosenstock I. The health belief model and preventive health behavior. Health Education Monograph. 1974;2:354–386. [Google Scholar]
- Rosenstock I, Kirscht JP. Why people seek health care. In: Stone G, Cohen F, Adler N, editors. Health Psychology. Jossey-Bass; San Francisco: 1979. pp. 161–188. [Google Scholar]
- Samejima F. Estimation of ability using a response pattern of graded scores. Psychometrika Monograph. 1969;34:100–114. (Suppl.) [Google Scholar]
- Samejima F. A general model for free-response data. Psychometrika Monograph. 1972;18 [Google Scholar]
- Samejima F. Graded response model. In: van der Linder WJ, Hambleton RK, editors. Handbook of item response theory. Springer; New York: 1996. pp. 85–100. [Google Scholar]
- Sampson A, Singh H. Min and max scorings for two-sample partially ordered categorical data. Journal of Statistical Planning and Inference. 2002;107:219–236. [Google Scholar]
- Smirnov NV. Approximate distribution laws for random variables, constructed from empirical data. Uspekhi Matematicheskikh Nauk (In Russian) 1944;10:179–206. [Google Scholar]
- Stanley RD. Enumerative combinatorics. 2nd Vol. 1. Cambridge University Press; Cambridge, UK: 2012. [Google Scholar]
- Tatsuoka C. Data analytic methods for latent partially ordered classification models. Journal of the Royal Statistical Society. Series C. 2002;51:337–350. [Google Scholar]
- Tatsuoka C, Varadi F, Jaeger J. Latent partially ordered classification models and normal mixtures. Journal of Educational & Behavioral Statistics. 2013;38:267–294. [Google Scholar]
- Thissen D, Steinberg L. A response model for multiple choice items. Psychometrika. 1984;49:501–519. [Google Scholar]
- Thissen D, Steinberg L. A taxonomy of item response models. Psychometrika. 1986;51:567–577. [Google Scholar]
- Thissen D, Chen W-H, Bock RD. MULTILOG 7 for Windows: Multiple-category item analysis and test scoring using item response theory [Computer software] Scientific Software International, Inc; Skokie, IL: 2003. [Google Scholar]
- Wilson M. The ordered partition model: An extension of the partial credit model. Applied Psychological Measurement. 1992;16:309–325. [Google Scholar]
- Wu ML, Adams RJ, Wilson MR. ConQuest: Multi-Aspect Test Software, [computer program] Australian Council for Educational Research; Camberwell: 1997. [Google Scholar]
- Zimowski MF, Muraki E, Mislevy RJ, Bock RD. BILOG-MG 3 for Windows: Multiple-group IRT analysis and test maintenance for binary items [Computer software] Scientific Software International, Inc; Skokie, IL: 2003. [Google Scholar]
- Zhang Q, Ip E. Generalized linear model for partially ordered data. Statistics in Medicine. 2012;31:56–68. doi: 10.1002/sim.4318. [DOI] [PMC free article] [PubMed] [Google Scholar]