Abstract
PURPOSE
High spatial-temporal four-dimensional imaging with large volume coverage is necessary to accurately capture and characterize liver lesions. Traditionally, parallel imaging and adapted sampling are used towards this goal, but they typically result in a loss of signal to noise. Furthermore, residual under-sampling artifacts can be temporally varying and complicate the quantitative analysis of contrast enhancement curves needed for pharmacokinetic modeling. We propose to overcome these problems using a novel patch-based regularization approach called Patch-based Reconstruction Of Under-sampled Data (PROUD).
METHODS
PROUD produces high frame rate image reconstructions by exploiting the strong similarities in spatial patches between successive time frames to overcome the severe k-space under-sampling. To validate PROUD, a numerical liver perfusion phantom was developed to characterize CNR performance compared to a previously proposed method, TRACER. A second numerical phantom was constructed to evaluate the temporal footprint and lag of PROUD and TRACER reconstructions. Finally, PROUD and TRACER were evaluated in a cohort of five liver donors.
RESULTS
In the CNR phantom, PROUD, compared to TRACER, improved peak CNR by 3.66 times while maintaining or improving temporal fidelity. In vivo, PROUD demonstrated an average increase in CNR of 60% compared to TRACER.
CONCLUSION
The results presented in this work demonstrate the feasibility of using a combination of patch based image constraints with temporal regularization to provide high SNR, high temporal frame rate and spatial resolution four dimensional imaging.
Keywords: Liver, Perfusion, Patch, Dictionary Learning, PROUD, Time-resolved, TRACER
INTRODUCTION
The ability to reliably capture the arterial phase in contrast enhanced imaging is crucial for the detection and characterization of liver lesions. Multiple phase imaging within a breath-hold has shown promise towards achieving this goal (1–3). To retain both high spatial and temporal resolution, parallel imaging techniques with adapted sampling schemes have been used, both with Cartesian (4–8) and radial (9–12) trajectories. The success of these techniques lies in the particular balance chosen between undersampling artifacts, signal to noise ratio (SNR), volume coverage, spatial resolution and temporal fidelity. TRACER (13), a nonlinear parallel imaging reconstruction (14) of golden ratio ordered variable density spiral acquisition, allows the reconstruction of volume covering the whole liver with a sub-second frame rate. The high temporal frame rate (equal to the time to acquire a single spiral leaf for all slice encodings) was achieved by assuming small changes of image content between frames, an assumption which is increasingly satisfied as the frame rate increases. Both in simulations and phantom experiments, a high agreement between the reconstructed and the true contrast enhancement curves was observed. However, the reconstructed images are susceptible to noise in the rapid spiral acquisition; the measured temporal footprint of each frame was found to be larger than the apparent frame rate; and residual undersampling artifacts resulted in flickering artifacts visible when viewed in cine mode.
Recently, patch-based image reconstruction methods using dictionary learning have shown promise in reconstructing both static and dynamic under-sampled MRI data (15–24) by exploiting local structure and similarity to a known dictionary. In these methods, an overcomplete basis is learned from prior measurements or the data itself during the reconstruction, using for instance the K-SVD algorithm (25–27). It is assumed that every patch in the unknown image can be written as a sparse linear combination – i.e. with very few non-zero coefficients – of elements in this basis, typically referred to as “atoms”. In this work, the computationally expensive dictionary learning step is replaced by an explicit construction of the dictionary, based on the assumption that image patches change little in structure and location between successive time frames. For every patch, a number of sets with a fixed number of patches are constructed by taking a patch around the same location (allowing for some translation) in a number of reference images, one of which is the time frame immediately preceding the frame to be reconstructed. Combined with an L2 temporal regularization, the resulting method is called Patch-based Reconstruction Of Under-sampled Data (PROUD) and is applied to dynamic imaging data with frames that are ~250 ms apart. Through phantom and in vivo studies, it is shown that PROUD is able to maintain the high spatial and temporal frame rate obtained with TRACER while allowing for increased SNR, reduction of temporal footprint, and reduced undersampling artifacts.
THEORY
The PROUD algorithm reconstructs dynamic highly undersampled data: in this work a single spiral leaf is used to reconstruct each frame, assuming a fully sampled image is available for the first time frame (see below). To allow a reconstruction, the regularization used in PROUD is based on the observation that the local structure of the image is largely preserved between successive frames in high frame rate dynamic imaging. An additional temporal regularization is used to suppress temporally varying residual undersampling artifacts. In previous approaches (13,14), differences between successive frames were constrained on a global, image based level. To constrain differences on a local level, we use image patches. Patch based image regularization has proven very successful in image processing algorithms such as denoising (26).
In this work, each n × n patch Ri,jv around pixel (i,j) of the unknown image v is assumed to be a linear combination of a small number of n × n patches taken from a dictionary of patches Pi,jD specific to the pixel (i,j). This dictionary is constructed by taking n × n patches from an m × m neighborhood around the pixel (i,j) selected by Pi,j from a set D constructed from NR reference images that are assumed to represent the local structure of the unknown image v well. For each pixel (i,j), the dictionary Dt contains a set of patches di,j. Each set di,j has NR patches of size n × n selected around pixel (i,j) in each of the NR reference images. Therefore, the dictionary Dt has size (Nx × Ny) × NR × (n × n), where Nx and Ny are the number of columns and rows of vt, respectively. Note that for pixels near the edge of the field of view, zero padding was used in the construction of patches when needed. Therefore, the following minimization problem was solved in order to obtain a solution for each time t = 1, …, T:
| [1] |
where yt is the sampled k-space data for all coils, T is the total number of time frames, S is the operator that multiplies the image vt with each of the coil sensitivities (si)i =1, …, Nc, Nc is the number of coils, F is the spatial Fourier transform, Ut is the projection of k-space unto the spiral leaf acquired at time t. Each vector αi,j,t has linear coefficients αi,j,t(p, r) with p = 1, …, Np and r = 1, …, Nr, with Np = (m − n + 1) × (m − n + 1) the number of overlapping patches of size n × n that fit within a m × m neigborhood. Note that, here, we index the vector αi,j,t with two indices for clarity. On the vectors αi,j,t, a composite L0 norm was defined as . Therefore, the constraint in Eq. 1 ensures that only one set of patches from the dictionary Pi,jDt is selected. This reflects the constraint that an image patch is expected to move only slightly between time frames and can change in scale (DC component) as well. The latter will be the case for contrast enhanced imaging. Note that, compared to conventional dictionary learning approaches, the number of non-zero linear coefficients is always set to NR and that only certain combinations of patches are allowed, i.e., those that were derived from the same pixel location in the NR reference images. In this work, Dt was constructed from the following reference images: the previously reconstructed image and a composite image reconstructed from all acquired data, which in dynamic imaging is fully sampled or even oversampled. In vivo, to further improve robustness to through plane motion, Dt included reference images derived from Nslices neighboring slices reconstructed from all acquired data as well. The minimization of the patch constraint term in Eq. 1 is simplified by orthonormalizing each set of patches from the dictionary Pi,jDt, such that the optimal linear combinations αi,j,t(p, r) can be computed using a simple projection (see last paragraph of Appendix B). A general depiction of Eq. 1 for one time frame is shown in Fig. 1. Note that in Fig. 1, the displayed set of patches is not orthonormalized for clarity of presentation only.
Figure 1.
A diagram of the PROUD reconstruction algorithm for one temporal frame. Patch size is 5×5 with a neighborhood size of 7×7.
As in TRACER (13), an initial guess v0 for the first frame was reconstructed from the first fully sampled set of data, which is typically available in dynamic imaging. For the contrast enhanced imaging application, this assumes no contrast agent has entered the field of view until after the first fully sampled set of data is acquired. This requirement can be considerably relaxed by taking the same fully sampled reconstruction image and perform a PROUD (or TRACER, see below) reconstruction backwards in time from the end of the fully sampled data set towards the beginning, after which the reconstruction is again performed now going forward in time. This allows a better guess for the first time frame. The coil sensitivities (si)i =1, …, Nc are derived by dividing low resolution coil images by their root sum of squares. These low resolution coil images were obtained from all acquired data in the dynamic acquisition, which typically is long enough to provide a highly oversampled, high SNR reconstruction. The determination of the regularization parameter λ is described below.
For high temporal resolution imaging, a new frame is reconstructed for each newly acquired set of k-space data (13), which is assumed to be acquired in a small time interval in order to satisfy the assumption of smooth temporal changes. With PROUD (and TRACER, see below), a single spiral leaf (collected for all slice encodings in the case of 3D imaging) is used to update each temporal frame, typically at a rate of ~250 ms. The angle between two successive spiral leaves is based on the golden ratio (13,28,29).
In a second step, temporal smoothness was enforced to overcome the temporally varying residual undersampling artifacts in the reconstructed images. This regularization provides smooth time courses for contrast enhancement curves simplifying post-processing. This was done by solving:
| [2] |
Eqs. 1&2 are solved by extending the method used in (24) to the multi-channel non-Cartesian case. A detailed derivation is shown in Appendix B. The solver algorithm iterates between solving for αi,j,t and solving for vt. Since spiral data was acquired in this study, nonuniform fast Fourier transforms were performed using NUFFT (30,31). The dictionary Dt for each frame vt was constructed in the same way as for Eq. 1.
The patch and temporal regularization parameters, λ and γ, were determined automatically by the solver. To find λ, we estimated a solution for by excluding the regularization term from Eq. 1:
| [3] |
Because of the severe undersampling by U1, which projects onto a single leaf, this was iteratively solved by using v0 as the initial guess and halting the iterations when the image update between iterations no longer decreased, similar to the stopping criterium used in TRACER (13). Next, a vector was found by solving (see Appendix B):
| [4] |
Using the discrepancy principle (32), the regularization parameter λ was then chosen such that the two terms in Eq. 1 were equal for the values of and obtained in Eqs 3 and 4, respectively. The value of λ was then kept constant for all remaining time frames. After Eq. 1 was solved for all time frames, the regularization parameter γ was obtained by demanding that the first term (data term) equaled the third term (temporal term) in Eq. 2 when and were set to the solutions of Eq. 1. Appendix A outlines the PROUD reconstruction algorithm in detail.
In the experiments below, the performance of PROUD will be compared TRACER, a previous method to perform high frame rate reconstructions. For clarity, a brief description of this method is included here. Using the notation introduced above, TRACER aims to solve the following equation:
| [4a] |
which is similar to the data term in Eq. 1 for a single time frame, except for the fact that the coil sensitivities are now considered to be unknown as well and are allowed to vary over time. This makes Eq. 4a a non-linear least squares problem in the variable xt,k = {vt,k, s1,t,k, … sNct,k}. It is solved using the Levenberg–Marquardt (LM) algorithm, which iteratively determines an update dxt,k = {dvt,k, ds1,t,k, … dsNc,t,k} to an initial guess xt,0:xt,k = xt,k − 1 + dxt,k}. To deal with the high undersampling, each frame xt was reconstructed using the previous frame as the initial guess xt,0 = xt − 1 and the iteration was stopped when the norm of the update ||dxt,k|| stopped decreasing (13). The underlying assumption is the change in image content dxt is small between successive time frames. Note that in contrast to PROUD the difference between successive frames is measured using a single norm of the entire image update. All reconstruction parameters were automatically determined based on the data as described in (13).
METHODS
Optimization of reconstruction parameters
To characterize the PROUD algorithm, a numerical phantom simulating dynamic liver perfusion was created (Fig. 2a) similar to the phantom in (13). The noiseless phantom was multiplied by simulated coil sensitivity maps (eight channels), and sampled with a spiral trajectory. For each time frame, a cutoff of rcutoff = 10−5 with a maximum of 100 and 5 iterations was used for the first (Eq. 1) and the remaining temporal iterations (Eq. 2), respectively. Five temporal iterations were used in solving Eq. 2. The patch size was determined by solving Eq. 1 for a range of sizes: square patches of size n = 3,6,7,9,11 and 13 pixels were tested. The root mean square error RMSE, defined as
Figure 2.

(A) A numerical phantom simulating liver perfusion indicating the various simulated organs, including the inferior vena cava (IVC) (B). Temporal footprint phantom with inner diameter = 0.5*FOV.
| [5] |
was calculated to determine the optimal patch size. The background of the phantom was excluded from the norm in Eq. 5. The neighborhood size was then set m = n+2 to reduce the increase in computation time while still allowing small local translational motions of image patches between successive time frames.
Numerical phantom SNR
Thirty sets of randomly generated Gaussian noise was added to the numerical phantom described above. A fully sampled first frame was assumed. The phantoms were then reconstructed using PROUD with the reconstruction parameters obtained above and using the TRACER algorithm (1) for comparison. A contrast-to-noise ratio CNR was computed as
| [6] |
where SNRaorta and SNRportal vein are the signal-to-noise ratios within a region of interest (ROI) in the respective anatomies. Pixel-wise SNR was computed at each time-point by taking the mean of each pixel in an ROI over the 30 reconstructions divided by the standard deviation of each pixel. The mean of the pixel-wise SNR values was then taken over the ROI.
Numerical phantom temporal footprint
Temporal phantoms were developed (Fig. 2b) to characterize the temporal response of the PROUD algorithm compared to TRACER. Each phantom consists of a central disk with diameter (DIA) equal to 0.125, 0.1875, 0.25, 0.3125, 0.375, 0.4375, 0.5, 0.5625, 0.625, 0.6875, 0.75, 0.8125, 0.875, 0.9375, 1 times the FOV superimposed onto a larger disk with diameter equal to the FOV. The contrast in the central disk was changing over time, such that the enhancement curve was Gaussian. The temporal footprint (TF), used to characterize the length of the enhancement curves, was defined as the full width-half maximum (FWHM) of the Gaussian curves: . The TF of the curves was varied between 0.5, 1, 2, 5, 7, 10, 15 and 20 seconds. This resulted in 120 unique numerical phantoms. These noiseless phantoms were multiplied by simulated coil sensitivity maps and sampled along a spiral trajectory. A fully sampled first frame was assumed and the phantom was reconstructed with PROUD and TRACER for comparison. For PROUD, the phantoms were reconstructed both with Eq. 1 and 2 to allow for analysis of the effects of temporal regularization. The phantoms allowed for the estimation of the temporal footprint and lag. The reconstructed curve was temporally shifted and compressed to maximize its cross-correlation with respect to the true simulated curve. The measured temporal footprint (TFMEAS) of the reconstructed curve was taken as the true temporal footprint divided by the obtained compression factor. The measured temporal lag was defined as the obtained temporal shift (in sec). Differences in the amplitude of the measured curve compared to the true curve were not taken into account.
In vivo liver MRI experiments
In vivo data were acquired using a golden angle 3D dynamic multi-phase spiral LAVA sequence using a stack of variable density spiral trajectory (1). Five candidate liver donors imaged with this acquisition were selected retrospectively in accordance with an institutionally approved IRB protocol. The acquisition acquired data continuously for 60 sec, while the patients were given repeated breath-hold instructions. Other imaging parameters were: 1.5T (Ge Healthcare, Waukesha, WI), 48 variable density spiral leaves (density of 2 in the center of k-space, 0.7 at the periphery), acquisition matrix 256×256× (34–60), slice thickness 5 mm, FOV 32–48cm, bandwidth ±62kHz, fat suppression, 8 channel cardiac coil, and Magnevist/Eovist (Bayer Healthcare) injected at a dose based on patient weight. Since breathing motion was present, additional high SNR images created from all sampled data at 3 slices above and below the reconstructed slice were added to the dictionary Dt.
CNR was computed in vivo as
| [7] |
where Saorta and SNRportal vein SPV is the mean signal in a ROI in the aorta and portal vein, respectively, and Nliver NL the signal standard deviation in an ROI of homogenous liver tissue near both the aorta and portal vein ROIs. This is computed for each time frame and is a surrogate measure for how well the arterial phase is visualized (13).
All PROUD and TRACER reconstructions were done either on a Dell Studio XPS 8100 (Intel i7 2.8 GHz processor, 16 GB RAM, Windows 7, Matlab R2011b) or a Dell PowerEdge R910 Server (64 cores, 64 GB RAM, Red Hat Linux, Matlab R2009a). Statistical significance (p <0.05) was determined by using a paired two-tailed student’s t-test in Microsoft Excel 2013.
RESULTS
Parameter selection
Optimal patch size was determined to be 7×7 pixels as it resulted in the smallest RMSE (Figure 3) and neighborhood size was then set to be 9×9 pixels.
Figure 3.
Root Mean Squared Error (RMSE) vs. patch size. 7×7 pixels was chosen to be the optimal patch size.
Phantom SNR test
Both algorithms provided similar contrast enhancement curves (Fig 4a). The PROUD aorta curve slightly preceded the TRACER aorta curve (Fig. 4a&b), but both lag the reference aorta curve. PROUD provided almost 3.66× higher peak CNR compared to TRACER (Fig. 4c). PROUD without the temporal regularization (denoted by PROUD γ = 0) obtained essentially the same peak CNR. The dip in the PROUD CNR was due to increased undersampling artifacts associated with rapid signal changes, such as the enhancing aorta and portal vein.
Figure 4.
Comparison of PROUD, PROUD γ = 0 (i.e., without temporal regularization) and TRACER in a numerical liver phantom (A) Average signal intensity of various regions of interest in the numerical phantom with noise standard deviation = 0.003. (B) Magnified region of interest showing the aorta enhancement curves around their peak enhancement. (C) CNR averaged over 30 noisy phantoms. The dip in CNR of the PROUD curve is due to increased reconstruction errors at the edges of the aorta and portal vein, which increase the standard deviation in the ROIs near the edges.
Phantom temporal footprint
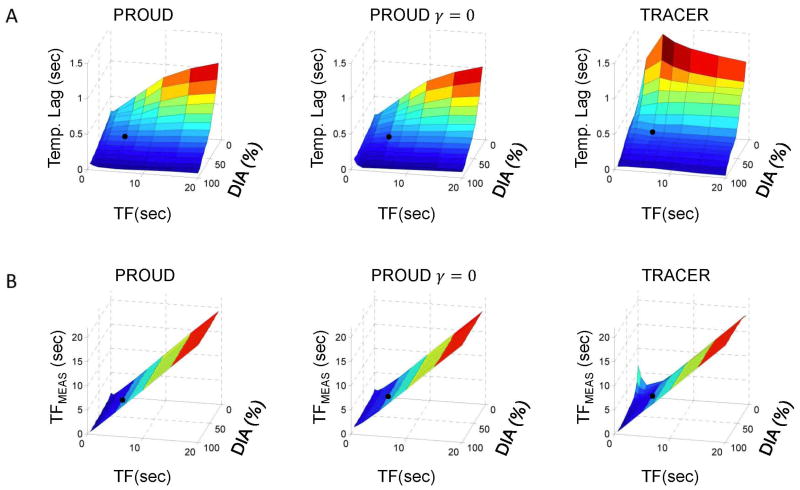
Fig. 5 shows the results from the testing of the temporal response of PROUD compared to TRACER. For larger objects (>50% FOV) and longer temporal footprint (> 5 sec) – indicated by a black dot in Fig. 5 – the curves reconstructed with TRACER and PROUD had measured temporal footprints that were very close to those of the reference curves and temporal lags below 0.5 seconds.
Figure 5.
(A) Temporal (Temp.) lag and (B) measured temporal footprint (TFMEAS) values determined using cross-correlations of the reconstructions from TRACER and PROUD compared to the true phantom curves with varying diameter (DIA) and temporal footprint (TF). PROUD γ = 0 is the solution to Eq. 1 and PROUD to Eq. 2. A black dot indicates the position corresponding to DIA>50% FOV and TF>5sec in each of the plots.
For all methods, temporal lag decreased for larger objects and increased for larger temporal footprint. Overall TRACER had a higher temporal lag than PROUD. In addition, there was a larger discrepancy between TRACER and PROUD for smaller objects (FOV 12.5%–43.8%). For larger objects (FOV = 81.3% and greater) with very short temporal events (0.5 – 1 sec temporal footprint), PROUD had a longer temporal lag than TRACER.
The measured temporal footprint for TRACER and PROUD were similar for objects of size 37.5% of the FOV and greater. The PROUD reconstruction using temporal regularization (Eq. 2) had a slightly larger measured temporal footprint compared to the PROUD reconstruction without (Eq. 1). In addition, for fast temporal events (~ 5 sec temporal footprint and less), there was some discrepancy in the methods. In general, for smaller objects TRACER had an increased measured temporal footprint. However, from objects sized equal or greater than 50% of the FOV, the temporal regularization of Eq. 2 made the measured temporal footprint larger than both TRACER and PROUD without the temporal regularization, with the largest difference around 1 sec. Finally for the three smallest objects (FOV = 12.5 – 25%), the measured TRACER temporal footprint is smaller than the true temporal footprint, when the latter exceeds 2 to 3 sec.
Fig. 6 shows examples for three of the curves analyzed in Fig. 5. In Fig. 6A for a short TF with small DIA, TRACER (TFMEAS =7.5s, Temp. Lag =1.9s), PROUD No Temp. Constr. (TFMEAS = 1.6s, Temp. Lag =1.6s) and PROUD w/ Temp. Constr. (TFMEAS =2.4s, Temp. Lag =1.4s) had large errors in reconstructing the true curve. In Fig. 6B as the TF and DIA grow, TRACER (TFMEAS =5.1s, Temp. Lag =1.8s), PROUD No Temp. Constr. (TFMEAS = 5.1s, Temp. Lag =1.4s) and PROUD w/ Temp. Constr. (TFMEAS = 5.3s, Temp. Lag =1.3s), had improved performance compared to the smaller DIA/TF. Finally in Fig. 6C with a large TF and DIA, all methods provided curves similar to the truth: TRACER (TFMEAS = 20.0, Temp. Lag =0.1s), PROUD No Temp. Constr. (TFMEAS = 20.0s, Temp. Lag =0.3s) and PROUD w/ Temp. Constr. (TFMEAS =20.1s, Temp. Lag =0.3s).
Figure 6.

Examples of curves analyzed in Fig. 5. (A) A very short temporal event (TF = 0.5 sec) with a small diameter object (12.5% FOV). (B) A medium size temporal event (TF = 5 sec) with a mid-sized diameter object (50% FOV). (C) A long temporal event (TF = 20 sec) with a large diameter object (100% FOV).
In vivo testing
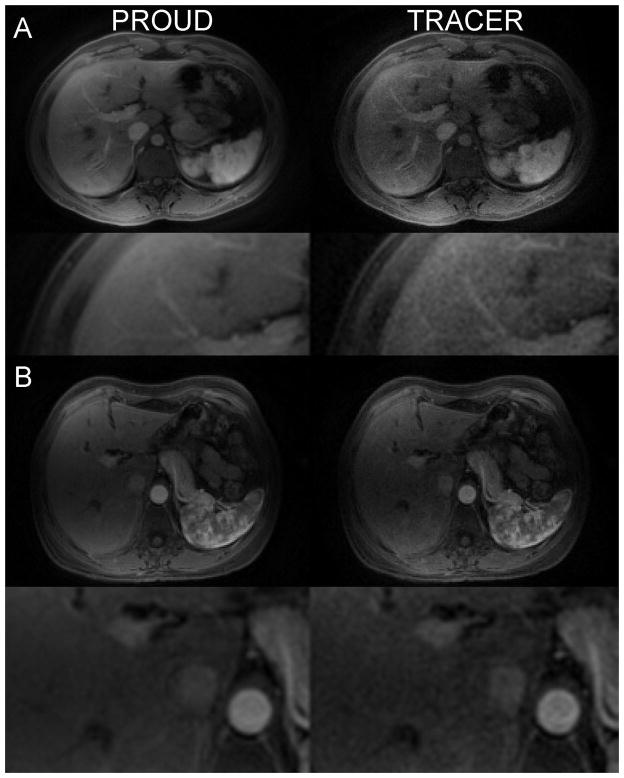
Over the 5 in vivo datasets, the images reconstructed using PROUD had a peak CNR of 42 ± 18 compared to 26 ± 12 using TRACER resulting in a 60% improvement in peak CNR (p = 0.008). Fig. 7 shows a single temporal frame reconstructed with the PROUD and TRACER methods in two patients. Improvements in SNR were seen using PROUD, while TRACER clearly suffered from increased noise in the reconstruction. The magnified regions of interest for each of the liver images indicates that PROUD allowed preservation of image detail. A video comparing PROUD and TRACER reconstructions in the same subject is available as online supplementary material.
Figure 7.
In vivo image reconstruction using PROUD and TRACER in two patients. Note the reduction in noise (increase in SNR) utilizing the PROUD method. The second row for each patient shows a magnified region of interest. Note that image details are preserved on PROUD compared to TRACER.
Fig. 8 shows the signal and CNR curves for patient in Fig. 7. In-vivo for Eq. 1, the preliminary pure Matlab (Natick, MA) implementation of PROUD took an average of 4.3 ± 0.1 minutes to reconstruct one temporal frame resulting in a total reconstruction time of 10.3 hours for 144 frames (as measured in one volunteer).
Figure 8.

(A) In vivo perfusion curves for aorta, portal vein and liver and (B) aorta—to—portal vein CNR curve for the same volunteer as in Fig. 7. A comparison is made between PROUD, PROUD γ = 0 (i.e., without temporal regularization) and TRACER.
DISCUSSION
The results presented in this work demonstrate the feasibility of using a combination of a patch based image constraint with a temporal regularization to provide improved CNR in phantoms while maintaining or improving temporal fidelity and to provide an increase in CNR of up to 60% in vivo compared to TRACER. This reduction in noise (as seen by the increase in CNR) can be attributed to the patch-based dictionary methods employed in the PROUD method. Patch level dictionary learning has previously been shown to be useful in de-noising problems (26,27) and has been shown to improve PSNR compared to a ground truth in MRI data (24).
Temporal characterization of PROUD against TRACER gave similar performance for larger objects and slower temporal events. For short temporal events or small objects there were some discrepancies between the methods. TRACER had increased temporal lag and somewhat larger measured temporal footprint with smaller object size at shorter temporal events. This may be due to differences in the reconstruction methods of TRACER and PROUD. Importantly, TRACER is subject to blurring of edges during fast signal changes. This is shown in Fig. 4d of (13), where the blurring of the aorta edge around peak aorta enhancement increased its apparent diameter. This blurring will effect smaller objects more and is most likely the cause of the increase in the measured temporal footprint and some of the temporal lag. This artifact was reduced in PROUD, however, since the dictionary-based method allows for a better delineation of edges during contrast changes. This is because this edge information is available in the image reconstructed from all available data which was used in the dictionary for each frame. In addition, with PROUD regularization is done on a local level while TRACER implements global image regularization. In our analysis, the method of determining the temporal lag and compression factor via compression and cross-correlation may be affected by the fact that response function in TRACER only is non-zero for positive time, see Fig. 3a in (13), while, due the temporal smoothness constraint, PROUD has a bi-directional temporal spread. These reasons may also explain the reason why TRACER exhibits an apparent negative lag for the three smallest objects (FOV = 12.5 – 25%), which is likely an artifact of the specific way in which lag was measured in this work. Overall it is important to note, that for both methods, temporal response was a factor of both the temporal event length and the size of the feature being evaluated.
Finally, in comparison to TRACER, PROUD is able to reduce residual temporal flickering artifacts due to the addition of Eq. 2. This temporal fidelity constraint forces neighboring frames to be similar over time therefore penalizing rapid temporal changes (e.g. flickering). There are differences to be noted however in the temporal performance of PROUD with Eq. 1 only and PROUD with Eq. 2. In general, Eq. 1 (and sometimes TRACER with larger objects) provided slightly better measured temporal footprint than Eq. 2. This is mainly due to the fact that the temporal term in Eq. 2. may introduce some degree of temporal blurring. The effect of temporal blurring was observed to be small, except in fast changing temporal signals. Improvement may be possible in future implementations replacing the L2-norm on the temporal term with an L1 norm, as was done in (23). It should be noted, however, that a small degree of temporal blurring is still present for large acceleration factors using this norm (23).
There were some limitations in this work. The size of the neighborhood in constructing the atoms for the dictionary was relatively small: 2 pixels larger than the patch size itself. This was done two reasons: 1) the assumption was made that the motion between frames was small, and 2) increasing the neighborhood increased the computational cost of the algorithm, since each patch in the unknown image would have to be compared with a larger number of atoms in the dictionary. In vivo validation was only done in subjects that were assumed to be healthy. Further studies may be warranted to evaluate the performance of PROUD in patients presenting with liver dysfunction (i.e. fibrosis, hepatocellular carcinoma, etc.). In addition, reconstruction time for the current pure Matlab implementation of PROUD was long (4.3 minutes to reconstruct one frame of one slice with Eq. 1). However, reconstruction time can be reduced through implementation in C code and GPU parallelization. Future implementations of PROUD may warrant automatic patch and neighborhood size determination, which could be done by analyzing the residual in Eq. 10a for varying patch/neighborhood size.
CONCLUSION
The proposed PROUD algorithm combines an image patch based regularization combined with a temporal regularization to enable high SNR, high temporal frame rate and spatial resolution 4D imaging that can improve in vivo peak CNR by up to 60% compared to previous methods while maintaining adequate temporal fidelity.
Supplementary Material
TABLE 1.
Symbols Used in the Text
| t | Time index | |
| i,j | Image space pixel locations | |
| ki,kj | K-space pixel locations | |
| vt | Image to be reconstructed at time t | |
| Nx | Number of columns of vt | |
| Ny | Number of rows of vt | |
| n | Patch size (in pixels) | |
| Ri,jvt | Selects an n × n patch centered around a pixel i,j | |
| m | Neighborhood size (in pixels). m ≥ n | |
| Dt | Image-based dictionary at time t | |
| NR | Number of reference images used for the reconstruction of the dictionaries Dt | |
| Pi,jvt−1 | Selects all sets of NR patches of size n × n with an m × m neighbourhood centered at pixel i,j | |
| yt | Multi-channel spiral k-space data acquired at time t | |
| Nc | Number of RF coils used | |
| si | Coil sensitivity map of the ith channel, i = 1, …, Nc | |
| S | Operator that maps an image v to the coil images (siv)i = 1, …, Nc | |
| F | Fourier transform | |
| Ut | Under-sampling operator projecting Cartesian k-space on the spiral k-space acquired at time t | |
| αi,j,t | Vector of dictionary coefficients for a patch at time t around pixel i,j | |
| Ns | Number of spiral leaves needed for a Nyquist reconstruction | |
| rcutoff | Relative change between successive solutions that will halt the iterative solver. | |
|
|
Number of temporal iterations for solving Eq. 2. | |
| TF | True temporal footprint (FWHM) of the numerical temporal phantoms | |
| TFMEAS | Measured temporal footprint of the numerical temporal phantoms | |
| DIA | Diameter (as a % of the FOV) of the central disk in the numerical temporal phantoms |
Acknowledgments
This research was supported in part by an NSF Graduate Research Fellowship (DGE-0707428) and the Joan & Irwin Jacobs Technion-Cornell Innovation Institute.
APPENDIX A: PROUD Reconstruction Algorithm
vt, αi,j,t ← PROUD (yt)
Reconstruct a reference v0 using the first Ns spiral leaves
Reconstruct a composite image vALL using all spiral leaves
Compute the coil sensitivity maps (si)i = 1, … ,Nc using vALL
Set λ such that the two terms in Eq. 1 are equal for the solutions in step 4.
-
Solve Eq. 1 for all time frames:
Set γ such that the terms 1 and 3 in Eq 2 are equal for the solutions obtained in step 5.
-
Solve Eq. 2 using the solutions obtained in step 5 as initial guess:
vt,1 ← vt and αi,j,t,1 ← αi,j,t for m = 2, …, for t =1, …, T va ← 1/2(vt−1,m + vt+1,m−1) Dt,m ← DICTIONARY (vt−1,m, vALL) find αi,j,t,m by fitting vt,m against the patch dictionary Dt,m using Eq. 10a&b create the patch averaged image compute new image estimate vt,m using Eq. 9b end end vt ← vt,m and αi,j,t ← αi,j,t,m
D ← DICTIONARY (v1, …, vNR)
From each v1, …, vNR, take a patch of size n × n around pixel (i,j) to form a set di,j.
Orthonormalize each set di,j
For every pixel (i,j) collect all sets da,b in an m × m neighborhood centered on pixel i,j
APPENDIX B
In the following, we detail the solver used for Eqs. 1&2. The method goes back and forward between solving for and solving for the patch weights αi,j,t.
Eqs. 1&2 are solved by extending the method in (24) to the multi-channel non-Cartesian case. We start by assuming αi,j,t to be fixed to some appropriate initial values. Then Eq. 1
A solution for is obtained by setting the derivative of the cost function to zero, resulting in
Where is equal to βI where β is a scaling factor equal to n2, after appropriately taking into account patches at the edge of the FOV. Therefore:
Note that SH FH FS = SH S = I, by the fact that the Fourier transform is unitary and the fact that SH S is a diagonal matrix with entries equal to (by construction). Therefore
By applying FS on both sides, we obtain
| [8] |
where is the “patch averaged image”. Here “zeroes out” any k-space that is not on the spiral trajectory corresponding to time frame t. By writing , we can apply the inverse of the diagonal matrix on both sides of Eq. 8:
is simply the sampled k-space locations zero-padded to the matrix size. β can be incorporated into λ such that we can substitute λ ← β λ as in (24). This can be simplified to
| [9a] |
The added temporal regularization term in Eq. 2 similarly leads to:
| [9b] |
Where . To speed up convergence, new estimates of are used in the initialization and in the regularization term for subsequent time frames as soon as they become available.
Once an updated guess for an image v is available, the patch weights αi,j,t are updated as follows. For every pixel (i,j), a set d* of NR patches is found that maximizes the projection of patch Ri,jv onto the set d*:
| [10a] |
where . Note that, by construction, each set d ∈ Pi,jD is an orthonormal basis with NR elements. Once the optimal patch set d* is found, the patch weights are set equal to the linear coefficients in this basis:
| [10b] |
References
- 1.Agrawal MD, Spincemaille P, Mennitt KW, Xu B, Wang Y, Dutruel SP, Prince MR. Improved hepatic arterial phase MRI with 3-second temporal resolution. J Magn Reson Imaging. 2013;37(5):1129–1136. doi: 10.1002/jmri.23920. [DOI] [PubMed] [Google Scholar]
- 2.Ito K, Fujita T, Shimizu A, Koike S, Sasaki K, Matsunaga N, Hibino S, Yuhara M. Multiarterial phase dynamic MRI of small early enhancing hepatic lesions in cirrhosis or chronic hepatitis: differentiating between hypervascular hepatocellular carcinomas and pseudolesions. AJR Am J Roentgenol. 2004;183(3):699–705. doi: 10.2214/ajr.183.3.1830699. [DOI] [PubMed] [Google Scholar]
- 3.Hong HS, Kim HS, Kim MJ, De Becker J, Mitchell DG, Kanematsu M. Single breath-hold multiarterial dynamic MRI of the liver at 3T using a 3D fat-suppressed keyhole technique. J Magn Reson Imaging. 2008;28(2):396–402. doi: 10.1002/jmri.21442. [DOI] [PubMed] [Google Scholar]
- 4.Saranathan M, Rettmann DW, Hargreaves BA, Clarke SE, Vasanawala SS. DIfferential Subsampling with Cartesian Ordering (DISCO): a high spatio-temporal resolution Dixon imaging sequence for multiphasic contrast enhanced abdominal imaging. J Magn Reson Imaging. 2012;35(6):1484–1492. doi: 10.1002/jmri.23602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Low RN, Bayram E, Panchal NJ, Estkowski L. High-resolution double arterial phase hepatic MRI using adaptive 2D centric view ordering: initial clinical experience. AJR Am J Roentgenol. 2010;194(4):947–956. doi: 10.2214/AJR.09.2507. [DOI] [PubMed] [Google Scholar]
- 6.Saranathan M, Rettmann D, Bayram E, Lee C, Glockner J. Multiecho time-resolved acquisition (META): a high spatiotemporal resolution Dixon imaging sequence for dynamic contrast-enhanced MRI. J Magn Reson Imaging. 2009;29(6):1406–1413. doi: 10.1002/jmri.21750. [DOI] [PubMed] [Google Scholar]
- 7.Wang K, Schiebler ML, Francois CJ, Del Rio AM, Cornejo MD, Bell LC, Korosec FR, Brittain JH, Holmes JH, Nagle SK. Pulmonary perfusion MRI using interleaved variable density sampling and HighlY constrained cartesian reconstruction (HYCR) J Magn Reson Imaging. 2013;38(3):751–756. doi: 10.1002/jmri.24018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Feng L, Srichai MB, Lim RP, Harrison A, King W, Adluru G, Dibella EV, Sodickson DK, Otazo R, Kim D. Highly accelerated real-time cardiac cine MRI using k-t SPARSE-SENSE. Magn Reson Med. 2013;70(1):64–74. doi: 10.1002/mrm.24440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Brodsky EK, Bultman EM, Johnson KM, Horng DE, Schelman WR, Block WF, Reeder SB. High-spatial and high-temporal resolution dynamic contrast-enhanced perfusion imaging of the liver with time-resolved three-dimensional radial MRI. Magn Reson Med. 2013;71(3):934–941. doi: 10.1002/mrm.24727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Feng L, Grimm R, Block KT, Chandarana H, Kim S, Xu J, Axel L, Sodickson DK, Otazo R. Golden-angle radial sparse parallel MRI: Combination of compressed sensing, parallel imaging, and golden-angle radial sampling for fast and flexible dynamic volumetric MRI. Magn Reson Med. 2013 doi: 10.1002/mrm.24980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Seiberlich N, Ehses P, Duerk J, Gilkeson R, Griswold M. Improved radial GRAPPA calibration for real-time free-breathing cardiac imaging. Magn Reson Med. 2011;65(2):492–505. doi: 10.1002/mrm.22618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wright KL, Lee GR, Ehses P, Griswold MA, Gulani V, Seiberlich N. Three-dimensional through-time radial GRAPPA for renal MR angiography. J Magn Reson Imaging. 2014 doi: 10.1002/jmri.24439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Xu B, Spincemaille P, Chen G, Agrawal M, Nguyen TD, Prince MR, Wang Y. Fast 3D contrast enhanced MRI of the liver using temporal resolution acceleration with constrained evolution reconstruction. Magn Reson Med. 2013;69(2):370–381. doi: 10.1002/mrm.24253. [DOI] [PubMed] [Google Scholar]
- 14.Uecker M, Zhang S, Frahm J. Nonlinear inverse reconstruction for real-time MRI of the human heart using undersampled radial FLASH. Magn Reson Med. 2010;63(6):1456–1462. doi: 10.1002/mrm.22453. [DOI] [PubMed] [Google Scholar]
- 15.Yanhua W, Yihang Z, Ying L. Undersampled dynamic magnetic resonance imaging using patch-based spatiotemporal dictionaries. Biomedical Imaging (ISBI), IEEE 10th International Symposium on; San Francisco, California, USA. 2013. pp. 294–297. [Google Scholar]
- 16.Awate SP, DiBella EVR. Spatiotemporal dictionary learning for undersampled dynamic MRI reconstruction via joint frame-based and dictionary-based sparsity. Biomedical Imaging (ISBI), 9th IEEE International Symposium on; Barcelona, Spain. 2012. pp. 318–321. [Google Scholar]
- 17.Lingala SG, Jacob M. Blind compressive sensing dynamic MRI. IEEE Trans Med Imaging. 2013;32(6):1132–1145. doi: 10.1109/TMI.2013.2255133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ding X, Paisley J, Huang Y, Chen X, Huang F, Zhang X-P. Compressed sensing MRI with Bayesian dictionary learning. Image Processing (ICIP), 20th IEEE International Conference on; Melbourne, Australia. 2013. pp. 2319–2323. [Google Scholar]
- 19.Liu Q, Wang S, Yang K, Luo J, Zhu Y, Liang D. Highly undersampled magnetic resonance image reconstruction using two-level bregman method with dictionary updating. IEEE Trans Med Imaging. 2013;32(7):1290–1301. doi: 10.1109/TMI.2013.2256464. [DOI] [PubMed] [Google Scholar]
- 20.Zhang T, Cheng JY, Potnick AG, Barth RA, Alley MT, Uecker M, Lustig M, Pauly JM, Vasanawala SS. Fast pediatric 3D free-breathing abdominal dynamic contrast enhanced MRI with high spatiotemporal resolution. J Magn Reson Imaging. 2013 doi: 10.1002/jmri.24551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Akçakaya M, Basha TA, Goddu B, Goepfert LA, Kissinger KV, Tarokh V, Manning WJ, Nezafat R. Low-dimensional-structure self-learning and thresholding: regularization beyond compressed sensing for MRI reconstruction. Magn Reson Med. 2011;66(3):756–767. doi: 10.1002/mrm.22841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Wang Y, Ying L. Compressed sensing dynamic cardiac cine MRI using learned spatiotemporal dictionary. IEEE Trans Biomed Eng. 2014;61(4):1109–1120. doi: 10.1109/TBME.2013.2294939. [DOI] [PubMed] [Google Scholar]
- 23.Caballero J, Price AN, Rueckert D, Hajnal JV. Dictionary Learning and Time Sparsity for Dynamic MR Data Reconstruction. IEEE Trans Med Imaging. 2014;33(4):979–994. doi: 10.1109/TMI.2014.2301271. [DOI] [PubMed] [Google Scholar]
- 24.Ravishankar S, Bresler Y. MR image reconstruction from highly undersampled k-space data by dictionary learning. IEEE Trans Med Imaging. 2011;30(5):1028–1041. doi: 10.1109/TMI.2010.2090538. [DOI] [PubMed] [Google Scholar]
- 25.Aharon M, Elad M, Bruckstein A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation. Ieee T Signal Proces. 2006;54(11):4311–4322. [Google Scholar]
- 26.Elad M, Aharon M. Image denoising via sparse and redundant representations over learned dictionaries. IEEE Transactions on Image Processing. 2006;15(12):3736–3745. doi: 10.1109/tip.2006.881969. [DOI] [PubMed] [Google Scholar]
- 27.Protter M, Elad M. Image Sequence Denoising via Sparse and Redundant Representations. IEEE Transactions on Image Processing. 2009;18(1):27–35. doi: 10.1109/TIP.2008.2008065. [DOI] [PubMed] [Google Scholar]
- 28.Winkelmann S, Schaeffter T, Koehler T, Eggers H, Doessel O. An optimal radial profile order based on the Golden Ratio for time-resolved MRI. IEEE Trans Med Imaging. 2007;26(1):68–76. doi: 10.1109/TMI.2006.885337. [DOI] [PubMed] [Google Scholar]
- 29.Kim YC, Narayanan SS, Nayak KS. Flexible retrospective selection of temporal resolution in real-time speech MRI using a golden-ratio spiral view order. Magn Reson Med. 2011;65(5):1365–1371. doi: 10.1002/mrm.22714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lustig M, Pauly JM. SPIRiT: Iterative self-consistent parallel imaging reconstruction from arbitrary k-space. Magn Reson Med. 2010;64(2):457–471. doi: 10.1002/mrm.22428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Fessler JA. On NUFFT-based gridding for non-Cartesian MRI. J Magn Reson. 2007;188(2):191–195. doi: 10.1016/j.jmr.2007.06.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.MOROZOV V. SOLUTION OF FUNCTIONAL EQUATIONS BY REGULARIZATION METHOD. Doklady Akademii Nauk Sssr. 1966;167(3):510. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.