Single Acquisition Electrical Property Mapping Based on Relative Coil Sensitivities: A Proof-of-Concept Demonstration

Abstract

Purpose

All methods presented to date to map both conductivity and permittivity rely on multiple acquisitions to compute quantitatively the magnitude of radiofrequency transmit fields, ${\mathrm{B}}_1^{+}$. In this work, we propose a method to compute both conductivity and permittivity based solely on relative receive coil sensitivities ${(\mathrm{B}}_1^{-})$ that can be obtained in one single measurement without the need to neither explicitly perform transmit/receive phase separation nor make assumptions regarding those phases.

Theory and Methods

To demonstrate the validity and the noise sensitivity of our method we used electromagnetic finite differences simulations of a 16-channel transceiver array. To experimentally validate our methodology at 7 Tesla, multi compartment phantom data was acquired using a standard 32-channel receive coil system and two-dimensional (2D) and 3D gradient echo acquisition. The reconstructed electric properties were correlated to those measured using dielectric probes.

Results

The method was demonstrated both in simulations and in phantom data with correlations to both the modeled and bench measurements being close to identity. The noise properties were modeled and understood.

Conclusion

The proposed methodology allows to quantitatively determine the electrical properties of a sample using any MR contrast, with the only constraint being the need to have 4 or more receive coils and high SNR.

INTRODUCTION

Noninvasive mapping of electrical conductivity (σ, reflecting the ability to conduct charge) and permittivity (ε, reflecting the ability to store charge) in vivo has promising potential applications in various fields, including Specific Absorption Rate (SAR) control in high field MRI (1), design of subject specific head models for transcranial magnetic stimulation (2), electroencephalography (3) and magneto-encephalography, and direct medical diagnostics. However, the mechanisms underlying conductivity and permittivity in tissues at the high frequencies probed by MR (over 65 MHz) is still largely unknown (4,5). Significant variations of conductivity have been observed in the brain following stroke (6) and in malignant tissues (4,7). Some of these variations have been associated with differing salt distributions, while permittivity above 100 MHz has been attributed to intracellular electrolytes and water concentration (8,9).

Many methods have been developed over the years in different fields of expertise to study tissue electrical properties. Electrical Impedance Tomography (EIT) was one of the first methodologies proposed (10–13) to calculate impedance images by applying an electrical potential in a surface electrode and observing its effect on distal electrodes. The calculation of the impedance maps, being based on limited surface measurements, is highly ill posed, which limits the resolution and robustness of the obtained resistance maps obtainable. One related technique that takes advantage of the ability of magnetic resonance to measure the effect of magnetic fields on the water signal phase is Magnetic Resonance Electrical Impedance Tomography (14–18). In this technique the additional magnetic flux B_z (along the direction of the main magnetic field B₀) generated inside the object at low frequencies by injecting currents at one or several surface electrodes is measured by means of changes in the local frequency shift and hence in the image phase. Other than the phase images with and without applied currents (or, alternatively, with opposed currents), at least one voltage measurement at the surface is needed to be able to compute quantitative conductivity maps (19).

An alternative method, which relies solely on conventional MR hardware and can be considered less invasive (without the need of using surface electrodes and injecting currents into tissue), was first described by Katscher et al (20) and dubbed Electrical Properties Tomography (EPT). Given that electrical properties influence the way in which electromagnetic waves and currents propagate through the body, one natural way to characterize those electrical properties is to measure their effect on the radiofrequency (RF) electromagnetic fields that are associated with either the excitation $({\mathrm{B}}_1^{+})$ or the detection $({\mathrm{B}}_1^{-})$ of the MR signal (20). The curvature of RF electromagnetic fields in an homogeneous region of the sample is described by the Helmholtz equation:

$$\frac{{\nabla }^2{\mathrm{B}}_1^{\pm }}{{\mathrm{B}}_1^{\pm }}=-(\mathrm{\mu }\mathrm{\epsilon }{\mathrm{\omega }}^2\pm \mathrm{i}\mathrm{\mu }\mathrm{\sigma }\mathrm{\omega })$$ [1]

where ω is the frequency of the RF fields, and μ is the magnetic permeability. This relationship is only valid in regions of constant conductivity, σ, and permittivity, ε. Note that if the ${\mathrm{B}}_1^{\pm }$ fields in Eq. [1] are modulated at the Larmor frequency, then σ and ε represent the electrical properties associated with that frequency. In the presence of an interface between materials with different electrical properties, the Maxwell Equations couple the magnetic fields along the three Cartesian directions. Because the longitudinal field component B_z at the Larmor frequency cannot easily be disentangled from MR measurements, the electrical property mapping problem is quite challenging in regions of varying properties. For this reason, and for another reason to be addressed in a moment, EPT was initially proposed for use near the center of long circularly polarized birdcage-like RF coils in which the z component of the RF field is negligible at baseline.

Although the problem of solving the Helmholtz Equation for σ and ε given known transmit and/or receive magnetic fields looks, at first glance, to be simple, there are a series of issues that hinder its applicability. First, second derivatives are extremely sensitive to noise and hence it is important to obtain very high SNR measurements of the RF magnetic fields. Second, most methods to obtain quantitative transmit magnetic fields maps rely on sequences that are rather long (due to the need to disentangle T₁ and other parameters from B₁), rely on multiple acquisitions (and hence are sensitive to subject movement) and are typically of fairly low SNR and/or are limited to relatively low spatial resolutions (21–27). Furthermore, quantitative transmit B₁ mapping methodologies are often limited, in terms of accuracy, to a limited range of B₁ intensities (25). On the other hand, absolute receive fields are virtually impossible to disentangle from any magnetization variations in the object. Third, and more fundamentally, quantitative ${\mathrm{B}}_1^{+}$ mapping techniques only give access to the amplitude of the transmit field, and if necessary to its phase relative to some reference transmitter, but not to its absolute phase. The phase of the signal measured from any given MR sequence depends not only on the RF phase of the transmitter, but also on the RF phase of the receiver, on sequence related eddy currents and, in the case of gradient echo sequences, on the local B₀ inhomogeneity. While the effects of the latter can be limited by using spin echo sequences (20,28,29), and care can be taken to minimize or correct for eddy currents (20,28,29), the separation between the transmit and receive phase is less trivial. All methods presented to date to map conductivity together with permittivity rely on multiple acquisitions to compute quantitative ${\mathrm{B}}_1^{+}$ field magnitudes, and either: (a) make assumptions regarding the phase of the RF field that are only valid for specific birdcage-like circularly polarized (CP) coil arrangements at lower field strengths (20,28,29) and away from tissue boundaries but break down at higher field strengths; (b) use multiple transmit coils to estimate absolute RF phase subject to additional symmetry assumptions (1); or (c) compute true absolute RF phase by combining ${\mathrm{B}}_1^{+}$ maps with receive ${\mathrm{B}}_1^{-}$ maps (30,31). The third approach, called Local Maxwell Tomography, has been shown to be capable in principle of mapping challenging regions of varying electrical properties without any inherent symmetry assumptions, but at the price of substantial added complexity and requirements for measurement accuracy (32).

In this work, we propose a formalism to compute electrical property maps (of both conductivity and permittivity) based solely on relative receive coil sensitivities. Relative receive coil sensitivities have the particularity that both the amplitude and phase are measurable from any single acquisition without the need to make assumptions on how to separate the receive and transmit phases. The feasibility of this approach is demonstrated in simulations and phantom data.

THEORY

Although absolute ${\mathrm{B}}_1^{-}$ fields cannot be measured, relative receive field between two coils, ${\mathrm{B}}_{1,\mathrm{i},\mathrm{ref}}^{\prime -}$, can be measured from any MR acquisition as:

$${{\mathrm{B}}^{\prime }}_{1,\mathrm{i},\mathrm{ref}}^{-}=\frac{{\mathrm{Signal}}_{\mathrm{i}}}{{\mathrm{Signal}}_{\mathrm{ref}}}=\frac{{\mathrm{B}}_{1,\mathrm{i}}^{-}}{{\mathrm{B}}_{1,\mathrm{ref}}^{-}}$$ [2]

where Signal_i is the MR signal measured by coil i. Given that the conductivity and permittivity distribution experienced by any of the measured receive B⁻_1,i fields is the same (i.e., the right-hand side of Eq. [1] is the same for all receive fields), and using the product law of differentiation or else expressing Eq. [1] in terms of derivatives of log quantities, it is possible to build a set of linear equations:

$$-2\nabla {{\mathrm{B}}^{\prime }}_{1,\mathrm{i},\mathrm{ref}}^{-}\times \frac{\nabla {\mathrm{B}}_{1,\mathrm{ref}}^{-}}{{\mathrm{B}}_{1,\mathrm{ref}}^{-}}={\nabla }^2{{\mathrm{B}}^{\prime }}_{1,\mathrm{i},\mathrm{ref}}^{-}$$ [3]

which can be solved for $\nabla {\mathrm{B}}_{1,\mathrm{ref}}^{-}/{\mathrm{B}}_{1,\mathrm{ref}}^{-}$. Note that this ratio now characterizes not a relative coil sensitivity, but the rate of change of the complex field associated with the coil used as reference. There are three complex unknowns associated with $\nabla {\mathrm{B}}_{1,\mathrm{ref}}^{-}/{\mathrm{B}}_{1,\mathrm{ref}}^{-}$, and one complex equation for each receive coil. Because one coil (or a suitable combination of coils) must be used as the reference, Eq. [3] has a unique solution if a total of four or more receive coils are available with sufficiently distinct relative sensitivities at each location of interest (one to define the reference, and three or more to define the equations).

Electrical properties can subsequently be computed by rewriting the Helmholtz equation as a function of the newly calculated ratio:

$$\begin{array}{l}\frac{{\nabla }^2{\mathrm{B}}_{1,\mathrm{ref}}^{-}}{{\mathrm{B}}_{1,\mathrm{ref}}^{-}}=\frac{\nabla {\mathrm{B}}_{1,\mathrm{ref}}^{-}}{{\mathrm{B}}_{1,\mathrm{ref}}^{-}}·\frac{\nabla {\mathrm{B}}_{1,\mathrm{ref}}^{-}}{{\mathrm{B}}_{1,\mathrm{ref}}^{-}}+\nabla ·\left(\frac{\nabla {\mathrm{B}}_{1,\mathrm{ref}}^{-}}{{\mathrm{B}}_{1,\mathrm{ref}}^{-}}\right)\\ =-(\mathrm{\mu }\mathrm{\epsilon }{\mathrm{\omega }}^2-\mathrm{i}\mathrm{\mu }\mathrm{\sigma }\mathrm{\omega })\end{array}$$ [4]

To see a complete derivation of both Eqs. [3] and [4], refer to the Appendix at the end of this manuscript.

METHODS

To test the validity of these equations and demonstrate them experimentally, electrical property mapping was performed in numerical simulations (NS) and experimental phantom data (PD).

Numerical Simulations

A transceive array with 16 loop elements surrounding a spherical (d = 160 mm) phantom (σ = 0.75 S/m and ε_rel = 65, with ε = ε_rel ε₀, where ε₀ is the permittivity of free space), as shown in Figure 1, that includes smaller spheres with varying conductivity (0.2–2.1 S/m) and relative permittivity (40–90) was simulated at 300 MHz using XFDTD v6.4 (Remcom, Inc.). The absolute B_1x and B_1y generated by each element of the RF coil was computed. Subsequently the transmit and receive magnetic fields were computed as ${\mathrm{B}}_1^{+}={\mathrm{B}}_{1\mathrm{x}}+\mathrm{i}{\mathrm{B}}_{1\mathrm{y}}$ and ${\mathrm{B}}_1^{-}={\mathrm{conj}(\mathrm{B}}_{1\mathrm{x}}-\mathrm{i}{\mathrm{B}}_{1\mathrm{y}})$ (33). To first test the validity of Eq. [4], taking advantage of the fact that in the case of numerical simulations all ${\mathrm{B}}_1^{-}$ fields, including the reference field, are known completely, the electrical properties of the phantom were computed either using Eq. [1] or Eq. [4]. Subsequently, to test the validity of Eq. [3], it was assumed that only relative receive coil sensitivities could be measured. Conductivity and permittivity maps using either different coils or combinations of coils as the reference, ${\mathrm{B}}_{1,\mathrm{ref}}^{-}$ were calculated.

FIG. 1.

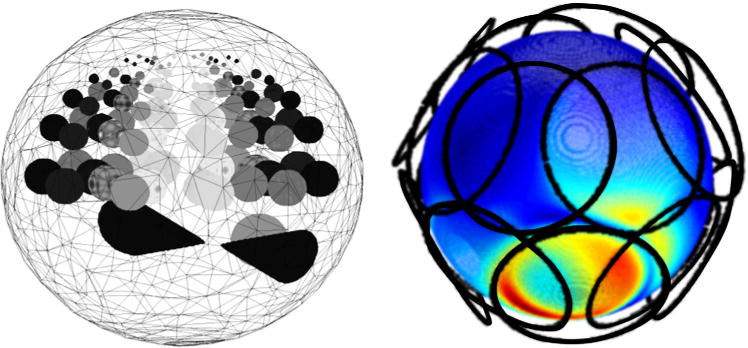
Simulation geometry. Left: 3D representation of the spherical model used in numerical simulations. The model was created with 1 mm resolution and the spherical inserts had varying diameters (17, 14, 10, 6, and 4 mm when passing from the middle slice to the top of the model). Right: Sixteen loop coils positioned around the numerical phantom were used to guarantee a spatial independence between the computed fields. As an example, the field generated by one of the loop coils at the surface of the numerical phantom is shown by surface color shading, with red indicating high amplitude and blue low amplitude. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

The sensitivity to noise amplification of the proposed method in comparison to simply using the Helmholtz equation with transmit ${\mathrm{B}}_1^{+}$ field maps, as in EPT, was evaluated. The SNR of the input data was defined as follows:

• For the standard Helmholtz equation methodology, a CP mode was created using the 16 independent transmit channels and making their fields in phase at the center of the phantom. Complex random Gaussian noise, uncorrelated between real and imaginary channels, was added to the transmit CP mode. The SNR of the transmit magnetic field was characterized as ratio of the mean ${\mathrm{B}}_1^{+}$ field in the center Region of Interest (ROI) and its standard deviation. This simple Gaussian noise model does not take into account any nonlinearities in methods which might be used to calculate transmit field distributions in practice (see Appendix C). The reconstruction assumes that the absolute phase of the CP mode ${\mathrm{B}}_1^{+}$ field is known, as mentioned earlier, this is not possible at 300 MHz and the standard transceiver approximations are not valid (see Appendix C).

• For the Single Acquisition Electrical Property (SAEP) mapping, complex Gaussian noise was added to each independent channel. The nominal SNR was calculated as being the mean over the ROI of the ratio between $\sqrt{{\sum }_{i=1}^{\mathit{Coils}}|B_{1i}^{-}(r)+\mathit{noise}{|}^2}$ and the standard deviation over 100 replicas.

This procedure was repeated for each method to evaluate the impact of an input SNR ranging from 100 up to 1e6. The two different methodologies were used to calculate the conductivity and permittivity maps and the SNR of the reconstruction of σ and ε_rel (defined as mean divided by standard deviation over the ROI) was calculated. Note that the final SNR results also depend upon the particular methodology used for computing derivatives (description to follow).

Phantom Data

Two 120-mm spherical phantoms were divided by 2 perpendicular planes of parafilm, which held in place 4 thin latex containers in each of the phantoms. One phantom was designed to study the variation of conductivity. Based on invasive and primarily ex vivo measurements, the conductivity of brain is expected to be approximately 0.34, 0.59, and 2.14 S/m for white matter, grey matter and CSF, respectively (5,34). The 4 compartments of the conductivity phantom were, therefore, filled with 2, 4, 8, and 12 g/L NaCl solution (further doped with 0.07 g/L MnCl₂ to match the T₁ of the solution to brain-like tissues) with the first two matching the expected grey and white matter conductivity and the 12 g/L solution expected to match the conductivity of CSF. Another phantom was designed to study variations in permittivity. The relative permittivity of the brain is expected to lie in the vicinity of 52, 73, and 84 for GM, WM, and CSF, respectively. The relative permittivity of the compartments was modulated by introducing various amounts of sugar. The different compartments were filled with a solution in which the following quantities of sugar were added per liter of water (doped with 0.07 g/L MnCl₂ and with a 3 g/L NaCl): 0, 0.66, 1.47, and 2.27 kg, respectively. The use of these two phantoms enabled modulation of both the conductivity and the permittivity in expected physiological variations.

The permittivity and conductivity values of the different solutions at 300 MHz were assessed with the use of a dielectric assessment kit (DAK1.2 planar P140 vector reflectometer, SPEAG, Switzerland) inside a 200-mL glass beaker.

All MR acquisitions were performed on a short-bore 7T MR scanner (Siemens Medical Solutions, Erlangen, Germany) equipped with a head-gradient insert, using a 32-element receive array (Nova Medical Inc).

Three different acquisitions were performed to test the robustness of the method to the sequence parameters used:

• 3DGRE with the following parameters TR/TE 6.5/3.0 ms (BW = 260 Hz/Pixel), α = 8 degree, res = 1 mm isotropic, matrix size 192 × 192 × 192, 3 averages, Tacq = 10 min.

• 2DGRE sequence with the following parameters TR/TE = 400/3.35 ms (BW = 260 Hz/Pixel), α = 60 degree, res = 1.5 mm isotropic, matrix size 128 × 128 × 60, 6 averages, Tacq = 5.09 min.

• 2DGRE multi echo sequence with the following parameters TR/TE = 400/3.35 ms, α = 60 degree, res = 2 mm isotropic, matrix size 256 × 182 × 60, 8 averages, Tacq = 5 min.

Processing Protocol

The electrical property (EP) mapping protocol applied to the numerical simulations and phantom data was the following:

1. EP calculations were performed in a sliding window of width L + 2K_Grad, where L was the displacement used for the sliding window (and the region where EP were actually calculated) (L 3) and K_Grad is the total size of the kernel used to calculate the derivatives (K_Grad = 3);

2. Coil modes were calculated by means of SVD decomposition in the sliding window and 8 relative ${{\mathrm{B}}^{\prime }}_{1,\mathrm{i},\mathrm{ref}}^{-}$ were computed using the first mode as reference (Eq. [3]). As will be discussed later, this coil recombination approach was used to avoid regions of low ${\mathrm{B}}_{1,\mathrm{ref}}^{-}$ amplitude, which can degrade the quality of the reconstructions;

3. Gradients and Laplacians were calculated using finite differences for the numerical simulations (along each Cartesian direction Gradient = [−1 0 1], Laplacian = [−1 2 −1]) (see Supporting Figure S1, which is available online, to see the resulting effective size of the gradient and Laplacian kernel when applied to the 1, 1.5, and 2 mm resolution data);

4. Equation [3] was solved by Moore-Penrose matrix inversion for each pixel introducing an additional weighting for each line of the system of equations (Eq. [3]) corresponding to the SNR of the corresponding mode SNR_1;i;ref.:

   $$-2{\mathrm{SNR}}_{1,\mathrm{i},\mathrm{ref}}·\nabla {{\mathrm{B}}^{\prime }}_{1,\mathrm{i},\mathrm{ref}}^{-}·\frac{\nabla {\mathrm{B}}_{1,\mathrm{ref}}^{-}}{{\mathrm{B}}_{1,\mathrm{ref}}^{-}}={\mathrm{SNR}}_{1,\mathrm{i},\mathrm{ref}}·{\nabla }^2{{\mathrm{B}}^{\prime }}_{1,\mathrm{i},\mathrm{ref}}^{-}$$ [5]

5. Equation [4] was computed using a second-stage application of the gradient algorithm described in (iii), and the electrical properties were calculated in the inner kernel of width L.

As derivatives (first and second order) are very sensitive to noise in high frequencies range of the Fourier spectrum, smoothing the original data is one approach to reduce the sensitivity of these operators to noise. Particularly, Gaussian smoothing has some important properties, amongst them the fact that it keeps the shape of the derivative operators in the Fourier space in the low frequency range intact. Hence, the phantom data processing chain was preceded by a Gaussian smoothing of the original multichannel data with a FWHM parameter set to 4 mm.

RESULTS

Simulations

Figure 2 shows that when using the Helmholtz equation on the numerical simulations to calculate directly the conductivity and permittivity (assuming that the complex ${\mathrm{B}}_1^{-}$ was known), an essentially perfect match between the calculated values and the true a priori values is found as long as the kernel used to calculate the Laplacian does not cross a boundary between structures with different conductivity or permittivity. In the regions where these boundaries are crossed by the Laplacian kernel, significant errors were observed in the electrical properties estimated (some examples are highlighted with red arrows in Figures 2b and 2h) because the Helmholtz Equation does not hold when either the conductivity or the permittivity are not homogeneous. When using the modified Helmholtz equation (Eq. [4]), regions where boundary artifacts were observed were extended (red arrows in Figures 2d and 2j) while artifacts also arise in regions where the amplitude of the B₁ field was very small (yellow arrows in Figures 2c and 2i). The first effect is due to the increased effective kernel size needed to compute the conductivity and permittivity by means of a second-stage divergence. While the Laplacian used for the Helmholtz equation (Eq. [1]) was a 3×3×3 kernel, using the SAEP method the calculation of the electrical properties is done in two stages: (i) Eq. [3] is used to calculate $\nabla {\mathrm{B}}_{1,\mathrm{ref}}^{-}/{\mathrm{B}}_{1,\mathrm{ref}}^{-}-$. Because this is done having initially calculated a Laplacian of the relative coil sensitivities, the minimum kernel size is again 3 × 3 × 3; (ii) the modified Helmholtz equation (Eq. [4]) is then applied to $\nabla {\mathrm{B}}_{1,\mathrm{ref}}^{-}/{\mathrm{B}}_{1,\mathrm{ref}}^{-}$, with the second term being a divergence operator, to guarantee that both terms are centered in the same voxel. The resulting kernel size is 5 × 5 × 5.

FIG. 2.

Comparisons of various methods for electrical property mapping in simulations. Conductivity and permittivity maps of a transverse slice across the numerical phantom are shown in the top and bottom rows, respectively. The columns show (a,g) – true property maps using model parameters; (b,h) – maps reconstructed when using Eq. [1] assuming complex ${\mathrm{B}}_1^{-}$ of all coils is fully known; (c,i) and (d,j) maps reconstructed using modified Helmholtz equation (Eq. [4]) using either one single coil sensitivity distribution (f) or using a locally phase matched coil combination (l) assuming complex ${\mathrm{B}}_1^{-}$ of all coils is fully known; (e,k) reconstructed maps using the proposed Single Acquisition Electrical Property mapping method, starting from relative receive coil sensitivities and using as the reference the main mode (represented by the top-ranked singular vector) in the sliding window kernel. For presentation purposes, the reference ${\mathrm{B}}_1^{-}$ maps (f,l) are shown in logarithmic scale. Red arrows highlight the artifacts present at tissue interfaces where the conductivity or permittivity are not constant. Yellow arrows highlight the sensitivity of the modified Helmholtz Equation to numerical errors arising from a low B_1ref, which can be overcome by choosing a reference mode devoid of such points in the kernel. A 2D cut through the 3D Laplacian kernel is shown under each version of the Helmholtz equation. The thin black squares in each kernel indicate the three-voxel effective spatial resolution of each method given these choices of derivative kernel. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

To minimize the effect of errors in regions of low B₁ (seen in Figures 2c and 2i) which result from the numerical instability associated with the second term in Eq. [4] (i.e., $\nabla {\mathrm{B}}_{1,\mathrm{ref}}^{-}/{\mathrm{B}}_{1,\mathrm{ref}}^{-}$ becomes very large and the derivatives will further propagate any error in $\nabla {\mathrm{B}}_{1,\mathrm{ref}}^{-}/{\mathrm{B}}_{1,\mathrm{ref}}^{-}$). These artifacts can be overcome by carefully choosing either the channel to which to apply the modified Helmholtz equation (avoiding regions of low B₁) or by building locally recombined modes which have a high B₁ amplitude (Fig. 2.l). (Note that within each kernel the coil combination is linear and consistent, so that Maxwell’s equations continue to hold for the recombined fields.) Once the whole reconstruction was performed using the protocol as described in the Methods section, it was possible to reconstruct electrical property maps where the only visible artifacts appear in the interface between regions with distinct electrical properties. Note that these artifacts are now different from those initially found when only computing the Helmholtz equation (Fig. 2a–c,h–j). Once again, this is a consequence of the fact that the SAEP methodology relies twice upon the validity of the Helmholtz equation, not only when solving the modified Helmholtz equation (Eq. [4]) but also when initially computing $\nabla {\mathrm{B}}_{1,\mathrm{ref}}^{-}/{\mathrm{B}}_{1,\mathrm{ref}}^{-}$ (Eq. [3]). In the regions where the whole effective kernel fell within the different compartment boundaries, a high correlation (0.99) was found between the calculated and the true electrical properties.

When comparing the effect of noise propagation of the different electrical property mapping methodologies in the ROI defined at the center of the numerical phantom, it is possible to conclude that, despite the inherently increased kernel size of the SAEP methodology, an inherent increase in noise sensitivity results from the fact that the SAEP methodology relies on a third order derivative (by means of the second pass divergence of a quantity derived from second derivatives) rather than a second order derivative as for the simple Helmholtz equation. This can be seen both on the electrical property maps of Figures 3e and 3f when compared with Figures 3b and 3c and on the plot of the SNR of the calculated maps as a function of the input SNR (see Figure 3g). It should be noted that relative coil sensitivities and quantitative ${\mathrm{B}}_1^{+}$ maps cannot be computed with the same SNR and in the same amount of time as ${\mathrm{B}}_1^{-}$ maps, and that the SNR of the ${\mathrm{B}}_1^{+}$ maps is highly dependent upon the underlying ${\mathrm{B}}_1^{+}$ amplitude at any given position. The spatially varying noise level in the EP maps resulting from the Helmholtz equation is due to the varying amplitude of the CP ${\mathrm{B}}_1^{+}$ field (see Figure 3a). Furthermore, systematic errors in quantitative transmit field maps and the assumption that the phase of the transmit field can be approximated by half of the transceiver coil sensitivities can, at high fields, introduce systematic errors that were not accounted on these simulations (see Supporting Figure S1).

FIG. 3.

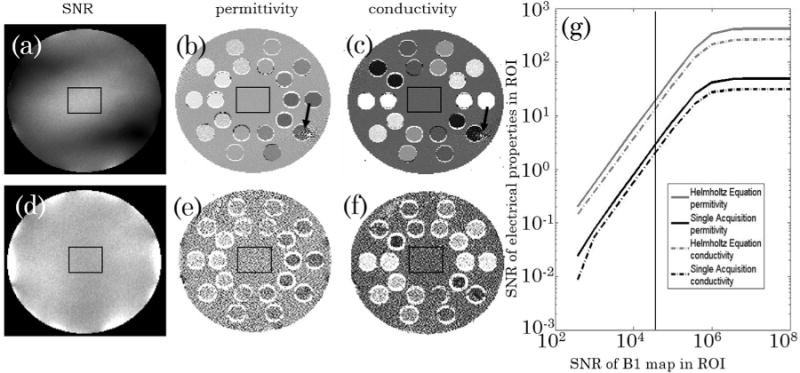
Calculated conductivity and permittivity maps of a transverse slice across the numerical phantom in the presence of white noise resulting in an SNR in the central ROI (black square) of 100,000 for the ${\mathrm{B}}_1^{+}$ (a) and for the combined receive ${\mathrm{B}}_1^{-}$ (d). The first row (b,c) shows the electrical properties calculated assuming the complex CP field is fully known and the Helmholtz equation can be used in a straightforward manner. The black arrow indicates a region of low B_1CP amplitude and hence increased noise on the electrical property map. The second row (e,f) shows the electrical properties calculated using the proposed single acquisition methodology. g: Plot of average measured SNR of the electrical properties in the ROI as a function of the average input SNR in the same ROI for the two different methodologies. The plateau on the right side reflects the inherent SNR of the simulation of ~5 × 10⁵.

Phantom Data

From the bench studies the conductivity and permittivity at 300MHz of the doped water solution was found to be σ_water = 0.022 S/m and ε_rel,water = 79. The dependence of the permittivity on the sugar concentration (g/L) was 12 per Kg/L of sugar. The dependence of the conductivity in the sodium concentration was of 0.16 S/m per g/L of NaCl, while the relative permittivity dependence was of −0.22 per g/L of NaCl.

Figure 4 shows a slice of the sugar phantom (top row) and of the salt phantom (bottom row) covering a region where the 4 different compartments are visible. As an example, the magnitude (Figures 4a and 4e) and phase (Figures 4b and 4f) of the first 4 coil modes are shown. Although 8 modes are not sufficient to explain the signal obtained by the 32 channels over the whole phantom, 8 modes are sufficient when compressing the data inside the sliding window. It is possible to observe that these channel modes have both different magnitude and different phase behavior throughout the object. When using the strongest mode as a reference it was possible to create 3 relative coils sensitivities (Figures 4c, 4d, 4g, and 4h) where all clear anatomical information both in terms of intensity (due to the different water fraction) and phase (due to either chemical shift or susceptibility artifacts) has vanished. While the coil modes shown in Figure 4 were calculated for the whole volume, those shown in Figure 5 correspond to the coil modes calculated inside a sliding window. While the first 4 modes over the whole phantom, Figure 4a, explain 72% of the data (29%, 23%, 11%, and 9%), those in a sliding window, Figure 5a, explain 98% of the data (81%, 8%, 5%, and 4%). In such a sliding window the compression of the data is thus justifiable and it can be seen that the different modes have very spatial patterns both in the magnitude and in the phase. Figure 5c shows the 3 Cartesian components of the calculated $\frac{\nabla {\mathrm{B}}_{1,\mathrm{ref}}^{-}}{{\mathrm{B}}_{1,\mathrm{ref}}^{-}}$ using Eq. [5]. Two features can readily be visible in these maps: the large values of the gradient close to the boundaries between different compartments (due to the erroneous assumption of the Helmholtz Equation); and the increased noise in regions of low SNR in the reference mode (see top left compartment).

FIG. 4.

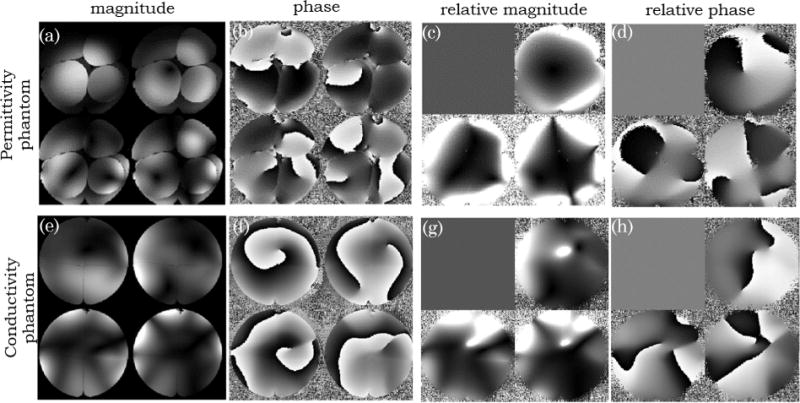
Images of the permittivity (sugar) phantom and conductivity (salt) phantom are shown on the top (a–d) and bottom row (e,h), respectively. Magnitude (a,e) and phase (b,f) images of the first 4 coil modes (calculated for the whole volume) in one transverse slice. The magnitude (c,g) and phase (d,h) coil sensitivities, in the same slice, relative to the first mode are also shown.

FIG. 5.

Axial Magnitude and Phase images of the permittivity (sugar) phantom are shown on the top and bottom row respectively. a: Images of the first 4 coil modes calculated in a sliding window of 7 × 7 × 7 voxels and the corresponding (b) 3 relative coil sensitivities. c: x, y, and z components of $\frac{\nabla {\mathrm{B}}_{1,\mathrm{ref}}^{-}}{{\mathrm{B}}_{1,\mathrm{ref}}^{-}}$. The values shown on the magnitude images of the local coil modes represent the fraction of the data explained by each mode with the first 4 modes explaining 98% of the data.

Using the processing protocol described in the methods section it was possible to generate the permittivity maps shown on Figures 6b and 6f and the conductivity maps shown in Figures 6c and 6g for the sugar and salt phantoms respectively. The maps shown in Figure 6 were obtained using the 3D GRE acquisition protocol with 1 mm isotropic voxels, followed by smoothing with a 4-mm FWHM Gaussian, therefore, each pixel has an effective full-width of ~8 mm isotropic. Using the magnitude data (see Figures 6a and 6e) and an edge detection algorithm it was possible to separate each compartment into a different ROI. Using information regarding the kernel size used to calculate the EP, the region where the Helmholtz equation holds was defined and, finally, the mean value of the electrical property maps and the standard deviation within each compartment were computed. All plots in Figure 6 show a noteworthy agreement between the mean values of the electrical property maps obtained in the different GRE experiments regardless of sequence dimensionality (2D versus 3D) or resolution with those measured using the dielectric probes in a bench experiment. The slope between the bench permittivity values and those measured by means of MRI was of 0.96 ± 0.01, 1.02 ± 0.02, and 1.01 ± 0.02 for the GRE3D, GRE2D with 1.5 and 2.0 mm protocols, respectively. The correlations for the conductivity for those 3 protocols was 0.98±6 0.05, 1.01 ± 0.02, and 1.00 ± 0.04. It should be noted effective resolution of the different reconstructions is different with the 3 protocols having an effective resolution of 8, 10, and 12 mm, respectively, which could responsible for the better correlation found with the lower resolution data.

FIG. 6.

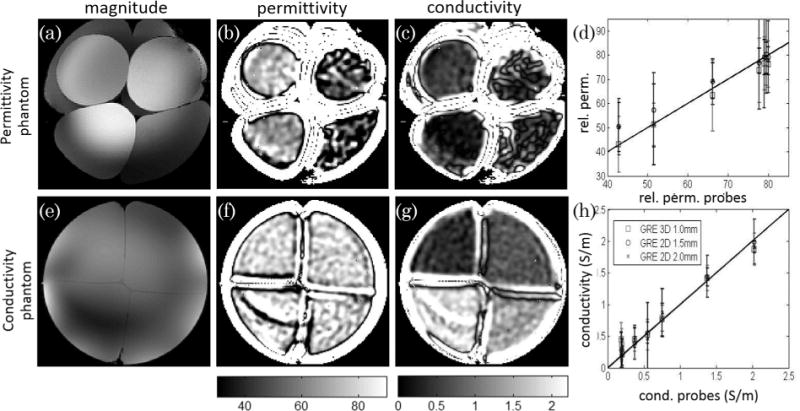
Sum of squares images of the permittivity (sugar) phantom and conductivity (salt) phantom are shown on the top (a) and bottom row (e) together with the calculated permittivity (b,f) and conductivity (c,g) maps calculated for the same slice. The plots shown on the right represent the mean and standard deviations of the electrical properties (ε, d; σ, h) obtained in the eight large 3D regions of interest designed on both phantoms (with expected homogeneous properties appropriate for use of the Helmholtz equation to be valid) with the three different datasets acquired plotted against the measured conductivity and permittivity values obtained by the bench probes.

DISCUSSION

The present study shows for the first time in simulations and experimentally that electrical property maps can be obtained based solely on the information from the relative receive sensitivity maps. The relative receive fields can be measured with the most SNR-efficient sequences which offsets the increased sensitivity to noise and derivative estimation error compared with other published methods. The presented experimental data was based on spoiled gradient echo acquisitions, but balanced steady state free precession sequences could also be considered for further increases in SNR.

Both conductivity and permittivity vary relatively slowly as a function of frequency in the typical range used in MRI (60–300 MHz) (5,34). Therefore, from Eq. [1], it can be concluded that with the increase of the magnetic field, there is an inherent approximately quadratic increase in the sensitivity to permittivity and an approximately linear increase in the sensitivity to conductivity. This estimate does not take into account the gains in SNR associated with the MR measurements, which can be supra-linear with B₀. Our data, acquired at 7T, seems to suggest that the measurement of permittivity is significantly more susceptible to errors than the measurements of conductivity. One factor that is expected to play an important role is that, at 7T, assuming that the real and imaginary components of the Helmholtz equation can be calculated with the same precision, a change in the relative permittivity of 10 should be measurable with the same SNR as a change of 0.17 S/m of the conductivity. This is in agreement with the relative size of the error bars shown on Figure 5 (mean of 11 and 0.23 for the permittivity and conductivity, respectively). Furthermore, the variations expected inside the brain in terms of permittivity are on the order of ~ 30 and variations in the conductivity are on the order of 1.8 S/m (31) (similar ranges were obtained with our setup). This suggests a 3 times greater sensitivity to maximal conductivity changes than to maximal permittivity changes in the brain at 300 MHz. Given the approximately quadratic dependence of permittivity on frequency as opposed to the linear dependence of conductivity, the relative sensitivity to permittivity should in principle increase with increasing static magnetic fields.

The strong agreement found between the measured electrical properties based on the SAEP and those obtained using the dielectric probes demonstrates the accuracy of the method while the large error bars seen in Figure 6 suggest the method has a low precision and high noise sensitivity. As it can be seen from Figure 3 and Figure 5 the SNR of the final and intermediate measurements is highly dependent on the available SNR in the original image. In the current experimental setup, the used spherical phantoms produce strong B₁ field inhomogeneities making the SNR available highly inhomogeneous. This problems could be mitigated by the use of parallel transmission, either to obtain a more spatially homogeneous transmit field (as in RF shimming) (35), or by acquiring various images with different RF shimming combinations that together could have a homogeneous SNR distribution (36) (the electric properties associated with each of the measurements could then be averaged).

The main source of noise of the current methodology is the implicit use of third order derivatives needed to calculate the electric properties. When using the ratio of different coil sensitivities, part of the interaction of the RF waves with the electric properties of the object might be cancelled out, and hence the method then relies on subtler imprints of this interaction. Another potential source of noise in the presented methodology could be the ill-condition nature of the inversion of Eq. [3]. For this system of equations to be ill-conditioned it would be necessary that the N-1 vectors $\nabla {{\mathrm{B}}^{\prime }}_{1,\mathrm{i},\mathrm{ref}}^{-}$ in a given pixel would lye on the same plane. Using a large number of surface arrays, as used throughout this manuscript, this is unlikely. The only scenario where this could be envisaged to happen is in the case where axially symmetric RF coils image perfectly axially symmetric object so that the receive field of the N coils have the same derivative along z and particularly this derivative would also have a zero in the same plane. In this plane, located at the center of the RF coil, the matrix inversion would be ill-posed. This behavior was not observed neither in our simulations nor in our data.

In the current study, the methodology used to control the noise amplification of the EP computation was based on Gaussian smoothing the original data before applying the differential kernels (also polynomial fits of unsmoothed relative coil sensitivities were performed – data not shown) which has the advantage of being extremely fast and computationally inexpensive, but has a high cost in terms of effective resolution (with the 1mm isotropic data, the electrical property maps obtained had an implicit footprint, FWHM, of 8mm). As can be seen in both the numerical and phantom results, the values of the conductivity and permittivity in regions where the derivative kernels cross the boundaries, making the Helmholtz Equation not valid, diverge by one or more orders of magnitude (intensities in the boundary between compartments appear clipped in Figures 2, 3, 4, and 6). When moving to in vivo applications, where the intricate shapes of the anatomy that is likely to have homogeneous electrical properties are not well suited to the large kernels used throughout this manuscript (for example, grey matter has an average thickness of ~4 mm), more advanced methodologies to perform denoising of the relative coil sensitivities will have to be implemented, or more compact derivative kernels have to be considered (the current effective derivative kernel is the convolution of the finite difference with the nontruncated Gaussian function – see Supporting Figure S1). In the future it could be envisaged using methods based on iterative denoising of the relative coil sensitivity maps, $B_1^{\prime }$, by simply minimizing the following quantity within the boundaries of EP homogeneity (indicated by a binary mask M_EP)

$${\mathit{min}}_{B_{1\mathit{DN}}^{\prime }}\Vert M_{\mathit{EP}}(B_{1\mathit{DN}}^{\prime }-B_1^{\prime }){\Vert }_2^2+\mathrm{\alpha }\Vert M_{\mathit{EP}}{\nabla }^2{B}_{1\mathit{DN}}^{\prime }{\Vert }_2^2$$ [6]

Here α is a regularization parameter that forces the denoised relative coil sensitivity to have a Laplacian with small norm (or alternatively with a smooth norm if the regularization term would be $\Vert M_{\mathit{EP}}\nabla {\nabla }^2{B}_{1\mathit{DN}}^{\prime }\Vert$). This would be based on the assumption that the large values of the Laplacian are mainly of noise origin and would guarantee that the first stage of noise amplification would be significantly reduced without the loss of resolution introduced by the Gaussian smoothing which is especially problematic close to boundaries. Denoising in the second stage could also be solved iteratively by first denoising $\frac{\nabla {\mathrm{B}}_{1,\mathrm{ref}}^{-}}{{\mathrm{B}}_{1,\mathrm{ref}}^{-}}$ so that the resulting electrical property maps have smooth and small values (unlike those seen in Figure 5 in regions where the kernel crosses the boundaries):

$$\begin{array}{l}{\mathit{min}}_{{\frac{\nabla {\mathrm{B}}_{1,\mathrm{ref}}^{-}}{{\mathrm{B}}_{1,\mathrm{ref}}^{-}}}_{\mathit{DN}}}{\Vert M_{\mathit{EP}}\left({\frac{\nabla {\mathrm{B}}_{1,\mathrm{ref}}^{-}}{{\mathrm{B}}_{1,\mathrm{ref}}^{-}}}_{\mathit{DN}}-\frac{\nabla {\mathrm{B}}_{1,\mathrm{ref}}^{-}}{{\mathrm{B}}_{1,\mathrm{ref}}^{-}}\right)\Vert }_2^2\\ +\mathrm{\alpha }{\Vert M_{\mathit{EP}}\nabla \left({\frac{\nabla {\mathrm{B}}_{1,\mathrm{ref}}^{-}}{{\mathrm{B}}_{1,\mathrm{ref}}^{-}}}_{\mathit{DN}}·\frac{\nabla {\mathrm{B}}_{1,\mathrm{ref}}^{-}}{{\mathrm{B}}_{1,\mathrm{ref}}^{-}}+\nabla ·{\frac{\nabla {\mathrm{B}}_{1,\mathrm{ref}}^{-}}{{\mathrm{B}}_{1,\mathrm{ref}}^{-}}}_{\mathit{DN}}\right)\Vert }_2^2\end{array}$$ [7]

Here α is a regularization parameter that forces the denoised $\frac{\nabla {\mathrm{B}}_{1,\mathrm{ref}}^{-}}{{\mathrm{B}}_{1,\mathrm{ref}}^{-}}$ to produce piecewise smooth electrical properties (note that the term inside the gradient of regularization terms is simply the modified Helmholtz Eq. [4]). Given that any acquisition pulse sequence can be used for the SAEP method, it might be of interest to use sequences that easily allow segmentation of the brain (37), guaranteeing that the binary mask M_EP is perfectly co-registered with the sensitivity maps needed to calculate the EP.

CONCLUSIONS

We conclude that it is possible to calculate electrical property maps from any single volumetric measurement without the need to measure ${\mathrm{B}}_1^{+}$ maps (whose accuracy and precision is limited) (20,28,29), or rely on specific coil/subject setups (1,20,28,29) provided that 4 or more coils are available for reception and without the need to correct for effects arising from frequency inhomogeneities or eddy currents (29).

APPENDIX

A – Derivation of Equations 3

Equation [3] can be derived by defining the second derivative of the relative receive field as a function of the absolute receive field:

$$\begin{array}{l}{\nabla }^2{{\mathrm{B}}^{\prime }}_{1,\mathrm{i},\mathrm{ref}}^{-}=\nabla ·(\nabla {{\mathrm{B}}^{\prime }}_{1,\mathrm{i},\mathrm{ref}}^{-})=\nabla ·(\frac{\nabla {\mathrm{B}}_{1,\mathrm{i}}^{-}}{{\mathrm{B}}_{1,\mathrm{ref}}^{-}}-{\mathrm{B}}_{1,\mathrm{i}}^{-}\frac{\nabla {\mathrm{B}}_{1,\mathrm{ref}}^{-}}{{{\mathrm{B}}_{1,\mathrm{ref}}^{-}}^2})\\ =(\frac{{\nabla }^2{\mathrm{B}}_{1,\mathrm{i}}^{-}}{{\mathrm{B}}_{1,\mathrm{ref}}^{-}}-{\mathrm{B}}_{1,\mathrm{i}}^{-}\frac{{\nabla }^2{\mathrm{B}}_{1,\mathrm{ref}}^{-}}{{{\mathrm{B}}_{1,\mathrm{ref}}^{-}}^2})+(-2\frac{\nabla {\mathrm{B}}_{1,\mathrm{i}}^{-}·\nabla {\mathrm{B}}_{1,\mathrm{ref}}^{-}}{{{\mathrm{B}}_{1,\mathrm{ref}}^{-}}^2}+2{\mathrm{B}}_{1,\mathrm{i}}^{-}\frac{\nabla {\mathrm{B}}_{1,\mathrm{ref}}^{-}·\nabla {\mathrm{B}}_{1,\mathrm{ref}}^{-}}{{{\mathrm{B}}_{1,\mathrm{ref}}^{-}}^3}).\\ =\frac{{\mathrm{B}}_{1,\mathrm{i}}^{-}}{{\mathrm{B}}_{1,\mathrm{ref}}^{-}}(\frac{{\nabla }^2{\mathrm{B}}_{1,\mathrm{i}}^{-}}{{\mathrm{B}}_{1,\mathrm{i}}^{-}}-\frac{{\nabla }^2{\mathrm{B}}_{1,\mathrm{ref}}^{-}}{{\mathrm{B}}_{1,\mathrm{ref}}^{-}})+2(-\frac{\nabla {\mathrm{B}}_{1,\mathrm{i}}^{-}}{{\mathrm{B}}_{1,\mathrm{ref}}^{-}}+{\mathrm{B}}_{1,\mathrm{i}}^{-}\frac{\nabla {\mathrm{B}}_{1,\mathrm{ref}}^{-}}{{{\mathrm{B}}_{1,\mathrm{ref}}^{-}}^2})·\frac{\nabla {\mathrm{B}}_{1,\mathrm{ref}}^{-}}{{\mathrm{B}}_{1,\mathrm{ref}}^{-}}\end{array}$$ [A1]

Using Eq. [1] and the fact that both fields ( ${\mathrm{B}}_{1,\mathrm{ref}}^{-}$ and ${\mathrm{B}}_{1,\mathrm{i}}^{-}$) experience the same electrical properties, the first term of Eq. [A1] cancels out, and the second term can be rewritten as a gradient of the relative coil sensitivities:

$$\begin{array}{l}{\nabla }^2{{\mathrm{B}}^{\prime }}_{1,\mathrm{i},\mathrm{ref}}^{-}=-2\nabla \left(\frac{{\mathrm{B}}_{1,\mathrm{i}}^{-}}{{\mathrm{B}}_{1,\mathrm{ref}}^{-}}\right)·\frac{\nabla {\mathrm{B}}_{1,\mathrm{ref}}^{-}}{{\mathrm{B}}_{1,\mathrm{ref}}^{-}}\\ =-2\left(\nabla {{\mathrm{B}}^{\prime }}_{1,\mathrm{i},\mathrm{ref}}^{-}\right)·\frac{\nabla {\mathrm{B}}_{1,\mathrm{ref}}^{-}}{{\mathrm{B}}_{1,\mathrm{ref}}^{-}}.\end{array}$$ [A2]

B – Derivation of Equation [4]

Equation [4] can be derived by noting that the Laplacian is by definition the divergence of a gradient and that $\nabla {\mathrm{B}}_{1,\mathrm{ref}}^{-}={\mathrm{B}}_{1,\mathrm{ref}}^{-}\frac{\nabla {\mathrm{B}}_{1,\mathrm{ref}}^{-}}{{\mathrm{B}}_{1,\mathrm{ref}}^{-}}$:

$$\begin{array}{l}\frac{{\nabla }^2{\mathrm{B}}_{1,\mathrm{ref}}^{-}}{{\mathrm{B}}_{1,\mathrm{ref}}^{-}}=\frac{\nabla ·\nabla {\mathrm{B}}_{1,\mathrm{ref}}^{-}}{{\mathrm{B}}_{1,\mathrm{ref}}^{-}}=\frac{\nabla ·\left({\mathrm{B}}_{1,\mathrm{ref}}^{-}\frac{\nabla {\mathrm{B}}_{1,\mathrm{ref}}^{-}}{{\mathrm{B}}_{1,\mathrm{ref}}^{-}}\right)}{{\mathrm{B}}_{1,\mathrm{ref}}^{-}}\\ =\frac{\nabla {\mathrm{B}}_{1,\mathrm{ref}}^{-}}{{\mathrm{B}}_{1,\mathrm{ref}}^{-}}·\frac{\nabla {\mathrm{B}}_{1,\mathrm{ref}}^{-}}{{\mathrm{B}}_{1,\mathrm{ref}}^{-}}+\nabla ·\left(\frac{\nabla {\mathrm{B}}_{1,\mathrm{ref}}^{-}}{{\mathrm{B}}_{1,\mathrm{ref}}^{-}}\right)\end{array}$$ [A3]

C – Limitations of Transmit field B1 Map and CP Coil Based Electrical Property Mapping Methods

To support the claims made throughout the study regarding the limitations of conventional Electrical Property Mapping Methods based on transmit B₁ field mapping and assumptions about the phase relationship between the receive and transmit RF phase at high fields, the following electrical calculations were performed. Using the simulations presented in the Methods section, a CP mode was built by adding a phase shift to each channel so that the ${\mathrm{B}}_1^{+}$ field of all 16 channels would be in phase at the center of the phantom. The same phases between the different channels was used to create the ${\mathrm{B}}_1^{-}$ CP field.

In a first reconstruction it was assumed that the complex transmit ${\mathrm{B}}_1^{+}$ field could be measured but that the method used introduced a small bias in the quantification of its magnitude. This can be the case in some methods due to, for example, different point spread function of the readouts (24,26,38); spatially varying frequency shifts (27); or deviations from the assumed average T₁ value of the sample (24). In the simulations shown in Figure 7, a sinusoidal deviation of the measured amplitude of transmit field was introduced (see Figure 7a). This deviation was limited to 3% of the nominal ${\mathrm{B}}_1^{+}$ amplitude.

FIG. 7.

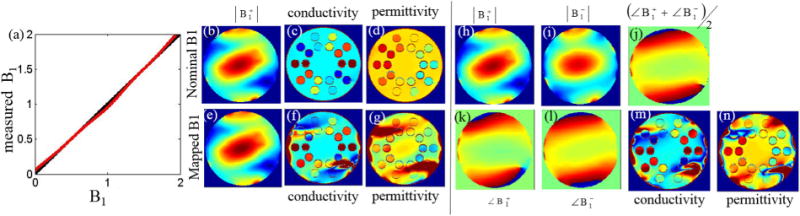
a: Plot of the measured ${\mathrm{B}}_1^{+}$ versus the real ${\mathrm{B}}_1^{+}$ values in the ideal case (black line) and in the presence of a 3% sinusoidal bias (red line). Nominal and Biased CP ${\mathrm{B}}_1^{+}$ mode (b,e) and the corresponding conductivity (c,f) and permittivity (d,g) maps calculated by solving the Helmholtz equation (Eq. [1]). h–l: Magnitude (h,i) and phase (k,l) of the transmit (h,k) and receive (i,l) CP mode and calculated transcieve phase (j). Conductivity (m) and permittivity (n) maps calculated by applying the Helmholtz equation to transmit field with the correctly measured amplitude (h) but assuming the transceiver phase (j).

In the second reconstruction, given the simulated ${\mathrm{B}}_1^{+}$ and ${\mathrm{B}}_1^{-}$ field, it was assumed that the transmit phase measured would be the sum of the transmit and receive phases divided by two (20,28,29).

In the bottom panel of Figure 7, it can be seen that a small variation (see Figure 7a red line), that is visually not discernible in the measured ${\mathrm{B}}_1^{+}$ map (see Figure 7e versus Figure 7b – ground truth), has large implications in the quantitative electrical property maps (Figs. 7f,g) that are not restricted to the regions of low transmit field, but that can be seen in all the compartments. The deviations of the electrical property maps from the ground truth (Figs. 7c and 7d) in the center of the phantom are smaller for the permittivity than for the conductivity as expected from the previous reports (28,29,39), which have noted that the conductivity in regions of small variations of ${\mathrm{B}}_1^{+}$ amplitude is primarily determined by the phase of the transmit field (which was not manipulated in this simulation) and not by the magnitude of the ${\mathrm{B}}_1^{+}$.

Figure 7i and l shows the amplitude and phase of the receive CP field, which, despite the phantom having a close to cylindrical symmetry and showing some similar overall patterns to the transmit field (see Figures 7h,k) has distinguishable features. The computed transceive phase divided by two is shown in Figure 7j. When calculating the conductivity and permittivity maps from a combination of the measured transmit amplitude (assuming a perfect B1 map – Fig. 7h) and transceive phase (Fig. 7j), the resulting electrical properties (Figs. 7m,n) significantly deviate from the maps computed if the transmit phase was known (Figures 7c,d).