Velocity alignment leads to high persistence in confined cells

Abstract

We study a simple model of a crawling cell as an active Brownian particle that aligns its polarity direction to its velocity, a mechanism that has been previously proposed to describe collective cell migration. We show that under quasi-one-dimensional confinement, velocity-aligning cells transition from a random-walk motility to a highly persistent crawling motion. This problem can be mapped to a classical diffusive escape over a barrier and analytically solved to determine the cell’s orientation distribution and repolarization rate. The cell’s repolarization time increases exponentially as the strength of the velocity alignment is increased. We relate this behavior to experiments showing that cells confined in microchannels and on adhesive micropatterns develop strong directional migration, and describe collective motion of quasi-one-dimensionally confined cells.

In traveling through the body, cells move through profoundly complex environments, interacting with nearby cells and extracellular matrix. By contrast, experiments on cell motility primarily study cells on two-dimensional homogeneous substrates. Understanding how cells alter their motility in response to confinement is an ongoing and crucial problem in biology that may be relevant to cancer cell migration, where cancer cells may follow preexisting structures or push through tissue [1, 2]. Confinement of cells may determine invasiveness [3] as well as changing cell motility modes [4]. To study the effects of confinement and adhesion in cell motility, controllable in vitro environments have been developed, including adhesive micropatterned substrates [5–7] and microchannels [2, 8, 9]. Cells in confinement can have strikingly different motion than on a substrate, including periodic migration [7, 10]. The presence of this confinement also can change the persistence of the cell’s direction: many cell types undergo persistent directed migration on narrow micropatterned adhesive stripes [5] and within small microchannels [2], even though they undergo primarily random motility on two-dimensional substrates.

Crawling cells under confinement are also an important example of how boundaries can lead to new and interesting behavior in the dynamics of active matter [11]. The effects of boundaries on active particles are still only beginning to be understood; new behaviors that arise include spontaneous circulation [12], rectification of motion [13], driving of gears [14], aggregation at boundaries [15–17], and other complex dynamics [18–21].

Recently, “velocity aligning” (VA) active particles and related models have been proposed to explain the origins of collective motility, including keratocytes flocking [22], streaming in endothelial monolayers [23], active jamming [24], wound healing [25], and many other collective cell motions [26–28]. These models can create collective motility even though a cell only “senses” its own velocity, not its neighbors’ orientation. In this work, we study a minimal velocity-aligning model of a cell as an active Brownian particle that aligns its polarity (direction of pushing) with its velocity; this model was introduced by Szabo et al. [22]. We show analytically that the combination of strong confinement and velocity alignment leads to a significant increase in persistence of cell motion. Surprisingly, the orientation of an active velocity-aligning cell under confinement can be mapped to a classical diffusion-over-a-barrier problem. This simple model demonstrates that physical confinement can dramatically alter a cell’s type of motility without requiring a different mechanism for free- and confined- cell migration.

In the overdamped active Brownian particle model we study here [22], the equations of motion for a velocity-aligning cell’s position r̃ = (x̃, ỹ) and polarity p̂ = (cos θ, sin θ) are ∂_t̃r̃ = υ₀p̂ + μF and ${\partial }_{\tilde{t}}\theta =\frac{1}{T}\text{arcsin}[{(\hat{\mathbf{p}}\times \hat{\mathbf{v}})}_z]+\zeta (\tilde{t})$, where v̂ = (∂_t̃r̃)/|∂_t̃r̃| is the unit vector of the cell’s velocity, μ is the cell’s mobility, υ₀ is the cell’s speed in the absence of external force, and F the external force. The Langevin noise ζ(t̃) has variance 〈ζ(t̃)ζ(t̃′)〉 = 2P⁻¹δ(t̃ − t̃′), where P is the cell’s angular persistence time. The aligning term T⁻¹arcsin [(p̂ × v̂)_z] = T⁻¹arcsin [cos θυ̂_y − sin θυ̂_x] makes the polarity direction θ relax to the velocity direction, θ_v = arg v with a time scale T; it is a periodic extension of −T⁻¹ (θ − θ_v) [24]. We describe a single velocity-aligning cell confined within a harmonic potential of stiffness k_s in the×direction. We rescale lengths and times as t = t̃/P and x = x̃/(υ₀P). In these units,

$${\partial }_t\mathbf{r}=\hat{\mathbf{p}}-\kappa x\hat{\mathbf{x}}$$ (1)

$${\partial }_t\theta =\frac{1}{\tau }\text{arcsin}[{(\hat{\mathbf{p}}\times \hat{\mathbf{v}})}_z]+\xi (t).$$ (2)

κ is the unitless measure of the strength of the cell’s confinement, κ = μk_sP. τ = T/P is the ratio of the time required to align the cell’s polarity to its velocity to the time scale for the cell’s orientation to randomly reorient; a smaller value of τ implies a more effective aligning mechanism. The Gaussian Langevin noise ξ(t) has zero mean and variance 〈ξ(t)ξ(t′)〉 = 2δ(t − t′).

Looking at the x component of our position equation, ∂_tx = cos θ − κx, we can solve to find x(t) as a functional of the angle θ(t), $x(t)={\int }_{-\infty }^{t}dt\prime e^{-\kappa (t-t\prime )}\text{cos}\theta (t\prime )$. We are modeling strongly confined cells (Fig. 1), and therefore assume κ ≫ 1. In this limit, $e^{-\kappa (t-t\prime )}\to \frac{1}{\kappa }\delta (t-t\prime )$ and we find κx(t) ≈ cos θ(t), i.e. the cell quickly crawls to its stall point where υ_x = 0. We make the approximation that υ_x = 0 and thus $\hat{\mathbf{v}}=\frac{\text{sin}\theta }{\left|\text{sin}\theta \right|}ŷ$. Our equation for θ thus becomes ${\partial }_t\theta =\frac{1}{\tau }\text{arcsin}\left[\frac{\text{cos}\theta \text{sin}\theta }{\left|\text{sin}\theta \right|}\right]+\xi (t)$. Using standard trigonometric identities, we can show that for θ ∈ [−π, π], arcsin $\text{arcsin}\left[\frac{\text{cos}\theta \text{sin}\theta }{\left|\text{sin}\theta \right|}\right]=-{\partial }_{\theta }W(\theta )$, where

$$W(\theta )=-\frac{\pi }{2}|\theta |+\frac{1}{2}{\theta }^2$$ (3)

For strong confinement, θ thus follows

$${\partial }_t\theta =-{\tau }^{-1}{\partial }_{\theta }W(\theta )+\xi (t)$$ (4)

where now we interpret W(θ) as the periodic extension of its definition in Eq. 3.

FIG. 1.

A: Velocity-aligning cell model originally proposed by Szabo et al. [22]. The cell is propelled along its internal polarity p̂; this polarity aligns itself to the direction of the cell’s velocity v: The cell moves under the combination of its motility and the force from confinement (Eqs. 1–2). B: Fibroblast on narrow adhesive microstripe; adapted from [5]. C: Human breast carcinoma in microchannel; adapted from [8]. Dashed lines indicate the stall point x = ±κ⁻¹ that the cell cannot cross.

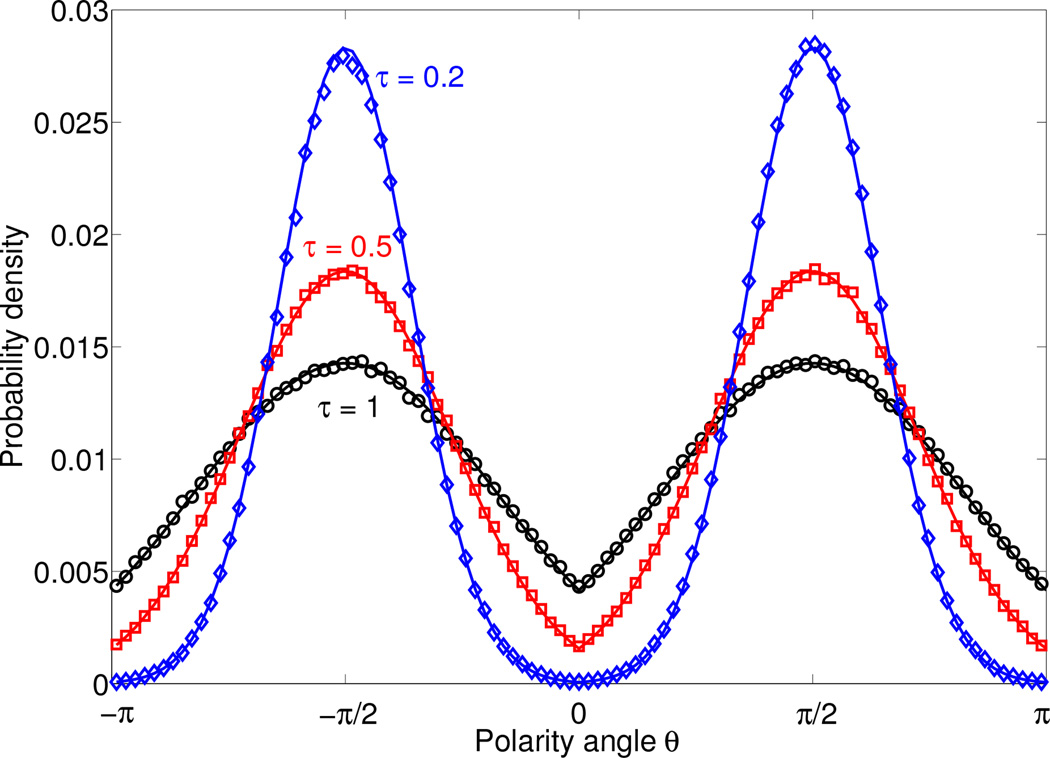
Eq. 4 provides us with a great deal of insight into the dynamics of the cell’s polarity θ: it is precisely the dynamics of a Brownian particle with unit temperature diffusing passively in a potential well τ⁻¹W(θ). The potential W(θ) has minima at ±π/2, when the cell polarity is aligned in the ±ŷ direction (along the channel). The velocity alignment parameter τ acts as an effective temperature: as τ → 0, the polarity of the cell becomes increasingly localized to the minima of W(θ), e.g. the ±ŷ directions. The distribution of angles (modulo 2π) is just the standard Boltzmann distribution, p(θ) ~ exp [−W(θ)/τ]. We show these distributions, and corresponding ones computed from direct Brownian dynamics simulation of Eqs. 1–2 in Fig. 2.

FIG. 2.

Probability distribution of cell polarity angles θ (modulo 2π) are given by the Boltzmann-like distribution p(θ) ~ exp [−W(θ)/τ]. Symbols are determined from Brownian dynamics simulations of our full model (Eqs. 1–2), lines are the Boltzmann distribution. Simulations performed with κ = 1000, Δt = 10⁻⁴, and a simulation time of 10⁶.

We can use Eq. 4 to compute the rate of spontaneous repolarization of our cells. In order for a cell to change its direction θ from π/2 to −π/2, it must cross the barrier at θ = 0. This rate will decrease strongly with decreasing τ, leading to increased persistence of the cell motion. Determining the rate of escape over a barrier is a classic problem; in one dimension, the mean first-passage times can be found exactly up to quadrature via the Smoluchowski equation corresponding to Eq. 4 and its adjoint [29–31]. The mean first passage time from θ = π/2 to absorbing boundaries at θ = 0, π is given by

$$t_{\mathrm{M}\mathrm{F}\mathrm{P}\mathrm{T}}=\frac{1}{2}{\int }_0^{\pi }dz{e}^{W(z)/\tau }{\int }_0^{z}dy{e}^{-W(y)/\tau }-{\int }_0^{\pi /2}dz{e}^{W(z)/\tau }{\int }_0^{z}dy{e}^{-W(y)/\tau },$$ (5)

using the symmetry of W(z) about π/2. This integral may be evaluated exactly using Mathematica,

$$t_{\mathrm{M}\mathrm{F}\mathrm{P}\mathrm{T}}=\frac{{\pi }^2}{8}{}_2{F}_2(1,1;\frac{3}{2},2;\frac{{\pi }^2}{8\tau })$$ (6)

where ₂F₂(a₁, a₂; b₁, b₂; z) is the generalized hypergeometric function. A more convenient and intuitive form that is asymptotically correct in the limit of τ → 0 can be found by applying the method of steepest descent to the integrals in Eq. 5,

$$t_{\mathrm{M}\mathrm{F}\mathrm{P}\mathrm{T}}\approx \sqrt{\frac{2}{\pi }}{\tau }^{3/2}\text{exp}\left(\frac{{\pi }^2}{8\tau }\right)$$ (7)

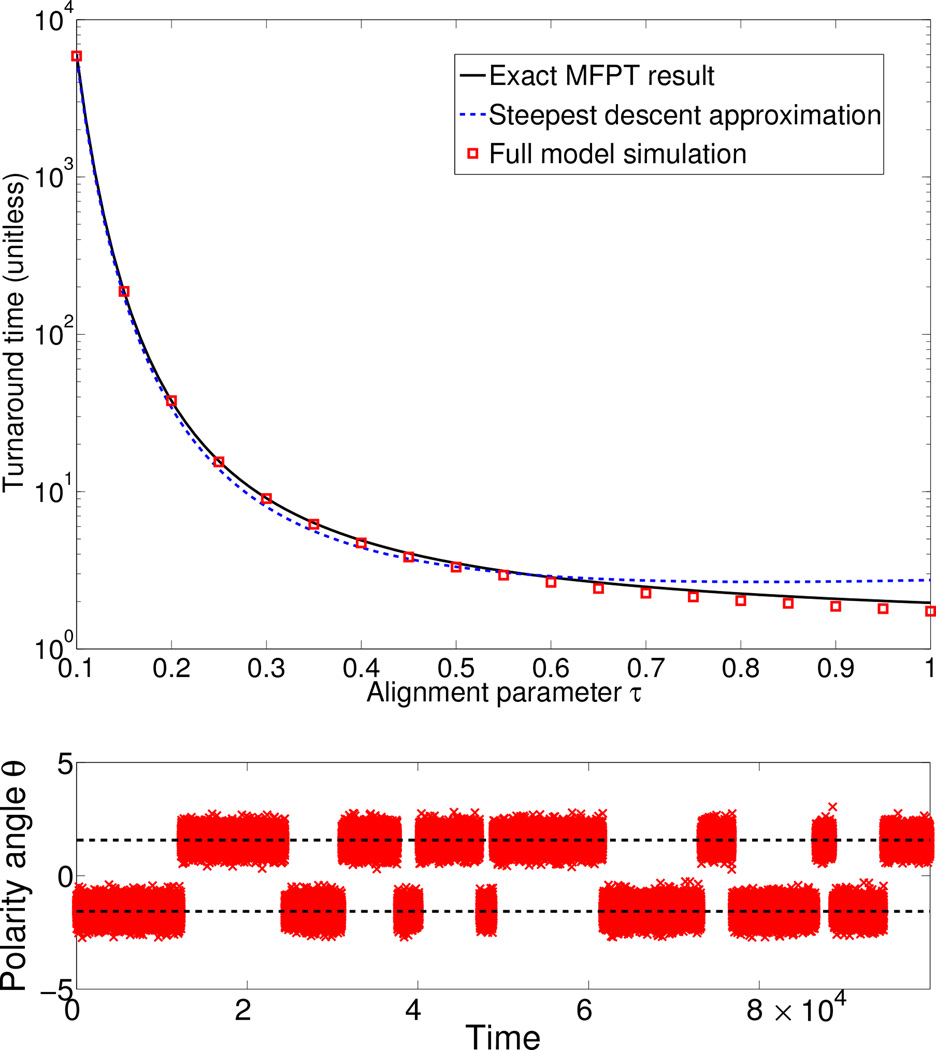
As expected from our analogy with diffusion over a barrier, the time to repolarize increases exponentially in 1/τ: the faster the cell aligns to its local velocity, the longer it takes to turn around. We compare Eq. 6 and Eq. 7 with mean first passage times (escape rates) observed in Brownian dynamics simulations of Eqs. 1–2 in Fig. 3, and find excellent agreement [32, 33].

FIG. 3.

When the alignment parameter τ is small, the time required for the cell to repolarize becomes extremely large. TOP: Repolarization times from simulation of Eqs. 1–2 (symbols) and theory; MFPT result is Eq. 5, steepest-descent result is Eq. 7. BOTTOM: Typical time trace for θ (modulo 2π) for τ = 0.1. Dashed lines indicate ±π/2. Simulations performed with κ = 1000, Δt = 10⁻⁴, and a simulation time of 10⁶.

While our MFPT theory very accurately predicts the Brownian dynamics simulation, there is some discrepancy at large values of τ. Here, the MFPT theory overestimates the time required to escape the potential well. This occurs because we have assumed that the escape rate for the entire well is effectively the same as the escape rate for the center, π/2. As τ becomes larger, this assumption begins to break down [32].

In the strong-confinement limit κ ≫ 1, the only controlling parameter for our model is τ. Can we estimate τ from experimental data? To determine τ from Eq. 6, we need to know 1) the rate of spontaneous reversals, and 2) the persistence time P that sets our unit of time. Desai et al. [34] have recently measured the rate of spontaneous reversal of NRK-52E rat epithelial kidney cells on micropatterned adhesive substrates, finding a rate of 0.08 ± 0.05 reversals per hour. The characteristic persistence time P for this system has not been measured, but we can estimate it. For a single cell without confinement (κ = 0), the alignment term of our model vanishes, as v̂ = p̂, and the Szabo model reduces to a generic self-propelled particle model with velocity-velocity correlation function (in dimensional units), $\langle \tilde{\mathbf{v}}(\tilde{t})·\tilde{\mathbf{v}}(0)\rangle ={\upsilon }_0^2{e}^{-\tilde{t}/P}$ [35, 36]. This form and the corresponding result for the mean-squared displacement have historically been used to analyze cell motion [37–40]. Persistence times range from tens of seconds (for neutrophils [40]) to the order of hours (fibroblasts [37] and endothelial cells [39]). Based on this information, and the trajectories of unconfined NRK-52E cells shown in [34], we estimate P ≈ 1 hour. Using this estimate, we fit to k_reversal = (2t_MFPTP)⁻¹, where t_MFPT is given by Eq. 6 [33]. We find τ ≈ 0.3 (i.e. T ≈ 0.3 hr). This is a measurement of the cell’s internal memory as well as the strength of cell-cell alignment in collective motility.

How does the increased persistence time alter the cell’s dispersal? For an unconfined cell, the mean-squared displacement increases ballistically as 〈|Δr|²〉 ~ t² at short times. At longer times, reorientation leads to a diffusive motion, 〈|Δr|²〉 ~ t [35]. We show in Fig. 4 the mean-squared displacement of a cell under increasing confinement κ. Interestingly, increasing κ changes cell dispersal non-monotonically. The presence of a nonzero κ significantly decreases the displacement of the cell (κ = 1 in Fig. 4, as confinement prevents the cell from traveling beyond x = 1/κ. As κ is increased, the cell’s persistence increases markedly, as studied above. The cell then maintains a steady crawling motion for much longer without reorienting, leading to an extended period of ballistic motion and a larger dispersal (Fig. 4). This mean-squared displacement begins to saturate as we reach the strong confinement limit for κ > 100.

FIG. 4.

Unitless mean-squared displacements 〈|Δr|²〉 of a cell from simulation of Eqs. 1–2 with τ = 0.3 and varying values of κ. The initial increase of κ from zero to one decreases the dispersal of the cell, due to its confinement. However, for larger values of κ, the confinement-induced persistence ensures that the cell persists in ballistic motion for a longer time before reorienting, increasing the cell dispersal.

Collective motion emerges in a simple extension of our model to multiple cells in confinement. We simulate multiple velocity-aligning cells, interacting only by a short-range repulsion force. In unitless variables, the force between cells i and j is F_ij = −κ_cell(2R − |r_ij|)Θ(2R − |r_ij|)r̂_ij, where r_ij = r_j − r_i, R the cell radius, and Θ is the Heaviside step function. As noted by Henkes et al., [24], simple repulsive interactions are sufficient to generate collective motion. We find trains of cells as observed in Desai et al. [34] (Fig. 5). For τ = 0.1, all cells quickly align into a single direction, and very rarely collectively reverse (observed once in a simulation of unitless time 10⁴). For the experimentally estimated value of τ = 0.3, we see occasional reversals of trains, generally consistent with the results of [34]. However, for τ = 1, no persistent collective motions occur and trains are transient. These results are similar to the observations of [34], but have an important caveat. Our simulations predict that cells reverse at a physical barrier; those studied in [34] do not. Our model may therefore be more appropriate for fibroblasts as studied in [5], which are observed to reverse at micropattern ends; we primarily study the results of Desai et al. because they have quantified the spontaneous repolarization rate.

FIG. 5.

Velocity-aligning cells with cell-cell repulsion develop “trains” consistent with [34]. TOP: representative snapshots of trains of cells when τ = 0.3; circles represent cell size while arrows represent cell polarity p̂. Each snapshot is separated by a unitless time of 5 (e.g. 5 hours if P = 1 hour). BOTTOM: Positions of cells are plotted over time for τ = 0.1, 0.3, 1. Trains are highly persistent for τ = 0.1, occasionally reverse for τ = 0.3, and are only transient if τ = 1. In this simulation, 25 cells of radius R = 1 are confined in a periodic system of length L = 100. The confinement strength κ = 1000, and the cell-cell repulsion is κ_cell = 100.

Our results show that in a velocity-aligning model, the increase in persistence time of a strongly confined cell and the interactions driving collective cell motility are intimately related. Balzer et al. have recently shown that human breast carcinoma (MDA-MB-231) is highly persistent in a confined channel, but that this persistence can be disrupted by interfering with microtubule polymerization or depolymerization by application of colchicine or paclitaxel (Taxol) [8]. This raises an interesting question: do Taxol and colchicine disrupt collective cell migration? Our model combined with the data of Balzer et al. [8] suggests that Taxol and colchicine would have similar effects on collective migration - even though they have opposing effects on the stability of microtubules. The idea that velocity alignment may be linked with microtubule dynamics is perhaps not surprising, given the known roles of microtubules in cell polarity [41].

While we have worked with the simplest possible model, our results may be extended to more complex cellular dynamics and potentially used to relate single-cell behavior under strong confinement with cell-cell interactions. To do this, we may have to generalize some aspects of this model. Experimental studies tracking cell motion have shown that velocity-velocity correlations have two distinct time scales, rather than being single-exponential as we have assumed here [38]; this feature may be added by adding a stochastic process corresponding to the desired speed of the cell varying, replacing υ₀ with υ(t) [35]. In our constant-speed model, υ₀ only rescales the lengths involved; if υ(t) does not frequently drop to zero, we expect the varying velocity to only affect our results minimally. We argue that the details of the confining potential are relatively unimportant; simulations with strong hard-wall confinement are consistent with Eq. 5 [32].

In this paper, we have shown that even in a very simple model, cell motility in confinement can take on a profoundly different character than on a two-dimensional substrate, without invoking different mechanisms for free- and confined- cell motility [42]. Our results may explain the origin of large persistence times experimentally observed for confined cells. We believe that these results may be useful as a baseline model for the analysis of cell crawling in confinement, as well as for making connections between single- and collective- cell motility. In particular, our technique provides an in principle straightforward way to determine the velocity-alignment timescale that is important for collective cell motion [22–25, 27] by the analysis of single-cell trajectories under strong confinement. This allows an interesting test of these minimal models of collective cell motions.