Abstract
There are several methods for conducting interfacial partitioning tracer tests to measure air-water interfacial area in porous media. One such approach is the mass balance surfactant tracer method. An advantage of the mass-balance method compared to other tracer-based methods is that a single test can produce multiple interfacial area measurements over a wide range of water saturations. The mass-balance method has been used to date only for glass beads or treated quartz sand. The purpose of this research is to investigate the effectiveness and implementability of the mass-balance method for application to more complex porous media. The results indicate that interfacial areas measured with the mass-balance method are consistent with values obtained with the miscible-displacement method. This includes results for a soil, for which solid-phase adsorption was a significant component of total tracer retention.
1. INTRODUCTION
There are multiple disciplines that require an understanding of fluid flow in multiphase systems. The need for considering fluid-fluid interfacial areas when characterizing and simulating fluid flow is well established (e.g., Skopp 1985; Hassanizadeh and Gray 1993; Gvirtzman and Roberts, 1991; Reeves and Celia 1996; Celia et al. 1998; Kawanishi et al., 1998). There are two primary methods available to measure fluid-fluid interfacial areas for porous media systems: imaging methods (e.g., microtomography) and interfacial partitioning tracer tests (IPTT). The latter method is the focus herein.
There are several alternative approaches available to implement an interfacial partitioning tracer test to specifically measure air-water interfacial area. One approach that has been used by several investigators is termed the mass balance surfactant tracer method, or mass-balance method for short (e.g., Schaefer et al., 2000; Anwar et al., 2000, 2001). For this method, a surfactant solution is introduced into a column packed with a selected porous medium. The test apparatus is then manipulated to allow drainage or imbibition, which generates unsaturated conditions for most of the column. The surfactant (interfacial) tracer will partition to the air-water interfaces present. Monitoring of surfactant concentrations in solution, along with measurement of tracer masses obtained from extraction of porous-medium samples collected along the column length provide a means to determine the surfactant load associated with the interfacial domain. These values are then used to calculate the interfacial areas, under assumptions of monolayer coverage.
An advantage of the mass-balance method compared to other IPTT methods is that a single test can produce multiple interfacial area measurements over a wide range of water saturations. In contrast, each test for other IPTT methods produces an interfacial-area measurement for a single water saturation. Thus, the mass-balance method can save a significant amount of experiment time. The mass-balance method has been used to date only for glass beads or for simple quartz sands that have been treated to remove associated organic matter. The purpose of this research is to investigate the effectiveness and implementability of the mass-balance method for application to more complex porous media such as natural soils.
2. MATERIALS AND METHODS
2.1 Materials
Sodium dodecylbenzene sulfonate (SDBS) (>95% purity, Tokyo Kasei Kogyo, Japan) was used as the partitioning tracer. The aqueous solution comprised SDBS (35 mg/L) and 0.01 M NaCl. The SDBS concentration is well below the critical micelle concentration of 414 mg/L. The interfacial tension function for SDBS was measured to determine the interfacial partition (adsorption) coefficient, Ki. A series of SDBS solutions was prepared in 0.01 M of NaCl, ranging between 15–105 mg/L. The surface tension was measured by a Surface Tensiomat (Fisher Scientific, model 21) using the ring method. The ring method determines the force required to detach a wire loop (i.e. ring) from the surface of a liquid (Adamson, 1982). The calculated Ki value is 2.99×10−3 cm for the 35 mg/L concentration used for the tracer tests.
Two porous media were used in this study. Vinton soil (sandy, mixed thermic Typic Torrifluvent), collected locally in Tucson, AZ., and a 45/50 mesh quartz sand (Accusand). Vinton soil was sieved to remove the fraction larger than 2 mm. The sand was not treated in any manner to remove naturally occurring organic or inorganic components. Relevant properties of the porous media are presented in Table 1.
Table 1.
Relevant physical properties of the porous media
| Medium | Sand | Silt | Clay | Median diameter | Uniformity coefficient Ua | Bulk density ρb | Porosity n | Ksat |
|---|---|---|---|---|---|---|---|---|
| ————%——— | (mm) | (--) | (g/cm3) | (--) | (cm/min) | |||
| Vinton | 97 | 1.8 | 1.2 | 0.23 | 2.4 | 1.50 | 0.376 | 0.2 |
| Sand | 100 | 0 | 0 | 0.35 | 1.1 | 1.65 | 0.326 | 1.3 |
U = (d60/d10).
2.2 Tracer Test Methods
An acrylic column composed of 20 stackable rings, 1.5 cm in height and 2.8 cm in diameter, was used for the study. The vertically placed column was packed with sand or soil, and then saturated with the SDBS solution using a recirculation system based on Anwar et al. (2000). The top of the column was open to the air. The bottom ring contained a porous plate and a hydrophilic membrane, and was connected to the solution reservoir. An initial flow rate of approximately 20 ml/min was used initially to equilibrate the packed column to the solution. The flow rate was reduced gradually in small increments of 0.5 ml/min to a final flow rate of approximately 2 ml/min, to promote drainage. The column was then maintained in recirculation mode for 7 (sand) or 14 (soil) days after drainage to promote attainment of an equilibrium distribution of SDBS. Replicate columns were used for the sand and triplicate for the soil. The data presented represent the composite of all experiments.
After the designated time, each ring was removed from the column and placed into a separate glass beaker and weighed. Each sample was then extracted using 2-d propanol following the procedure used by Schaefer et al. (2000). The samples were sealed and placed on a shaker table for 3–4 hours. Aliquots of the supernatant were analyzed for SDBS concentration. The concentration of SDBS in solution was also measured. SDBS concentrations were measured using a UV-Vis Spectrophotometer (Shimadzu model 1601) at 223 nm wavelength. After extraction, the porous-medium samples were dried in an oven to determine dry soil weight and water saturation.
2.3 Data Analysis
The total mass of SDBS in the system (MT) is the sum of the mass of tracer in solution (Mw), the mass of tracer sorbed by the porous media (Ms-w), and the mass of tracer accumulated at the air-water interface (Ma-w):
| (1) |
where subscripts w, a, s denote water, air, and solid phase respectively. It is assumed that the surfactant does not partition into the non-wetting phase (air). The surface excess Γ (mol/cm2) is related to aqueous phase concentration (C) using the Gibbs equation (e.g., Adamson 1982):
| (2) |
where Ki represents the interfacial partition (adsorption) coefficient, γ is the surface tension (dyn/cm), C represents the aqueous phase concentration (mol/cm3), and R is the gas constant (erg/mol ° K). For adsorption at the air-water interface, the mass loading is related to the magnitude of the air-water interfacial area, aa-w (cm2):
| (3) |
The total mass of SDBS for each ring (MT) is the mass of SDBS extracted from each individual ring. The final aqueous SDBS concentration provides, along with the water saturations, the means to determine the mass of SDBS in solution present in each ring (Mw). The mass sorbed by the solids (Ms-w) is obtained from the saturated (bottom) ring. If the ring is saturated, it follows that there is no air-water interface present in the system. Thus, the difference between MT and Mw provides the mass of surfactant sorbed. The mass accumulated at the air-water interface (Ma-w) is determined by subtracting Mw and Ms-w from MT. The Γ is obtained by using the adsorption isotherm (equation 2), Γ = KiC, where Ki is obtained from the measured surface-tension function. Equation 3 is then used to determine aa-w. The aa-w values are then divided by the volume of the respective porous-medium samples to determine the volume-normalized specific air-water interfacial areas, Aaw (cm−1).
3. RESULTS & DISCUSSION
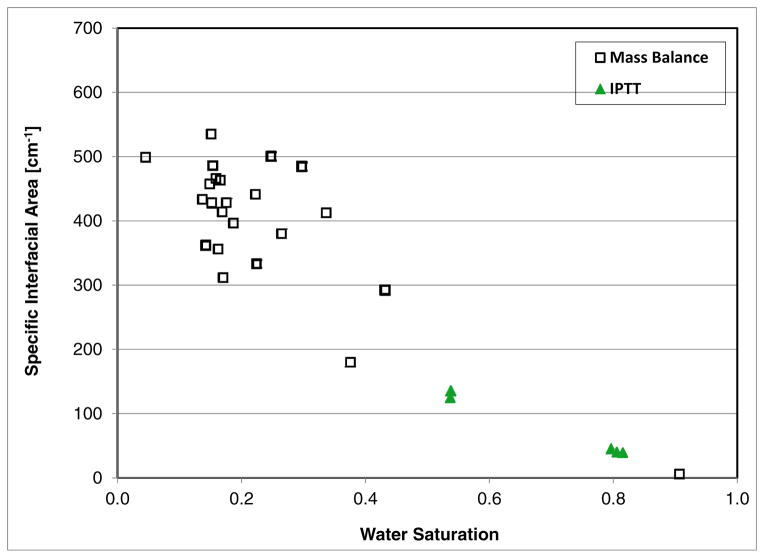
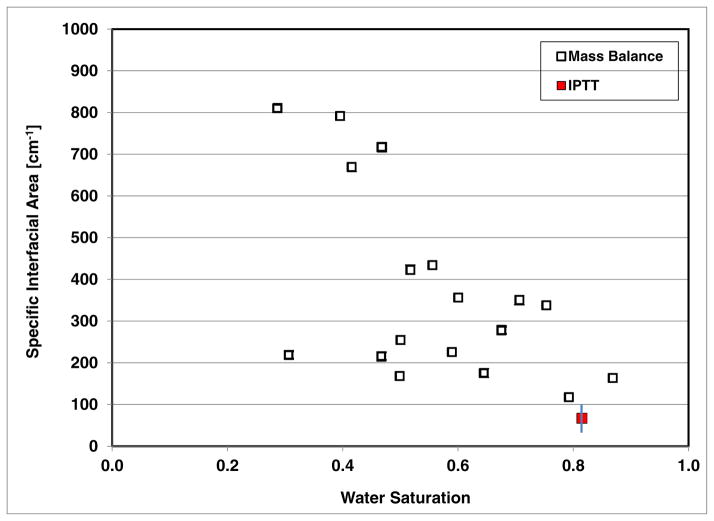
The results of the tests are presented in Figures 1 and 2 for the sand and soil, respectively. The data display a fair amount of scatter, consistent with prior reports (e.g., Anwar et al., 2000; Schaefer et al., 2000). The interfacial areas are generally larger for lower water saturations as would be expected. In addition, the values for a given water saturation are larger for Vinton, which is consistent with the difference in median grain diameter between the two media (Anwar et al., 2000; Costanza-Robinson and Brusseau, 2002; Cho and Annable, 2005; Brusseau et al., 2009, 2010). These results indicate that the method produced values that are consistent with what is expected.
Figure 1.
Air-water interfacial areas measured with the mass-balance method for the sand; also included are literature values measured with the miscible-displacement IPTT method, designated in the legend as “IPTT” (Brusseau et al., 2007, 2015).
Figure 2.
Air-water interfacial areas measured with the mass-balance method for the soil; also included are literature values measured with the miscible-displacement IPTT method, designated in the legend as “IPTT” (Brusseau et al., 2007, 2015).
Another means by which to assess the robustness of the method is to compare SDBS Kd values determined from the saturated rings in the mass-balance tests to independently measured Kd values. The mass-balance test produced a measured Kd for SDBS adsorption of 0.05 for the sand. This is identical to the independently measured value. The mean measured Kd determined from the mass-balance tests for Vinton is 0.51, which is very similar to the independently measured value of 0.5 (Brusseau et al., 2007, 2015). These results indicate that the test procedures (extractions, chemical analysis) produced robust measures of tracer distribution.
Included in Figures 1 and 2 are interfacial areas measured for the respective porous media using the miscible-displacement IPTT method (e.g., Kim et al., 1997; Saripalli et al., 1997; Brusseau et al., 2007, 2015). For this method, miscible-displacement tests are conducted under unsaturated flow conditions using an aqueous tracer solution. The concentrations of the tracers in the column effluent are monitored to construct breakthrough curves, which are used to determine the retardation of the tracer that partitions to the interface relative to that of a non-reactive (non-partitioning) tracer. The magnitude of the retardation corresponds to the magnitude of the interfacial area. The miscible-displacement (MD) IPTT data presented in the figures were previously reported by Brusseau et al. (2007, 2015).
The MD-IPTT values are observed to fall along the curve associated with the mass-balance data for the sand. The MD-IPTT data point for the soil represents the mean of 8 individual test measurements. This value is observed to fall within the range of values obtained with the mass-balance method. These results indicate that the two sets of interfacial areas obtained with the two methods are consistent for both media.
As noted above, prior applications of the mass-balance method used glass beads or treated quartz sand. Issues associated with adsorption of the surfactant by the solids are insignificant for these media, given that adsorption is typically minimal. This was the case for the sand used in this study. Conversely the soil exhibits significant adsorption of SDBS. Thus, solid-phase adsorption was a significant component for the tracer tests conducted for the soil, contributing approximately half of total retention of the tracer. The consistency between the mass-balance and MD-IPTT interfacial areas suggests that the mass-balance method provided reasonable measures of interfacial area for the soil, a system for which solid-phase adsorption was significant.
4. SUMMARY
The objective of this study was to investigate the efficacy of the mass-balance method for measurement of air-water interfacial area in unsaturated natural porous media. The results indicate that interfacial areas measured with the mass-balance method are consistent with values obtained with the miscible-displacement method. This includes the results for the soil, for which solid-phase adsorption was a significant component of total tracer retention.
An advantage of the mass-balance method is the ability to measure multiple interfacial areas for a range of water saturations with a single test. This is anticipated to save time compared to using the miscible-displacement method. For this study, however, the time savings was reduced by the need to extend the equilibration time to 2 weeks for the soil. Another issue observed was that interfacial areas were essentially indeterminate for water saturations higher than approximately 0.9. This is attributed to the small relative magnitudes of Ma-w for samples with small magnitudes of interfacial area. Similar results were reported by Schaefer et al. (2000). Finally, the measurements produced with the mass-balance method, both herein and in the literature, appear to exhibit greater uncertainty compared to the measurements obtained with the MD-IPTT method. A number of factors may contribute to this uncertainty. One possible factor is inter-ring variability in surfactant phase distribution caused by factors other than differences in water saturation (such as inter-ring variability in physical and geochemical properties of the media). Other possible factors include extraction efficiency impacts and the impacts of adsorption of the surfactant by the solids. These factors would be anticipated to be of greater significance for natural media.
Highlights.
The mass-balance method is used to measure air-water interfacial area for two porous media
The interfacial areas are compared to values measured with the MD-IPTT method
Advantages and disadvantages of the mass-balance are discussed
Acknowledgments
This research was funded by the NIEHS Superfund Basic Research Program (Grant # E504940). We thank the reviewers for their comments.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Adamson AW. Physical chemistry of surfaces. 4. xviii. J. Wiley; New York: 1982. p. 664. [Google Scholar]
- Anwar A, Bettahar M, Matsubayashi U. A method for determining air-water interfacial area in variably saturated porous media. J Contam Hydrol J Contam Hydrol. 2000:129–146. [Google Scholar]
- Anwar AHMF. Experimental determination of air-water interfacial area in unsaturated sand medium. New Approaches Characterizing Groundwater Flow; Proceedings. of XXXI IAH Congress; Munich, Germany. September 10–14; 2001. pp. 821–825. [Google Scholar]
- Brusseau ML, Peng S, Schnaar G, Murao A. Measuring air-water interfacial areas with X-ray microtomography and interfacial partitioning tracer tests. Environ Sci Technol. 2007:1956–1961. doi: 10.1021/es061474m. [DOI] [PubMed] [Google Scholar]
- Brusseau ML, Narter M, Schnaar S, Marble J. Measurement and estimation of organic-liquid/water interfacial areas for several natural porous media. Environ Sci Technol. 2009:3619–3625. doi: 10.1021/es8020827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brusseau ML, Narter M, Janousek H. Interfacial Partitioning Tracer Test Measurements of Organic-Liquid/Water Interfacial Areas: Application to Soils and the Influence of Surface Roughness. Environ Sci Technol. 2010:7596–7600. doi: 10.1021/es101312n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brusseau ML, ElOuni A, Araujo JB, Zhong H. Novel methods for measuring air–water interfacial area in unsaturated porous media. Chemosphere. 2015:208–213. doi: 10.1016/j.chemosphere.2015.01.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Celia MA, Gray WG, Montemagno CD, Reeves PC. On the inclusion of interfacial area in models of two-phase flow in porous media. In: Herbert M, Kovar K, editors. IAHS-AISH P. 1998. pp. 81–87. [Google Scholar]
- Cho J, Annable MD. Characterization of pore scale NAPL morphology in homogeneous sands as a function of grain size and NAPL dissolution. Chemosphere. 2005:899–908. doi: 10.1016/j.chemosphere.2005.04.042. [DOI] [PubMed] [Google Scholar]
- Costanza-Robinson MS, Brusseau ML. Air-water interfacial areas in unsaturated soils: Evaluation of interfacial domains. Water Resour Res 2002 [Google Scholar]
- Gvirtzman H, Roberts PV. Pore Scale Spatial-Analysis of 2 Immiscible Fluids in Porous-Media. Water Resour Res. 1991:1165–1176. [Google Scholar]
- Hassanizadeh SM, Gray WG. Toward An Improved Description Of The Physics Of 2-Phase Flow. Adv Water Resour. 1993:53–67. [Google Scholar]
- Kawanishi T, Hayashi Y, Roberts PV, Blunt MJ. Fluid-fluid interfacial area during two and three phase fluid displacement in porous media: a network model study. IAHS-AISH P. 1998;(250):89–96. [Google Scholar]
- Kim H, Rao PSC, Annable MD. Determination of effective air-water interfacial area in partially saturated porous media using surfactant adsorption. Water Resour Res. 1997:2705–2711. [Google Scholar]
- Reeves PC, Celia MA. A functional relationship between capillary pressure, saturation, and interfacial area as revealed by a pore-scale network model. Water Resour Res. 1996:2345–2358. [Google Scholar]
- Saripalli KP, Kim H, Rao PSC, Annable MD. Measurement of specific fluid - Fluid interfacial areas of immiscible fluids in porous media. Environ Sci Technol. 1999:932–936. [Google Scholar]
- Schaefer CE, DiCarlo DA, Blunt MJ. Experimental measurement of air–water interfacial area during gravity drainage and secondary imbibition in porous media. Water Resour Res. 2000:885–890. [Google Scholar]
- Skopp J. Oxygen Uptake and Transport in Soils: Analysis of the Air-water Interfacial Area. Soil Sci Soc Am J. 1985:1327–1331. [Google Scholar]