Modeling Regional Vulnerability to Alzheimer Pathology

Abstract

Latent growth curve (LGC) models estimate change over time in a cohort's serially obtained measurements. We have applied LGC techniques to a spatial distribution of Alzheimer's disease (AD) pathology using autopsy data from 435 participants in the Honolulu-Asia Aging Study. Neurofibrillary tangle (NFT) and neuritic plaques (NP) were distributed across differently ordered sets of anatomical regions. The gradient of spatial change in NP (dNP), was significantly associated with that of NFT (dNFT), but weakly and inversely (r = -0.12, p <0.001). Both dNFT and dNP correlated significantly and inversely with Braak stage. 61% of the variance in Braak stage was explained by dNFT independent of covariates. Only dNFT was significantly associated with longitudinal change in cognition. Only dNP was associated with apolipoprotein (APOE) e4 burden. This is the first application of LGC models to spatially ordered data. The result is a quantification of the inter-individual variation in the inter-regional vulnerability to AD lesions.

1. Introduction

Latent “class” or growth curve (LGC) and growth mixture models (GMM) represent the state of the art in longitudinal data analysis. LGC estimate the trajectory of change over time in a cohort's serially obtained measurements (Willett & Sayer, 1994). GMM can be used to define subsets among a cohort with homogenous trajectory parameters. Through them, it is possible to use intra- and inter-individual change over time as outcome variables or as predictors, e.g., in structural equation models (SEM) (McArdle & Epstein., 1987; Willet & Sayer, 1994). This allows one to assess mediating /moderating effects on longitudinal outcomes. Another valuable feature of LGC models is that measurement error is explicitly assessed, and removed from the latent construct. This can strengthen statistical power and improve model fit.

However, it may also be possible to extend the application of these techniques beyond temporally ordinal datasets, i.e., to measures repeated across spatial dimensions. Particularly useful applications might be in the analysis of neuropathological or neuroimaging data (Royall, 2007). For example, Braak and others have suggested that neurofibrillary tangles (NFT) and Lewy Body lesions propagate transynaptically within neuronal networks (Saper et al., 1985; Pearson & Powell, 1989; Braak & Braak, 1991; Braak et al., 2006). The interconnections of those networks may thus determine the exquisite regional, and even laminar vulnerability of neuronal populations to NFT (Arnold et al., 1991; Armstrong, Carins & Lantos, 2001). These networks can be conceived as an ordinally arranged sequence of anatomical regions along a hierarchical gradient of interregional vulnerability. As such, the three dimensional propagation of neuropathology through the network may be amenable to modeling with LGC and GMM techniques.

If applied to NFT counts, this approach would result in two latent parameters, the network's “intercept” (e.g., the estimated mean NFT count within the first in a hierarchically arranged sequence of anatomical regions that together define the Braak neuropathological hierarchy) and its “slope” (e.g., the mean change in NFT counts across regions, from the most to the least vulnerable in the sequence). Both parameters would have associated estimates of variability about those means, and both linear and non-linear gradients in NFT counts across the network could be independently estimated. These “slope” parameters can be interpreted as representing the network's “vulnerability” to, or alternatively, its resistance against, penetration by the AD process. Biomarkers, genes or other variables could then be tested as determinants of this vulnerability.

If there is significant variability about the estimated mean change in NFT counts across the network, then GMM could be employed to identify homogeneous subgroups within the cohort with significantly different network intercepts and vulnerability gradients. These could be interpreted as subpopulations within the cohort with differing risks of AD pathology. Thus, the variables responsible for those differences could also be identified, in regression models of trajectory class membership. Associating these gradients with longitudinal change in cognitive measures, i.e., in SEM, may eventually allow the direct quantification of cognitive reserve and its related biomarkers. In this paper, we demonstrate the feasibility of this approach using autopsy and clinical data from the Honolulu-Asia Aging Study (HAAS).

2. Methods

2.1 HAAS

Autopsy tissue and clinical data were obtained from HAAS (White et al., 2005). HAAS began in 1991 as an add-on to the Honolulu Heart Program (HHP). It is a longitudinal study of heart disease and stroke established in 1965 with the examination of 8006 Japanese-American men born 1900-1919. Brain autopsy and cognitive exams have been performed continuously since 1991.

2.2 HAAS autopsy material

838 autopsies had been performed prior to May, 2010. These represent approximately 20% of HAAS deaths since 1991. The current analyses are limited to autopsies obtained between1991 and 2001. Microscopic examinations performed since 2001 have been done by a different team of neuropathologists, and have not yet been pooled for common analyses. Complete microscopic data generated by the first team are available in 493. 437 of those with complete microscopic data also have premorbid clinical information related to dementia and neuropsychological test performance. Results presented here are from these 437 decedents. The generalizability of autopsied decedents to the larger HAAS sample has been detailed elsewhere (White et al., 2002).

2.3 Pathological materials

The HAAS pathological methods have been detailed elsewhere (Petrovitch et al., 2001). Brains were fixed by submersion in 10% neutral formalin. Tissue samples were embedded in paraffin. Slides were cut at 8 micron thicknesses and stained as mentioned. Modified Bielschowsky, Gallyas, Hematoxylin and Eosin (H&E), and α-synuclein-stained slides were examined to quantify diffuse plaques (DP), neuritic plaques (NP), neurofibrillary tangle (NFT), cortical Lewy bodies (CLB), and to determine Braak stage. NP were defined as extracellular accumulations of abnormal agyrophilic and anti-amyloid staining aggregates containing a central amyloid core and identifiable neurites (abnormal dark, coarse, tangled or irregular neuritic processes). DP were defined as unformed and amorphous plaques that lack identifiable neurites. NFT were defined by intraneuronal, cytoplasmic dense accumulations of agyrophilic (Bielschowsky or Gallyus stain) filamentous material that may be globoid, circumferential or flame-shaped. Extracellular or “tombstone” neurofibrillary tangles were interpreted as indicating that the neuron in which the NFT had developed had died and deteriorated. CLB were defined by round to oval, single or multiple intraneuronal, cytoplasmic accumulations of synuclein immunoreactive material.

NP, DP, and NFT were enumerated in 5 fields for each anatomical region, with post-assessment adjustment to produce counts standardized to areas of 1 square millimeter. Fields with the highest counts (2-dimensional densities) were selected for either the total plaque count (neuritic plus diffuse) or the total NFT count. Mean NP, DP, and NFT counts were calculated across 20 isocortical fields, from the right frontal, parietal, temporal, and occipital lobes. Total CLBs were counted in defined segments of the cortical gray ribbon of the four main lobes, plus the insula and anterior cingulate cortex, in order to create a total cortical Lewy body score and a standard McKeith Lewy body score (McKeith et al, 1996).

2.4 Cognitive Abilities Screening Instrument (CASI)

The CASI was developed by merging an expanded MMSE (the 3MS) with the Hasegawa dementia scale (Hasegawa, Honma & Ima, 1986). The resulting measure has been rescaled to 100 points (higher score is better), and contains items addressing 9 cognitive domains, including long-term and short-term memory, attention, concentration, orientation, visuospatial abilities, judgment and abstract thinking, word fluency and language.

2.5 Statistical approach

2.5.1. Latent Growth Curves of Lesion Propagation through Neuronal Networks

Our first step was to empirically determine the relative vulnerability of selected anatomical regions to AD pathology. Separate models were developed for NFT and NP. Mean lesion counts averaged across five fields were calculated for each subject, in each anatomical region. These means were then averaged across subjects within each region. They were then rank ordered by descending mean lesion counts (figure 1).

Figure 1. Frequency Counts of NP and NFT Lesions by Anatomical Region.

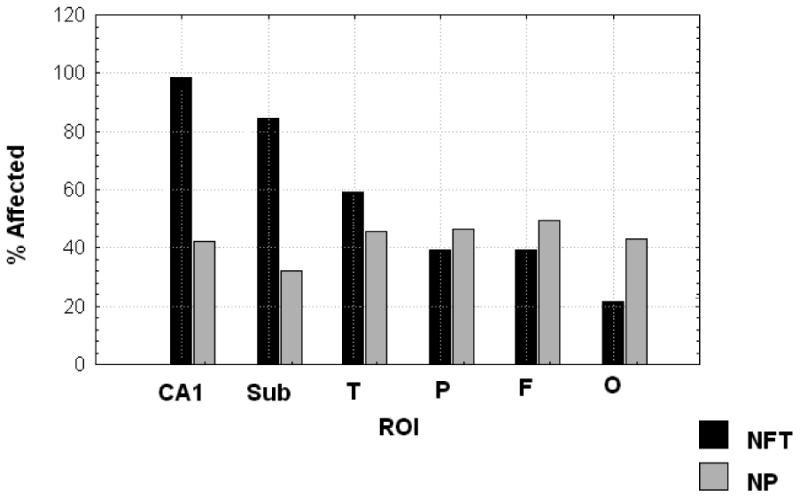
Frequency Counts of NP and NFT Lesions by ROI

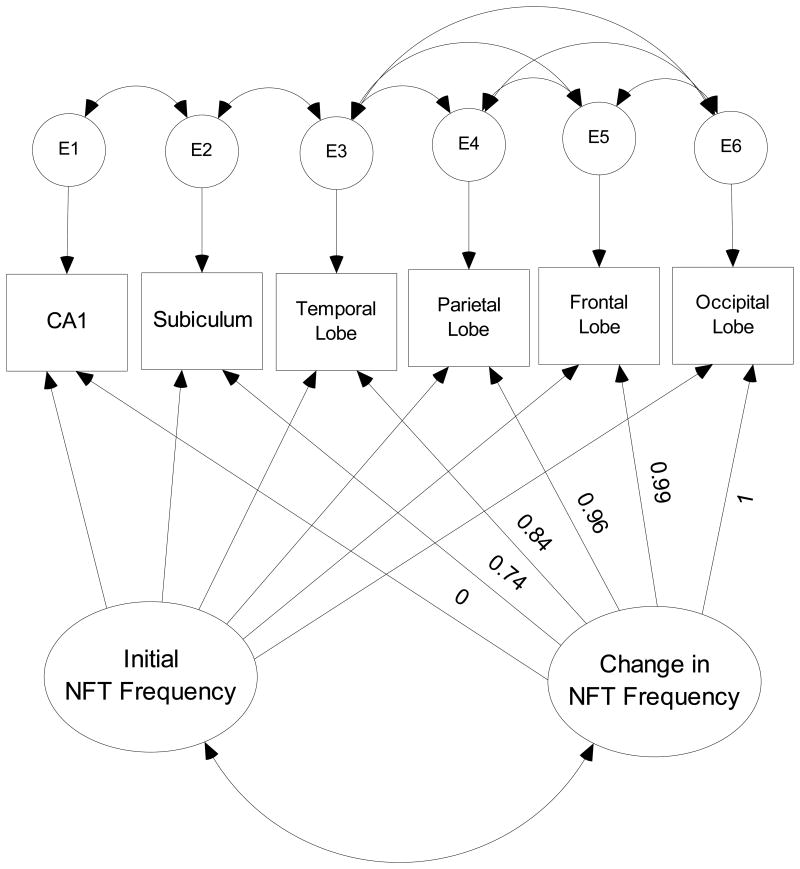
We next built growth curve models of latent variables describing the distribution of these lesions across their respective networks (Figure 2). In this figure, square objects represent observed variables. Oval objects represent unmeasured latent variables derived from the observed variables. Round objects represent residual “measurement” error uniquely associated with each observed variable, but not explained by the latent variables. The arrows represent the regression weights associating each variable in the model.

Figure 2. Latent Growth Curve Model of NFT Formation.

The “distance” between anatomical regions is not evenly spaced, as it would be in a temporal model with equally spaced follow-ups. Therefore, we determined the spacing between them empirically, by forcing the loadings of the most and least commonly affected regions to 0.0 and 1.0, respectively. This locates each intermediate region as a fraction of this maximum difference in mean lesion counts. The intercorrelations amongst the residuals were determined empirically to achieve an acceptable fit.

The final models provide parameters for the “intercept” and “rate of change” in lesion counts as a function of each region's relative “distance” down a hierarchically arranged gradient of regional lesion vulnerability. In the case of NFT counts (Figure 2), the intercept can be interpreted as the mean NFT count in CA1, the most commonly and severely affected region in the HAAS dataset. The “slope” reflects the mean change in NFT counts across the gradient. It could be interpreted as the vulnerability of this specific spatially ordered network to penetration by the AD process. Lower (negative) slope parameters would represent greater resistance to AD pathology, while greater (positive) slopes would represent greater vulnerability.

2.5.2. Fit Indices

The validity of structural models was assessed using three common test statistics. A nonsignificant chi-square signifies that the data are consistent with the model (Bollen & Long, 1993). A root mean square error of approximation (RMSEA) of 0.05 or less indicates a close fit to the data, with models up to 0.10 viewed as acceptable fit (Browne & Cudeck, 1993). The comparative fit index (CFI), with values ranging between 0 and 1, compares the specified model with a model of no change (Bentler, 1990). CFI values below 0.95 suggest model misspecification. Values of 0.95 or greater indicate adequate to excellent fit. All three fit statistics should be simultaneously considered to assess the adequacy of the models to the data.

3. Results

Sample characteristics are presented in Table 1. Mean NFT and NP counts by anatomical region are presented in Table 2. From these, we developed LGC models of NFT and NP distributions over space, and CASI performance over time. As can be seen in figure 1, the rank ordered frequency of dichotomously rated NFT neatly recapitulate Braak's model. 97% of autopsy cases had NFTs in CA1. Less than 28% had NFTs in the occipital lobe. As shown in Table 1, there was also a descending gradient in mean NFT counts, ranging from 22.5 ± 30.8 in CA1 to 1.1 ± 4.6 in the occipital cortex. The frequency distribution of NP is very different, and does not clearly correspond to Braak's model, as has been previously noted (Armstrong et al., 1993). Mean NP counts ranged from 2.0 ± 4.6 in the temporal lobe to 0.55 ± 1.7 in the subiculum (Table 2).

Table 1. Demographic Features.

	N	Mean	SD
Baseline Age (yrs)	436	79.6	5.1
Education (yrs)	436	10.4	3.4
Baseline CASI Score	436	76.7	21.3
Last CASI Score Before Death	436	61.6	29.1
Age at Death (yrs)	436	85.9	5.3
Braak Stage	393	3.7	1.3
Brain Weight (g)	435	1229.9	120.8

Table 2. NFT and NP Counts by Anatomical Region.

NFT Counts by Anatomical Region	N	Minimum*	Maximum*	Mean*	SD
CA1	431	0	203.51	22.54	30.77
Subiculum	429	0	189.42	6.63	13.57
Temporal	432	0	92.15	4.50	10.98
Parietal	433	0	71.08	1.73	6.10
Frontal	434	0	76.76	1.19	5.12
Occipital	434	0	46.76	1.09	4.57

NP Counts by Anatomical Region	N	Minimum*	Maximum*	Mean*	SD
Temporal	432	0	37.05	2.04	4.61
Parietal	433	0	25.68	1.80	3.89
Frontal	435	0	25.47	1.65	3.71
Occipital	434	0	17.00	1.61	3.36
CA1	431	0	24.21	0.97	2.20
Subiculum	429	0	17.68	0.55	1.65

^*Average of five fields

Each model displayed excellent fit (Table 3). Each model's estimated mean and slope was significant (Table 4), as was the variability about all estimates except the gradient of spatial change in NP (dNP) (Table 5). This suggests the presence of subgroups within the HAAS sample with discriminable differences in their vulnerability to NFT pathology, and discriminable rates of change in cognitive performance over time. These will be further examined through GMM in a future communication.

Table 3. Model Fit.

Model	χ2	df	p	RMSEA	CFI
1: NFT	9.50	4	0.05	0.02	0.995
2: NP	23.65	5	≤ 0.001	0.03	0.992
3: CASI	8.05	5	0.15	0.04	0.990

Table 4. Model Parameter Estimates.

	Estimate	p
Model 1:
Mean NFT at Origin	22.38	<0.001
dNFT	-21.35	<0.001
Model 2:
Mean NP at Origin	2.06	<0.001
dNP	-1.45	<0.001
Model 3:
Baseline CASI	76.73	<0.001
dCASI	-6.18	<0.001

Table 5. Model Variance Estimates.

Variances	Estimate	p
Baseline CASI	371.61	<0.001
dCASI	28.24	<0.001
Mean NFT at Origin	695.48	<0.001
dNFT	592.19	<0.001
Mean NP at Origin	16.51	<0.001
dNP	1.13	0.76

The relative “distance” between anatomical regions in the NFT and NP networks was estimated empirically from the data. Thus, for NFT (Figure 2), the subiculum was estimated to be “located” 74% of the distance between CA1 and the occipital lobe, the temporal lobe at 84% of that distance, the parietal lobe at 96% and the frontal lobe at 99%. The validity of this specific order is supported by the ordinal reduction in the variability in mean NFT counts across the network (Table 2), consistent with a ‘filtering” effect. Attempts to impose an alternative sequence on the data (i.e., by switching the order of the frontal and parietal cortex) results in a dramatic loss of fit (data not shown). The non-cardinal distribution of the regions reflects their relative vulnerabilities to NFT lesions. Mean NFT counts drop dramatically between CA1 and the subiculum (Table 2), but there is less marked interregional differences in mean NFT counts across the neocortex. This suggests a non-linear diathesis in a subset of cases with CA1 NFT pathology, followed by widespread neocortical dissemination.

Similarly, NP seemed to be distributed across a differently ordered set of structures. In the case of NP, the temporal lobe is the most heavily affected structure. The parietal lobe was located 8% of the distance between the temporal lobe and the subiculum, the frontal lobe 19%, the occipital lobe 36% and CA1 90%. The validity of this sequence is again supported by an ordinal reduction in the variability in mean NP counts across the network (Table 2).

Figures 3 and 4 present the individual NFT and NP growth trajectories (respectively). NFTs exhibited an estimated mean of 22.38 /mm² in CA1 (the network's intercept) and a decline of -0.214 NFT / percentile unit change across the network. NP exhibited a prevalence of 2.06 / mm² in the temporal cortex, and a decline of -0.015 / percentile unit change across its network. Mean CASI scores at baseline were 76.7 /100 and declined at an annualized rate of – 0.613 CASI points / year, over the ten year period of CASI score surveillance.

Figure 3. Individual Growth Trajectories: NFT.

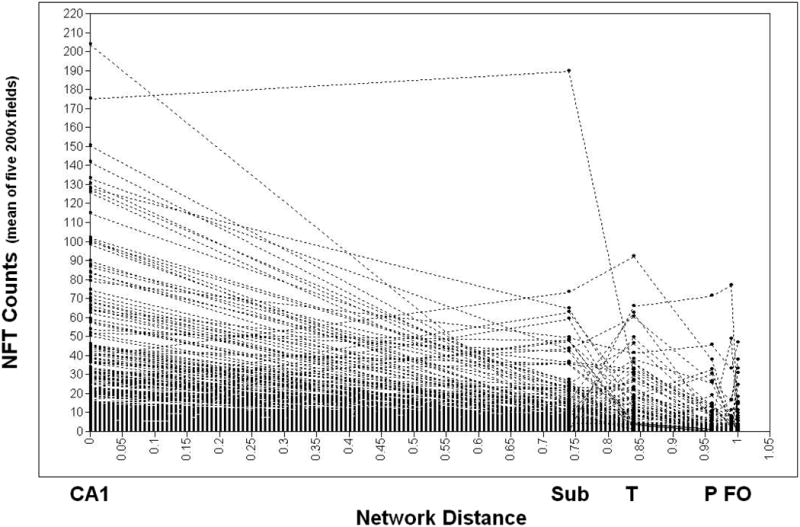
Individual Growth Trajectories of NFT Formation, N = 435 Honolulu Asia Aging Study (HAAS)

Figure 4. Individual Growth Trajectories: NP.

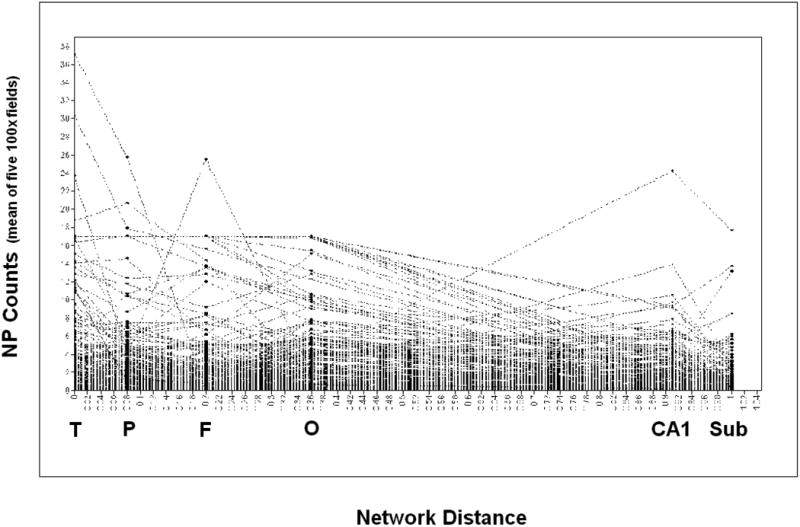
Individual Growth Trajectories of NP Formation, N = 435 Honolulu Asia Aging Study (HAAS)

Next we examined the associations between the gradient of spatial change in mean NFT counts (dNFT), dNP, and Braak stage. dNP was significantly inversely associated with dNFT, but weakly (r = -0.12, p <0.001). In a multivariate regression model, where Braak stage was adjusted for age at death and last CASI, dNFT and dNP were significantly, inversely, and independently associated with Braak stage (Table 6). dNFT was strongly associated with Braak stage (partial r = -0.63, p <0.001). Given a common intercept, each decrease by 10 NFT in mean change in NFT counts across the network was associated with a 0.4 increase in Braak stage.

Table 6. Multivariate Regression Model of Braak Stage.

Regression Model of Braak Stage	β	p
dNFT	-0.63	<0.001
dNP	-0.15	<0.001
Age at Death	0.06	0.15
Last CASI	-0.06	0.25

Next, we examined the correlation between apolipoprotein e (APOE) genotype, dNP and dNFT. APOE e4 allele burden correlated significantly with dNP (r = 0.29, p < 0.001), but not with dNFT (r = 0.00, p = ns).

Finally, we examined the correlations between dNFT, dNP, and change in CASI performance (dCASI). dNFT was most strongly correlated with dCASI. In a multivariate regression model adjusted for age and baseline CASI scores, only dNFT was significantly associated with dCASI (Table 7).

Table 7. Multivariate Regression Model of Change in CASI scores over 10 years (R = 0.29).

Regression Model of dCASI	β	p
dNFT	0.23	<0.01
dNP	0.01	0.26
Age at Baseline	0.04	<0.001
Baseline CASI	0.48	<0.001

4. Discussion

We have presented a novel approach to the analysis of autopsy data by treating the distribution of lesions within a neuronal network as a growth process across a spatial, rather than a temporal dimension. This allows us, for the first time, to apply advanced LGC and GMM modeling techniques to autopsy data.

Our models replicate familiar aspects of AD neuropathology. In the case of NFT, our model empirically recapitulates the hierarchical vulnerability of these regions to NFT formation, as previously described by Braak (Braak & Braak, 1998; 2000). We have also confirmed that regional vulnerability to either NFT or NP can be associated with both cross-sectional and longitudinal cognitive test performance. Similar to previous studies (Neary et al., 1986; Arnold et al., 1991; Arriagada et al., 1992; Berg et al., 1993; Bierer et al., 1995; Nagy et al., 1995; Berg et al., 1998), dNFT was a stronger correlate of cognition than was dNP, and dNP had no significant effect on cognition independently of dNFT (Arnold et al., 1991; Bennett et al., 2004). Conversely, only dNP was significantly related to APOE e4 burden (Kok et al., 2009).

Our analysis also demonstrates that NFT and NP are arranged in distinct spatial arrangements (Armstrong et al., 1993). The hippocampal structures (CA1 and subiculum) are more vulnerable to NFT than neocortical regions. The reverse is true of NP. However, both models agree that CA1 is more vulnerable to AD lesions than the subiculum. Both models also agree with regard to the specific relative vulnerability of the neocortical regions (i.e., temporal > parietal > frontal > occipital). This pattern replicates that reported in Corder et al.'s (2000) grade of membership analysis (GOM) of 249 Swedish autopsy cases. Similarly, in our earlier work (Royall et al., 2002), we demonstrated that these regions are similarly relatively vulnerable to paired helical filament tauopathy (PHF-τ). Thus, the relative vulnerabilities of these anatomical regions to the AD process appears to be conserved, both across neuropathologies, in the current models, and between study populations (Japanese American men vs. Swedish and French geriatric patients of both genders).

The timing of NP relative to NFT involvement of the same R0I cannot be determined from this analysis. However, neuroimaging with Pittsburg compound B (¹¹C) (PiB)-positron emission tomography (PET) suggests that amyloid affects the neocortex before dementia can be diagnosed (Li et al., 2008). Our earlier work suggests that NFT affect these regions coincident with dementia (Royall et al., 2002). Thus, NP formation probably precedes NFT formation, at least in the neocortex. However, a model forcing NP counts into the specific order exhibited by NFT failed to show acceptable fit (data not shown). This indicates that NFT and NP have different spatial origins and undermines the notion that NFT necessarily follow NP formation in the same structure.

Also consistent with our model, in vivo PiB-PET suggests that NP appear throughout the neocortex before the hippocampus is affected (Li et al., 2008). Further analyses may be able to test whether regional NFT vulnerability evolves linearly over the period of observation in HAAS, or non-linearly, as has been suggested by recent studies (Lovell et al., 2002; Engler et al., 2006; Jack et al., 2009).

The current analysis displays significant variability about the modeled gradients. This is to be expected in a population based sample, and may reflect AD variants, which could differ markedly from the average hierarchical patterns we have described here (von Guten et al., 2006, Jellinger & Attems, 2007; Petrovitch et al. 2009). The characterization of such variants could be facilitated by the application of GMM to these data, or even by simple visual inspection of the raw growth curves. Alternatively, significant variability about the modeled gradients could reflect contemporaneous or sequential interactions between multiple lesion forming processes in the same brains.

Finally, this approach lends itself to even more sophisticated modeling of the brain's regional vulnerability to AD lesions. For example, the comorbid occurrence of AD and ischemic lesions is a vexing pathological issue (Jellinger, 2007). It has been suggested that ischemic lesions contribute to cognitive decline and dementia independently of AD lesions, that ischemic lesions partially mediate the association between AD lesions and dementia, that AD lesions modulate the association between ischemic lesions and cognitive decline, and conversely that ischemic lesions modulate the temporo-spatial evolution of AD lesions.

SEM using latent variables derived from autopsy data is ideally suited to examine such issues. By using SEM and LGC modeling, the intercept and growth parameters from LGC models of AD and ischemic lesions can be used in multivariate regression models of temporal change in cognitive performance. The regression parameters will be informed by the variance in cognitive change across the entire sample, and statistical power should be greatly increased relative to multivariate regression models in complete cases (Launer et al., 2008; White, 2009). Moreover, the slope parameters from each pathological lesion type could be tested for their covariance, to determine whether or not one set of lesions affected the spatial evolution of the other (s).

There are some intrinsic limitations on these models. First, the regions available to us are not exhaustive, and limited to those selected by HAAS for study. NFT are found in many structures not sampled by HAAS. Second, these tissues were available by convention only from the L hemisphere. However, regional lesions counts may also be determined by interhemispheric projections from the contralateral side. Moreover, the exquisitely non-random distribution of NFT in particular implies that even the laminar distribution of NFT within a single anatomical region may vary across cases as a function of the specific sequence of regions affected earlier in the course of NFT development (Vogt et al., 1998). Thus, the models’ fit might have been further improved had other anatomical regions been available to us, or had more detailed assessments been available on these anatomical regions.

Finally, there are a wide range of technical limitations to the interpretation of autopsy data. These include issues such as the time between death and brain harvesting, technical limitations on the orientation of the region at cutting, potential selection biases in the cases that come to autopsy, etc. Never the less, our use of LGC has the potential to offset many of these. Latent variables are “error free” in the sense that the “residual” variance in each measured variable that is unexplained by the latent construct is specifically estimated. This variance is thought to include any non-systematic measurement error. Thus, the parameters of interest in a LGC model are less influenced by random technical problems than would be direct statistical descriptions of the observed variables.

In summary, we describe a methodological advance. This is the first application of LGC models to spatially ordered data. The result is a quantification of the inter-individual variation in the inter-regional vulnerability to AD lesions. We can now model biomarkers or other AD risk factors as determinants of this vulnerability, or use GMM to define subsets in our cohort with discriminably different vulnerabilities to these lesions.