Estimating the Temporal Evolution of Alzheimer’s Disease Pathology with Autopsy Data

Abstract

The temporal growth of Alzheimer’s disease (AD) neuropathology cannot be easily determined because autopsy data are available only after death. We combined autopsy data from 471 participants in the Honolulu-Asia Aging Study (HAAS) into latent factor measures of neurofibrillary tangle (NFT) and neuritic plaque (NP) counts. These were associated with intercept and slope parameters from a latent growth curve (LGC) model of 9-year change in cognitive test performance in 3244 autopsied and non-autopsied HAAS participants. Change in cognition fully mediated the association between baseline cognitive performance and AD lesions counts. The mediation effect of cognitive change on both AD lesion models effectively dates them within the period of cognitive surveillance. Additional analyses could lead to an improved understanding of lesion propagation in AD.

Introduction

Alzheimer’s Disease (AD) is characterized by specific neurodegenerative lesions: the neurofibrillary tangle (NFT) and the neuritic plaque (NP). Both are associated with cognitive impairment. However, it remains unclear whether these lesions develop gradually over many years, or non-linearly. It is also unclear whether they develop in concert or sequentially, and if the latter, then which lesion precedes the other, and whether the sequence of their development varies by region.

Autopsy studies suggest that AD pathology does in fact develop slowly, over many years, possibly decades. This is supported by the documentation of NP and NFT in mid-life among non-demented persons at low-grade Braak stages [1]. It is also supported by in vivo imaging of amyloid deposits in non-demented persons, and an increased burden among those who subsequently convert to AD dementia [2].

However, carbon¹⁴ has been used to more precisely date the formation of NP and NFT relative to symptom onset and subsequent autopsy in a small number of AD cases [3]. In that study, which has yet to be replicated, NFT and NP appeared to be formed coincidently with the onset of clinical symptoms, and up to a decade before the autopsy tissues were obtained. The timing of NFT relative to NP could not be determined. However, the variation about these means was surprisingly small (± 1.0 years) compared to the mean period of follow-up. This suggests that both NP and NFT may be formed in an abrupt non-linear diathesis that occurs relatively early in the clinical course of AD.

Non-linear development of NP lesions is supported by studies of serial neuroimaging with Piitsburgh Imaging Compound B (PiB) positron emission tomography (PET). PiB is thought to specifically bind fibrillary beta-amyloid, which comprises NP. These studies show little change in PiB burdens over time in AD and Mild Cognitive Impairment (MCI) cases, and weak correlations with prospective change in cognitive measures [4–5].

Cognitive change may be mediated through structural volume losses instead [5]. Serial MRI scans show a “wave” of cortical volume loss travelling across the brain in time scales as small as two years [6]. This wave is associated with a five point decline in MMSE score. MMSE scores themselves evolve non-linearly in older persons [7] and begin to decline in a non-linear diathesis up to six years before the diagnosis of AD is made [8]. The relationship between these in vivo changes and autopsy findings is not clear.

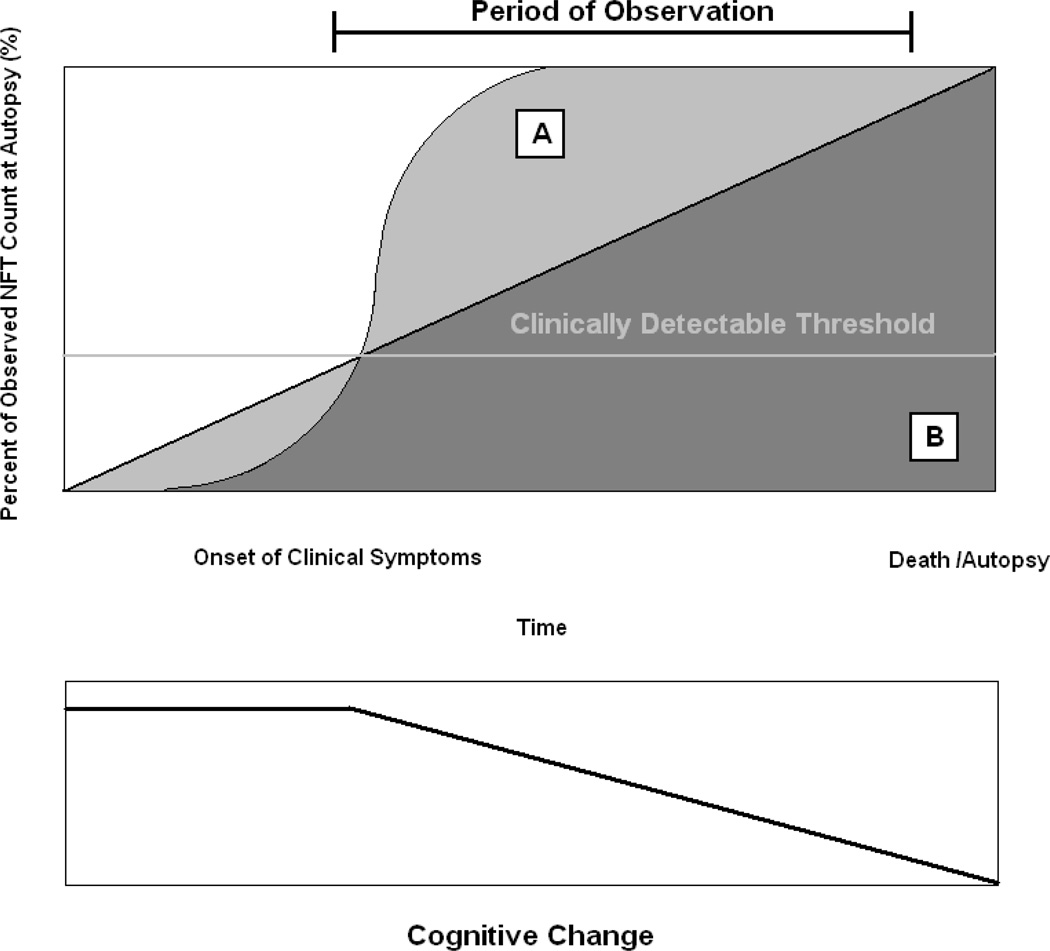
This has caused us to reconsider the roles that neurodegenerative lesions may play in cognitive decline, and the temporal evolution of their development. Because autopsy data are by definition cross-sectional, they cannot distinguish between a slow steady development of AD lesions (Figure 1:A) and an early non-linear diathesis (Figure 1:B). Neither does an observed gradual decline in cognition over the period of observation necessarily imply steady NFT formation. A “flash” of early NFT formation might be linked to subsequent longitudinal cognitive decline through down-stream inflammation, apoptosis, loss of synaptic density or other processes.

Figure 1.

Hypothetical Models of AD Lesion Development

Symptom onset may begin once AD pathology reaches a critical threshold, and progress linearly from there (below). It remains an empirical question whether AD lesions cross this threshold as part of a non-linear diathesis (above A) or a steady linear growth process (above B). Autopsy cannot distinguish these alternatives.

Longitudinal clinical data are often available in the years preceding the subject’s death. Never the less, we know of no study that has associated in vivo change in cognitive function with neurodegenerative changes at autopsy. Instead, the available literature associates neuropathology with cross-sectional cognitive performance, usually the last measurement obtained before death [9].

The state of the art for the longitudinal measurement of cognitive data is latent growth curve (LGC) and growth mixture models (GMM) [10]. Both provide separate estimates of the cohort’s intercept and its mean rate of change over the period of observation. Linear and non-linear rates of change can be independently estimated, and used as either outcomes or predictors in regression models.

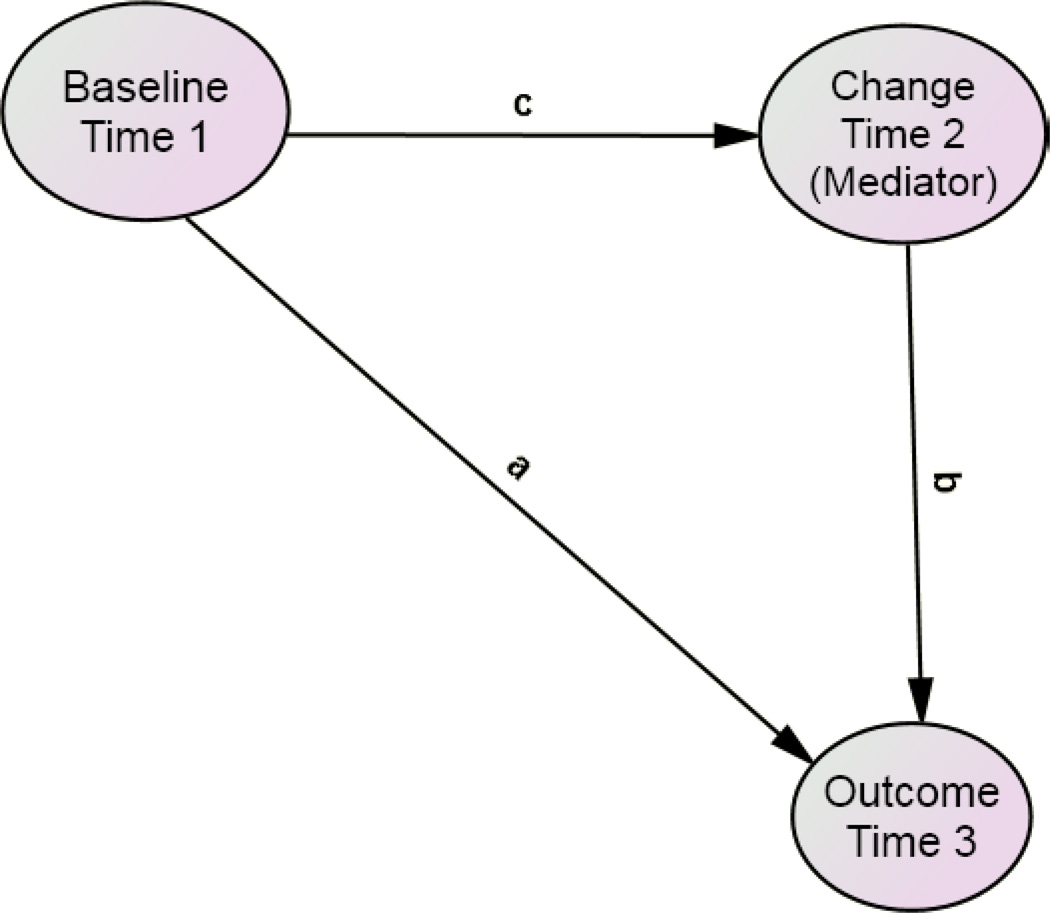
These models would again be limited by the fact that neuropathology is only available after death (i.e., temporally following the cognitive changes in question). However, it has occurred to us that the intercept, slope parameter(s) (i.e., from LGC models of change in cognition) and autopsy findings can all be arranged in a temporal sequence which allows the formal testing of in vivo cognitive change as a potential mediator of the association between the intercept and autopsy findings (Figure 2). Moreover, such models can arguably be interpreted as “causal” [11].

Figure 2.

Proposed Mediation Model

Partial or complete mediation effects can be calculated from the attenuation of the direct path “a” after adjustment for the indirect paths “c” + “b”. When the mediator variable is sampled intermediately in time, between baseline and outcome measurements, the mediation effect is arguably causal.

Thus, if AD lesions develop linearly in time, neuropathology at autopsy should be more strongly associated with the change parameter in a LGC model of cognitive decline, than with its intercept, and the rate of change in cognitive test performance may either partially or wholly mediate the significant unadjusted association (if any) between cognition and neuropathology. On the other hand, if neuropathology develops in a “flash”, early in the disease process, then the lesions at autopsy many years later may be more strongly associated with a coincident intercept than the intervening cognitive change.

Moreover, this logic could be used to test the development of each neurodegenerative change individually, or the entire range of neuropathological lesions simultaneously, in fully adjusted structural equation models. Finally, concurrently obtained biomarkers could be included as potential mediators of the associations between the cognitive intercept and neuropathology, or between cognitive change and neuropathology. This analysis provides “proof of concept” that mediation models employing LGC models of longitudinal clinical change can be used to estimate the temporo-spatial development of neuropathology.

Methods

The Honolulu-Asia Aging Study (HAAS): Autopsy tissue and clinical data were obtained from HAAS [12]. HAAS began in 1991 as an add-on to the Honolulu Heart Program (HHP) which is a longitudinal study of heart disease and stroke established in 1965 with the examination of 8006 Japanese-American men born 1900–1919. Brain autopsy and cognitive exams have been performed continuously since 1991.

HAAS autopsy material

838 autopsies had been performed prior to May, 2010. These represent approximately 20% of HAAS deaths since 1991. Demented decedents with autopsies do not differ significantly on several demographic and clinical measures from those who have not been autopsied, and non-demented and autopsied decedents were similar to autopsied, non-demented decedents. Although a diagnosis of dementia increased the likelihood that family members would contact the HAAS and /or agree to autopsy at the time of death, previous analyses indicate a general comparability across the two groups (demented and non-demented) with regard to clinical and demographic features [13]. The current analyses are limited to autopsies obtained between1991 and 2001. Microscopic examinations performed since 2001 have been done by a different team of neuropathologists, and have not yet been pooled for common analyses. Complete microscopic data generated by the first team are available in 493 decedents. Of those with complete microscopic data, 471 also have “normal” baseline neuropsychological test performance. Pathological data are limited to these 471 decedents.

The gross exams include external measurements and examination of 1 cm thick coronal sections of the entire brain for lacunes and large infarcts. The microscopic exam includes multiple stains for each of 38 tissue blocks from the brainstem and left hemisphere [14]. These are typically stained using Hematoxylin and Eosin (H&E) staining, Bielschowshi, Gallyas, and anti-Aβ stains. Anti-α-synuclein staining was done on isocortical sections from brains in which Lewy bodies were observed in H & E stained sections from the substantia nigra and /or locus ceruleus, and on a sample of brains in which no brainstem Lewy bodies were observed.

Microscopic AD pathology data include NFT counts, neuritic and diffuse (non-neuritic) amyloid plaque densities, vascular amyloid indices, substantia nigra neuronal counts, and anti-α-synuclein assessments of isocortical Lewy bodies.

Focal ischemic lesions assessed included large cortical infarctions, small grey and white matter lacunes and “microinfarcts” (i.e., ischemic lesions visible only on light microscopy).

Pathological materials

Brains were fixed by submersion in 10% neutral formalin. Tissue samples were embedded in paraffin. Slides were cut at 8 micron thicknesses and stained as mentioned. Modified Bielschowsky, Gallyas and α-synuclein-stained slides were examined to quantify diffuse plaques (DP), neuritic plaques (NP), neurofibrillary tangles (NFT), cortical Lewy bodies (CLB), and to determine Braak stage. NP were defined as extracellular accumulations of abnormal agyrophilic and anti-amyloid staining aggregates containing a central amyloid core and identifiable neurites (abnormally dark, coarse, tangled or irregular neuritic processes). DP were defined as unformed and amorphous plaques that lacked identifiable neurites. NFT were defined by intraneuronal, cytoplasmic dense accumulations of agyrophilic (Bielschowsky or Gallyas stain) filamentous material that may be globoid, circumferential or flame-shaped. Extracellular or “tombstone” neurofibrillary tangles were interpreted as indicating that the neuron in which the NFT had developed had died and deteriorated. CLB were defined by round to oval, single or multiple intraneuronal, cytoplasmic accumulations of synuclein immunoreactive material.

NP, DP, and NFT were enumerated in 5 fields for each anatomical region, with post-assessment adjustment to produce counts standardized to areas of 1 square millimeter. Fields with the highest counts (2-dimensional densities) were selected for either the total plaque count (neuritic plus diffuse) or the total NFT count. Mean NP, DP, and NFT counts were calculated across 20 isocortical fields, from the right frontal, parietal, temporal, and occipital lobes. Total CLBs were counted in defined segments of the cortical gray ribbon of the four main lobes, plus the insula and anterior cingulate cortex, in order to create a total cortical Lewy body score and a standard McKeith Lewy body score [15].

Cognitive Abilities Screening Instrument (CASI)

The CASI was developed by merging the Modified Mini-Mental Stae Examination (3MS) with the Hasegawa dementia scale [16–17]. The resulting measure has been rescaled to 100 points (higher score is better), and contains items addressing 9 cognitive domains, including long-term and short-term memory, attention, concentration, orientation, visuospatial abilities, judgment and abstract thinking, word fluency and language. CASI scores are available on 3736 HAAS participants at baseline. Of these, 3244 had “normal” performance at baseline, defined by a CASI score >70/100. Cognitive variables are limited to this subset.

Statistical Approach

Latent Neuropathology Measures

We used latent neuropathology measures derived from observed regional lesion counts supplied by HAAS. The raw pathological data were submitted to an exploratory factor analysis, with promax rotation. Five factors were obtained, most labeled by a single lesion type. Together, they explained 68.0% of the total variance in the neuropatholgical variables.

NFT counts from the hippocampus (CA1, subiculum), and temporal (T), frontal (F), parietal (P) and occipital (O) neocortex co-labeled a single factor with factor loadings ranging from 0.64 – 0.87 (data not shown). In addition, limbic NP counts (CA1 and the subiculum) loaded moderately on the same factor (r = 0.51 and 0.63 respectively).

In contrast, neocortical NP counts co-labeled a distinct orthogonal factor (range r = 0.75 – 0.92). Similarly, CLB from each of the above neocortical anatomical regions and the cingulate gyrus loaded on a single factor with strong loadings (0.63 – 0.98). Limbic and neocortical diffuse plaque counts loaded strongly on a single factor (0.61 – 0.85). Finally, small vessel vascular lesions (lacunes, microlacunes and microinfarcts) loaded strongly on a single factor (0.64 – 0.88). The high factor loadings across distinct orthogonal factors within lesion type support the use of latent neuropathology variables as outcomes in this analysis. To reduce the number of parameters to be estimated, we restricted both the NP and NFT latent factors to neocortical lesions (i.e., O, T, P, F).

Latent Growth Curves

CASI data were submitted to latent growth curve LGC modeling. In contrast to multiwave autoregressive models, which estimate interindividual rates of change across measurements, LGC models estimate the full trajectory of change across each individual’s measurement points (Willet and Sayer, 1994). The first four factor loadings on the latent-growth parameter were fixed at two year intervals. The last time-point loading was freely estimated from the data. The residual covariances were assumed to be uncorrelated over time, except when empirically better fit was achieved. Then, the covariance was estimated. Multivariate normality and linear associations were also asummed. All observed variables were adjusted for age at death, education and brain weight at autopsy.

Missing data

This analysis was performed using Analysis of Moment Structures (AMOS) software [18]. AMOS uses Full Information Maximum Likelihood (FIML) methods to address missing data. FIML uses the entire observed data matrix to estimate parameters with missing data. FIML assumes the data are “missing at random” (MAR). In this cohort, the data are likely missing not at random (MNAR) as the autopsied decedents were selected by mortality. However, FIML uses all the available data to improve parameter estimates relative to complete cases. This effctively preserves the overall power of the analysis, and is currently the accepted state-of-the-art method in addressing issues of missing data [19–20]. Morever, these models were adjusted for mortality-related covariates. We emirically tested whether FIML and our covariates yielded unbiased parameter estimates.

Goodness of fit

The fit of each structural model was assessed using three common test statistics. A nonsignificant chi-square signifies that the data are consistent with the model [21]. A root mean square error of approximation (RMSEA) of 0.05 or less indicates a close fit to the data [22]. The comparative fit index (CFI) compares the specified model with a model of no change [23]. CFI values below 0.95 suggest model misspecification. Values >0.95 indicate adequate to excellent fit. The Browne Cudeck Criteria (BCC) [24] address the issue of parsimony and is useful for comparing two models that are not necessarily nested, with lower BCC values indicating better fit.

All models were restricted to cases with “normal” baseline CASI scores > 70. Additionally, all observed variables were adjusted for age at death, education and autopsied brain weight. The analyses were repeated with logarithmic transformation of the highly skewed pathological variables, but this did not substantially alter the results (data not shown).

Mediation Models

We assessed mediation effects in three nested models for each lesion (NFT Models 1–3 and NP Models 1–3). For each lesion, we first assessed the significance of the “direct” path between CASI intercept and autopsy findings (Model 1, Figures 2 and 3, paths labeled as "a"). Given that this path was significant, we next tested CASI slope as an independent predictor of the autopsy findings (Model 2, Figures 2 and 3, paths labeled as "b"). Finally, we tested the “indirect” path (Model 3, Figures 2 and 3, paths labeled as "c" + “b”) as a mediator of the direct path a. The mediation effect is demonstrated by an attenuation of the direct effect after adjustment for significant indirect effects. “Complete” mediation requires a complete attenuation of the direct effect.

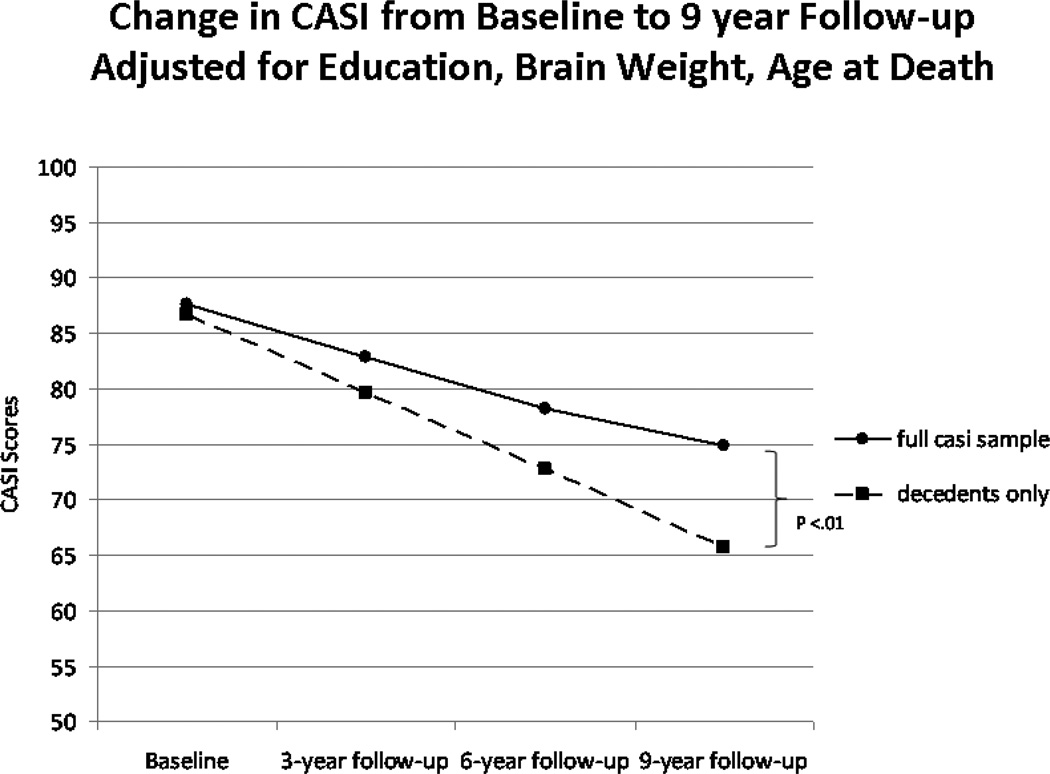
Figure 3.

Estimated Mean Change in CASI Scores*

Latent Growth Curve estimated mean change in CASI scores in the entire HAAS cohort (N = 3244) with baseline CASI > 70 vs. autopsied decedents (N = 471)

*Observed last CASI before death in autopsied decedents = 72.1 at a mean of 8.5 years of follow-up at time of death.

CASI = Cognitive Abilities Screening Instrument; HAAS = Honolulu-Asia Aging Study.

Results

Sample characteristics are presented in Tables 1 and 2. Mean lesion counts by anatomical region have been reported elsewhere [25]. Mean CASI scores fell linearly by −1.75 points / year (Figure 3). A non-linear slope was estimated, and found not to be significant independent of linear CASI change. The rate of change in CASI scores was significantly faster among the decedents (−2.30 points / year) (N = 471) than in all cases (N = 3244). Baseline CASI was significantly correlated with change in CASI (r = 0.31, p < 0.001).

Table 1.

Demographic Features of the HAAS Cohort^*

	N	Mean	Min	Max	SD
Baseline Age (yrs)	3271	77.16234	71	93	4.15
Education (yrs)	476	11.03361	3	22	3.29
Baseline CASI Score (ca. 1991)	3271	87.06472	70	100	6.70
CASIX5 (ca. 1994)	2506	82.81026	1	100	11.23
CASIX6 (ca. 1997)	1897	79.18846	0	100	15.55
CASIX7 (ca. 2000)	1474	78.80068	0	99	15.26

^*Restricted to subjects with CASI > 70/100 at baseline.

Ca = circa; CASI = Cognitive Abilities Screening Instrument; HAAS = Honolulu-Asia Aging Study. CASIx5 = CASI score at Exam 5, etc.

Table 2.

Demographic Features of Autopsied Decedents^*

	N	Mean	SD
Baseline Age (yrs)	471	77.8	4.4
Education (yrs)	471	11.1	3.3
Baseline CASI Score	471	86.8	6.6
Last CASI Score Before Death	440	72.1	22.4
Age at Death (yrs)	440	86.3	5.1
Braak Stage	240	3.6	1.3
Brain Weight (g)	471	1233.7	123.5

^*Restricted to subjects with CASI > 70/100 at baseline.

CASI = Cognitive Abilities Screening Instrument; HAAS = Honolulu-Asia Aging Study.

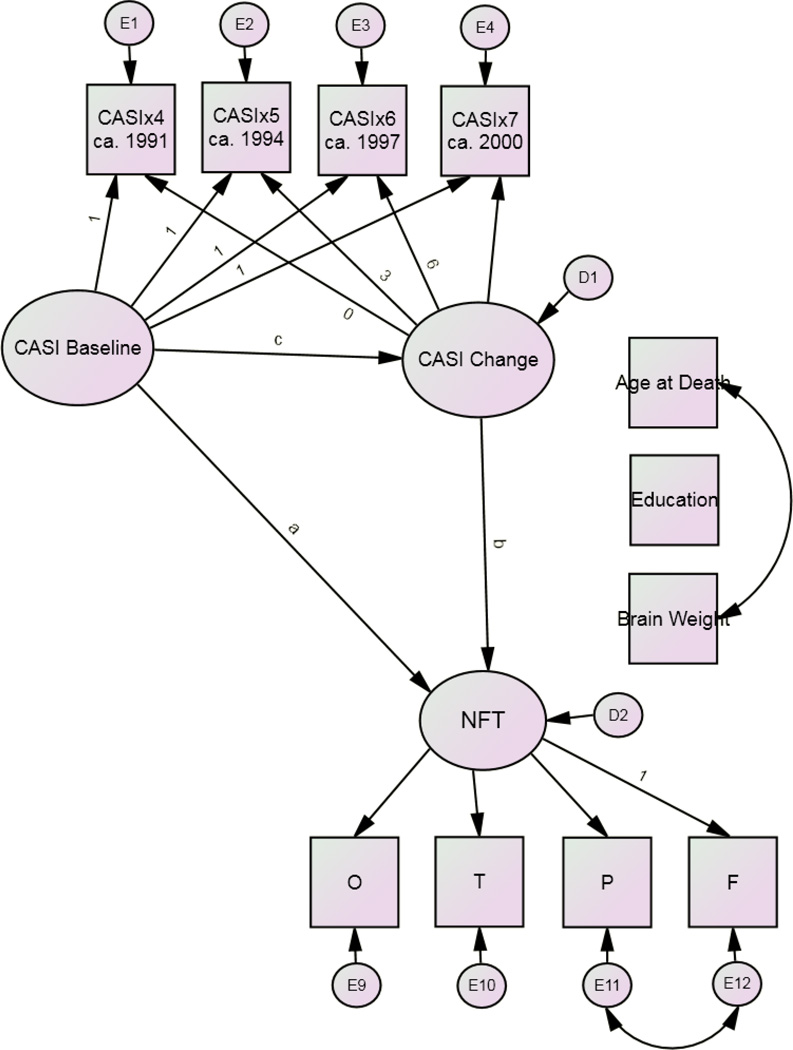
Tables 3–5 present the mediation models (Figure 4). Table 3 shows excellent fit for all models. The final models fit the data best. 10.4% of the variance in neocortical NFT counts was explained by NFT Model 3. 7.4% of the variance in neocortical NP counts was explained by NP Model 3.

Table 3.

Relative fit of NFT Models
Model	χ2:df	RMSEA	CFI	BCC
1	83.40:26, p <0.001	0.026	0.988	185.78
2	51.14:25, p = 0.002	0.018	0.994	155.53
3	51.14:25, p = 0.002	0.018	0.994	155.53
Relative fit of NP Models
Model	χ2:df	RMSEA	CFI	BCC
1	77.38:26, p <0.001	0.025	0.991	179.76
2	51.21:25, p = 0.002	0.018	0.995	155.21
3	51.21:25, p = 0.002	0.018	0.995	155.21

BCC = Browne Cudeck Criteria. Lower values indicating better fit; CFI = Comparative Fit Index. CFI values >0.95 indicate excellent fit; df = degrees of freedom; NFT = Neurofibrillary tangle factor; NP = Neuritic Plaque Factor; RMSEA = root mean square error of approximation. RMSEA values ≤ 0.05 indicate a close fit to the data.

Table 5.

NP Mediation Model^† for Baseline CASI Predicting NP Pathology at Autopsy: Rate of Change in CASI as the Mediator

	Model 1				Model 2				Model 3
	Path	B	(se)	stb	Path	B	(se)	stb	Path	B	(se)	stb
Baseline CASI predicting NP at autopsy.	a	−0.065	(0.03)*	−0.14	a	0.023	(0.03)	0.05	a	0.023	(0.03)	0.05
Rate of CASI change predicting NP at autopsy					b	−0.359	(0.10)***	−0.28	b	−0.359	(0.10)***	−0.28
Baseline CASI predicting rate of CASI change									c	0.110	(0.02)***	0.31

B = un-standardized regression weight; CASI = Cognitive Abilities Screening Instrument; NP = Neuritic Plaque Factor; se = standard error; stb = standardized regression weight (interpretable as a partial correlation).

^*= p ≤ 0.05,

^**= p ≤ 0.01;

^***= p <0.001

^†Adjusted for age at death, education and autopsy brain weight, and restricted to CASI > 70 at baseline. R = 0.074.

Age at death significantly related to CASIx4, education to CASIx4, CASIx5 and CASIx6, and brain weight to CASIx6 and CASIx7. All asssociations were statistically “weak” except between education and CASIx4 (partial r = 0.33, p < 0.001).

Figure 4.

Final Model*

*Restricted to subjects with CASI > 70/100 at baseline.

The unadjusted “direct” path from baseline CASI to NFT counts is significant (Table 4). However, change in CASI fully mediates the association between baseline CASI and NFT counts. Thus, cognitively relevant neocortical NFT formation appears to have been limited to the period of longitudinal CASI surveillance, and not before. NP results are similar to those obtained for NFT (Table 5). Thus, cognitively relevant neocortical NP formation also appears to have been limited to the period of longitudinal CASI surveillance, and was thus contemporaneous with NFT formation. Both lesions are inversely related to change in CASI.

Table 4.

NFT Mediation Model^† for Baseline CASI Predicting NFT Pathology at Autopsy: Rate of Change in CASI as the Mediator

	Model 1				Model 2				Model 3
	Path	B	(se)	stb	Path	B	(se)	stb	Path	B	(se)	stb
Baseline CASI predicting NFT at autopsy.	a	−0.150	(0.04)***	−0.24	a	−0.018	(0.04)	0.03	a	−0.018	(0.04)	−0.03
Rate of CASI change predicting NFT at autopsy					b	−0.504	(0.14)***	−0.31	b	−0.504	(0.14)***	−0.31
Baseline CASI predicting rate of CASI change									c	0.109	(0.02)***	0.31

B = un-standardized regression weight; CASI = Cognitive Abilities Screening Instrument; NFT = Neurofibrillary Tangle Factor; se = standard error; stb = standardized regression weight (interpretable as a partial correlation).

^*= p ≤ 0.05,

^**= p ≤ 0.01;

^***= p <0.001

^†Adjusted for age at death, education and autopsy brain weight, and restricted to CASI > 70 at baseline. R = 0.104.

Age at death significantly related to CASIx4, education to CASIx4, CASIx5 and CASIx6, and brain weight to CASIx6 and CASIx7. All asssociations were statistically “weak” except between education and CASIx4 (partial r = 0.33, p < 0.001).

To confirm the stability of the parameter estimates, the final mediation models were repeated in autopsied decedents only. While these models did not fit well, they resulted in near identical parameter estimates and supported identical interpretations (data not shown).

Discussion

We have found that the significant associations between baseline CASI performance (ca 1991) and AD pathologies at autopsy were mediated entirely by the observed linear change in CASI scores over the intervening nine years of longitudinal surveillance. However, these models explain relatively little variance in either neuropathology. Thus, they do not offer a comprehensive description of AD’s development. Nevertheless, they provide proofs of concept that LGC can be leveraged to produce a model of a pathology’s temporo-spatial evolution.

We found that the cognitively-salient fractions of NP and NFT developed concurrently in the HAAS cohort decade or less before death, and not before.

This finding does not rule out a non-linear diathesis within this time frame. However, by systematically re-iterating these models across smaller, and /or lagged temporal frames we can we can examine that possibility empirically.

If there is a non-linear diathesis, two conditions should arise. First, the intercept should most stongly predict neuropathology when placed coincidently with the diathesis. Second the slope should no longer completely mediate the intercept’s association when the intercept is placed coincidently with or after the diathesis. Because the significant direct effect was completely mediated in these analyses, we can conclude that the diathesis, if there was one, occurred after 1991 and before 2001.

These models do have limitations. First, each addresses only the fraction of these lesions that is related to the growth process under study. Thus, our finding that NFT and NP developed concurrently in the decade before death applies only to the cognitively salient fractions of those lesions. Cognitively “silent” AD pathology cannot be interrogated by these models and might have a different temporal evolution.

As an example, Arriagada et al. [26] have reported NFTs to be regionally distributed across two factors. The first contained the amygdala and hippocampus. NFT burden in these regions was not associated with cognition, as measured by the Blessed Dementia Rating Scale (BDRS). The second cluster contained neocortical regions, including Brodmann Areas 7, 8, 9, 17, 20, and 21. NFT burden in these regions correlated r = −0.66, with the BDRS (p < 0.05). Our analysis might apply only to the latter regions of interest. In fact, we may have detected a mediation effect on NFT because our NFT factor was limited to overlapping neocortical structures.

Moreover, we modeled linear cognitive change. HAAS’ cohort did not manifest non-linear growth in CASI scores, but if it had, that growth process might be related to yet another cognitively salient fraction of these lesions. We were further limited to HAAS’ use of CASI scores. Other psychometric measures might be associated with other populations of AD lesions evolving independently of or in concert with these. Finally, we might have modeled non-cognitive behavioral, neuropsychiatric, or affective changes, which might reveal still other pathological substrates and temporal histories. In a richer dataset, we could have assembled a more comprehensive view of AD lesions, and explained a greater share of each lesion’s variance. Moreover, this approach could be applied to other expensive or difficult to acquire cross-sectional data, i.e., neuroimaging or biomarkers.

Regardless, this approach remains a methodological advance. Within the constraints above, we can systematically catalog the temporo-spatial evolution of these lesions, as well as Lewy Bodies (which were not considered here), or indeed any lesion available in HAAS’ dataset. Moreover, multiple lesions can be considered simultaneously in systems level models of pathological interaction.

Furthermore, our method has other notable advantages. For example, the measurement “error free” modeling of latent pathological data circumvents many familiar limitations to the interpretation of autopsy data. These include the time between death and brain harvesting, technical limitations on the orientation of the anatomical regions at cutting, potential selection biases in the cases that come to autopsy, etc.

Our approach is not immune to systematic measurement issues. HAAS, for example, measured NP and NFT counts in fields selected for their higher lesion densities, rather than randomly selected fields. Such methodological choices could affect our factor loadings. However, this would be an issue only if the differences between these methods were invariate across structures. It seems more likely that the resulting differences would vary significantly by region. In that case, the latent constructs under investigation would be unaffected. In theory then, this method is limited only by pathologies documented and the regions available, and might be applied within anatomical regions at the laminar level. Thus, “error free” estimates of change in NFT or NP counts across a wide range of structures, or even within lamina, can be modeled relative to longitudinally measured cognitive, behavioral or other clinical changes.

Furthermore, because we have used FIML to achieve these analyses, the effects of attrition and mortality selection bias are mitigated. CASI scores are available on over 3000 HAAS subjects at Exam 4 while less than 500 go on to provide autopsy data. CASI performance may be missing in some waves among decedents, with or without autopsies, especially those that died soon after the cohort’s inception. And yet, not only is FIML capable of handling such “real world” missing data issues [20], the large amount of longitudinally available cognitive performance data in this sample has demonstrably improved our power to model these associations without meaningfully affecting the parameter estimates.

Because the major variables, baseline CASI, change in CASI, and autopsy lesions are temporally distinct and ordered observations, the final analyses also represent strong mediation models, and can be interpreted to imply causal effects [11, 27].

Finally, the signs of these parameter estimates bear mentioning. Both unadjusted mediation models suggest that higher baseline CASI scores are related to lower lesion counts at autopsy. The mediation effects suggest that the association between baseline CASI scores and neuropathology is mediated by incident, and not baseline neuropathology.

Both models agree that faster rates of decline in CASI scores are associated with higher (neocortical) lesion burdens at autopsy. However, we did not model the interactions between these lesions. Prior studies suggest that NP have no association with cognition independent of NFT counts [28]. Similarly, another analysis we have performed in this cohort suggests that change in CASI is not related to NP counts independently of NFT [29].

It remains to be seen if NP moderate NFT’s association with cognitive decline. HAAS data suggest that it does. In our first LGC model of HAAS’ pathology [25], interregional vulnerability to NFT was found to be inversely related to that of NP, suggesting that neocortical NP resist the advance of NFT through neuronal networks. Consistent with this, NFT’s association with change in CASI appears to be weakened by adjustment for NP (partial r = −0.31 in the present unadjusted model vs. −0.23 in an NP adjusted model) [29].

In summary, our analysis represents a methodological advance. We have used change in cognition to demonstrate, in a formal and arguably causal mediation model, that the fraction of AD lesions related to linear in vivo cognitive change are evolving concurrently in time. This supports a model of contemporaneous neocortical and NFT and NP formation over at most 9 years of CASI surveillance. Additional analyses have the potential to construct a comprehensive picture of AD’s temporo-spatial development using difficult or expensively acquired cross-sectional data referenced to easily acquired longitudinal clinical assessments.