Detection of the lunar body tide by the Lunar Orbiter Laser Altimeter

Abstract

The Lunar Orbiter Laser Altimeter instrument onboard the Lunar Reconnaissance Orbiter spacecraft collected more than 5 billion measurements in the nominal 50 km orbit over ∼10,000 orbits. The data precision, geodetic accuracy, and spatial distribution enable two-dimensional crossovers to be used to infer relative radial position corrections between tracks to better than ∼1 m. We use nearly 500,000 altimetric crossovers to separate remaining high-frequency spacecraft trajectory errors from the periodic radial surface tidal deformation. The unusual sampling of the lunar body tide from polar lunar orbit limits the size of the typical differential signal expected at ground track intersections to ∼10 cm. Nevertheless, we reliably detect the topographic tidal signal and estimate the associated Love number h₂ to be 0.0371 ± 0.0033, which is consistent with but lower than recent results from lunar laser ranging.

Key Points

• Altimetric data are used to create radial constraints on the tidal deformation

• The body tide amplitude is estimated from the crossover data

• The estimated Love number is consistent with previous estimates but more precise

1. Introduction

The Lunar Reconnaissance Orbiter (LRO) mission [Chin et al., ²⁰⁰⁷] was launched in June 2009 to provide the high-resolution data sets needed to prepare for future human exploration, such as topography [Smith et al., ^2010a] and visible and thermal imagery. After a successful 1-year Exploration mission and a 2-year Science mission, LRO continues to operate in its 2-year Extended Science mission, still producing a wealth of new data.

The Lunar Orbiter Laser Altimeter (LOLA) [Smith et al., ^2010a] is the first multibeam space laser altimeter. With its five-beam cross pattern and 28 Hz firing frequency, it mapped the Moon's topography at higher resolution and better accuracy in a few months' time [Smith et al., ^2010b] than any previous lunar mission [e.g., Araki et al., ²⁰⁰⁹]. The altimetric data of the LOLA instrument, precise to ∼10 cm, were also invaluable in enabling precise orbit reconstruction significantly better (<20m total position error) than the original position knowledge requirements (50 m) [Chin et al., ²⁰⁰⁷], through the use of altimetric crossovers in the orbit determination process [Mazarico et al., ²⁰¹²].

More recently, our knowledge of the lunar gravity field has taken a quantum leap with the successful Gravity Recovery and Interior Laboratory (GRAIL) mission [Zuber et al., ^2013a]. Beyond the important geophysical implications [Zuber et al., ^2013b; Wieczorek et al., ²⁰¹³; Andrews-Hanna et al., ²⁰¹³], the improved lunar gravity field resolution and accuracy yield even more precise orbits for lunar orbiters such as LRO [Mazarico et al., ²⁰¹³].

1.1. Rationale

The more accurate spacecraft orbit determination enables new scientific goals for LOLA, as the orbit reconstruction error level becomes comparable to the altimeter intrinsic precision. The detection of the tidal deformation of the lunar shape was not part of the LOLA instrument objectives because of its difficulty: in addition to the specific sampling geometry from orbit, the typical radial surface deformation expected between two recurring observations is less than 10 cm, whereas the individual altimetric measurement noise is ∼10 cm and the radial position knowledge was anticipated to be no better than ∼1m. Nevertheless, after a focus on orbit accuracy [Mazarico et al., ²⁰¹²], and with nearly 4 years of near-continuous measurements resulting in millions of ground track intersections, we will show that we detected the tidal surface deformation signal in the raw LOLA elevation data set.

This direct detection is important because it does not depend on but can support other complex models of the lunar interior that can rely on lunar laser ranging (LLR) measurements which are not as sensitive to the effect of the body tide alone [Williams et al., ²⁰⁰⁸]. In addition, if the lunar tidal response is not uniform spatially, the LLR results would be insensitive, due to the retroreflectors being concentrated on the nearside and at low latitudes. On the other hand, the LOLA data are global and more uniformly distributed.

1.2. Tide Modeling

Lunar body tide models can be complex, such as Williams et al. [2008, 2010, 2013] in which the orbit and orientation of the Moon are integrated numerically and tidal parameters concurrently fit to the LLR data. Here we use a simple analytical model, driven by the DE421 ephemerides and lunar orientation model [Williams et al., ²⁰⁰⁸] to calculate the degree-2 tidal potential, V, due to the Earth and Sun from their Moon-fixed positions [Kaula, ¹⁹⁶⁶]. The tidal displacement at the surface, written here for clarity ignoring the Sun, is given by

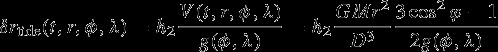where t, r, φ, and λ are the time, radius, longitude, and latitude, respectively; ϕ is the angle to the sub-Earth point and D the distance between the Earth and the Moon centers; g is the surface gravity; and h₂ is the tidal Love number describing the efficiency of the response in terms of radial deformation. In this work, we use an a priori h₂ value of 0.03786, equal to the DE421 value derived from a constrained fit to LLR data [Williams et al., ²⁰⁰⁸]. The DE421 ephemeris is also used by the LRO project and the LOLA science team for processing and data archival to the Planetary Data System.

Although the Moon is rotating synchronously around the Earth, the sub-Earth point can shift by 7–8° in longitude and latitude from its average position, due to optical librations. The eccentricity of the Moon's orbit also moderates the amplitude of the bulge, causing time-variable radial displacements.

Thus, while the maximum displacement is ∼50 cm, it is mostly static and effectively part of the background topography, whose range is ∼20 km. Small oscillations around that mean deformation are due to the eccentricity and pole orientation, but solar perturbations on the Moon's orbit and orientation produce additional longer-period signals.

1.3. Outline

We will first describe the LOLA instrument characteristics, its in-flight performance (section 2.1) and the reconstructed spacecraft position accuracy (section 2.2). In section 2.3, we will then discuss the distribution of the altimetric crossovers and show how they can be used to obtain precise relative position information between pairs of LOLA profiles. We will compare the radial crossover offsets directly to the tidal model predictions (section 3.1) and present a more comprehensive method to distinguish the tidal signal from remaining orbital errors (section 3.2). Finally, we will discuss these results (section 3.3) and summarize our findings (section 4).

2. Data Description

2.1. The LOLA Instrument

Designed to provide short-wavelength terrain and slope data to enable future landings on the lunar surface, the LOLA instrument is a high-frequency multibeam system. A diffractive optical element at the end of the laser beam expander produces a cross-shaped far-field pattern composed of five spots. At the nominal 50 km altitude, each spot is 5 m wide and the spot centers are 25 m apart [Smith et al., ^2010a, Figure 2]. The cross pattern is rotated by 26° with respect to the flight direction, to optimize the coverage of the surface with the five profiles: each profile is separated by about 10 m cross-track, and the average along-track distance between spots is also 10 m. The multibeam configuration enables proper two-dimensional sampling of the surface topography, which was not the case with previous laser altimeters. The cross-track information can help match two independent topographic profiles around their intersection point, removing or reducing the ambiguities that exist with purely one-dimensional profiles.

As explained in Smith et al. [2010b], the thermal blanket protecting the LOLA instrument from the space environment was tightly attached to both the beam expander and the receiver telescope. As the spacecraft transitions from the dayside to the cold nightside, the strong outer layer of the blanket contracts and pulls the beam expander out of alignment from the five detector fields of view. Fortuitously however, this displacement is such that two out of the five laser spots fall inside the nominal fields of view of two other spots. Consequently, LOLA continues to collect altimetry over the nightside but in diminished mode (two profiles, or ∼40% of nominal returns).

This complicates the analysis of the LOLA data by introducing time-dependent thermally driven signals to the LOLA pointing. It affects the quality of the altimetric crossovers, primarily by reducing the number of cross-track profiles from five to two when on the nightside.

2.2. LRO Position Knowledge

Before the GRAIL gravity fields [Zuber et al., ^2013b] became available, the LRO orbit determination relied on bootstrapped gravity solutions tuned to minimize orbital overlaps [Mazarico et al., ²⁰¹²]. These models performed better geodetically than the Lunar Prospector models [Konopliv et al., ²⁰⁰¹; Mazarico et al., ^2010a], with an orbit consistency of about 20 m in total position and less than 1.5 m radially. With the degree and order 420 GRAIL gravity field of Zuber et al. [2013a], the accuracy of the orbits determined from the LRO radiometric tracking data improved further in the nominal orbit phase, to ∼10m in total position and about 50 cm radially [Mazarico et al., ²⁰¹³]. The LOLA altimetric profiles that we use here are geolocated from those high-quality orbits, in order to minimize the impact of orbit reconstruction errors on the results.

2.3. Altimetric Crossovers

2.3.1. Definition and Distribution

Crossovers are locations where two spacecraft ground tracks intersect. They are advantageous when an altimeter is operating because the altimetric data can be transformed into geodetic constraints on the spacecraft trajectory, the instrument pointing, and the changes in surface height. Except for those, the two measurements should yield the same planetary radius.

The number of crossovers grows quadratically with the number of orbits, so naturally we maximize the temporal baseline of our data set. Because LOLA cannot reliably measure laser returns at ranges larger than ∼120 km, the altimetric data are exclusively concentrated in the Southern Hemisphere in the elliptical commissioning orbit (July–September 2009) and the quasi-frozen orbit to which LRO was transitioned in December 2011. In order to limit the heterogeneity of the crossovers included in the tide estimation, we restrict our analysis to the LOLA nominal orbit data, e.g., September 2009 to December 2011.

As noted by Rowlands et al. [2009], because the Moon is a slow rotator and the LRO orbit has a near-polar inclination, the crossover distribution is very different from what the Mars Orbiter Laser Altimeter encountered at Mars [Neumann et al., ²⁰⁰¹]. The primary effect is that few crossovers occur at low latitudes. Moreover, to minimize the effects of thermally related pointing offsets and possible measurement biases due to uncalibrated range walk at lower pulse energies (section 2.1), we only consider the crossovers where both tracks reliably measure the five spots (i.e., both tracks are on the dayside and away from the terminator). This considerably reduces the number of selected crossovers, in particular in the polar regions. Despite those restrictions designed to retain only the most promising LOLA crossovers, with 9902 orbits in our study period, our initial sample consists of nearly 500,000 crossovers (Figure 1).

Figure 1.

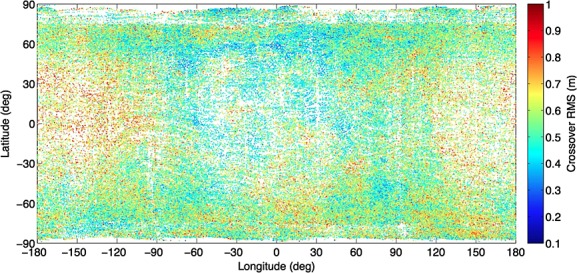
Spatial distribution of the selected LOLA crossovers. Color indicates the radial residual root-mean-square (RMS) of fit after crossover adjustment (section 2.3.3) and is correlated with surface roughness. Only half of the crossovers are shown for clarity.

2.3.2. Crossover Adjustment Method

At every crossover location, we estimate the relative offset between the two altimetric profiles following the method described in Mazarico et al. [2010b]. Briefly, the concept is to interpolate the points from each track onto the other track and to minimize the residual height differences by estimating a single three-dimensional displacement between both tracks, in a local stereographic projection. Typically, each track contains between 200 and 1000 altimetric ranges in the common intersection area. The multibeam pattern of the LOLA ground track is especially important for the low-latitude crossovers, where intersecting tracks are nearly parallel. If no cross-track information was available (single-beam altimeter case), this geometry would prevent any realistic use of these crossovers.

We use the raw LOLA elevation data, without any prior correction for tide or geoid. As the cost function is not necessarily well behaved because of the interpolations involved, we improved the algorithm by initiating the minimization from 50 random guesses, more than enough to reach consensus and avoid local minima. Thus, for each crossover, we obtain a three-dimensional offset vector that brings both altimetric segments in best agreement and associated error estimates.

2.3.3. Results

After excluding crossovers with poor fits, high radial errors (> 1 m), large slopes (> 20°), and high off-nadir angles (> 5°), the total sample size is 354,840. The radial residual root-mean-square (RMS) improves by a factor of 3 after applying each crossover's best-fit offset vector, decreasing from 1.78 ± 2.11 m to 0.56 ± 0.12 m (Figure 2a). The lunar farside generally has higher RMS (Figure 1), likely indicating that the remaining residuals are the inevitable result of interpolating a rough surface from spots tens of meters apart.

Figure 2.

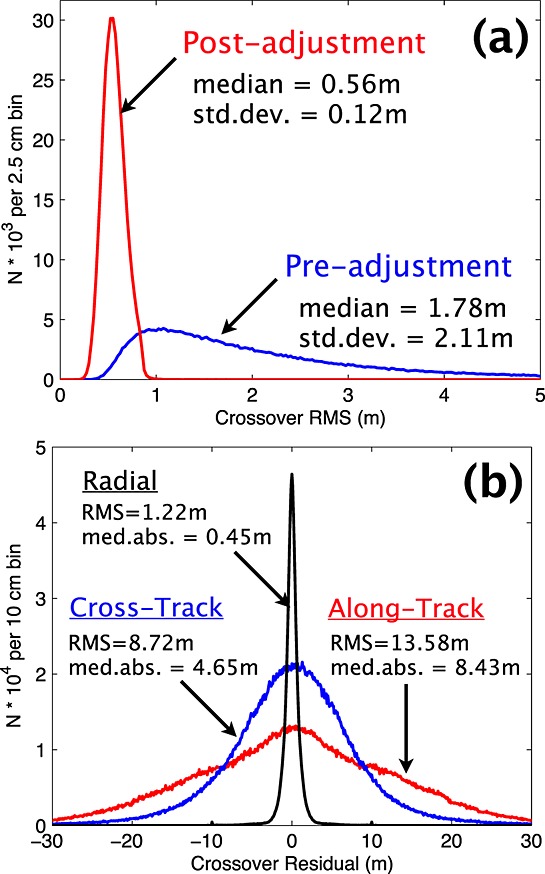
(a) Distribution of RMS radial residuals before (blue) and after (red) adjustments. (b) Distribution of radial (black), cross-track (blue), and along-track (red) offsets. For clarity, the counts for the cross-track and along-track distributions are multiplied by 5.

Figure 2b shows the distributions of the relative offsets estimated by the crossover adjustment during minimization. Their statistics are consistent with the orbit reconstruction accuracy given by Mazarico et al. [2013]. The offset distributions in the horizontal directions are widened due to aliasing between the LOLA boresight model errors (20–150μrad) and the seasonal spacecraft yaw flips. In the present study, we focus solely on the radial offsets, which are the new data we will use to detect the body tide. The detection of the body tide in the horizontal direction is unlikely at present given the large spread in horizontal crossover offsets (Figure 2b). M. K. Barker et al. (manuscript in preparation, 2014) will focus on the recovery of the boresight model corrections from the horizontal crossover adjustments.

3. Detection of the Body Tide

3.1. Initial Comparison to Tidal Model

To assess the quality of the new crossover measurements, we directly compare the relative radial displacements we obtained in section 2.3.3 to the radial deformation differences predicted at the crossover times by our simple tidal deformation model (section 1.2) with an a priori h₂=0.03786. Figure 3a shows a two-dimensional histogram of both sets, with warmer colors indicating a higher density. Because most crossover time separations are multiples of ∼14 days, the predicted radial offsets are generally small. The vertical scatter, an order of magnitude larger than the expected tidal signal amplitude, is due to the remaining orbital errors. Nevertheless, the crossover measurements appear qualitatively consistent with the model (1:1 line).

Figure 3.

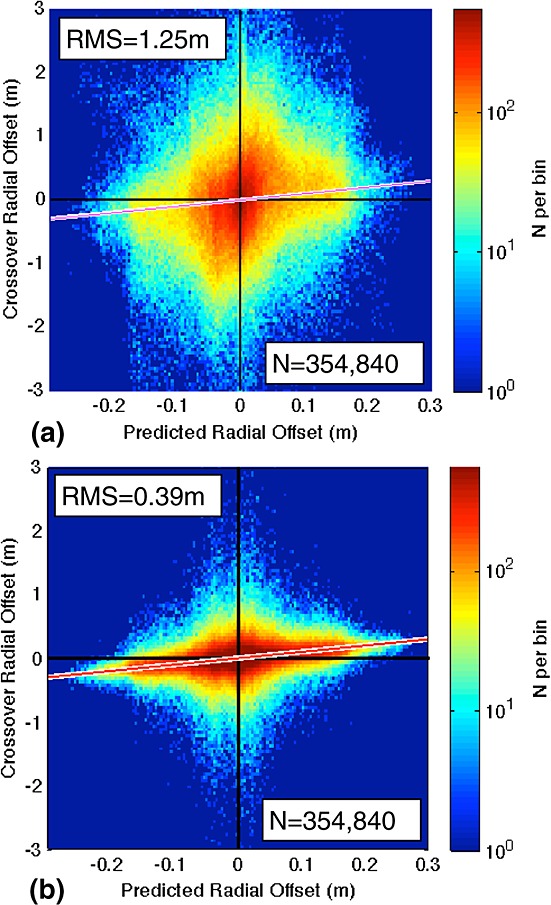
(a) Two-dimensional histogram of measured and predicted radial offsets. The red line is the 1:1 line, not a fit. (b) Same as Figure 3a but after subtracting the orbital errors estimated by least squares (section 3.2).

3.2. Comprehensive Least Squares Inversion

We follow this first look at the crossover offsets with a more formal least-squares inversion. In addition to our parameter of interest, h₂, we estimate a large number of “nuisance” parameters designed to absorb the effects of time-dependent orbital errors with frequencies higher than the tidal period. Due to the long temporal support of the crossovers (more than 2 years), it is not practical to directly model the orbital errors with a fine time step (e.g., enough to sample an orbit period) [Neumann et al., ²⁰⁰¹]. Instead, because orbital errors are typically once-per-revolution perturbations whose amplitude (A) and phase (ψ) vary slowly with time, we use the associated parameters u=A sin(ψ) and v=A cos(ψ), sampled every orbit (∼2 h). This is supported by the temporal signature of the radial crossover offsets, initially dominated by the orbital errors. In total, we have 9799 u and 9799 v orbital parameters and one tidal parameter, h₂. These empirical parameters also guard against the low-degree gravity coefficients used for the LRO orbit determination, including the Love number k₂, affecting our results.

For a given crossover with associated times t₁ and t₂, the modeled radial offset is δr(t₁)−δr(t₂) with

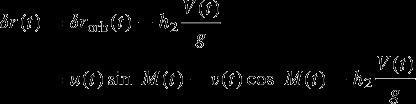where M(t) is the LRO true anomaly and V(t) the tidal potential, both known quantities.

The partial derivatives of the radial offset with respect to h₂ and the u, v parameters are trivial, and we accumulate the partial derivatives for all 354,840 crossover measurements into a normal equation. Before inverting the system, we add a second-derivative smoothing constraint that favors slow changes in the u and v parameters. In addition to preventing singularities in the original matrix for the few 2 h periods with no crossover, it yields less noisy time series for the orbital errors and more importantly guards against overfitting the data. The combined matrix is inverted using Cholesky decomposition, and we obtain the solution and its associated covariance matrix.

The estimated orbital errors closely follow the individual crossover offsets. The recombined radial amplitude 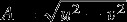, not shown, has a median value of 51 cm and a standard deviation of 1.26 m. Its magnitude and temporal behavior are consistent with the orbit overlap results of Mazarico et al. [2012]. The correlations of the u and v parameters with h₂ are very small (RMS <0.05, and a maximum less than 0.14). We also computed the variance inflation factor (VIF), which measures the multicolinearity and possible aliasing among model parameters. We obtained a VIF of 2.9, which is below the threshold of 5 for sufficient orthogonality recommended by Rogerson [2001], itself significantly more restrictive than the more commonly used value of 10 [Hair et al., ¹⁹⁹⁵]. This suggests that the estimated h₂ value is not significantly affected by colinearity with the u and v parameters.

3.3. Results

Figure 3b shows the same 2-D histogram after removing the contribution of the estimated orbital errors from the measured crossover radial offsets. The vertical scatter due to orbital errors is significantly reduced, bringing the overall RMS from 1.25 m to 0.39 m. The largest fit residuals occur near the poles where the predicted tidal signal is smallest, but where fluctuations in instrument temperature may start to affect the coalignment of the LOLA receiver telescope and beam expander.

It is clear that the signature of the radial deformation due to the tide is detected from the LOLA crossover data. The estimated Love number is h₂=0.0371, with a formal uncertainty of 0.0011 (or 3%). We obtained a similar uncertainty (0.0007) with a bootstrapping technique, by performing the inversion of 500 random resamplings of the full population. This estimated h₂ is 2% smaller than the a priori value from Williams et al. [2008] h₂=0.03786 ± 0.0076 (20% uncertainty) [Williams et al., ²⁰¹⁰], but we note that more recent interior models derived from LLR and GRAIL data inferred larger values: 0.0476 ± 0.0064 [Williams et al., ²⁰¹³] and 0.04240 (Williams et al., Lunar interior properties from the GRAIL mission, under review). We scale our formal uncertainty by a factor of 3 to avoid incompatibility with these values obtained from models that used the latest GRAIL k₂ results [Lemoine et al., ²⁰¹³; Konopliv et al., ²⁰¹³], resulting in an estimate of h₂=0.0371 ± 0.0033. However, we note that while the LLR data are sensitive to a variety of effects, the LOLA crossover data are more directly sensitive to the body tide itself.

4. Summary and Future Work

We analyzed ∼350,000 LOLA crossovers to obtain accurate relative displacements between track pairs at intersection locations. We can account for the radial displacements as the combined effects of body tide surface deformation and of errors in spacecraft position reconstruction. The latter are modeled as high-frequency parameters to enhance the recovery of the tidal Love number h₂. After least squares inversion of the LOLA crossover data, we obtained an h₂ value of 0.0371 ± 0.0033, which is consistent with recent estimates based on LLR data.

In future work we will improve the calibration of the nightside two-spot tracks to increase the number of usable crossovers and provide a more uniform temporal sampling. We will assess the spatial homogeneity of the surface deformation response to the forcing potential. Differences would reveal asymmetries in the lunar interior, which could have remained undetected by the nearside LLR data.