Skip to main content
PMC home page
Wiley Open Access Collection logoLink to Wiley Open Access Collection
. 2014 May 30;41(10):3367–3374. doi: 10.1002/2014GL060178

High-resolution local gravity model of the south pole of the Moon from GRAIL extended mission data

Sander Goossens 1,2, Terence J Sabaka 2, Joseph B Nicholas 2,3, Frank G Lemoine 2, David D Rowlands 2, Erwan Mazarico 2,4, Gregory A Neumann 2, David E Smith 4, Maria T Zuber 4
PMCID: PMC4459178  PMID: 26074637

Abstract

We estimated a high-resolution local gravity field model over the south pole of the Moon using data from the Gravity Recovery and Interior Laboratory's extended mission. Our solution consists of adjustments with respect to a global model expressed in spherical harmonics. The adjustments are expressed as gridded gravity anomalies with a resolution of 1/6° by 1/6° (equivalent to that of a degree and order 1080 model in spherical harmonics), covering a cap over the south pole with a radius of 40°. The gravity anomalies have been estimated from a short-arc analysis using only Ka-band range-rate (KBRR) data over the area of interest. We apply a neighbor-smoothing constraint to our solution. Our local model removes striping present in the global model; it reduces the misfit to the KBRR data and improves correlations with topography to higher degrees than current global models.

Key Points

  • We present a high-resolution gravity model of the south pole of the Moon

  • Improved correlations with topography to higher degrees than global models

  • Improved fits to the data and reduced striping that is present in global models

Keywords: lunar gravity, local analysis, GRAIL, planetary geodesy

1. Introduction

The Gravity Recovery and Interior Laboratory (GRAIL) mission was designed to map the structure of the lunar interior through high-precision global gravity mapping [Zuber et al., 2013a]. The mission was composed of two spacecraft with Ka-band intersatellite tracking as the single science instrument, complemented by tracking from Earth using the Deep Space Network (DSN) [Asmar et al., 2013]. The mission consisted of two phases: a primary mission which lasted from 1 March 2012 to 29 May 2012, during which the spacecraft had a mean altitude of 55 km above lunar surface, and an extended mission which lasted from 30 August 2012 to 14 December 2012. In the extended mission, the spacecraft had a mean altitude of 23 km above lunar surface until 18 November. After that, they were lowered to 20 km and finally to 11 km on 6 December. Initial analysis of the primary mission data resulted in a gravity field model in spherical harmonics of degree and order 420 [Zuber et al., 2013b], showing high correlations with topography up to high degrees and improving on the pre-GRAIL lunar gravity models such as those by Konopliv et al. [2001], Matsumoto et al. [2010], and Goossens et al. [2011], which were based on Lunar Prospector, Selenological and Engineering Explorer (SELENE), and other historical data. Subsequent analysis of the primary mission data resulted in models of degree and order 660 [Konopliv et al., 2013; Lemoine et al., 2013]. Owing to the much lower average altitudes above lunar surface in the extended mission, recent analysis has resulted in further improvements, in the form of models of degree and order 900 as presented by Konopliv et al. [2014] and Lemoine et al. [2014]. Both models have variable spatial resolution between degrees 600–680 over the central farside of the Moon to degree 900 at the poles. This variable spatial resolution of the gravity field is due to spacecraft altitude and ground track spacing [Konopliv et al., 2014]. Aliasing and relatively higher fits for the low-altitude part of the extended mission indicate that there is remaining signal in the Ka-band range-rate (KBRR) data even beyond degree 900. However, global spherical harmonics are not optimal when the spatial data coverage is heterogeneous, which is the case here at short wavelengths.

In instances where global models require a large number of parameters to describe high-resolution features, the estimation of these parameters may become unstable, and local representations can be of great utility: they have the potential to extract high-resolution information from the data, while not demanding the computational burden of determining a full global model of similar resolution. In satellite geodesy there is a long history of local representations that have been applied successfully to different data types from satellites orbiting various planetary bodies. Examples include analysis for Venus [Barriot and Balmino, 1992], Mars [Beuthe et al., 2006], and Jupiter's moon Ganymede [Anderson et al., 2004; Palguta et al., 2005], without even mentioning the many applications to Earth-orbiting satellites. Prior to the SELENE and GRAIL missions the tracking data distribution for the Moon was extremely asymmetrical with no farside data available, and thus, the Moon was especially suitable for the application of local methods, mostly using Lunar Prospector data: Sugano and Heki [,] and Goossens et al. [,] estimated anomalies while Han [2008] and Han et al. [2011] used localized spherical harmonic functions to model the nearside gravity field. These same functions were used by Goossens et al. [2012] to estimate the gravity field over the South Pole-Aitken basin on the farside of the Moon using SELENE data. In addition, local representations allow one to use constraints other than the spectral constraints often used in global gravity modeling [e.g., Rowlands et al., 2010; Sabaka et al., 2010].

The goal of the research presented here is to extract more information from the tracking data than can be modeled reasonably using global spherical harmonics. In the case of GRAIL KBRR data, our interest is especially in areas where the altitude of the spacecraft was low and/or where the coverage was dense. Both Konopliv et al. [2014] and Lemoine et al. [2014] show that the degree strength of their models is at the maximum degree at the poles because of the confluence of tracks. Therefore, we estimated a local gravity field model for the south pole of the Moon covering a cap of 40° radius, as adjustments to a global background model, at a resolution of 1/6° by 1/6° in both longitude and latitude, which is equivalent to the resolution of a degree and order 1080 model in spherical harmonics (spatial block size = 5 km).

2. Data and Methods

GRAIL data consist of both DSN tracking (both in two-way and one-way modes) and intersatellite KBRR. While DSN data mostly determine the absolute positioning of the satellites, it is the contribution of KBRR data acquired at low altitudes that has resulted in the unprecedented GRAIL model sizes. KBRR data in the extended mission have a sampling of 2 s. Because we aim to estimate local parameters in one area of the Moon, we choose to use only KBRR data over the area of interest, excluding DSN tracking altogether. It is well known that each KBRR observation from the Gravity Recovery and Climate Experiment (GRACE) and GRAIL missions is approximately directly proportional to the difference in gravity potential at the two satellite locations. This makes KBRR data ideal for estimating local parameters from a subset of the entire mission data set [Rowlands et al., 2005]. KBRR data outside the region do not contribute, and data inside the region do not contain significant information from outside the region.

Our analysis of the GRAIL extended mission KBRR data is based on the technique of Rowlands et al. [2002]. They showed that a short-arc analysis using KBRR data only is capable of recovering the underlying gravity field model. They used a baseline representation of the 12 parameters describing the difference vector between the two satellites and the state vector of the midpoint of the two satellites, instead of using the Cartesian inertial state vectors of the two satellites, all at the initial epoch. They showed that KBRR data are only sensitive to a subset of these baseline parameters, facilitating the coestimation of gravity parameters and orbit parameters from short arcs. This approach has been used successfully in the determination of monthly gravity solutions using GRACE data, for example Rowlands et al. [2005]; Luthcke et al. [2006], and later publications.

Since we adjust gravity parameters on a spherical cap at the south pole, and since the GRAIL satellites were in polar orbits, each orbit passes over the area and each arc covering the area is approximately 25 min long. Using the orbits from a global gravity field model (GRGM900A, a predecessor to the GRGM900C model discussed in Lemoine et al. [2014]), we create short arcs over the south pole area with initial conditions and other parameters from these orbits and then adjust only the baseline parameters to the KBRR data. We emphasize that in this baseline analysis, we do not use the DSN data. The baseline parameters we adjust are those given in Rowlands et al. [2002] as being most sensitive to the KBRR data: the pitch of the GRAIL A-B position baseline, the magnitude of the GRAIL A-B velocity baseline, and the pitch of the GRAIL A-B velocity baseline. We use the NASA Goddard Space Flight Center's (GSFC) GEODYN II Orbit Determination and Geodetic Parameter Estimation Program [Pavlis et al., 2013] for the short-arc analysis. We adjust only the three baseline parameters for the short arcs, and once these arcs are converged we use GEODYN again to generate the partial derivatives of the KBRR data points with respect to the adjusted baseline parameters and the chosen gravity parameters.

We represent local gravity as gravity anomalies on a regular grid of 1/6° by 1/6°. This resolution is equivalent to that of a degree and order 1080 expansion in spherical harmonics, and it was chosen in order to assess whether or not we could increase the resolution of our current global models (which are degree and order 900). For a cap of 40° radius (with a 1/6° of a degree cap on the south pole itself), this leads to the estimation of a total of 518,401 anomalies over the selected area, for which we use 992,080 KBRR data points from the extended mission. This means that the ratio of observations and parameters is less than two and that constraints will be important for the solution. We discuss the constraints below, and we discuss their influence on the solutions in section 3. Despite the fact that the longitudinal size of the grid cells physically decreases toward the pole, we did not compensate for this by decreasing the number of grid cells. Results in section 3 will show we do not see artifacts in this dense south pole grid.

Our gravity anomalies Δg are related to the disturbing potential T (from W = U + T, where W is the gravity potential and U the normal potential of a reference field) in the following way: in a spherical approximation, the anomaly can be expressed as a function of T through Δg =− ∂T/∂r − 2T/r, with r the spherical coordinate for radial distance. The potential T at a point P can be expressed in terms of anomalies Δg(Q) at points Q on an exterior boundary σas

graphic file with name grl0041-3367-m1.jpg 1

where R is the reference radius of the surface (1738 km in our case) and the kernel S(P,Q) is the Stokes-Pizetti kernel [Heiskanen and Moritz, 1984]. If the disturbing potential is expressed in spherical harmonics, and the anomalies are global, then both anomalies and standard spherical harmonics are completely equivalent, and anomalies can be expressed in spherical harmonics, with the anomalies carrying a factor (l − 1)in their expansion, where l is the degree.

The partial derivatives of KBRR data with respect to the anomalies can be constructed from the acceleration on the satellite, by differentiation of equation 1. When computing the acceleration contribution per anomaly (from which the partial derivative is also computed), we approximate the integral in equation 1 by a summation. For the integration over each separate anomaly in equation 1, each block (of size 1/6° by 1/6°) is divided into four subblocks (1/12° by 1/12°; except for 36 subblocks in the shape of wedges for the polar cap), and the integration is then approximated by the sum of the kernel function S(P,Q)evaluated at each center point of the subblock multiplied by the area of the subblock. This assumes that there are no anomaly contributions from outside of the chosen grid, which, in general, leads to boundary effects on the local solutions. This is further discussed in section 3.

Once the partial derivatives of the data with respect to all parameters are generated, the normal equation system is formed. Due to the size of the problem, we use the supercomputers of the NASA Center for Climate Simulation (NCCS) at NASA GSFC. We apply a neighbor-smoothing constraint to our solutions following Rowlands et al. [2010] and Sabaka et al. [2010]. These spatial constraints are straightforward: each anomaly pair is forced to be equal, but each constraint equation is only given a weight Wc,ij that decreases with increasing distance between the ith and jth anomalies, according to Wc,ij= exp(1 − dij/D) with dij being the distance between the two anomalies (computed from their center points), and D being the correlation distance, which was here set equal to the latitudinal size of each grid cell (which is thus the same for all anomalies because the grid is regular). We discuss these constraints further in section 3. We apply the smoothing constraint to the full anomaly field, i.e., on Δgglobal+Δgadj where Δgglobal is the vector with anomalies corresponding to the global spherical harmonics starting model and Δgadj is the vector with gravity anomalies for the adjustment. We apply the constraint to the full field (not just to the estimated gravity anomaly parameters) because the anomalies from GRGM900A show stripes (cf. Figure S1 in the supporting information). Once the constraint system is formed, it is added to the data system with a scaling factor μ, resulting in the following equation:

graphic file with name grl0041-3367-m2.jpg 2

where Ais the matrix with the partial derivatives of the data with respect to the parameters, Wd is the data weight matrix, Dis the matrix with partial derivatives of the constraints, Wc the constraint weight matrix with elements Wc,ij as defined above, rd is the vector with data residuals, and rc is the vector with constraint residuals which is expressed as rc=−DΔgglobal. The partial derivatives A and the data residuals rd are evaluated using orbits determined with the global field GRGM900A. The anomalies for the global field are computed from its spherical harmonics expansion. The baseline parameters are not included in Δgadj but are accounted for by a modification of the data weight matrix Wd (by taking into account their Schur complement), following Sabaka et al. [2010]. The baseline parameters are unconstrained and free to adjust.

Figure 1.

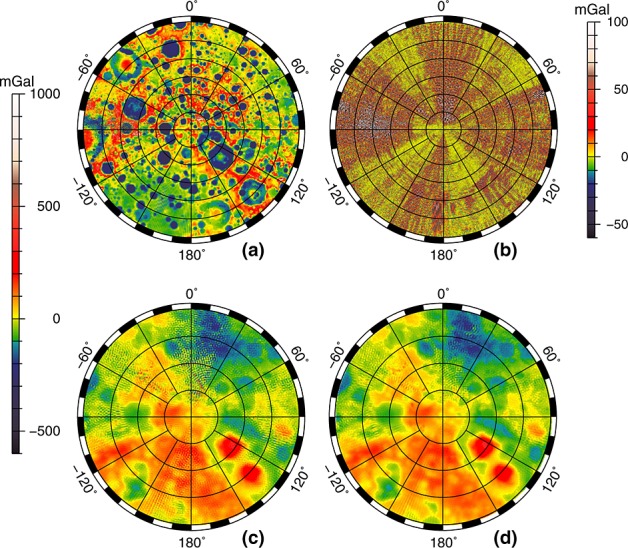
Figure 1

Open in a new tab

Maps in stereographic projection centered at the south pole for (a and b) free-air anomalies (up to 50°) and (c and d) Bouguer disturbances (up to 70°S). The local model is shown in Figure 1a, the difference between the local model and GRGM900A is shown in Figure 1b, GRGM900A (l = 7–900) is shown in Figure 1c, and a spherical harmonic transform of the local model (l = 7–900) is shown in Figure 1d.

3. Results

We processed the GRAIL extended mission data as outlined in the previous section. We had 1388 short arcs covering the selected south pole area. Our global starting gravity field model was GRGM900A. We weighted KBRR data at 0.1 μm/s throughout the entire extended mission because that is the level of fit with our current global models, but as in the processing of those models [Lemoine et al., 2014], we noted improvements when the low-altitude data were relatively downweighted. A factor of 0.5 on the normal system for the December arcs was found to give the best results in terms of data fit, anomaly patterns, and correlations with topography (all of which will be shown and explained below). We also experimented with the weight of the constraint system, denoted as μ in equation 2, and we found that a value of μ = 1·10−4 leads to the best overall results. We discuss this further at the end of this section.

Figure 1 shows free-air anomalies and Bouguer disturbances (the latter of which are related to the disturbing potential through δg =− ∂T/∂r, with a factor of (l + 1) in their spherical harmonic expansion, as opposed to the (l − 1)factor for anomalies) for our preferred local solution (Figures 1a and 1d for free air and Bouguer, respectively), Bouguer disturbances for GRGM900A (Figure 1c), and anomaly differences between the local solution and GRGM900A (Figure 1b). The free-air anomalies are shown up to 50°S, whereas the Bouguer disturbances are shown up to 70°S in order to focus on features close to the south pole. We also refer to Figures S2–S5 which show enlargements of these anomaly maps. The local model shows far fewer stripes than the global model, as the stripes in the difference map (Figure 1b) negate stripes in the anomaly map of GRGM900A (cf. Figure S1). We attribute this to our short-arc analysis where we adjust the orbit for each track, and, more importantly, to the neighbor smoothing that was applied to the full anomaly field, thus including the anomalies from the starting model. We also tested solutions with either a damping constraint (a diagonal constraint system, thus without neighbor smoothing) or with the neighbor smoothing applied to the adjustments only, and both solutions show more stripes in the anomalies. We also tested a neighbor-smoothing constraint with a varying correlation distance D (see section 2), where D was multiplied by the cosine of the latitude of the grid cell center point to account for varying size toward the pole. While this may slightly improve anomalies further away from the pole, the resulting small correlation distance at the pole leads to more striping in the solution there. An optimum between a constant and varying correlation distance may be found,but this was outside the scope of our current analysis. We also note that despite the decreasing physical size in longitude of the grid cells toward the pole, there are no apparent artifacts, likely thanks to the constant correlation distance applied.

Bouguer disturbances were computed by subtracting the contributions of topography to gravity, expressed in the same principal axis frame as gravity, using the formulation of Wieczorek and Phillips [1998]. We used Lunar Orbiter Laser Altimeter (LOLA) topography [Smith et al., 2010] archived in the Planetary Data System (LOLA/PDS Data Node, http://imbrium.mit.edu). We used a density of 2400 kg/m3 to account for the observed decrease in crustal density with higher degrees [Wieczorek et al., 2013; Han, 2013]. In order to compare two solutions of the same size so we can subtract the same topography-induced gravity potential, we generated global spherical harmonics for our local solution through a spherical harmonic transformation using Gauss-Legendre (GL) quadrature. We interpolated the adjustments Δgadj on a GL grid appropriate for a degree and order 1079 model, applied the spherical harmonic transformation, and constructed an updated global model by adding the resulting coefficients to the background global model. Our local model thus becomes a global model with a maximum size of degree and order 1079 which is only attained in the south pole area; elsewhere it is equivalent to the background model. For the Bouguer disturbances in Figure 1 we used both models up to degree 900. The Bouguer map for the local model shows fewer speckles and clearer features when compared to the map for the global model, which can help facilitate the geophysical interpretation of the structure of small-scale features [e.g., Zuber et al., 2014].

The free-air anomalies for the local solution in Figure 1a show a nonphysical speckle pattern at longitude 270°E, which is also where the adjustments are largest (Figure 1b). This is the area just below Mare Orientale where GRAIL attained its lowest altitudes above topography. We have indications that for these areas the current resolution of 1/6° by 1/6° of a degree is not sufficient to extract the full signal in the data [Zuber et al., 2014]. The speckle pattern is not as pronounced in the Bouguer disturbances in Figure 1, indicating that it appears beyond l = 900.

The fits to the KBRR data for the global and local models, using short arcs over the selected area for both, are shown in Figure 2. The fits for the local model were computed by adding the acceleration contributions of the adjustments Δgadj using equation 1 to the global model GRGM900A in the short-arc orbit determination. This shows that our local model fits the KBRR data better than the global starting model, sometimes by a considerable amount: on average, the fits improve by 12% for the whole extended mission and by 43% for the low December arcs only. There are still high fits for certain periods, most notably around 5 and 8 December, where the GRAIL satellites had their lowest periapsis heights. This indicates that information beyond degree and order 1080 is still present in the data, especially considering that the fit for those arcs is still well above the intrinsic noise levels of the data, which is thought to be between 0.05 and 0.07 μm/s (N. Harvey, Jet Propulsion Laboratory, Pasadena, CA, unpublished data, 2013). Figure 2 shows the fits for the last part of the GRAIL extended mission because the improvements are most clear there. The fits also improve for the earlier arcs in the extended mission, although there they are very close to the global model fits, at ∼0.12μm/s.

Figure 2.

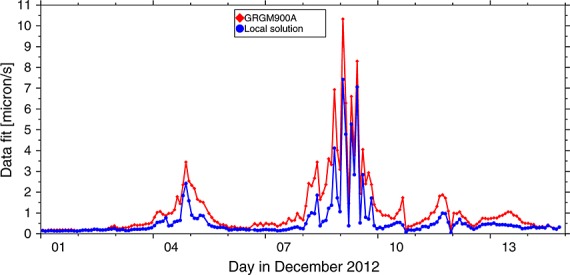
Figure 2

Open in a new tab

The root-mean-square (RMS) of fit to the KBRR data for GRGM900A and the local model, for the December arcs where the satellite altitude above topography was at its lowest.

Figure 3 shows correlations of various models (we again used the spherical harmonic transform for the local solution) with the gravity potential generated from topography. We show correlations localized over the south pole, following Wieczorek and Simons [2005], using a cap of 30°, with one taper and a concentration factor of 0.9999, resulting in a windowing function with Lwin=13. We chose the radius of 30° to avoid possible boundary effects at the edges of the solution, arising from the fact that we only use data over the area of interest, whereas data points close to the edge also contain information for unaccounted anomalies just beyond the grid. By testing small overlapping solutions, we found that the negative edge effects extend a few degrees at most, so our 10° cutoff is probably conservative.

Figure 3.

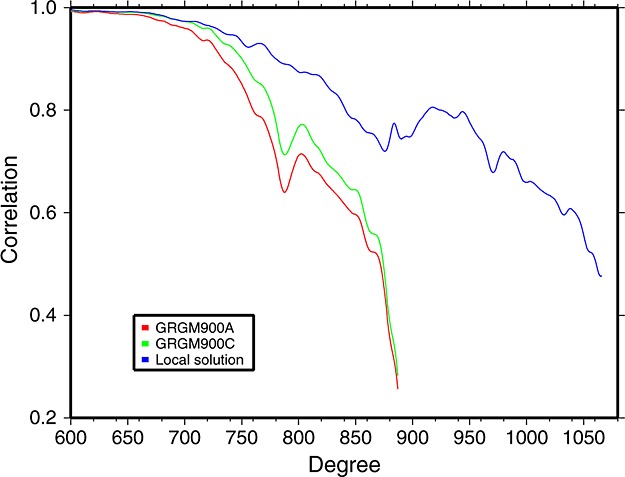
Figure 3

Open in a new tab

Localized correlations with topography-induced gravity for various gravity field models. The localization used a cap with a radius of 30° centered on the south pole.

Figure 3 shows that the local model improves the correlations with topography considerably, and extends them to higher degrees. We also included the correlations for GRGM900C, a more recent model than GRGM900A, to show that the local solution also has higher correlations than that global model. Such high correlations are indicative of the pervasive fracturing of the lunar crust [Zuber et al., 2013b]. These results indicate that the smoothness of the maps in Figure 1 captures real gravity information and is not only the expression of the neighbor-smoothing constraint.

Our solutions depend strongly on the data weights Wd and the scaling factor μ for the constraint system; cf. equation 2. We generated solutions with various weights for the December data and with various scaling factors μ. We found that while anomaly maps for μ = 1·10−3, in general, look smoother (they do not show as many stripes below the Mare Orientale area), such solutions do not fit the data well, nor do they maintain correlations with topography as high as the μ = 1·10−4 solution. To assess the contribution of the constraints to the solution, we decomposed the gradient component of equation 2 into two parts, one describing the data (ATWdrd) and one describing the constraints (μDTWcrc). We then computed two separate solutions, each with only one of these components as a right-hand side to the equation system, which otherwise was the same for both solutions (thus including the constraint equation system μDTWcD). These solutions indicate the contribution of each component to the final solution. These solutions are shown in the Figure S6, showing that the data largely influence anomalies in areas where the spacecraft were low and that the constraints largely influence the anomalies where GRGM900A showed stripes. Finally, downweighting the December normal system reduces the striping in the area south of Mare Orientale, yet using a factor of 1.0 rather than 0.5 slightly increases the correlations with topography. This again indicates information present in the data beyond our current resolution. However, the KBRR fits for such a solution in arcs other than the December arcs, especially earlier ones at slightly higher altitudes, are not as good as that for a solution using a factor 0.5, and often even higher than the fits for the starting model. For these reasons, a solution using a factor of 0.5 on the December system and a scaling factor of μ = 1·10−4 is our preferred solution. For future solutions we might increase the grid resolution (in certain areas) to account for the information present in the low-altitude data.

4. Summary

We presented a local model of the gravity field of the Moon over the south pole estimated from GRAIL extended mission data. Our model is expressed as gridded gravity anomalies with a resolution of 1/6° by 1/6°, covering a cap over the south pole with a radius of 40°. We estimated the anomalies from a short-arc analysis using only KBRR data. We applied a neighbor-smoothing constraint to obtain our solution. Our local model removes striping present in the global models, and it improves fits to the KBRR data. We also transformed our local anomalies into spherical harmonics using Gauss-Legendre quadrature. This facilitates the comparison of Bouguer disturbances between the local and global models, and it allows us to compute correlations with topography. Our local model shows improved correlations with topography up to higher degrees than the global models. The spherical harmonic transformation from the original anomaly grid also has the benefit that it is easier to produce gravity disturbances and to compute gradients. Due to increased resolution and extended high correlations with topography, maps of the lunar gravity field such as from our local south pole model have the potential to improve the geophysical interpretation of small-scale features on the Moon.

Acknowledgments

The data used in this analysis are available at the Geosciences Node of the Planetary Data System (http://pds-geosciences.wustl.edu/missions/grail/default.htm). This work was supported by the GRAIL Project under the auspices of the NASA Discovery Program, performed under contract to the Massachusetts Institute of Technology and the Jet Propulsion Laboratory, California Institute of Technology. This work made extensive use of the supercomputers of the NASA Center for Climate Simulation (NCCS) at NASA Goddard Space Flight Center, and we acknowledge their support. Localized correlations were computed using the freely available SHTOOLS library (http://shtools.ipgp.fr). All figures were generated with the free Generic Mapping Tools (GMT) software [Wessel and Smith, 1991].

The Editor thanks two anonymous reviewers for their assistance in evaluating this paper.

Supporting Information

Readme

grl0041-3367-sd1.txt (3.4KB, txt)

Figures S1

grl0041-3367-sd2.pdf (4.5MB, pdf)

Figures S2

grl0041-3367-sd3.pdf (4.2MB, pdf)

Figures S3

grl0041-3367-sd4.pdf (7.5MB, pdf)

Figures S4

grl0041-3367-sd5.pdf (1.2MB, pdf)

Figures S5

grl0041-3367-sd6.pdf (910.5KB, pdf)

Figures S6

grl0041-3367-sd7.pdf (6.7MB, pdf)

References

  1. Anderson J D, Schubert G, Jacobson R A, Lau E L, Moore W B. Palguta J L. Discovery of mass anomalies on Ganymede. Science. 2004;305:989–991. doi: 10.1126/science.1099050. [DOI] [PubMed] [Google Scholar]
  2. Asmar SW. The scientific measurement system of the Gravity Recovery and Interior Laboratory (GRAIL) mission. Space Sci. Rev. 2013;178(1):25–55. doi:10.1007/s11214-013-9962-0. [Google Scholar]
  3. Barriot J P. Balmino G. Estimation of local planetary gravity fields using line of sight gravity data and an integral operator. Icarus. 1992;99(1):202–224. [Google Scholar]
  4. Beuthe M, Rosenblatt P, Dehant V, Barriot J -P, Pätzold M, Häusler B, Karatekin O, Maistre S L. van Hoolst T. Assessment of the Martian gravity field at short wavelength with Mars Express. Geophys. Res. Lett. 2006;33 L03203, doi:10.1029/2005GL024317. [Google Scholar]
  5. Goossens S, Visser P N A M. Ambrosius B A C. A method to determine regional lunar gravity fields from earth-based satellite tracking data. Planet. Space Sci. 2005a;53:1331–1340. [Google Scholar]
  6. Goossens S, Visser P N A M, Heki K. Ambrosius B A C. Local gravity from Lunar Prospector tracking data: Results for Mare Serenitatis. Earth Planets Space. 2005b;57(11):1127–1132. [Google Scholar]
  7. Goossens S. Lunar gravity field determination using SELENE same-beam differential VLBI tracking data. J. Geod. 2011;85:205–228. doi:10.1007/s00190-010-0430-2. [Google Scholar]
  8. Goossens S, Ishihara Y, Matsumoto K. Sasaki S. Local lunar gravity field analysis over the South Pole-Aitken basin from SELENE farside tracking data. J. Geophys. Res. 2012;117 E02005, doi:10.1029/2011JE003831. [Google Scholar]
  9. Han S -C. Improved regional gravity fields on the Moon from Lunar Prospector tracking data by means of localized spherical harmonic functions. J. Geophys. Res. 2008;113 , E11012, doi:10.1029/2008JE003166. [Google Scholar]
  10. Han S -C. Determination and localized analysis of intersatellite line of sight gravity difference: Results from the GRAIL primary mission. J. Geophys. Res. Planets. 2013;118:2323–2337. , doi:10.1002/2013JE004402. [Google Scholar]
  11. Han S -C, Mazarico E, Rowlands D D, Lemoine F G. Goossens S. New analysis of Lunar Prospector radio tracking data brings the nearside gravity field of the Moon with an unprecedented resolution. Icarus. 2011;215(2):455–459. doi:10.1016/j.icarus.2011.07.020. [Google Scholar]
  12. Heiskanen W A. Moritz H. Physical Geodesy. Graz, Austria: Institute of Physical Geodesy; 1984. , and . (Original edition by W. H Freeman and Company, San Francisco, Calif., 1967.) [Google Scholar]
  13. Konopliv A S, Asmar S W, Carranza E, Sjogren W L. Yuan D N. Recent gravity models as a result of the Lunar Prospector mission. Icarus. 2001;150:1–18. [Google Scholar]
  14. Konopliv AS. The JPL lunar gravity field to spherical harmonic degree 660 from the GRAIL Primary Mission. J. Geophys. Res. Planets. 2013;118:1415–1434. doi:10.1002/jgre.20097. [Google Scholar]
  15. Konopliv AS. High-resolution lunar gravity fields from the GRAIL primary and extended missions. Geophys. Res. Lett. 2014;41:1452–1458. doi: 10.1002/2014GL060027. doi:10.1002/2013GL059066. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Lemoine FG. High-degree gravity models from GRAIL primary mission data. J. Geophys. Res. Planets. 2013;118:1676–1698. doi:10.1002/jgre.20118. [Google Scholar]
  17. Lemoine FG. GRGM900C: A degree-900 lunar gravity model from GRAIL primary and extended mission data. Geophys. Res. Lett. 2014 doi: 10.1002/2014GL060027. doi:10.1002/2014GL060027. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Luthcke S B, Rowlands D D, Lemoine F G, Klosko S M, Chinn D. McCarthy J J. Monthly spherical harmonic gravity field solutions determined from GRACE inter-satellite range-rate data. Geophys. Res. Lett. 2006;33 L02402, doi:10.1029/2005GL024846. [Google Scholar]
  19. Matsumoto K. An improved lunar gravity field model from SELENE and historical tracking data: Revealing the farside gravity features. J. Geophys. Res. 2010;115 E06007, doi:10.1029/2009JE003499. [Google Scholar]
  20. Palguta J, Anderson J D, Schubert G. Moore W B. Mass anomalies on Ganymede. Icarus. 2005;180(2):428–441. doi:10.1016/j.icarus.2005.08.020. [Google Scholar]
  21. Pavlis D E, Wimert J. McCarthy J J. GEODYN II system description, vol. 1–5. 2013. Contractor Report, SGT Inc., Greenbelt, Md.
  22. Rowlands D D, Ray R D, Chinn D S. Lemoine F G. Short-arc analysis of intersatellite tracking data in a gravity mapping mission. J. Geod. 2002;76:307–316. [Google Scholar]
  23. Rowlands D D, Luthcke S B, Klosko S M, Lemoine F G R, Chinn D S, McCarthy J J, Cox C M. Anderson O B. Resolving mass flux at high spatial and temporal resolution using GRACE intersatellite measurements. Geophys. Res. Lett. 2005;32 L04310, doi:10.1029/2004GL021908. [Google Scholar]
  24. Rowlands D D, Luthcke S B, McCarthy J J, Klosko S M, Chinn D S, Lemoine F G, Boy J -P. Sabaka T J. Global mass flux solutions from GRACE: A comparison of parameter estimation strategies—Mass concentrations versus Stokes coefficients. J. Geophys. Res. 2010;115 B01403, doi:10.1029/2009JB006546. [Google Scholar]
  25. Sabaka T J, Rowlands D D, Luthcke S B. Boy J -P. Improving global mass flux solutions from Gravity Recovery and Climate Experiment (GRACE) through forward modeling and continuous time correlation. J. Geophys. Res. 2010;115 B114033, doi:10.1029/2010JB007533. [Google Scholar]
  26. Smith DE. Initial observations from the Lunar Orbiter Laser Altimeter (LOLA) Geophys. Res. Lett. 2010;37 doi: 10.1002/2013GL059085. L18204, doi:10.1029/2010GL043751. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Sugano T. Heki K. High resolution gravity anomaly map from the Lunar Prospector line-of-sight acceleration data. Earth Planets Space. 2004a;56:81–86. [Google Scholar]
  28. Sugano T. Heki K. Isostasy of the Moon from high-resolution gravity and topography data: Implication for its thermal history. Geophys. Res. Lett. 2004b;31 L24703, doi:10.1029/2004GL022059. [Google Scholar]
  29. Wessel P. Smith W H F. Free software helps map and display data. Eos Trans. AGU. 1991;72:441–444. [Google Scholar]
  30. Wieczorek M A. Phillips R J. Potential anomalies on a sphere: Applications to the thickness of the lunar crust. J. Geophys. Res. 1998;103(E1):1715–1724. [Google Scholar]
  31. Wieczorek M A. Simons F J. Localized spectral analysis on the sphere. Geophys. J. Int. 2005;162:655–675. doi:10.1111/j.1365-246X.2005.02687.x. [Google Scholar]
  32. Wieczorek MA. High-resolution estimates of lunar crustal density and porosity from the GRAIL extended mission. Abstract 1914, presented at 44th Lunar and Planetary Science Conference, 18–22 Mar., The Woodlands, Tex. 2013 , et al. ( [Google Scholar]
  33. Zuber M T, Smith D E, Lehman D H, Hoffman T L, Asmar S W. Watkins M M. Gravity Recovery and Interior Laboratory (GRAIL): Mapping the lunar interior from crust to core. Space Sci. Rev. 2013a;178(1):3–24. doi:10.1007/s11214-012-9952-7. [Google Scholar]
  34. Zuber MT. Gravity field of the Moon from the Gravity Recovery and Interior Laboratory (GRAIL) mission. Science. 2013b;339(6120):668–671. doi: 10.1126/science.1231507. doi:10.1126/science.1231507. [DOI] [PubMed] [Google Scholar]
  35. Zuber MT. A high-resolution view of the Orientale basin and surroundings from the Gravity Recovery and Interior Laboratory (GRAIL) Abstract 2061, presented at 45th Lunar and Planetary Science Conference, 17–21 Mar., The Woodlands, Tex. 2014 , et al. ( [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Readme

grl0041-3367-sd1.txt (3.4KB, txt)

Figures S1

grl0041-3367-sd2.pdf (4.5MB, pdf)

Figures S2

grl0041-3367-sd3.pdf (4.2MB, pdf)

Figures S3

grl0041-3367-sd4.pdf (7.5MB, pdf)

Figures S4

grl0041-3367-sd5.pdf (1.2MB, pdf)

Figures S5

grl0041-3367-sd6.pdf (910.5KB, pdf)

Figures S6

grl0041-3367-sd7.pdf (6.7MB, pdf)

Articles from Geophysical Research Letters are provided here courtesy of Wiley

RESOURCES