Rising atmospheric CO₂ leads to large impact of biology on Southern Ocean CO₂ uptake via changes of the Revelle factor

Abstract

The Southern Ocean is a key region for global carbon uptake and is characterized by a strong seasonality with the annual CO₂ uptake being mediated by biological carbon drawdown in summer. Here we show that the contribution of biology to CO₂ uptake will become even more important until 2100. This is the case even if biological production remains unaltered and can be explained by the decreasing buffer capacity of the ocean as its carbon content increases. The same amount of biological carbon drawdown leads to a more than twice as large reduction in CO_2(aq) concentration and hence to a larger CO₂ gradient between ocean and atmosphere that drives the gas exchange. While the winter uptake south of 44°S changes little, the summer uptake increases largely and is responsible for the annual mean response. The combination of decreasing buffer capacity and strong seasonality of biological carbon drawdown introduces a strong and increasing seasonality in the anthropogenic carbon uptake.

Key Points

• Decrease of buffer capacity leads to stronger summer CO₂ uptake in the future

• Biology will contribute more to future CO₂ uptake in Southern Ocean

• Seasonality affects anthropogenic carbon uptake strongly

1. Introduction

The global ocean takes up about a quarter of current CO₂ emissions [Le Quéré et al., ²⁰¹⁴]. The ocean can take up more CO₂ from the atmosphere than expected for an inert gas (such as oxygen and nitrogen) because CO₂ reacts with seawater. An equilibrium comes into place:

(1)

and only 1% of the CO₂ that was taken up as a gas remains in the form of CO_2(aq). This property of the carbonate system is known as buffering and can be quantified using the Revelle factor, R [Revelle and Suess, ¹⁹⁵⁷]:

(2)

The Revelle factor R is the ratio of the relative change of seawater pCO₂ (or, alternatively, CO_2(aq)) to the relative change of dissolved inorganic carbon (DIC, the sum of CO_2(aq), HCO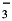 and CO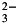) [Zeebe and Wolf-Gladrow, ²⁰⁰¹; Egleston et al., ²⁰¹⁰]. It varies between 8 in warm and 15 in cold waters [Broecker et al., ¹⁹⁷⁹]. The lower the Revelle factor, the more efficient is the anthropogenic CO₂ uptake [Völker et al., ²⁰⁰²; Sabine et al., ²⁰⁰⁴]. As the ocean continues to take up CO₂, the carbonate system is pushed toward higher CO_2(aq) concentrations and the Revelle factor increases [Zeebe and Wolf-Gladrow, ²⁰⁰¹]. Consequently, the buffer capacity of the ocean and its CO₂ uptake capacity decrease. This is a positive feedback limiting the increase of the ocean CO₂ sink in the future [Wallace, ²⁰⁰¹].

The Southern Ocean turned from a source of CO₂ in preindustrial times into a CO₂ sink, today being the key region for CO₂ uptake together with the North Atlantic. It is the strong uptake of anthropogenic carbon [Khatiwala et al., ²⁰⁰⁹] that nearly balances the outgassing of natural carbon and results in a net CO₂ sink [Gruber et al., ²⁰⁰⁹]. The contemporary CO₂ flux is characterized by a strong seasonality driven by deep winter mixing and photosynthesis in summer [Takahashi et al., ²⁰⁰⁹]. The Southern Ocean is a CO₂ source in winter and a CO₂ sink in summer [Lenton et al., ²⁰¹³] highlighting the importance of biological carbon drawdown in summer [Bakker et al., ¹⁹⁹⁷]. The effect of seasonal temperature variability on the solubility of CO₂ would work in the opposite direction and is apparently of secondary role in the Southern Ocean [Takahashi et al., ²⁰⁰²].

In this study we will show that the seasonal drawdown of carbon by biological production will contribute an even larger share to total CO₂ uptake as the Revelle factor increases toward the end of the century. Our analysis focuses on the Southern Ocean, a key region for global carbon uptake, but the process might be at work in all regions governed by strong seasonality.

2. Model

We use the Massachusetts Institute of Technology general circulation model (MITgcm) [Marshall et al., ¹⁹⁹⁷; Massachusetts Institute of Technology General Circulation Model Group, ²⁰¹⁴] with a state-of-the-art sea ice model [Losch et al., ²⁰¹⁰] coupled to the Regulated Ecosystem Model with two phytoplankton classes (REcoM-2). The horizontal resolution is 2° in longitude and 0.38 to 2° in latitude, with the higher resolution in the Southern Ocean and at the equator. The thickness of the vertical layers is 10 m at the surface, increasing downward to 500 m at a depth of 3700 m. Eddies are parameterized, using the Gent and McWilliams [1990] formulation. REcoM-2 carries 21 prognostic tracers, including dynamic intracellular pools of carbon, chlorophyll, nitrogen, and silicate (for diatoms) for the two phytoplankton classes (nanophytoplankton and diatoms) [Geider et al., ¹⁹⁹⁸] as well as actively advected detritus carbon, nitrogen, and silicate pools. Iron is taken up by the cells in a fixed ratio to carbon. CO₂ gas exchange across the air-sea interface considers chemical enhancement [Wanninkhof, ¹⁹⁹²]. More details on the ocean and ecosystem model setup and present-day validation is given in Hauck et al. [2013a].

The future simulation of the period 2011 to 2100 is started from a hindcast of the period 1948-2010 [Hauck et al., ^2013a] that was preceded by a 47 year spin-up. The 6-hourly atmospheric forcing fields are obtained from the Model for Interdisciplinary Research on Climate (MIROC5) Representative Concentration Pathway 8.5 scenario (RCP8.5) simulation that is available from the Coupled Model Intercomparison Project phase 5 (CMIP5) archive [Watanabe et al., ²⁰¹¹].

The atmospheric CO₂ concentration follows the RCP8.5 scenario [Meinshausen et al., ²⁰¹¹] in the standard model run (RCP85). In an additional simulation (CONST), atmospheric CO₂ is kept constant at the preindustrial concentration of 278 ppm. Both simulations experience climate change as projected by the MIROC5 atmospheric fields.

Results will be presented in three latitudinal bands following RECCAP protocols [Lenton et al., ²⁰¹³]. The region south of 58°S refers to the Antarctic Zone south of the Polar Front; a latitudinal band between 44°S and 58°S spans large parts of the subantarctic and polar frontal zones and includes the polar front itself. The zonal band between 30°S and 44°S consists of the subtropical zone, with a minor contribution from the subantarctic zone.

3. Results

Figure 1 depicts the time series of CO₂ fluxes in the RCP85 and CONST simulations as well as their mean seasonal cycle for the beginning and end of the simulations. There is a general increase of CO₂ uptake in RCP85 as expected from increasing atmospheric CO₂ concentrations.

Figure 1.

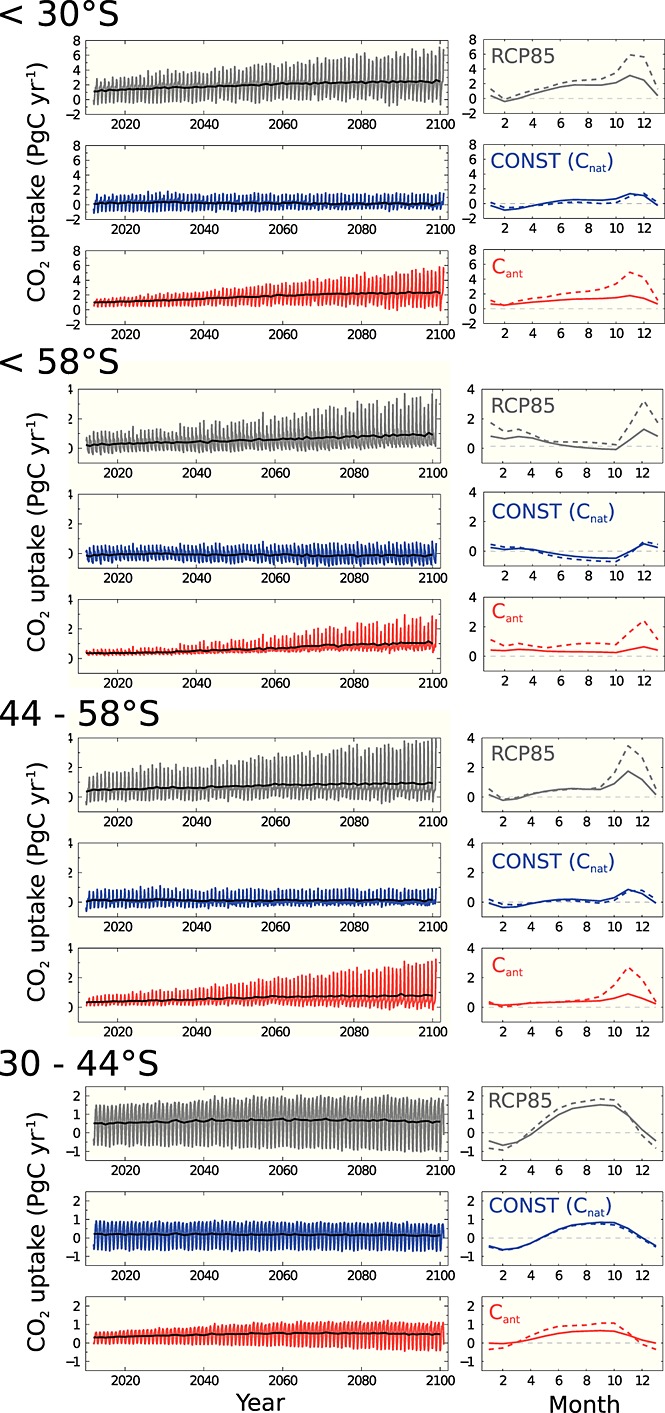
(first column) Monthly time series of CO₂ uptake in the model simulations following the RCP8.5 scenario (RCP85, dark grey), in the scenario with constant atmospheric CO₂ (CONST, equivalent to natural CO₂ flux, blue) and the difference between the two simulations (anthropogenic CO₂ flux, red) in MITgcm-REcoM-2 averaged over the full Southern Ocean (<30°S), and the subregions <58°S, 44°S–58°S, and 30°S–44°S as indicated in the figures. The annual mean is overlain in black. (second column) The mean seasonal cycle of CO₂ uptake for the periods 2012–2031 (line) and 2081–2100 (dashed) in the same regions and model runs. January is shown as the first and again as the last month of the seasonal cycle.

More surprisingly, the amplitude of the seasonal cycle increases in all subregions of the Southern Ocean in RCP85. The CONST simulation does not exhibit this behavior. In the regions south of 44°S, the strong summer CO₂ uptake drives the annual mean increase with winter CO₂ uptake changing only little (Figure 1, second column). The absence of this effect in the CONST simulation demonstrates that the strengthening of the seasonal cycle is not a response of biology to changing climate and altered resource availability. This implies that (1) the change in the integrated Southern Ocean CO₂ uptake is to a large part driven by changes in anthropogenic CO₂ flux, i.e., by the increase of atmospheric CO₂ itself and only to a smaller degree by circulation changes that are expected to occur in the Southern Ocean [e.g., Le Quéré et al., ²⁰⁰⁷; Hauck et al., ^2013a] and that (2) future CO₂ uptake has a strong seasonality that becomes more important toward the end of the century.

The peak of CO₂ uptake occurs in November to January (south of 58°S) and October to December (44°S–58°S, Figure 1, second column). This coincides with the peak of carbon drawdown by biological production in these regions (Figure 2).

Figure 2.

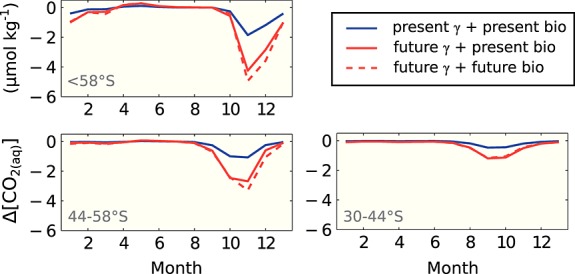
Effect of buffer factor on CO_2(aq) drawdown by biology calculated as in equation (4). Blue: CO₂ drawdown with present-day buffer factor and biological carbon drawdown (gross primary production minus respiration minus remineralization). Red: future buffer factor and present-day biological carbon drawdown. Red, dashed: future buffer factor and future biological carbon drawdown. Present day: mean seasonal cycle 2012 to 2031, future: 2081 to 2100. Change in buffer factor has a much larger effect on CO_2(aq) drawdown (and hence CO₂ uptake) than increase in biological production. January is shown as the first and again as the last month of the seasonal cycle.

We explain this emergent strengthening of seasonality in CO₂ uptake by the increase of the Revelle factor over the course of the century (Figure 3) that brings the system into a new state, which is less well buffered and therefore more sensitive to seasonal DIC variations [Riebesell et al., ²⁰⁰⁹; Egleston et al., ²⁰¹⁰]. As a consequence, the summer DIC drawdown by biology leads to a stronger decrease in CO_2(aq). As it is the CO_2(aq) concentration (and not DIC concentration) that controls the gas exchange with the atmosphere, this allows more CO₂ to be taken up by the ocean. In other words, the same amount of biological production leads to a stronger CO₂ uptake at the end of the century than at the beginning of the simulation. An increase of export production south of 44°S apparent in our model simulation reinforces this effect, yet the buffer factor is driving it.

Figure 3.

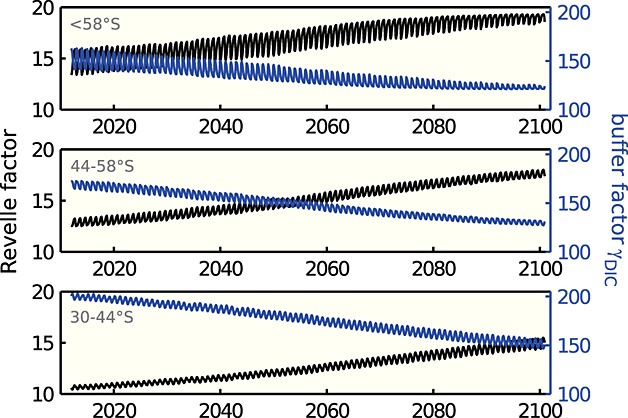
Monthly time series of Revelle factor (black, unitless) and buffer factor γ_DIC (blue, μmol kg⁻¹) [Egleston et al., ²⁰¹⁰] for the RCP8.5 scenario in the period 2012 to 2100 and the regions <58°S, 44°S–58°S, and 30°S–44°S as indicated in the figures.

This is illustrated in Figure 2 where we use the mean surface carbonate system from REcoM-2 for the periods 2012–2031 and 2081–2100 to calculate the sensitivity of aqueous CO₂ concentration [CO_2(aq)] to DIC perturbations using the buffer factor γ_DIC which is linked to the Revelle factor via

(3)

an can be explicitly derived from the carbonate system parameters [Egleston et al., ²⁰¹⁰]. The decrease of the buffer capacity that is described by an increase in the Revelle factor manifests itself as a decrease in the buffer factor γ_DIC (Figure 3). The reduction in [CO_2(aq)] due to biological carbon drawdown is then calculated as

(4)

where ΔDIC is the carbon drawdown by biological production in the top 100 m layer of the ocean taken from REcoM-2 (as gross primary production minus remineralization minus respiration). The total CO_2(aq) drawdown by biology integrated over the year increases by a factor of 2.3, 2.5, and 2.6 due to changes in the buffer factor for the regions <58°S, 44–58°S, and 30–44°S, respectively (calculated as Δ[CO_2(aq)]^{2081 − 2100}/Δ[CO_2(aq)]^{2012 − 2031}). The contribution of altered biological production is small as indicated by similar numbers for the combined effects of production and buffer capacity changes (2.7, 2.9, and 2.5 from south to north, Figure 2).

North of 44°S, summer outgassing of CO₂ becomes stronger and the amplitude of the seasonal cycle widens in both directions. The Revelle factor is still lower than in the other two regions, so that the buffer effect on CO_2(aq) drawdown is smaller in absolute numbers in this region (Figure 2). As the buffer capacity of the system decreases, the system reacts stronger to DIC perturbations, but biology is only one factor among others and seasonality is not as pronounced as in the other regions. The source minus sink term for DIC becomes positive after the spring bloom, leading to (stronger) outgassing of CO₂ in the less well-buffered system in austral summer (January and February).

4. Discussion

The increase of the Revelle factor with rising pCO₂ acts as a strong positive feedback, reducing potential CO₂ uptake in the ocean in the future [Wallace, ²⁰⁰¹]. The other side of the coin, however, is that CO_2(aq) becomes more sensitive to DIC variations as pCO₂ rises, such that a strong seasonal drawdown of DIC is responsible for the increasing CO₂ uptake. This is particularly relevant in systems with a strong seasonality such as the high latitudes where darkness inhibits biological production in winter.

The buffer factor γ_DIC reaches its theoretical minimum of 120 μmol kg⁻¹in winter in the region <58°S at the end of the simulation. The buffer factor has a minimum when alkalinity approximately equals DIC or in other words when the system is equally distant from both pK values [see Egleston et al., ²⁰¹⁰]. Based on this concept, we would expect that the buffer capacity would further decrease in the regions 30°S–44°S and 44°S–58°S beyond 2100 (assuming constant alkalinity, note that alkalinity is not expected to increase strongly in the Southern Ocean as carbonate sediments are sparse [Hauck et al., ^2013b]). The buffer capacity south of 58°S would rise again with further CO₂ uptake after the system passed through the minimum.

In the literature the concept of so-called natural and anthropogenic CO₂ is used recurrently [e.g., Sarmiento et al., ¹⁹⁹²]. The natural CO₂ (C_nat) flux describes the CO₂ exchange between ocean and atmosphere in preindustrial times at an atmospheric CO₂ concentration of 278 μatm. The concept assumes that this background flux is today overlain by an uptake of anthropogenic CO₂(C_ant) which is not affected by biology and/or seasonal variability. (however, Rodgers et al. [2008] and Gorgues et al. [2010] demonstrate that there is a seasonality of C_ant uptake at present). Indeed, the seasonal cycle of C_ant uptake that can be explicitly simulated in the model (RCP85 − CONST) is smaller than the seasonal cycle of C_nat uptake at the beginning of the simulation (Figure 1).

In the Southern Ocean, CO₂ is taken up from the atmosphere when biology draws down carbon in spring and summer. As the Revelle factor increases due to anthropogenic CO₂ emissions, seasonality becomes more important and the peak CO₂ uptake is evident in the anthropogenic carbon flux (Figure 1). A strong seasonal amplitude in C_ant flux is established which becomes larger than the seasonal amplitude of C_nat uptake after approximately 2050. This implies that biological processes impact anthropogenic CO₂ uptake, and this effect becomes more important as time and emissions progress.

We would like to note that typical methods for calculating anthropogenic carbon (based on DIC or CFC measurements) that implicitly assume that biologically induced carbon fluxes do not change C_ant uptake [e.g., Wallace, ¹⁹⁹⁵; Gruber et al., ¹⁹⁹⁶; Goyet et al., ¹⁹⁹⁹; Touratier and Goyet, ²⁰⁰⁴; Friis et al., ²⁰⁰⁵; Waugh et al., ²⁰⁰⁶] might become biased in the future. While this was observed previously [Goodkin et al., ²⁰¹¹], we propose that this is due to the increased importance of the biological carbon pump for CO₂ uptake. The same amount of biological production and hence nutrient uptake leads to more CO₂ uptake per buildup of biomass in the future. This questions the basic assumption that anthropogenic carbon can be calculated from the DIC concentration after applying a correction for biological production based on a linear relationship between nutrients and carbon. In contrast, we show that anthropogenic carbon is directly affected by nutrient variability or seasonality when taken as a proxy for biological production (Figure 1). To demonstrate this point, we calculate the C_ant inventory using the extended multiple regression method (eMLR) method [Friis et al., ²⁰⁰⁵] with the parameters potential temperature, alkalinity, and nitrate from the RCP85 simulation (Figure 4, see supporting information for details of calculation). There is an increasing gap between the C_ant inventory as simulated with the model (RCP85 −CONST) and that calculated using the eMLR method. We ascribe this to the impact of biology on C_ant uptake that is not accounted for by the method. We hypothesize that other methods that are based on the assumption of a linear and constant relationship between either carbon and nutrients or possibly carbon and CFCs (biology does impact uptake of CO₂ but not of CFCs) may experience similar problems, but leave this to be tested in future work.

Figure 4.

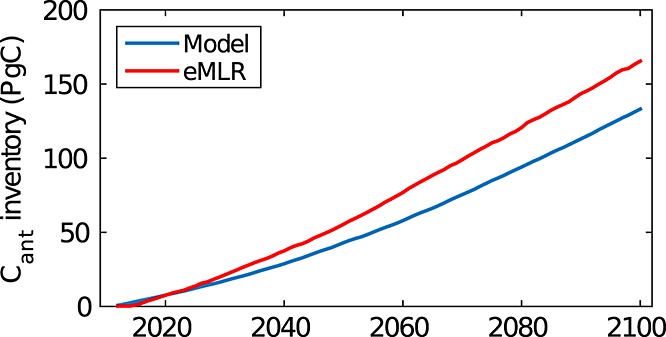
Buildup of C_ant inventory (Pg C) relative to the reference year 2011 as simulated with the model (blue, RCP85 − CONST) and as calculated with the eMLR method from the RCP85 simulation using the parameters theta, alkalinity, and dissolved inorganic nitrogen (red). See supporting information for details of eMLR calculation.

Biology will contribute substantially more to CO₂ uptake as the buffer capacity decreases. We demonstrate this in an example calculation using model output (Figure 2). While the timing and magnitude of the described effect is model dependent, the underlying carbonate chemistry is well understood [Zeebe and Wolf-Gladrow, ²⁰⁰¹; Egleston et al., ²⁰¹⁰], and this is an intrinsic feature of the carbonate system.

Supporting Information

Text S1