Skip to main content
PMC home page
Wiley Open Access Collection logoLink to Wiley Open Access Collection
. 2014 May 29;41(10):3382–3389. doi: 10.1002/2014GL060027

GRGM900C: A degree 900 lunar gravity model from GRAIL primary and extended mission data

Frank G Lemoine 1, Sander Goossens 1,2, Terence J Sabaka 1, Joseph B Nicholas 1,3, Erwan Mazarico 1,4, David D Rowlands 1, Bryant D Loomis 1,5, Douglas S Chinn 1,5, Gregory A Neumann 1, David E Smith 4, Maria T Zuber 4
PMCID: PMC4459205  PMID: 26074638

Abstract

We have derived a gravity field solution in spherical harmonics to degree and order 900, GRGM900C, from the tracking data of the Gravity Recovery and Interior Laboratory (GRAIL) Primary (1 March to 29 May 2012) and Extended Missions (30 August to 14 December 2012). A power law constraint of 3.6 ×10−4/ℓ2 was applied only for degree ℓ greater than 600. The model produces global correlations of gravity, and gravity predicted from lunar topography of ≥ 0.98 through degree 638. The model's degree strength varies from a minimum of 575–675 over the central nearside and farside to 900 over the polar regions. The model fits the Extended Mission Ka-Band Range Rate data through 17 November 2012 at 0.13 μm/s RMS, whereas the last month of Ka-Band Range-Rate data obtained from altitudes of 2–10 km fit at 0.98 μm/s RMS, indicating that there is still signal inherent in the tracking data beyond degree 900.

1. Introduction

The twin spacecraft of the NASA Discovery Gravity Recovery and Interior Laboratory (GRAIL) mission mapped the gravity field of the Moon in two phases: during the Primary Mission (1 March to 29 May 2012) from a mean altitude of 55 km and during the Extended Mission (30 August to 14 December 2012) from a mean altitude of 23 km [Zuber et al., 2013a, 2013b]. The main data produced by GRAIL include the Ka-Band Range-Rate (KBRR) data between the two satellites, acquired by the GRAIL Lunar Gravity Ranging System and the Doppler data from the antennae of the Deep Space Network (DSN) that tracked the spacecraft in lunar orbit from the Earth [Asmar et al., 2013; Klipstein et al., 2013].

Initial analysis of the GRAIL Primary Mission data led to spherical harmonic models complete to degree and order 420 [Zuber et al., 2013c] that improved on the pre-GRAIL gravity models derived from Lunar Prospector, Kaguya, and other historical data [Konopliv et al., 2001; Matsumoto et al., 2010] by a factor of 3 to 4 in spatial resolution, and 3 to more than 5 orders of magnitude in quality. Subsequently, more detailed analyses of the Primary Mission data by the GRAIL gravity teams at the Jet Propulsion Laboratory (JPL), and the NASA Goddard Space Flight Center (NASA GSFC), produced models to degree 660 in spherical harmonics, GL0660B [Konopliv et al., 2013] and GRGM660PRIM [Lemoine et al., 2013]. This paper describes GRGM900C, a lunar gravity solution to degree and order 900 in spherical harmonics (resolving spatial blocks of 6 km) obtained from the analysis of the Primary and Extended Mission data by the NASA GSFC GRAIL gravity team. The JPL GRAIL gravity team solution to degree 900 is described by Konopliv et al. [2014]. The degree 900 models developed by the two gravity teams differ in terms of the orbit determination software used, a priori models, data editing, and parameter estimation strategies.

2. Extended Mission Summary

During GRAIL's Extended Mission, the GRAIL spacecraft orbits were maintained within a tight band of apoapse and periapse altitudes. From 30 August to 17 November 2012 the minimum periapse altitude ranged from 10 to 20 km and the apoapse altitude from 25 to 35 km. From 17 November 2012 through the end of the mission, the periapse altitude generally ranged from 5 to 10 km while the apoapse altitude ranged from 15 to 25 km. The low altitude of the GRAIL spacecraft made the mission operations more complex, requiring sometimes as many as three maneuvers per week to maintain the desired orbit [Sweetser et al., 2012; Ryne et al., 2013]. The end-of-mission operations from 4 December 2012 onward included orbits where the GRAIL spacecraft were targeted to fly within 5–10 km over part of Orientale [Zuber et al., 2013b]. The orbit maneuvers also maintained the spacecraft separation between 40 and 60 km in order to reduce KBRR signal multipath, whereas during the Primary Mission the spacecraft separation ranged from 70 to 200 km. The Extended Mission included effectively 3 1/2 mapping cycles, compared to three for the Primary Mission. A mapping cycle is a complete rotation of the Moon with respect to the ascending node of the GRAIL spacecraft orbits. The GRAIL Extended Mission ground tracks were interleaved to improve the longitudinal sampling of the lunar gravity field. However, the lunar gravity field was not sampled uniformly in terms of the periapse altitude. Whereas a swath of longitudes just east of Orientale was sampled at 5–10 km periapse height, both the South Pole Aitken Basin (due partially to its depth) and a swath of longitudes in the central nearside (∼335°E to ∼5°E) are sampled at about 20 km of periapse altitude. (See Figure S1 in the supporting information.)

3. Data, Modeling, and Method of Solution

3.1. Data Overview

The Deep Space Network (DSN) tracking data (two-way tracking at S band and one-way tracking at X band) and the intersatellite Ka-Band Range-Rate (KBRR) data obtained during the Extended Mission are similar to those obtained in the Primary Mission [Asmar et al., 2013; Lemoine et al., 2013]. We used the Level 1B tracking data, which are a derived product based on the dual one-way Ka-Band ranging between the two satellites [Klipstein et al., 2013]. The GRAIL Level 1B data are time-tagged in Barycentric Dynamic Time using a procedure outlined by Kruizinga et al. [2012]. The time-tagging of the data is dependent on the quality of the reconstructed orbits, and so the Level 1B team produced several versions of the intersatellite tracking data, as improved lunar gravity models were developed [Kruizinga et al., 2013]. The GRGM900C gravity solution discussed in this paper was based on the processing of the version 3 Level 1B KBRR data. The Primary Mission Level 1B KBRR data had a sampling of 5 s, whereas the Extended Mission data had a sampling of 2 s. As a consequence, the noise floor of the Primary Mission KBRR data is thought to be 0.03 μm/s, but for the Extended Mission the noise floor is thought to be 0.05–0.07 μm/s (N. Harvey, Jet Propulsion Laboratory, unpublished data, 2013).

3.2. Force Modeling

The gravity field potential due to the Moon is modeled as a spherical harmonics series [Kaula, 1966; Heiskanen and Moritz, 1967],

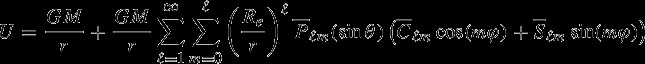graphic file with name grl0041-3382-m1.jpg 1

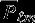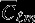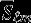where G is the Universal constant of gravitation, M is the mass of the Moon, Inline graphic are the normalized associated Legendre polynomials, Re is the reference radius (1738 km), ϕ, θ and r are the longitude, latitude, and radius at the evaluation point. Inline graphic and Inline graphic are the normalized Stokes coefficients. Our solution, GRGM900C, estimates the lunar GM and the normalized Stokes coefficients to degree and order 900. In addition, we also estimated the degree 2 Love number k2. The model, GRGM900C, is based on the DE421 lunar and planetary ephemerides [Williams et al., 2008].

Other aspects of the force modeling follow the strategy used for the Primary Mission [Lemoine et al., 2013]. The modeling of the solar radiation pressure for GRAIL requires the detailed modeling of the Sun's shadow function, since the shape of the topography can alter this function over that predicted from a spherical or ellipsoidal Moon, especially for near-full-Sun orbits where grazing transitions are long [Lemoine et al., 2013]. We derived the shadow function for the Extended Mission, taking into account the GRAIL spacecraft trajectories and the lunar topography determined by the altimeter data from the Lunar Reconnaissance Orbiter, Lunar Orbiter Laser Altimeter (LOLA) [Smith et al., 2010], archived in the Planetary Data System (LOLA/Lunar Reconnaissance Orbiter Radio Science Planetary Data System Data Node, http://imbrium.mit.edu). The planetary radiation pressure, including the reflected solar radiation due to the lunar albedo, and the radiation from the lunar thermal emission are modeled as described in Lemoine et al. [2013]. The relative magnitudes of these radiation pressure accelerations on GRAIL are discussed by Park et al. [2012].

3.3. Solution Development

We used the NASA GSFC GEODYN II Orbit Determination and Geodetic Parameter Estimation Program [Pavlis et al., 2013] to analyze the GRAIL tracking data and to compute the partial derivatives of the adjusted parameters. Because GEODYN uses a fixed-step Cowell integrator, the only change introduced with respect to Lemoine et al. [2013] was to reduce the integration step size from 1.0 to 0.5 s, in order to provide an adequate sampling of the gravitational potential field of the Moon for the degree and order 900 fields, given the mean spacecraft orbital velocity of ∼1.7 km/s.

The solutions were derived using the QR method, which allows for a numerically stable way of solving the normal equations in terms of a Cholesky square root matrix [Golub and van Loan, 1989]. The degree 900 solutions included estimates for 811,808 common parameters, and used up to 4080 processors and 6 terabytes of memory belonging to the supercomputers of the NASA Center for Climate Simulation (NCCS) at the NASA Goddard Space Flight Center. The arc lengths were 2.5 days for the data of the Primary Mission, where the arcs were bounded by spacecraft angular momentum desaturation events. For the Extended Mission data, we used 1 day arcs to limit the buildup of dynamical errors. Initially, these dynamical errors were mostly due to gravity mismodeling, especially in the first interim gravity solutions we developed with the Extended Mission data. We note that mismodeling of radiation pressure (both the direct solar radiation pressure, and the planetary radiation pressure) will also be accommodated by the estimation of empirical accelerations. The set of estimated arc parameters included the satellite initial state, a KBRR bias, and a KBRR time-tag bias per arc, and empirical accelerations. It is necessary to estimate a time-tag bias for the KBRR data to accommodate any residual time offsets between these data and the time tags of the DSN data [Kruizinga et al., 2013]. The KBRR time-tag bias is stable over a data arc and typically of the order of a few milliseconds. We note that as updated versions of the KBRR Level1B data were made available, the values and the dispersion in these estimated KBRR time-tag biases were reduced [e.g., Fahnestock et al., 2013]. We estimated empirical accelerations along track and cross track to the orbit, every quarter revolution, for each satellite. Acceleration parameters in time periods ti and tj are tied together with an exponentially decaying weight factor that has a time correlation of one-quarter revolution [Lemoine et al., 2013, cf. equation (5)]. An a priori sigma, σA of 1.0 ×10−9, was assigned to control the amplitude of the estimated accelerations. The number of observations and data weights used in the GSFC degree 900 solutions are summarized in Table S1 of the supporting information.

Using the Primary and the Extended Mission data, we developed successively several interim models of varying size (e.g.,660 × 660, 720 × 720, and 900 × 900). Each time we obtained a new global solution, we reconverged the orbits and recomputed the partial derivatives before obtaining the subsequent model. The processing that resulted in the first degree and order 900 model, called GRGM900A, was based on a starting model of degree and order 720. Then GRGM900A was used to produce the set of partial derivatives that were used to develop the degree 900 models that are the subject of this paper, GRGM900B and GRGM900C. For all the solutions we applied a constraint on the total coefficient power per spherical harmonic degree, known as a Kaula power law constraint. For the degree 900 solutions we applied the Kaula constraint only above degree 600, after verifying the behavior of the unconstrained solution. We applied a power law constraint of 2.5 ×10−4/ℓ2 for GRGM900B, and a constraint of 3.6 ×10−4/ℓ2 for GRGM900C. Also, for GRGM900C we downweighted the data after 18 November 2012 (when the spacecraft had lower periapse altitudes), by applying a factor of 0.316 to the end-of-mission Cholesky square root matrix, which meant the data were effectively downweighted (both DSN and KBRR) by a factor of 10, from the nominal weights of 0.12 mm/s (for the DSN data) and 0.1 μm/s (for the KBRR data).

In addition to deriving the models, we also calibrate the a posteriori parameter error-covariance matrix by estimating a scalar multiplicative factor, s2, which corresponds to treating all data and constraints as a single statistical unit via the formula

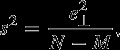graphic file with name grl0041-3382-m2.jpg 2

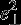where Inline graphicis the a posteriori weighted residual variance, N is the number of observations plus the Kaula constraint, and M is the number of parameters. The effect of calibration is to bring the formal errors into agreement with those actually observed [cf. Kusche, 2003; Lemoine et al., 2013, sections 4.2.4 and section 5.4].

4. Results

4.1. Power Spectrum for GRAIL Gravity Solutions

We compute the root-mean-square (RMS) power of the coefficients, RMSℓ(U), and RMS power of the coefficient standard deviations following Kaula [1966]:

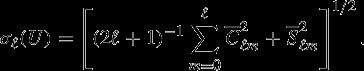graphic file with name grl0041-3382-m3.jpg 3

The RMS power for the GRAIL gravity solutions GRGM660PRIM and GRGM900C are shown in Figure 1. We show the coefficient power spectra as well as the calibrated spectrums of the solution standard deviations for GRGM900C and GRGM660PRIM. In addition, we show the RMS power of the coefficients for the GRGM900C unconstrained solution, where no Kaula constraint was applied. In Figure S2, we show the coefficient differences between the constrained and unconstrained solutions to degree 900, normalized by GRGM900C. Since the unconstrained solution begins to deviate from a smooth power law around degrees 630–650, we chose ℓ = 600 to be the degree above which we applied a Kaula constraint in GRGM900C. Note also that the power spectrum of GRGM660PRIM starts to drop more steeply after degree 400, indicating that there is not enough resolving power in the Primary Mission data for a global model of degree and order 660. The impact of the Extended Mission data can be seen in the improved error estimates of the midrange degrees (ℓ=200 to 500) by 2–3 orders over GRGM660PRIM.

Figure 1.

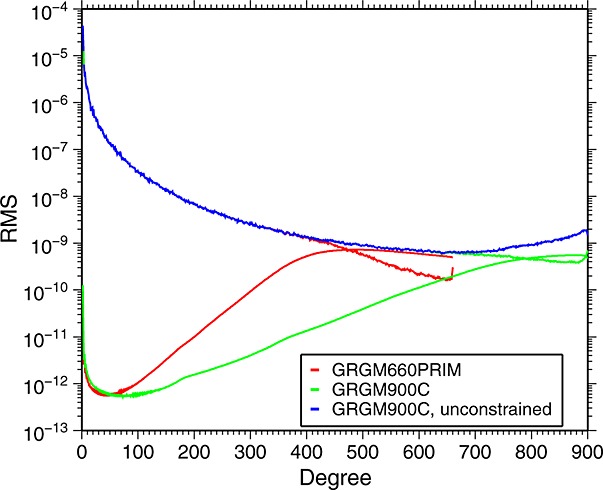
Figure 1

Open in a new tab

Power spectra of the Primary Mission GRAIL gravity solution, GRGM660PRIM [Lemoine et al., 2013], GRGM900C, the new solution including Extended Mission data, and the unconstrained version of GRGM900C, where no Kaula constraint was applied. The power spectra of the coefficient standard deviations for GRGM660PRIM and GRGM900C are also shown.

The calibrated errors of GRGM900C cross the coefficient power spectrum at ℓ = 790 (Figure 1), whereas the uncalibrated errors do not intersect the coefficient power spectrum. Referring to equation 2, the calibration factors are 3.20 for GRGM900B and 1.93 for GRGM900C and directly scale the uncalibrated formal errors from the two solutions. They show that the downweighting of the end-of-mission data has reduced the systematic errors in the solution. This indicates the importance of data weighting and solution calibration on the estimation of the error spectrum.

The low-degree errors for GRGM900C are close to and even slightly above those of GRGM660PRIM. In addition, we report that the lunar gravitational parameter GM for GRGM900C is 4.90279997×1012±14147 m3/s2, and the degree 2 potential Love number k2 is 0.024116 ± 0.000108. For both these values the errors are actually higher than those reported for GRGM660PRIM in [Lemoine et al., 2013]. This is mostly due to the 1 day arcs which we used in the processing of the Extended Mission data, which slightly degrade the sensitivity with respect to these parameters. Future models will extend the length of these arcs and increase the sensitivity with respect to the lower degrees.

4.2. Correlations With Topography

The gravity solutions from the GRAIL Primary Mission showed high correlations of gravity and topography. We also evaluate this correlation for the new Extended Mission models. We compute the gravity induced by topography following Wieczorek and Phillips 1998, assuming a uniform density of 2560 kg/m3[Wieczorek et al., 2013], using the topography expansion to the ninth power. We see in Figure 2 that the addition of the Extended Mission data has extended the range of degrees with high correlations. For GRGM660PRIM, the correlations begin to decrease below 0.98 after ℓ= 320, whereas for the two Extended Mission models, correlations ≥ 0.98 extend to ℓ≈ 638. The two Extended Mission models, GRGM900B and GRGM900C, differ in their treatment of the end-of-extended-mission data and the magnitude of the Kaula constraint. By relaxing the Kaula constraint and slightly downweighting the Extended Mission data after 18 November 2012, we modestly improve the global correlations, while maintaining the same levels of postfit residuals (see section 4.4). For this reason, our preferred solution is GRGM900C.

Figure 2.

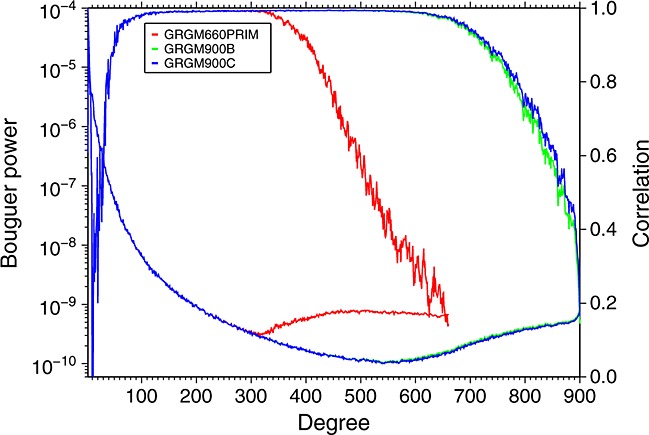
Figure 2

Open in a new tab

Correlations between gravity solutions and gravity computed from LOLA topography, and Bouguer power spectrum. The top curves (referred to the right axis) show global correlations for the Primary Mission model, GRGM660PRIM, and the models including Extended Mission data, GRGM900B and GRGM900C. The bottom curves (referred to the left axis) show the spectrum of the Bouguer power for the three gravity models.

4.3. Bouguer Gravity

The Bouguer gravity, which highlights subsurface structures, is computed by subtracting the gravity predicted from topography, as just described, from the estimated geopotential coefficients. The RMS power is computed according to equation 3.

The Bouguer power (see bottom curves of Figure 2) begins to increase around ℓ=300 for GRGM660PRIM, and around ℓ≈570 for GRGM900B and GRGM900C. These degrees represent, in global terms, where spurious power in the geopotential coefficients begins to affect the global geophysical interpretation based on the gravity solutions.

We also compute the Bouguer coefficient amplitude 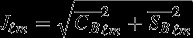Inline graphic. This is illustrated in Figure 3 for two gravity solutions, GRGM900C without application of a Kaula constraint and the final solution GRGM900C. The solution derived without Kaula illustrates which degrees are most reliably determined by the KBRR data. As pointed out by Floberghagen [2002], since the Moon is a slow rotator, resonances occur only at high degrees (ℓ≈ 350–370, and ℓ≈700–740). In the unconstrained solution, it is these resonance and near-resonance orders that develop excess power in the Bouguer coefficients (see Figure 3a). In these GRAIL solutions, the lower-order coefficients (m less than 300) are better determined than the “wings” of the gravity model (high degrees and high orders). This phenomenon is also a characteristic of solutions for the Earth gravity derived from GRACE data [Rowlands et al., 2002]. The Kaula constraint successfully reduces some of the spurious power in the coefficients (Figure 3b), however, a signature remains in the RMS Bouguer coefficient power spectrum (bottom curves of Figure 2).

Figure 3.

Figure 3

Open in a new tab

Amplitude of Bouguer gravity coefficients (a) based on GRGM900C-unconstrained (no Kaula constraint applied), and (b) based on GRGM900C, with a Kaula constraint of 3.6 × 10−4/ℓ2 applied for degree ℓ greater than 600.

4.4. Data Fit

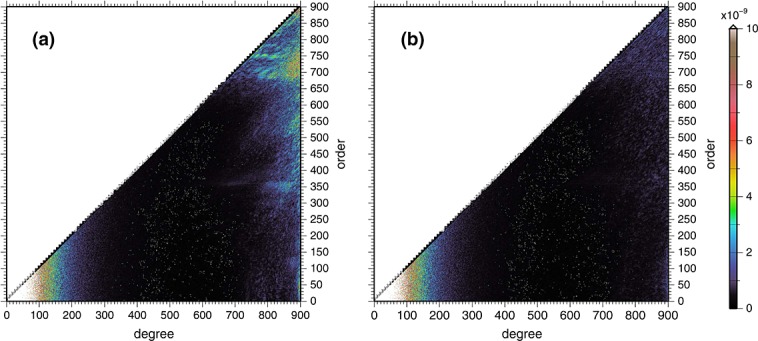
In addition to examining the correlations with topography and the power spectra of the solutions, we also computed the a posteriori orbital fits to the tracking data. The fits to GRGM900C are very similar to those of GRGM900B, even though we note an improvement in the topography correlations with GRGM900C (see section 4.2). The GRGM900C fits to the Primary Mission KBRR data are largely unchanged from those obtained with the model GRGM600PRIM and are in the range 0.04–0.06 μm/s. The GRGM900C a posteriori fits to the Extended Mission KBRR data through 18 November 2012 are in the range of 0.10–0.17 μm/s, whereas the fits to the data beyond 18 November 2012 range from 0.2 to 3.2 μm/s. We illustrate the Extended Mission KBRR data fits for GRGM900C in Figure 4, together with the periapse height for each data arc. The RMS fits to the DSN S band data (not shown) are in general close to the data weights of 0.12 mm/s, except for the latter part of the Extended Mission where they reach RMS fits of 0.5 mm/s. The low-periapse altitude of 5–10 km dramatically increases the gravity signal inherent in the satellite-tracking data. In certain regions and along some orbital tracks, the inherent resolution is more than can be accommodated in a global spherical harmonic model of degree and order 900.

Figure 4.

Figure 4

Open in a new tab

RMS residuals of the KBRR data per data arc in the Extended Mission with the gravity model GRGM900C, shown together with the periapse altitude for each orbital arc.

4.5. Anomaly Errors and Degree Strength

The propagation of the gravity field errors into a map of anomaly errors is helpful for evaluating the model's performance geographically and aids the geophysical interpretation using that model. However, the propagation of a full covariance matrix of a degree and order 900 field is computationally prohibitive. Instead, we have applied a Monte Carlo approach which uses the Cholesky square root matrix from QR to compute an ensemble of statistically consistent members, or “clones,” to replace the error-covariance matrix in these calculations. We have verified this procedure by comparing its gravity anomaly errors for the SGM150J model [Goossens et al., 2011] with those obtained from using the full error-covariance matrix and have found the convergence rate to be the expected 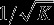Inline graphic, where K is the ensemble size. An example of the use of Monte Carlo calculations to propagate error functions for large covariances can be found in Gundlich et al. [2003]. In Figure S3 in the supporting information, we show the anomaly errors to ℓ=720 for GRGM900C. The total global RMS error to degree and order 720 is 8.49 mGal. This compares to an RMS global anomaly error from GRGM660PRIM to degree and order 660 of 30.49 mGal [Lemoine et al., 2013].

We also seek to evaluate the spatial variability in the model resolution. We do this by computing the degree strength of the solution following Konopliv et al. [1999]. First, we evaluate the anomaly error at each degree for each geographic location using the Monte Carlo approach just described, and then we determine at what degree the anomaly error matches the Kaula law signal strength. The result is a map that illustrates the resolution of GRGM900C (see Figure 5). We see that the lowest degree strength is 550–600 over a broad swath of the central farside. It is possible that the slight deweighting of the post 18 November 2012 data affects the degree strength over the farside. Over Orientale, the degree strength of the model is 700–725; however, we note that the KBRR data obtained from the lowest altitudes at the end of the mission over Orientale have been deweighted in this solution. The model has the highest resolution (degree strength of 900) over the polar regions due to the extra sampling that comes from the convergence of the orbital ground tracks.

Figure 5.

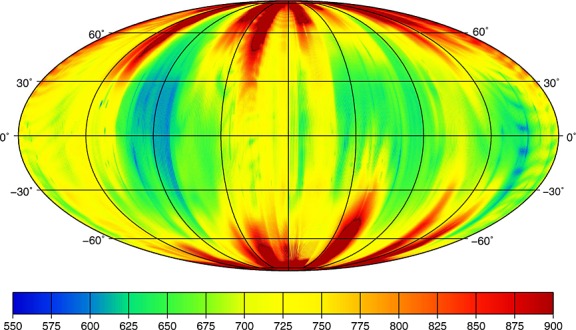
Figure 5

Open in a new tab

Degree strength of the GRGM900C gravity model. The map shows spatially at what degree the gravity field errors match the expected signal power from the applied Kaula power law. The map is a Mollweide projection centered on 270°E, with the lunar farside to the left of the figure center, and the lunar nearside to the right of the figure center.

5. Summary

Using the method of QR factorization, we have derived a gravity field of the Moon from the GRAIL primary and Extended Mission data complete to degree and order 900 in spherical harmonics. The tracking data, in particular the GRAIL KBRR data, completely resolve the coefficients below ℓ = 600 (9 km block size). A power law constraint of 3.6 ×10−4/ℓ2 was applied for ℓ≥600. The inclusion of the Extended Mission GRAIL data improves the lunar gravity field resolution by 2–3 orders of magnitude over the midrange degree bands, compared to the Primary Mission GRAIL model, GRGM660PRIM. The variable sampling of the Moon at low altitude (see Figure S1 in the supporting information) combined with the RMS of fit to the KBRR data that is higher than the intrinsic noise, especially for the data from the last month of the Extended Mission, suggest that a degree 900 model does not capture all the signal inherent in the tracking data. Future work should expand the solutions to higher degree to obtain improved resolution or should assess the utility of local solutions over bounded regions to fully extract the signal inherent in the KBRR tracking data.

Acknowledgments

The work described herein was supported by the GRAIL Project and the NASA Discovery Program. We acknowledge Gerhard Kruizinga and his team at the Jet Propulsion Laboratory (JPL) for their meticulous work in developing the GRAIL Level 1B data sets. We also acknowledge the NASA Center for Climate Simulation (NCCS) at the NASA Goddard Space Flight Center for their assistance in optimizing the performance of the supercomputers to obtain the GRAIL degree 900 solutions. The GRAIL Level 1B data used in this study are available from the Geosciences Node of the Planetary Data System http://pds-geosciences.wustl.edu/missions/grail/default.htm.

The Editor thanks Rune Floberghagen and an anonymous reviewer for their assistance evaluating this paper.

Key Points

  1. New gravity model of the Moon obtained to degree and order 900

  2. The model is obtained from analysis of GRAIL intersatellite data

  3. The degree strength of the model ranges from 575–900

Supporting Information

Readme
grl0041-3382-sd1.txt (2.2KB, txt)
TableS1 pdf
grl0041-3382-sd2.pdf (22KB, pdf)
FigureS1
grl0041-3382-sd3.eps (218.3KB, eps)
FigureS2
grl0041-3382-sd4.eps (1.8MB, eps)
FigureS3
grl0041-3382-sd5.eps (30.3MB, eps)
grl0041-3382-sd6.txt (354B, txt)
grl0041-3382-sd7.txt (498B, txt)
grl0041-3382-sd8.txt (278B, txt)

References

  1. Asmar SW. The scientific measurement system of the Gravity Recovery and Interior Laboratory (GRAIL) mission. Space Sci. Rev. 2013;178(1):25–55. , et al. (, doi: 10.1007/s11214-013-9962-0. [Google Scholar]
  2. Fahnestock E. 2013. , et al. ( GRAIL science data system orbit determination: Approach, strategy, and performance, AAS 13-271 presented at AAS/AIAA Spaceflight Mechanics Meeting, 10–14 Feb., Lihue, Hawaii.
  3. Floberghagen R. Lunar Gravimetry, Astrophysics and Space Science Library. Dordrecht, The Netherlands: Kluwer Acad; 2002. , vol. 273, [Google Scholar]
  4. Golub GH. van Loan CF. Matrix Computations. Baltimore, Md: The John Hopkins Univ. Press; 1989. , and. [Google Scholar]
  5. Goossens S. 2011. , et al. ( Improved high-resolution lunar gravity field model from SELENE and historical tracking data, Abstract P44B-05 presented at 2011 Fall Meeting, AGU, 5–9 Dec., San Francisco, Calif.
  6. Gundlich B, Koch K-R. Kusche J. Gibbs sampler for computing and propagating large covariance matrices. J. Geod. 2003;77(9):514–528. , and, doi: 10.1007/s00190-003-0350-5. [Google Scholar]
  7. Heiskanen W. Moritz H. Physical Geodesy. San Francisco, Calif: W. H. Freeman and Co; 1967. , and. [Google Scholar]
  8. Kaula WM. Theory of Satellite Geodesy. Waltham, Mass: Blaisdell Publishing Co; 1966. (republished by Dover, New York, 2000) [Google Scholar]
  9. Klipstein WM, Arnold BW, Enzer DG, Ruiz AA, Tien JY, Wang RT. Dunn CE. The lunar gravity ranging system for the Gravity Recovery and Interior Laboratory (GRAIL) mission. Space Sci. Rev. 2013;178(1):57–76. , and, doi: 10.1007/s11214-013-9973-x. [Google Scholar]
  10. Konopliv AS, Banerdt WB. Sjogren WL. Venus Gravity: 180th degree and order model. Icarus. 1999;139(1):3–18. , and, doi: 10.1006/icar.1999.6086. [Google Scholar]
  11. Konopliv AS, Asmar SW, Carranza E, Sjogren WL. Yuan DN. Recent gravity models as a result of the Lunar Prospector mission. Icarus. 2001;150(1):1–18. , and, doi: 10.1006/icar.2000.6573. [Google Scholar]
  12. Konopliv AS. The JPL lunar gravity field to spherical harmonic degree 660 from the GRAIL primary mission. J. Geophys. Res. Planets. 2013;118:1415–1434. , et al. (, doi: 10.1002/jgre.20097. [Google Scholar]
  13. Konopliv AS. High resolution lunar gravity fields from the GRAIL Primary and Extended Mission. Geophys. Res. Lett. 2014;41:1452–1458. doi: 10.1002/2014GL060027. , et al. (, doi: 10.1002/2013GL059066. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Kruizinga G, Bertiger W. Harvey N. 2012. JPL D-75620 Pasadena, Calif, and Timing of science data for the GRAIL mission, Jet Propulsion Laboratory, California Institute of Technology, [Available at http://pds-geosciences.wustl.edu/grail/grail-l-lgrs-3-cdr-v1/grail_0101/document/grail_timing.pdf.]
  15. Kruizinga G. 2013. AAS Paper 13-270, et al. ( The role of GRAIL orbit determination in preprocessing of gravity science measurements, presented at the AAS/AIAA Space Flight Mechanics Conference, 10–14 Feb., Lihue, Hawaii.
  16. Kusche J. Noise variance estimation and optimal weight determination for GOCE gravity recovery. Adv. Geosci. 2003;1:81–85. , doi: 10.5194/adgeo-1-81-2003. [Google Scholar]
  17. Lemoine FG. High-degree gravity models from GRAIL data. J. Geophys. Res. Planets. 2013;118:1676–1698. , et al. (, doi: 10.1002/jgre.20118. [Google Scholar]
  18. Matsumoto K. An improved lunar gravity field model from SELENE and historical tracking data: Revealing the farside gravity features. J. Geophys. Res. 2010;115 , et al. (, E06007, doi: 10.1029/2009JE003499. [Google Scholar]
  19. Park RS, Asmar SW, Fahnestock EG, Konopliv AS, Lu W. Watkins MW. Gravity recovery and interior laboratory simulations of static and temporal gravity field. J. Spacecraft Rockets. 2012;49(2):390–400. , and, doi: 10.2514/1.A32117. [Google Scholar]
  20. Pavlis DE, Wimert J. McCarthy JJ. 2013. Contract. Rep Greenbelt, Md, and GEODYN II system description, vols. 1–5, SGT Inc.,
  21. Rowlands DD, Ray RD, Chinn DS. Lemoine FG. Short arc analysis of intersatellite tracking data in a gravity mapping mission. J. Geodesy. 2002;76:307–316. , and. [Google Scholar]
  22. Ryne M, Antreasian P, Broschart S, Criddle K, Gustafson E, Jefferson D, Lau E, Wen HY. You T-H. 2013. 148, and GRAIL orbit determination for the science phase and the extended mission, AAS Paper 13-269, Advances in the Astronautical Sciences,, Univelt Inc., San Diego, Calif.
  23. Smith DE. Initial observations from the Lunar Orbiter Laser Altimeter (LOLA) Geophys. Res. Lett. 2010;37 doi: 10.1002/2013GL059085. , et al. (, L18204, doi: 10.1029/2010GL043751. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Sweetser TH, Wallace MS, Hatch SJ. Roncoli RB. 2012. , and Design of an extended mission for GRAIL, AIAA Paper 2012-4429, AIAA/AAS Astrodynamics Specialist Conference, 13–16 Aug., Minneapolis, Minn., doi:10.2514/6.2012-4429.
  25. Wieczorek MA. Phillips RJ. Potential anomalies on a sphere: Applications to the thickness of the lunar crust. J. Geophys. Res. 1998;103(E1):1715–1724. , and, doi: 10.1029/97JE03136. [Google Scholar]
  26. Wieczorek MA. The crust of the Moon as seen by grail. Science. 2013;339(6120):671–675. doi: 10.1126/science.1231530. , et al. (, doi: 10.1126/science.1231530. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Williams JG, Boggs DH. Folkner WM. 2008. Rep. IOM 335-JW,DB,WF-20080314-001 Pasadena, Calif, and DE421 lunar orbit, physical librations, and surface coordinates, Jet Propul. Lab.,
  28. Zuber MT, Smith DE, Lehman DH, Hoffman TL, Asmar SW. Watkins MM. Gravity Recovery and Interior Laboratory (GRAIL): Mapping the lunar interior from crust to core. Space Sci. Rev. 2013a;178(1):3–24. , and, doi: 10.1007/s11214-012-9952-7. [Google Scholar]
  29. Zuber MT. 2013b. , et al. ( Gravity Recovery and Interior Laboratory (GRAIL): Extended Mission and Endgame status, Abstract 1777, 44th Lunar and Planetary Science Conference, 18-22 March, The Woodlands, Tex.
  30. Zuber MT. Gravity field of the Moon from the gravity recovery and interior laboratory (GRAIL) mission. Science. 2013c;339(6120):668–671. doi: 10.1126/science.1231507. , et al. (, doi: 10.1126/science.1231507. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Readme
grl0041-3382-sd1.txt (2.2KB, txt)
TableS1 pdf
grl0041-3382-sd2.pdf (22KB, pdf)
FigureS1
grl0041-3382-sd3.eps (218.3KB, eps)
FigureS2
grl0041-3382-sd4.eps (1.8MB, eps)
FigureS3
grl0041-3382-sd5.eps (30.3MB, eps)
grl0041-3382-sd6.txt (354B, txt)
grl0041-3382-sd7.txt (498B, txt)
grl0041-3382-sd8.txt (278B, txt)

Articles from Geophysical Research Letters are provided here courtesy of Wiley

RESOURCES