Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2015 Jun 8.
Published in final edited form as: J Gambl Stud. 2011 Jun;27(2):317–330. doi: 10.1007/s10899-010-9209-x

Differential Item Functioning of Pathological Gambling Criteria: An Examination of Gender, Race/Ethnicity, and Age

Paul Sacco 1,✉, Luis R Torres 2, Renee M Cunningham-Williams 3, Carol Woods 4, G Jay Unick 5
PMCID: PMC4459593  NIHMSID: NIHMS692821  PMID: 20623329

Abstract

This study tested for the presence of differential item functioning (DIF) in DSM-IV Pathological Gambling Disorder (PGD) criteria based on gender, race/ethnicity and age. Using a nationally representative sample of adults from the National Epidemiologic Survey on Alcohol and Related Conditions (NESARC), indicating current gambling (n = 10,899), Multiple Indicator-Multiple Cause (MIMIC) models tested for DIF, controlling for income, education, and marital status. Compared to the reference groups (i.e., Male, Caucasian, and ages 25–59 years), women (OR = 0.62; P < .001) and Asian Americans (OR = 0.33; P < .001) were less likely to endorse preoccupation (Criterion 1). Women were more likely to endorse gambling to escape (Criterion 5) (OR = 2.22; P < .001) but young adults (OR = 0.62; P < .05) were less likely to endorse it. African Americans (OR = 2.50; P < .001) and Hispanics were more likely to endorse trying to cut back (Criterion 3) (OR = 2.01; P < .01). African Americans were more likely to endorse the suffering losses (OR = 2.27; P < .01) criterion. Young adults were more likely to endorse chasing losses (Criterion 9) (OR = 1.81; P < .01) while older adults were less likely to endorse this criterion (OR = 0.76; P < .05). Further research is needed to identify factors contributing to DIF, address criteria level bias, and examine differential test functioning.

Keywords: MIMIC modeling, Differential item functioning, Pathological Gambling Disorder, Diagnostic criteria

Introduction

Pathological Gambling Disorder (PGD) leads to distress and dysfunction at the individual, familial, and societal levels (National Research Council 1999). Clinical features may include preoccupation, restlessness/irritability when unable to gamble, and loss of control over gambling, and these may lead to adverse consequences for gamblers and their families (American Psychiatric Association 1994). Societal costs of PGD are estimated at almost $5 billion annually due to workplace, treatment, health and criminal justice systems burdens (Gerstein et al. 1999).

PGD prevalence rates range from 0.4 to 2.0%. However, those experiencing problems below the minimum threshold of five criteria, (American Psychiatric Association 1994), but who endorse at least one gambling related problem (typically known as Problem, Subthreshold, or Level 2) gamblers (PG), have prevalence rates twice as high (Cunningham-Williams et al. 1998; Petry et al. 2005; Shaffer et al. 1999). Rates vary by gender, race/ethnicity, and age suggesting socio-demographic disparities in prevalence. Epidemiological studies report increased rates of disordered gambling among racial and ethnic minority groups (Welte et al. 2004). Findings from the National Epidemiologic Survey on Alcohol and Related Conditions (NESARC) suggest that African Americans are at higher risk of PGD (Petry et al. 2005), while Welte and colleagues, also in a nationally-representative study, found higher than average rates of PG/PGD among African Americans, Latinos, and Asians (Welte et al. 2002). Such results concur with community based studies of drug-using gamblers reporting elevated rates by race/ethnicity (Cunningham-Williams et al. 2000), but other studies have found that these racial/ethnic variations in elevated risk disappeared when adjusting for other socio-demographic factors (Cunningham-Williams et al. 2005).

Similar disparities have been reported by gender (Petry et al. 2005). Using NESARC data, Blanco and colleagues identified higher rates of both problem and pathological gambling in men compared to women (Blanco et al. 2006). They compared criterion endorsement by gender and found that women were more likely to endorse gambling to escape or relieve a depressed mood, while men were more likely to endorse chasing losses and preoccupation with gambling.

Studies reporting age-related differences exist, albeit with contradictory findings. Some studies suggest that middle age groups (ages 30–64) have the highest risk of PGD (Petry et al. 2005; Welte et al. 2002) with lower rates of PGD among younger and older adults. Other studies have found young adults at higher risk (National Research Council 1999). Shaffer and colleagues compared prevalence rates between various age groups across multiple samples and found higher risks for Levels 2 and 3 gambling (analogous to PG and PGD, respectively) among adolescents and college students versus adults (Shaffer et al. 1999).

Gender, racial/ethnic, and age disparities in PGD likely reflect a combination of both true group differences as well as artifacts of how these disorders are conceptualized and measured. Our previous work found higher proportions of African Americans than Caucasians endorsed various symptoms including preoccupation, chasing losses, loss of control, financial bailout, interference with life responsibilities, and illegal behaviors (Cunningham-Williams et al. 2007). Yet, further exploration needs to clarify whether such disparities are the results of true differences or group-based measurement idiosyncrasies. Knowledge of whether group memberships impact how individuals interpret the meaning of items in standardized diagnostic assessments (American Educational Research Association et al. 1999) can be used to refine PGD diagnostic criteria (Toce-Gerstein et al. 2003), foster culturally informed models of prevention, outreach and treatment (Crisp et al. 2004; Raylu and Oei 2004; Tang et al. 2007), and improve screening among racial/ethnic, gender and age subgroups (Cunningham-Williams et al. 2007).

Differential Item Functioning

Differential item functioning (DIF) analysis is a statistical technique designed to detect different probabilities of item or symptom endorsement for people with the same level of the latent trait, in this case gambling pathology, but who differ along other characteristics such as socio-demographic factors. In this context socio-demographic factors are construct-irrelevant dimensions, and differential response probabilities between groups are known as item bias (Gierl 2005).

DIF analysis is based on the assumption that persons with similar levels of an underlying construct (i.e., gambling pathology) should respond to individual test items the same, regardless of group affiliation (e.g., race). In other words, DIF occurs when people with different group affiliations (e.g., age, race, ethnicity, or gender) and the same latent trait (e.g., knowledge of a particular subject or PGD diagnosis) have a different probability of endorsing a given response to a specific question on a survey or a test item (Embretson and Reise 2000). By separating group differences from item response probabilities, DIF techniques can detect group-based item bias even when there are large group differences in the prevalence of the latent trait (i.e. gambling pathology).

Strong and Kahler (2007) examined the PGD criteria for DIF using Rasch modeling techniques and found that after controlling for severity, there was a differential probability of reporting some criteria by age and gender. Specifically, women were more likely than men to report “gambling as a way of escaping from problems,” and younger gamblers were more likely than older gamblers to report “chasing losses.”

This report builds on Strong and Kahler’s (2007) work by executing a DIF analysis of the NESARC data using an alternate methodology with several advantages, Multiple-Indicator Multiple-Cause (MIMIC) modeling. MIMIC modeling techniques for detecting DIF also allow for the inclusion of covariates that have been associated with disordered gambling (e.g. income, marital status, and education) (Gerstein et al. 1999; Welte et al. 2004). A further advantage of MIMIC modeling is that it allows for comparison of multiple groups simultaneously such as racial/ethnic groups.

In this study, we used the 2-parameter logistic item response model. Unlike the Rasch model (Bond and Fox 2007), it does not constrain all items to have the same discrimination parameter, effectively assuming that they are equally related to disordered gambling. Rasch modeling, on the other hand, may be problematic for detecting DIF if the discrimination parameters vary across items as is common in health-related data (Teresi 2006). We tested the following hypothesis: Differential item functioning is present in DSM-IV pathological gambling criteria based on race/ethnicity, younger and older age and gender. This is the first report examining differential item functioning of PGD criteria based on age, race/ethnicity, and gender while adjusting for sociodemographic factors. This research adds to the limited literature using DIF to understand disordered gambling using a large, nationally representative sample that includes older adult, Latino, and Asian respondents.

Method

NESARC Sample

The NESARC is a nationally representative sample of 43,093 non-institutionalized individuals 18 years and older (Grant and Dawson 2005; Grant et al. 2003). The survey gathered information regarding alcohol use and a variety of comorbid conditions from individuals throughout the U.S. The NESARC utilized a multistage sampling structure, oversampling Latinos, African Americans, and young adults (18–24) in the interest of obtaining reliable and precise statistical estimation in these populations, and to ensure appropriate representation of racial and ethnic groups (Grant et al. 2003). The overall response rate for NESARC was 81% (Blanco et al. 2006). The weighted NESARC data adjusts for oversampling and non-response on variables including age, race/ethnicity, sex, region, and place of residence. Data were also adjusted to be nationally representative (based on region, age, race, and ethnicity) according to the 2000 U.S. Census (U.S. Census Bureau 2004).

DSM-IV Gambling Criteria

Interviewers used laptops to administer the Alcohol Use Disorder and Associated Disabilities Interview Schedule—DSM-IV version (AUDADIS-IV). This instrument has excellent internal consistency reliability in assessing DSM-IV PGD in the general population (Grant et al. 1995). Using the AUDADIS-IV, interviewers asked 15 gambling-related questions to individuals who endorsed gambling five times in any 1 year of their lives (n = 11,153). For each item, respondents were first asked if they ever experienced the gambling symptom, with two probes regarding timeframe (within the past 12-months and prior to the past 12-months). Lifetime and past year prevalence were based on endorsement of the follow up questions. Please see Table 1 for a list of DSM-IV Pathological Gambling Disorder criteria.

Table 1.

DSM-IV diagnostic criteria

Persistent and recurrent maladaptive gambling behavior as indicated by five (or more) of the following:

  1. Is preoccupied with gambling (e.g., preoccupied with reliving past gambling experiences, handicapping or planning the next venture, or thinking of ways to get money with which to gamble)

  2. Needs to gamble with increasing amounts of money in order to achieve the desired excitement

  3. Has repeated unsuccessful efforts to control, cut back, or stop gambling

  4. Is restless or irritable when attempting to cut down or stop gambling

  5. Gambles as a way of escaping from problems or of relieving a dysphoric mood (e.g., feelings of helplessness, guilt, anxiety, depression)

  6. After losing money gambling, often returns another day to get even (“chasing” one’s losses)

  7. lies to family members, therapist, or others to conceal the extent of involvement with gambling

  8. has committed illegal acts such as forgery, fraud, theft, or embezzlement to finance gambling

  9. Has jeopardized or lost a significant relationship, job, or educational or career opportunity because of gambling

  10. Relies on others to provide money to relieve a desperate financial situation caused by gambling

Open in a new tab

Analysis

MIMIC modeling was used to test for DIF. To adjust for the sampling structure of NESARC, Mplus (Muthén and Muthén 1998–2009) was used to analyze MIMIC models, and SUDAAN (Research Triangle Institute 2004) was used for bivariate analyses. Mplus and SUDAAN were chosen because they have features to estimate parameters derived from complex survey designs, important in deriving unbiased estimates (Hahs-Vaughn and Lomax 2006). All MIMIC models were parameterized as two-parameter logistic item response models and fitted to the data using the robust maximum likelihood estimator (i.e., MLR).

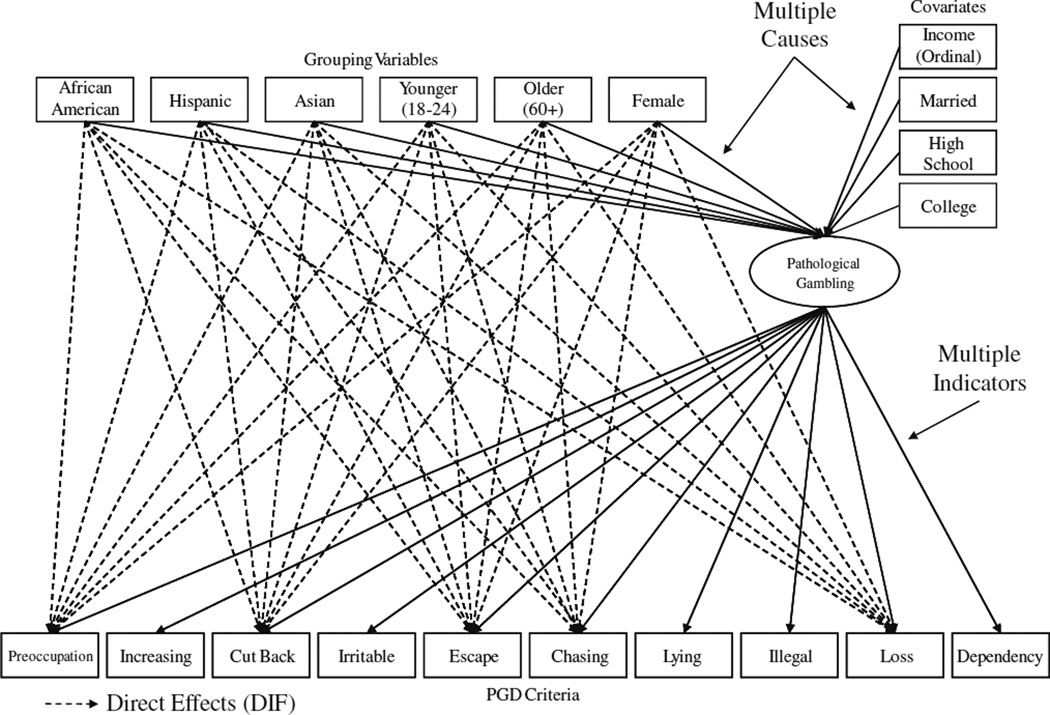
Initially, confirmatory factor analysis was performed to assess whether PGD criteria represent a single factor. Gambling criteria were loaded on a single factor we labeled gambling problems. In the MIMIC models, the gambling factor was regressed on a series of grouping variables, which adjusted for group mean differences (see Table 1). The gambling criteria serve as the “multiple indicators” of the latent construct while the grouping variables and covariates are the “multiple causes”. Items (indicators) were tested for DIF by regressing them directly on the grouping variables (causes). Dichotomous grouping variables included female gender (compared with male gender), older adult status (60+) and young adult status (≤25) (compared with ages 25–59). These age thresholds were defined based on both practical and theoretical considerations. We chose the younger age grouping based on the NESARC’s oversampling of this age group. In addition, theoretical considerations emphasize focusing on the late teenage years and early twenties as a distinct period of development (Arnett 2000). The age cutoff for older adults was based on the work of Levinson (1986), who described age 60–65 as “Late Adult Transition” and 65+ as “Late Adulthood”. Based on the variations in life events in older adulthood, such as retirement, we opted to include the transition period as defined by Levinson. Compared with Caucasians, three binary variables measured race/ethnicity, namely, African Americans, Asians, and Latinos (Fig. 1).

Figure 1.

Figure 1

Open in a new tab

MIMIC model path diagram

MIMIC models included covariates (i.e., educational attainment, income, and marital status) to adjust for socio-demographic influences on the latent variable. Two dichotomously coded variables operationalized education: high school education/GED, and college attendance, with less than a high school education as the reference. We rescaled the annual family income variable, based on past-year, so estimates represent increments of $10,000. Marital status was dichotomized based on being currently married/cohabitating or not currently married.

Using the strategy recommended by Woods (2009), we first tested preliminary models for each criterion to identify DIF free criteria on all the grouping variables, presuming that all other items are DIF free. Criteria presumed DIF-free become reference criteria (i.e., “anchors”) in subsequent DIF testing. We analyzed DIF by adding a regression path from each of the grouping variables to each item, one at a time. This regression coefficient represents a difference in the responses by the groups (e.g. African Americans) controlling for differences in the latent construct of gambling. We tested each criterion in a separate model, and criteria found to have non-significant direct effects were considered DIF free reference items (which were not tested for DIF in the subsequent models).

We then used nested MIMIC models to test the remaining or “studied” criteria for DIF, one at a time. For example, to test for DIF on Criterion 1, a model with direct effects to each studied criterion was compared to a model without the estimation of a direct effect on Criterion 1. If removing the direct effect for Criterion 1 significantly diminished model fit, there was evidence of differential functioning.

Likelihood ratio (LR) difference tests compared model fit between the nested MIMIC models using a special procedure for robust maximum likelihood estimation described at the Mplus website (www.statmodel.com/chidiff.shtml). To control the false discovery rate, the Benjamini and Hochberg (1995; Thissen et al. 2002) procedure was applied to the studied items. We then constructed a final MIMIC model using the items with significant DIF in nested models. The model provides estimates of discrimination parameters (a), threshold parameters (τ), group mean differences on the latent gambling factor estimates of covariate effects on the latent variable (γ), DIF effects (β), and odds ratios (OR).

Results

Stage I Analysis

Table 2 shows criteria endorsement rates of the studied groups. Additionally, individuals missing on all gambling criteria (n = 36; 0.32%) were excluded from the analysis, leaving an analysis sample of n = 10,899. Table 3 presents the results of the Confirmatory Factor Analysis (CFA) model of PGD criteria. A single factor model fit the data well (χ2 = 61.72; P < .001; TLI = 0.995; CFA = 0.994; RMSEA = 0.008) (Table 3). Due to large sample size, the chi-square value was inflated, but other fit statistics indicated excellent model fit. Therefore, the MIMIC models used a single latent construct of gambling pathology.

Table 2.

Prevalence of symptom endorsement by gender, race, and age groupa

Endorsed criteria Male,
n (wt%)		 Female,
n (wt%)		 Caucasian,
n (wt%)		 African-American,
n (wt%)		 Asian,
n (wt%)		 Hispanic,
n (wt%)		 Older adult,
n (wt%)		 Young adult,
n (wt%)
Totala 6007 (58.65) 5146 (41.35) 6906 (75.18) 2155 (10.78) 292 (3.50) 1582 (8.02) 2975 (23.54) 980 (9.45)
1. Preoccupation 884 (14.62) 470 (8.21) 773 (11.28) 328 (15.46) 40 (12.75) 179 (11.80) 295 (9.92) 165 (16.17)
2. Increasing 421 (7.04) 293 (5.15) 372 (5.43) 185 (8.82) 34 (12.42) 108 (7.47) 134 (4.17) 113 (10.97)
3. Cut back 203 (2.76) 123 (1.96) 129(1.76) 119 (5.83) 11 (2.98) 59 (3.48) 65 (1.90) 40 (3.89)
4. Irritable 82 (1.18) 53 (0.74) 58 (0.77) 49 (2.15) 6 (1.72) 17 (1.18) 30 (0.87) 11 (1.14)
5. Escape 305 (4.85) 364 (6.35) 356 (4.87) 167 (8.16) 18 (8.85) 108 (5.73) 125 (4.01) 59 (5.50)
6. Chasing 519 (8.79) 271 (4.89) 413 (6.07) 205 (10.81) 39 (14.98) 111 (8.70) 117 (3.78) 151 (14.49)
7. Lying 235 (3.89) 138 (2.33) 184 (2.78) 105 (4.55) 17 (7.50) 56 (3.57) 66 (2.05) 50 (4.65)
8. Illegal 27 (0.48) 15 (0.20) 22 (0.30) 14 (0.76) 1 (0.95) 5 (0.23) 8 (0.37) 2 (0.21)
9. Loss 82 (1.13) 34 (0.60) 48 (0.71) 47 (2.43) 1 (0.55) 19 (1.14) 16 (0.53) 15 (1.02)
10. Dependency 91 (1.33) 54 (0.90) 78 (1.05) 47 (2.17) 4 (1.89) 14 (0.58) 21 (0.50) 19 (1.67)
Open in a new tab
a

Gambled +5 times in 1 year

Table 3.

CFA model of PGD criteria

Criterion Factor loadings SE z
1. Preoccupation 0.823 0.013 65.85
2. Increasing 0.813 0.016 51.01
3. Cut back 0.842 0.019 43.69
4. Irritable 0.994 0.017 57.16
5. Escape 0.692 0.022 31.80
6. Chasing 0.858 0.015 55.91
7. Lying 0.866 0.017 49.52
8. Illegal 0.819 0.038 21.65
9. Loss 0.842 0.027 31.27
10. Dependency 0.880 0.022 40.42
Open in a new tab

n = 10,924; χ2 = 61.719; P <.0001; TLI = 0.995; CFI = 0.994; RMSEA = 0.008 All the loadings are significant (P <.0001)

We ran 10 separate MIMIC models to identify DIF free items using all other criteria as anchors. Criteria 2, 7, and 8 had non-significant direct effects. In subsequent models, they were used as reference criteria. Nested Chi-square difference tests on all the other gambling criteria detected significant DIF on Criteria 1, 3, 5, 6, and 9 (Table 4), after adjustment for false discovery. In the final MIMIC model, we estimated direct effects from the grouping variables to these studied criteria only.

Table 4.

Differential item functioning tests and item parameter estimates for lifetime PGD

Criterion χ2 P PBH a (SE) τ (SE)
1. Preoccupation 40.53 <.0001 <.0001 2.62 (.14) 1.61 (.42)
2. Increasing – – – 2.57 (.14) 3.46 (.45)
3. Cut back 31.17 <.0001 .0001 2.77 (.21) 5.60 (.55)
4. Irritable 12.92 .044 .052 4.85 (.51) 9.64 (1.23)
5. Escape 50.30 <.0001 <.0001 1.86 (.10) 4.17 (.34)
6. Chasing 16.05 .013 .019 3.01 (.18) 3.25 (.52)
7. Lying – – – 3.08 (.24) 5.04 (.61)
8. Illegal – – – 2.90 (.31) 7.81 (.76)
9. Loss 18.61 .005 .009 3.01 (.31) 6.40 (.75)
10. Dependency 9.96 .127 .127 3.50 (.30) 7.22 (.73)
Open in a new tab

PBH Benjamini–Hochberg corrected P-value, a discrimination parameter, τ difficulty parameter, “–” anchor item

Stage II Analysis: Final MIMIC Model

Regression of the latent construct of gambling on grouping variables and covariates showed significant group mean differences (see Table 5). Being female (c = −0.240; z = −4.778; P < .001), older age (c = −0.194; z = −3.467; P < .001), and currently married (c = -0.190; z = −4.421; P < .001) were all associated with lower mean levels of the latent gambling variable. In contrast, being African American (c = 0.274; z = 4.886; P < .001), Asian American (c = 0.473; z = 3.584; P < .001), and younger (c = 0.177; z = 2.667; P < .05) were all associated with higher mean levels.

Table 5.

Covariate and group mean differences in PGD criteria endorsement

Variable γ SE z
Grouping variables
   Gender (reference = male) −0.240 .05 −4.778***
   African-American (reference = Caucasian)   0.274 .06   4.886***
   Asian-American (reference = Caucasian)   0.473 .13   3.584***
   Hispanic (reference = Caucasian)   0.081 .07   1.251
   Older adults (reference = age 25–60) −0.194 .06 −3.467***
   Young adults (reference = age 25–60)   0.177 .07   2.667**
Covariates
   High school (reference = less than HS) −0.001 .05 −0.027
   College (reference = less than HS) −0.065 .05 −1.312
   Marital status (reference = unmarried) −0.190 .04 −4.421***
   Income (per $10,000) −0.006 .01 −1.412
Open in a new tab
**

P <.01;

***

P <.001

Table 6 shows parameter estimates of DIF effects. Similar to regression, DIF coefficients and odds ratios adjusted for differences on model covariates and group differences in gambling pathology. Controlling for covariates and group differences in the latent construct, women were significantly less likely to endorse Criterion 1 (OR = 0.62), but more than two times as likely (OR = 2.22) to endorse Criterion 5 than Caucasian males aged 25–59. In terms of race/ethnicity DIF, Asian Americans had a decreased probability of endorsing Criterion 1 (OR = 0.34). Compared to the reference group (Caucasian males age 25–59), African Americans were more than twice as likely to endorse Criterion 3 and Criterion 9 and showed no evidence of negative DIF on any studied item. Hispanics showed positive DIF on Criterion 3, with almost two times greater odds of endorsing this criterion, compared to the reference group (Caucasian males aged 25–59). Young adults (18–24) were less likely to endorse Criterion 5 (OR = 0.62), but more likely to endorse Criterion 6 (OR = 1.81).

Table 6.

Uniform DIF tests for lifetime PGD criteria

Criterion Gender African-American Asian Hispanic Older adult Young adult
1 −0.48 (.15)***[0.62] −0.19 (.15) −1.08 (.29)***[0.34] −0.29 (.18)   0.20 (.15) −0.21 (.18)
3   0.13 (.18)   0.92 (.21)***[2.50] −0.50 (.36)   0.69 (.22)**[2.01]   0.36 (.24)   0.05 (.26)
5   0.79 (.14)***[2.22]   0.04 (.14) −0.06 (.31)   0.06 (.16) −0.15 (.16) −0.48 (.21)*[0.62]
6 −0.28 (.17)   0.10 (.17)   0.28 (.23)   0.10 (.22) −0.41 (.20)*[0.76]   0.60 (.23)**[1.81]
9 −0.32 (.36)   0.82 (.29)**[2.27] −1.52 (.93)   0.30 (.40) −0.20 (.43) −0.64 (.46)
Open in a new tab
*

P< 05;

**

P<.01;

***

P<.001;

DIF effects, (SE), [OR]

Discussion

We found evidence of DIF relative to gender, race/ethnicity, and age, after adjusting for group mean differences in gambling pathology. For female and young adults, DIF was present in both directions, with decreased likelihood of endorsing certain criteria and increased likelihood of endorsing other criteria (Table 6). In contrast, analysis of racial/ ethnic subgroups identified DIF in a single direction. African Americans showed twice the likelihood of endorsing two PGD criteria, and Hispanics showed positive DIF on one item. Asian Americans and older adults showed DIF reflecting decreased likelihood of endorsing specific criteria.

The presence of DIF is of particular importance in light of racial/ethnic disparities in the prevalence of PGD. Recent epidemiological studies, including the NESARC survey (Grant and Dawson 2005; Grant et al. 2003) used for this analysis, have found higher rates of PGD among African Americans compared to the general population (Welte et al. 2001). It is possible that DIF in DSM-based instruments such as the AUDADIS contribute to racial differences in prevalence rates between African Americans and Caucasians. Nonetheless, we found significantly higher levels of gambling pathology in the African American subsample, even when correcting for the DIF, suggesting that DIF is not singularly responsible for racial/ethnic disparities in disordered gambling (Cunningham-Williams et al. 2007). For clinical practitioners and prevention experts, these findings suggest that DIF should be a consideration in addressing age, gender and ethnic disparities in Pathological Gambling. Prevention and intervention resources should target groups at identified higher risk of gambling problems as our results indicate that these differences may not be attributable to measurement bias.

We found gender-based DIF specifically for chasing losses/gains and for gambling to escape. Our finding that women show greater likelihood of endorsing gambling is consistent with the findings of Strong and Kahler (2007). Factor analysis indicated that this criterion did not load as strongly on a single gambling factor (see Table 3) as did other criteria. These findings suggest that escape gambling is less strongly associated with the unidimensional construct of PGD as analyzed, but is associated with female gender. Gambling to escape may represent a second dimension of the gambling construct important in identifying gambling pathology in women, or this criterion may inadvertently tap comorbid pathology related to affectivity such as anxiety and mood disorders. Recent studies have reported higher levels of anxiety and depression comorbidity among female subclinical and pathological gamblers (Blanco et al. 2006). Desai and Potenza (2008), studying the NESARC sample (Grant et al. 2003), found that associations between PG/PGD and Major Depression, Dysthymia, and Panic Disorder were statistically stronger in women than in men. Further theorizing about the nature of the PGD construct itself will be necessary to determine whether gender-based DIF is a function of PGD as a multidimensional construct or actual item bias relative to gender.

Less pronounced was the finding of age-related DIF for older adults. After accounting for differences in PGD pathology in the model, DIF occurred only for the chasing losses criterion. Model estimates indicated that older adults had significantly lower gambling pathology (Table 5) than the reference group (Caucasian males age 25–59). This suggests that overall, lower prevalence rates of PGD in older adults are not the result of item bias. As opposed to older adults, young adults showed greater likelihood of endorsing the “chasing” criterion. Chasing may be a gambling behavior more common in younger pathological gamblers. Younger gamblers may be driven by sensation seeking but this may be less important among older adults (Stinchfield and Winters 1998). A study by Nower et al. (2004) found that gambling-disordered youth displayed preferences for “intensity seeking” and “novelty seeking”.

Some of our findings contrast with those of Strong and Kahler’s (2007) DIF analysis of gambling criteria. These differences are likely the result of differing approaches to the sample and the method used in assessing for DIF. Using MIMIC modeling, we were able to adjust for the complex survey design of the NESARC (Grant and Dawson 2005; Grant et al. 2003), including weighting, stratification and clustering of the data. Researchers have found that structural equation models yield statistically different model fit statistics and parameter estimates when design effects are included compared to when they are ignored (Hahs-Vaughn and Lomax 2006). The use of complex survey methods also allowed for accurate estimation of standard errors. Use of complex survey analyses was especially important in our analysis, where the focal groups (African Americans, Hispanics and young adults) were oversampled. Thomas and Cyr (2002) reported that exclusion of complex sample design from IRT analyses could lead to DIF when groups of interest are oversampled.

We also estimated a 2-parameter logistic model as opposed to a 1-parameter logistic model (Rasch Model) estimated by Strong and Kahler (2007). We opted for a 2-parameter model because the assumption of equal discrimination parameters inherent in the Rasch model may be too strict for health-related items (Teresi 2006) such as DSM-IV criteria. Additionally, since gambling criteria are already in use, the removal of items that contribute to misfit would be unrealistic.

We also adjusted for covariates in the models (e.g. income); this may have been particularly important in controlling for latent mean differences on gambling pathology between focal and reference groups accounted for by the covariates. One such covariate was marital status. By adjusting for marital status, we controlled for potential focal/reference group differences in marriage/cohabitation and their influence on gambling problems. Inclusion of these variables helped ensure that estimates of differential item function were not a result of group differences in income, education level, or marital status.

Our research has a number of limitations. Although the 2-parameter logistic model estimated discrimination parameters, these MIMIC models do not assess for non-uniform DIF. There is the potential that non-uniform DIF is present in PGD criteria and not detected in our analyses. Overall, PGD criteria had low rates of endorsement. This led in some cases to wide standard errors for certain focal groups such as Asian Americans. Additionally, our MIMIC models did not adjust for differences in other psychiatric comorbidity; it is possible that DIF was the result of racial/ethnic, gender, or age differences in psychiatric comorbidity.

Despite these limitations, we conducted DIF analyses for PGD on new subgroups (i.e. older adults, Hispanics, Asian Americans), and our findings on African Americans yielded evidence of previously undetected DIF in this population. Replication is necessary (in other samples and using alternate methods) to further assess estimates of DIF (Camilli and Shepard 1994). Additionally, follow up studies such as cognitive interviewing may identify factors contributing to DIF (Napoles-Springer et al. 2006). Further research will suggest future steps, if any, needed to address criteria level bias in PGD criteria. Moreover, future investigations should examine differential test functioning to determine whether criterion level DIF on multiple criteria influence the performance of PGD criteria as a whole (Raju et al. 1995).

Acknowledgement

The National Epidemiological Survey on Alcohol and Related Conditions (NESARC) was conducted and funded by the National Institute on Alcohol Abuse and Alcoholism (NIAAA), with supplemental support from the National Institute on Drug Abuse (NIDA).

Contributor Information

Paul Sacco, Email: psacco@ssw.umaryland.edu, School of Social Work, University of Maryland-Baltimore, 525 West Redwood Street, Baltimore, MD 21201, USA.

Luis R. Torres, Graduate College of Social Work, University of Houston, Houston, TX, USA

Renee M. Cunningham-Williams, George Warren Brown School of Social Work, Washington University in St. Louis, St. Louis, MO, USA

Carol Woods, Department of Psychology, Washington University in St. Louis, St. Louis, MO, USA.

G. Jay Unick, School of Social Work, University of Maryland-Baltimore, 525 West Redwood Street, Baltimore, MD 21201, USA.

References

  1. American Educational Research Association, American Psychological Association, & National Council on Measurement in Education. Standards for educational and psychological testing. Washington, DC: 1999. [Google Scholar]
  2. American Psychiatric Association. Diagnostic and statistical manual of mental disorders: DSM-IV. 4th ed. Washington, DC: American Psychiatric Association; 1994. [Google Scholar]
  3. Arnett JJ. Emerging adulthood: A theory of development from the late teens through the twenties. American Psychologist. 2000;55(5):469–480. [PubMed] [Google Scholar]
  4. Benjamini Y, Hochberg Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing. Journal of the Royal Statistical Society. Series B (Methodological) 1995;57(1):289–300. [Google Scholar]
  5. Blanco C, Hasin DS, Petry N, Stinson FS, Grant BF. Sex differences in subclinical and DSM-IV pathological gambling: Results from the national epidemiologic survey on alcohol and related conditions. Psychological Medicine. 2006;36(7):943–953. doi: 10.1017/S0033291706007410. [DOI] [PubMed] [Google Scholar]
  6. Bond TG, Fox CM. Applying the Rasch model: Fundamental measurement in the human sciences. 2nd ed. Mahwah, NJ: Lawrence Erlbaum Associates; 2007. [Google Scholar]
  7. Camilli G, Shepard LA. Methods for identifying biased test items. Thousand Oaks, CA: Sage Publications; 1994. [Google Scholar]
  8. Crisp BR, Thomas SA, Jackson AC, Smith S, Borrell J, Ho W-y, et al. Not the same: A comparison of female and male clients seeking treatment from problem gambling counselling services. Journal of Gambling Studies. 2004;20(3):283–299. doi: 10.1023/B:JOGS.0000040280.64348.d1. [DOI] [PubMed] [Google Scholar]
  9. Cunningham-Williams RM, Cottler LB, Compton WM, Spitznagel EL. Taking chances: Problem gamblers and mental health disorders—results from the St. Louis Epidemiological Catchment Area study. Journal of Public Health. 1998;88:1093–1096. doi: 10.2105/ajph.88.7.1093. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Cunningham-Williams RM, Cottler LB, Compton WM, Spitznagel EL. Problem gambling and comorbid psychiatric and substance use disorders among drug users recruited from drug treatment and community settings. Journal of Gambling Studies. 2000;16(4):347–376. doi: 10.1023/a:1009428122460. [DOI] [PubMed] [Google Scholar]
  11. Cunningham-Williams RM, Grucza RA, Cottler LB, Womack SB, Books SJ, Przybeck TR, et al. Prevalence and predictors of pathological gambling: Results from the St. Louis personality, health and lifestyle (SLPHL) study. Journal of Psychiatric Research. 2005;39(4):377–390. doi: 10.1016/j.jpsychires.2004.09.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Cunningham-Williams RM, Ostmann EL, Spitznagel EL, Books SJ. Racial/ethnic variation in the reliability of pathological gambling disorder. Journal of Nervous and Mental Disease. 2007;195(7):551–559. doi: 10.1097/NMD.0b013e318093ed13. [DOI] [PubMed] [Google Scholar]
  13. Desai R, Potenza M. Gender differences in the associations between past-year gambling problems and psychiatric disorders. Social Psychiatry and Psychiatric Epidemiology. 2008;43(3):173–183. doi: 10.1007/s00127-007-0283-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Embretson SE, Reise SP. Item response theory for psychologists. Mahwah, NJ: Lawrence Erlbaum Associates; 2000. [Google Scholar]
  15. Gerstein D, Hoffman J, Larison C, Engelman L, Murphy S, Palmer A, et al. Gambling impact and behavior study (no. 0160594715) New York, NY: National Gambling Impact Study Commission; 1999. [Google Scholar]
  16. Gierl MJ. Using dimensionality-based DIF analyses to identify and interpret constructs that elicit group differences. Educational Measurement: Issues and Practice. 2005;24(1):3–14. [Google Scholar]
  17. Grant B, Dawson D. Introduction to the national epidemiologic survey on alcohol and related conditions. Alcohol Research and Health. 2005;29(2):74. [Google Scholar]
  18. Grant BF, Harford TC, Dawson DA, Chou PS, Pickering RP. The Alcohol and Associated Disability Interview Schedule (AUDADIS): Reliability of alcohol and drug modules in a general population sample. Drug and Alcohol Dependence. 1995;39:37–44. doi: 10.1016/0376-8716(95)01134-k. (Instrument Validation) [DOI] [PubMed] [Google Scholar]
  19. Grant BF, Kaplan K, Shepard J, Moore T. Source and accuracy statement for wave 1 of the 2001–2002 National Epidemiologic Survey on Alcohol and Related Conditions. Bethesda, MD: National Institute on Alcohol Abuse and Alcoholism; 2003. [Google Scholar]
  20. Hahs-Vaughn DL, Lomax RG. Utilization of sample weights in single-level structural equation modeling. Journal of Experimental Education. 2006;74(2):163–190. [Google Scholar]
  21. Levinson DJ. A conception of adult development. American Psychologist. 1986;41(1):3–13. [Google Scholar]
  22. Muthén LK, Muthén BO. Mplus users guide. 4th ed. Los Angeles, CA: Muthén & Muthén; 1998–2009. [Google Scholar]
  23. Napoles-Springer AM, Santoyo-Olsson J, O’Brien H, Stewart AL. Using cognitive interviews to develop surveys in diverse populations. Medical Care. 2006;44(11):S21–S30. doi: 10.1097/01.mlr.0000245425.65905.1d. [DOI] [PubMed] [Google Scholar]
  24. National Research Council. Pathological gambling: A critical review. Washington, DC: National Academy Press; 1999. [Google Scholar]
  25. Nower L, Derevensky JL, Gupta R. The relationship of impulsivity, sensation seeking, coping and substance use in youth gamblers. Psychology of Addictive Behaviors. 2004;18(1):49–55. doi: 10.1037/0893-164X.18.1.49. [DOI] [PubMed] [Google Scholar]
  26. Petry NM, Stinson FS, Grant BF. Comorbidity of DSM-IV pathological gambling and other psychiatric disorders: Results from the National Epidemiological Survey on Alcohol and Related Conditions. Journal of Clinical Psychiatry. 2005;66(5):564–574. doi: 10.4088/jcp.v66n0504. (Research) [DOI] [PubMed] [Google Scholar]
  27. Raju NS, van der Linden WJ, Fleer PF. IRT-based internal measures of differential functioning of items and tests. Applied Psychological Measurement. 1995;19(4):353–368. [Google Scholar]
  28. Raylu N, Oei TP. Role of culture in gambling and problem gambling. Clinical Psychology Review. 2004;23(8):1087–1114. doi: 10.1016/j.cpr.2003.09.005. [DOI] [PubMed] [Google Scholar]
  29. Research Triangle Institute. SUDAAN language manual, release 9.0. Research Triangle Park, NC: Research Triangle Institute; 2004. [Google Scholar]
  30. Shaffer H, Hall MN, Vander Bilt J. Estimating the prevalence of disordered gambling behavior in the United States and Canada: A research synthesis. American Journal of Public Health. 1999;89(9):1369–1376. doi: 10.2105/ajph.89.9.1369. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Stinchfield R, Winters KC. Gambling and problem gambling among youths. Annals of the American Academy of Political and Social Science. 1998;556:172–185. [Google Scholar]
  32. Strong DR, Kahler CW. Evaluation of the continuum of gambling problems using the DSMIV. Addiction. 2007;102(5):713–721. doi: 10.1111/j.1360-0443.2007.01789.x. [DOI] [PubMed] [Google Scholar]
  33. Tang C, Wu A, Tang J. Gender differences in characteristics of Chinese treatment-seeking problem gamblers. Journal of Gambling Studies. 2007;23(2):145–156. doi: 10.1007/s10899-006-9054-0. [DOI] [PubMed] [Google Scholar]
  34. Teresi JA. Different approaches to differential item functioning in health applications. Advantages, disadvantages and some neglected topics. Medical Care. 2006;44(11):S152–S170. doi: 10.1097/01.mlr.0000245142.74628.ab. [DOI] [PubMed] [Google Scholar]
  35. Thissen D, Steinberg L, Kuang D. Quick and easy implementation of the Benjamini-Hochberg procedure for controlling the false positive rate in multiple comparisons. Journal of Educational and Behavioral Statistics. 2002;27(1):77–83. [Google Scholar]
  36. Thomas DR, Cyr A. Applying item response theory methods to complex survey data; Paper presented at the Proceedings, Statistical Society of Canada, Section on Survey Research Methods; Hamilton, ON. 2002. [Google Scholar]
  37. Toce-Gerstein M, Gerstein DR, Volberg RA. A hierarchy of gambling disorders in the community. Addiction. 2003;98(12):1661–1672. doi: 10.1111/j.1360-0443.2003.00545.x. [DOI] [PubMed] [Google Scholar]
  38. U.S. Census Bureau. 2000 Census of population and housing, population and housing unit counts PHC-3-1 United States summary. Washington, DC: U.S. Census Bureau; 2004. [Google Scholar]
  39. Welte JW, Barnes GM, Wieczorek WF. Gambling participation in the U.S.—results from a national survey. Journal of Gambling Studies. 2002;18(4):313–337. doi: 10.1023/a:1021019915591. [DOI] [PubMed] [Google Scholar]
  40. Welte JW, Barnes GM, Wieczorek WF, Tidwell MC. Gambling participation and pathology in the United States—a sociodemographic analysis using classification trees. Addictive Behaviors. 2004;29(5):983–989. doi: 10.1016/j.addbeh.2004.02.047. [DOI] [PubMed] [Google Scholar]
  41. Welte JW, Barnes GM, Wieczorek WF, Tidwell M-C, Parker J. Alcohol and gambling pathology among U.S. adults: Prevalence, demographic patterns and comorbidity. Journal of Studies on Alcohol. 2001;62(5):706–712. doi: 10.15288/jsa.2001.62.706. (Research) [DOI] [PubMed] [Google Scholar]
  42. Woods CM. Empirical selection of anchors for tests of differential item functioning. Applied Psychological Measurement. 2009;33(1):42–57. [Google Scholar]

RESOURCES