Confounders of mutation-rate estimators: selection and phenotypic lag in Thermus thermophilus

Abstract

In a recent description of the rate and character of spontaneous mutation in the hyperthermophilic bacterium Thermus thermophilus, the mutation rate was observed to be substantially lower than seen in several mesophiles. Subsequently, a report appeared indicating that this bacterium maintains an average of about 4.5 genomes per cell. This number of genomes might result in a segregation lag for the expression of a recessive mutation and might therefore lead to an underestimate of the rate of mutation. Here we describe some kinds of problems that may arise when estimating mutation rates and outline ways to adjust the rates accordingly. The emphasis is mainly on differential rates of growth of mutants versus their parents and on various kinds of phenotypic lag. We then apply these methods to the T. thermophilus data and conclude that there is as yet no reliable impact on a previously described rate.

1. Introduction

Estimating a mutation rate experimentally typically requires measuring the frequency of mutants in a population, knowing the growth history of that population, understanding the geometry with which the genome is replicated (exponential, stamping-machine [1], or a mixture thereof), assessing potential measurement confounders, and having in hand a theory able to weave these partials into a rate in the form of mutations for a site, a gene, or a genome per chromosome replication, per cell division, per sexual generation, or per unit of time. The large numbers and uniformity of cells in laboratory cultures, combined with strong selections for particular mutants, give micro-organisms important advantages for the experimental analysis of spontaneous mutation. Examining diverse microbial species also enables the mutation process to be compared across wider phylogenetic distances and ranges of environmental conditions than is feasible with multicellular organisms [2–4]. However, probing such extremes may introduce biological properties that complicate mutation analysis. Here we examine the basis and quantitative impact of two such complications (selection and phenotypic lag), outline appropriate corrections, and then apply the insights to a somewhat complicated example, mutation in Thermus thermophilus. Because the T. thermophilus rate [4] and that from Sulfolobus acidocaldarius [2] suggest a fundamental difference between mutation rates in thermophiles and mesophiles [5], the present analysis is of general interest.

2. Theory and occasional confounders

One of the most powerful methods of calculating rates of growth-dependent spontaneous mutation in exponentially growing cultures originated with Luria and Delbrück in 1943 [6]. The simple portion of their formulation starts with the assumption that the occurrence of mutations is random among cells and in time (which may be expressed as generations). In the absence of confounders, mutations arise at a constant rate μ per cell or chromosome duplication that is independent of the population size; previously arisen mutants replicate at the same rate as do non-mutants; and the mutant frequency remains small enough so that neither reverse mutation nor the loss of non-mutants to the growing pool of mutants need be taken into account. The measurements are made using a number of parallel cultures inoculated with sufficiently few cells that no mutants are included. At first, only rare cultures experience a mutation event; later, at a per-culture population size in the neighborhood of the reciprocal of the mutation rate, many cultures will have experienced one or a few mutation events; and, as growth continues, all cultures will eventually have accumulated many mutation events.

The total number of cell or chromosome duplications required to produce a final population of size N starting from a single cell or chromosome is N – 1 ≈ N. Therefore, the number of mutations per cell or chromosome replication (the mutation rate) is μ = m/N where m is the average number of mutation events per culture. The random distribution of mutation events across cultures can be described by the Poisson distribution, P(x) = m^xe^–m/x!, so that the fraction of cultures without mutants is given by P(0) = e^–m and m = –ln[P(0)]. This procedure is often called the “null-class” or “P-zero” method and it works best when P(0) ≈ 0.5.

The change in numbers of mutants M during the growth of a population can be easily described as the increments of newly arising mutants plus the growth of previously arisen mutants: dM = (μ + M/N)dN. Substituting the mutant frequency f = M/N, the equation integrates to the simple expression μ = f/ln(N/N₀) where f is the final mutant frequency.

The striking characteristic of mutation frequencies that stimulated these insights of Luria and Delbrück was the tendency of some cultures to contain anomalously large numbers of mutants (“jackpot” cultures). These high frequencies are driven by the infrequent occurrence of the first mutation event early in the growth of a culture, when μN << 1. Luria and Delbrück and their successors devised complex “fluctuation test” methods to estimate m under these conditions, but the calculations were always tedious and are now most easily performed by simulators such as the on-line FALCOR calculator at http://www.mitochondria.org/protocols/FALCOR.html. The distribution of mutant frequencies among large numbers of cultures displays a long tail with values far above those for central measures such as the mean or the mode. However, use of the median frequency considerably relieves the impact of this tail on m. In addition, if one ignores the few mutation events that occurred before N ≈ 1/μ and replaces N₀ with 1/μ in the above equation, the result is the estimator μ = f/ln(Nμ) where the median value of μ is reported [7]. This method generates the same value as the more complicated “gold standard” calculations of Luria and Delbrück and their elaborators provided that m ≥ 30 [8], that is, provided that the cultures have grown at least 4 generations beyond N ≈ 1/μ and thus have experienced at least 1 + 2 + 4 + 8 + 16 = 31 mutation events.

These ways of estimating mutation rates can be confounded by either or both of two classically recognized complications, sometimes in different directions. The following simple methods were also treated previously in a computationally more complex way [9].

2.1 Differential growth rates

One of the classical confounders is differential growth, when the mutants and their non-mutant progenitors grow at different rates, and which is sometimes called selection. Depending on the direction of the bias, differential growth can lead to mutant frequencies that either underestimate or overestimate mutant events and therefore mutation rates. The impact of selection on mutation frequencies is nil for the null-class method because only the presence or absence of mutants is relevant. The impact of selection on cultures grown to N >> 1/μ (sometimes called the accumulation method) can be assessed by a simple modification of “dM = (μ + M/N)dN” by starting with dM = [μ + (1 – s)M/N]dN where s is the “coefficient of selection”, s = 1 corresponding to lethality (the mutants being unable to grow) and s < 0 corresponding to a growth advantage compared to the non-mutants [10]. As before, setting f₀ = 0, integrating, and replacing N₀ with 1/μ leads to μ = sf/[1 – e^–sln(Nμ)]. s can be estimated by reconstruction experiments, that is, by growing mixtures of parental and mutant organisms (where the proportion of the latter is substantially higher than produced by mutagenesis alone) for g generations, measuring the initial and final mutant frequencies, and calculating s from f/f₀ = (1 – s)^g.

2.2 Phenotypic lag

The other classical confounder is the delayed expression of newly arisen mutations, which may result from factors such as the number of additional chromosome replications required to reduce a recessive mutation to homozygosity, or the extent of macromolecular turnover required to reduce the amount of non-mutant gene product to an ineffectual level. Such delays cause mutation frequencies to be underestimated. Originally called “delayed phenotypic expression” [11], the term “phenotypic lag” is now often used for the delayed expression of newly arisen mutations, and the more specific term “segregation lag” is sometimes used for the delayed achievement of homozygosity.

The following formulations can be obtained using simple inductive reasoning for populations of cells whose chromosomes replicate and then segregate into the two daughter cells. As generations (g) increase, both population sizes and numbers of new mutation events each increase by the factor 2^{(g – 1)}. Total mutants increase (by the sum of mutagenesis and replication) by a factor of g2^{(g – 1)}; importantly, each generation contributes equally to the final yield of mutants. In the presence of phenotypic lag, mutants fractionate into the expressed and the unexpressed. For a lag of L generations, no new mutants are expressed for L generations. Thereafter, the number of expressed mutants is (g – L)2^{(g – 1)} and of unexpressed mutants is L2^{(g – 1)}. The fraction of expressed mutants is (g – L)/g for g ≥ L, at first being 0 and asymptotically approaching 1 with increasing generations. A simple way to correct μ for phenotypic lag of length L in a culture that had already grown to size N₂ and had accumulated >30 mutational events L generations back when it was of size N₁ is to note that the final measured f (based on only expressed mutants) will be the same as was the total f (including expressed and unexpressed mutants) L generations back, because both M_expressed and N will increase by 2^L in that interval; the additional mutations newly arising over those L generations will not be detected. However, N₁ will be only N₂/2^L at that time, so that the corrected μ = f/ln(μN₂/2^L), or simply μ = f/ln(μN/2^L).

For strongly recessive mutations, mutants cannot be detected until they achieve homozygosity. In the case of a bacterium with multiple copies of its genome, the number of cell divisions required for reduction to homozygosity depends on the mode of chromosome segregation, of which there are several possibilities.

1. Consider an asexual microbe with an array of four sister chromosomes, [  ], one of which ( ) contains a newly arisen mutation. If, after a synchronous division of all four chromosomes to [ □    ], the left four and the right four chromosomes segregate to different daughter cells, one cell receives both mutant chromosomes, [  ]. After the next cell division, one cell achieves homozygosity, [  ]. In this case, the phenotypic lag from segregation is L = 2. More generally, whenever the number of chromosome copies n is a power of 2, L = ln(n)/ln(2), but if n is not a power of 2, segregation continues indefinitely as a minority contributor to the mutant frequency.

2. If, instead, each pair of newly replicated mutant chromosomes segregates into a different daughter cell, then [  ]→ 2[  ]→ 4[  ] and so on, and a recessive mutation will never be detected by conventional phenotypic methods.

3. If the chromosomes segregate randomly, then there are many individual paths to homozygosity and the average value of L may best be estimated by simulation. An example is given below for a population comprised of cells with four copies of their genomes, each of which replicates once per cell generation and four of whose daughter genomes are then distributed at random to each of the two daughter cells.

Because the null-class method for estimating mutation rates necessarily depends on cultures that have experienced an average of at most a few mutation events, it is particularly vulnerable to phenotypic lag. The classical fluctuation test, in which most cultures have usually experienced one or several mutation events, is also vulnerable. In contrast, the accumulation method can be rather insensitive to phenotypic lags of up to several generations depending on the mode of chromosome segregation into daughter cells, provided the cultures are grown to sufficiently large values of N; a probable exception is extreme values of L as in the case of Haloferax volcanii [3]. Thus, a mutation rate derived by the accumulation method that is larger than one determined by the null-class method or the fluctuation test signals the possible impact of phenotypic lag. In the case of fluctuation tests, the quartiles method of Koch [8] can also signal phenotypic lag. One experimental test for detecting and quantifying phenotypic lag consists of treating briefly with a mutagen and then monitoring the time to the appearance of new mutants.

2.3 Other confounders

An unusually early origin of the first mutation in a culture strongly enhances the mutation frequency, the event originally designated a jackpot [6]. The usual way to avoid the consequences of jackpots when estimating mutation rates is to use the median value. In a manner evocative of the impact of increasing N on phenotypic lag, the continual addition of new mutants to a culture can dilute the impact of an early mutation, but a large jackpot is difficult to thusly dilute to a mutation frequency close to the median value. If we let f₀ = the constant mutant frequency established by the jackpot event alone, and f_N = the increasing mutant frequency due to recurrent mutation = μln(Nμ), then the total mutation frequency is f = f₀ + f_N. The factor R by which the jackpot increases the mutant frequency over the typical value is then (f₀ + f_N)/f_N = 1 + f₀/μln(Nμ). For values of f₀/μ = 10, increasing N from 10/μ to 1000/μ decreases R from 5.3 to 2.4, whereas for values of f₀/μ = 100, increasing N from 10/μ to 1000/μ decreases R from 44 to 15. Thus, the impact of a pronounced jackpot upon a particular culture cannot be squelched even by greatly increasing N, even though it can be countered by using the median value from many cultures.

Microbial mutants are often detected by selective plating in the presence of an agent that either blocks the growth of, or kills, the non-mutant parents. Sometimes, however, the cells can continue to replicate for one or a few generations and express the mutations that arise in those replications. Various schemes exist or can be devised to detect and measure the residual growth; see, for instance, the case of canavanine-resistant mutant in yeast [12]. This behavior has the effect of increasing the final population size and can be accordingly countered arithmetically.

3. Mutation in Thermus thermophilus

In the course of determining the kinds and rates of spontaneous mutation in extremophiles, we examined T. thermophilus [4]. Mutation rates were estimated from frequencies of pyrE and pyrF uracil auxotrophs that survived plating in the presence of 5-fluoroorotic acid and were confirmed by sequencing, and the final value was the average of determinations using fluctuation tests and the accumulation method and was expressed as μ^g, the genomic rate in mutations per genome duplication. Calculating this value requires not only the formulations already discussed here, but also a method that takes into account the fact that, while virtually all indels are detected, most base-pair substitutions (BPSs) go undetected. Provided that sufficient mutants have been collected and sequenced, the preferable way to do this is to estimate the BPS rate solely from chain-terminating BPSs that, like indels, are detected with high efficiency (at the cost of small sample sizes). That rate for T. thermophilus was μ^g = 0.00093 and was of interest because it was several-fold lower than rates characteristic of nonthermophiles, which cluster around 0.003– 0.004 for DNA-based microbes [5, 7]. The T. thermophilus rate was based on the average of (i) a genic rate from the accumulation method with N = 10¹⁰ and, for the median culture with a central f = 1.745 × 10^–6, μ = (2.26 ± 0.66) × 10^–7 and (ii) a rate using a fluctuation test yielding μ = (4.34 ± 2.92) × 10^–7. The average rate was ?μ = (3.30 ± 2.12) × 10^–7 which was then scaled by 73/75 to account for a small fraction of mutations that did not localize to the mutation-reporter genes by DNA sequencing, yielding ?μ = (3.21 ± 2.06) × 10^–7.

3.1 Differential growth

Two tests for differential growth rates between mutant and wild-type cells were reported for T. thermophilus [4]. In a series of turbidometric tests, the growth rates of separately grown mutant and parental cultures were monitored and the mean ratio of mutant to wild-type growth rates was 0.98 ± 0.29. In eight reconstruction controls using mixtures of mutant and wild type cells, the mean ratio of mutant to wild-type growth rates was 1.20 ± 0.23. These values revealed no significant difference in growth rates but did hint that mutant cells might grow more rapidly than wild-type cells when supplemented by a nutrient (uracil) specifically essential for the mutants. Note that the mixed-growth method may be intrinsically more accurate than the turbidometric comparisons and that the growth rate of a small minority of mutants might better reflect the environment of a newly arisen mutant. If the value of 1.20 were correct, then the selection coefficient in the mutation-accumulation method would be s = –0.20 and the solution to μ = sf/[1 – e^–sln(Nμ)] would correspond to a genomic mutation rate of μ^g that is 1.21-fold lower than posted in ref. [5]. Assuming that the fluctuation test rate was not affected by differential growth because of the small number of generations that newly arisen mutants could grow (see also ref. [9]), the average rate for the fluctuation and accumulation methods would be ?μ = (2.65 ± 2.02) × 10^–7, a (clearly insignificant) 1.21-fold decrease from the uncorrected value.

3.2 Phenotypic lag

Two results were reported in the T. thermophilus analysis suggesting that phenotypic lag was not an important factor [4]. One was that the measured mutation rate was modestly although insignificantly higher from the fluctuation tests than from the accumulation method, [(4.34 ± 2.92)/(2.26 ± 0.66)] = 1.92-fold, whereas phenotypic lag would have produced an opposite effect. The other was that the use of the quartile method [9] failed to signal phenotypic lag. However, our calculations of mutation rates implicitly assumed that the number of copies of the genome was small, one or two per cell, in which case only one or two generations would suffice for mutant expression and phenotypic lag would have little impact on our rate estimations. In contrast to this assumption, T. thermophilus was later reported to harbor an average of 4.5 genomes per cell [13], which might have led to significant phenotypic lag.

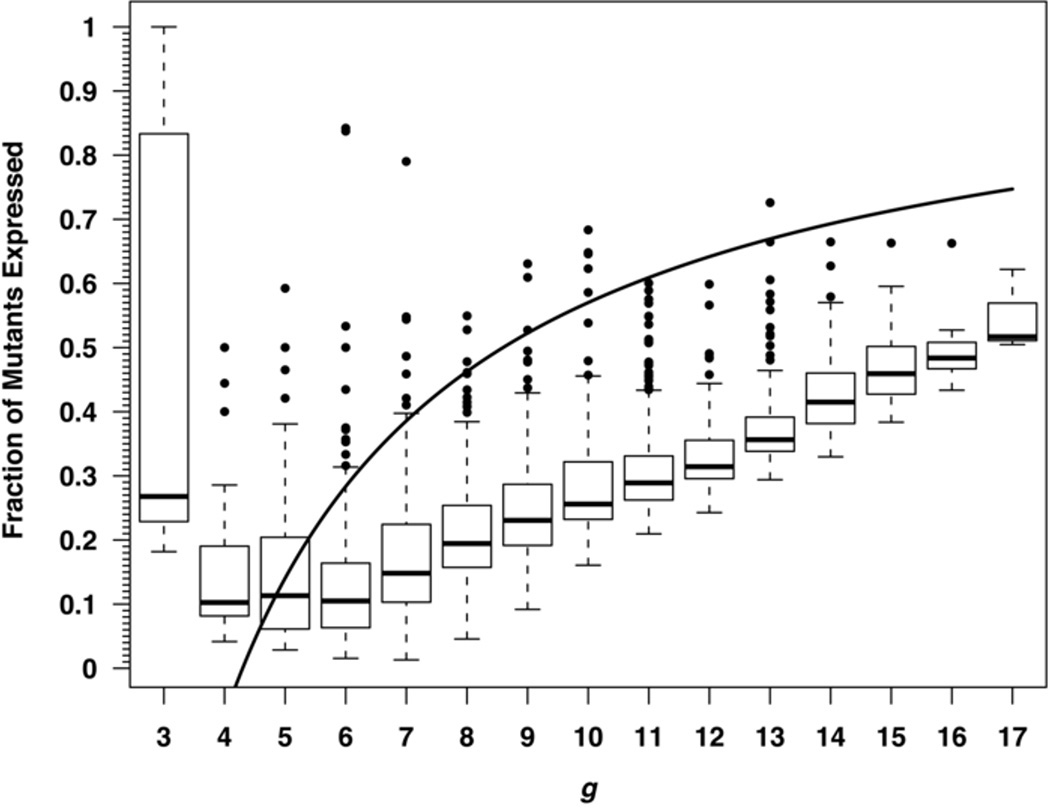
In the absence of information concerning the pattern of chromosome segregation in T. thermophilus, we examined the consequences of two models. The first uses the expression described previously, μ = f/ln(μN/2^L) with L = 4.5, where the accumulation method had N = 10¹⁰ and f = 1.745 × 10^–6 for the median μ, and the corrected μ = (1.745 × 10^–6)/ln(μ10¹⁰/2^4.5) = (3.47 ± 2.23) × 10^–7, a value 1.55-fold higher than the posted value of 2.26 × 10^–7. The second used a simulation method based on random segregation of genomes into progeny cells (Fig. 1). Both estimates predict an impact on the T. thermophilus analysis. For μ = 3×10^–7 per cell division, the first mutation arises at about 22 generations of growth; this was followed by 3–4 generations in the fluctuation assays and 11 generations in the mutant-accumulation assays [4]. As shown in Fig. 1, both phenotypic-lag calculations yield modest detection efficiencies under these conditions, ranging from 0.1 for the fluctuation cultures predicted by the computational simulation, to 0.6 for the mutant-accumulation cultures predicted by the (g-L)/g method. The presumably more reliable estimator (the simulation) argues that the number of cells containing a pyrE or pyrF mutation may have been 3- to 10-fold higher in the T. thermophilus cultures than indicated by the number of FOA-resistant colonies.

Fig. 1.

Simulation of phenotypic lag in a bacterial population composed of cells maintaining four initially identical copies of their genome, typically as one circular chromosome per genome. In each generation, all copies replicated and each cell divided into two daughter cells, each receiving four chromosome copies. Mutations occurred randomly at a rate per gene copy per cell division of μ = 3.468 × 10^–7 (a value reflecting the T. thermophilus estimate) and genomes were allocated to each pair of daughter cells at random. The horizontal axis (g) shows the number of generations after the first mutation occurred in each simulated culture. Production of the first cell containing four mutant genomes (which is when the phenotype was first expressed in at least one progeny of the first-mutated cell) followed within a few generations and continued cell division was simulated for at least nine generations after that time. The numbers of cells in the mutant lineage containing 0, 1, 2, 3, or 4 mutant chromosomes were tabulated and expressed as a function of g. The entire simulation was repeated 200 times. The solid curve is the fraction of mutations that were expressed as predicted by the expression (g – L)/g in section 2.2. At each generation, the top and bottom vertical dashed lines mark 1.5 interquartile ranges outside of the 75^th and 25^th percentiles, respectively, and values indicated by dots are considered to be outliers. The boxes indicate the middle 50% of values and the horizontal bars within the boxes mark the medians. The median value at g = 3 is based on tiny numbers of mutants and is correspondingly unreliable, that it, is itself an outlier that should be ignored.

Multiple chromosome copies per cell create another complication, independent of phenotypic lag, in which gene replications outnumber cell divisions by a corresponding ratio. This makes it important to identify the relevant basis on which to express mutation rates. Molecular aspects of spontaneous mutation are usually viewed in terms of gene or chromosome replication, and the focus of the T. thermophilus analysis was specifically on genome replication. The genic mutation rate calculated previously was based implicitly on a minimum number of chromosomes per cell, which would be about 1.5 when averaged over a bacterial cell-division cycle. Correcting for the reported 4.5 chromosomes per cell [13] would therefore decrease the previously calculated genic mutation rate by a factor of about 3.

3.3 Thesis, antithesis, synthesis?

We are left with three contrasting measures by which the T. thermophilus mutation rate may have been misestimated: i) a roughly 1.2-fold overestimate arising from a possible growth advantage of mutants arising within a population of non-mutant cells, ii) a possible several-fold underestimate from phenotypic lag due to complementation by multiple copies of the genome, and iii) and a roughly threefold overestimate reflecting the number of gene replications per cell division. However, the overestimate due to growth advantage lacks statistical significance, while the underestimate due to phenotypic lag is contradicted by the observations that the accumulation method produced a rate lower than that produced by the fluctuation tests (whereas phenotypic lag would produce the opposite result), and the fluctuation test revealed no hint of phenotypic lag by quartile analysis. Additional perspectives come from the results of other investigations. An earlier study had found that thermophilic prokaryotes evolve more slowly than do mesophilic ones [14], an observation suggesting that thermophiles achieve lower base-substitution rates than do mesophiles because more base substitutions are deleterious at higher temperatures and thus invite stronger selection for lower base substitution mutation rates [5]. On this basis, T. thermophilus is expected to have a lower mutation rate than the characteristic value of 0.003–0.004 for mesophiles. In addition, base substitutions consistently strongly outnumber indel mutations in mutation spectra of mesophiles based on protein-coding genes, whereas the reverse is seen in the two thermophiles examined to date [2, 4]; this reversal may reflect the almost universally deleterious nature of indels in coding regions, in contrast to base substitutions. In the case of S. acidocaldarius, the lack of MutSL homologues may also contribute, because MutSL-dependent mismatch repair preferentially removes the slipped-strand events that occur in mononucleotide runs and similar simple repeats [15]. However, this hypothesis does seem relevant to T. thermophilus, because its genome encodes intact MutS and MutL homologues [http://archaea.ucsc.edu; 16]. Overall, therefore, the confounders of mutation-rate measurements that we could identify in the T. thermophilus analysis seemed to exert limited and largely offsetting effects.

The mutation-rate corrections applied here should have wider relevance for experimental analyses of genetic fidelity. For instance, certain situations require analyzing mutation in multi-copy plasmids, where the quantitative effects of phenotypic lag can be addressed as described. We also note that several micro-organisms have been found to maintain multiple identical copies of their genomes during normal cell division. To cite an extreme example, the aerobic nitrogen-fixer Azotobacter vinelandii can maintain 40–80 copies of its chromosome per cell, yet recessive mutations and introduced genetic markers are detected with apparently high efficiency [17]. This paradox raises questions as to whether certain prokaryotes may have mechanisms which selectively silence the expression of certain genes or chromosomes, co-segregate daughter chromosomes, or divide with pronounced asymmetry, thereby countering the expected consequences of genetic redundancy [18].

Highlights.

The measurement of microbial mutation rates is peppered with hazards.

These include diverse kinds of phenotypic lag and differential growth.

Ways are described to counter such problems.

These methods are applied to the case of Thermus thermophilus.

The methods are generally applicable.