Recovery of rhythmic activity in a central pattern generator: analysis of the role of neuromodulator and activity-dependent mechanisms

Abstract

The pyloric network of decapods crustaceans can undergo dramatic rhythmic activity changes. Under normal conditions the network generates low frequency rhythmic activity that depends obligatorily on the presence of neuromodulatory input from the central nervous system. When this input is removed (decentralization) the rhythmic activity ceases. In the continued absence of this input, periodic activity resumes after a few hours in the form of episodic bursting across the entire network that later turns into stable rhythmic activity that is nearly indistinguishable from control (recovery). It has been proposed that an activity-dependent modification of ionic conductance levels in the pyloric pacemaker neuron drives the process of recovery of activity. Previous modeling attempts have captured some aspects of the temporal changes observed experimentally, but key features could not be reproduced. Here we examined a model in which slow activity-dependent regulation of ionic conductances and slower neuromodulator-dependent regulation of intracellular Ca²⁺ concentration reproduce all the temporal features of this recovery. Key aspects of these two regulatory mechanisms are their independence and their different kinetics. We also examined the role of variability (noise) in the activity-dependent regulation pathway and observe that it can help to reduce unrealistic constraints that were otherwise required on the neuromodulator-dependent pathway. We conclude that small variations in intracellular Ca²⁺ concentration, a Ca²⁺ uptake regulation mechanism that is directly targeted by neuromodulator-activated signaling pathways, and variability in the Ca²⁺ concentration sensing signaling pathway can account for the observed changes in neuronal activity. Our conclusions are all amenable to experimental analysis.

Introduction

Neural networks that produce rhythmic patterns of activity are commonly involved in behaviors serving basic biological functions, including breathing, heartbeat, locomotion, digestion, etc. (Frere et al., 2004; Golowasch and Marder, 1992; MacKay-Lyons, 2002; Marder, 2000) and most of our understanding derives from work on central pattern generators (CPGs) (Marder and Calabrese, 1996; McCrea and Rybak, 2008; Selverston, 2010). CPGs are often capable of generating robust activity but can also adapt to drastically changing environments. This is accomplished by a readjustment of neuronal intrinsic and synaptic properties (Bucher et al., 2005; Marder and Bucher, 2001; Tryba et al., 2003). One example of such a system is the pyloric network localized in the stomatogastric ganglion (STG) of the crustacean central nervous system (Selverston and Moulins, 1986).

Under normal circumstances the rhythmic activity of the pyloric network depends obligatorily on neuromodulatory substances released by terminals of axons entering the STG via a single input nerve. If action potential transmission along this nerve is blocked (i.e. the STG is ‘decentralized’), rhythmic pyloric activity ceases (Russell, 1979). However, a pattern of activity closely resembling the original pyloric pattern recovers spontaneously in the absence of neuromodulatory input within several hours (Golowasch et al., 1999; Luther et al., 2003; Thoby-Brisson and Simmers, 1998). In the crab Cancer borealis, this recovery follows a complex temporal dynamical process that involves the alternating onset and termination of the rhythm, or ‘bouting’ (Luther et al., 2003). This bouting activity can last several hours, after which a stable pyloric pattern emerges that distinguishes itself from the control pattern only by its somewhat lower frequency (Golowasch et al., 1999; Luther et al., 2003).

We have previously shown that the bouting phase of the recovery of rhythmic pyloric activity after decentralization can be accounted for by the relatively fast activity-dependent regulation of voltage-gated calcium and potassium currents (Golowasch et al., 1999), or even only of voltage-gated calcium currents (Zhang et al., 2009). In these studies we used conductance-based models to further show that, whether only calcium currents or both calcium and potassium currents are regulated, no transition to a stable pattern of activity can be observed in the absence of an additional regulatory mechanism that operates at a much slower time scale (Zhang and Golowasch, 2007; Zhang et al., 2009). Under these conditions, the resulting recovery process meets most of the signature features of recovery in biological preparations (Luther et al., 2003). Nevertheless, these models show two important attributes that are not observed in biological preparations (Luther et al., 2003): 1) individual bout durations gradually increased until stable recovery, 2) a correlation is observed between the extent of bouting activity and delay to stable recovery

In this paper, we used a modified version of our original model (Zhang and Golowasch, 2007) to examine the process of functional recovery of the rhythmic activity of a pacemaker cell using phase plane analysis. In order to accomplish this, this model was modified to both remove non-essential elements for the recovery process, thus reducing it to a two dimensional system. It was additionally modified to reproduce experimentally observed features. The results of this study confirm that activity-dependent feedback to a single conductance, that need not be a calcium conductance, is a sufficient condition to elicit bouting activity, and that the rate of intracellular Ca²⁺ sequestration plays a critical role in controlling the appearance of a stable pyloric rhythm. We find that during bouting, the system alternates its behavior between a limit cycle (within bouts) and a stable fixed point (within interbouts). The switch between these two states occurs via a subcritical Hopf bifurcation, while the transition to the stable recovery occurs as the Ca²⁺ pump rate increases, making the system transition to a state from which it cannot switch back to the stable fixed point. Our results show that, as observed experimentally, the stable recovery of rhythmic activity is fully decoupled from the appearance of bouting. Nevertheless, bouting always precedes the stable recovery. In our model this is forced by the slow nature of the mechanism controlling the stable recovery. Finally, the introduction of low level noise into the system reduces constraints on slow regulatory processes, making the model more physiologically realistic. We discuss possible biological mechanisms that may mediate these two regulatory pathways.

Methods

Electrophysiological recordings were carried out exactly as described before (Luther et al., 2003). Pyloric rhythm activity was measured from extracellular recordings of motor nerves (Fig. 1A).

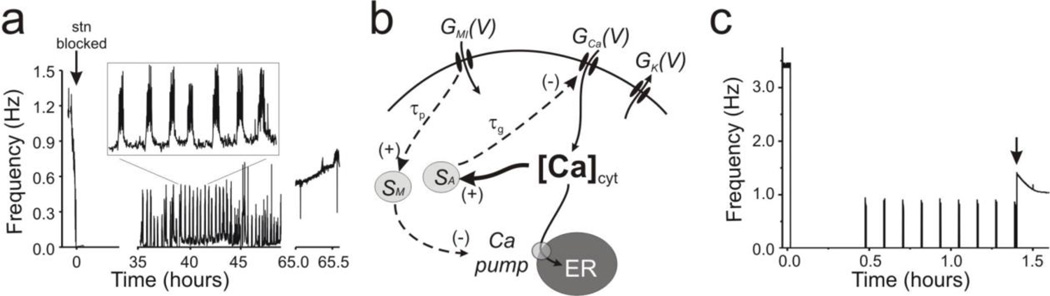
Fig. 1. Decentralization effects in biological and model systems.

(a) Frequency changes over time during the recovery process of the pyloric network rhythmic activity. At time = 0 the input nerve carrying neuromodulatory inputs to the STG was severed (stn blocked, arrow). Inset: expanded view of bouting activity as marked. Stable pyloric activity was recovered in this case after ~65 hours. (b) Schematic diagram of intracellular activity- and neuromodulator-dependent regulation pathways and target molecules. G_K(V) (including both G_A and G_Kd) and G_Ca(V) are the voltage-dependent conductances of I_K and I_Ca, respectively; G_MI(V) is the voltage-dependent conductance of the modulator activated inward current, I_MI, which activates via a neuronal receptor upon binding to a ligand such as proctolin (not shown), and is assumed to directly regulate S_M. All conductances have fast kinetics of activation. S_A is the activity-dependent intracellular Ca²⁺ sensor and in turn (negatively) regulates G_Ca with slow kinetics given by τ_g. S_M is the neuromodulator-dependent sensor that detects changes in G_MI, and in turn (negatively) regulates the endoplasmic reticulum Ca²⁺ pump with slow kinetics given by τ_p > τ_g. G_MI(V) and [Ca]_cyt positively regulate the intracellular sensors S_M and S_A, respectively. ER represents the endoplasmic reticulum or any intracellular Ca²⁺ store. (C) Frequency changes over the recovery process in the full model when E_Ca was set to vary freely with [Ca]_cyt

We built a pacemaker neuron with only a soma/neurite (S/N) compartment generating slow-wave oscillations. Since it has been observed that action potentials produced by an axonal compartment (Zhang and Golowasch, 2007; Zhang et al., 2009) does not make a significant contribution to the recovery process, no axonal compartment was added and only the following currents necessary for slow wave oscillations were included in the S/N compartment: leakage current (I_leak), voltage-gated Ca²⁺ current (I_Ca), voltage-gated delayed rectifier K⁺ current (I_Kd), transient A-type K⁺ current (I_A), and a voltage-gated, neuromodulator-dependent, inward current found in pyloric neurons in crab STG, I_MI, which represents the neuromodulator input from adjacent ganglia (Swensen and Marder, 2000). Decentralization is implemented by turning Ḡ_MI to zero.

$$C_m\frac{dV}{dt}=-(I_{\mathit{\text{Ca}}}+I_{Kd}+I_A+I_{MI}+I_{\mathit{\text{leak}}})$$ [1]

The equations were adapted from those described by Zhang et al. (2007; 2009) for the pacemaker neuron. The parameters describing these currents are included in Table 1.

Table 1.

Voltage dependence of ionic channels in the original full model neuron.

$I_{\mathit{\text{Ca}}}=\overline{G_{\mathit{\text{Ca}}}}{m}_{\mathit{\text{Ca}}}^3{h}_{\mathit{\text{Ca}}}(V-E_{\mathit{\text{Ca}}})$	$I_{Kd}=Ḡm_{Kd}^4(V-E_K)$
${\tau }_{m\mathit{\text{Ca}}}\frac{d{m}_{\mathit{\text{Ca}}}}{dt}=m_{\infty \mathit{\text{Ca}}}-m_{\mathit{\text{Ca}}},\hspace{1em}{\tau }_{h\mathit{\text{Ca}}}\frac{d{h}_{\mathit{\text{Ca}}}}{dt}=h_{\infty \mathit{\text{Ca}}}-h_{\mathit{\text{Ca}}}$	${\tau }_{mKd}\frac{d{m}_{Kd}}{dt}=m_{\infty Kd}-m_{Kd}$
$m_{\infty \mathit{\text{Ca}}}=\frac{1}{1+{\mathrm{e}}^{0.205(-60.6-\mathrm{V})}},\hspace{1em}{h}_{\infty \mathit{\text{Ca}}}=\frac{1}{1+{\mathrm{e}}^{-0.15(-75-\mathrm{V})}}$	$m_{\infty Kd}=\frac{1}{1+{\mathrm{e}}^{0.065(-35-\mathrm{V})}}$
${\tau }_{m\mathit{\text{Ca}}}=30-\frac{5}{1+{\mathrm{e}}^{0.2(-65-\mathrm{V})}}\mathrm{m}\text{sec},{\tau }_{h\mathit{\text{Ca}}}=150\mathrm{m}\text{sec}$	${\tau }_{mKd}=2+\frac{55}{1+{\mathrm{e}}^{0.125(-54-\mathrm{V})}}$
$E_{\mathit{\text{Ca}}}=12.6\text{ln}\frac{{[\mathit{\text{Ca}}]}_{\mathit{\text{ext}}}}{{[\mathit{\text{Ca}}]}_{\mathit{\text{cyt}}}}\mathrm{m}\mathrm{V},{[\mathit{\text{Ca}}]}_{\mathit{\text{ext}}}=13\mathrm{m}\mathrm{M}$	ḠKd =10.2 µS, EK= −80 mV
$I_A={Ḡ}_A{m_A}^3{h}_A(V-E_K)$	Ileak = Gleak (V − ELeak) Gleak = 0.03 µS Eleak = −68 mV
${\tau }_{mA}\frac{d{m}_A}{dt}=m_{\infty A}-m_A,\hspace{1em}{\tau }_{hA}\frac{d{h}_A}{dt}=h_{\infty A}-h_A$
$m_{\infty A}=\frac{1}{1+e^{0.2(-60-V)}},\hspace{1em}{h}_{\infty A}=\frac{1}{1+e^{-0.18(-68-V)}}$
τmA = 0.1 msec, τmA = 50 msec, ḠA = 0.45 µS
$I_{MI}=\overline{G_{MI}}{m}_{MI}(V-E_{MI}),$	Cm = 0.2 nF
${\tau }_{mMI}\frac{d{m}_{MI}}{dt}=m_{\infty MI}-m_{MI},\hspace{1em}{m}_{\infty MI}=\frac{1}{1+{\mathrm{e}}^{0.2(-55-\mathrm{V})}}$
τmMI = 6msec, ḠMI = 0.02 µS, EMI = −10 mV

A schematic diagram of the intracellular signaling mechanisms is shown in Figure 1B, and the parameters that determine these mechanisms are given in Table 2. The intracellular cytoplasmic calcium concentration [Ca]_cyt was used as an activity monitor since it can faithfully represent the status of neuronal activity. A single activity sensor, S_A depends sigmoidally on [Ca]_cyt and rises when [Ca]_cyt increases:

$$S_A=\overline{S_A}{M_A}^4$$

$$M_A=\frac{1}{1+e^{M_{\mathit{\text{thr}}\_A}-{[\mathit{\text{Ca}}]}_{\mathit{\text{cyt}}}}}$$ [2]

S̅_A is the maximal value of S_A, and M_{thr_A} represents the [Ca]_cyt for half maximal activation of M_A.

Table 2.

Conductance and calcium pump regulation

[Ca]cyt-dependent activity sensor:
$S_A=\overline{S_A}{M_A}^4\hspace{1em}{M}_A=\frac{1}{1+e^{M_{\mathit{\text{thr}}\_A}-{[\mathit{\text{Ca}}]}_{\mathit{\text{cyt}}}}}$	S̅A = 8 Mthr_A = 0.9 µM
[Ca]cyt kinetics:
$d\frac{{[\mathit{\text{Ca}}]}_{\mathit{\text{cyt}}}}{dt}=-\gamma I_{\mathit{\text{Ca}}}-R_{\mathit{\text{pump}}}\frac{{[\mathit{\text{Ca}}]}_{\mathit{\text{cyt}}}^2}{{[\mathit{\text{Ca}}]}_{\mathit{\text{cyt}}}^2+{\alpha }_{\mathit{\text{pump}}}^2}$	γ = 0.00678 µM nA−1msec−1 αpump = 0.2 µM
ḠCa regulation:	ḠCa_min = 0.069 µS ḠS_Ca = 0.12 µS Sthr_A = 0.13, rS = 0.02, τA = 500 sec
${Ḡ}_{\mathit{\text{Ca}}}={Ḡ}_{\mathit{\text{Ca}}\_\mathit{\text{min}}}+G_{S\_\mathit{\text{Ca}}}\hspace{1em}{\tau }_A\frac{d{G}_{S\_\mathit{\text{Ca}}}}{dt}=\frac{{Ḡ}_{S\_\mathit{\text{Ca}}}}{1+e^{\frac{S_A-S_{\mathit{\text{thr}}\_A}}{r_S}}}-G_{S\_\mathit{\text{Ca}}}$
Calcium pump activity regulation:
Rpump = Rpump_min + F(M)	Rpump_min = 0.0026 µMmsec−1 Rpump_M = 0.006 µMmsec−1 Mthr = 0.1331, rM = 0.00001 Gthr = 0.01 µM, rG = 0.00001 τM = 2500 sec
$F(M)=\frac{R_{\mathit{\text{pump}}\_M}}{1+e^{-\frac{M_{\mathit{\text{thr}}}-M}{r_M}}}\hspace{1em}{\tau }_M\frac{dM}{dt}=\frac{1}{1+e^{\frac{G_{\mathit{\text{thr}}}-{Ḡ}_{MI}}{r_G}}}-M$

Although [Ca]_cyt dynamics in biological neurons is regulated by many components, its major changes were here assumed to be due to two main processes: calcium influx via I_Ca, and calcium uptake by an intracellular calcium pump located in the endoplasmic reticulum membrane, ER. This is described by:

$$\frac{d{[\mathit{\text{Ca}}]}_{\mathit{\text{cyt}}}}{dt}=-\gamma I_{\mathit{\text{Ca}}}-R_{\mathit{\text{pump}}}\frac{{[\mathit{\text{Ca}}]}_{\mathit{\text{cyt}}}^2}{{[\mathit{\text{Ca}}]}_{\mathit{\text{cyt}}}^2+{\alpha }_{\mathit{\text{pump}}}^2}$$ [3]

where γ is the current-to-concentration conversion factor. R_pump is the activity rate of the calcium pump in the ER (in µM msec⁻¹). α_pump is the [Ca]_cyt for half maximal pump rate (Zhang and Golowasch, 2007).

As in our previous model, the activity sensor S_A regulates the maximal calcium conductance Ḡ_Ca (Fig. 1B).

$${Ḡ}_{\mathit{\text{Ca}}}={Ḡ}_{\mathit{\text{Ca}}\_\mathit{\text{min}}}+G_{S\_\mathit{\text{Ca}}}$$

$${\tau }_{\mathrm{A}}\frac{d{G}_{S\_\mathit{\text{Ca}}}}{dt}=\frac{{Ḡ}_{S\_\mathit{\text{Ca}}}}{1+e^{\frac{S_A-S_{\mathit{\text{thr}}\_A}}{r_S}}}-G_{S\_\mathit{\text{Ca}}}$$ [4]

τ_A is the time constant of Ca²⁺ conductance regulation and Ḡ_{Ca_min} represents the minimal value of Ḡ_Ca, which is determined by the intrinsic properties of Ca²⁺ channels in the plasma membrane and the Ca²⁺ pump activity in the ER. G_{S_Ca} represents the portion of Ḡ_Ca that is activity sensor-dependent, and is a decreasing function of S_A. S_{thr_A} is the half maximal value of G_{S_Ca} and r_S represents the steepness of G_{S_Ca} regulation. Ḡ_{S_Ca} represents the maximal value that Ḡ_Ca can achieve via activity-dependent regulation.

The regulation of R_pump (Fig. 1B) has been modified relative to previous versions of our model for two main reasons. First, although we have already established that the increase of R_pump plays a critical role in the emergence of stable recovery (but lesser or none on bouting properties) (Zhang and Golowasch, 2007; Zhang et al., 2009), previous models show a gradual increase in the duration of both individual bouts and interbouts with time until stable recovery is achieved, which is not a behavior that is observed experimentally (Luther et al., 2003). Second, experimental observations have not revealed evidence of correlations between duration of bouting activity and overall time to stable recovery (Luther et al., 2003), while our previous models do (Zhang and Golowasch, 2007; Zhang et al., 2009). In order to account for these observations we have here assumed that the regulation of Ḡ_Ca and R_pump occurs through two separate pathways. Thus, here R_pump does not depend on [Ca]_cyt, but depends on neuromodulator activity:

$$R_{\mathit{\text{pump}}}=R_{\mathit{\text{pump}}\_\text{min}}+F(M)$$

$$F(M)=\frac{R_{\mathit{\text{pump}}\_M}}{1+e^{\frac{M-M_{\mathit{\text{thr}}}}{r_M}}}$$ [5]

$${\tau }_M\frac{dM}{dt}=\frac{1}{1+e^{-\frac{{Ḡ}_{MI}-G_{\mathit{\text{thr}}}}{r_G}}}-M$$

R_pump depends on two components: R_{pump_min}, the minimal value of R_pump (determined by the intrinsic properties of the Ca²⁺ pump), and F(M) representing the portion of R_pump sensitive to modulator receptor regulation via some second messenger pathway. M represents the activation of such a second messenger pathway, and F(M) is a decreasing sigmoid function of M. M_thr is the value of M for half maximal activation of F(M), and r_M is the steepness of F(M). R_{pump_M} is the maximal value of the modulator-dependent portion of R_pump. Hence, R_pump is bounded by R_{pump_min} and R_{pump_min} + R_{pump_M}. The time constant τ_M, the rate of change of M, determines the time for stable recovery. A large value of τ_M ensures that R_pump changes slowly (and remains near its low initial value of 10⁻⁵) for a long time after decentralization (Fig. 2C).

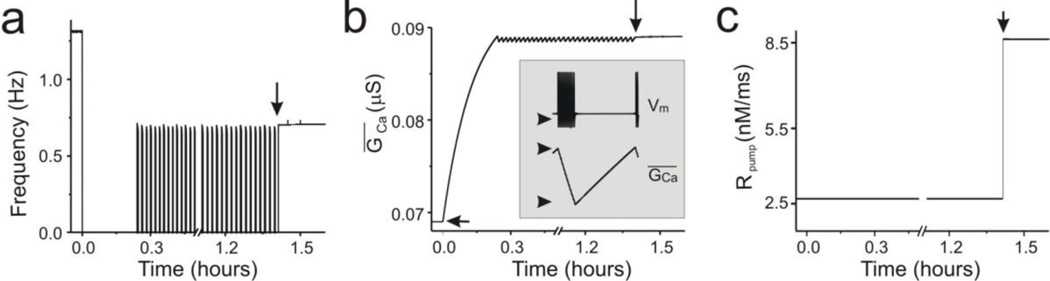
Fig. 2. Activity of the simplified model.

(a) Frequency changes over the recovery process in the simplified model with E_Ca fixed at +128mV. As in the full model (Fig. 1C), bouting ensued after a silent period followed by a stable rhythm (vertical arrow). (b) G_Ca changes in the simplified model with E_Ca fixed at +128mV. Horizontal arrow point at a baseline G_Ca = 0.069 µS. Inset: Magnified V_m and G_Ca changes during bouting. Arrows point at V_m = −70 mV, and G_Ca = 0.08845 and 0.08895 µS (min and max, respectively). (c) R_pump activity in the simplified model. Notice that stable neuronal activity coincides with the abrupt increase of R_pump at around 1.4 hours (vertical arrows in A–C). Decentralization is indicated by the time = 0 marks, and corresponds to setting G_MI = 0

For simplicity, M directly detects the changes of Ḡ_MI, which represents the neuromodulatory input, including neuromodulator receptors, but receptor activation is not explicitly represented, and Ḡ_MI activation is assumed to be very fast. M is 1 when Ḡ_MI is turned on. After Ḡ_MI turns to zero, M gradually decreases towards zero until it crosses M_thr making F(M) increase abruptly.

For the purpose of speeding the computations, τ_A and τ_M were adjusted so that the time course of recovery is scaled down by approximately 30 to 50-fold compared to that observed in the biological system (Luther et al., 2003). No differences in general behavior of the model were observed when the time constants were given more realistic values.

The model neuron was built using XPP. The phase plane and bifurcation analysis were performed using the XPP/Auto software (Ermentrout, 2002).

Results

Simplification of the model neuron

An example of the frequency changes during the recovery process after decentralization of the biological system are shown in Figure 1A. This preparation in particular remained quiescent for ~35 hours, at which time the alternating turning on and off of oscillations characteristic of bouting ensued (see Fig. 1 inset). After ~30 hours of bouting activity, the pyloric rhythm became stable with a frequency about 50% lower than the control typical of this process (Luther et al., 2003). In our full model a similar process is observed (Fig. 1C) and after an initial silent period of 0.46 hours bouting activity started. The bouts and interbouts were regular and did not change noticeably their duration throughout the bouting phase, with a ratio of mean individual bout duration to the mean individual interbout duration of 0.06, which is comparable to the value of 0.08 observed in the biological system (Luther et al., 2003). Oscillations became stable following a long period of bouting, with a frequency approximately 30% of that of control (1.04 ± 0.01 Hz compared to 3.44 ± 0.04 before decentralization). A similar ratio (38% of control) is observed in biological preparations (Luther et al., 2003). Stable recovery did not occur until R_pump sharply increased 1.4 hours after decentralization (Figs. 1C, 2C). Thus, the recovery process in our model satisfies most of the signature features observed in the recovery process of biological preparations (Luther et al., 2003). This occurs in the model via activity-dependent regulation of Ḡ_Ca (which plays a critical role in determining bouting activity), and neuromodulator-dependent regulation of Ca²⁺ pump activity (which is necessary for the recovery of stable activity). Both of these regulatory mechanisms have slow kinetics (τ_A and τ_M ≥ 500 sec). All other dynamical processes in the system correspond to voltage-gated ionic currents and have much faster kinetics (τ of any ionic conductance < 0.5 sec). Since these times scales are at least two orders of magnitude different, the voltage-dependent regulation of most ionic currents can be analyzed separately from the regulation process of Ḡ_Ca and R_pump. For this, we set all the ionic currents, except for I_Kd, to activate or inactivate instantaneously, i.e. m_i = m_∞i and h_i = h_∞i. I_A was found to be unnecessary to generate bouting or stable recovery and was eliminated (Table 3).

Table 3.

Voltage dependence of ionic channels in the simplified model neuron.

$C_m\frac{dV}{dt}=-(I_{\mathit{\text{Ca}}}+I_{Kd}+I_{MI}+I_{\mathit{\text{leak}}})$
$I_{\mathit{\text{Ca}}}={Ḡ}_{\mathit{\text{Ca}}}{m}_{\infty \mathit{\text{Ca}}}^3{h}_{\infty \mathit{\text{Ca}}}(V-E_{\mathit{\text{Ca}}})$	$I_{Kd}={Ḡ}_{Kd}{m}_{Kd}^4(V-E_K)$
$m_{\infty \mathit{\text{Ca}}}=\frac{1}{1+{\mathrm{e}}^{0.185(-60.6-\mathrm{V})}},h_{\infty \mathit{\text{Ca}}}=\frac{1}{1+{\mathrm{e}}^{-0.15(-65-\mathrm{V})}}$ ECa = +128 mV	${\tau }_{mKd}\frac{d{m}_{Kd}}{dt}=m_{\infty Kd}-m_{Kd}$
	$m_{\infty Kd}=\frac{1}{1+{\mathrm{e}}^{0.05(-35-\mathrm{V})}}$
	τmKd = 400 msec, ḠKd = 10.2 µS, EK = −80 mV
IMI = ḠMIm∞MI(V−EMI)	ILeak = Gleak(V−Eleak)
$m_{\infty MI}=\frac{1}{1+{\mathrm{e}}^{0.2(-55-\mathrm{V})}}$	Gleak = 0.03 µS, Eleak = −68 mV
ḠMI = 0.02 µS, EMI = −10 mV	Cm = 0.2 nF

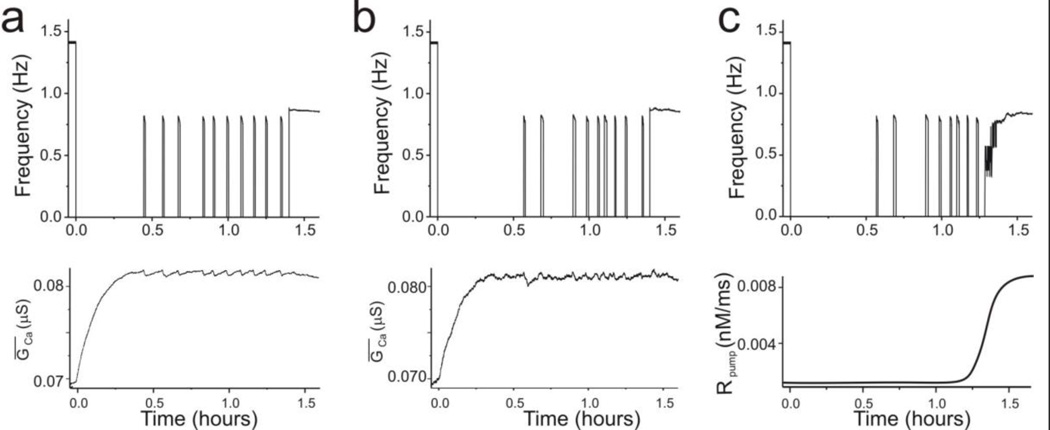
In our full model, variations of Ḡ_Ca appeared to be required to ensure the transition from a post-decentralization quiescent state to bouting. We considered the possibility that variations in E_Ca due to changes in [Ca]_cyt may be responsible instead. To test this possibility, Ḡ_Ca was held constant after decentralization at around values near those observed in the full model and E_Ca was left to vary according to Eq. 3 and Table 1 (top-left). E_Ca changes alone could not generate either bouts or stable recovery under these conditions (not shown). In contrast, Ḡ_Ca was the critical element for the generation of bouting activity. Therefore, we chose to fix E_Ca at its time-averaged value of +128 mV, and study the pattern of Ḡ_Ca changes during the recovery process (with Ḡ_{S_Ca} now set to 0.026 µS to prevent the oscillations from stopping due to the fixed E_Ca).

Figures 1C and 2A show the difference in the recovery process in the full model with E_Ca set free to change with [Ca]_cyt (Fig. 1C) and the recovery process in the simplified model with E_Ca fixed at +128 mV (Fig. 2A). Even though bouting activity occurred at a higher frequency in the simplified model neuron with fixed E_Ca, no qualitative differences were observed in the recovery of activity. For this reason, the simplified model was used for the analysis of activity recovery after decentralization.

When E_Ca was fixed at +128mV and Ḡ_{S_Ca} at 0.026µS, Ḡ_Ca increased from 0.069 µs before decentralization to values that varied slightly below 0.089 µS (Fig. 2B) during the bouting phase of activity, with the highest level marking the beginning of a bout and the lowest level marking the beginning of an interbout (Fig. 2B inset). Ḡ_Ca increased during each interbout and decreased during each bout. The beginning of the stable activity (recovery) brought Ḡ_Ca to a fixed value close to 0.089 µS. As a consequence, after turning off the feedback system, Ḡ_Ca can be treated as a parameter, the simplified model neuron becomes governed by only two dynamical variables (V and m_Kd ; Table 3), and the whole system can be examined in the phase plane.

Phase plane analysis of the rhythmic activity recovery process

The process of recovery of rhythmic activity is characterized by changes both in the shape and displacement along the vertical axis of the V-nullcline due to subtle changes in Ḡ_Ca induced by a direct activity-dependent regulation, and by an indirect neuromodulator-dependent regulation of the intracellular calcium pump (see Fig. 1B).

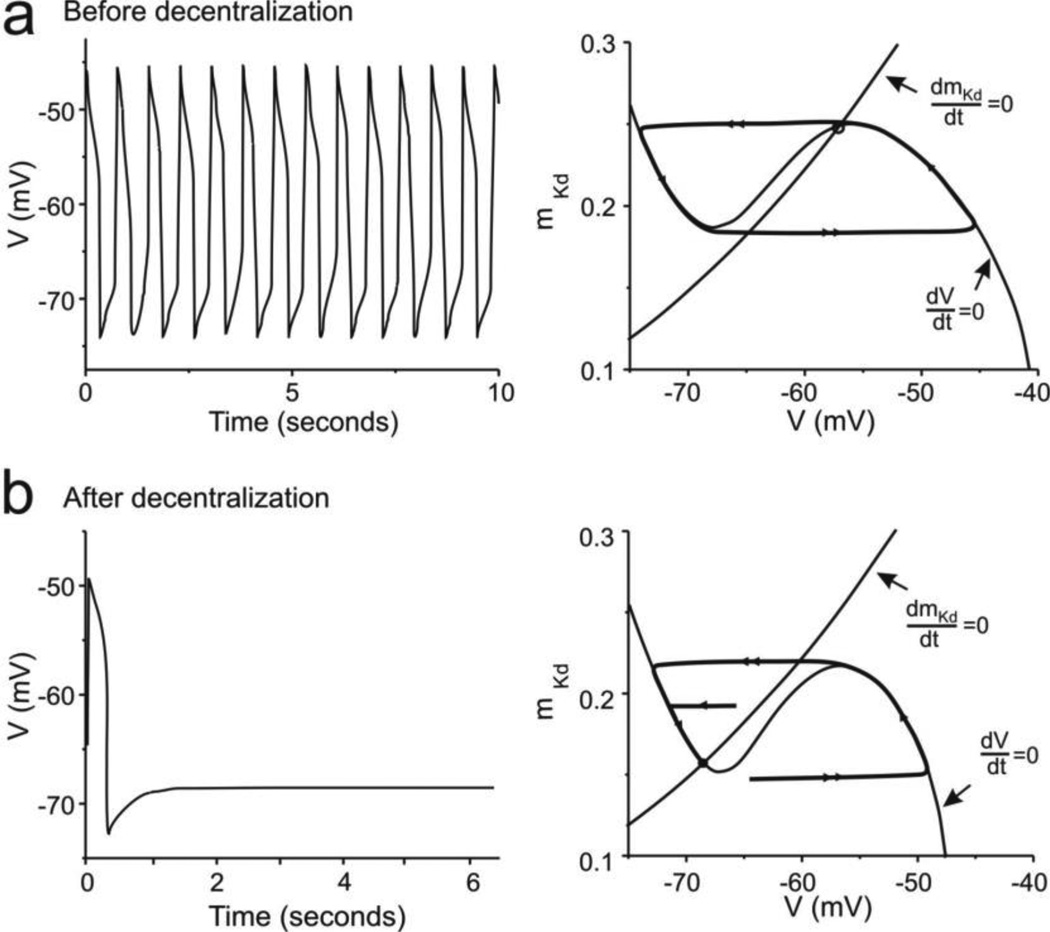
The neuronal activity, and phase portrait plus trajectories of the system in the pre-decentralization (control) state are shown in Figure 3A (with fixed Ḡ_Ca = 0.06900 µS). The activity of the neuron is a rhythmic oscillation with a frequency of 1.3 Hz in the simplified model with fixed E_Ca (Fig. 3A, left). The V- and m_Kd-nullclines intersect at a fixed point located in the middle branch of the V-nullcline (Fig. 3A, right) characterized by positive eigenvalues (Table 4). As a consequence, a limit cycle characteristic of a relaxation oscillation dominates the activity of the system in this state. Immediately after decentralization neuronal activity rapidly ceases due to the elimination of neuromodulators, here modeled as the loss of I_MI (Fig. 3B, left). The phase portrait changes immediately due to the loss of I_MI as shown in Figure 3B (right) even though the more slowly regulated Ḡ_Ca remains at the same level (Ḡ_Ca = 0.06900 µS). While the m_Kd-nullcline remains unchanged, the V-nullcline drops and the V- and m_Kd-nullclines intersect uniquely at a stable fixed point (see Table 4) on the left branch of the V-nullcline towards which all trajectories converge (Fig. 3B, right).

Fig. 3. Modifications of activity and the phase plane during the early stages of the recovery of rhythmic activity.

Left panels show membrane potential changes over time; right panels show the phase plane with both the V-nullcline (dV/dt = 0) and m_Kd-nullcline (dm_Kd/dt = 0) indicated. The system’s trajectories are shown by thick curves. (a) Before decentralization the model cell expresses rhythmic activity (left) that corresponds to a limit cycle in the phase plane (right). (b) Immediately after decentralization the cell falls silent (left), which corresponds to the system’s trajectory converging onto a stable fixed point on the left branch of the V-nullcline

Table 4.

The stability of fixed points at different Ḡ_Ca values.

Condition	ḠCa (µS)	Fixed points	Eigenvalues	Stability
Before decentralization	0.06900	Upper level of the middle branch (−57.12mV, 0.2486)	0.1253, 0.0106	unstable node
Immediately after decentralization	0.06900	Left branch(−68.53mV, 0.1576)	−0.0696, −0.0048	stable node
During bouting	0.08845	Upper level of the middle branch (−58.65mV, 0.2346)	0.2275, 0.0030	unstable node
		Center of middle branch(−63.83mV, 0.1913)	0.2517, −0.0007	saddle node
		Lower level of middle branch(−67.64mV, 0.1636)	−0.0008+0.0137i, −0.0008−0.0137i	stable spiral
	0.08860	Upper level of the middle branch (−58.62mV, 0.2349)	0.2254, 0.0031	unstable node
		Center of middle branch(−63.87mV, 0.1910)	0.2476, −0.0007	saddle node
		Lower level of middle branch(−67.63mV, 0.1636)	−0.0003+0.0135i, −0.0003−0.0135i	stable spiral
	0.08870	Upper level of the middle branch (−58.60mV, 0.2350)	0.2240, 0.0031	unstable node
		Center of middle branch(−63.90mV, 0.1908)	0.2463, −0.0007	saddle node
		Lower level of middle branch(−67.62mV, 0.1637)	0.00002+0.0135i, 0.00002−0.0135i	unstable spiral
	0.08885	Upper level of the middle branch (−58.57mV, 0.2353)	0.2219, 0.0032	unstable node
		Center of middle branch(−63.94mV, 0.1905)	0.2444, −0.0007	saddle node
		Lower level of middle branch(−67.61mV, 0.1638)	0.0005+0.0134i, 0.0005−0.0134i	unstable spiral
	0.08895	Upper level of the middle branch (−58.56mV, 0.2355)	0.2205, 0.0033	unstable node
		Center of middle branch (−63.96mV, 0.1903)	0.2432, −0.0007	saddle node
		Lower level of middle branch (−67.60mV, 0.1638)	0.0009+0.0134i, 0.0009−0.0134i	unstable spiral
	0.08900	Upper level of the middle branch (−58.55mV, 0.2355)	0.2175, 0.0034	unstable node
		Center of middle branch(−63.98mV, 0.1902)	0.2448, −0.0007	saddle node
		Lower level of middle branch(−67.60mV, 0.1639)	0.0019+0.0131i, 0.0019−0.0131i	unstable spiral

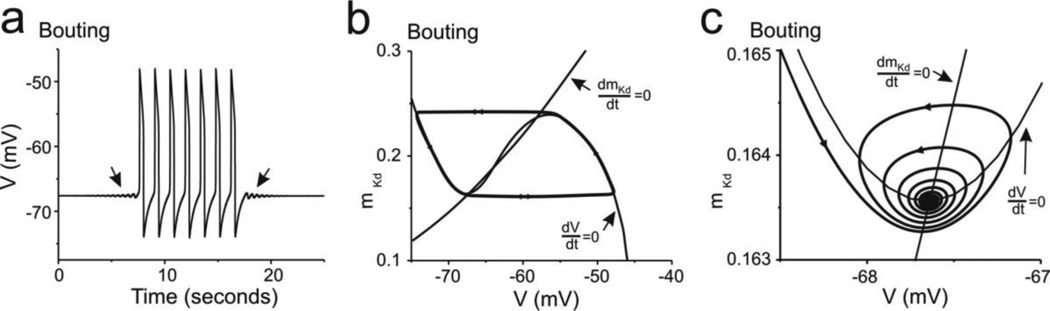
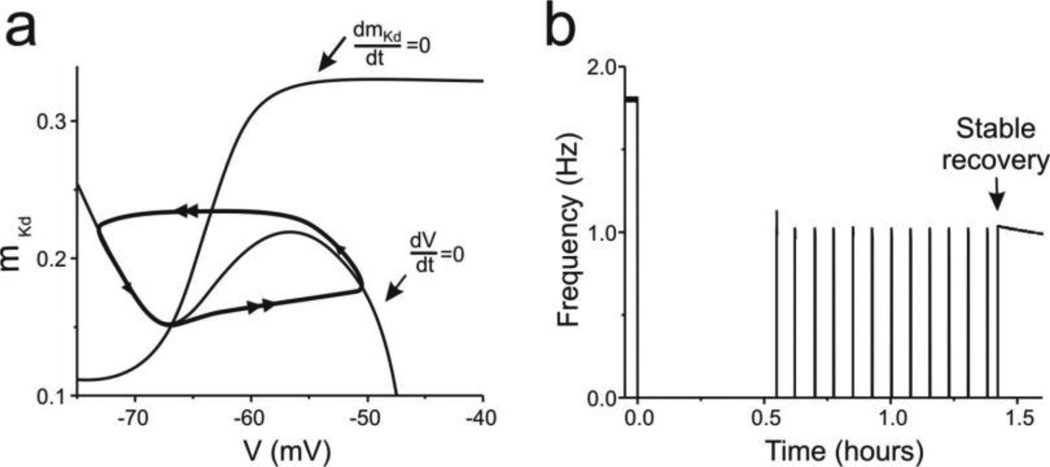
As shown in Figure 2B, Ḡ_Ca began to slowly increase after decentralization until a value near 0.08845 µS was reached, at which point three fixed points were created and bouting activity started (Fig. 2A and Fig. 4A). During the bouting period, Ḡ_Ca oscillated between 0.08845 µS and 0.08895 µS (Fig. 2B) and the V-nullcline shifted up (when Ḡ_Ca increased) and down (when Ḡ_Ca decreased). During this period two of the fixed points were located on the middle branch, and one near the knee between the left and middle branches of the V-nullcline (Fig. 4B). Among the three fixed points, the one located near the knee between the left and middle branches was the only one that changed its stability as Ḡ_Ca varied (Table 4, Fig. 4). When Ḡ_Ca increased, it switched from a stable spiral to an unstable spiral via a subcritical Hopf bifurcation occurring at Ḡ_Ca = 0.08870 µS. During the whole bouting phase, the fixed point located on the upper level of the middle branch of the V-nullcline retained the properties of an unstable node (positive real eigenvalues, Table 4) ensuring the existence of a limit cycle that generated oscillatory activity or a return to a low voltage state (Fig. 4A). The fixed point located at the center of the middle branch always retained the properties of a saddle (Table 4).

Fig. 4. Modifications of activity and the phase plane during the bouting phase of rhythmic activity recovery.

(a) Membrane potential changes over time; arrows point to damped subthreshold oscillations leading to and emerging from the period of bursting. (b) Phase plane showing both the V-nullcline (dV/dt = 0) and m_Kd-nullcline (dm_Kd/dt = 0). The system’s trajectory is shown by the thick curve. (c) Phase plane as in (b) but zoomed in on the region around the left-most fixed point at the time of transition from bursting to silence (right handside arrow in (a))

As Ḡ_Ca varied during the bouting phase of activity, the V-nullcline moved up (as Ḡ_Ca increased) and the left-most fixed point moved to the right. At Ḡ_Ca = 0.08870µS the fixed point developed two complex eigenvalues and became an unstable spiral (Table 4) whose amplitude grew the more Ḡ_Ca increased, leading to a full blown limit cycle and regular membrane potential oscillations (Fig. 4B). As shown in Figure 2B, Ḡ_Ca began to decrease once it reached 0.08895µS, and the V-nullcline began to shift down. The system continued to oscillate even below the critical value of Ḡ_Ca = 0.08870 µS. With further decrease of Ḡ_Ca, the lower-left fixed point became a stable decreasing spiral that attracted the trajectory to towards it (Fig. 4C, Table 4) leading to the end of a bout and the beginning of the silent interbout (Figs. 4A, C). As Ḡ_Ca reached its lowest point at 0.08845 µS Ḡ_Ca began to grow again repeating the bout-interbout cycle. This critical fixed point is weak and, as a consequence, oscillations do not stop or appear abruptly. This also leaves time for the critical point, because of the V-nullcline’s dependence on Ca²⁺, to move slightly to the left of the attractor (or to the right of the repeller) as the oscillations are destroyed (or generated, respectively), creating a small degree of hysteresis.

The fixed points located at the medium and upper levels of the middle branch of the V-nullcline retained the same stability throughout (Table 4). The transition into and out of a burst of activity during this bouting period always occurred via a Hopf bifurcation and thus subthreshold damped oscillations can be observed at these transition points (Fig. 4A, arrows).

Such cycles continued until R_pump increased, driven by its own neuromodulator-dependent dynamics (Eqs. 5 and Table 2), which stopped the oscillation of Ḡ_Ca and led to the increase of Ḡ_Ca to a near-steady state value of 0.08900 µS (Fig. 2B). The left-most fixed point became permanently consolidated as a relatively strong repeller (Table 4), and a new limit cycle was generated characterized by stable rhythmic activity with a slower frequency than before decentralization (see Fig. 2B).

The role of two fixed points located at the middle branch of the V-nullcline

Throughout the bouting period, it was the fixed point located near the knee between left and middle branch of the V-nullcline that changed its stability via a Hopf bifurcation. The other two fixed points didn’t change their stability during the entire bouting period (Table 4). To examine whether these two fixed points played a role in the generation of bouting activity we generated a biologically unrealistic equation of m_Kd, to make it a steeper sigmoid function of V:

$$m_{\infty Kd}=\frac{0.22}{1+e^{0.5(-64-V)}}+0.11$$

As a consequence, the V- and m_Kd-nullclines intersect at a single fixed point located near the knee between the left and middle branch of the V nullcline (Fig. 5A). As shown in Fig. 5B, the modified model neuron still exhibited a recovery process similar to that shown in Figures 1C and 2A, even though the bouting frequency is somewhat slower. Phase plane analysis shows that a Hopf bifurcation occurs at this fixed point, regardless of the absence of the other two fixed points. Thus, all the evidences indicate that eliminating these two fixed points does not affect the recovery process.

Fig. 5. Stable rhythmic activity recovery only requires one fixed point.

(a) Phase plane showing both the V-nullcline (dV/dt = 0) and m_Kd-nullcline (dm_Kd/dt = 0) during bouting phase. The system’s trajectory (thick curve) shows a limit cycle in the absence of additional fixed points. (b) Membrane potential changes over time show bouting and a stable recovery of bursting activity

The limits of m_Kd (0.11 and 033 rather than 0 and 1) were chosen so that the excursions of m_Kd activation remained approximately the same as when the previous equation was used. Alternatively, m_Kd varied much more widely and other equations in the model had to be modified as well. In this manner we could test the effect of the steepness of the activation (and thus of the number of fixed points) specifically.

Noise analysis

As shown before, the characteristics of bouting activity are determined by how Ḡ_Ca oscillates within a narrow range around the transition point of stability of the system (Fig. 2B). The regularity of the bouting process is one feature never observed in the biological system. To examine the origin of this variability we tested if a small amount of variability (noise) in some of the system’s parameters could account for it. For this, low amplitude noise was added to Ḡ_Ca and the activity after decentralization measured. Wiener noise (Ermentrout, 2002), was added to Ḡ_Ca by modifying Eq. 4 as follows:

$${\tau }_{\mathrm{g}}\frac{d{G}_{S\_\mathit{\text{Ca}}}}{dt}=\frac{{Ḡ}_{S\_\mathit{\text{Ca}}}}{1+e^{\frac{S_A-S_{\mathit{\text{thr}}\_A}}{r_S}}}+A·W·{Ḡ}_{S\_\mathit{\text{Ca}}}{\tau }_{\mathrm{g}}-G_{S\_\mathit{\text{Ca}}}$$

W is the Weiner noise term and A is an amplification factor. The recovery process of the model with noise added to Ḡ_Ca is shown in Figure 6. The coefficient of variation (SD/mean) of the individual bout and of the interbout durations for noise levels in Ḡ_Ca between 0 and 2% increase nearly linearly (not shown). This indicates that with modest increases of noise, the irregularity of bouting activity increased substantially. The irregular bouting activity generated with 2% noise in Ḡ_Ca (Fig. 6B) closely matches experimental observations (Luther et al., 2003), with the noise level in Ḡ_Ca not significantly affecting the average time to stable recovery. However, it did affect how the recovery reaches its stable activity in one significant way. In the previous modeling work, R_pump was designed to have a gradual increase as a function of activity sensor. However, the gradual increase of R_pump caused a gradual increase of individual bout durations before the stable recovery. As indicated before, this is not observed experimentally (Luther et al., 2003). To avoid this, the only successful solution we could find was to increase R_pump, which depends on the neuromodulator sensor, abruptly (Eq. 5, Table 2). Although this led to recovery of a stable rhythm at a time after decentralization similar to what has been observed experimentally, such an abrupt increase of R_pump is not biologically realistic. Thus, we asked what effect a gradually increasing R_pump would have in the presence of Ḡ_Ca noise. We found that with 2% noise added, the irregularity of bouting activity allows for a major relaxation of the constraint imposed on how R_pump could transition during the activity change occurring from the bouting to the stable state (Fig. 6C). In fact, the rate of change of R_pump could be decreased more that 10-fold, resulting in transitions that are very similar to what is observed in the biological system. This indicates that in the presence of a small level of noise in the system R_pump does not need to have an unrealistically sharp dependence on the neuromodulator sensor for the stable recovery to occur.

Fig. 6. Effect of noise on the dynamics of bouting.

Low-level noise was added to the maximum Ca²⁺ conductance and recovery from decentralization followed. (a). 1% noise slightly increases the variability of the bouting phase of activity. Bottom panel shows evolution of Ḡ_Ca. (b) 2% noise added to Ḡ_Ca. (c) 2% noise added to Ḡ_Ca and a more than 10-fold reduction in the steepness of the increase of R_pump. The transition from bouting to stable recovery is gradual and the bouting frequency changes are not regular, as observed experimentally

Activity-dependent regulation of other conductances

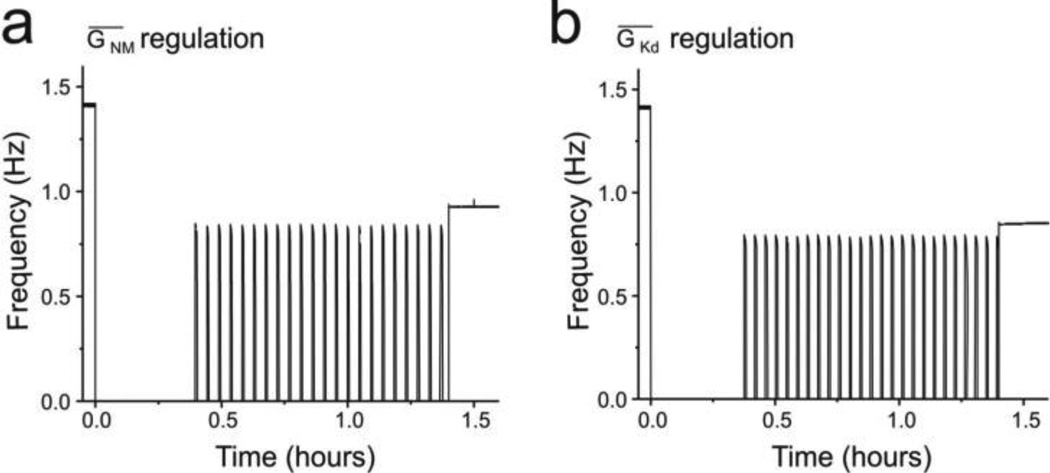
We have previously shown that activity-dependent regulation of a single Ca²⁺ current (Zhang et al., 2009) or of both a Ca²⁺ and a K⁺ current (Golowasch et al., 1999; Zhang and Golowasch, 2007) could account for the generation of bouting and the eventual recovery of stable rhythmic activity. However, in the biological system several other ionic currents undergo changes in amplitude during the process of activity recovery after decentralization (Khorkova and Golowasch, 2007). Thus, we asked if activity-dependent regulation of currents other than a Ca²⁺ current could be responsible for the generation of bouting and stable rhythmic activity recovery.

To test this we modified the activity-dependent regulation of the model to target separately Ḡ_MI and Ḡ_Kd, the only remaining voltage-gated conductances in the model, rather than Ḡ_Ca. For this Ḡ_Ca was fixed at 0.06900 µS and Ḡ_MI was modified in a manner similar to that used to represent activity-dependent regulation of Ḡ_Ca before (see Eqs. 4 and Table 2) as follows:

$${Ḡ}_{MI}=G_{MI\_\text{min}}+G_{S\_MI}$$

$${\tau }_A\frac{d{G}_{S\_NM}}{dt}=\frac{0.005}{1+e^{\frac{S_A-S_{\mathit{\text{thr}}\_A}}{r_S}}}-G_{S\_MI}$$

With G_{MI_min} = 0.02 µS before decentralization. To represent decentralization Ḡ_MI was decreased by 0.02 µS, which resulted in the cessation of oscillatory activity (Fig. 7A) and the beginning of an upregulation of Ḡ_MI via the activity sensor S_A, in a similar way as that of Ḡ_Ca regulation. This modified model could successfully produce bouting activity and the eventual stable recovery of rhythmic activity when R_pump increased (Fig. 7A) in a manner qualitatively indistinguishable from that observed when Ḡ_Ca was the target of activity-dependent regulation (compare Fig. 7A to Fig. 2A). As is the case with Ḡ_Ca regulation, the activity sensor S_A slowly raises Ḡ_MI. When Ḡ_MI reaches around 0.0044 µS, with Ḡ_Ca fixed at 0.06900 µS, the system approaches the critical fixed point and its stability is modified through a Hopf bifurcation as before, and bouting ensues. Ḡ_MI oscillates in a narrow range between 0.00431 µS and 0.00439 µS during the bouting phase, and stabilizes at around a value of 0.00437 µS.

Fig. 7. Several currents can be the target of slow conductance regulation.

(a). Positive regulation of the I_MI current induces bouting and stable recovery. (b). Negative regulation of the I_Kd current induces bouting and stable recovery

In a similar manner, we tested if Ḡ_Kd activity-dependent regulation via the activity sensor S_A could reproduce the observed phenomena. Ḡ_Ca was fixed at 0.069µS and Ḡ_Kd was negatively regulated by activity (to allow for an increase in excitability) as follows:

$${Ḡ}_{Kd}=G_{Kd\_\text{min}}-G_{S\_Kd}$$

$${\tau }_A\frac{d{G}_{S\_Kd}}{dt}=\frac{2.75}{1+e^{\frac{S_A-S_{\mathit{\text{thr}}\_A}}{r_S}}}-G_{S\_Kd}$$

With G_{Kd_min} = 10.2 µS before decentralization, and decentralization was again represented as done originally by setting Ḡ_MI = 0 µS. The modified model produced a recovery process that was qualitatively indistinguishable from that observed (compare Fig. 7B to Figs. 2A and 7A) when either Ḡ_Ca or Ḡ_MI were the targets of activity-dependent regulation. Similar to the case with Ḡ_Ca and Ḡ_MI, Ḡ_Kd oscillated in a narrow range between 7.8664 µS and 7.9289 µS during bouting phase, and stabilized at a steady state level near 7.8740 µS.

Discussion

It is important to understand to what extent neurons and networks can recover their normal function if it is lost due to trauma, disease or other perturbations, and to identify the mechanisms that allow this to happen. Rhythmic neuronal activity patterns are typically found to be involved in basic biological functions, such as breathing, heartbeat, digestion, locomotion, etc. (Frere et al., 2004; Golowasch and Marder, 1992; MacKay-Lyons, 2002; Marder, 2000). Thus, recovery of activity is all the more crucial. The pyloric network located in the stomatogastric ganglion of decapods crustaceans is capable of just such a recovery when its rhythmic activity is disrupted as a consequence of the loss of central neuromodulatory input (Luther et al., 2003; Thoby-Brisson and Simmers, 1998) and may provide insights that may be applicable to other systems. Here we propose a model to account for some important features observed experimentally that we could not reproduce with previous models (Golowasch et al., 1999; Zhang and Golowasch, 2007; Zhang et al., 2009), suggesting possible line for experimental work aimed at understanding the mechanisms involved. The most important difference with previous models is the uncoupling of the activity-dependent regulation of ionic conductances from the neuromodulator-dependent regulation of intracellular Ca²⁺ concentration (cf. (Zhang and Golowasch, 2007; Zhang et al., 2009)). This allowed us to eliminate the dependency of the recovery of stable periodic activity from the duration of episodic (bouting) activity that ensues soon after decentralization. Furthermore, the added assumption that low level noise is present along the biochemical pathway(s) underlying activity-dependent regulation of conductances allows the relaxation of a major (and biologically unrealistic) restriction in the kinetics of the neuromodulator-sensitive mechanism. With these changes, we can now account for all the kinetic features observed experimentally (Luther et al., 2003) during the entire process of recovery: loss of activity immediately after decentralization, appearance of slow bouting activity after a long silent period, and the delayed transition from bouting to a stable rhythmic state that does not involve a progressive reduction in the bout duration, which was a major shortcoming in previous models. The uncoupling of the two regulatory pathways allowed us also to account for an additional feature observed during the recovery of a stable rhythmic state that previous model could not explain: the transition to a stable state almost always follows a period of bouting activity but it does not depend on any property of the bouting phase (such as bout or interbout durations). We propose that this is simply due to the very different time scales of the activity-dependent mechanisms, which are relatively fast, and the neuromodulator-dependent mechanisms, which are slower. This could explain why on rare occasions a preparation will recover a stable pyloric rhythm without first undergoing bouting, or sometimes express an overlap of bouting and of the onset of steady rhythmic activity, as a consequence of different relative kinetics of the neuromodulatory- and the activity-dependent pathways.

Our assumption that the activity-dependent regulatory pathway, represented in our model by an activity sensor that regulates the maximal conductance of one ionic current, could have variable activity may be the result of stochastic fluctuations in biochemical pathways as has been proposed for many molecular systems in recent years (Levine and Hwa, 2007; Shahrezaei and Swain, 2008). This can easily arise from the operation of pathways in which certain molecules are maintained at very low concentrations (Cao and Liang, 2007). We modeled such source of variability by adding noise to the maximal conductance of I_Ca. This has two consequences that mirror experimental observations: it makes the bouting activity more variable, and it greatly relaxes the biologically unrealistic constraints otherwise necessary on the separate and independent biochemical pathway regulated by neuromodulators.

What biologically plausible mechanisms could underlie the activity-dependent regulation of ion channels and the activity-independent regulation of a Ca²⁺ pump? Because stable recovery from decentralization is a very slow process that expresses itself only after a long delay (many hours), direct regulation of channels and pumps by second messengers or enzymes is deemed unlikely. However, regulation of protein synthesis and/or transcription are possible mechanisms, especially since transcription has been shown to be involved in the control of recovery from decentralization in a related species (Thoby-Brisson and Simmers, 2000). Additionally, it has been shown that neuronal activity can control (i.e. switch) the expression of calcium ATPase isoforms in axons of a different crustacean species, crayfish (Lnenicka et al., 1998) as well as in vertebrate muscle (Briggs et al., 1990; Leberer et al., 1989) with time courses comparable to those of the phenomenon we study (many hours). Ca²⁺ pumps (e.g. SERCA) are regulated by the protein phospholamban (Simmerman and Jones, 1998), whose expression also appears to be transcriptionally regulated and to participate in activity-dependent muscle type switching with similar time course (Hu et al., 1995). Several mechanisms have been identified in different systems that can mediate activity-dependent transcriptional regulation of these proteins (Mellstrom et al., 2008). Other, non-activity-dependent, regulatory mechanisms that can be linked to neuromodulator receptor activation have been characterized as well (Gudi et al., 2002). Specifically for instance, it has been reported that both phospholamban and a Ca²⁺ ATPase are controlled by thyroid hormone in heart, with hormonal concentration changes leading to very large changes in expression in mRNA levels of both molecules over the course of days (Nagai et al., 1989). Long-term adenylyl cyclase regulation (Sugano et al., 2011) has also been shown to regulate sarcoplasmic calcium in heart via several different components, including phospholamban phosphorylation. cGMP, a molecule that is regulated by a number of modulators, is also known to regulate transcription of different molecules in several systems (Gudi et al., 2002; Martel et al., 2010; Ota et al., 2010; Pilz and Casteel, 2003). Additional intracellular signaling pathways have been shown to regulate SERCA2 expression, such as calcineurin A (Prasad and Inesi, 2011), which is also known to be regulated by several neuromodulatory systems. Finally, neuromodulator-mediated regulation of other types of pumps, i.e. Na⁺/K⁺ ATPase are known to exist in vertebrate as well as invertebrates (Aizman et al., 2000; Catarsi and Brunelli, 1991; Catarsi et al., 1993; Therien and Blostein, 2000; Tobin and Calabrese, 2005). Although these are all short-term regulatory processes, it is not inconceivable that they may also mediate long-term processes such as the one proposed here given that pathways know to activate transcription are involved in many of them (i.e. cyclic nucleotides). In sum, although direct information for our system is clearly lacking at this time, there are a number of possible paths through which, Ca²⁺ pumps or their regulatory proteins can themselves be regulated by products of G-protein coupled receptors, which the neuropeptide receptors in the STG are likely to be, and the intracellular signaling molecules activated by them. Furthermore, a time course of many hours is possible (even likely) if transcription and translation of pumps and regulating molecules are involved. A sudden increase in molecular activity, such as that of an ATPase, could also be expected after a slow buildup of several independent interacting regulatory components past a threshold. In the absence of detailed experimental evidence, we propose that such a mechanism may be at work here.

Episodic activity somewhat similar to bouting activity has been characterized in other systems, particularly in developing networks of the spinal cord, retina, neocortex and hippocampus (O'Donovan, 1999; O'Donovan et al., 1998; Vladimirski et al., 2008; Yuste et al., 1995). Such episodic activity depends on network interactions via depressing excitatory synapses or via gap junctions, which sometimes determine temporal relationships between episodes and interepisodic silent activity. While the pyloric network’s recovery of activity does not appear to require synaptic modifications (Luther et al., 2003) and we do not observe such temporal relationships during the bouting phase, one feature that appears common to both phenomena is that intracellular Ca²⁺ concentration changes are involved (Garaschuk et al., 1998; Gu et al., 1994; Spitzer et al., 1994; Yuste et al., 1995). Our results suggest that intracellular Ca²⁺ concentration changes may be necessary. This is directly supported by the observation of Ca²⁺- dependent ionic conductance regulation in cultured pyloric neurons (Haedo and Golowasch, 2006), crayfish neurons (Hong and Lnenicka, 1995), as well as in numerous other systems. We propose that, similar to what is observed in developing vertebrate networks, the episodic activity of the pyloric network requires intracellular Ca²⁺ concentration changes, which regulate ionic conductances, and that the system is extremely sensitive to these changes. Our model shows oscillations of Ḡ_Ca of no more than 1% being sufficient to explain all the temporal changes observed. However, the model predicts intracellular Ca²⁺ concentration changes of over 100% (not shown). While 1% changes in Ḡ_Ca would be extremely hard to resolve, 100% changes in intracellular Ca²⁺ concentration changes should be relatively easy to detect. These predictions can be experimentally tested.

Our results suggest that the Ca²⁺ current conductance does not need to be the sole target of activity-dependent regulation. Although we show that Ḡ_Ca regulation is sufficient for the recovery process, other currents can equally mediate the effects of an activity sensor in generating temporal changes of the rhythmic pattern characteristic of the pyloric network. In fact, it has been shown before that the conductance of multiple ionic currents, including Ca²⁺ and K⁺ conductances, undergoes changes during the process of recovery from decentralization (Khorkova and Golowasch, 2007; Thoby-Brisson and Simmers, 2002). Our conclusions do not exclude possible synaptic changes within the pyloric network or ionic conductance changes of non-pacemaker neurons of the network. Both of these types of changes could act synergistically to modify the properties of the network, and need to be examined experimentally. Here we have aimed to show that all the changes necessary to account for the temporal features of pyloric activity observed during the recovery of function after decentralization can be accounted for by excitability and intracellular Ca²⁺ regulation changes in the pacemaker neuron.

Our phase plane analysis shows that the critical fixed point located near the knee between the left and middle branches of the V-nullcline alone can generate the bifurcations needed for the model neuron to switch between bouting and interbout silence. Our model however, shows three fixed points. The possible roles of the additional two fixed points located along the middle branch of the V-nullcline are unclear. Although they are not required for the generation of the bouting activity and stable recovery, they may play roles in other attributes of neuronal activity. For instance, in the biological system the onset of individual bouts is characterized by a rapid acceleration of the pyloric rhythm and typically a slow decay to the interbout low frequency or silence (Luther et al., 2003). This is not captured in our simplified model neuron. It is possible that while I_Ca plays a crucial role in the activation of the bouts, other currents control their oscillation frequency and/or termination. A full model neuron, perhaps including axonal compartments, might be required to explain such details of neuronal activity, including the predicted small oscillations of the neuron’s voltage at both the beginning and at the end of each bout (Fig. 4A), which we have never observed in the biological system.

In a previous study we explored the effects on the pyloric activity of disrupting its activity prior to decentralization (Zhang et al., 2009). A model was proposed to explain the observed responses in which both an activity-dependent signaling pathway and a neuromodulator-dependent pathway regulate ionic conductances directly. In order to attempt to dissect out the possible mechanisms that explain the temporal properties of the network activity recovery process in the present study we did not incorporate the neuromodulator-dependent regulatory pathway of ionic conductances. It would be interesting to now combine the two approaches by adding a direct neuromodulator-dependent regulation path of ionic conductances to the present model with the goal of obtaining a full account of all the currently known responses of the system to decentralization.

The functional role of bouting activity

Episodic activity comparable to bouting is a common behavior found in the development of neural networks (O'Donovan, 1999). They are found in various parts of nervous system and at different stages of development, supplying the spatial and temporal cues for appropriate innervation, supporting the proper differentiation of neuronal phenotypes, guiding neurite extensions, and regulating the wiring of the synaptic contacts during early postnatal development (Garaschuk et al., 1998; Meister et al., 1991; Murphy et al., 1992; O'Donovan, 1999; O'Donovan et al., 1998; Wong et al., 1995). The bouting activity of the decentralized pyloric network shares some similarity with those in the development of neonatal nervous system but there is no known role of bouting in the pyloric network. It is interesting to note that bouting in the pyloric network occurs in the adult animal, and has not been observed during development (Casasnovas and Meyrand, 1995). It is possible that bouting activity is just a side effect of the instability of neuronal intrinsic activity at a time when ionic conductances have lost part of their regulation by neuromodulators. However, bouting activity may play a role in maintaining activity-dependent properties within acceptable limits to generate pyloric-like activity (e.g. ionic conductances) while other changes occur that will allow the system to eventually stabilize (e.g. intracellular Ca²⁺ concentration regulation).

In conclusion, our modeling approach accounts for all major temporal features observed in the pyloric network of decapods crustaceans in response to decentralization. We predict that experimental measurements should reveal changes in intracellular Ca²⁺ concentration uptake mechanisms as a consequence of decentralization, that intracellular Ca²⁺ regulation mechanisms are likely to be directly controlled by neuromodulators, that intracellular Ca²⁺ concentration changes are thus likely to be observed, and that ionic conductance regulation as a function of activity is sensitively dependent on intracellular Ca²⁺ concentration.