Parallel MR Imaging

Abstract

Parallel imaging is a robust method for accelerating the acquisition of magnetic resonance imaging (MRI) data, and has made possible many new applications of MR imaging. Parallel imaging works by acquiring a reduced amount of k-space data with an array of receiver coils. These undersampled data can be acquired more quickly, but the undersampling leads to aliased images. One of several parallel imaging algorithms can then be used to reconstruct artifact-free images from either the aliased images (SENSE-type reconstruction) or from the under-sampled data (GRAPPA-type reconstruction). The advantages of parallel imaging in a clinical setting include faster image acquisition, which can be used, for instance, to shorten breath-hold times resulting in fewer motion-corrupted examinations. In this article the basic concepts behind parallel imaging are introduced. The relationship between undersampling and aliasing is discussed and two commonly used parallel imaging methods, SENSE and GRAPPA, are explained in detail. Examples of artifacts arising from parallel imaging are shown and ways to detect and mitigate these artifacts are described. Finally, several current applications of parallel imaging are presented and recent advancements and promising research in parallel imaging are briefly reviewed.

MAGNETIC RESONANCE IMAGING (MRI) is a medical imaging modality that creates images with adjustable soft-tissue contrast for anatomical and functional assessment. While MRI has been used in the clinic to make images of all areas of the body, the primary disadvantage of MRI is that it requires a relatively long time to capture all of the data needed to make an image as compared to computed tomography (CT) or ultrasound. For some types of scans it can take several minutes to acquire the necessary data. Lengthy scan times are uncomfortable for patients and introduce the potential for motion, which causes artifacts in the images. Long acquisition times also make it difficult to acquire images of structures which move (for instance, the heart) or in which contrast changes over time (for instance, the flowing blood in an MR angiography examination).

The advent of parallel imaging has changed the way MRI is used in the clinic. Parallel imaging is a robust way to accelerate MRI data acquisition, making MRI feasible as an imaging method for many new types of clinical applications. This article introduces the basic concepts of parallel imaging and explains how it has been implemented on clinical MRI scanners. To this end, the basics of MRI data collection and k-space are described and the concept of aliasing in MR images is introduced. The two parallel imaging methods most commonly used on clinical scanners today, sensitivity encoding (SENSE (1)) and generalized autocalibrating partially parallel acquisitions (GRAPPA (2)), are detailed, and the artifacts that can arise as a result of using parallel imaging are shown, along with strategies to identify and mitigate these artifacts. Finally, some of the many applications of these methods are examined to illustrate the impact of parallel imaging on clinical MRI.

K-SPACE AND THE MR IMAGE

In MRI, information about the image is not gathered directly. Instead, MRI data are collected in k-space, which contains spatial frequency information and is related to the actual image through a mathematical operation called the Fourier transform (3). K-space data are generated by using spatially varying magnetic field gradients superimposed on the main magnetic field of the MRI scanner. Once all of the data are collected, the Fourier transform is used to convert the k-space data to an image.

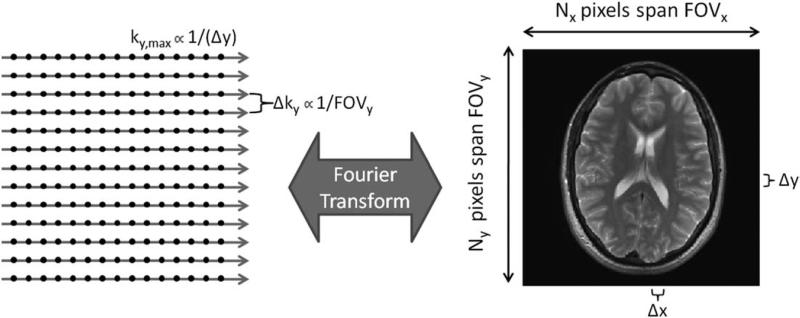
The spacing between k-space points in each direction is inversely proportional to the field-of-view (FOV) in that direction (Fig. 1). For example, decreasing the spacing in the y-direction of k-space will result in an increase in the FOV in the y-direction of the image. The highest frequency collected in k-space (k_x,max or k_y,max) is inversely proportional to the image resolution, or spacing between points in the image domain (Δx or Δy, respectively). Therefore, increasing k_y,max will result in decreasing Δy and increasing resolution in the y-direction of the image. The FOV and resolution of the resulting image can be manipulated by changing the number of points acquired in k-space, the spacing between these points, and the k-space extent spanned by these points.

Figure 1.

Data in k-space are usually collected on a Cartesian grid (left). The Fourier transform is used to convert the k-space to an image of size N_x by N_y pixels (right). The extent of k-space covered (k_x,max and k_y,max) is inversely proportional to the image resolution (Δx and Δy). The spacing between adjacent samples in k-space (Δk_x and Δk_y) is inversely proportional to the field-of-view (FOV_x and FOV_y).

In general, k-space data are collected line-by-line in order to fill a grid of points, where in this case the k_x direction is the read (or frequency-encoding) direction, and the k_y direction is the phase-encoding direction (as illustrated in Figs. 1, 2). In a 3D scan, there would be an additional k_z direction, which would correspond to partition encoding, essentially a second phase-encoding direction. The total acquisition time (T_A) needed to collect a 2D dataset can be written as:

$${\mathrm{T}}_{\mathrm{A}}={\mathrm{T}}_{\mathrm{R}}\times {\mathrm{N}}_{\mathrm{PE}}$$ [1]

where T_R is the repetition time, or the time needed to acquire one line of k-space along the k_x direction, and N_PE is the number of phase-encoding lines in the k_y direction in the dataset (in a 3D acquisition, the number of partition-encoding lines N_PART would also be included). The T_R helps to determine the contrast in the image, and N_PE determines the resolution of the image in the phase-encoding direction, as described above.

Figure 2.

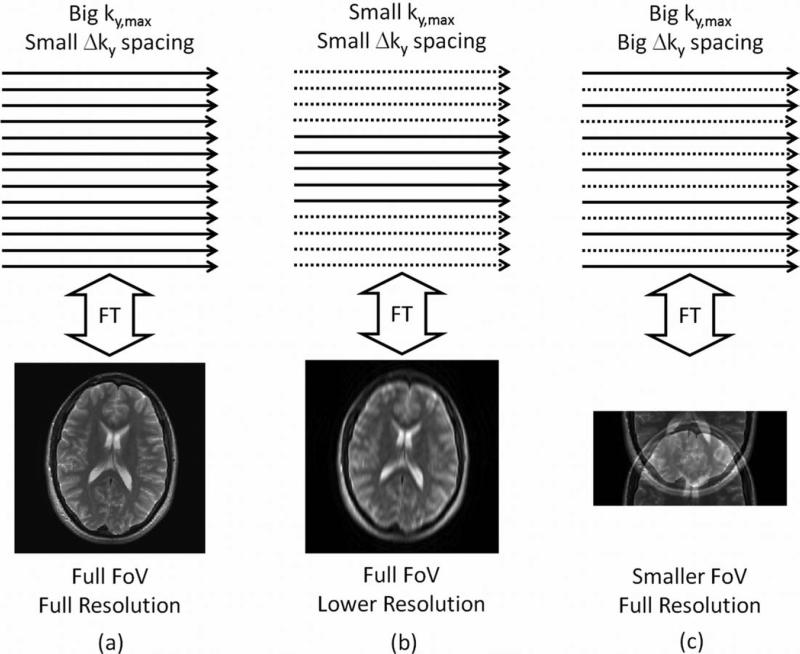
a: A high-resolution image covering the full FOV requires collection of data along closely-spaced lines that span a large region of k-space. b: Reducing k_y,max maintains the FOV but decreases the image resolution. c: Increasing Δk_y while holding k_y,max constant maintains image resolution but decreases the FOV, resulting in spatial aliasing artifacts in the corresponding image.

In order to reduce the acquisition time, either the k-space data must be collected more quickly (reducing the T_R in Eq. [1]) or the amount of k-space data collected must be decreased (reducing the N_PE). The speed at which k-space data can be collected is determined by the desired image contrast and the strength of the magnetic field gradients needed to encode the k-space data. For some types of scans (spin echo, for instance), the T_R must be left long in order to generate the desired contrast. For other types of scans (such as spoiled gradient echo or balanced steady-state free-precession sequences), it is possible to reduce the T_R while still maintaining image contrast. However, in these cases the electrical power required to run the magnetic field gradients significantly faster than the current speed would be massive. There is also a physiologic limit: rapidly switching high-strength magnetic field gradients on and off can induce electrical currents in the patient, potentially causing peripheral nerve stimulation (4–6). Additionally, when using some fast multiecho pulse sequences at high magnetic field strengths, most notably fast spin echo at 3T and higher, the specific absorption rate (SAR) can limit the minimum achievable T_R, which constrains the speed at which data can be acquired (7).

The other approach to decreasing the T_A is to reduce the amount of k-space data collected; in other words, N_PE must be reduced. One method to achieve this is to simply decrease k_y,max while keeping the same Δk_y spacing (Fig. 2b). Because the resolution is proportional to 1/k_y,max, this option will lead to a reduction in image resolution. If image resolution must be maintained for clinical assessment of the images, another option is to remove some phase-encoding lines (Fig. 2c). Because removing lines implies increasing the Δk_y spacing, the result is a reduction in the FOV, which can lead to spatial aliasing if the object is larger than the reduced FOV.

UNDERSAMPLING AND ALIASING

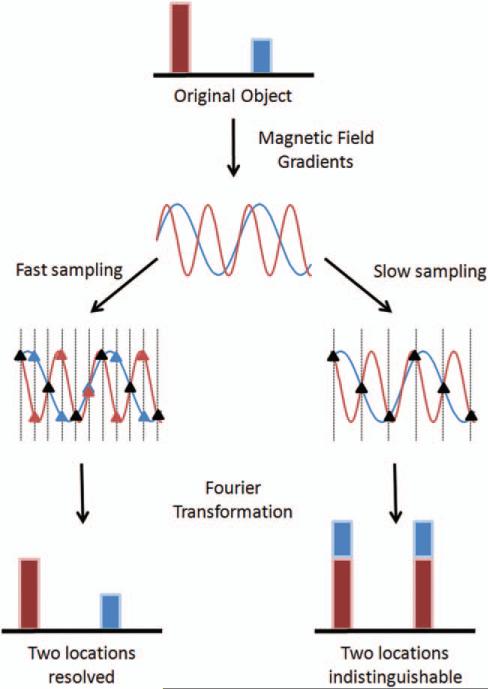
In order to understand the concept of spatial aliasing, it is important to first look at the relationship between k-space and the MR image. Figure 3 shows a typical example of MRI encoding. The top row shows a 1D “object” containing two signal sources, shown here in blue and red. When a magnetic field gradient is applied, these two sources will give rise to signals with different frequencies because they are in different locations. The two-frequency signal arising from the two different locations is shown schematically in the second row of Figure 3; the lower frequency (blue) stems from the blue source, and the higher frequency (red) from the red source.

Figure 3.

A 1D object with two signal sources at two different locations (red and blue in the top row) gives rise to two signals oscillating at different frequencies (second row). These signals are sampled at a high rate (third row left) and at a lower rate (third row right), where the sampling time is indicated by vertical dotted lines. The points sampled are denoted as triangles; at some sampling times, the two signals appear the same (black triangles). If the signals are sampled at a high enough rate (left bottom), the frequencies can be distinguished from one another and the two locations can be resolved. If the signals are sampled too slowly (right bottom), or undersampled, the two frequencies appear the same at these sampled points and the two locations cannot be distinguished.

In the data collection process, the MRI signal is sampled at discrete timepoints, which are shown by the vertical dotted lines overlaying the frequency signal (third row of Fig. 3). The sampling rate is determined by the user, and can be fast (left side) or slow (right side). In order to get back to an image from the sampled data, a Fourier transform is applied to the sampled points (the bottom row of Fig. 3).

The left side of Figure 3 shows the results of the Fourier transform when many measurements are made of the signal. Because the two frequencies can be distinguished using this sampling rate, the two different signal sources can be separated from one another (bottom left). If fewer measurements are made, which is shown on the right side of Figure 3, the samples of these two signals appear to be identical (the vertical lines fall at places where the signals overlap). The frequencies are not actually the same, but at this lower sampling rate they cannot be distinguished from one another. In this case, the data are said to be undersampled. When the Fourier transform is used on these undersampled data, the signal from both locations appears at both locations because they cannot be differentiated (bottom right). The resulting image is said to contain aliasing artifacts due to the low sampling rate.

This same phenomenon can occur in k-space data in MRI if the lines are not sampled often enough in the phase-encoding direction. If the k-space data are undersampled, a high-frequency signal originating from one part of the object is indistinguishable from a low-frequency signal originating from another part of the object, and the two locations will overlap in the image. Undersampling in k-space reduces the FOV and leads to aliasing in the image domain.

Recalling the relationships between k-space and the image domain from Figure 1, the spacing between points in k-space needs to be small enough that the frequencies from different locations within the object can be distinguished from one another. In other words, the FOV (as determined by the spacing of the phase-encoding lines) should be at least as large as the size of the object. This requirement on the FOV (and the k-space sampling interval) is known as the Nyquist criterion. If the Nyquist criterion is satisfied in both the k_x and k_y directions, an image can be reconstructed from the k-space data without spatial aliasing (Fig. 2a). However, if fewer phase-encoding lines are collected, then the k_y direction is undersampled (Fig. 2c). This undersampling results in reduction of the FOV and aliasing in the phase-encoding direction of the image.

PARALLEL IMAGING METHODS

While it is possible to accelerate MRI data acquisition by collecting fewer phase-encoding lines in k-space, the resulting spatial aliasing must be removed before the images can be used for clinical purposes. Parallel imaging has been developed to address this issue. All parallel imaging methods share some common characteristics, which are listed below:

1. K-space data are undersampled in the phase-encoding direction (and potentially also the partition-encoding direction in 3D imaging) to reduce the scan time. The acceleration factor (or reduction factor), R, is defined as the ratio of the amount of k-space data required for a fully sampled image to the amount collected in an accelerated acquisition (if every other line in k-space is collected, the acquisition is accelerated by factor R = 2). If the Nyquist criterion is not met (and the FOV becomes smaller than the object), the result is an aliased image.

2. Data are acquired using an array of independent receiver channels instead of using a large homogeneous volume receive coil (Fig. 4). Each receiver coil is more sensitive to the specific volume of tissue nearest to the coil, which means that the coils provide an additional source of spatial information for image reconstruction.

3. A special algorithm, which requires some knowledge of the individual coil sensitivities, is used to combine the undersampled data from each of the receiver coils into an unaliased reconstructed image with the full FOV.

Figure 4.

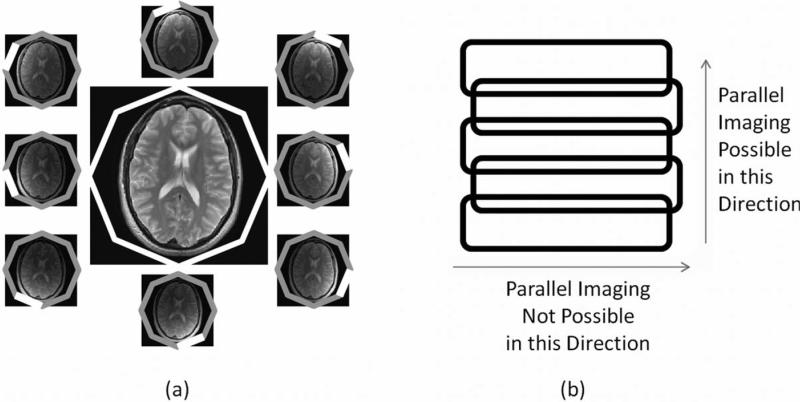
(a) An example head coil array made up of eight independent receiver coils arranged around the object in a circle. Each coil is more sensitive to signal originating from the tissue closest to it, and can be used to form its own image (small images). The independent coil images can be combined into a single image with uniform sensitivity (large center image). (b) An example linear array made up of five coils, where the sensitivity profile of each array is similar in the horizontal direction, but the sensitivity decreases with distance along the vertical direction. When using such a coil, acceleration can only be performed in the vertical direction where there is substantial variation in the coil sensitivities.

It is important to note that parallel imaging is not a specialized pulse sequence, but instead a reconstruction technique that can be used to reconstruct under-sampled data from nearly any type of pulse sequence. Additionally, the number of receiver channels in the coil array limits the maximum acceleration factor; in general, the acceleration factor cannot be higher than the number of coils in the array, although this parameter is usually chosen to be much smaller in order to generate images of clinical quality.

Many different parallel imaging algorithms exist, and the three characteristics detailed above are shared by all. These methods can be subdivided into those that work with the aliased image (such as SENSE) and those that reconstruct the missing k-space data (such as GRAPPA). While many techniques have been proposed and been essential along the path of developing robust parallel imaging methods, not all are routinely employed on clinical MRI scanners. This article focuses on the two methods (and their variations) that are used most commonly in the clinical setting: SENSE-type algorithms, and GRAPPA-type algorithms. As a basic example of how parallel imaging works, the PILS method (8) will also be discussed, although this method is not commonly used in clinical imaging.

RECEIVER COIL ARRAYS

Before discussing specific parallel imaging methods, it is important to examine the essential hardware required for parallel imaging, namely, the multichannel receiver array. A single receiver channel in an array is sensitive to signal from a limited spatial region, as can be seen in Figure 4. The coil sensitivity describes how sensitive a given channel is to a specific point in space; this sensitivity is often dependent on the object in the receiver coil, and therefore can vary from patient to patient.

The individual receiver coils are arranged in an array such that the sensitivity profiles cover the desired FOV. When performing a scan with multiple coils, all of the images resulting from the multiple channels must be combined to form a single image. This can be performed using a sum-of-squares operation (9), or using other techniques that result in a homogeneous signal after combination (see, eg, (10)). Arrays can be arranged in a planar form, as in a spine array, or in a circular form, as in the head coil shown in Figure 4a (9,11). Typical arrays used in a clinical setting contain from four to more than 32 independent channels and have sensitivity variations in two- or three-dimensions. Because parallel imaging relies on these coil sensitivity differences, acceleration can only practically take place in directions with coil sensitivity variations. For instance, if an array is made up of five channels arranged in a line (illustrated in Fig. 4b), data acceleration can occur along the direction of the array (where there are sensitivity differences between the coils), but not parallel to the individual coils in the array (where there are almost no differences in sensitivity). When a coil array is designed for a specific part of the body, great care is taken to construct a geometry that allows maximum acceleration in standard phase-encoding directions. Overlap between the different channels in the array, which reduces the amount of spatial information provided by the array, is also avoided.

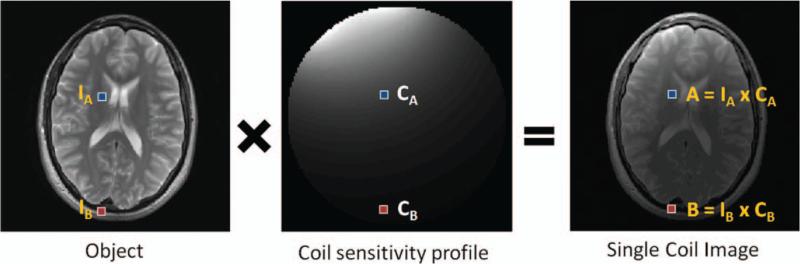
Figure 5 shows how a nonhomogeneous coil sensitivity profile modifies an MR image. Given the coil sensitivity profile shown in the center, which is representative for a receiver coil placed at the right frontoparietal area of the head, and the object shown at the left, the resulting single coil image will exhibit the shading shown in the image on the right-hand side of the figure. In mathematical terms, each pixel in the object image is multiplied by the appropriate pixel in the coil sensitivity map. Thus, pixel A shown on the right-hand image can be described as the result of multiplying the coil sensitivity at location A, namely, C_A, with the object pixel at location A, namely, I_A:

$$\mathrm{A}={\mathrm{C}}_{\mathrm{A}}\times {\mathrm{I}}_{\mathrm{A}}$$ [2]

Figure 5.

The object pixels (left) are weighted, ie, multiplied, by the sensitivity of the receiver coil (center) to yield the single-coil image (right).

The same is true for pixel B:

$$\mathrm{B}={\mathrm{C}}_{\mathrm{B}}\times {\mathrm{I}}_{\mathrm{B}}$$ [3]

Thus, the single coil images are simply a result of multiplying the object with the coil sensitivity maps.

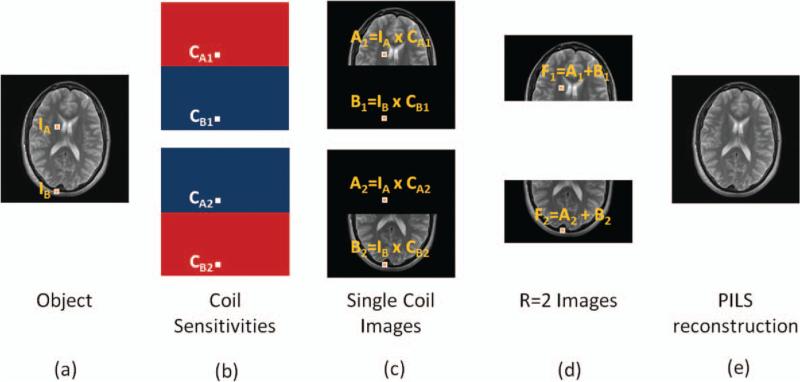
Figure 6 illustrates that the limited FOV of each element in a coil array can be used to accelerate imaging through the simple example of the PILS reconstruction (8). Consider a full k-space acquisition with a two-channel receiver array, where each receiver is homogeneously sensitive to a local portion of the object and these sensitivities do not overlap. Two images result from this acquisition, one from each receiver coil, where again, each single coil image is simply the product of the object and the appropriate coil sensitivity map as in Figure 5. Each image will display only the part of the object that was within the region of sensitivity of one coil. Because each coil is sensitive to only half the volume of interest, the FOV can be reduced by a factor of two by acquiring every other line in k-space, which cuts the total acquisition time in half. There will still formally be aliasing (specifically, pixel F₁ is the sum of pixels A₁ and B₁ and pixel F₂ is the sum of pixels A₂ and B₂), but because one of the aliased pixels will have no signal, the result is a smaller FOV image, but one without any overlapping information. The PILS reconstruction involves simply putting the two images together to create a full FOV image. While this example serves to illustrate how parallel imaging works in general, it is not a practical approach. This is because the sensitivity profiles of the coils would have to be completely nonoverlapping, and the sensitivity of each individual coil completely homogeneous. As these two requirements are not practically feasible, more complex parallel imaging strategies have been developed.

Figure 6.

The data acquisition for the object shown in (a) can be performed using a two-channel receiver array (b) where each receiver is sensitive to a localized region and sensitivity regions do not overlap. Each receiver coil gives rise to one fully sampled image where each pixel is the product of the object location and the coil sensitivity map (c). In the case of B₁, for instance, the coil sensitivity value at location B, namely C_B1, is zero. If the scan is accelerated by a factor of 2, the FOV in each single-coil image is decreased by a factor of 2 (d). These accelerated single-coil images are aliased (pixel F₁ is the sum of pixels A₁ and B₁), but because one of the aliased pixels comes from outside the region of sensitivity, it will contribute no overlapping signal. The full FOV image can be reconstructed by piecing together the accelerated single-coil images (e).

SENSITIVITY ENCODING (SENSE)

The SENSE technique (1) is one of the methods commonly used in the clinic. Unlike PILS, SENSE does not require homogeneous and nonoverlapping coil sensitivities, making it useful for commercially available receiver coil arrays. In SENSE, the maps of the coil sensitivities must be known; this information is usually gathered using a prescan at the beginning of the MRI examination.

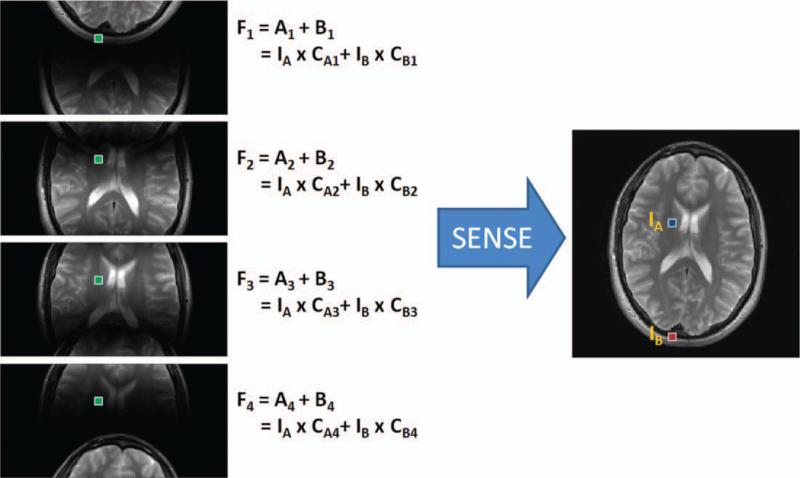
As in all parallel imaging techniques, the first step in SENSE is to acquire undersampled k-space data, which results in an aliased image. A schematic example using a four-channel linear array is shown in Figure 7, where the data acquisition has been accelerated by a factor of R = 2. In this case, two pixels alias (or fold) on top of one another in each of the single channel images because the FOV has been decreased by one-half. However, each of these pixels is multiplied by the appropriate coil sensitivity value before they are added together in the aliased image:

$$F_1=A_1+B_1=I_A{C}_{A1}+I_B{C}_{B1}$$ [4]

where F₁ is the aliased pixel for coil 1, C_A1 and C_B1 are the coil sensitivities for coil 1 in locations A and B, and I_A and I_B are the values of the pixels in the desired image at locations A and B. In this equation, even if the values of the coil sensitivities C_A1 and C_B1 are known (from the calibration step above), there is still only one known value F₁ (the aliased pixel from the acquired undersampled data) to solve for two unknown values (the actual pixel values I_A and I_B). However, because the data acquisition was performed using a multichannel receiver array, there will be similar equations for each of the four coils, as depicted in Figure 7. Note that each of the coil sensitivity entries (the C_A1, C_A2, etc.) are different because each of the coils has a different sensitivity value at these two pixel locations, but the actual pixel values I_A and I_B stay the same because there is only one underlying object. Now, given that the coil sensitivity values are known, there are four known values (the folded pixels for each of the coils), and only two unknown values (the actual pixels I_A and I_B). Using linear algebra and matrix inversion methods, it is possible to solve for the actual pixels I_A and I_B. This same operation is performed for each set of aliased pixels in the folded images to arrive at the final unaliased image.

Figure 7.

A four-channel linear array is used to acquire an image with acceleration factor R = 2. This results in four single-coil images where two pixels, I_A and I_B, are aliased. The aliased pixels, F₁ through F₄, in each single-coil image are sums of the two pixels weighted by the appropriate coil sensitivity values. Given that the coil sensitivity values (the C_A and C_B terms) are known, SENSE solves the resulting system of equations with four known values (F₁, F₂, F₃, and F₄) and two unknown values (I_A and I_B) to unfold the aliased single-coil images into a full FOV image. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

With the help of the equations in Figure 7, some of the properties of parallel imaging can be better understood. Any system of equations can only be solved if there are more known values than unknown values. Thus, the maximum number of pixels that can be unaliased from one another (or the maximum acceleration factor) cannot be larger than the number of receiver coils. This means that larger numbers of receiver coils in an array offer the potential for higher acceleration factors. Second, each of the receiver coils must have a sensitivity profile that is different from all the other coils, or else two of the equations in the system will be the same. Finally, parallel imaging is usually associated with a drop in the signal-to-noise ratio (SNR). For SENSE, this SNR reduction can be written as follows:

$$SN{R}_{PI}=\frac{SNR}{g\sqrt{R}}$$ [5]

where R is the acceleration factor and g is the coil geometry factor. These two terms come from different sources. The √R stems from the fact that R-times fewer data points are acquired, which reduces the SNR. The geometry factor, or “g-factor,” which is always greater than or equal to one, arises from the properties and geometry of the receiver coil array. If the coil sensitivities from two receiver coils are highly correlated, the aliased pixels will in general be harder to separate, which reduces the SNR of the SENSE reconstruction. This g-factor-related SNR loss is different from pixel to pixel, and generally appears largest in the center of the reconstructed image where many pixels overlap and the coil sensitivities are most similar. Examples of images showing SNR loss due to high g-factors are shown below.

The only major drawback to the SENSE reconstruction is the need for an accurate coil sensitivity map. Errors in the coil sensitivity map will cause artifacts in the form of residual aliasing in the reconstructed full FOV image. There are many factors that can cause the sensitivity maps to be inaccurate. The coil sensitivity profiles depend on the placement of the coils relative to the anatomy being imaged. If the patient moves during the course of the examination, the coil sensitivities may change, and the resulting images can contain artifacts. These artifacts can be mitigated by reacquiring the information needed to calculate the sensitivity map and using these new maps in the reconstruction. Additionally, in regions with low signal levels, for instance, the lungs or sinuses, it can be difficult to determine the sensitivity map due to the high noise in these areas. By assuming that the coil sensitivity profile must be smooth, small areas of discontinuity in the coil sensitivity maps can be estimated using approximation methods (1).

Despite the potential challenges when working with coil sensitivity maps, SENSE and variations on SENSE (such as mSENSE (12) and ASSET) are used daily to accelerate clinical MRI scans. Several examples of SENSE-accelerated images are shown in the clinical section below.

GENERALIZED AUTOCALIBRATING PARTIALLY PARALLEL ACQUISITION (GRAPPA)

GRAPPA (2), unlike SENSE, seeks to regenerate the phase-encoding lines that were left out of the k-space data acquisition in order to accelerate the MRI scan. Once the missing lines have been restored, the Fourier transform is applied to arrive at the final image. Because the method is applied to the raw k-space data, GRAPPA is said to work with the undersampled k-space, whereas SENSE works on the aliased image.

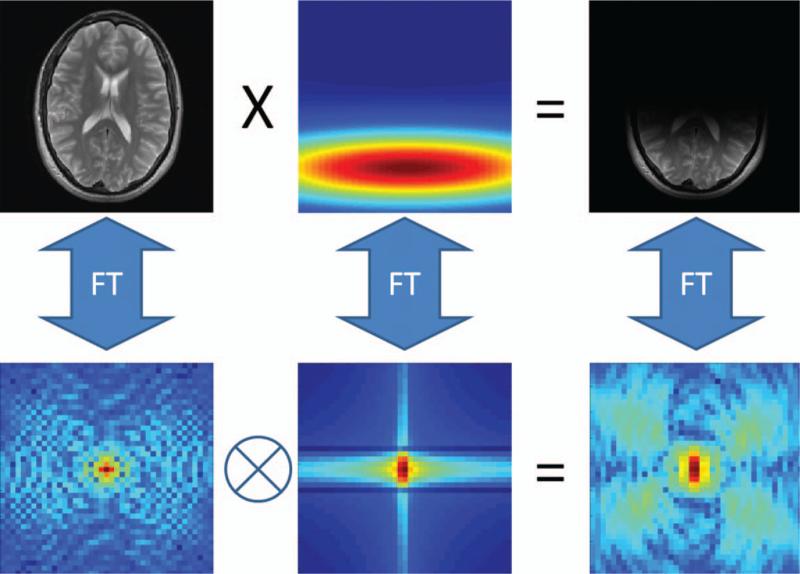
The idea behind GRAPPA is to use portions of the acquired k-space to calculate the portions that were not acquired. As illustrated in Figure 8, the signal intensity at each point in the image acquired using a receiver array is multiplied (or weighted) by the appropriate coil sensitivity profile. The consequence of this in k-space is a smearing of information across neighboring k-space points. The same smearing pattern is found everywhere in k-space. GRAPPA is based on the notion that because of this smearing, some information about any given k-space point is also contained in the neighboring k-space points. Therefore, any missing data point can be recovered by combining neighboring points together in the appropriate way.

Figure 8.

In the image domain (top row), a fully sampled image (left) multiplied by a localized coil sensitivity profile (center) results in a single-coil image (right). Looking at the same relationship in k-space (bottom row), the k-space of the object (left) is smeared (or convolved) with the k-space of the coil sensitivity (center), resulting in spreading of the k-space data across several points in the single-coil k-space (right).

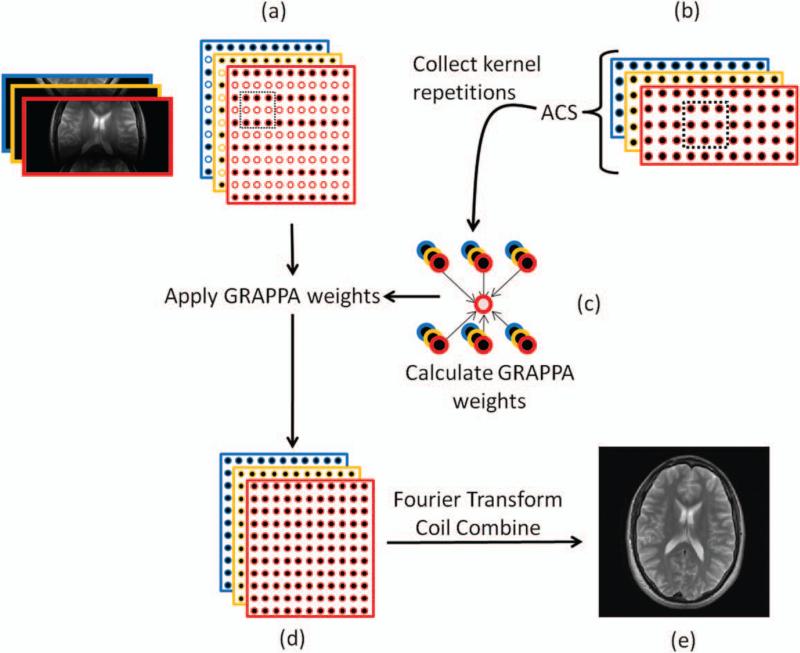
A schematic diagram of the GRAPPA algorithm is shown in Figure 9. In order to be able to use GRAPPA, the appropriate combination of each of the acquired points (or source points) must be found in order to recover the missing points (or target points). The weighting factors (or weights) in this combination are determined by using an additionally acquired portion of k-space known as the autocalibration signal (ACS). The ACS usually is a patch of k-space with the same desired k-space spacing / image FOV as the final reconstructed image, but with a lower resolution. While the ACS lines can be obtained before, during, or after the lines for the accelerated acquisition, they are most frequently collected during the accelerated scan, which is why GRAPPA is known as an “autocalibrated” method. It is also important to note that the ACS lines can be acquired with a different contrast than the accelerated scan, which is useful in cases where the scan to be accelerated is slow due to the desired contrast (spin echo, for example). A GRAPPA kernel is then defined, which describes the number and arrangement of source points to be used for the reconstruction. For example, Figure 9 depicts the kernel as a box spanning two sampled phase-encoding lines and three readout points, where the source points are filled circles and the target points are white empty circles. This GRAPPA kernel appears in both the undersampled k-space data and the ACS data. Then, using the ACS data, the appropriate GRAPPA weighting factors can be determined. By sliding the kernel throughout the entire ACS region, many examples of the kernel of source and target points can be found. Using these multiple kernels, the GRAPPA weight set can be calculated by determining the mathematical relationship between the source and target points in the ACS.

Figure 9.

a: Undersampled k-space data are collected from each coil, where the different coils are shown with different colors. The kernel (outlined by the dotted black box) consisting of some source points (solid circles) and target points (empty circles) defines the neighborhood of k-space points that will be used for the GRAPPA reconstruction. b: Additional data (auto-calibration signals, or ACS) are collected, usually near the center of k-space. c: The repetitions of the kernel through the ACS region are used to calculate the GRAPPA weights. d: The GRAPPA weights are then applied to fill in the missing k-space data from each coil to produce fully sampled single-coil data. e: The Fourier transform is used to obtain single-coil images, which are then combined to form a reconstructed full-FOV image. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Once the GRAPPA weights have been determined, the kernel is moved to the undersampled region of k-space. Because the same k-space smearing pattern exists in all regions of k-space, the weights determined from the ACS data can be applied to the under-sampled k-space to fill in the lines skipped during the accelerated acquisition. This step results in a fully sampled k-space for each coil in the receiver array. The Fourier transform is used to make an image for each coil, and the individual coil images are then combined into a composite image, as illustrated in Figure 9 (9,10).

GRAPPA is widely employed, and various versions and implementations of this algorithm have been adopted for clinical imaging (including ARC (13)). Because this method does not rely on exact knowledge of the coil sensitivities, GRAPPA is robust in cases where it might be difficult to obtain a coil sensitivity map, such as images with areas of low signal, and in regions that are subject to patient motion. Additionally, GRAPPA can sometimes lead to images with fewer artifacts when there is aliasing in the full FOV image (14,15). GRAPPA is also flexible, as parameters such as the number of ACS lines or the size of the kernel can be adjusted to form the best result in each imaging scenario. As a general rule of thumb, increasing the ACS size results in more accurate GRAPPA weights (although more time is needed to acquire them). Increasing the kernel size may result in a more accurate fit for the target points, but if the kernel becomes too large, there will not be enough repetitions of the kernel through the ACS for an accurate estimate of the weights.

As in all parallel imaging, the SNR of a GRAPPA-reconstructed image depends on the acceleration factor, R, and on the spatially varying noise characteristics, quantified by the GRAPPA g-factor (16). Like the SENSE g-factor, the GRAPPA g-factor also describes the pixel-by-pixel SNR losses in the reconstructed image. Unlike the SENSE g-factor, which is derived from explicit knowledge of the coil sensitivity profiles, the GRAPPA g-factor is calculated using the GRAPPA weights. While the GRAPPA g-factor and SENSE g-factor are not identical because the techniques are not the same, they tend to be quite similar as the g-factor originates from the coil sensitivities, which are used in similar ways in both parallel imaging methods.

So far, this article has only described data acceleration in the phase-encoding dimension. However, when performing 3D imaging, which includes a partition direction, acceleration can take place in both the phase-encoding and the partition-encoding directions. Research has shown that it is possible to reduce the g-factor and improve the reconstruction by undersampling in both directions. For instance, it may be preferable to accelerate by a factor of R = 2 in the phase-encoding direction and R = 2 in the partition-encoding direction compared to R = 4 in the phase- or partition-encoding direction alone, as it is possible to take advantage of coil sensitivity variations in multiple directions (depending on the coil array used). Additionally, by using methods such as CAIPIRINHA, where the acquired k-space points are offset from the normal grid-like sampling to shift aliasing artifacts, the g-factor losses can be further mitigated (17,18). Examples of several GRAPPA and CAIPIRINHA patterns are shown in Figure 10, where the black dots are the source points and the gray dots are the target points for these patterns.

Figure 10.

Examples of R = 4 GRAPPA kernel patterns for 3D imaging, where the black points are the source points and the gray points are the target points. The phase-encoding direction is up-down, the partition-encoding direction is left-right, and the frequency-encoding (or read) direction is into the plane of the page. a: The entire R = 4 acceleration is performed in the phase-encoding direction, which can lead to residual aliasing artifacts and high g-factor losses depending on the coil configuration. b: The acceleration has been split up such that the phase and partition-encoding directions each experience R = 2, leading to a total acceleration of R = 4. This type of acceleration can lead to an improved image quality compared to the pattern in (a). c: A CAIPIRINHA pattern, where the acceleration has been split up as in (b), but the acquired points are offset (the so-called R_phase = 2, R_partition = 2, delta = 1 pattern). Such a pattern causes the aliasing to be shifted and can lead to lower g-factors and more robust GRAPPA reconstructions than the patterns in either (a) or (b).

ARTIFACTS AND MITIGATION

Artifacts due to parallel imaging generally fall into one of two categories: residual aliasing and noise enhancement. Both of these artifact types can arise from the same underlying mechanism, namely, that the acceleration factor is too high for the coil geometry and too many pixels must be unfolded from one another. However, the physical manifestation of the two is quite different. Residual aliasing appears as ghosts inside or outside the object of interest. Noise enhancement makes structures in the image appear grainy, and may be more severe in some regions of the object than in others. While these two types of artifacts are discussed separately below, it is important to note that the same effects can cause both, and one rarely appears without the other. Examples of both are shown in Figure 11; notice that the artifacts increase in severity as the acceleration factor is increased.

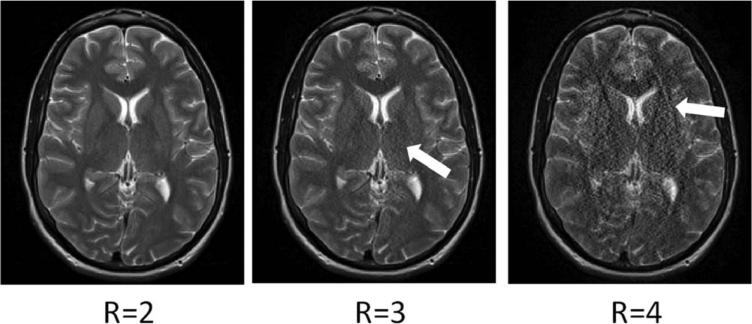
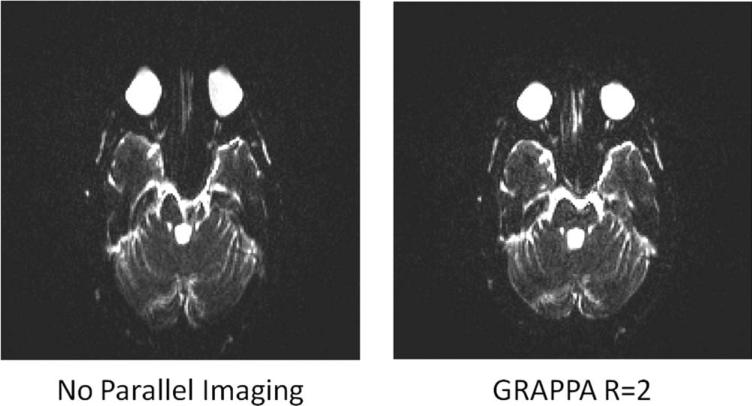
Figure 11.

Example GRAPPA reconstructions of head images using acceleration factors R = 2, R = 3, and R = 4 and 24 ACS lines. A total of 12 receiver coils were used to acquire these data. Note that as the acceleration factor increases, the noise enhancement increases (compare R = 2 and R = 3), and residual aliasing artifacts start to appear (R = 4). Similar artifacts appear in the equivalent SENSE reconstructions.

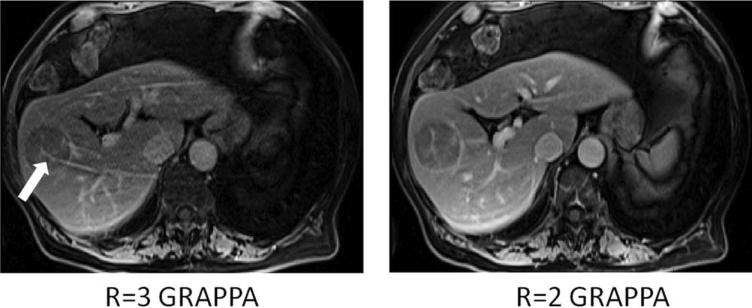
Residual aliasing can appear wherever there is an error in the unfolding process of the parallel imaging reconstruction. These artifacts are especially evident when the edge of the object is bright (eg, a T_1⁻ weighted abdominal image), causing a bright ridge to appear through the anatomy of interest (Fig. 12). In order to determine if a feature in an image is a consequence of residual aliasing, it is important to know what acceleration factor was used and which direction was accelerated (phase-encoding, partition-encoding, or both). In this way, the location and direction of any aliasing artifacts can be determined and the artifacts themselves identified.

Figure 12.

T₁-weighted abdominal images acquired with R = 3 (left) and R = 2 (right) in the up-down direction and reconstructed using GRAPPA. Note the residual aliasing in the left image, which could appear to be abnormal vasculature in the liver lesion. Decreasing the acceleration factor removes these artifacts, as can be seen in the image on the right.

Residual aliasing occurs in SENSE-type algorithms if the coil sensitivity map is not accurate (and if the acceleration factor is too high, as in GRAPPA). These errors can occur if the patient moves after the pre-scan, and can be corrected by reacquiring the sensitivity map information. Errors in the coil sensitivity map can also occur if the coil sensitivity profiles are not accurate in areas of low signal, such as lung tissue or sinuses. Small inaccuracies in the coil sensitivity maps due to low signal may be removed by interpolating or smoothing the coil sensitivity profile (1,19).

Residual aliasing occurs in GRAPPA-type algorithms if there is error in the GRAPPA weights. This can occur if the acceleration factor is too high for the specific coil used, or if there are not enough ACS lines acquired to accurately determine the proper values of the GRAPPA weights. In the first case, the only option is to reduce the acceleration factor in order to remove the aliasing artifacts. In the second case, more ACS lines can be acquired, yielding more accurate GRAPPA weights.

Noise enhancement can occur for many of the same reasons as residual aliasing artifacts (acceleration factor too large, geometric configuration of the coil array is not optimal). This results when regions of the coil sensitivity profiles are too similar. These areas tend to lie in the center of the image, because many pixels are folded on top of one other and the coil sensitivities are the most similar in these parts of the image, as depicted in Figure 11. Much effort is placed in optimal coil design in order to reduce noise enhancement, and specialized arrays are designed for the geometry of specific anatomies such as dedicated cardiac arrays (20), spine arrays (21), neck coils (22), and breast coils (23).

As mentioned above, there are many possible ways to reduce residual aliasing artifacts and noise enhancement due to parallel imaging. Either the method can be adjusted (reacquisition of the coil sensitivity map for SENSE, acquisition of more ACS lines for GRAPPA), or the acceleration factor can be reduced. Another possibility is to change the direction of the phase encoding. This can help if the coil array has more elements in one direction than in the other, making the parallel imaging reconstruction more robust in that direction. Changing the direction of the phase encoding (and thus the acceleration) is also a way of determining whether an image feature is an artifact or part of the anatomy. If a 3D scan is employed, it is often beneficial to accelerate in both the phase and the partition-encoding directions. If the total acceleration factor is R = 4, the acceleration can be applied all in the phase-encoding direction, all in the partition-encoding direction, or R = 2 in each of the phase- and partition-encoding directions. Such a 3D reconstruction can be performed using SENSE, GRAPPA, or a combination of the two. As illustrated in Figure 13, CAIPIRINHA can be used in 3D scans to reduce the number of pixels that alias on top of each other, thereby reducing the g-factor-related noise enhancement in the parallel imaging reconstruction (17,18). Finally, both SENSE and GRAPPA can be implemented with an additional mathematical technique known as regularization to reduce noise enhancement (24–27). Regularization determines how noise in the data affects the final reconstructed image, and it can be used during the unfolding of the aliased pixels in SENSE or in the determination of the GRAPPA weights. While regularization can reduce noise enhancement, this improvement is often accompanied by increased aliasing or other image artifacts, and therefore this technique must be used carefully. Thus, even in cases of severe artifacts or noise enhancement, adjustments can generally be made to improve the quality of the accelerated image.

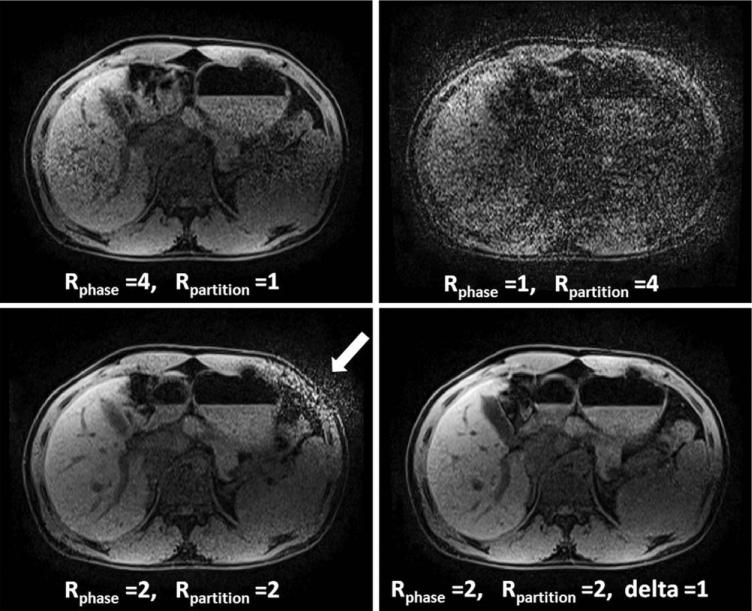
Figure 13.

Examples of GRAPPA-reconstructed partitions from a 3D abdominal scan with acceleration factors of R = 4. Top left: All of the acceleration is performed in the phase-encoding direction (up-down), leading to noise enhancement (GRAPPA kernel shown in Fig. 10a). Top right: All of the acceleration is performed in the partition-encoding direction (head-foot). Because the coil array is more suited to acceleration in the up-down direction, this arrangement leads to a poorer reconstruction than when accelerating only in the phase-encoding direction. Bottom left: The acceleration has been split up between the phase and partition-encoding directions (kernel shown in Fig. 10b), thereby improving the reconstruction quality. Note the residual aliasing artifacts outside the body near the stomach and spleen. Bottom right: By using a CAIPIRINHA pattern where the acquired k-space points are offset with respect to one another (kernel shown in Fig. 10c), the g-factor is reduced and a clinically acceptable R = 4 image is generated.

CLINICAL APPLICATIONS OF PARALLEL IMAGING

Parallel imaging has had a profound impact on clinical imaging. Techniques such as SENSE and GRAPPA can be applied to nearly any sequence, and can be used to provide a reduction in overall scan time or an improvement in image quality in almost all imaging protocols. This section seeks to provide an overview of different clinical areas that have benefited from parallel imaging acceleration, and by no means is meant as a comprehensive treatment of all applications of parallel imaging in the clinic. For a detailed look at how parallel imaging is used for specific types of MRI scans, the authors recommend Parallel Imaging in Clinical MR Applications, edited by Schönberg et al (28).

As mentioned above, the acquisition time for a single image is determined by the number of phase-encoding lines, N_PE, and the repetition time, T_R. Parallel imaging can be used to improve clinical imaging protocols in four ways:

1. Reduced acquisition time with fixed spatial resolution: Parallel imaging allows fewer phase-encoding lines to be acquired over the same span of k-space, thereby reducing the time it takes to acquire a static image without sacrificing spatial resolution. For static imaging, this results in a shorter scan time with fewer artifacts due to motion and/or a shorter breath-hold time, and for dynamic imaging, parallel imaging can yield a higher temporal resolution as each frame can be acquired more quickly.

2. Improved spatial resolution with fixed acquisition time or temporal resolution: Instead of acquiring fewer lines in k-space that are spaced farther apart, the same number of lines can be acquired with wider spacing such that a larger span of k-space is covered. This scheme increases the final image resolution for a fixed acquisition time or temporal resolution.

3. Improved spatial and temporal resolution: Parallel imaging can be used to balance the scan time increase that accompanies the collection of high-spatial-resolution images (acquiring data over a larger region of k-space) with accelerated data acquisition to improve spatial and temporal resolution simultaneously.

4. Improved image quality from reduced echo train length: In some imaging sequences (fast gradient echo, fast spin echo, and echo-planar imaging), multiple echoes are generated in one readout train to speed the imaging process. These techniques can suffer from susceptibility artifacts, blurring, and distortions due to T₂ and ${\mathrm{T}}_2^{\ast }$ decay over the duration of the long echo train. Parallel imaging is frequently used to reduce the interecho spacing or overall echo train length, thereby reducing these artifacts.

The reduction in scan time for a fixed spatial resolution is the most common application of parallel imaging. This is the type of acceleration shown in Figure 11, where the scan time without parallel imaging is 97 seconds, and acceleration by a factor of 2 with 24 ACS lines reduces this time to 57 seconds. This acceleration is especially useful for imaging scenarios in which patient motion poses a significant problem. For example, pediatric patients (29) and patients with neurodegenerative diseases (30) often do not comply with commands to hold still. Even compliant patients may start to fidget or become uncomfortable during a longer scan, and acquisition of the MR image in a fraction of the time using parallel imaging can reduce the risk of patient movement during these longer scans. Finally, patients frequently have difficulty with completing lengthy breath-hold maneuvers required for cardiothoracic or abdominal imaging. Parallel imaging is often used to accelerate thoracic and abdominal scans in order to shorten the breath-hold duration, resulting in improved patient compliance and reduced motion artifacts.

The benefits of reduced image acquisition time and high temporal resolution afforded by parallel imaging have been demonstrated repeatedly in cardiovascular applications. Parallel imaging is frequently used to reduce breath-hold duration and increase comfort for patients with advanced cardiac disorders. The improvements in temporal resolution have increased frame rates in cardiac cine imaging (31), allowing a better examination of cardiac morphology, wall motion abnormalities, and valve diseases (32). Spatial and temporal resolution improvements have contributed to more accurate assessments of cardiac function (33,34) and myocardial perfusion (35,36). These clinical indicators are important for assessment of conditions such as hypertrophic cardiomyopathy (37) and ischemic heart disease (38). Improved temporal resolution has also contributed to improvements in aortic and pulmonary artery flow quantification (39), time-resolved blood velocity mapping (40), detection of intracranial aneurisms (41), and coronary angiography (42).

As with cardiothoracic imaging, abdominal imaging has benefited from the reduced breath-hold duration, shortened echo train length, and improvements in spatial and temporal resolution achieved by using parallel imaging. For example, Figure 13 shows abdominal images that were acquired in 10 seconds using CAIPIRINHA; without parallel imaging the total scan time would be 35 seconds, which is too long a breath-hold for most patients. Parallel imaging has also been used to accelerate renal imaging, allowing for larger volume coverage (43) and quantitative assessment of parenchymal lesions (44).

Systemic angiography is an important area for applications of parallel imaging due to improvements in both the spatial and temporal resolution. MR angiography (MRA) is frequently conducted after bolus injection of a contrast agent. In order to obtain images of the arterial tree without venous contamination from this injection, it is crucial that all images collected in the angiography imaging sequence are obtained during the first pass of the bolus. This restriction demands imaging over a short time window with high temporal resolution. Recent work has demonstrated high-temporal-resolution angiography with acceleration factors of up to 16 with parallel imaging applied in two directions (45). Parallel imaging can also be used to improve spatial resolution of MRA, and has been applied to image renal artery stenosis (46) and for planning of endovascular interventional treatment (47). The combination of improved spatial and temporal resolution through 2D parallel imaging has been applied to increase the spatial coverage of abdominal angiography (48). Recently, parallel imaging has been coupled with modified pulse sequences such as gradient echo and inversion recovery to improve SNR efficiency (49) and to perform noncontrast angiography (50,51). The combination of partial Fourier techniques and view-sharing with parallel imaging has also led to the availability of time-resolved angiography examinations of the vessels of the brain (52), lower extremities (53), and kidneys (54).

Parallel imaging techniques have improved the performance of rapid, multiecho imaging sequences such as echo-planar imaging (EPI) or turbo spin echo (TSE) by shortening the total echo train length, thereby reducing both geometric distortions and sometimes increasing the resulting SNR. In these multiecho sequences, several phase-encoding lines are acquired in each T_R. Each phase-encoding line requires an echo, and when many phase-encoding lines are needed, many echoes must be acquired in the T_R (the so-called echo train must be long). Because T₂ and ${\mathrm{T}}_2^{\ast }$ relaxation effects cause geometric distortions and lead to a loss in SNR when the echo train is long, shortening the echo train length and the effective echo time with parallel imaging leads to improved image quality. As an example, an EPI sequence with an echo train of 192 echoes was acquired with an effective echo spacing of 1280 μs; a representative image is shown on the left side of Figure 14. Using GRAPPA and R = 2, shown at the right, the echo train length was reduced to 96 echoes with an effective echo spacing of 650 μs. As can be seen in Figure 14, reducing the echo train length leads to a reduction in geometric distortion artifacts. In functional MRI (fMRI), combining parallel imaging with multiecho acquisitions has not only reduced geometric distortions (55), but has also improved temporal resolution (56,57), and reduced ghosting artifacts due to T₂ decay (58). Parallel imaging has been used to increase sensitivity to blood oxygenation level-dependent (BOLD) effects (59), improve the accuracy of functional localization (60), and examine the oxygen supply and demand from cerebral vasculature (61). Accelerated diffusion-weighted EPI sequences have also been employed in the liver to image focal lesions (62,63).

Figure 14.

Left: The long echo train length of an unaccelerated EPI sequence used in diffusion-weighted imaging creates severe geometric distortions. Right: The use of parallel imaging allows for a shortened echo train length, thereby reducing geometric distortions and restoring the image to diagnostic quality.

Another advantage to using parallel imaging with multiecho sequences such as TSE is the potential to limit SAR and total energy deposition, especially at magnetic field strengths of 3T and higher. TSE pulse sequences require the rapid application of many high powered RF pulses, which can lead to a high SAR. When employing parallel imaging, fewer pulses are required, as fewer lines in k-space are collected. The parallel imaging acceleration can then be invested in either decreasing the total acquisition time or in increasing the spacing between the echo trains, which would leave the total acquisition time constant but lengthen the TR. If the acceleration is used to increase the TR of the TSE scan, the SAR of the sequence can be reduced, as fewer RF pulses are played out per unit time (64). If the TR is held constant and the total acquisition time reduced with parallel imaging, the SAR maintains constant, but the total amount of energy deposited is reduced. Parallel imaging for energy deposition reduction has been shown to be especially beneficial when performing cardiac imaging at 3T (65).

While lung imaging by MR poses challenges due to low proton density and short T₂ species, the ability to accelerate data acquisition with parallel imaging has made it possible to examine the anatomical structure and function of lung abnormalities. Parallel imaging techniques provide sufficient spatial and temporal resolution for dynamic imaging of chest wall movement, small pulmonary vessel angiography, and lung perfusion. Reduction in scan time allows for free-breathing scans or reduced breath-hold time. As in the fMRI applications discussed previously, the shortened echo train length of multiecho sequences that use parallel imaging reduces the blurring effects and SNR losses due to tissues with short T₂ and ${\mathrm{T}}_2^{\ast }$ values in the lungs (66). Clinically, the accelerated lung imaging protocols can be used to identify and quantify lesions originating from nodules (67), tumors (68), and embolisms (69).

In addition to these specific areas of application, parallel imaging has been utilized in a multitude of other imaging protocols. High-resolution parallel imaging has been used to identify atherosclerotic plaques in carotid arteries (70), perform tractography on the spinal cord (71), aid in the imaging of biomarkers such as choline and creatinine in gliomas (72), and study the structure (73) and spatial variation (74) of articular cartilage. Accelerated imaging with high temporal resolution has been applied to correct for metal artifacts (75), develop more accurate pharmacokinetic models for dynamic contrast-enhanced imaging (76), and perform fetal cine imaging (77). Reduction in scan time has allowed for volumetric imaging of various organs, from the breast imaging (78) to whole-body imaging of parasites (79).

FUTURE DIRECTIONS OF PARALLEL IMAGING IN THE CLINIC

While this article has focused on standard parallel imaging methods that are commonly used in the clinic, newer methods that use parallel imaging are slowly becoming available to the physician. When performing dynamic imaging, it is often possible to acquire several sets of undersampled k-space data where the missing lines are interleaved with respect to one another. These interleaved datasets can be combined to form a fully sampled k-space, which can be used for calibration. This method is known as TGRAPPA, and has been shown to be useful for cardiac imaging (80). A similar method, known as TSENSE (81), can be used to determine coil sensitivity maps in the same way, also eliminating the need for an additional calibration scan. Techniques that exploit temporal information as well as coil sensitivity information, including k-t SENSE (82) and k-t GRAPPA (83), have moved into the clinic on some platforms.

Additionally, the field of non-Cartesian parallel imaging is an emerging area with great potential clinical benefit. Non-Cartesian MRI involves collecting the MRI data not along straight lines (as shown in Figs. 1 and 2), but instead along trajectories such as radial, spiral, or PROPELLER (84). The special properties of these trajectories, such as continuous repeated sampling of the center of k-space (radial), efficient k-space coverage (spiral), and intrinsic motion correction (PROPELLER), makes them advantageous for specific applications. In order to accelerate non-Cartesian MRI acquisitions, regions of k-space are not sampled, as in Cartesian undersampling. Non-Cartesian parallel imaging seeks to reconstruct images from these undersampled non-Cartesian data. However, because these trajectories lead to more complicated aliasing patterns, SENSE and GRAPPA cannot be used.

Luckily, many methods have been proposed to reconstruct images from undersampled non-Cartesian data, including CG SENSE (85), radial GRAPPA (86,87), spiral GRAPPA (88,89), zig-zag GRAPPA (90), 1D non-Cartesian GRAPPA (91), pseudo-Cartesian GRAPPA (92), through-time non-Cartesian GRAPPA (93,94), PARS (95), APPEAR (96), and IRGN (97,98). While these methods are not currently used routinely in the clinic, there are a variety of applications that would benefit from their implementation. Real-time imaging is one such area, as it is advantageous to visualize nonperiodic motions such as swallowing, complex joint movement, or cardiac arrhythmias. Current approaches to real-time imaging utilize parallel imaging in conjunction with non-Cartesian trajectories, especially radial imaging (93,94,97,98), and acquisition strategies that exploit correlations both in k-space and through time (99–101). The addition of temporal information into parallel imaging and the use of non-Cartesian trajectories are expected to lead to massive speed improvements in clinical imaging, enabling the use of MRI for more complex applications such as real-time interventional imaging.

CONCLUSION

In this review several concepts related to parallel imaging have been discussed. These ideas can be summarized in the following take-home points:

• The FOV and spatial resolution of an MR image can be manipulated by changing the k-space sampling.

• The acquisition time can be shortened by under-sampling k-space in the phase-encoding (and partition-encoding) direction, which leads to spatial aliasing in the image domain.

• Parallel imaging relies on the use of an array of receiver coils to collect undersampled k-space data and on specialized algorithms to reconstruct full FOV images.

• SENSE uses knowledge of the coil sensitivity profile to perform the unfolding and reconstruction steps in the image domain.

• GRAPPA uses autocalibration signals and a convolution kernel (or neighborhood of points) in k-space to perform reconstruction of the missing lines in k-space.

• Artifacts such as residual spatial aliasing and noise enhancement can be mitigated by choosing an appropriate coil array and reconstruction algorithm and by optimizing the parallel imaging parameters (such as the acceleration factor, FOV, number of ACS lines, or GRAPPA kernel type).

• Parallel imaging is used clinically to improve acquisition time, spatial resolution, temporal resolution, image quality, or combinations of these four factors. These techniques have been well adopted with multiecho sequences and dynamic imaging protocols, and are frequently used clinically in applications throughout the body.