Investigating attention in complex visual search

Abstract

How we attend to and search for objects in the real world is influenced by a host of low-level and higher-level factors whose interactions are poorly understood. The vast majority of studies approach this issue by experimentally controlling one or two factors in isolation, often under conditions with limited ecological validity. We present a comprehensive regression framework, together with a matlab-implemented toolbox, which allows concurrent factors influencing saccade targeting to be more clearly distinguished. Based on the idea of gaze selection as a point process, the framework allows each putative factor to be modeled as a covariate in a generalized linear model, and its significance to be evaluated with model-based hypothesis testing. We apply this framework to visual search for faces as an example and demonstrate its power in detecting effects of eccentricity, inversion, task congruency, emotional expression, and serial fixation order on the targeting of gaze. Among other things, we find evidence for multiple goal-related and goal-independent processes that operate with distinct visuotopy and time course.

1 Introduction

Visual attention encompasses more-or-less automatic processes driven by sensory parameters, such as visual saliency (Itti and Koch, 2001), as well as processes informed by motivated volition, such as instructed search (Yarbus, 1967). On top of these, visual field location, the history of previous fixations to a given stimulus, and of the occurrence and arrangement of specific features (e.g., those influencing serial vs. parallel search) are bound to influence where gaze is directed. Although the study of attention is one of the oldest sub-disciplines of Psychology, when and how each of these putative factors exerts its effect remains unclear. Attention to faces has been a topic at the center of the controversy, with studies arguing both for (Theeuwes & Van der Stigchel, 2006) and against (Brown, Huey, & Findlay, 1997) efficient detection of faces from similar distractors. More recent work utilizing eye movement data has shown that saccades are preferentially targeted to faces over other non-face objects as early as 120 ms after onset of the stimulus (Cerf, Harel, Einhäuser, & Koch, 2008; Fletcher-Watson, Findlay, Leekam, & Benson, 2008; Kirchner & Thorpe, 2006). These studies, however, compare selection of faces over non-face objects, still leaving open the possibility that the responses are driven by lower-level image statistics associated with faces (Honey, Kirchner, & VanRullen, 2008; VanRullen, 2005) and leaving unanswered many other questions about the scope and specificity of peripheral face detection.

Small portions of the larger question, what information guides attention, have typically been addressed by experimentally manipulating factors in isolation. But even simple effects depend on their interactions with context (i.e., all of the other factors), leaving numerous questions unanswered when only one or two factors can be studied at a times. Eye-movement responses hold the promise of a sensitive and detailed index of attentional behavior through which one might hope to resolve the tangle of possible influences. But the very richness of eye-movement data makes their proper statistical treatment a non-trivial and highly context-dependent problem. For this reason, no comprehensive framework for the analysis of eye movement data has yet emerged, which allows a large number of simultaneous effects to be modeled and compared across a wide range of conditions.

An optimal descriptive model ought to have a number of properties: sufficient flexibility to handle a variety of measures, robustness to bias, relative ease of implementation and interpretation, methods for hypothesis testing which minimize type I and type II errors, and reliable techniques for testing goodness of fit. Second, model fitting should generate statistics that may be interpreted in light of formal computational models of attention. We show that an approach fulfilling each of these criteria can be developed from the theory of point processes, and describe its implementation in a software toolbox for Matlab. Point process models have a well established track record of application to neural spiking data (Dayan & Abbott, 2001; Truccolo, Eden, Fellows, Donoghue, & Brown, 2005), and spatial and spatiotemporal point process models have been among standard tools for modeling geophysical phenomena (Ogata, 1988) and ecological data (Stoyan & Penttinen, 2000). Their formal application to eye movement data has gained attention comparatively recently (Barthelmé, Trukenbrod, Engbert, & Wichmann, 2013; Kovach, 2008). Barthelmé et al. have reviewed the application of point process models to gaze selection, hilighting the flexibility of the approach, and giving a comprehensive overview of how point processes might be applied to fixation data. Our present aim is is narrower in scope, to demonstrate the implementation of a point process model as a generalized linear regression model (GLM) and to describe novel results from its application to visual search for faces.

A key goal of this work will be distinguishing the numerous simultaneously operating influences that may drive saccadic selection (Tatler, Hayhoe, Land, & Ballard, 2011). Models that readily account for concurrent influences allow for more efficient experimental design and may be crucial for avoiding flawed interpretation (Simpson, 1951) (see also Discussion section 4.1.1). Commonly used approaches to modeling the distribution of fixations require some form of binning or smoothing of fixation density within the space of some dependent measures of interest, such as scene plane coordinates. In many instances, however, summary measures based on binning and smoothing may prove critically biased, making it necessary to discard large quantities of data (as, for example, in the common practice of discarding all fixations but the first in a trial in order to control for bias related to the serial dependence of fixations).

At its heart, modeling gaze response overlaps with the problem of modeling discrete choice behavior. Of the statistical models routinely applied to the latter, those that handle categorical outcomes, such as the conditional logit, have proven most useful (McFadden, 1973). Such models have more recently been adapted to the analysis of visual fixations (Barr, 2008; Kovach, 2008). However, in the context of the gaze response, the requirement of a categorical dependent measure may impose certain limitations. The space of visual fixations is not inherently discrete, nor is there any reason to assume that stimulus properties influencing gaze should be bundled into discrete units. While binning is straightforward enough, the choice of bin location and dimension and the assignment of stimulus properties to bins may create implicit assumptions. The present application therefore generalizes the conditional logit to continuous decision spaces by way of a spatiotemporal point-process model. By doing so, it overcomes a number of limitation of discrete models, including the need to define a priori regions of interest in visual space.

The relationship to the conditional logit also links this approach to a broad family of formal decision models (Luce, 1959; Shepard, 1964), which encompass, among other things, a promising computational model of visual attention (Bundesen, 1990; 1998). These models share a common form that relates the probability of a given response to the proportional strength of a signal driving the response. The theoretical attraction of such models comes from the way in which they allow processes that compute signal strength for each option to operate independently from each other as well as from the process charged with selecting the outcome, leading to the property of independence of irrelevant alternatives (IIA)(Luce, 1959). It is not hard to envision how such a model might be implemented in the brain by way of functionally specialized populations that compute a decision signal for stimuli within their receptive fields (Bundesen, Habekost, & Kyllingsbaek, 2005). Normalization of local responses with respect to the summed population activity is another ubiquitous property of neural responses in the cortex (Carandini & Heeger, 2012), pointing to the importance of proportional response coding. These considerations offer some reason to hope that conditional logit models, beyond providing a useful descriptive framework, may at least loosely approximate dynamics of underlying mechanisms and so yield measures with physiological relevance. Although violations of IIA are well known and the conditional logit takes IIA as a starting assumption, in principle, the regression framework may also allow many types of deviations from IIA to be evaluated by way of appropriately constructed interactions terms.

As a test case, we applied the conditional logit model to an investigation of the factors that guide attention to faces during visual search. We found that saccades may select target faces from among inverted distractors, showing that attentional shifts can be guided by the configural information that distinguishes face orientation. On top of the target selection effect, we observed a weaker intrinsic bias towards upright faces, which evolved with a time-course and visual field distribution distinct from the task-related effect. The influence of memory manifested as strong inhibition of return to previously visited distractors, with variable inhibition and facilitation to previously visited targets. These results address a number of open questions and emphasize the dependence of effects on time, visual field location and the history of prior fixations, whose separate influences can be distinguished with the current method. Beyond showcasing the promise of this framework, we also provide a matlab toolbox for its implementation and for visualization of the results.

2 Materials and Methods

2.1 Statistical framework and analysis

Fixations are treated as discrete events in space and time, whose occurrence is governed by a spatiotemporal point process with an intensity function, λ, that gives the rate and density of events. The most basic point process models assume that events are mutually independent; by the Poisson formula, the probability P_A of observing n independent events within a region of the sampling space, A, is

$$P_A(n)=\frac{{\Lambda }^n}{n!}{e}^{-\Lambda }\text{where}\Lambda ={\int }_A\lambda (x)dA\text{and}\lambda (x)\ge 0$$ (1)

Further elaborations of the point process framework address various forms of dependence among the events, generally by making the dependence between events explicit in the model. In the case of serial dependence in time, this extension is straightforward, as past events can be assumed to affect future events but not vice versa. Thus one may specify an intensity function, λ, conditioned on the history of events up to the point of observation (Daley & Vere-Jones, 2005)

$${\lambda }^{*}(t,x)=\lambda (t,x|x_1\dots x_n,t_1\dots t_n)$$ (2)

Adding a vector of model parameters, θ, the log likelihood function for model M is given by

$${\ell }_M(\theta )=\sum _{i=1}^N\text{log}{\lambda }_M^{*}(x_i,t_i|\mathbf{\theta })-{\int }_A{\lambda }_M^{*}(x,t|\mathbf{\theta })dA$$ (3)

where N is the number of observations in{x_i,t_i} and A is the extent of the spatiotemporal sampling space. For linear and log linear models, the log likelihood function is well behaved, exhibiting at most a single unique maximum, which can be found using algorithms for numerical maximization (Ogata, 1978). Here we consider log linear models, of the form:

$$\text{log}(\lambda (t,x))=\sum _k{\theta }_k{\varphi }_k(x,t)$$ (4)

where {ϕ_k} is a set of known regressors, yielding a generalized linear model, with canonical parameters θ.

In order to make model estimation more computationally tractable, various approaches can be taken to simplify the form of the intensity function λ. Under the assumption that the rate of events is independent of their spatial distribution, spatial effects can be treated separately from rate, while still allowing the dependence of spatial distribution on time. In the present case, for the sake of simplicity, we will consider the serial temporal order of fixations and their spatial distribution, but not their precise arrangement in absolute time.

The model may be further simplified under a discrete piecewise constant approximation for λ, yielding a conditional logit, according to which the probability of fixating region j is given by

$$P_j=\frac{e^{{\sum }_k{\theta }_k{\varphi }_{jk}+{\mu }_j}}{{\sum }_i{e}^{{\sum }_k{\theta }_k{\varphi }_{ik}+{\mu }_i}}$$ (5)

Concretely, parameter estimate θ̂_k represents the influence of regressor ϕ_k on the log odds ratio of fixating a target with respect to some baseline. ϕ_k may represent main effects or interactions among any of a large number of regressors representing nominal, ordinal or continuous measures (Agresti, 2014). The term µ_j is equal to log area of bin j and is needed to correct for variations of bin area when bins are not uniform in area. A more detailed derivation is provided in the Supplementary Material.

Conditional logit models have long been applied to various kinds of decision behavior involving discrete choice sets (Luce, 1959; McFadden, 1978) and are related to logistic regression, which addresses the case of dichotomous outcomes. In their application to gaze patterns they typically require coarse binning of visual space in order to avoid model overparameterization (Barr, 2008), which in turn requires some a priori assumptions about where gaze is likely to be distributed . We overcome this limitation in the present application and extend the conditional logit model to serial choices over a continuous decision space using continuous spatial basis functions.

2.1.1 Binning

While spatial basis functions allow the underlying distribution to be continuous, bins are still necessary to cast the data into the space of discrete outcomes handled by the conditional logit, with the density of spatial sampling limited by computational cost. In this context, equation 5 becomes a piecewise-uniform approximation to a continuous exponential-family distribution over the space encoded by the regressors. The summation over bins in the denominator of equation 5 is then equivalent to numerical integration with the rectangle rule. A more formal discussion of this relationship is given in the Supplementary Material.

A question worth considering in this context is how to optimally construct bins to minimize approximation error. Smaller and more compact bins might naturally be expected to result in a better approximation, however for a given number of bins, optimal bin size will not be uniform, in general, but vary according to distribution. A closely related problem is that of signal block quantization (Lloyd, 1982), which addresses how to optimally select thresholds when digitizing a continuous multivariate signal. For a two dimensional signal, such as gaze coordinates recorded by an eye tracker, squared error is minimized when bin size varies according to the square root of the probability density of the signal (Gersho, 1979). In the context of linear model estimation, optimal binning also depends on properties of the regressors and the expected Fisher information (see Supplementary Material). As average expected fixation density will typically be unknown at the outset, optimization must proceed iteratively (Du, Faber, & Gunzburger, 1999). The usefulness of any such approach depends on whether the added computational complexity improves on simpler alternatives, such as uniformly increasing bin density at the outset. Although we hope to address optimal binning in future work, for the present application we do not attempt any formal optimization of this sort, rather we use these results to inform general rules of thumb for constructing bins. In particular, they provide the rationale for placing bins more densely around salient targets.

A simple method to construct suitably compact bins involves selecting a set of points spaced according to the anticipated or observed fixation density and applying a Delaunay tessellation or Voronoi diagram to construct bins (Du et al., 1999). The Delaunay tessellation assigns 3 points as the vertices of a triangular bin if their circumcircle does not enclose any other point, and the Voronoi diagram creates polygonal bins containing the area that is closer to the associated point than any to other. Whereas the Voronoi diagram provides better control of the placement of bin centers and creates optimally compact bins, the Delaunay tessellation allows for somewhat greater control of bin edges, and the triangular bins it generates may be simpler to handle during analysis than the irregular polygons returned by the Voronoi diagram. Both algorithms are routinely implemented in software packages for scientific computing, and the application of Voronoi diagrams in optimal binning has been extensively studied (Du et al., 1999).

2.1.2 Hypothesis testing and model comparison

Conditional logit models come with the family of likelihood-based inferential procedures that apply broadly to generalized linear models. For nested models, the log likelihood ratio test derives from the asymptotic convergence of the log ratio of the maximum likelihoods to a chi-squared distribution (Agresti, 2014). A somewhat less reliable but often more easily computed statistic, the Wald statistic, may also be used for hypothesis testing and confidence intervals (Pawitan, 2000). The latter is based on the asymptotic normal distribution of the likelihood function with variance-covariance matrix given by the inverse Fisher information at θ̂. When the likelihood function deviates from the normal distribution, as when sample sizes are small, the Wald tests tend to elevate type II errors (Pawitan, 2000).

Alternatives to classical null-hypothesis testing include model comparison techniques that estimate the posterior probability of alternate models under different kinds of prior assumptions. Two commonly used criteria are the Bayes-Schwartz information criterion (BIC) (Schwarz, 1978) and Akaike information criterion (AIC) (Akaike, 1974). The difference of BIC between two models approximates the posterior log Bayes factor comparing them, while AIC asymptotically approaches decision criterion obtained with cross-validation (Stone, 1977).

2.1.3 Hierarchical modeling

Such inferential tests depend critically on the assumption of conditional independence, and data are often clustered in ways that may give rise to obvious violations of this assumption. For example, inference at the group level requires accounting for subject-related random effects. The most general form of the problem is addressed through hierarchical modeling (Barr, Levy, Scheepers, & Tily, 2013). Model fitting for hierarchical models is computationally more intensive than for simple fixed-effects models, and may quickly become intractable for highly parameterized nongaussian GLMs (Barr, 2008). Recent advances in statistical modeling of latent Gaussian models, show considerable promise in the efficient handling of random effects for hierarchical point-process models (Rue, Martino, & Chopin, 2009), which may prove valuable for modeling fixation data (Barthelmé et al., 2013).

In the present case, we turn to a computationally and conceptually simpler approximation, the summary statistic procedure (Penny, Holmes, & Friston, 2003), which applies univariate or multivariate statistics at the second level to parameter estimates for clusters obtained at the first. While this procedure assumes equal variance of the first level of estimates across clusters, it is generally robust to deviations from this assumption even at modest sample sizes (Penny et al., 2003). In the present case, summary statistics were computed for univariate contrasts, which represent spatially localized effects at points in the visual field, as fitted by basis functions. In order to account for the resulting large number of multiple comparisons, we applied the false discovery rate (FDR) (Benjamini & Hochberg, 1995) correction to p-values at each point, which avoids overly penalizing multiple comparisons among correlated tests.

2.1.4 Non-parametric model fitting

Likelihood-based decision criteria can be used with non-parametric model fitting as well (Karabatsos, 2006). When {ϕ_k} represents a basis set chosen in a manner that asymptotically spans the set of all functions meeting basic criteria of differentiability, then model fitting is non-parametric, asymptotically approaching the unknown true model. In the present analysis, non-parametric modeling of spatial effects was carried out by choosing the lowest order of polynomial and sinusoidal basis functions that minimized AIC across subjects.

2.1.5 Application of the point-process framework to visual search

In the present case, we sought to model the influences of task relevance, stimulus orientation, distance from the fovea, and memory for previously fixated locations on the probability of generating a fixation to a given location. These effects were modeled as linear terms in a conditional logit regression over a discretized sampling of the visual field. Interactions between inversion and facial expression were also included in the model. The model was fit separately for each of 26 subjects, and group-level statistical tests were carried out on parameter estimates across subjects. The visuotopic spatial dependence of these effects was estimated with polynomial basis functions that included a semi-parametric spatial function, modeled with additive radial and angular components. The radial component, modeling eccentricity from the fovea, was fit with a 3^rd order polynomial, and the angular component, representing clock-face angle relative to the fovea, was fit with a first order sinusoid (that is, the simple sine and cosine over angle). Interactions among radial and angular components were included as well, allowing differences across hemifields to be distinguished. The respective polynomial and sinusoid orders were selected based on lowest observed AIC, combined across subjects, for different orders.

2.1.6 GazeReader

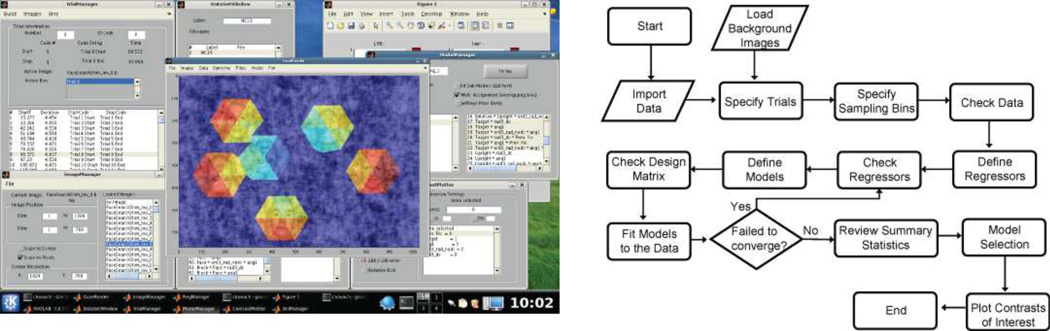
All GLM analysis of the current data were carried out using a software toolbox (the GazeReader toolbox developed by the first author under Matlab (Mathworks, Nattick, MA), which may be downloaded at http://www.nitrc.org/projects/gazereader/. Data loading, model specification, fitting and review are organized into a sequence of events, each of which is handled by a separate module in the toolbox. Figure 1 illustrates the steps as they are implemented in the toolbox and gives an example of the graphical interface developed in Matlab (Kovach, 2008).

Figure 1.

Overview of the GazeReader toolbox, with a schematic diagram of processing steps implemented in the toolbox (right panel) and an illustration of the user interface (left panel).

2.2 Procedure

2.2.1 Subjects

Subjects for experiment 1 were recruited from the University of Iowa Hospitals and Clinics community and participated following voluntary informed consent in accordance with requirements of the University of Iowa biomedical internal review board and the Code of Ethics of the World Medical Association (Declaration of Helsinki). 24 healthy subjects (12 female, 2 left handed and 5 unknown handedness) participated with median age of 27 and range 20 to 58. Median education was 16 years with a range of 12 to 19. Data for three subjects were excluded due to technical failures or poor signal quality. This left a total of 21 subjects in Experiment 1.

For experiment 2, 5 subjects (3 female, 1 left handed) were recruited from the University of Iowa student community, 4 of whom received course credit for participating. Median age was 18. One of the participants was an author (CK) of the present study.

2.2.2 Task

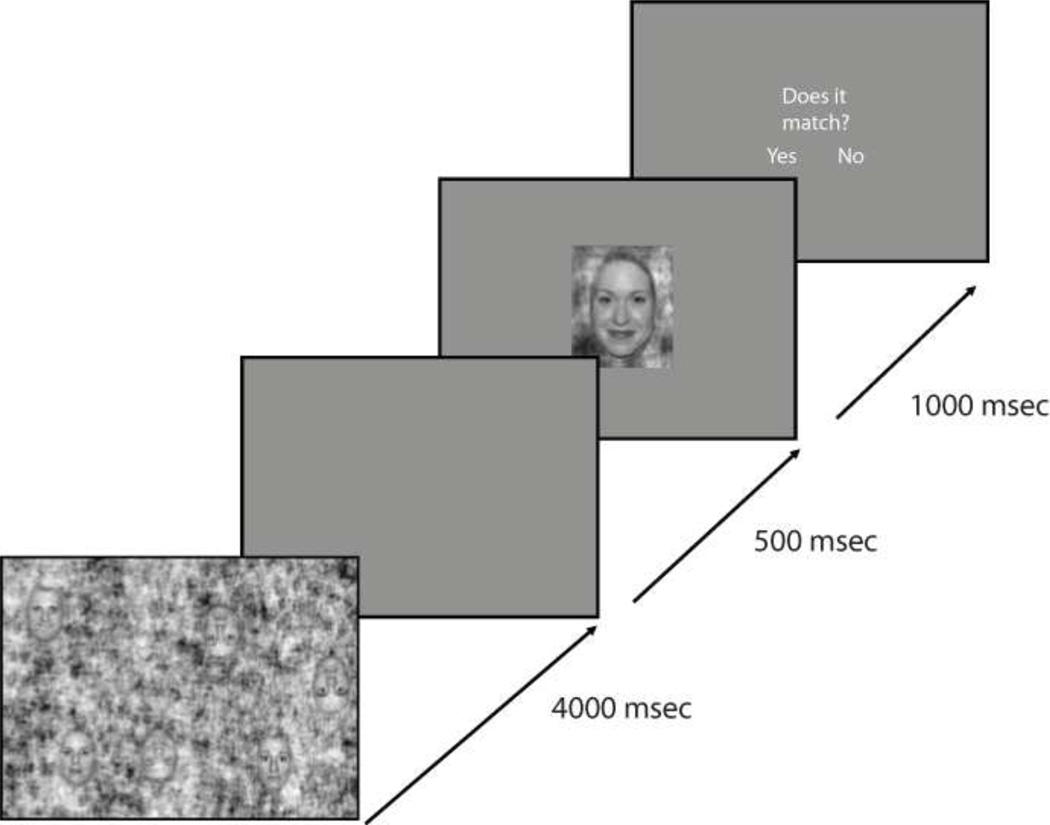
In experiment 1, 24 subjects participated in two versions of a task requiring visual search for upright and inverted faces (Figure 2). Each trial began with a fixation cross for 500 ms followed by a field containing 6 pseudo-randomly arranged faces, 3 upright and 3 inverted, presented against a background equated in spectral content and histogram with the faces (Fig. 2). The search field remained visible for 4 seconds and was followed by a probe face after a 500 ms delay. The probe remained visible for 1000 ms, after which a prompt appeared. Following the prompt, subjects identified with a yes or no button response whether the probe face had been among those in the search field. Trials were divided between two blocks. In block 1 all probe faces were upright, and in block 2 probe faces were inverted. Before each block subjects were informed of the orientation of probe faces for that block, thus faces of the same orientation as the probe were target stimuli while faces of the other orientation served as distractors. Each block contained 72 trials, and block order was counterbalanced across subjects.

Figure 2.

Structure of the task. Probe faces were either upright or inverted depending on experimental block.

The task for the 5 participants in experiment 2 was the same as for experiment 1 excepting one modification: because the use of pseudo-random stimuli in experiment 1 may raise the concern that comparisons pooled across subjects will amplify random differences between the stimulus sets, face positions were re-randomized online before each trial.

2.2.3 Stimuli

Stimuli were constructed by converting face images to gray-scale, normalizing the mean spectral power of each image to the average spectral power, followed by matching the histogram distribution of pixel values to the average histogram. Faces were randomly arrayed on a background composed of phase randomized noise matched in spectral power and pixel distribution (Figure 2). This design served to increase the difficulty of visual search and decrease the influence of elementary scene statistics on saccade targets. Each search field contained 3 upright and 3 inverted faces. Within each orientation, faces were of three different identities expressing each of 3 basic emotions: fear, neutral and happy. All faces were modified from the MacBrain Face Stimulus Set developed by Nim Tottenham and supported by the John D. and Catherine T. MacArthur Foundation Research Network on Early Experience and Brain Development, downloaded from http://www.macbrain.org/resources.htm/. The search array stimuli sets were generated using Matlab (Nattick, MA).

For experiment 1 stimuli were displayed using Presentation® software (Version 0.70, www.neurobs.com). Two sets of pseudo-random stimuli were used and participants were tested using a randomly chosen set, with the order of search arrays randomized for each subject. Stimuli were presented on a 21 inch CRT monitor at 40 inches distance. Faces subtended approximately 3.0 degrees of visual arc, while the scene plane covered 18 by 23 degrees. Faces were spaced with a minimum center-to-center distance of 4 deg.

Stimuli for experiment 2 were presented using the Matlab psychophysics toolbox on a 17 inch CRT monitor at 27 inches distance. Faces subtended approximately 3.5 degrees of visual arc, while the scene plane covered 21 by 28 degrees. Faces were spaced with a minimum center-to-center distance of 4.5 deg.

2.2.4 Eye tracking

For the group of 24 subjects in experiment 1, eye movements were recorded with a video based Purkinje eye tracking system (Applied Science Laboratories, Bedford, MA) with 60 Hz sampling rate and 1–2 degrees of resolution. Fixation extraction was carried out offline using dispersion criteria and visually checked against the raw trace of gaze position to ensure that fixations were accurately identified. The onset of a fixation was marked when the standard deviation of any sequence of 6 data points fell within 0.5 deg, and termination was marked when at least three sequential samples fell beyond 1 deg from the average following fixation onset. Fixation position was computed as the average coordinate of points between onset and termination, excluding outliers falling more than 1.5 deg. from the initial fixation position.

For the group of 5 subjects in experiment 2, data were recorded with an Eyelink 1000 system (SR Research, Ottawa, Ontario), using a chin rest for head stabilization to reduce measurement error and data dropout. Data were sampled at 1000 Hz and typical resolution was .5 deg or better. Fixation extraction was carried out by Eyelink vendor software, which applied velocity, acceleration and distance thresholds to determine saccade onsets. Onsets were marked when eye rotation velocity exceeded 30 deg/s or when acceleration exceeded 8000 deg/s², and position deviated at least 0.15 deg. from the previous point of fixation. Fixation onsets were marked at saccade termination. The use of different equipment from experiment 1 in this case was motivated by the wish to verify that results are robust to details of sampling, signal quality and fixation criteria, in addition to stimulus randomization.

2.3 Model construction

2.3.1 Sampling

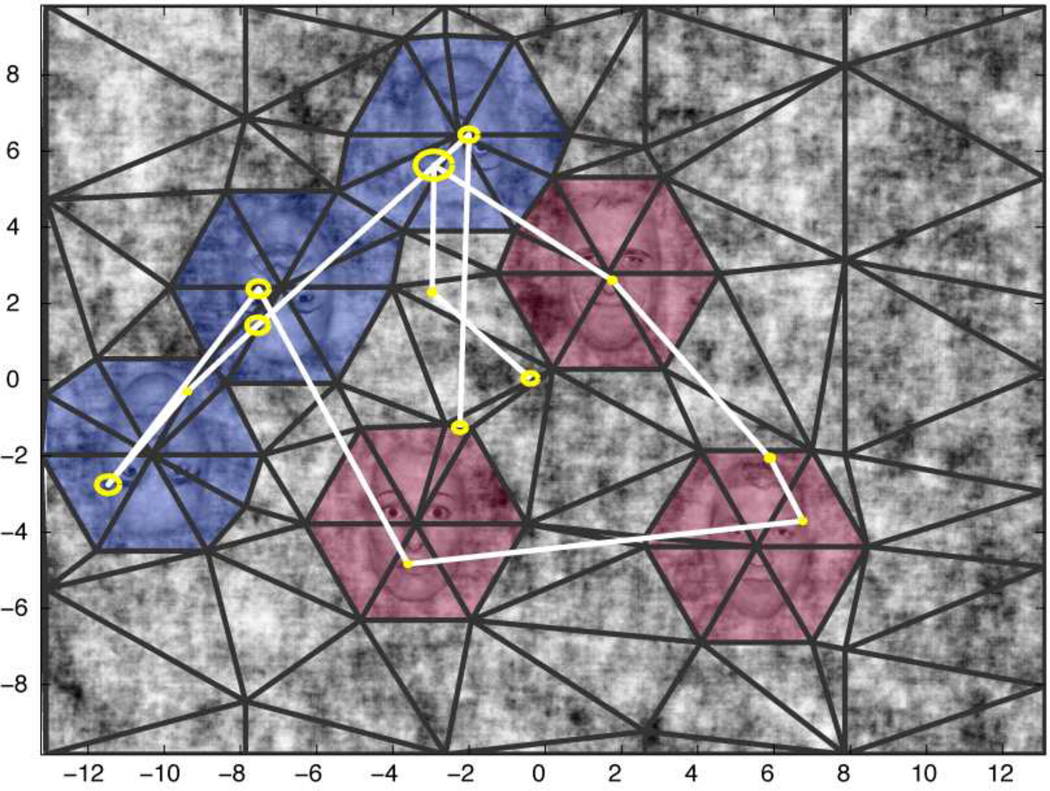
For each trial, the scene plane was sampled according to an irregular tessellation, constructed in the following manner. An array of hexagonally spaced vertices was placed on the scene plane with inter-vertex distance of approximately 5.4 degrees of visual arc. Additional vertices were added around each face, one at the center of the face and six at the vertices of a hexagon with edges of approximately 2.2 degrees. Triangular sampling bins were generated by applying a Delaunay tessellation to vertices, using the DELAUNAY function in Matlab. Optimal binning requires the density of bins to vary with the square root of the density of fixations (see Supplementary Material); although we did not attempt formal optimization, the present binning procedure was devised to bin more densely around faces, where we anticipated the greatest density of fixations, which was subsequently verified in the model (see section 3.2.2). The Delaunay tessellation connects vertices such that the circumcircle enclosing each simplex contains no other vertex, thus dividing the scene into compact triangular bins. All resulting bins whose centers fell within the hexagon of points surrounding each face were associated with the face. In most cases, the bins associated with each face corresponded to the original six simplexes within the hexagonal array of points added to the face in the previous step. Bins that were not associated with any face following this procedure were regarded as belonging to the background. An example of the resultant binning is shown in Figure 3.

Figure 3.

Example of the binning and scanpath for a single trial. Fixations over the course of the trial are binned within outlined simplexes. A sample scanpath is shown by the white line with relative fixation duration indicated by yellow circles. Colors indicate the value of the regressor, Target, for each bin: .5 is red, −.5 is blue, and 0 is unshaded. Numbers show screen coordinates in degrees of visual arc.

2.3.2 Spatial Basis Function

GLM covariates modeled effects of interest as a function of visual field location using spatial basis functions. Basis functions were chosen to be polynomials of eccentricity and sinusoids of azimuth:

$$\varphi (r,\alpha )=\left[1r{r}^2{r}^3\right]\otimes \left[1\text{sin}\alpha \text{cos}\alpha \right]$$ (6)

where r is the eccentricity of the sampling bin from the current point of fixation, α is the azimuthal angle in the scene plane, increasing clockwise from vertical upward meridian, and the symbol ⊗ denotes the Kronecker tensor product, whose output is a 12 dimensional vector in which each element is a product of two elements of the operands. The order of basis functions was chosen by adjusting the polynomial and sinusoidal order and refitting the model until minimum AIC was found; the chosen values gave minimum AIC in a majority of subjects.

2.3.3 Modeling effects of stimulus type

The properties of the face associated with each bin, such as orientation and task relevance, were modeled in their interactions with the spatial basis function, thus treating them as a function of visual field location. Properties associated with faces were represented by indicator variables, which were centered across all faces by subtracting the mean value for all face bins. For example the regressor target assumed a value of .5 for bins associated with task-relevant (target) faces and −.5 for bins associated with irrelevant distractor faces. Bins associated with the background were given a value of zero for all of the face properties; therefore fixations that fell within background bins did not contribute to the estimation of effects nested in the face bins. The regressor face indicated bins associated with faces, and had a value of 1 for face bins and 0 for background bins. The following additional indicator variables were specified for each face: orientation, facial expression, block and previous fixations. Each of these indicator regressors was incorporated into the model through the interaction with the spatial basis set, where s_i is the vector of indicator variables for the i^th object:

$${\varphi }_s(r_i,{\alpha }_i)={\mathbf{s}}_i\otimes \varphi (r_i,{\alpha }_i)$$ (7)

Interactions among the indicator variables, such as the interaction of previous fixation with task relevance or facial expression with orientation were likewise incorporated by computing the three-way interaction between the two indicator variables and the spatial basis set. Table 1 provides a list of all of the terms in the model and the number of parameters accounted to each.

Table 1.

List of regressors in the individually fitted models, with number of associated terms.

	Regressor Label	# Par	Description	Group
1	Rad3_nodc	3	Eccentricity polynomial (no DC term)	Visual Field Main Effect
2	Ang1	2	Azimuth sinusoid
3	Rad3 * ang1	6	Eccentricity × Azimuth
4	Prev. Fix. * rad3_dc	4	Eccentricity × Previous Fixation
5	Prev. Fix. * ang1	2	Azimuth × Previous Fixation
6	Prev. Fix. * rad3_nodc * ang1	6	Eccentricity × Azimuth × Previous Fixation
7	Target * rad3_dc	4	Target × Eccentricity	Target × Visual Field interaction
8	Target * ang1	2	Target × Azimuth
9	Target * rad3_nodc * ang1	6	Target × Eccentricity × Azimuth
10	Target * rad3_dc * Prev. Fix.	4	Target × Eccentricity × Previous Fixation
11	Target * ang1 * Prev. Fix.	2	Target × Azimuth × Previous Fixation
12	Target * rad3_nodc * ang1 * Prev. Fix.	6	Target × Eccentricity × Azimuth × Previous Fixation
13	Upright * rad3_dc	4	Orientaion × Eccentricity	Orientation × Visual Field interaction
14	Upright * ang1	2	Orientaion × Azimuth
15	Upright * rad3_nodc * ang1	6	Orientaion × Eccentricity × Azimuth
16	Upright * rad3_dc * Prev. Fix.	4	Orientaion × Eccentricity × Previous Fixation
17	Upright * ang1 * Prev. Fix.	2	Orientaion × Azimuth × Previous Fixation
18	Upright * rad3_nodc * ang1 * Prev. Fix.	6	Orientaion × Eccentricity × Azimuth × Previous Fixation
19	Face * rad3_dc	4	Face × Eccentricity	Face × Visual Field interaction
20	Face * ang1	2	Face × Azimuth
21	Face * rad3_nodc * ang1	6	Face × Eccentricity × Azimuth
22	Block * Face * rad3_dc	4	Block × Eccentricity	Block × Face × Visual Field interaction
23	Block * Face * ang1	2	Block × Azimuth
24	Block * Face * rad3_nodc * angl	6	Block × Eccentricity × Azimuth
25	Block * Face * rad3_dc * Prev. Fix.	4	Block × Eccentricity × Previous Fixatio
26	Block * Face * ang1 * Prev. Fix.	2	Block × Azimuth × Previous Fixation
27	Block * Face * rad3_nodc * angl * Prev. Fix.	6	Block × Eccentricity × Azimuth × Previous Fixation
28	Emotion * rad3_dc	8	Emotion × Eccentricity	Emotion × Visual Field interaction
29	Emotion * ang1	4	Emotion × Azimuth
30	Emotion * rad3_nodc * ang1	12	Emotion × Eccentricity × Azimuth
31	Emotion * rad3_dc * Prev. Fix.	8	Emotion × Eccentricity × Previous Fixation
32	Emotion * ang1 * Prev. Fix.	4	Emotion × Azimuth × Previous Fixation
33	Emotion * rad3_nodc * ang1 * Prev. Fix.	12	Emotion × Eccentricity × Azimuth × Previous Fixation
34	Emotion * Upright * rad3_dc	8	Emotion × Orientation × Eccentricity	Emotion × Orientation × Visual Field × Previous Fixation interaction
35	Emotion * Upright * ang1	4	Emotion × Orientation × Azimuth
36	Emotion * Upright * rad3_nodc * ang1	12	Emotion × Orientation × Eccentricity × Azimuth
37	dist to −2 fix	2	Distance to the penultimate fixation
38	dist to −3 fix	2	Distance to the antepenultimate fixation
39	Face Grid Poly.	2	Distribution within face
	Total	185

2.3.4 Revealing spatial effects

From fitted model parameters, spatial dependence of effects may be shown by applying the value of spatial basis functions at given locations as contrasts on the parameter estimates, and error estimates can similarly be obtained by applying the contrast to the inverse Fisher information matrix. To examine dependence on visual field location in greater detail, we plot effects in polar coordinates as a function of eccentricity and azimuth with respect to the point of fixation. Terms that represent interactions with eccentricity show effects averaged over all azimuthal angles, a consequence of the fact that the sinusoidal basis functions integrate to zero over azimuths. While this analysis may show dependence on visual field, to support the claim that any apparent differences are statistically significant it is necessary to also compute a direct contrast. We address visual field differences with two contrasts: the Left-Right (LR) -contrast gives the difference of log odds ratios between points equidistant from the vertical meridian, which represents the contribution of the antisymmetric azimuthal interactions (in this case with sin(α)):

$${\eta }_T(r,\alpha )-{\eta }_T(r,-\alpha )=2[{\theta }_{10}+\sum _j{\theta }_{1j}{\varphi }_j(r)]\text{sin}(\alpha )$$ (8)

The π-contrast gives the difference between points equidistant along the line intersecting the origin, offset from each other by π radians. It therefore represents the combination of symmetric and antisymmetric azimuthal interactions:

$${\eta }_T(r,\alpha )-{\eta }_T(r,\alpha +\pi )=2[{\theta }_{10}+\sum _j{\theta }_{1j}{\varphi }_j(r)]\text{sin}(\alpha )+2[{\theta }_{10}+\sum _j{\theta }_{2j}{\varphi }_j(r)]\text{cos}(\alpha )$$ (9)

3 Results

3.1 Individual fits

For individual subjects, Table 2 shows the result of omnibus likelihood ratio tests and pseudo-R² statistics for each main group of regressors. Statistical thresholds were adjusted for multiple comparisons across subjects using FDR. In every individual, the full model is heavily favored over the null model, which assumes uniform selection probability across all bins. The following effects were significant at false discovery rate (FDR Q <0.01) in all subjects: the main effect of visual field location, the effect of distance from the previous point of fixation, and the effect of the presence of a face. The effect of task relevance reached significance in 23 participants, and the effect of inversion, separate from the task-relevance effect was also significant (Q < .05) in 9 subjects, while the effect of experimental block was significant in 18 subjects. The effect of previous fixation on the likelihood of fixation was likewise significant (Q < .01) in all subjects, and the interaction of previous fixation and other modeled effects is significant in 24 of 26 subjects. The effects of facial expression and interactions between facial expression and orientation or task relevance approached significance in 2 subjects.

Table 2.

Significance tests and pseudo-R² for major regressor groups for all subjects.

Subject	Full model (185)	Vis. field main (23)	Target (24)	Upright (24)	Block (24)	Face (12)	Emotion (48)	Emotion intxn (24)	Prev. fix main (12)	Prev. fix intxn (60)
1	*** 0.21	*** 0.035	*** 0.0039	*** 0.0037	*** 0.019	*** 0.038	0.0013	0.0011	*** 0.0046	*** 0.0093
2	*** 0 27	*** 0.052	*** 0.0023	0.0010	*** 0.0022	*** 0.11	0.0015	0.0016	*** 0.024	*** 0.0098
3	*** 0 23	*** 0.063	*** 0.0024	0.0009	*** 0.0021	*** 0.019	0.0012	0.0013	*** 0.0034	0.0043
4	*** 0 34	*** 0.053	* 0.0014	0.0008	0.0014	*** 0.11	0.0015	0.0014	*** 0.016	*** 0.0095
7	*** 0.22	*** 0.049	*** 0.0059	0.0002	*** 0.0019	*** 0.035	* 0.0020	0.0010	*** 0.0053	* 0.0045
8	*** 0.25	*** 0.055	*** 0.0043	0.0007	0.0017	*** 0.076	0.0020	0.0021	*** 0.016	* 0.0076
9	*** 0 27	*** 0.057	*** 0.0021	0.0008	0.0009	*** 0.079	0.0012	0.0015	*** 0.017	*** 0.0059
11	*** 0 29	*** 074	*** 0.0038	0.0009	0.0009	*** 0.12	0.0011	0.0017	*** 0.037	*** 0.0073
12	*** 30	*** 0.046	*** 0.0053	* 0.0015	0.0009	*** 0.11	0.0011	0.0011	*** 0.025	*** 0.0089
13	*** 0.26	*** 0.034	*** 0.0070	0.0008	*** 0.0024	*** 0.053	0.0015	0.0010	*** 0.013	*** 0.0069
14	*** 0.31	*** 0.049	*** 0.0033	* 0.0018	0.0008	*** 0.11	0.0012	0.0008	*** 0.024	*** 0.0095
15	*** 0 24	*** 0.061	*** 0.0029	0.0006	** 0.0015	*** 0.045	0.0008	0.0016	*** 0.0086	** 0.0052
16	*** 0.30	*** 0.057	*** 0.0048	0.0004	*** 0.0042	*** 0.056	0.0014	0.0011	*** 0.024	*** 0.0089
17	*** 0 24	*** 0.050	*** 0.0039	0.0007	*** 0.0030	*** 0.027	0.0013	0.0012	*** 0.0090	** 0.0062
18	*** 0 27	*** 0.054	*** 0.0052	0.0007	*** 0.0030	*** 0.097	0.0013	0.0015	*** 0.022	*** 0.0086
19	*** 0 23	*** 0.075	0.0010	* 0.0014	* 0.0014	*** 0.018	0.0013	0.0022	*** 0.0044	0.0047
20	*** 0.26	*** 0.043	*** 0.0030	0.0007	*** 0.012	*** 0.018	0.0015	0.0019	*** 0.010	*** 0.011
21	*** 0.26	*** 0.058	*** 0.0037	0.0007	0.0005	*** 0.095	0.0006	0.0021	*** 0.023	*** 0.0083
22	*** 0.26	*** 0.054	0.0011	* 0.0016	0.0014	*** 0.089	* 0.0028	0.0018	*** 0.018	*** 0.0092
23	*** 0 24	*** 0.037	*** 0.0051	0.0011	** 0.0023	*** 0.095	0.0023	0.0019	*** 0.014	*** 0.011
24	*** 0 32	*** 0.065	*** 0.0043	0.0010	0.0011	*** 0.097	0.0015	0.0012	*** 0.030	*** 0.0063
25	*** 0.35	*** 0.028	0.0007	0.0004	0.0005	*** 0.13	0.0012	0.0009	*** 0.014	*** 0.011
26	*** 0 43	*** 0.022	*** 0.0027	* 0.0012	0.0009	*** 0.087	0.0012	0.0012	*** .010	*** 0.012
27	*** 0.38	*** 0.012	*** 0.0019	0.0008	0.0006	*** 0.11	0.0009	0.0013	*** 0.0053	*** 0.0075
28	*** 0 41	*** 0.028	** 0.0013	0.0004	* 0.0009	*** 0.093	0.0014	0.0009	*** 0.0091	*** 0.0050
29	*** 0 37	*** 0.028	*** 0.0017	0.0007	* 0.0012	*** 0.13	0.0011	0.0019	*** 0.017	*** 0.010

For each regressor group and subject, the left column indicates FDR corrected significance level: q < .001 (***), q < .01 (**), q< .05 (*), q > .05 (empty). The right column shows pseudo-R² values. Data for 5, 6 were excluded. Subject 10 was retested as subject 24. Results for s. 1 to 24 (above dashed line) are for experiment 1 and for s. 25 to 29 are for experiment 2. Models are identical in both experiments.

3.1.1 Comparison of Experiment 1 and Experiment 2

The purpose of Experiment 2 was to verify that the results in Experiment 1 were robust to the use of pseudo-randomized stimuli and to differences in sampling rate, signal quality and processing stream between eye tracking systems. The pattern of results were broadly consistent between the two experiments (Table 2). In keeping with higher sampling rate and superior average spatial resolution of the Eyelink system relative to the ASL, model fits on average were better in data collected with the Eyelink systems. Measured as pseudo-R², the average goodness of fit for the full model was .232 for Experiment 1 and .355 for Experiment 2 (Wilcoxon rank-sum P<.001). The separate contributions of regressor groups, visual field main effect and face × visual field interaction differed significantly (Wilcoxon rank-sum P < .01), in both cases with better average fit for data from Experiment 2. A corresponding group-level difference is visible in Figure 4B, which shows at eccentricities below 10 deg, the log odds ratio for fixations to faces over background regions is consistently greater for subjects in experiment 2. None of the other terms in the model differed between experiments with respect to both goodness of fit measures and group level effects. Therefore, for the group-level analyses to follow, we present data pooled over Experiments 1 and 2.

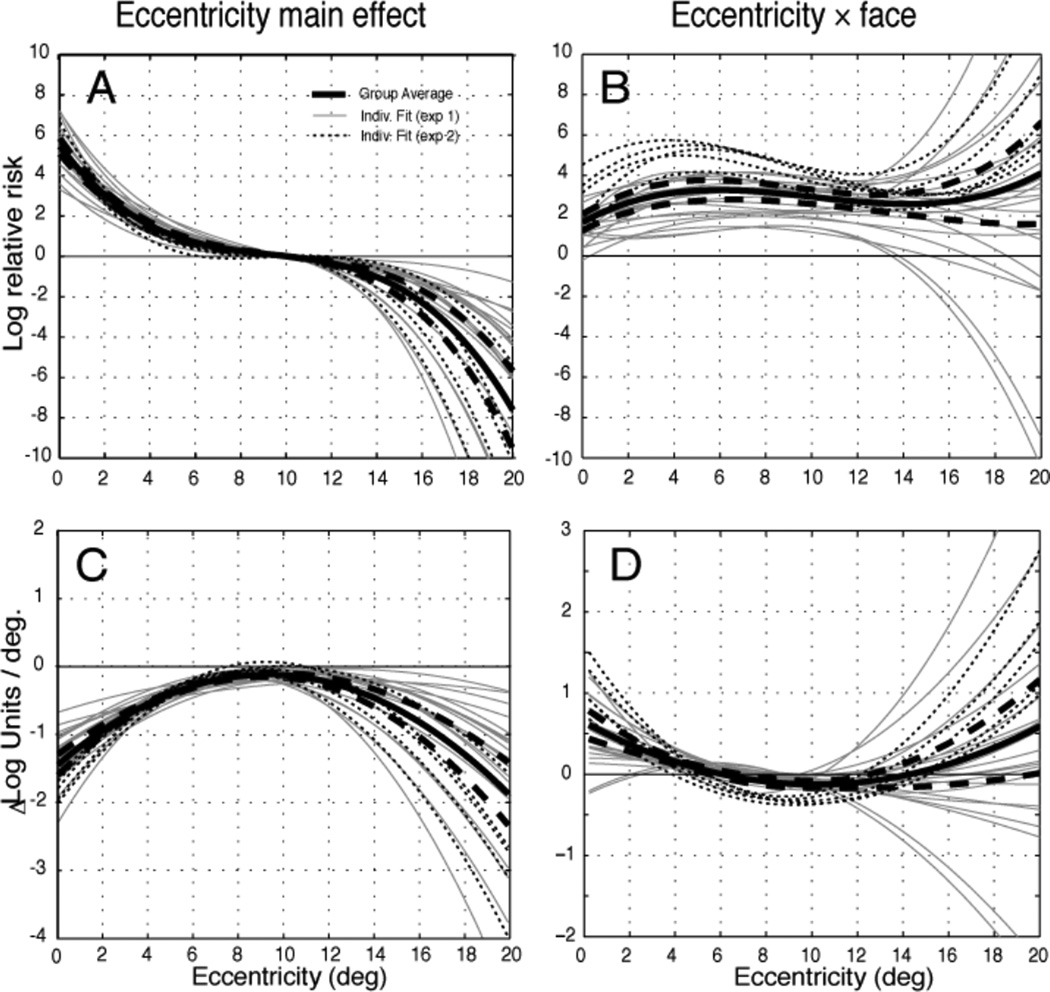
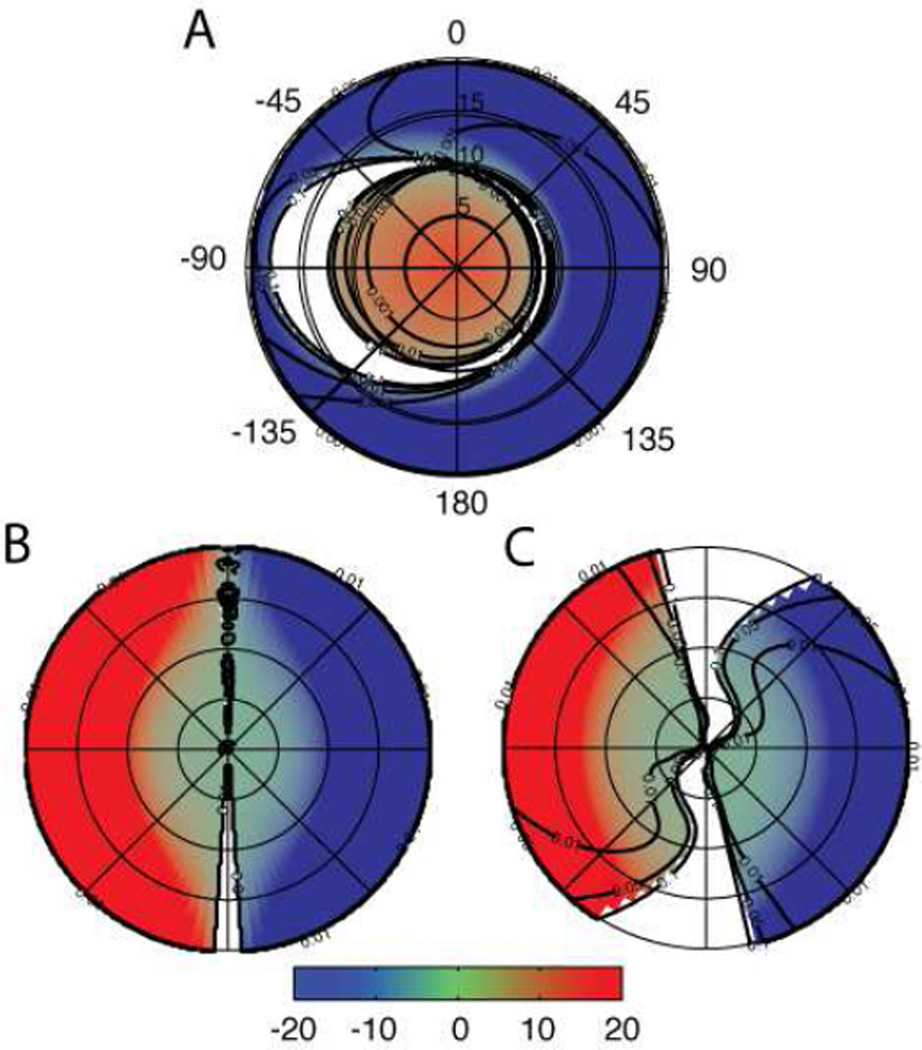
Figure 4.

Effects related to eccentricity and gaze bias towards faces over background. A. The main effect of eccentricity is shown as log relative risk of fixation averaged over all azimuthal angles, normalized to 10°. B. The interaction between eccentricity and face shows the log odds ratio of selecting a face bin over a non-face bin as a function of eccentricity. Derivatives of the respective curves reveal a monotonically decreasing trend in the main effect (C) but no monotonic trend in the face interaction (D). Group averages (thick black lines) and ± 2 SEM (thick dashed lines) are computed from model fits to individual subject data (gray and dotted lines). Units are in natural log base.

3.2 Group-level results

3.2.1 Saccades are biased towards locations near the fovea

The main effect of eccentricity, which represents the relative risk of a fixation falling within a bin as a function of eccentricity, reveals a monotonically decreasing curve (Figure 4A). The mean slope across subjects (Figure 4B) was negative and convex over the fitted range, with a minimum magnitude near eight degrees. This result indicates a strong bias towards locations near the current point of fixation, irrespective of other stimulus attributes.

3.2.2 Selectivity for faces over background is similar across eccentricities

The model confirmed that saccades are targeted more frequently to faces than background at all eccentricities (Figure 4C). In contrast to the main effect of eccentricity, face selectivity showed only modest dependence on eccentricity (Figure 4D), with average log odds ratio varying between 2 and 4 in natural base units across all observed eccentricities and no sign of a trend with respect to eccentricity.

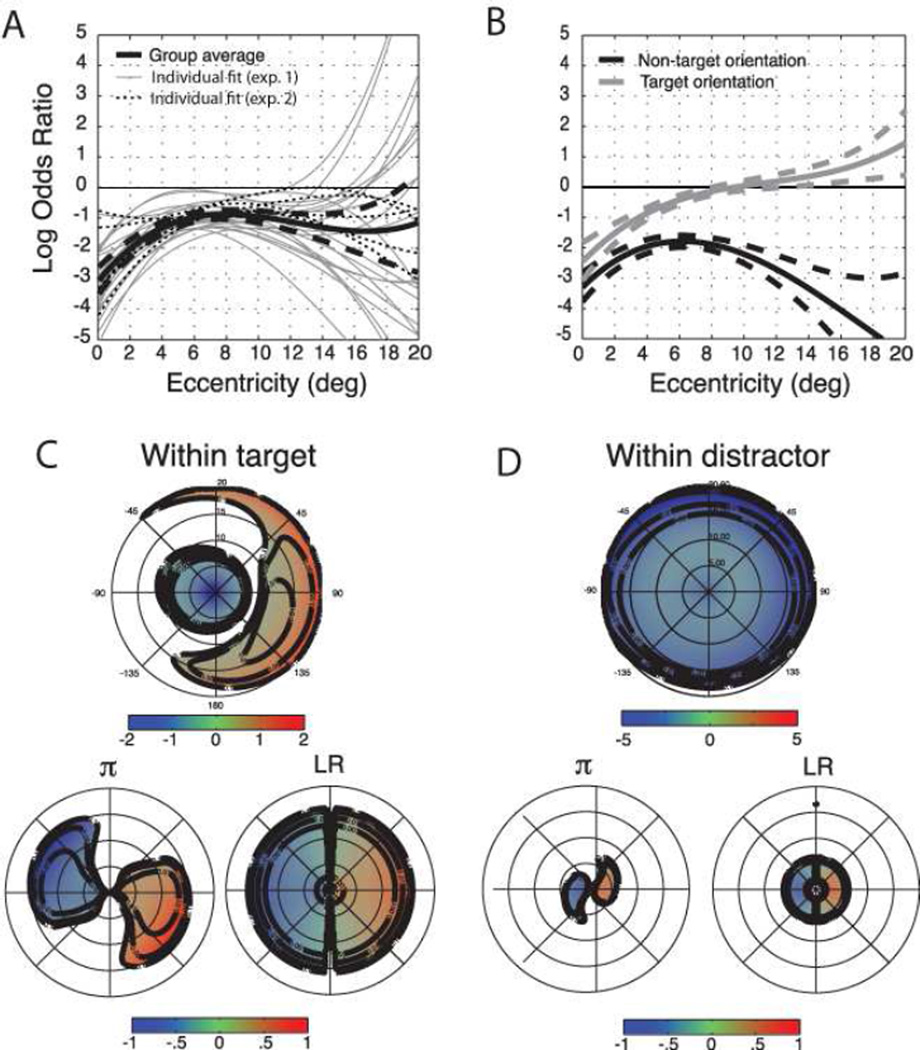
3.2.3 Saccades select the target orientation with increasing efficiency as a function of eccentricity

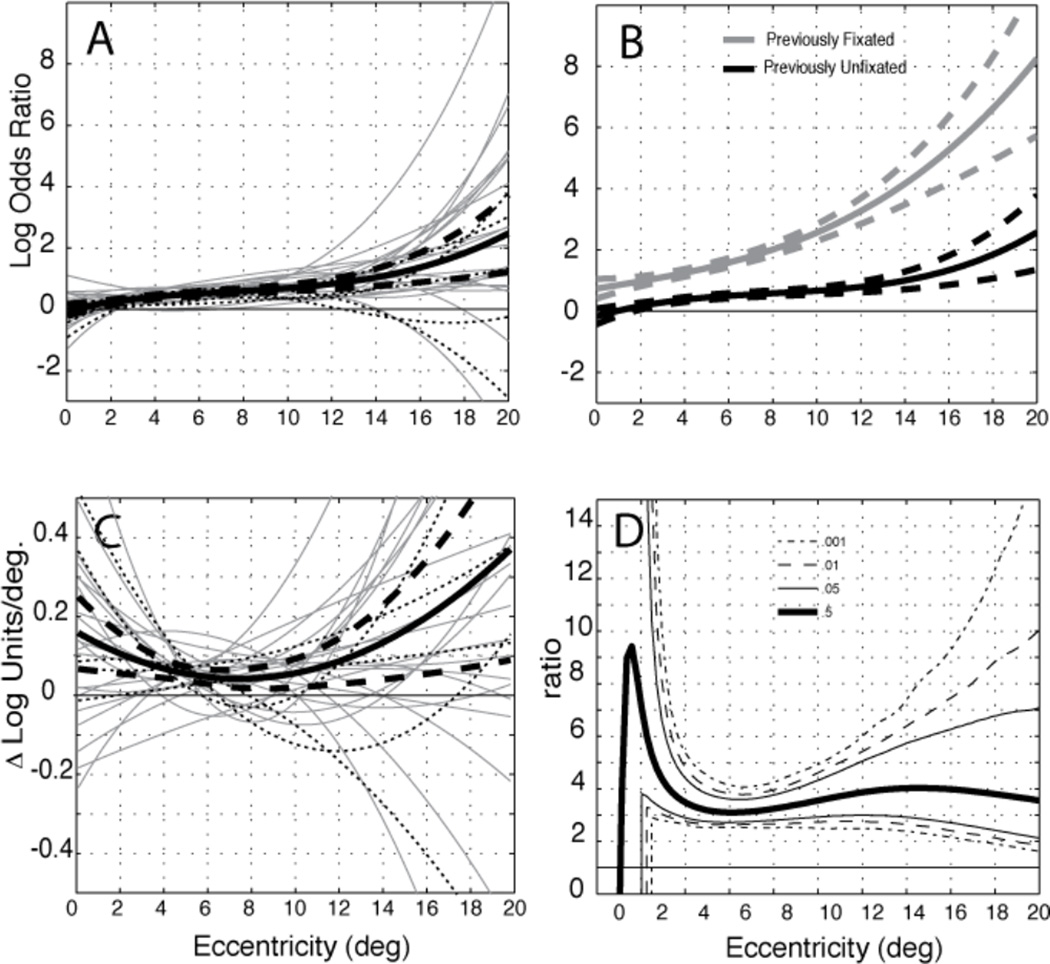
Saccades select the task relevant orientation over the distractor orientation (upright or inverted) both for faces that have been previously fixated and for faces that have not (Figure 5). This effect increases substantially for return fixations, shown by the interaction of task relevance and previous fixation (Figure 5B). A second noteworthy observation is that selectivity for the target orientation is an increasing function of eccentricity. This fact is confirmed in Figure 5C, which shows that the mean derivative of the task-relevance effect is significantly positive at all eccentricities. Across eccentricities, the ratio of the effect for first and return fixations in the group average is nearly constant (Figure 5D), thus the effect of previous fixation resembles a multiplicative 3- to 4-fold gain on the effect for first fixation. Breaking the effect down further by visual field shows it to be uniformly positive both for initial (Figure 6A) and return (Figure 6D) fixations and uniformly greater for return fixations (Figure 6G). As described next, hemifield contrasts in Fig. 6 also reveal noteworthy difference between LVF and RVF.

Figure 5.

Effect of task relevance with respect to eccentricity. A. Individual fits for experiment 1 (gray) and experiment 2 (dotted line) and group averages ±2 SEM (black) for previously unfixated faces. B. Group average and ±2 SEM for previously unfixated faces (black) in comparison to fixated faces (gray). C. Individually fitted curves and group average ±2 SEM for the slope of the task-relevance effect (as shown in panel A) with respect to eccentricity. D. Ratio of the task-relevance effect for return and initial fixations in the group averages (as shown in B); lines represent quantiles of a bootstrapped distribution for the ratio computed on group means, using 10,000 boostrap samples.

Figure 6.

Target selectivity as a function of visual field for initial and return fixations. A. For initial fixations, target faces are more likely to be selected across the visual field. Both hemifield contrasts, comparing log odds ratios between points offset by 180° azimuth (B) and comparing points equidistant from either side of the vertical meridian (C) reveal greater target selectivity in the LVF. D. Return fixations similarly show uniformly positive target selectivity, however hemifield contrasts (E,F) reveal no evidence for hemifield differences (FDR Q > .22). G. As shown by the interaction term, selectivity is uniformly greater for return fixations compared to initial fixations across the visual field. Hemifield contrasts (H,I) reveal a relatively larger difference in the RVF implying that the difference of hemifield effects for target and distractor stimuli is significant. Color scales represent natural log units thresholded at FDR Q ≥ .1, and contours indicate FDR significance regions of .1, .05, .01, and .001. In panels D, C, H, I, the color scale represents the difference of log odds ratios between corresponding points of the hemifields.

3.2.4 Target selectivity is greater in the LVF than in the RVF for previously unfixated faces but not previously fixated faces

For initial fixations on previously unfixated faces, both the LR- and π-contrasts reveal significantly greater selectivity for targets in the LVF compared to RVF (Figure 6B,C). On the other hand, no points in the hemifield contrasts reach significance for return fixations (FDR Q > .22) (Figure 6E,F). The hemifield contrasts for the interaction between previous fixation and task relevance are significant (Figure 6H,I), verifying that hemifield differences are less for return fixations than first fixations. The results of these tests therefore show a left visual hemifield advantage for previously unfixated target faces, which disappears for return fixations.

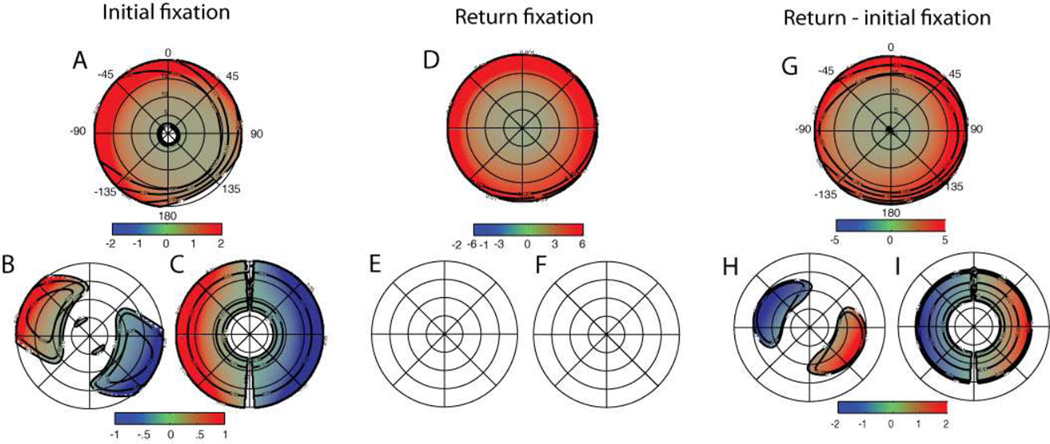
3.2.5 Memory affects saccadic guidance through suppression of return fixations to previously visited distractors

The interaction of previous fixation and target selectivity can also be combined with the previous fixation main effect to give the contrast that represents the previous fixation effect within each target category. Having previously fixated a face results in a negative log odds ratio of returning across all eccentricities in the main term (Figure 7A), implying a net suppression of return fixations across face types. As described in section 3.2.3, previous fixation also produces a large increase in the effect of task relevance, which offsets the suppression of return fixations to faces of the target orientation. While return fixations to distractors are suppressed, there is little net suppression for targets in the periphery (Figure 7B). For distractor faces, on the other hand, prior fixation results in large suppression of return fixations. For target faces, suppression is present perifoveally at eccentricities less than about 8 deg. The combination of these effects thus implies that memory exerts a role largely through the suppression of return fixations to task irrelevant locations, resembling inhibition of return (Klein & MacInnes, 1999; Rafal, Calabresi, Brennan, & Sciolto, 1989).

Figure 7.

Effect of previous fixation on the log odds ratio of refixation for target and distractor faces. A. Main effect of previous fixation with respect to eccentricity for individual subjects (gray and dotted lines) and the group average ± 2 SEM (thick black lines). B. Effect of previous fixation ± 2 SEM separated by category: target (gray) and distractor (black). C,D. Previous fixation effect within the target (C) and distractor (D) categories broken down by visual field and hemi-field contrasts below. The effect for target faces is characterized by RVF lateralized facilitation of return, whereas return to distractors is inhibited in both fields. Color scale shows log odds ratio thresholded at FDR≥ .1 and contours show FDR significance thresholds of .1, .05, .01, and .001.

3.2.6 Fixations to targets in the RVF are biased towards previously visited faces

Breaking down the effect in the previous section by visual field location reveals a hemifield-dependence for target objects (Figure 7C). Among fixations directed to target stimuli in the periphery of the LVF, there is no apparent bias towards or away from previously fixated faces. On the other hand, for fixations directed to targets in peripheral RVF, there is a bias towards previously fixated faces. Among distractors, a modestly greater suppression is present in the LVF for small eccentricities of five degrees and less (FDR Q < .01), while for all other eccentricities the effect does not reach FDR-corrected significance (Q>.1).

3.2.7 No evidence for saccadic bias related to facial expression

To examine whether any effects related to facial expression were discernible at the group level, two contrasts were computed across eccentricities: an arousal contrast, .5*(H+F)-N, and a valence contrast H-F, where H,F, and N represent the categorical variables for happy, fearful and neutral, respectively. None of the contrasts reached FDR-corrected significance at any eccentricity (Q > .05), and neither did the interactions with respect to orientation or previous fixation. Thus the data provide no evidence that saccade targeting was influenced by facial expression.

3.2.8 Saccades are biased towards upright faces

At the group level, there is a bias towards the upright faces among previously unfixated faces, reaching statistical significance (Q < .05) in the periphery, beyond 7 degrees (Figure 8). For return fixations, no significant effect (Q > .1) was observed at any eccentricity. However, because the interaction of previous fixation and orientation was also not significant at any eccentricity (Q > .1), it can’t be concluded that the effect differed for first and return fixations. As described in following sections, a stronger effect emerged when fixation order was taken into account.

Figure 8.

The effect of face orientation for initial fixations on previously unfixated faces. Color scale indicates log odds ratio of fixating upright faces over inverted faces.

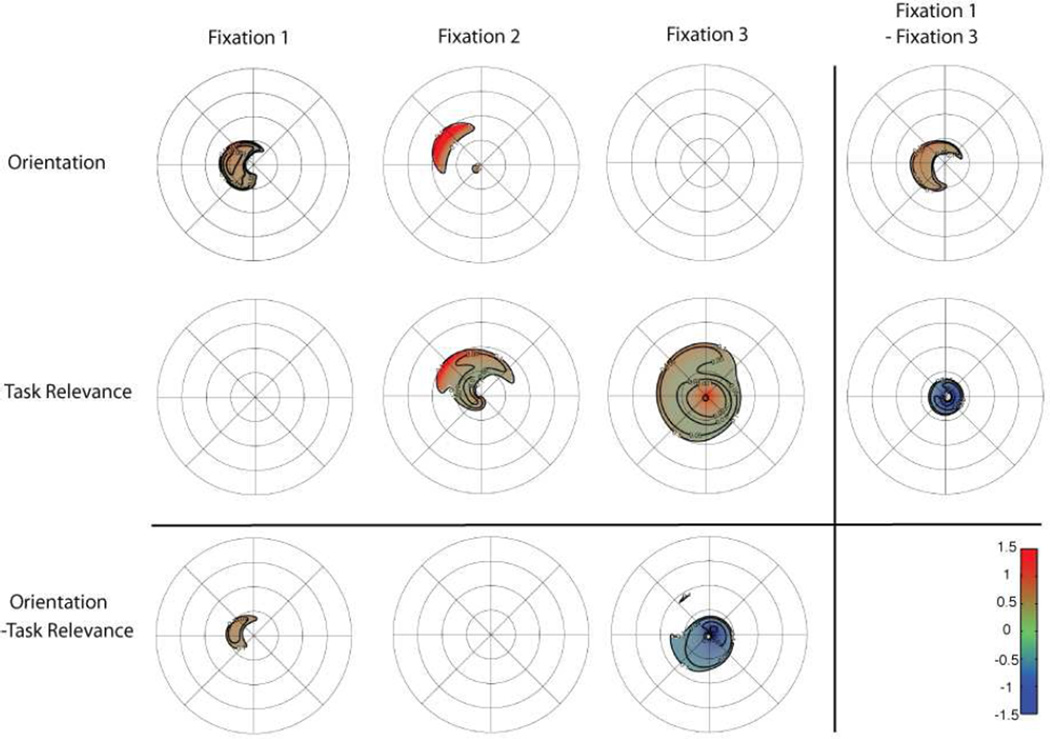
3.2.9 Effects specific to early fixations

The first fixation in each trial happens under very different conditions from all the others, as it follows a change of the visual stimulus from the fixation cross to the search array with an accompanying widely distributed visual transient. In order to examine the dependence of specific effects on early fixations, the data from the first 3 fixations were fit separately to a model that included the main effects of visual field and the task relevance and orientation interactions.

The first fixation in each trial was strongly biased towards the LVF (Figure 9), consistent with a left-to right scanning strategy, as has been commonly observed in western subjects accustomed to left-to-right reading (Abed, 1991; Spalek & Hammad, 2005). With respect to stimulus selectivity, an initial bias towards upright faces in the LVF appears for the first fixation at 5 deg. eccentricity and diminishes over the second and third (Figure 10, top row). Meanwhile, the first fixation shows no sign of a task-relevance effect, which first emerges over the second and third (Figure 10, second row). The time courses of these effects are confirmed as statistically significant in the contrasts between third and first fixations, as are the differences between orientation and task-relevance effects (Figure 10, 4^th column). The orientation, task relevance and eccentricity effects strongly imply a qualitative difference between the first saccade and subsequent saccades, a fact which is likely to be important in interpreting studies that rely on the initial saccade within the trial, e.g. (Brown et al., 1997) and (Parkhurst, Law, & Niebur, 2002).

Figure 9.

A. Main effect of visual field location for the first fixation in the trial. A large LVF bias is apparent in the LR-contrast (B) and π-contrast (C).

Figure 10.

Orientation and task-relevance effects evolve over the first three fixations. At the first fixation, a prominent bias towards upright faces appears in the LVF at 5 deg. eccentricity, and diminishes over subsequent fixations (top row). The growing task-relevance effect emerges at the second fixation (second row). The far right column and bottom row represent contrasts of these effects between, respectively, the first and third fixation and orientation and task relevance terms. Plots are thresholded as previously. Effects are plotted relative to the point of fixation (center), and circles mark radial distance at 5 deg. intervals.

3.2.10 Effect of block

In fifteen participants, the likelihood ratio test revealed significant interactions with block, indicating that spatial interactions with the face regressor differed between experimental blocks. At the group level, none of the planned spatial contrasts approached significance (FDR Q > .1), nor did any univariate tests on parameters across individuals, yielding no evidence that effects were systematic across individuals.

4 Discussion

We have applied a generalized linear regression framework developed from a log-linear point process model towards revealing the influence of visuotopic location, task relevance, orientation, and facial expression on the probability of fixating face stimuli. Viewed as a conditional logit, our approach generalizes methods that employ logistic regression (Barr, 2008). It improves upon these by allowing for both discrete and continuous variables to serve as both dependent and independent measures. Although the dependent measure is binned, bins can be arbitrarily small, as computational limits allow. As a result, the distribution modeled over the dependent measure may be decoupled from binning scheme, while model complexity can be optimally adjusted through semi-parametric model selection of basis functions. Although amenability to full hierarchical modeling is bound to be more limited than for simpler parametric GLMs, we have addressed subject-level random effects by way of the summary-statistic procedure (Penny et al., 2003) applied to spatial contrasts. In addition, many sources of conditional dependence, such as serial dependence of gaze position, can be directly addressed within the point-process framework by modeling conditional intensity.

Beyond demonstrating the application of the method, we obtained several intriguing results that deserve further consideration. Among these is evidence for pre-saccadic detection of face-like objects in the periphery over similar but inverted distractors (Figure 6), a question, which has generated conflicting answers in the past (Brown et al., 1997; Theeuwes & Van der Stigchel, 2006; Wolfe & Horowitz, 2004). The present work suggests a possible resolution, that targeting of saccades to faces based on configural information depends on a low threshold process, which still performs substantially better than chance, and which varies across the visual field. Moreover, we find clear evidence for at least two mechanisms that use configural information distinguishing upright from inverted faces: the guidance of saccades in accordance with momentary task-related goals, and a task-independent bias towards certain stimuli over others, in this case towards upright over inverted faces, which operate with distinct time courses with respect to the onset of the stimulus (Figure 10), showing also differing dependence on visual field. The view suggested by the present study is that attentional control towards faces encompasses multiple separable systems, which handle different aspects of orienting towards relevant information in the visual environment (Kovach, Sutterer, Rushia, Teriakidis, & Jenison, 2014; Morton & Johnson, 1991). Our results emphasize the non-uniformity of these effects over the visual field with respect to both laterality and eccentricity, as well in their evolution over time.

These effects may be a source of significant unaccounted variability in studies that neglect to consider them, affecting both the power and interpretation of results (Simpson, 1951). We have demonstrated the viability of the GLM approach as a means of disentangling multiple factors influencing attention, allowing the actions of respective systems to be more clearly distinguished. One potential advantage of this approach that may benefit future applications is that it allows effects to be studied under more ecologically meaningful conditions than are often required to gain experimental control of the same variables.

4.1.1 Relevance to visual search and orienting to faces

A number of the findings deserve further comment. With respect to foveal eccentricity, we found that the visual field is segmented into distinct zones wherein goal-related and stimulus-related effects influence gaze orienting to different degrees. Contrary to what might be expected, accuracy of saccade targeting to task-relevant stimuli is not a simple function of stimulus discriminability; this is shown by the fact that the bias towards task-relevant stimuli was lowest near the fovea where discriminability ought to be greatest, increasing smoothly towards the periphery (Figure 5). At first glance, this result may seem paradoxical, but given that the costs of generating a saccade, in metabolic terms and in the degree and duration of the visual disruption, are bound to scale with amplitude (Stevenson, Volkmann, Kelly, & Riggs, 1986), this finding might plausibly be explained by a higher threshold of certainty about the target identity, which needs to be overcome to trigger larger amplitude saccades. It therefore points towards an evaluation of biological cost in target selection during visual search, which also accords with the large bias towards targets near the fovea (Figure 4).

A second observation is that the biases towards upright and task-relevant faces emerge with distinct time courses Figure 10. The first fixation in the trial is biased towards upright faces lying near the fovea, particularly in the LHF, regardless of task relevance. At the second fixation the effect of orientation spreads towards the periphery to 10 degrees, while effects of task relevance emerge closer to the fovea. By the 3^rd fixation, task relevance becomes the dominant effect. These observations suggest early pre-attentive parafoveal selection of upright faces that spreads to the periphery concurrently with the emergence of a task-relevance effect near the fovea, which also then spreads peripherally.

The current results also have bearing on the controversial topic of the role of memory in visual search (Horowitz & Wolfe, 2003; Horowitz & Wolfe, 1998; Klein, 2000). Previous fixations clearly affected the likelihood of return fixations, which took the form both of inhibition of return (IOR) to distractors and facilitation of return (FOR) to target stimuli. IOR to irrelevant distractors spanned the visual field while FOR to task-relevant stimuli depended on laterality. IOR to distractor faces was reflected in a large, uniform, approximately 3-fold negative gain observed in the interaction of task relevance and eccentricity (Figure 7D). For targets, IOR appeared perifoveally, within 10 degrees, but not beyond, with instead modest FOR in the RVF (Figure 7C). It is possible that parafoveal inhibition in this case reflects an unmodeled dependence of IOR on recency of fixation, which future work may consider in greater detail.

Finally, among the most striking effects were those of laterality, revealed by interactions with azimuth (clock-face angle). First, for faces that had not previously been foveated, a clear left hemifield advantage was observed in target selection: saccades targeted to the left were more likely to be directed to task-relevant faces than those to the right. Such an LHF advantage for previously unfoveated targets agrees with a right-hemispheric advantage in face perception (Hay, 1981; Hillger & Koenig, 1991; Perrett et al., 1988) and with hemispheric specialization for guiding attention to previously unattended targets (Corbetta & Shulman, 2002; Mangun et al., 1994). Less expected is the reversal of hemifield advantage for return fixations, for which the model implies a rightward bias towards targets and, to a lesser extent, distractors. A handful of studies have found RHF perceptual advantages in the context of face naming (Marzi & Berlucchi, 1977) and in the “analytic” processing of isolated facial features (Patterson & Bradshaw, 1975; Sergent & Bindra, 1981), yet none of these seem directly related to the present observation. A study of lateralized visual search for simple shapes in callosotomy patients found RHF advantage when the target belonged to a subset of items identified by a common feature (Kingstone, Enns, Mangun, & Gazzaniga, 1995). Such an effect could arise from left hemispheric specialization for tracking the properties of attended objects during visual search, as suggested in the present case, a possibility that deserves further investigation. Finally, studies have also shown culturally dependent patterns of laterality in scanning and inhibition of return (Abed, 1991; Spalek & Hammad, 2005), related to scan-direction during reading. Although the present result has no obvious explanation in simple biases of scan pattern, neither can a relationship be ruled out, warranting further study, as well.

4.1.2 An example of Simpson’s paradox

Linear regression affords a way to distinguish among otherwise confounded effects, one of the main reasons regression analyses have become a staple of behavioral research. Failing to account for important effects may have a number consequences, of which the most severe is “Simpson’s paradox,” the situation in which excluding a given independent measure from the analysis results in a drastic change of the apparent effect related to another measure, possibly leading the researcher to an entirely different and erroneous set of inferences (Blyth, 1972; Simpson, 1951). Simpson’s paradox comes about through correlations among the predictors, as a result of which variance properly explained by one loads onto the other if the first is not included in the model. The complexity of gaze behavior easily creates many such correlations, which are difficult to disentangle outside a regression framework. Moreover, in contrast to the normal linear model, such correlations for non-normal generalized linear models may depend on the parameters of the distribution, and therefore often cannot be predicted or controlled in advance through experimental design, which requires adaptive optimization (Chaloner & Verdinelli, 1995).

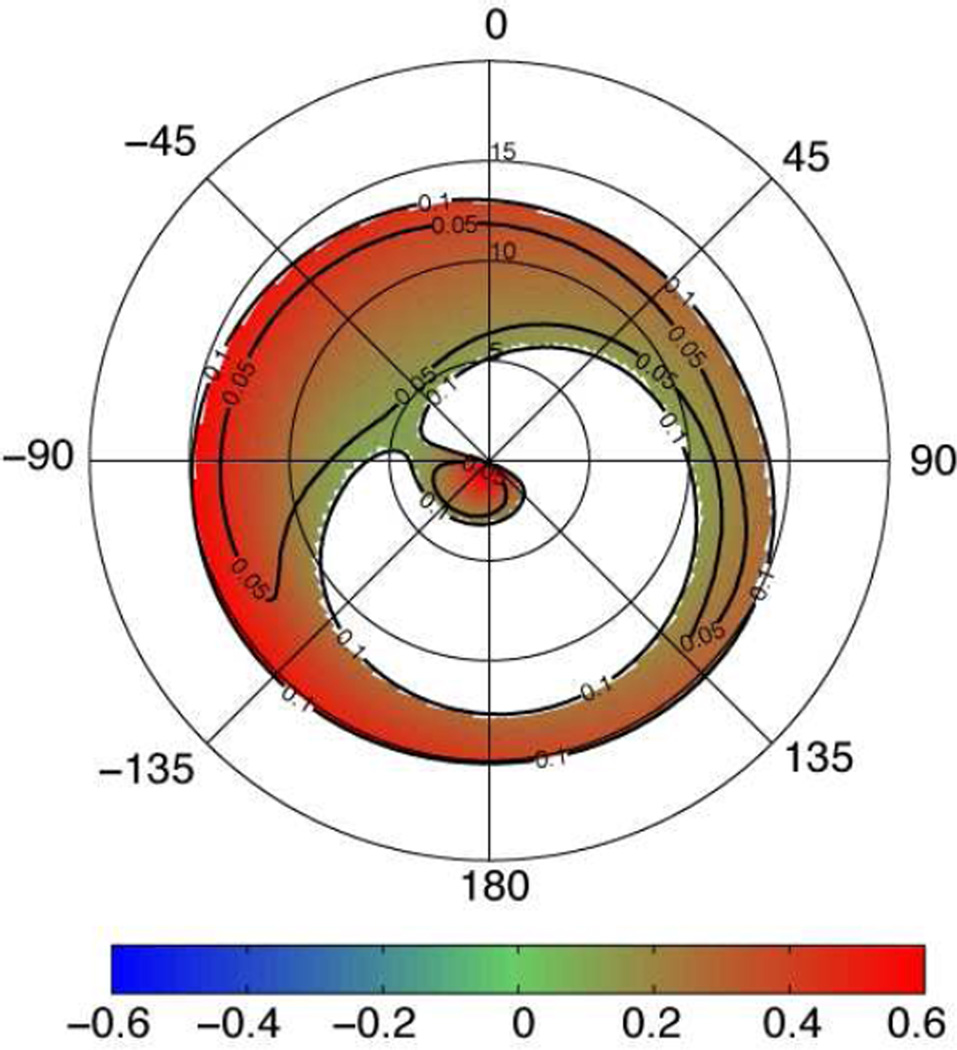
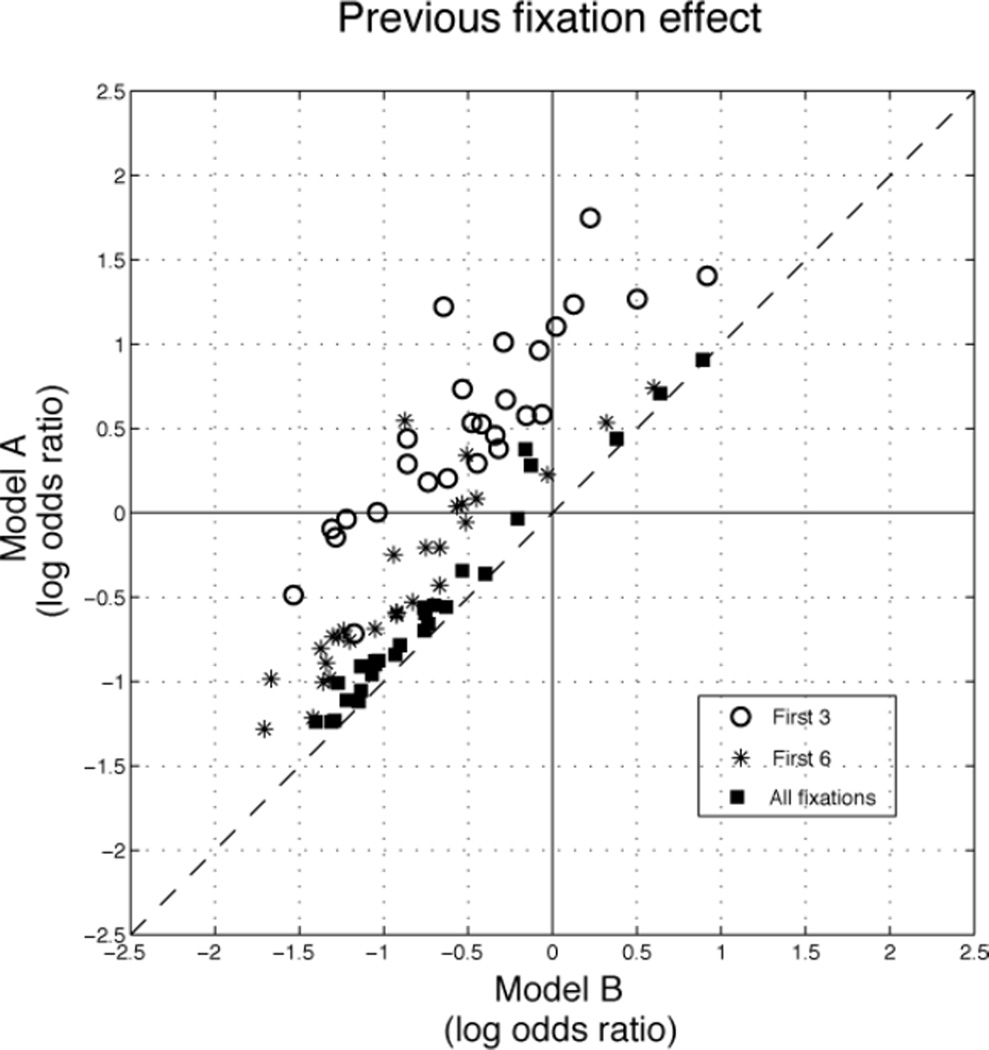
We highlight an example of Simpson’s paradox to illustrate some strengths of our approach. As described in section 3.2.5, having previously fixated a face leads to inhibition of return, a net decrease in the relative log-odds of a return fixation, all other factors equal (Figure 7). At the same time, we observe a strong bias towards objects near the fovea (Figure 4). In general, the large foveal bias dominates the previous fixation effect, meaning that a previously fixated face lying near the fovea will often remain a more probable target for the subsequent fixation than an unfixated face lying in the periphery. As a consequence of the same foveal bias, previously fixated faces lie on average closer to the fovea than previously unfixated faces. As shown in Figure 11, if one neglects to model eccentricity effects, this correlation creates a positive bias in the previous fixation effect, which may result in an apparent reversal of the effect, particularly when trials contain only a small number of fixations. In other words, previously visited faces may appear more likely to be selected than previously unfixated faces due not to a bias towards previously fixated faces but to their proximity to the current point of foveation. This effect will tend to mask inhibition of return in any analysis that does not account for eccentricity. By correcting for foveal bias through the eccentricity main effect, IOR emerges as a large and unambiguous effect in the GLM even when only the first three fixations are included, the minimum needed to observe return fixations. Thus, an appropriate regression model recovers this effect when fixations per trial are sparse and the distribution of fixations within each trial highly non-ergodic due to sequential dependence. This example illustrates the usefulness of the current approach in both distinguishing otherwise confounded effects and making efficient use of the data.

Figure 11.

Foveal bias can mask inhibition of return (IOR) when the effect of eccentricity is neglected. IOR manifests as diminished odds of fixating a previously visited face relative to unfixated faces at the same eccentricity. Markers show a comparison of the previous fixation effect as estimated by two models; the first (model A, shown on the y-axis), includes only the intercepts for previous fixation, target and face regressors, and the second (model B, shown on the x-axis) includes, in addition, the main effect of foveal eccentricity as a 3^rd order polynomial. To ensure that effects in both models are related to transitions between faces rather than refixations to the most recent target, fixations following saccades of less than 3 deg. amplitude were excluded from model fitting. Model A’s failure to correct for foveal bias results in a positive displacement in the previous fixation effect, a consequence of the fact that previously fixated faces tend on average to be closer to the current point of fixation. This displacement decreases as the number of fixations per trial increases due to convergence towards ergodicity. With three fixations per trial, the minimum required to observe any return fixations, model B still reveals IOR, while model A shows an effect with reversed (positive) sign, an example of Simpson’s paradox.

4.1.3 Limitations

While comprehensive in principle, our approach, as with any regression analysis, requires some judicious reductions in complexity. For instance, we did not model all possible higher-order interactions, nor the detailed interactions with time among all fixations. Portions of each of these additional components could, in principle, be added to the model, illustrating its flexibility—but at the cost of increased model complexity, which may lead to overparameterization and interpretive difficulties or run into computational constraints on model fitting. As with any regression analysis, it generally will be neither feasible nor desirable to model all higher-order interactions, and one will limit interactions to a given order or to those that are most relevant for a given question

Our approach also incorporates a number of more specific assumptions, which may be subject to doubt. The log-linear model we have adopted relates the linear component of the model to the logarithm of the mean of the response variable. Other link functions might more accurately reflect how regressors influence fixation probability. Likelihood-based inference assumes conditional independence among events, which is strictly true only if the explicit model of conditional dependence is correct and complete. There may be numerous unmodeled sources of dependence with the potential to affect the validity of any inferential procedure. Moreover, standard inferential tests apply asymptotic assumptions, and non-Gaussian generalized linear models tend to be less robust to these assumptions than their Gaussian counterparts (Pawitan, 2000). For these reasons, such tests should be treated with due caution. Although, the ratio of data points to model degrees of freedom should ideally be large enough to meet the asymptotic assumptions of any employed hypothesis tests, well-known approaches to regularization or Bayesian model estimation allow fitting over-parameterized models, while robust alternatives to asymptotic hypothesis tests, such as permutation tests, remain valid when asymptotic assumptions are not met. Caveats of this sort apply to any regression analysis, but they tend to be amplified in the GLM setting, where robustness to deviations from modeling assumptions is less well understood. As these topics apply generally to regression analyses and are addressed at length in standard textbooks (Agresti, 2014), we do not review them here in further detail. Finally, some of these limitations might be addressed, at the price of added complexity, by more flexible variants of the point-process framework, such as those that apply recent advances in modeling Gaussian latent variables (Barthelmé et al., 2013; Rue et al., 2009).

Highlights.

• We describe a way to distinguish influences on attention during visual search.

• We apply the method to visual search for faces.

• Orientation, task, memory and visual field influence the targeting of gaze.

• These influences depend differently on time course and visual field.