Effect of warming temperatures on US wheat yields

Significance

This study provides insights for wheat breeding efforts, public policy, and agricultural decision making related to climate change. Our findings provide opportunities for the international wheat breeding community to intensify research efforts to increase resistance to heat stress during focused developmental stages. These efforts could result in net positive warming effects since reduced exposure to freeze was found to be a yield-enhancing benefit of warming. Our results indicate that advancements in heat resistance could come at the expense of higher average yields, and that there is currently limited scope for producer adaptation through alternative variety selection. Our results also suggest that irrigation could help mitigate the effects of warming, which has implications for policies focused on the conservation of increasingly scarce water resources.

Abstract

Climate change is expected to increase future temperatures, potentially resulting in reduced crop production in many key production regions. Research quantifying the complex relationship between weather variables and wheat yields is rapidly growing, and recent advances have used a variety of model specifications that differ in how temperature data are included in the statistical yield equation. A unique data set that combines Kansas wheat variety field trial outcomes for 1985–2013 with location-specific weather data is used to analyze the effect of weather on wheat yield using regression analysis. Our results indicate that the effect of temperature exposure varies across the September−May growing season. The largest drivers of yield loss are freezing temperatures in the Fall and extreme heat events in the Spring. We also find that the overall effect of warming on yields is negative, even after accounting for the benefits of reduced exposure to freezing temperatures. Our analysis indicates that there exists a tradeoff between average (mean) yield and ability to resist extreme heat across varieties. More-recently released varieties are less able to resist heat than older lines. Our results also indicate that warming effects would be partially offset by increased rainfall in the Spring. Finally, we find that the method used to construct measures of temperature exposure matters for both the predictive performance of the regression model and the forecasted warming impacts on yields.

The potential impact of global warming and climate change on socioeconomic outcomes has become an important and growing area of scientific study and evaluation. Separate lines of study include quantifying the likely impact of climatic change on measures of civil conflict (1–5) and agricultural land values, profitability, and/or production efficiency (6–22). Both lines of literature continue to measure, discuss, and debate the effects of warming temperature. An issue that has received much attention in both sets of literature is how best to quantify exposure to extreme temperatures. This is an important concern, as many studies rely on historical spatial and temporal variations in weather outcomes to identify the effects of weather extremes. If these historical extremes are not measured correctly, estimates of their impacts will not be credibly identified, thereby raising doubts regarding any climate change projections based on these impacts.

Here we use regression analysis to estimate wheat yields as a function of observed weather variables and forecast yield impacts under a variety of weather scenarios. Our main findings are as follows. First, the effect of temperature exposure varies across the September−May growing season, with the biggest drivers of yield loss being freezing temperatures in the Fall and extreme heat in the Spring. Second, the net effect of warming on yields is negative, even after accounting for the benefits of reduced exposure to freezing temperatures. Third, there exists a tradeoff between mean yield and ability to resist extreme heat across varieties, and more-recently released varieties are less able to resist heat than older ones. Fourth, warming effects are partially offset by increased rainfall in the Spring. Fifth, the method used to construct measures of temperature exposure matters for both the predictive performance of the regression model and the forecasted warming impacts.

We focus on wheat as it is one of the first domesticated food crops, forms the basic staple food of major civilizations in Europe, West Asia, and North Africa, and is the most widely planted crop globally. With a 2013 harvest of 8 million hectares, the Great Plains of the United States form the largest contiguous area of low-rainfall winter wheat in the world. Five states (Kansas, Oklahoma, Texas, Colorado, and Nebraska) produce nearly all high-quality hard red winter wheat in the United States. In 2013, Kansas production generated 378 million bushels of wheat at a value of 2.8 billion US dollars. Kansas production value represents 15% of all wheat grown in the United States.

Our empirical approach uses data that combine variety-specific wheat yield observations with weather data from the exact location of the field trial. This permits two major advances for estimating the relationship between weather and wheat yield: (i) Location-specific weather data purge the results of aggregation bias that might be present in studies that use weather averages (or other aggregates) across space, and (ii) variety-specific yield responses provide information about the impact of climate on a large number of past, present, and future wheat varieties. Ref. 11 discusses limitations of gridded weather data sets, which have been used extensively because there is not often a weather station in each location of interest. Our data avoid the five pitfalls associated with gridded weather datasets (11). In addition, we find that the warming effects estimated using these field trial data are consistent with effects estimated from on-farm yield data, thereby providing external validity for the results presented here.

Results

The raw data include observed wheat yields matched by location with daily min/max temperatures and total precipitation. There are 268 observed seed varieties in the sample (SI Appendix, Table S1). The yield and weather data vary substantially in-sample (SI Appendix, Table S2 and Figs. S1−S5). Here and throughout the analysis, the 9-mo September−May wheat growing period is divided into 3-mo seasons: Fall (September−November), Winter (December−February), and Spring (March−May). Degree days are calculated using a sinusoidal interpolation of temperature exposure within each day and are hereafter referred to as Interpolated Degree Days (IDD). Extending the approaches of refs. 13 and 20, we also include variables that measure time exposure to freezing temperatures. There exists substantial variation in the IDD and freeze variables across both locations and years (SI Appendix, Figs. S6 and S7, Top).

Regression analyses that control for precipitation, technological change, location-specific unobserved factors, and seed variety suggest that degree days measured using interpolations between daily minimum and maximum temperatures (13, 20) are a more accurate predictor of wheat yield than average daily temperatures and an alternative measure of degree days calculated using daily mean temperatures (23–27). Thus, we focus on the interpolated degree day approach here, but include findings for the latter two approaches in SI Appendix, section S1. The results presented in that section suggest that average temperature and degree days calculated based on mean daily temperatures do not fully capture variations in temperature exposure and consequently misrepresent the effect of a warming climate on wheat yields.

Optimal Degree Day Thresholds for Yield Prediction Differ Across the Fall, Winter, and Spring Months.

It is not clear from the literature what the appropriate degree day thresholds for wheat are, as these can potentially vary depending on the method used for constructing degree days and the season under consideration. We follow the piecewise linear approach of ref. 13 and allow for two separate degree day thresholds within each season. We directly control for exposure to freezing temperature separately, and thus restrict our attention to thresholds above zero. We estimate the regression model over all possible thresholds and select as optimal the ones generating the best fit for the model (highest r-squared). The lower threshold is restricted to be at least five degrees above zero and ten degrees below the maximum observed temperature, while the upper threshold is restricted to be five degrees above the lower threshold and five degrees below the maximum. These restrictions are used to ensure that the thresholds are not too close to each other, nor too close to the endpoints of the piecewise linear function. We evaluate the robustness of these restrictions below.

Under the piecewise linear approach, the upper and lower thresholds are used to construct three measures of temperature exposure: IDD between 0 °C and the lower threshold, IDD between the lower and upper thresholds, and IDD above the upper threshold. The optimal thresholds were estimated to be 10 °C and 17 °C in the Fall, 5 °C and 10 °C in the Winter, and 18 °C and 34 °C in the Spring. Although the sample average for IDD above 34 °C in the Spring is slightly less than 1 (SI Appendix, Table S3), it exhibits substantial variation as the coefficient of variation is greater than 1. This variable is nonzero in two thirds of the location−years in the data.

Freezing Temperatures in the Fall and Extreme Heat in the Spring Are the Biggest Drivers of Yield Loss.

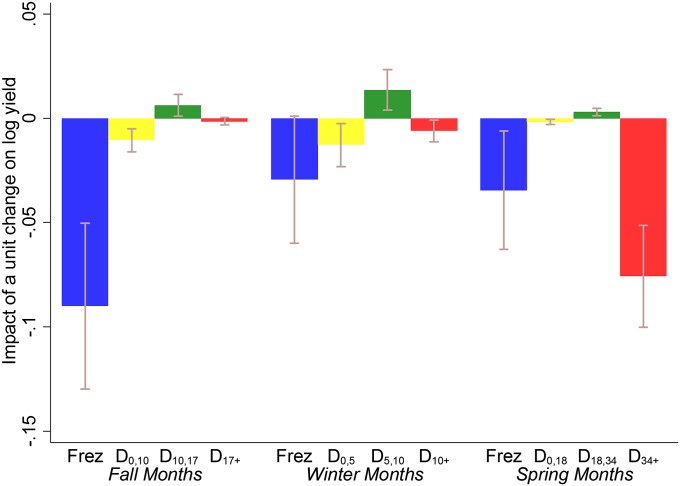
The parameter estimates for the preferred IDD model are reported in SI Appendix, Table S4, column 3. An additional day of freezing temperatures in the Fall is associated with a 9% yield reduction (Fig. 1). Fall growth can be slowed by cold weather, and wheat will be pushed toward dormancy, shutting down tiller formation, and thus reducing yield. The upper degree day threshold in the Spring is 34 °C, above which an additional degree day is associated with a 7.6% yield reduction. Effects on fertility of high temperatures in the Spring just before or during flowering can affect seed set, and exposure later in the season during the grain-filling phase causes the plant to start to senesce and shortens the amount of time the plant can fill grain. Among positive temperatures, springtime exposure above 34 °C is associated with the largest yield reductions (SI Appendix, Fig. S8). Precipitation has an inverted U shape in the Winter and Spring, whereas it is upward sloping at an increasing rate in the Fall (SI Appendix, Fig. S9). The precipitation variables are jointly significant (P = 0.02). The location and variety fixed effects are each statistically significant (SI Appendix, Table S5) and thus capture important variation across trial locations and seed varieties. Restricting the temperature coefficients to be the same across seasons is not supported by the data, nor is restricting the low, medium, and high degree day coefficients to be the same within each season (SI Appendix, Table S5).

Fig. 1.

Impacts of freezing and degree day temperature variables on wheat yield for the preferred model (SI Appendix, Table S4, column 3), expressed per 24 h (days). D_x,y refers to the degree day variables created from the IDD variables for the thresholds x and y. Each four-bar cluster shows impacts for the Fall, Winter, and Spring months. Bars show 95% confidence intervals using SEs clustered by year and variety.

The Overall Effect of Warming on Yields Is Negative, and Ignoring the Effects of Warming on the Exposure to Freezing Temperatures Overstates This Effect.

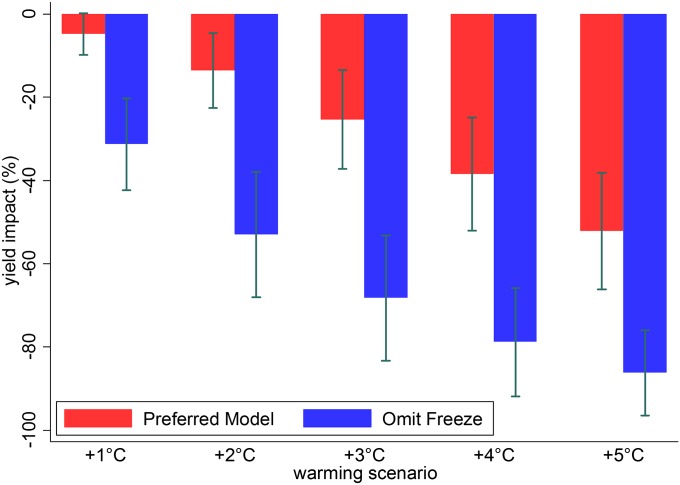
Fig. 1 implies that warming temperatures have potentially off-setting effects, as they reduce exposure to freezing temperatures while simultaneously increasing exposure to extreme heat. To evaluate which effect dominates, we predict yield impacts for a range of uniform temperature changes across the entire Fall−Spring growing season (Fig. 2). All scenarios suggest that warming is associated with net yield reductions, implying that the detrimental effect of extreme heat is larger than the beneficial effect of freeze reduction. All warming impacts are statistically significant at the five percent level, with the exception of the +1 °C warming scenario, which is significant at the ten percent level (P = 0.084). The warming effects are robust to the restrictions on the degree day thresholds discussed above (SI Appendix, Fig. S10). We also find that warming effects will be substantially overstated if one ignores the effects of reduced exposure to freezing temperatures (Fig. 2).

Fig. 2.

Predicted warming impacts on wheat yields under alternative uniform temperature changes across the entire Fall−Winter−Spring growing season. Impacts are reported as the percentage change in yield relative to historical climate. Each two-bar cluster shows estimates for a given scenario across different regression model specifications. The preferred model (SI Appendix, Table S4, column 3) estimates the warming effects using all temperature variables, whereas the alternative holds all effects from the Freeze Days variables at zero. Bars show 95% confidence intervals using SEs clustered by year and variety.

The Overall Effect of Warming on Yields Varies Across the Growing Season.

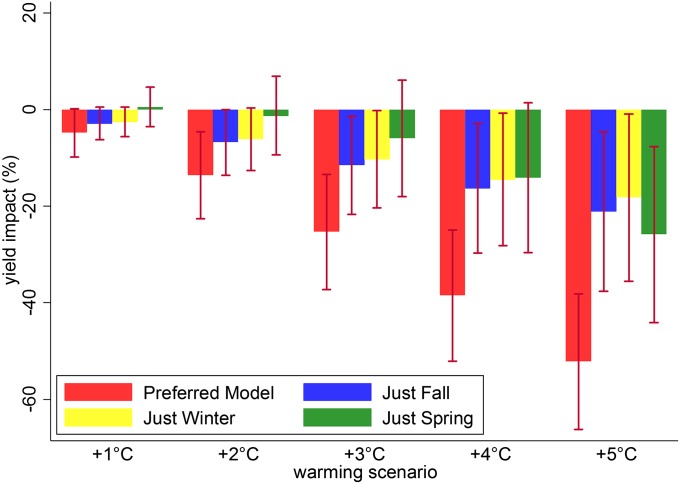
Fig. 3 decomposes the overall warming effect across the Fall, Winter, and Spring months. Within each season, the negative effects of warming are larger than the beneficial effects of reduced exposure to freezing. The one exception is Spring under the 1 °C warming scenario, which shows a net positive effect. The biggest drivers of yield reductions are associated with the Fall and Winter months until the 5 °C warming scenario, at which point the Spring effects are largest. These findings imply that looking at any one season in isolation can misrepresent the overall effects of warming, as can only focusing on the marginal effects from a regression model (i.e., Fig. 1).

Fig. 3.

Predicted warming impacts on wheat yields under alternative uniform temperature changes across subsets of the growing season. Each four-bar cluster shows estimates from the preferred model accompanied by alternatives that restrict subsets of these effects to be zero. Just Fall ignores temperature effects in the Winter and Spring. Just Winter ignores temperature effects in the Fall and Spring. Just Spring ignores temperature effects in the Fall and Winter. Bars show 95% confidence intervals using SEs clustered by year and variety.

The Warming Effects Estimated from Field Trial Yield Data Are Consistent with Effects Estimated from County-Level Aggregate Yield Data.

Management practices for the field trials vary by location and year. Production methods are considered, “best management practices” for each location−year and are designed to eliminate all yield-reducing features such as nutrient deficiencies or toxicities, damage from insect pests and disease, and competition from weeds. These optimal growing practices potentially differ from the production practices of real farmers, who base management decisions on profitability. To investigate the external validity of our results, we reestimate the preferred model (SI Appendix, Table S4, column 3) using county-level yield data for dryland hard winter wheat from the National Agricultural Statistics Service (NASS). The 11 trial locations form a small but representative sample of all Kansas wheat-producing counties (SI Appendix, Table S6). Average county-level farm yields are lower than field trial yields on average, which is consistent with the existence of a yield gap between field trial and on-farm production efficiency (28). We match the NASS yield observations with the weather from the field trial location in that county. The location and variety fixed effects from the preferred model are replaced with county fixed effects. We find that the temperature coefficient estimates and associated warming effects remain largely unchanged relative to our preferred model (SI Appendix, Figs. S11 and S12). This provides evidence of external validity for the results reported here.

There Exists a Tradeoff Between Mean Yields and the Ability to Resist Heat, and Newer Varieties Are Less Heat Resistant than Older Ones.

We consider whether the ability to resist high temperatures in the Spring varies across wheat varieties. We first consider a varying-slope multilevel model (29) where the fixed portion of the model takes the same form as our preferred model (SI Appendix, Table S4, column 3), but we allow the effect of degree days above 34 °C in the Spring to vary across varieties. We were not able to estimate this version of the model due to a small number of observations for many included varieties (SI Appendix, Fig. S13). We instead group varieties by the year in which they were released to the public and use this clustering in both the fixed and random components of the multilevel model. This allows us to estimate Spring heat resistance across 42 release year groupings between 1964 and 2014 (SI Appendix, Table S7). From this model, two findings emerge. First, there exists a tradeoff between the ability to resist heat and mean yield, with higher-yielding varieties less able to resist temperatures above 34 °C (SI Appendix, Fig. S14). We find that if the least resistant variety is switched to the most resistant variety, average (mean) yield is reduced by 6.6% and heat resistance is increased by 17.1%. Second, newer varieties are less able to resist temperatures above 34 °C than older varieties (SI Appendix, Fig. S14). We estimate warming effects for the most and least heat resistant varieties, and find that the effects differ by an average of three percentage points (SI Appendix, Fig. S15). This implies that there is limited scope for producer adaptation through alternative variety selection from a historical perspective. However, future breeding efforts could make this a more feasible strategy.

Interactions Between Temperature and Precipitation in the Spring Imply That Warming Effects Are Partially Offset by Increased Rainfall.

Our preferred specification (SI Appendix, Table S4, column 3) uses log yield as the dependent variable, which allows for the level change in yields as a result of warming to be a function of both temperature exposure and precipitation. However, the percent-change impacts—which are of interest here—are restricted to be independent of precipitation. Thus, we consider a more general specification that includes interactions between the degree day variables and precipitation for each of the Fall, Winter, and Spring seasons. This generalization is not supported by the data in the Fall and Winter (joint P values of 0.69 and 0.19, respectively), but is supported for the Spring (joint P value of 0.00). A further extension to quadratic interactions is not warranted (joint P values of 0.77, 0.54, and 0.90 for the Fall, Winter, and Spring, respectively). Thus, we include linear interactions for the Spring degree day and precipitation variables, and predict warming effects holding precipitation at the 25th, 50th, and 75th percentiles of the sample data (SI Appendix, Fig. S16). Results suggest that additional Spring precipitation can partially offset the negative effect of warming, as the warming impacts are 11 percentage points larger under the low-precipitation (25th percentile) versus the high-precipitation scenario (75th percentile).

Discussion

Scientific evidence continues to demonstrate the future importance of climate change on production of food, fiber, and fuel (30). With the exception of potatoes, wheat is the food crop most affected by climate change (31), and as such, greater knowledge and understanding of the agronomic relationship between weather outcomes and wheat yields is crucial to our ability to forecast, understand, and respond to potential future increases in temperature. This knowledge provides agronomists and plant breeders with information about genetic traits that could lead to increased heat resistance in future crop varieties. Knowledge of the impact of potential climate changes on economic variables such as agricultural land values allows policy makers, agriculturalists, and economists to better forecast and plan for a future that differs from the past. This is of great importance with regards to wheat, given that it is the largest source of vegetable protein in low-income countries. These important and significant gains in knowledge have caused the large growth in research efforts and results in the area of climate change effects on agricultural yields.

Our findings indicate that wheat yields have become less resistant to high Spring temperatures over time. These temperatures likely coincide with critical developmental stages such as flowering and grain filling; thus the finding provides opportunities for the wheat breeding community to intensify research efforts to increase resistance to heat stress during focused developmental stages to minimize damages projected under future warming scenarios. Efforts to mitigate damages associated with heat could potentially result in net positive warming effects, as our results indicate that reduced exposure to damaging freezes is a yield-enhancing benefit of a warming climate. Thus, incorporating higher tolerance to heat stress during critical developmental stages is identified as a major research direction for crop scientists. This parallels recent evidence suggesting that active selection and breeding for atmospheric CO₂ responsiveness among cereal varieties is a feasible adaptation strategy (32).

Our results indicate that advancements in heat stress resistance could come at the expense of higher average yields. The estimated tradeoff between yield and heat resistance is an important outcome that has implications for breeding efforts, which have recently placed particular emphasis on stress tolerances associated with anticipated environmental and climatic changes (33). Maintenance breeding is an important and constantly evolving objective among breeders (34–36). Our results also indicate that newer varieties are less heat resistant than older varieties. Newer varieties have longer grain-filling periods, which increases yield potential under ideal weather conditions but introduces additional susceptibility to high temperature exposure during this critical period. This reinforces the need for more focused breeding efforts, as our results suggest that there is currently limited scope for producer adaptation through alternative variety selection.

Our results also indicate that additional rainfall in the Spring can partially offset the negative effects of warming. This has important implications for devising agronomic and water management options to provide supplemental irrigation through sprinklers or aerial watering coinciding with expected extreme heat events during critical growth stages of the wheat plant to help mitigate significant crop losses. Thus, this study provides direction for policy making decisions, particularly for heat-prone wheat production areas in the United States and elsewhere. Furthermore, in considering an adaptation strategy based on irrigation, both producers and policy makers should take into account costs associated with water resource depletion.

In evaluating heat resistance across varieties, we were not able to estimate a separate resistance for each variety. Instead, we focused on the variety release year, a proxy for the imbedded seed technology available at that point in time. This potentially confounds the sensitivity estimate for years in which multiple varieties were released. A more realistic grouping scheme—perhaps based on genetic markers—could aid in the identification of heterogeneous heat sensitivities and associated warming impacts across varieties. Future research might also consider the role of heterogeneous precipitation effects in predicting overall effects of warming, as we found evidence of interactions between cumulative precipitation and temperature exposure. In addition, future efforts might also consider the timing of the weather outcomes within the growing season. Two consecutive days of high temperature exposure could have a more damaging effect on yield then two separate days, as could hot daytime temperatures followed by a hot night versus a hot day followed by a cool night. The timing of precipitation events also matters, as it can provide heat stress relief if it follows a period of high temperatures. Upon addressing these issues, more realistic forecasts of the effects of climate change on wheat yields could be pursued based on the approaches outlined in ref. 11.

Another important finding relates to the manner in which degree days are calculated from daily temperature observations. Previous studies for wheat have typically relied on average daily temperatures for constructing degree days (23–27). We find that first interpolating the distribution of temperature exposures within each day and then calculating degree days provides a statistically significant improvement in model performance, both in and out of sample. Previous approaches in the literature, such as a nonlinear function of average temperature or degree days constructed from mean temperatures, misrepresent the underlying variation in temperature and its associated impacts on yields. We further show that this misrepresentation has important consequences for predicting the impacts of warming temperatures, as it understates the negative effects of extreme heat, and thus warming.

Further research is needed to better understand the potential existence and magnitude of threshold values for measuring degree days. Our findings suggest that there are large negative yield effects at temperatures above 34 °C in the Spring. This threshold was previously used in ref. 20 for wheat production in India and ref. 9 for US farmland values; however, these studies assumed this threshold ex ante whereas our finding is ex post to a thorough statistical analysis of alternative threshold values. This complements the findings in ref. 13, which used a similar data-driven empirical exercise and found thresholds of 29 °C, 30 °C, and 32 °C for corn, soybeans, and cotton, respectively. Although exposures to 34 °C are somewhat rare in most wheat-growing regions, global warming has the potential to increase their frequency. Future research on climate change’s effects on wheat production might benefit from the application of our methodology at a larger spatial scale, augmenting our approach with the elements that improve prediction on a regional scale.

The relationship between temperature and plant growth is likely to be more complex than modeled here, depending on the crop, growth stage, location, and the interaction of other weather variables including humidity, vapor pressure, and solar radiation. This is particularly true for winter wheat, given the long growing period that spans three distinct weather seasons. Greater understanding of extreme weather events is also needed to further our ability to forecast the potential impacts of climate change on crop yields. Further research could devote more attention to improving specifications of the magnitude, duration, and frequency of extreme weather events. Our results also indicate that net warming effects will be substantially overstated if one ignores the effects of reduced exposure to freezing temperatures. Crop improvement will continue to advance with better knowledge of these differential impacts of weather on wheat varieties.

This study is only one part of a larger effort to develop sustainable wheat production worldwide. Achieving this goal in the face of climate change requires integrated approaches across economic, agronomic, soil, biological, hydrologic, and other scientific disciplines whose research can be guided by the results provided in this study. Continued observation of the interaction between increasingly variable weather conditions and wheat production outcomes will allow refinement and enhancement of this modeling approach and provide plant breeders, agricultural policy makers, and private enterprises with important direction for sustaining wheat production in an increasingly hot future.

Methods

Data.

Weather data were taken from Kansas Weather Library. Daily temperature observations correspond to each field trial location. Following ref. 13, a sinusoidal distribution was fitted between daily minimum and maximum temperatures to estimate hourly exposure for each degree Celsius. These exposures were then summed for each month during the wheat growing season, September through May (harvest typically occurs during June). A sine function was fit from daily minimum temperature to the daily maximum temperature, and then a second sine curve was fit from the maximum temperature to the next day’s minimum temperature. Therefore, a “day” is defined as the time between the minimum temperature (early AM) and the next day's minimum temperature. We also collect daily precipitation, which, along with the temperature exposures, is summed up to a cumulative measure for the Fall (September−November), Winter (December−February), and Spring (March−May) seasons. Wheat yield data are from Kansas Performance Tests with Winter Wheat Varieties for the years 1985–2013. All yield data are for dryland (nonirrigated, rainfed) Hard Red Winter Wheat, with some observations of Hard White Wheat. All yield data are in bushels per acre.

Regression Models.

The data vary temporally across growing seasons and cross-sectionally across field trial locations and seed varieties. Time-invariant factors such as soil quality may vary across locations. Although we do not directly observe these invariant factors in the data, we can control for them using location fixed effects. We also include seed variety fixed effects, as the mean yields will vary across this dimension. These variety fixed effects directly control for changes in technology over time, as newer varieties are typically associated with higher yields. We also considered location-by-variety fixed effects instead, but found our results robust across this alternative (SI Appendix, Figs. S17 and S18). A quadratic time trend is included to measure changes in the experimental design of the field trials over time, which could result from changes in best management practices (e.g., more timely fertilizer applications). The trend parameters suggest a slight increase in yields over time at a decreasing rate; however, the parameters are not statistically significant (P > 0.10).

We used multiple regression to estimate the following statistical model:

$$y_{ijt}={\alpha }_i+{\alpha }_j+{\alpha }_{t1}t+{\alpha }_{t2}{t}^2+f({\mathbf{w}}_{jt};\mathbf{\beta })+{\epsilon }_{ijt},$$

where $y_{ijt}$ is log yield for variety i at location j in trial year t, ${\alpha }_i$ and ${\alpha }_j$ capture fixed effects across varieties and locations, ${\alpha }_{t1}t+{\alpha }_{t2}{t}^2$ captures the trend component, and $f({\mathbf{w}}_{jt};\mathbf{\beta })$ captures the (potentially nonlinear) effects of location-specific weather ${\mathbf{w}}_{jt}$ on yields. It is likely that the error terms ${\epsilon }_{ijt}$ are heteroskedastic and autocorrelated. We therefore cluster SEs by year and seed variety using multiway clustering, which allows for errors to be heteroskedastic, spatially correlated within each year, and temporally correlated within each variety (37). We find that this is an important consideration, as SEs are 3.6 times larger when clustering by year alone relative to unclustered (but heteroskedasticity robust) errors, and 3.8 times larger when clustering by year and variety. Future research might also consider clustering by location, which is not feasible here because we only have 11 locations. Previous research suggests that having only 10 clusters, either in a single or multiway framework, can lead to inaccurate statistical inference (37).

We fix the growing season to the months September through May. The length of the growing season, and associated distinction in plant growth stages, makes identifying weather effects difficult in practice. Given these various stages—Fall growth followed by Winter dormancy, and then jointing, booting, heading, and grain development in the Spring—weather impacts can vary substantially across seasons. Thus, our preferred specification for the weather effects is based on seasonal ($s=\mathrm{1,2,3}$ for Fall, Winter, and Spring) weather outcomes for temperature and precipitation.

The specification for the average temperature (AT) model is given by

$$f({\mathbf{w}}_{jt};\mathbf{\beta })={\displaystyle \sum _{s=1}^3{\beta }_{1s}tem{p}_{jst}+}{\displaystyle \sum _{s=1}^3{\beta }_{2s}tem{p}_{jst}^2+}{\displaystyle \sum _{s=1}^3{\beta }_{3s}{p}_{jst}}+{\displaystyle \sum _{s=1}^3{\beta }_{4s}{p}_{jst}^2},$$

where $tem{p}_{jst}$ and $p_{jst}$ are average daily temperature and cumulative precipitation, respectively. Following the piecewise linear degree day approach of ref. 13, the specification for the degree day model is given by

$$f({\mathbf{w}}_{jt};\mathbf{\beta })={\displaystyle \sum _{s=1}^3{\beta }_{1s}Fre{z}_{jst}}+{\displaystyle \sum _{s=1}^3{\beta }_{2s}DDlo{w}_{jst}}+{\displaystyle \sum _{s=1}^3{\beta }_{3s}DDme{d}_{jst}}+{\displaystyle \sum _{s=1}^3{\beta }_{4s}DDhg{h}_{jst}}+{\displaystyle \sum _{s=1}^3{\beta }_{5s}{p}_{jst}}+{\displaystyle \sum _{s=1}^3{\beta }_{6s}{p}_{jst}^2},$$

where $Fre{z}_{jst}$ measures exposure in days to freezing temperatures, $DDlo{w}_{jst}$ measures degree days between zero and the lower threshold, $DDme{d}_{jst}$ measures degree days between the lower and upper threshold, and $DDhg{h}_{jst}$ measures degree days above the upper threshold. As an example, in SI Appendix, Table S4, the lower and upper thresholds in the Fall under the IDD model are 10 °C and 17 °C. We first calculate degree days above 0 °C, 10 °C, and 17 °C, call these DD0, DD10, and DD17, and then construct the regression covariates as $DDlow=DD0-DD10$, $DDmed=DD10-DD17$, and $DDhgh=DD17$, respectively.

The predicted yield impacts when the average weather variables change from the 1985–2013 average ${\overline{\mathbf{w}}}_0$ to the new values ${\overline{\mathbf{w}}}_1$ are derived as the percentage change in yield relative to baseline climate, $impact=100[e^{({\overline{\mathbf{w}}}_1-{\overline{\mathbf{w}}}_0)\mathbf{\beta }}-1]$. We simulate new values for each 1 °C increase up to 5 °C by increasing the observed daily maximum and minimum temperatures and then recalculating the appropriate weather variables. The regression estimates from SI Appendix, Table S4, are used as values for $\mathbf{\beta }$.

To investigate heterogeneous effects of high Spring temperatures across varieties, we first estimated the multilevel model

$$y_{ijt}={\alpha }_j+{\alpha }_{t1}t+{\alpha }_{t2}{t}^2+f({\mathbf{w}}_{jt};\mathbf{\beta })+u_{0i}+u_{1i}DDhg{h}_{j3t}+{\epsilon }_{ijt},$$

where $f({\mathbf{w}}_{jt};\mathbf{\beta })$ is the same as above except that high degree days above 34 °C in the Spring $\left(DDhg{h}_{j3t}\right)$ are removed and their effect is allowed to vary across each variety i. We assume that the random effects $(u_0,u_1)$ are distributed $N(\mathbf{0},\sum )$ where $\sum$ is a diagonal matrix with ${\sigma }_0$ and ${\sigma }_1$ along the diagonal. This model was estimated using the “mixed” command in STATA 13. The model converged but the estimate of the hyperparameter ${\sigma }_1$ was numerically zero, as were the Best Linear Unbiased Predictors for the $u_{1i}$. Thus, we instead focused on the multilevel model

$$y_{irjt}={\alpha }_j+{\alpha }_{t1}t+{\alpha }_{t2}{t}^2+f({\mathbf{w}}_{jt};\mathbf{\beta })+u_{0r}+u_{1r}DDhg{h}_{j3t}+{\epsilon }_{ijt},$$

where the $DDhg{h}_{j3t}$ parameter is instead allowed to vary across the release year r of the variety.