Ionic Current Variability and Functional Stability in the Nervous System

Abstract

Identified neurons in different animals express ionic currents at highly variable levels (population variability). If neuronal identity is associated with stereotypical function, as is the case in genetically identical neurons or in unambiguously identified individual neurons, this variability poses a conundrum: How is activity the same if the components that generate it—ionic current levels—are different? In some cases, ionic current variability across similar neurons generates an output gradient. However, many neurons produce very similar output activity, despite substantial variability in ionic conductances. It appears that, in many such cells, conductance levels of one ionic current vary in proportion to the conductance levels of another current. As a result, in a population of neurons, these conductances appear to be correlated. Here, I review theoretical and experimental work that suggests that neuronal ionic current correlation can reduce the global ionic current variability and can contribute to functional stability.

Plasticity (box 1) in the nervous system is essential in order for it to remain flexible and adaptive in response to both external challenges, such as sensory stimuli or injury, and internal changes, such as growth, aging, or molecular turnover, and is therefore crucial to the survival of an animal. However, too much plasticity can destabilize a system. We know from personal experience, as well as from experimental observations, that individuals maintain a relatively stable identity (engrained, e.g., in our personality, physical traits, and mental abilities) that can be traced over many years without drastic changes, unless we are hit by some catastrophic event. Such identity is also observed at the level of individual neurons and of functional neuronal networks (figure 1; Bucher et al. 2005, Schulz et al. 2006, Goaillard et al. 2009, Norris et al. 2011), and it is maintained over timescales that are much longer than the lifetimes of individual molecules, intercellular connections, or other components of neurons and neuronal circuits. Furthermore, stability is concurrent with the plasticity required of the nervous system to perform effectively; this fact requires that we uncover the mechanisms that enable the simultaneous expression of both plasticity and stability of cellular and network function. Although many forms and mechanisms of plasticity have been characterized, some in great detail, the mechanisms that ensure stability of function are far from understood. Furthermore, disease and aging leads to the breakdown of functional stability and reduced plasticity. Unraveling the processes that underlie functional stability may allow us to improve our understanding of both normal neuronal function and the pathological breakdown of functional stability in the context of aging and disease.

Box 1. Glossary.

Coefficient of variation: A measure of the variance of a variable, obtained by normalization of the variance by the mean value of the variable—the standard deviation divided by the mean.

Conductance correlation: The combination of pairs or subsets of ionic conductances (or currents or messenger RNA levels of the channels that generate these currents) that appear correlated when measured over multiple individuals or cells. These correlations have mostly been shown to be linear and positive.

Global variability: The variability of a biophysical or physiological parameter after the correlated variance of related parameters is taken into account. Specifically here, it refers to the combined variance of all ionic currents in a population of cells in which correlations between currents is observed. Because the currents that generate activity in a cell are additive, their variances would also be additive, unless the currents are correlated. In such a case, the variances are also correlated, and, as a consequence, the global variability is lower by a factor related to the correlation strength between the currents.

Homeostasis: The active maintenance of physiological variables or features, such as body temperature and neuronal excitability, within physiologically appropriate boundaries.

Individual variability: The variability of a specific physiological variable within an individual that may arise from experience, modulation, activity-dependent mechanism, or time-dependent mechanism.

Plasticity: The phenomenon of regulated change of a physiological variable. Many mechanisms have been described, such as synaptic plasticity, synaptic scaling, intrinsic plasticity, metaplasticity.

Population variability: Variability of a specific variable (e.g., the maximum conductance of an ionic current) among individuals in a homogeneous population. This has been called animal-to-animal variability in the literature (Bucher et al. 2005, Goaillard et al. 2009, Roffman et al. 2012, Williams et al. 2013) and relies on the assumption—or on evidence—that the variable is measured in a uniquely identified cell across individuals..

The classic term homeostasis (box 1) refers to the active maintenance of physiological features, such as body temperature and blood sugar levels, within physiological boundaries. The term homeostasis or homeostatic plasticity will be used here to refer to cellular mechanisms that generate stability of neuronal function at the cellular and network levels. Neurons are endowed with mechanisms that constantly monitor and respond to the state of the system. Therefore, these mechanisms continuously and actively contribute to the present state of the system but are typically best revealed when they respond to large deviations of a physiological variable from a basal state in such a way as to bring the system back to its functional range. This is achieved through changes in the expression of key cellular and network components, such as voltage-gated and synaptic ion channels. It is well known that many of these changes are dependent on activity and on the state of the system and are therefore likely to result in highly variable expression levels across individuals as they go through different life histories. Unless it is properly harnessed, this variability poses a serious threat to the stability of the system and must, therefore, somehow be controlled. Key effector molecules that are ultimately the target of regulatory mechanisms are the ion channels that carry electric current across the membrane. Changes in the numbers of different ion channels embedded in the cytoplasmic membrane will result in variable ionic conductance and current levels and, therefore, potentially change the electrical behavior of the neuron.

Variability in ionic current levels can occur during the lifetime of an animal or a cell, and we refer to this as individual variability (box 1). However, the variability of ionic current or conductance levels between unambiguously identified neurons between individuals is being reported in a growing list of different preparations (Khorkova and Golowasch 2007, Olypher and Calabrese 2007, Schulz et al. 2007, Leao et al. 2012, Ransdell et al. 2012, Temporal et al. 2012, Unal et al. 2012), including in genetically identical animals (Liss et al. 2001, Swensen and Bean 2005, Etheredge et al. 2007). This variability across individuals will here be referred to as population variability (box 1). Other biophysical properties of ion channels—for example, voltage dependences, time constants (McAnelly and Zakon 2000, Amendola et al. 2012)—have also been observed to express high levels of population variability. Surprisingly, such variability often has little effect on basic electrical and physiological behavior.

Here, I will discuss this source of variability in the nervous system and how it may affect or even determine neuronal function, under the assumption that ionic currents fully determine neuronal activity. My fundamental claims are that ionic current population variability is an integral element of the function of the nervous system and that neurons and neuronal networks have developed mechanisms that make use of it to generate functional and stable output. In the absence of such mechanisms, the affected system (e.g., a given signaling pathway, the electrical properties of a neuronal class, a specific functional neuronal network) will probably become destabilized with detrimental—and potentially fatal—consequences for the organism as a whole.

In the study of the biological sources of variability, we are beginning to discover a whole new field of inquiry. New mechanisms of stability control are being uncovered that portray a neuron as an even more complex unit than was previously thought.

Variability

The population variability in ion channel expression levels (i.e., mRNA [messenger RNA] copies or conductance levels) and ion current biophysical properties (i.e., activation or inactivation voltage thresholds, activation and deactivation time constants) increasingly being reported in different preparations requires the unequivocal identification of cell types to ensure that the measured variability is not due to sampling different cell types. Such accuracy can, at present, best be achieved only in invertebrate preparations, which, in many cases, contain a very small copy number of unambiguously identifiable neurons (e.g., the leech heartbeat central pattern generator, the stomatogastric ganglion [STG] and cardiac ganglion of decapod crustaceans, molluscan ganglia). In these systems, neurons often occur as single copies, and identification is completely unambiguous. However, advances in the molecular tagging of neurons according to cell-type-specific markers promise measurements in much more complex neuronal systems that can be trusted to belong to well-defined and relatively uncontaminated neuronal populations. Using this approach, large degrees of variability in conductance levels have been shown, for example, in mouse cholinergic forebrain neurons (Unal et al. 2012). Old-fashioned cell identification through localization or anatomical and electrophysiological criteria, sometimes followed by immunocytochemical confirmation, has also yielded quite convincing results (McAnelly and Zakon 2000, Liss et al. 2001, Swensen and Bean 2005, Li and Baccei 2011, Amendola et al. 2012, Leao et al. 2012). However, the data from cell types that are present in multiple copy numbers must be regarded with extreme caution, given that even seemingly well-identified neurons can belong to different cell types. This can, for instance, easily occur on the basis of differential distribution of ionic channels over the dendritic tree (Nusser 2009). Function should be the key cell identification criterion, with molecular and anatomical characteristics serving as supporting criteria, and not the other way around, because function is ultimately what matters to the cell, the neuronal network, and the individual as a whole.

There are instances in which the variability of ionic current parameters in seemingly homogeneous cell populations correlates well with distinct outputs. In such cases, population variability may not be the best term to describe the observed variability, if we follow the dictum stated above that function should be the primary criterion to define cell identity. Such is the case of weakly electric fish electrocytes, which show a wide range of voltage-dependent activation and inactivation time constants of their sodium ion (Na⁺) and potassium ion (K⁺) currents across animals (McAnelly and Zakon 2000). This wide variation of kinetic parameters correlates tightly with the frequency of the electric organ discharges (EOD) that each fish uses for communication and navigation, which is unique for each animal. As a consequence, this variability is of extreme behavioral importance for the animals and is tightly regulated. Furthermore, animals can rapidly change their EOD frequency by modifying the kinetic parameters of these same currents during social interactions, and EOD frequency also depends on the fish's sex and perhaps on its developmental stage or age, because these variations are at least in part mediated by several different hormones (Zakon et al. 1999). This indicates that electrocytes possess a high degree of plasticity with regard to these currents, which serves an important communication function, and also that the variability is at least in part constrained or even determined by sensory and social feedback.

Another example of high variability in a well-defined neuronal population is the different densities and kinetics of voltage-sensitive calcium ion (Ca⁺⁺) and Ca⁺⁺-activated K⁺ channels of hair cells in the vertebrate cochlea. These currents play a fundamental role in the tuning of the hair cells to different input frequencies along the length of the cochlea (Wu and Fettiplace 1996). In this case, it may appear that the cells constitute a homogeneous population, but, strictly speaking, this is not a case of population variability, because hair cells in the cochlea come from a population of cells from one individual, and their distinct properties are constrained and perhaps even determined by both mechanical and molecular gradients along the cochlea.

Although the variability of ionic current properties between same-type cells in electrocytes or cochlear hair cells appears to be directly related to their function, in many instances, such a link is much less obvious. This is best exemplified in systems in which neurons are found in single copy. For example, in the stomatogastric and cardiac ganglia of the crab Cancer borealis, identified neurons express highly variable conductance and mRNA levels of well-defined ionic currents (Liu et al. 1998, Khorkova and Golowasch 2007, Schulz et al. 2007, Ransdell et al. 2012, Temporal et al. 2012). However, what feature of activity each ionic current determines—­or, inversely, which currents each activity trait in the system is determined by—is not clear for any system. It is unquestionable that each ionic current expressed by a neuron affects some (and perhaps many) features of activity, as can be seen from the effects of modifying specific individual currents by pharmacological, molecular, or electrophysiological means. It is also expected that the specific constellation of ion channels expressed by a neuron correlates with the type of activity it expresses (Toledo-Rodriguez et al. 2004, Schulz et al. 2007). However, at the more detailed quantitative level, it has never been shown with what activity feature, if any, the natural population variability of any of the ionic currents expressed by these cells is correlated. In contrast, it has been shown in two different crustacean species (the crab C. borealis and the lobster Homarus americanus) that at least some activity traits of a neuronal network, the different phase relationships of bursting activity between neurons in the pyloric network, are highly conserved across individuals (Bucher et al. 2005, Goaillard et al. 2009). Interestingly, the phase maintenance observed in the pyloric system is also observed in a number of other rhythmic systems: gill ventilation (Dicaprio et al. 1997), leech heartbeat (Roffman et al. 2012), and lamprey swimming (Cohen et al. 1992). Given that the phase is probably influenced by a number of voltage-gated and synaptic currents, which can all be quite variable, the challenge is to explain how this is possible. Phase maintenance in pattern-generating networks is crucial for the generation of the correct behavior, because it determines the orchestrated movement of muscles in their correct sequence at different oscillation frequencies. Therefore, it appears that systems may need to develop compensatory mechanisms to adjust for variable ionic current expression. A dramatic example of functional stability in response to the variable expression of ionic currents is observed in experiments in which an entire ion channel gene is eliminated by knockout techniques or mutagenesis (Guo et al. 2005, Vähäsöyrinki et al. 2006, Etheredge et al. 2007, Nerbonne et al. 2008). The effects of removing the whole ion channel population in these examples had only limited effects, which suggests that compensatory mechanisms are present that balance the effects of changes in one component. Conversely, activity changes in an individual are well known to greatly affect ionic current expression, sometimes homeostatically, to restore output to a stable state (Thoby-Brisson and Simmers 1998, Turrigiano et al. 1998, Luther et al. 2003, Davis 2006, Haedo and Golowasch 2006).

Variability, itself, may define neuronal output or function. Li and Baccei (2011) reported a two- to threefold range of persistent sodium conductance and leak conductance in rat spinal cord lamina I bursting nociceptor neurons. Nonbursting neurons in the same area display a significantly larger range of sodium conductances (more than 25 times larger) but also a higher mean leak conductance. Therefore, the variability of sodium conductance, with no difference in the mean conductance values, appears to be related to the expression of a specific pattern of activity, with lower variability associated with bursting and higher variability with silent or tonic firing activity. In a different study, GABAergic (i.e., ©-aminobutyric acid–producing) interneuron inhibitory input to CA1 (Cornu Ammonis area 1) pyramidal cells was modeled using a conductance-based model that is, itself, based on experimentally measured biophysical parameters. The model showed that the variability of Na⁺, Ca⁺⁺, leak, and synaptic currents and that of the resting membrane potential of the CA1 neurons were as strong a determinant of the effectiveness of the inhibition that they received as were the mean values of these currents (Aradi et al. 2002). The mechanism behind this effect appears to be the nonlinear actions that inhibitory postsynaptic currents can have on action potential generation. The authors also conclude that increased parameter variability in the interneuron population can lead to a desynchronized state akin to epilepsy (Aradi and Soltesz 2002). In general, the conclusion of this and related work is that variability can play a role in neuronal function, even though this type of variability can sometimes be linked to pathological states (Santhakumar and Soltesz 2004). In summary, high degrees of variable expression of individual ion channels are, by now, very well documented in many systems. It was traditionally thought that such variability represented experimental error, but recent data showing similar variance levels and, sometimes, correlated variances between ionic conductances or between the copy numbers of the mRNA species coding for those channels (Schulz et al. 2006) indicate that variability is sometimes—and perhaps often—large and real. Although high variability levels may sometimes be associated with pathologies, evidence suggests that it is a biological phenomenon frequently not associated with disease. The mechanisms by which neurons use such variability to influence output are at this time unknown.

Conductance variability and network function

The ubiquity of variable ion channel expression presents a significant problem for neurons whose stable activity is required for normal function. Such is the case of pacemaker neurons, or neurons belonging to networks that generate rhythmic activity. Most rhythmically active networks control or underlie vital behaviors (e.g., heartbeat, respiration, locomotion, digestion). In such networks, stable phase relationships or bursting activity are typically observed (Cohen et al. 1992, Dicaprio et al. 1997, Bucher et al. 2005, Goaillard et al. 2009, Norris et al. 2011, Mulloney and Smarandache-Wellmann 2012) and are probably crucial to generating appropriate behavior while remaining able to be modulated into different levels or patterns when required by distinct and transient demands on the system. Therefore, it is to be expected that neurons and networks of neurons should be endowed with mechanisms that maintain the activity features that characterize these patterns within relatively narrow functional limits. The question is how the neurons that make up these networks are able to accomplish this. One set of mechanisms that have been shown to be involved in the maintenance of phase constancy operates at the level of the individual. Circuit interactions, short-term synaptic plasticity, and interactions between depressing synapses and intrinsic currents can all contribute to maintaining phase constancy when the frequency of the rhythm varies (e.g., Manor et al. 2003, Greenberg and Manor 2005). A different set of mechanisms is likely to operate across individuals whose phase relationships are very similar, in spite of the large population variability of ionic current levels.

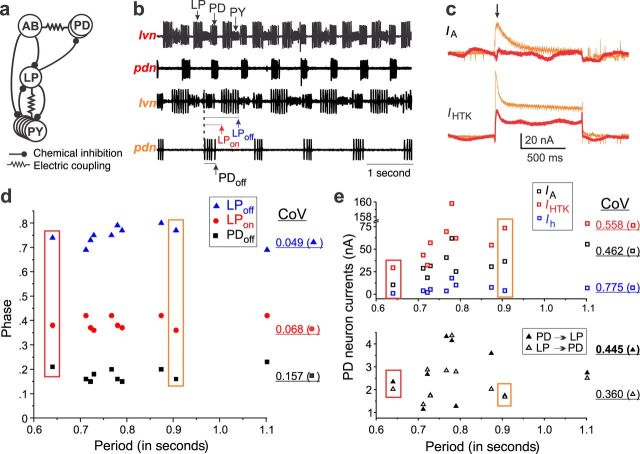
Although the average levels of ionic currents or ion channel mRNA copy numbers are often used to define distinct cellular types (e.g., Schulz et al. 2007, Unal et al. 2012), the important point to take from these and other studies is how remarkably well preserved activity can be in spite of the great variability at both transcript (i.e., mRNA) and current (i.e., protein) levels. Figure 1 shows a clear example of the stability of the rhythmic activity of the pyloric network of crustaceans (figure 1a) in the face of high variability in underlying ionic currents. In figure 1b, the pyloric rhythmic patterns of two animals (top and bottom) observed in vitro and in the absence of any known sensory feedback are shown to be clearly different in period; however, they are remarkably constant in the phase relationships of neuronal firing between the neurons of the network (figure 1d), as is characterized by very low coefficients of variation (CoVs) of the average phase levels at different periods (CoVs in figure 1d; also see Bucher et al. 2005, Goaillard et al. 2009). In contrast, the ionic current levels expressed by the cells of the network (ionic currents of the pyloric dilator neurons are shown in figure 1c, 1e) are quite variable, with CoVs nearly an order of magnitude higher than those of the phase values. As was stated before, we are assuming that the pyloric network activity, including features such as period and phase relationships, depends completely on the intrinsic and synaptic ionic currents expressed by the neurons of the network. It may, of course, be argued that the sample of currents shown in figure 1 is not complete, that only one cell is characterized, and that including other cells and currents may better explain phase constancy. However, all other currents (or channel mRNA levels) measured to date in this system show equally large degrees of variability (Liu et al. 1998, Golowasch et al. 2002, Khorkova and Golowasch 2007, Schulz et al. 2007, Goaillard et al. 2009, Temporal et al. 2012). Therefore, phase constancy among animals must be explained within a context of very large population variability of the underlying ionic currents in this system.

Figure 1.

Constancy of activity with variable currents. (a) Partial schematic diagram of the pyloric network of the crab Cancer borealis, including the pacemaker (AB), two pyloric dilator (PD), the lateral pyloric (LP), and the pyloric constrictor (PY) neurons. (b) Extracellular recordings from two pyloric motor nerves (lvn and pdn) from two different animals (the different color labels). Notice the different periods of the rhythmic activity. (c) Ionic currents I_A (top) and high-threshold potassium ion current, I_HTK (bottom) from PD neurons of the two preparations (red and orange) shown in panel (b). Notice the large amplitude differences. (d) Phase values (i.e., the proportion of the period, beginning with the first spike of the PD burst), for the end of PD burst (PD_off) and the beginning and end of LP burst (LP_on, LP_off) as indicated in panel (b), as a function of the period. The coefficient of variation (CoV) for each phase is indicated at the right. Note the low CoVs for each phase value; n = 9. (e) The maximal current levels (measured at the peak; e.g., the arrow in panel [c]) for intrinsic currents in PD: I_A, I_HTK, and I_h (top panel) and synaptic currents between PD and LP (bottom panel) as a function of the pyloric rhythm period in the same preparation as in panel (d). Note that the CoV values (right) are approximately one order of magnitude higher than those for the phase values shown in panel (d). The colored boxes in panels (d) and (e) highlight the phase and ionic current values, respectively, of the animals whose activity is shown in panel (b) and whose raw currents are shown in panel (c). Abbreviations: ms, milliseconds; nA, nanoamperes.

One possible answer was suggested by a large-scale computer simulation study in which pyloric network activity similar to that observed in lobsters was modeled (Prinz et al. 2004). That study proved that, given the large number of components (intrinsic and synaptic currents) involved and the nonlinearities of each of these components (e.g., voltage dependencies), many solutions could be found that resulted in the same phenotype (Prinz et al. 2004). A question that emerges from these observations is whether all of the solutions that can generate similar behavior lie in a connected continuum in multidimensional parameter space such that slight changes in one parameter still produce the same pattern (Taylor et al. 2006). Alternatively, many discontinuous but appropriate solutions may be generated because of the large number of combinations of highly nonlinear components. In that case, slight modifications of a subset of parameters would not necessarily generate similar patterns of activity. Such a mechanism may explain the intermittent nature (bouting) of the recovery of the pyloric rhythm after it is lost because of the removal of all neuromodulatory input (Luther et al. 2003): The system visits solutions that occupy discontinuous regions in parameter space as the individual conductances vary more or less continuously in response to this perturbation (Khorkova and Golowasch 2007). However, a different alternative would emerge if the regulation of expression of different ionic channels were coupled.

Ionic current coregulation

Even when the variance of a single current appears to correlate with a phenotype, such as the EOD frequency in electric fish (McAnelly and Zakon 2000) or the cochlear hair cell tuning frequency (Wu and Fettiplace 1996), random variability of other currents expressed by these cells could disrupt the precision necessary to ensure the appropriate phenotype. Therefore, a finely regulated coexpression of these currents may be required. In fact, such is the case between the Na⁺ and K⁺ current properties underlying action potentials and the EOD: A close correlation of voltage-dependent activation and deactivation time constants of a delayed rectifier K⁺ current and between the K⁺ current activation and Na⁺ current inactivation kinetics has been reported (McAnelly and Zakon 2000). In a system in which regulating the shape of the EOD is essential, it can easily be envisioned that changing only one or another of the parameters that control the kinetics of their action potentials could alter the properties of the EOD. Confirmation that the observed correlations are essential to generating appropriate behavior, such as by using computational models of this phenomenon, remains to be produced. Similarly, in cochlear hair cells, the conductances of the voltage-dependent Ca⁺⁺ current and the Ca⁺⁺-activated K⁺ current increase in proportion to the resonant frequency of the cell but also in proportion to each other, thus maintaining a fixed ratio between these conductances along a range of conductance values (Wu and Fettiplace 1996). That this relationship is essential to producing the right hair cell frequency tuning was shown with computational models by Wu and Fettiplace (1996).

However, in neurons in which the phenotype is relatively constant and high ionic current level population variability is observed (Liu et al. 1998, Swensen and Bean 2005, Khorkova and Golowasch 2007, Schulz et al. 2007, Norris et al. 2011, Temporal et al. 2012, Ransdell et al. 2013), a tight regulation of parameters between ionic currents could be an even more crucial requirement to ensuring functional stability, because modifying individual ionic currents can profoundly affect some activity traits (Lien and Jonas 2003, MacLean et al. 2003, 2005, van Welie et al. 2004, Zhao et al. 2010).

Invariance of activity and current correlations

One can ask whether the correlated expression of variable ionic currents in these systems can render specific activity features invariant. This question applies equally to cases of individual variability and to those of population variability, although the mechanisms that may generate these two distinct classes of variability could differ. Theoretical work predicts that this should be the case (Burdakov 2005, Olypher and Calabrese 2007, Taylor et al. 2009, Ball et al. 2010, Hudson and Prinz 2010, Soofi et al. 2012, Lamb and Calabrese 2013). Most of these studies show that linear or nearly linear combinations of the maximal conductances of two or more ionic currents (conductance correlations) define regions in parameter space in which activity traits are fixed, although linear relations are not always what is needed. For example, the work by Taylor and colleagues (2009) does not show linear correlations but shows, instead, that nonlinear (higher-order) conductance combinations can specify fixed activity. The important message here is that many forms of conductance combinations can, in principle, stabilize activity within narrow limits (Prinz et al. 2004). Other interesting results from these computational studies indicate a prominent place for correlations of Ca⁺⁺ conductances with other conductances and indicate negative correlations between conductance pairs in specifying constant activity features. Surprisingly, to date, nearly all experimental studies have revealed the existence of linear and positive correlations between mRNA levels that code for different ion channels (Schulz et al. 2006, 2007, Tobin et al. 2009, Ransdell et al. 2012, Temporal et al. 2012) and between maximal conductances or maximal currents of a number of ionic currents in different cell types (MacLean et al. 2003, 2005, Schulz et al. 2006, Khorkova and Golowasch 2007, Ransdell et al. 2012, Temporal et al. 2012). Only a single exception has been reported showing a negative correlation between mRNA levels of two A-type K⁺ currents (Bergquist et al. 2010). Another case of negative correlation was reported between two K⁺ currents (Ransdell et al. 2012), which show positive correlations, however, at the mRNA level, suggesting posttranscriptional regulation of these correlations.

The studies of MacLean and colleagues (2003, 2005) were perhaps the first to directly show that the cross-regulation of two ionic currents leads to the stabilization of an activity feature in a cell. They showed that the overexpression of one ionic current (Shal-mediated I_A) in a pyloric neuron of the lobster STG led to a compensatory enhancement of a different current (I_h), which set postinhibitory spiking latency at a nearly constant value. When the I_h enhancement was pharmacologically prevented, significant increases in postinhibitory spiking latency were observed. At first glance, a fast, transient, depolarization-activated outward current, such as I_A, does not seem to be an obvious candidate to be functionally complementary to a slow hyperpolarization-activated and noninactivating current, such as I_h, as these results suggest. However, they seem to do the trick, because the current levels generated by each during a depolarization depend on their level of deinactivation and activation, respectively, at negative voltages. However, there are a number of current pairs that have been found to be correlated that do not seem to be functional antagonists but are positively correlated (e.g., I_Na and I_h [Schulz et al. 2007], I_Ca and I_Na [Tobin et al. 2009], I_A and I_HTK [high-threshold potassium current; Khorkova and Golowasch 2007]). The role of these correlations remains largely unknown.

An elegant test of the idea that currents can balance each other to restrict phenotypical variability was recently reported by Ransdell and colleagues (2013). These authors showed that the large-cell (LC) motor neurons of the crab cardiac ganglion produce bursts of activity that are very similar in shape even though each one of the five different LC neurons within each animal expresses highly variable ionic conductance levels. Therefore, they predicted that throwing these conductances out of balance by a similar amount in all LC neurons (by applying a pharmacological blocker of one of the LC neuron's ionic currents) should result in each cell's producing a different output. By recording from several cells simultaneously, this is precisely what they observed (Ransdell et al. 2013), which implies that each cell finely balances its ionic currents individually to produce a similar activity phenotype.

The previous example illustrates how, at a single-cell level, activity can be stabilized by conductance coregulation. This has led to the prediction that a balance of intrinsic and synaptic currents will lead to the stabilization of network activity. Grashow and colleagues (2010) combined a biological and a computational approach to manipulate the maximal conductances of intrinsic and synaptic currents of STG neurons using the dynamic clamp technique. As was expected, they found maximal conductance combinations of synaptic and intrinsic currents that produced similar rhythmic activity, which suggested that neurons are sensitive to—and, therefore, effectively monitor—the activity of their network neighbors through synaptic interactions and somehow adjust conductances, accordingly giving rise to high degrees of individual current variability. However, as was indicated before, activity features have also been shown to be remarkably constant among different animals (figure 1; Bucher et al. 2005, Goaillard et al. 2009, Norris et al. 2011), in spite of large degrees of conductance variability in identified neurons among different animals (Liu et al. 1998, Khorkova and Golowasch 2007, Schulz et al. 2007, Norris et al. 2011, Ransdell et al. 2012, Temporal et al. 2012). This is a complex and as yet unresolved problem, because it implies that neurons in a network can monitor network activity and bring a large number of conductances to a point in a parameter space of high dimensionality that defines activity constancy. Alternatively, species may have evolved to endow individuals with a mechanism that somehow forces each one of them into a parameter space region that ensures activity constancy (e.g., phase constancy; figure 1) for all members of a population. How this can be achieved is not known. In a recent report, O’Leary and colleagues (2013) showed, however, a remarkably simple mechanism by which the correlated expression of ion channels may be achieved. They showed that a homeostatic rule that controls the expression of ion channels in an activity-dependent manner will result in a distribution of correlated maximum conductances that are both highly variable and distributed along linear relations in a population of independent individuals whose initial values are randomly distributed.

In a leech, the heart beat is controlled by a neuronal network that generates two distinct behaviors: synchronous and peristaltic heartbeats (Norris et al. 2011). In the peristaltic mode, the motoneurons that drive each consecutive segment of the heart to contract fire in phase progression, and the phase is well maintained across individuals. However, some motoneurons from different but adjacent segments receive inputs from exactly the same set of interneurons. Moreover, a large degree of variability in synaptic strength is observed among those inputs. So, how is phase progression achieved? Norris and colleagues (2011) examined the hypothesis that this is achieved by controlling the relative synaptic conductances that each motoneuron receives from the interneurons that synapse on them. If the conductance of the different synaptic inputs that each motoneuron receives is different, identical phase progressions in different animals may be achieved by ensuring a balanced input of relative synaptic conductances. They tested this in an experimental tour de force in which three motoneurons were voltage clamped in succession to measure the synaptic conductance that each received from each of four interneurons, and they also measured the activity output of the entire network. Surprisingly, they observed no relationship between the relative conductances and phases of activity. The authors concluded that each animal probably arrived at a solution to generate fixed phases that is unique to each cell and that depended on all or, at least, a large set of the voltage-gated ionic and synaptic conductances that each motoneuron expresses (Norris et al. 2011).

As was described above, a similar phenomenon is observed in the pyloric network of crustaceans, in which the phase relationship of bursting activity of the cell types that compose the pyloric network is remarkably preserved across animals (figure 1; Bucher et al. 2005, Goaillard et al. 2009), despite huge levels of variability of all the conductances expressed by these cells, including synaptic and voltage-gated currents. In an effort to explain this, Goaillard and colleagues (2009) measured nine conductance levels (or their underlying mRNA levels) in two key neurons of the network. Although they did observe some clear correlations between certain activity features and conductance levels, they found no clear link that could explain phase constancy. Although many ionic currents were measured, something was still missing. Some of the ionic currents that play a central role in neuronal activity are Ca⁺⁺ currents, which theoretical studies indicate may be crucial. However, they are notoriously hard to measure in pyloric neurons because of their small amplitude and space clamp limitations.

These two studies highlight the importance of measuring as complete a set of conductances and their parameters in each animal as is possible in order to obtain a satisfactory explanation for a phenomenon such as phase progression in the leech heart or phase constancy in the pyloric network. If theoretical studies are an indication, conductance correlations may hold the key to explaining the important phenomenon of phase constancy in rhythmic systems. However, the static measurements of ionic currents obtained with the voltage clamp technique or (especially) ion channel mRNA copy numbers measured with single-cell quantitative polymerase chain reaction may be part of the problem. It is possible that neurons can adjust their effective ionic current levels (both synaptic and intrinsic) during the ongoing activity of a cell, thanks to their voltage-dependent activation and inactivation properties or activity-dependent mechanisms to achieve a similar phenotype between animals independent from their starting level. Such mechanisms are not known at the moment, but there are indications that they could, in principle, be the mechanisms to adjust the relative current levels in a dynamic manner. As was mentioned before, Ransdell and colleagues (2012) showed that an A-type K⁺ current and a Ca⁺⁺-dependent K⁺ current express a negative functional relationship at the conductance level, whereas they are positively correlated at the mRNA level (Ransdell et al. 2012). Temporal and colleagues (2012) also found that mRNA-level relationships between currents and conductance-level relationships between the same currents are different and that this can be influenced both by the neuromodulatory environment and by activity. All of this suggests the possibility that real-time adjustments of the effective currents involved in shaping activity override the underlying basal values of conductance or mRNA levels that available technology allows us to measure.

Another interesting observation made in neurons from the crab pyloric network suggests that neurons can control the balance between ionic conductances in order to achieve functional stability. When neuromodulatory input to the pyloric network is removed, its rhythmic activity ceases (Thoby-Brisson and Simmers 1998, Luther et al. 2003). If neuromodulators are restored, rhythmic activity returns immediately (Zhao et al. 2010), which indicates that the role of some of these neuromodulators is pattern generation, itself, through the activation of a specific ionic current (Zhao et al. 2010). If neuromodulators are permanently removed, rhythmic activity is homeostatically restored by a very different mechanism, which involves changes in the expression of several ionic currents (Thoby-Brisson and Simmers 1998, Luther et al. 2003, Khorkova and Golowasch 2007). Moreover, this rhythmic pattern of activity is restored to a state that very strongly resembles the control state (Luther et al. 2003), even though neuromodulators are no longer present and are, therefore, no longer part of the pattern-­generation mechanism itself. Therefore, it appears that, somehow, the system is capable of readjusting its components to produce an indistinguishable pattern through two very different mechanisms. However, it was also found that some of the correlations normally observed between several of the ionic currents in these cells are lost when neuromodulators are absent. This indicates, on one hand, that some correlations are under neuromodulatory control (Khorkova and Golowasch 2007, Temporal et al. 2012). On the other hand, it also suggests that the correlated expression of ionic currents (when neuromodulators are present) may restrict the possible balance among currents that a cell needs in order to generate a specific type of activity. Once the variabilities of the currents are no longer coupled, the system may be able to find a new solution in a less restricted parameter space to produce pyloric-type activity.

Cellular mechanisms

A number of important questions arise at the level of the cellular and molecular mechanisms that underlie the phenomena described thus far, but an extensive description and analysis of these mechanisms would merit a separate review. Briefly, it is crucial that the following questions be experimentally examined: What mechanisms may generate variability of ionic current expression? What mechanisms may determine the correlated expression of ion channels in a cell or across a population of cells? Are there distinct rules that govern how synaptic or intrinsic variability is generated and handled by an organism?

Mechanisms that generate ionic current variability at the individual level may include well-known mechanisms of transcription, translation, or posttranslational regulation and their interactions. For example, the alternate activation of activity-dependent regulation of channel density and the action of some hormone or neuromodulator on the level of those same channels may result in varying degrees of channel expression, depending on the relative timing of those interactions. At the population level, variations among individuals will be the consequence of the same mechanisms acting on individuals but recorded at different times in their lives after undergoing different regulatory experiences over that time.

A surprisingly simple mechanism that explains how variable levels of different ionic currents may be correlated across a population was recently reported by O’Leary and colleagues (2013) and was described earlier. Starting with randomly different initial values of different channel populations, correlated expression results very simply if the levels of those channels are regulated by activity. This is not restricted to one pair but can affect multiple channel types, as long as they are all regulated by activity. Another recently discovered mechanism is the transcriptional coupling of ion channels (Bergquist et al. 2010). This mechanism was shown to homeostatically limit the total amount of transient K⁺ current in Drosophila neurons.

About whether distinct rules govern synaptic or intrinsic variability, there is no a priori reason for which that should necessarily be the case. Both channel types can, for example, be regulated by activity. A good example comes from work from Turrigiano and colleagues (1998, Desai et al. 1999), who showed that not only synaptic currents but also intrinsic currents in rat cortical pyramidal neurons are homeostatically regulated by the same activity modifications. The exact molecular mechanisms involved in the regulation of each class of channels, however, may not be exactly the same, but that still needs to be fully worked out in that and many other systems.

Do multiple current correlations generate stability of multiple activity traits?

Intrinsic excitability may sometimes be homeostatically maintained at the single-cell level, whereas the network that these same cells belong to may not be able to maintain stable activity, as is the case in some forms of epilepsy (Echegoyen et al. 2007, Howard et al. 2007). Mossy cells in the rat dentate gyrus undergo numerous changes in intrinsic and synaptic properties that are consistent with cellular homeostatic plasticity (Howard et al. 2007), but, overall, the tissue remains hyperexcitable, and network function is not restored. A similar situation occurs with the pyloric network of crabs and lobsters, in which pyloric activity is largely restored in response to the complete removal of neuromodulators, except for some activity features, such as oscillation period (Thoby-Brisson and Simmers 1998, Luther et al. 2003). This highlights the need to examine all aspects of function, some of which may correlate with certain conductance changes, whereas others may not. This was addressed with the use of the dynamic clamp technique and one identified cell of the crab pyloric network (Zhao and Golowasch 2012). The conductance levels of a subset of the ionic currents expressed by this cell were varied around their endogenous levels. The key of the experiment was to vary the conductance levels of each current relative to those of other currents (while staying within the range of values observed in the natural population). The authors observed that correlated changes in a set of three conductances could account for a significant part of the variability (from 50% to 76%) of 10 different features of pyloric rhythm activity. This suggests that neurons somehow globally tune the currents that they express to optimize many features of activity simultaneously but also hierarchically (some more stringently than others; Zhao and Golowasch 2012). What role this serves is not clear. One possibility is that neurons globally tune their ionic currents to respond to certain inputs that they normally receive (synaptic, modulatory) in a way that preferentially optimizes some activity traits over others. Which activity traits are optimized and for what purpose is an open question, and the answer almost certainly depends on the function of the network.

Conclusions

Neurons of the same type express variable ionic current levels, but they typically express similar activity, sometimes to a remarkable degree. It is clear by now that this variability is not due only to experimental error but that it is intrinsic. Although the roles of this variability are understood in some cases, for the most part, variability appears to be a major challenge that neurons must deal with in order to achieve similar activity. Likewise, it is a major challenge for us to understand how variability is generated and how it is controlled. Furthermore, we still have a long way to go before we can understand the functional consequences of ionic current coregulation and coexpression. At first glance, however, it appears that regulating conductance correlation may be a way to control global variability both for individual neurons and for functional neuronal networks.