Modelling highly variable environmental factors to assess potential microbial respiration in complex floodplain landscapes

Abstract

The hydrological exchange conditions strongly determine the biogeochemical dynamics in river systems. More specifically, the connectivity of surface waters between main channels and floodplains is directly controlling the delivery of organic matter and nutrients into the floodplains, where biogeochemical processes recycle them with high rates of activity. Hence, an in-depth understanding of the connectivity patterns between main channel and floodplains is important for the modelling of potential gas emissions in floodplain landscapes. A modelling framework that combines steady-state hydrodynamic simulations with long-term discharge hydrographs was developed to calculate water depths as well as statistical probabilities and event durations for every node of a computation mesh being connected to the main river. The modelling framework was applied to two study sites in the floodplains of the Austrian Danube River, East of Vienna. Validation of modelled flood events showed good agreement with gauge readings. Together with measured sediment properties, results of the validated connectivity model were used as basis for a predictive model yielding patterns of potential microbial respiration based on the best fit between characteristics of a number of sampling sites and the corresponding modelled parameters. Hot spots of potential microbial respiration were found in areas of lower connectivity if connected during higher discharges and areas of high water depths.

1. Introduction

River systems can be viewed as open ecosystems dynamically linked along the river network and within the riverine landscape at the catchment scale. The water exchange conditions and the linkage to the hydrological regime at the local (i.e. reach) scales determine matter transport, cycling and transformation (Tockner et al., 2000). Within riverine landscapes, riparian wetlands and floodplains are key areas for biogeochemical cycling, where the hydrological dynamics affect the temporal variability and spatial heterogeneity (Amoros and Bornette, 2002, Cook, 2007). The constant adaptation to changing hydrology and nutrient inputs occurring within in the floodplains create a variety of processes occurring at different scales and interfaces (Ward et al., 1999). As a result, these riverine landscape features, where physical sedimentation and biological activities occur, act as biogeochemical hot spots, in particular for carbon and nitrogen cycling (McClain et al., 2003). Consequently, this variability at the local scale has been shown to impact global elemental cycles (Seitzinger et al., 2006, Battin et al., 2009). Especially, the roles of river networks and within rivers, the role of different landscape elements such as floodplains, have been recently discussed for their contribution to global estimates of carbon cycling (Battin et al., 2009).

The delivery patterns of carbon and nutrient inputs and carbon dioxide emission along river ecosystems are strongly related to surface connectivity (Hein et al., 2004, Preiner et al., 2008). While the input of nutrients, sediment and organic matter occurs mainly via surface flow from upstream, significant amounts of these materials are deposited during floods. The transfer and storage of materials in floodplains are largely under the control of the connectivity pattern within the river landscape as well as of the magnitude, frequency and duration of floods (Pinay et al., 2002, Richardson et al., 2004). In dynamically connected retention areas, the pattern of surface and sub-surface flow provides the basis for intensive microbial processing, in particular the frequency, duration, timing and intensity of floods directly affect carbon turnover in sediments and alluvial soils (Pinay et al., 1995, Pinay et al., 2000, Pinay et al., 2007).

As a result of flood protection engineering, riverine floodplains in urban or agricultural areas are often decoupled from the main river, thus changing their connectivity patterns and nutrient cycling regimes. Restoration by reconnection is an attempt to recreate the nutrient processing potential of floodplains (Klocker et al., 2009). However, created and restored sites, due to homogenous sediment characteristics and changing hydrological regimes, may not return to the full potential of undisturbed, heterogeneous systems (Bruland et al., 2006, Orr et al., 2007).

Understanding changing environmental conditions and predicting the resulting effects requires integrated modelling of river systems (e.g. Arheimer et al., 2004, Poole et al., 2004, Laursen and Seitzinger, 2005, Hollander et al., 2006, Johnson et al., 2007, Metcalf et al., 2010). It is necessary to integrate the understanding of river ecosystems, nutrient dynamics and microbial processing, while considering the possible effects of restoration in order to evaluate the impact of restoration. While hydrological models have been widely applied for traditional engineering solutions in water management, the use as tools for river restoration is a recent development, which has been used to answer habitat requirements, hydrodynamics, changes in biodiversity and nutrient transformation (Trepel and Palmeri, 2002, Jones et al., 2006, Liu et al., 2008, Groffman et al., 2009).

However, modelling of the actual underlying processes has shown to be particularly challenging. In Zeng et al. (2006), a process-based biogeochemical model was applied to study nutrient cycling in a small impoundment. Kondolf et al. (2006) proposed the use of process-based conceptual models in order to facilitate ecological restoration. A catchment-scale modelling study of surface water–groundwater interaction and nitrate attenuation in riparian zones was presented by Rassam et al. (2008) using various water quality model components. Despite these process-based approaches a modelling framework determining in high spatial detail the environmental factors responsible for biogeochemical processes, eventually allowing an assessment on the landscape scale, has not been available so far.

This paper presents such a modelling framework and its underlying modules that aim at predicting spatially detailed system connectivity and related output patterns of potential microbial sediment respiration leading to CO₂ emissions in complex floodplain landscapes. The predictive model integrates hydrology and morphology. It is based on morphological input derived from LiDAR, bathymetric and terrestrial surveys, a long-term hydrograph of the main river, and biogeochemical and physical characteristics of sediment samples taken in the field. In a first step, connectivity patterns and wetting/drying cycles of natural floodplain environments were determined for a computation mesh based on the output of 2-D steady-state hydrodynamic modelling combined with a long-term discharge hydrograph of 30 years using a gauge transformation technique. This allowed for an automatic analysis of flow events, eventually yielding statistically relevant statements regarding connectivity probabilities and the respective duration of connection and disconnection cycles for every mesh node within the computational domain. These properties were assigned to field samples according to the sampling location. In a final step, the model linked the properties of every computation node to those of the field samples employing a best-fit approach based on least square errors. The predictive power of the modelling approach was applied to two study sites located in the Alluvial Zone National Park of the Austrian Danube East of Vienna.

2. Modelling approach

The modelling framework relies on five fundamental prerequisites: (i) a high-quality digital elevation model of the study area, derived from LiDAR and combined with additional bathymetric and terrestrial measurements; (ii) a computation mesh representing the topography reasonably well, i.e. by applying local mesh refinement; (iii) water surface elevations for several characteristic river discharges derived from hydrodynamic modelling; (iv) a long-term discharge hydrograph, covering 30 years or more, for a gauge either within the computational domain or used as boundary condition for the hydrodynamic model; (v) a statistically relevant number of field sediment samples and their biogeochemical properties measured in the lab.

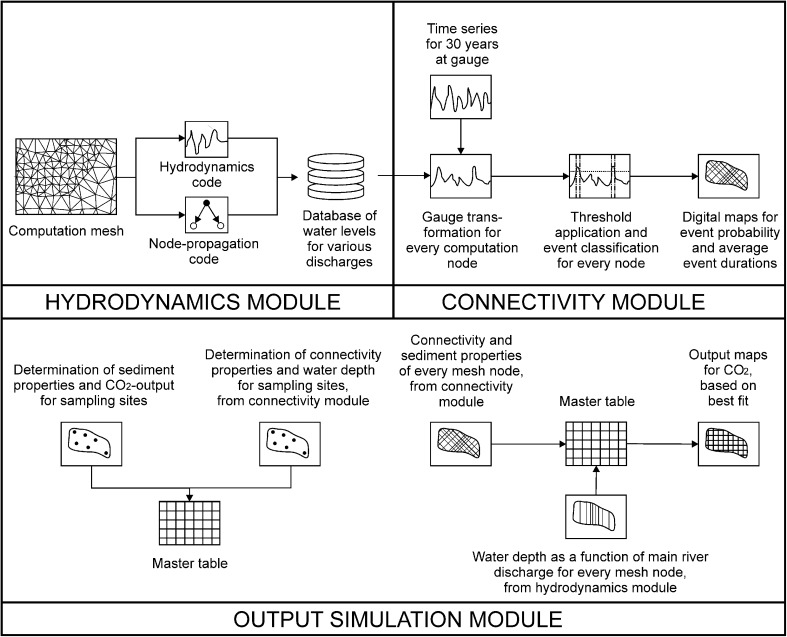
Within the modelling framework, data processing was performed in three modules (Fig. 1): (a) a hydrodynamics module, used for computing water surface elevations in the floodplain for characteristic river discharges; (b) a connectivity module, linking the output of the hydrodynamics module with a long-term hydrograph and performing an automatic event classification to yield connectivity properties of every computation node; (c) an output simulation module, calculating the potential microbial respiration for the entire mesh based on the best fit of hydrological and morphological properties at sampling sites.

Fig. 1.

Modules, components and flow chart of the modelling framework.

2.1. Hydrodynamics and node-propagation module

Any hydrodynamic model capable of delivering steady-state water surface elevations for a 2-D domain is suitable for this module, which particularly includes all 2-D and 3-D numerical models. If the number of model boundary conditions is reduced to one – as in some backwaters or flood retention pools – the dynamic component could be dropped from the flow equations and a simple node-propagation technique could be applied to obtain the water surface elevations.

In the study presented here, the 2-D hydrodynamics code Current2D (Milbradt, 2002) was used to obtain water surfaces for characteristic discharges between low and high flow conditions. It solved the shallow water equations using stabilized finite elements on a triangular mesh. Turbulence was modelled by means of the Smagorinsky (1964) eddy-viscosity approach. In this approach, the molecular viscosity of water is augmented by an eddy viscosity, which is calculated from local derivatives of the velocity field and thus encounters for the spatially varying effect of turbulence in every element of the computation mesh. Time discretisation was conducted by an explicit Euler technique; in this method, the temporally varying flow field and water surface elevations are calculated for a large number of small time steps, requiring that every time step is completed before calculation of the variables for the next time step commences, since they depend on the previously determined values. In elements with a water depth of less than 0.1 m only a standard Galerkin approximation was performed, which means that a horizontal water surface was assumed and its level was approximated by the water levels of surrounding elements. Among other studies, the numerical model was successfully applied in an analysis of the large flood of 2002 in the Danube river basin (Tritthart and Milbradt, 2003).

In simulation domains (i.e., study sites) characterised by inflow and outflow through the same cross-section profile, resulting in only one boundary condition, a node-propagation technique was employed using the RSim-GUI graphical pre-processor of the RSim-3D hydrodynamic model (Tritthart and Gutknecht, 2007a, Tritthart and Gutknecht, 2007b): similar to a particle tracing approach (Tritthart et al., 2009), a given water surface elevation – or flood wave crest height – was propagated from a computation node to its dry neighbours provided sufficiently low bed elevation. This procedure was realised using a binary tree data structure which guaranteed very fast execution time, particularly in comparison to a fully 2-D shallow water model. As only the final steady-state water surface was of interest, such a calculation without dynamic components did not introduce additional error.

The calculated water surfaces for every node and characteristic discharge were inserted into a database used by the connectivity and output simulation modules. In addition to these results of steady-state simulations, a minimum water surface was calculated for every node, corresponding to the lowest possible water level at this location. This minimum water surface was identical to the terrain elevation for nodes that could actually fall dry, while it corresponded to the horizontal pool water level in all regions within the computational domain that remained wet due to pool conditions in the hypothetical case of the main river falling completely dry. The minimum water surface was determined by computing a stepwise water-level drawdown from a high starting level, either by hydrodynamics or node-propagation: whenever the model predicted a node to be wet at a higher water surface elevation and dry at a lower water surface elevation, even though its elevation allowed it to be wet under these conditions, pool conditions were present for that node. In such a case, the corresponding pool water surface was found iteratively between the two elevations. The calculated minimum water surface elevations directly correspond to the threshold of connectivity for every node: whenever a node encounters a water surface elevation higher than the minimum water surface, it must necessarily be connected to the main river. All connectivity threshold elevations for every node were inserted into the database as well.

2.2. Connectivity module

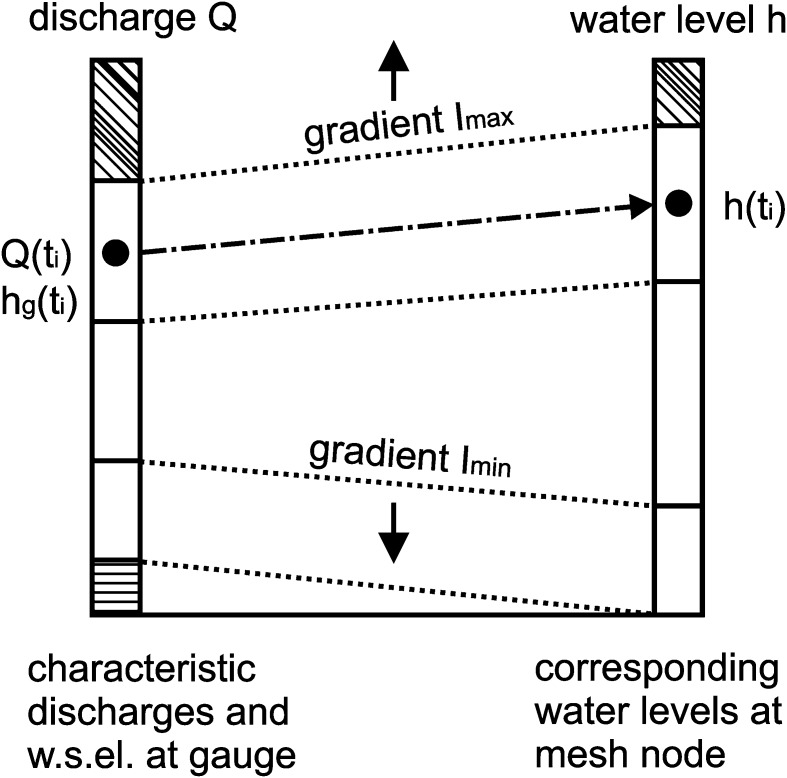
Using the water surface elevations determined by the steady-state hydrodynamic simulations, a relationship between characteristic discharges at a gauge and the corresponding water levels at each mesh node could be established (Fig. 2). A linear interpolation within the water level range encompassed by the characteristic discharges higher and lower than the discharge for the current time step within the discharge hydrograph was usually sufficient to yield the local water level. Water levels for runoff higher than the maximum simulated discharge were extrapolated based on the water surface gradient of the maximum simulated discharge (I_max). The same technique was applied for the lowest simulated discharge and the corresponding gradient I_min.

Fig. 2.

Diagram representing the gauge transformations: based on steady-state numerical modelling of water surface elevations (w.s.el.) for characteristic discharges Q, the unknown water levels h for specific points in time t_i at arbitrary locations within the computational domain can be derived from known water surface elevations at the gauge h_g; maximum (I_max) and minimum gradients (I_min) for every location are applied for water levels above the highest or below the lowest modelled discharge, respectively.

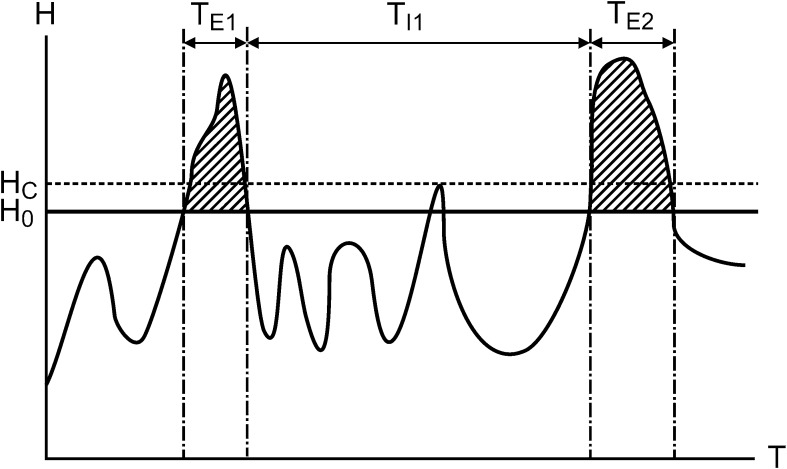
This procedure, referred to as gauge transformation, was applied to a hydrograph covering a statistically relevant period; usually 30 years or longer. As result of this procedure a local, virtual hydrograph of water levels H was obtained for every computation node (Fig. 3). Applying the respective connectivity threshold H₀, calculated individually for each node within the hydrodynamics module, this stage hydrograph was then converted into a time series of binary information for each node, corresponding to a connected or disconnected state. Subsequently, by analysis of the binary state changes, the time series was broken down into events. This allowed calculating event duration T_Ei and interval between events T_Ii. However, while the connectivity threshold was a reasonably good limiting value for the calculation of event durations, smaller flow events may not have reached the respective computation node, due to levelling caused by retention effects during wave propagation which were not covered in the modelling approach. Therefore, an event was only counted at an individual node if its peak was sufficiently higher than the connection threshold H₀ for this node. This correction for hydrologic retention was realised by introducing a critical connection threshold H_C for each node. This threshold was obtained from: H_C = H₀ + c, where c is a system-wide constant which must be calibrated according to gauge readings but is usually small, i.e. in the range of 0.05 to 0.10 m.

Fig. 3.

Diagram representing the event analysis in the connectivity module: events are defined as sections of the hydrograph exceeding the connectivity threshold H₀ as derived from the computation of a minimum surface by numerical modelling of a water surface drawdown; in order to account for retention leading to levelling of comparably small peaks in the hydrograph, events are counted only if exceeding a critical water surface elevation H_C. Event duration is denoted by T_Ei, intervals between events by T_Ii.

After a statistical evaluation of frequency and duration of event occurrence, the resulting parameters were obtained: (i) probability of connection (connectivity); (ii) average connection duration; (iii) average disconnection duration. This statistical information was then stored for every computation node, and used for plotting maps of connectivity properties.

The connectivity module outlined here comprised a number of simplifications regarding the actual fluvial processes encountered during the exchange of mass between a river and its riparian zones. These simplifications are therefore only applicable under several premises:

• 1.Negligible hysteresis effects in the study area. Water levels were assumed to be equal for the same discharge during the ascending and descending limb of the flood hydrograph.
• 2.No sharp increase or drop in water levels. The approach was based on quasi-steady state hydrodynamic modelling results. Therefore, the temporal change in water levels must be smooth at any time.
• 3.Comparably small size of the domain of interest or study reach. The propagation time of flood waves through the computation domain must be of the same order/scale as the time resolution of the input hydrograph, as otherwise significant errors would be introduced.

If the abovementioned assumptions are not met, the hydrodynamic model must be run in unsteady mode for the entire duration of the input hydrograph instead. In such a case the node-propagation code cannot be used.

2.3. Output simulation module

The output simulation module connected the output of the hydrodynamics and connectivity modules with sediment properties in order to predict the potential biogeochemical output of the entire system. This was performed in a two-stage procedure (Fig. 1): (i) assemble the master table, which linked physical, biogeochemical and hydromorphological parameters of all samples taken; (ii) calculate the best fit for properties at an arbitrary mesh node as a function of main river discharge and corresponding water depths.

The output simulation module was based on the parameters given in Table 1, derived from the hydrodynamics module (Hy), the connectivity module (Co) or field sampling (Sa). Parameters 1 through 5 were input parameters, whereas parameter 6 was a model output parameter. For each of the input parameters, the minimum and maximum values were determined in order to allow for deriving dimensionless parameters through standardisation. For every computation node i and every row of the master table, corresponding to sampling point j, the residual R_i,j was evaluated according to Equation (1),

$$R_{i,j}=W_{\text{H}}{\left(\frac{H_i-H_j}{H_{\max }-H_{\min }}\right)}^2+W_{\text{D}50}{\left(\frac{D_{50,i}-D_{50,j}}{D_{50,\max }-D_{50,\min }}\right)}^2+W_{\text{PC}}{\left(\frac{P_{\text{C},i}-P_{\text{C},j}}{P_{\text{C},\max }-P_{\text{C},\min }}\right)}^2+W_{\text{TC}}{\left(\frac{T_{\text{C},i}-T_{\text{C},j}}{T_{\text{C},\max }-T_{\text{C},\min }}\right)}^2+W_{\text{TD}}{\left(\frac{T_{\text{D},i}-T_{\text{D},j}}{T_{\text{D},\max }-T_{\text{D},\min }}\right)}^2$$ (1)

where W_H, W_D50, W_PC, W_TC and W_TD were weighting factors of the parameters water depth, median sediment grain size, connectivity, average connection duration and average disconnection duration, respectively. The sampling point j featuring the minimal residual R_i,j was assumed to be representative for the computation node i, and the corresponding output parameters for potential microbial respiration were set for the mesh node. Once the output for all nodes had been derived, output maps of the computation domain could be plotted.

Table 1.

Parameters of the output simulation module; Hy = hydrodynamics module, Co = connectivity module, Sa = field sampling.

Parameter #	Parameter description	Hy	Co	Sa
1	Water depth, H	m
2	Median sediment grain size, D50			mm
3	Connectivity, PC		%
4	Average connection duration, TC		days
5	Average disconnection duration, TD		days
6	Potential carbon dioxide (CO2) output OCO2			mg m−2 h−1

In the study presented here, the weighting factors were derived from a Mantel Test on the entire master table, yielding the corresponding influence of the input on the output parameters (Table 2). In general, a Mantel Test is a statistical test of the correlation between two matrices. Welti et al. (submitted for publication) used Mantel Tests to explain the relationship between hydrology and geomorphology on potential denitrification and microbial respiration (substrate induced respiration), demonstrating the underlying hierarchy. Mantel statistics do not have to be large, i.e. close to 1 or −1, to be statistically significant. Significance of path coefficients was assessed by randomizing all involved matrices using 10⁴ permutations, building randomized distributions for each path coefficient, and computing probabilities for observed path coefficients with the percentile method (Manly, 2006). All calculations were done in R 2.9. (R-Development-Core-Team, 2005), using the packages vegan (Oksanen et al., 2010) and sem (Fox et al., 2010). Mantel and partial Mantel (controlling for effects of hydrology) statistics were used to test for associations between metavariables, and causal modelling on dissimilarity matrices (i.e. path analysis using Mantel statistics treated as correlation coefficients) to relate the various metavariables in the hypothesized causal framework (Legendre and Legendre, 1998, King et al., 2005). These tests were based on matrices containing measured parameters describing floodplain morphology, hydrology, organic carbon sources and nutrient availability in the floodplain sediments during a two year study in the floodplain study sites. These links demonstrated to which extent the relationship between the floodplain hydrology and the potential respiration was mediated by the geomorphological context of the area. The weights for Equation (1) were derived from the Mantel Test results (Table 3) for the floodplain systems investigated, creating a general statistical model for potential microbial activity. The hydrology metavariable included the parameters connectivity, average connection duration and average disconnection duration; physical descriptors included sediment grain size, temperature and water depth (Table 2). As temperature was considered constant to remove the effects of seasonality, allowing for a generalised view on the output processes, the weights were derived from the associations between metavariables. Following the requirement that weights for parameters combined under the same metavariable must be equal to each other, this resulted in W_H = W_D50 = W₁ and W_PC = W_TC = W_TD = W₂. As the weights must sum up to unity, we obtained the conditional equation: 2W₁ + 3W₂ = 1, or W₂ = 0.333 (1–2W₁). Given that the metavariable association between the physical template and output processes was determined as 0.13, whereas the association between hydrology and output processes was calculated as 0.08 (Table 3), the ratio between W₂ and W₁ could be calculated: W₂ = 0.08/0.13 W₁ = 0.615W₁. Substituting this ratio for W₂ in the conditional equation resulted in the following coefficients: W_H = 0.26; W_D50 = 0.26; W_PC = 0.16; W_TC = 0.16; W_TD = 0.16.

Table 2.

Metavariable dissimilarity (distance) matrices and underlying variables. All matrices are Euclidean distance matrices calculated on standardized variables (from Welti et al., submitted for publication).

Metavariable	Underlying variables
Physical template	Depth of the water body (m)	Water temperature (°C), conductivity (μS/m) pH	Dissolved oxygen (%)	Sediment size (D50) (mm)
Hydrology	Duration of connection (days)	Duration of Disconnection (days)	Connection (days year−1)	Water age (days)
Processes	Substrate induced respiration (SIR) (mg CO2 m−2 h−1)

Table 3.

Associations between metavariable dissimilarity matrices as expressed by Mantel statistics. Mantel (upper diagonal) and partial Mantel (lower diagonal) statistics (controlling for hydrology), significant values printed bold, P-values not corrected for multiple testing.

	Physical template	Nutrients	Organic carbon sources	Processes
Hydrology	0.5	0.22	0.14	0.08
	P < 0.01	P < 0.01	P < 0.01	P < 0.03
Physical template		0.18	0.22	0.13
		P < 0.01	P < 0.01	P < 0.01
Nutrients	0.09		0.4	−0.09
	P = 0.05		P < 0.01	P = 0.99
Organic carbon sources	0.17	0.38		−0.01
	P < 0.002	P < 0.001		P = 0.55
Processes	0.11	−0.11	−0.02
	P < 0.007	P = 1	P = 0.59

3. Study sites

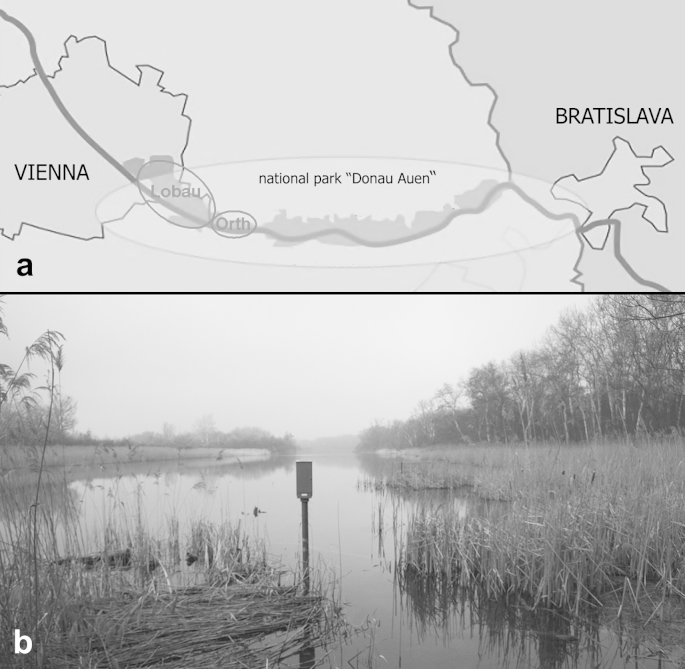
Two study sites were selected: Lobau and Orth. Both are situated within the Alluvial Zone National Park at the Danube East of Vienna (Fig. 4a). This river reach is characterised by a mean discharge of 1930 m³ s⁻¹, an annual flood discharge of 5300 m³ s⁻¹ (Table 4) and a strong seasonality controlled by the regime of its alpine catchment (Tockner et al., 1999). Before the major regulation scheme of 1875, the river stretch was originally an anabranched section consisting of a main stem and a channel-network of numerous small and large branches (Nanson and Knighton, 1996, Hohensinner et al., 2004). Ecological degradation of the river led to constrained side arm connectivity and loss of riverine habitats due to floodplain aggradation. Nowadays the river is under major restoration efforts which aim at improving the ecological status of the river (Habersack et al., 2007).

Fig. 4.

(a) Location of the study sites, i.e. Lobau and Orth within the Austrian national park “Donau Auen” between Vienna and Bratislava; (b) Photograph of a typical lake environment and gauge in the Lobau study area, near sampling site EW (see Fig. 5).

Table 4.

Characteristic discharges of the Danube River East of Vienna.

Identifier	Description	Discharge [m3 s−1]
RNQ	Regulated low flow	915
MQ	Mean flow	1930
HSQ	Highest navigable flow	5060
HQ1	Annual flood	5300
HQ30	30 year flood	9340
HQ100	100 year flood	10,400

3.1. Lobau

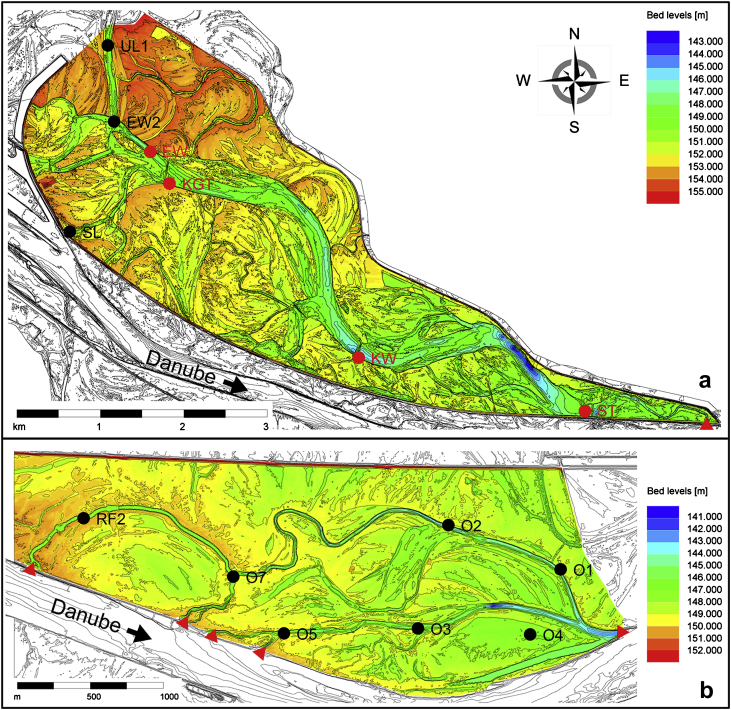
The Lobau is a floodplain of the Danube River located on the left river bank downstream of Vienna. It covers an area of approximately 23 km². Except for groundwater-surface water exchange and a small upstream inflow, the primary water exchange with the main river takes place through an artificial breach in the flood levee encompassing the Lobau’s southern side (Fig. 5a). Three major retention structures with culverts prevent the side arms to fall completely dry during low flow periods, resulting in reservoir-like conditions (Fig. 4b). Several gauging stations, most of them gauge boards, but some also equipped with automatic recorders, are present in the Lobau; however, time series of gauge readings without major data gaps are only available for gauges located in the reservoir-like sections constituting the main stem of the floodplain system. Time series of different gauges within each of these sections are highly intercorrelated. Hence, out of the gauges available, four have been selected – one per section in the main stem of the river system – to validate the model (Fig. 5a). Modelling of the Lobau was performed on a mesh comprised of approximately 150,000 nodes using the node-propagation module, based on hydrographs of a gauge in the Danube River located 250 m downstream of the inlet.

Fig. 5.

Digital Elevation models of the study sites (a) Lobau and (b) Orth; shaded areas indicate the floodplain modelling domain. Inflow and outflow cross-sections are represented by triangles; aquatic sampling sites are marked by filled circles; sampling sites with associated gauge recordings used for validation are coloured in red (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.).

3.2. Orth

The side-arm system of Orth is located just downstream of the Lobau. It covers approximately 5.5 km² (Fig. 5b), and features very diverse flow characteristics. Some side arms are characterised by a through-flow at runoff just above estival mean flow, while others are connected at much higher flow conditions. Most of the historical retention structures present in this river system have been removed in recent years as the inlets of the side-arms have been improved by lowering the bank heights to 1 m above low water level, thus increasing the side-arm discharge significantly as well as the connection duration. There are four main inlets and one outlet connecting this sidearm system to the main river. Modelling of the Orth study area was conducted using 2-D hydrodynamic modelling on a mesh of approximately 55,000 nodes, including the main river itself. The computation mesh was refined along the side arms and coarser in the floodplain regions. The model was calibrated on characteristic water levels of the Danube River in Austria (KWD) (Austrian Federal Waterways Authority, 1997), an official catalogue of water levels for characteristic discharges for every river kilometre obtained from gauges, hydrodynamic models and standard interpolation methods.

4. Field sampling and analyses

A total of 25 sampling sites of different flow and connectivity characteristics have been selected within the two side-arm systems. Sampling took place during three consecutive growing seasons (May–October) in 2006, 2007 and 2008; hence, the output rates modelled based on sampled data are valid only for the growing season. Triplicate sediment cores of 5-10 cm were taken using a PVC corer (inside diameter 5 cm) in deep and shallow aquatic areas of each of the 25 sampling sites. Among the 25 sites, 10 were terrestrial sites of 1 m² each, where 10 cm² triplicate samples in the top 5 cm soil layer were taken. Aquatic sampling occurred in 15 sites (Fig. 5) during different flow conditions and contrasting dry and wet periods. Grain size diameter D₅₀, organic carbon and nitrogen content of the sediment and potential respiration were determined in the laboratory.

Dried sediments obtained at each site were sieved through a sieve tower (20.00, 6.30, 2.00, 1.00, 0.50, 0.125, and 0.063 mm sieve sizes) to determine sediment size fractions and calculate D₅₀. From each sediment core, a 0.5 ml subsample of dried sediment was acidified with HCl to remove inorganic carbon and 1 to 2 mg of each sample were weighed into tin capsules and analysed for organic N and C concentration at the Department of Chemical Ecology and Ecosystem Research, University of Vienna.

Substrate induced respiration (SIR) was measured according to Beare et al. (1990). Three subsamples of 10 g of wet sediment were weighed into three 100 ml Schott glass flasks and closed with a silicon insert lid and received a 5 g C l⁻¹ (as glucose) amendment. All flasks were incubated at room temperature in the dark for 4 h. A 10 ml gas sample was taken from each flask and injected into an evacuated 10 ml headspace glass vial. Gas samples were analysed using a gas chromatograph (Agilent 6890N coupled with an Agilent G1888 Headspace sampler) and the results calculated according to Bauernfeind (1996). Initial CO₂ concentrations were assumed to be zero, so the concentration after 4 h was the rate of SIR.

Substrate induced respiration (SIR) was measured in the laboratory within 2 days after sampling. These potential activities represent the state of enzyme pools present at the sampling time with no other limiting factor, and without de novo enzyme synthesis and cell multiplication. In the framework of our study, these potential activity measurements were more relevant than actual in situ rates (flux measurements) since (i) actual fluxes cannot be accurately measured under in vitro conditions and (ii) variations in actual activities can reflect short-term variations in environmental conditions (e.g. temperature, water content) whereas variations in potential activities reflect deeper modifications of the sediment microbial functioning such as a modification of the level of enzyme synthesis involved in the carbon degradation, a modification of the density and/or diversity of the microbial community responsible for a given biotransformation (Beare et al., 1990).

5. Validation study

A validation of the modelled stage hydrographs for sites within the Lobau study region calculated by the connectivity module was conducted by comparing the corresponding module output to gauge readings. The objective was to verify whether the assumptions on which the connectivity module is based are justified and to confirm validity of its implementation.

The period chosen for validation was the hydrologic year 2007, starting November 1, 2006 and ending October 31, 2007. This period was selected as it is the only hydrologic year for which data without major gaps were available at four different gauges. The corresponding sites are located in different reservoirs of the Lobau (Fig. 5a).

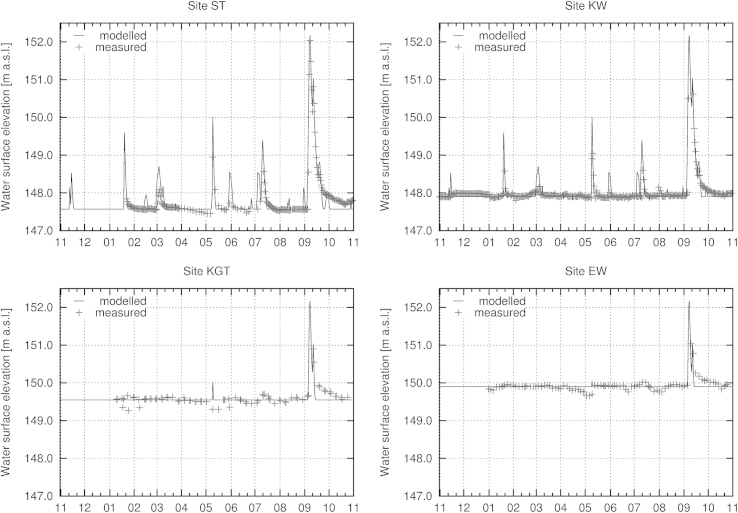
Fig. 6 depicts a comparison between modelled and measured hydrographs at all four sites. The diagrams indicate that the calculated minimum water surface – which is found if no flood event has taken place for significant time – represented adequately the measured data. It confirms that the concept of a minimum surface, the node-propagation technique applied to calculate it, as well as the underlying Digital Elevation Model was appropriate. The minimum surface was also not subject to large fluctuations, indicating that evaporation was not a major issue in these study sites to be considered in the modelling framework. In general, the timing of events was properly modelled, even though the magnitude was overestimated for some events at most sites. However, the nature of the gauge readings available, i.e. two manuals (KGT and EW) and two automatic (ST and KW) might not represent the reality of the water level during high flood events. Indeed, during flood events, gauges are often inaccessible for personnel while automatic gauge recorders may stop operating; therefore the peak of a flood wave may be missed. This fact was particularly evident for the flood event taking place during September 2007, when the highest water levels noted at site EW, near the upper end of the Lobau, exceeded those recorded at site KW, much closer to the inlet, which was contrary to the pattern retention effects would cause. Moreover, the readings showed the correctly modelled peak of the event at site ST to decrease by 1.5 m within the distance of 2.5 km to site KW, which cannot be credited to retention alone. However, while the magnitude of the events in terms of water levels was sometimes overestimated, the event duration important for connectivity calculations was generally well predicted. Only for very large events, the duration of the falling limb of the hydrograph was underestimated by the model; however, in terms of functional connectivity with the main river, it was unlikely to see any river water input into the system during that period as the flow direction was inverted during that phase.

Fig. 6.

Comparison of measured and modelled water surface elevations for the hydrological year 2007 (November 2006–October 2007) at four sites within the Lobau study area.

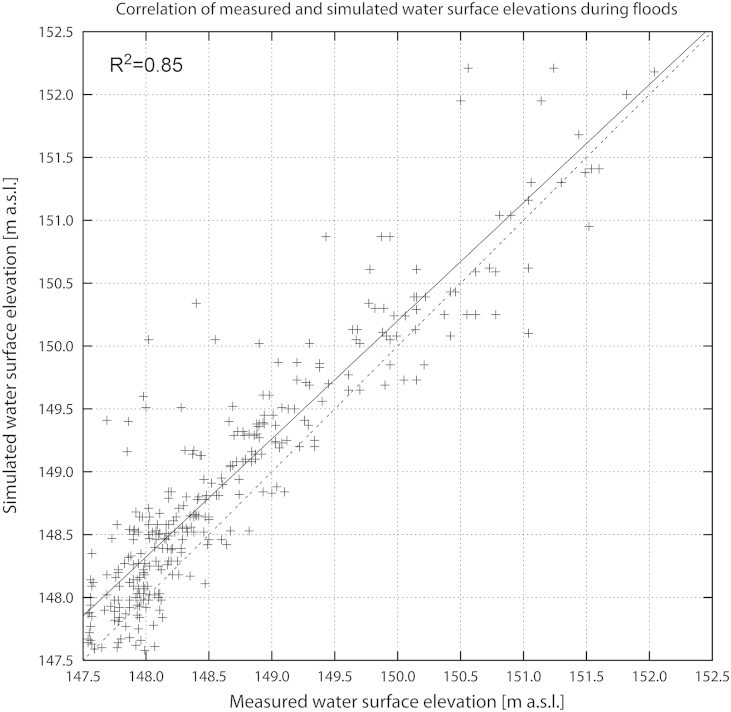
In order to obtain a quantitative indicator of model performance, the correlation between measured and simulated water surface elevations at all four gauges was calculated and is presented in Fig. 7. The analysis was performed on data covering the entire years of 2006 and 2007, after removing stage data corresponding to the respective pool surfaces, i.e. by only considering flood events exceeding these levels. The correlation diagram indicated a minor tendency towards overestimation of water surface elevations – and thus inundation areas and connectivity – for smaller flood events, whereas larger events were captured more precisely. Overall, the investigation yielded a correlation coefficient of R² = 0.85, which is similar to the values reported for hydrodynamic studies in literature (cf. Tritthart et al., 2009). Therefore the results of the validation study indicated that the model assumptions were justifiable and correct.

Fig. 7.

Correlation between measured and simulated water surface elevations during flood events in the years 2006 and 2007 at four gauges within the Lobau study area; the dashed line signifies the line of perfect agreement; the continuous line is fitted to the data using a least-squares regression.

6. Results and discussion

6.1. Connectivity

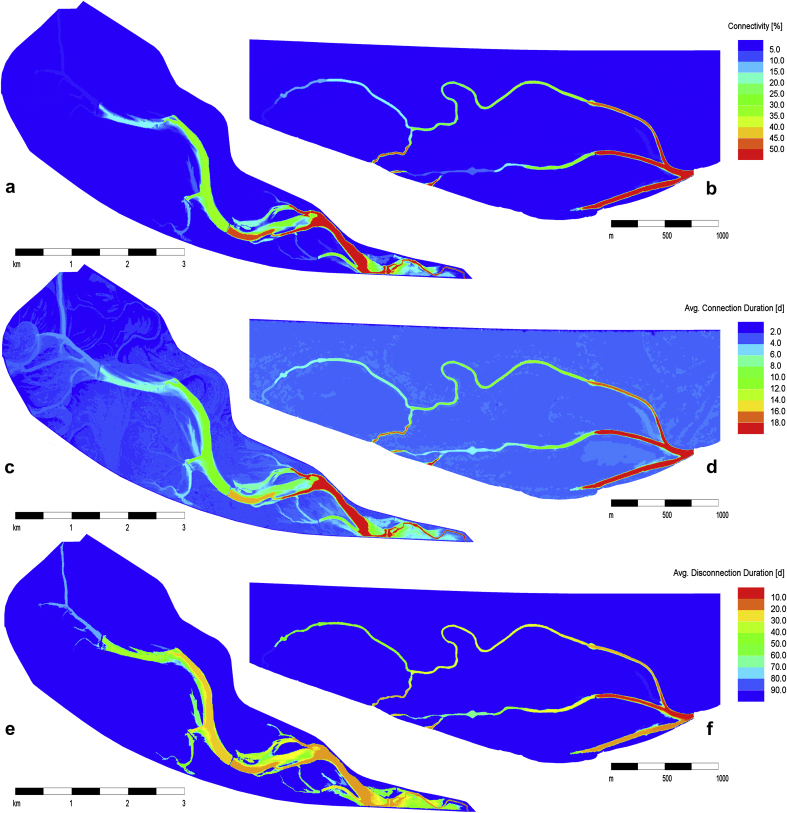
Connectivity, average connection duration and average disconnection duration for both study regions are depicted in Fig. 8. In the Lobau study area, the region close to the exchange inlet/outlet was characterised by connection probabilities of well above 50% (Fig. 8a). However, the morphology of the floodplain and the presence of the retention structures reduced this parameter to 30% and even 10% in the regions of the study area characterised by higher terrain altitudes. In contrast, the connectivity for the Orth study area (Fig. 8b) followed a different pattern as this region was dominated by through-flow rather than backwater flow. Due to the absence of functional retention structures, only the natural morphological features presented an obstacle to the flow and therefore to connectivity. While the reach close to the outlet was permanently connected, side arms with more frequent through-flow conditions featured connectivity probabilities of 30%; those dominated by backwater conditions were characterised by a connectivity of around 10%.

Fig. 8.

Modelling results of the connectivity module: Connectivity map of the Lobau (a) and Orth (b) study areas; Map of average connection duration in the Lobau (c) and Orth (d) study areas; Map of average disconnection duration in the Lobau (e) and Orth (f) study areas.

The duration of average connection or disconnection cycles were only dependent on the morphology of the study area and the long-term hydrologic conditions; hence they were independent from each other and from the connectivity probability. In the Lobau study area the average connection duration of the region close to the exchange cross-section was more than 30 consecutive days (Fig. 8c); Connection duration reduced to 6–10 days in the middle reach and less than 2 days in the upper section due to the retention structures. In Orth, side arms which were not permanently connected presented average connection durations between 4 and 18 days (Fig. 8d).

The average duration of disconnection was less than 10 consecutive days in the lower part of the Lobau, between 15 and 30 days in the middle section and almost 90 days in the upper reach (Fig. 8e). In the Orth study area (Fig. 8f), this parameter ranged between 20 and 60 days in most of the side arms, with a smaller reach dominated by backwater conditions characterised by up to 90 days of disconnection.

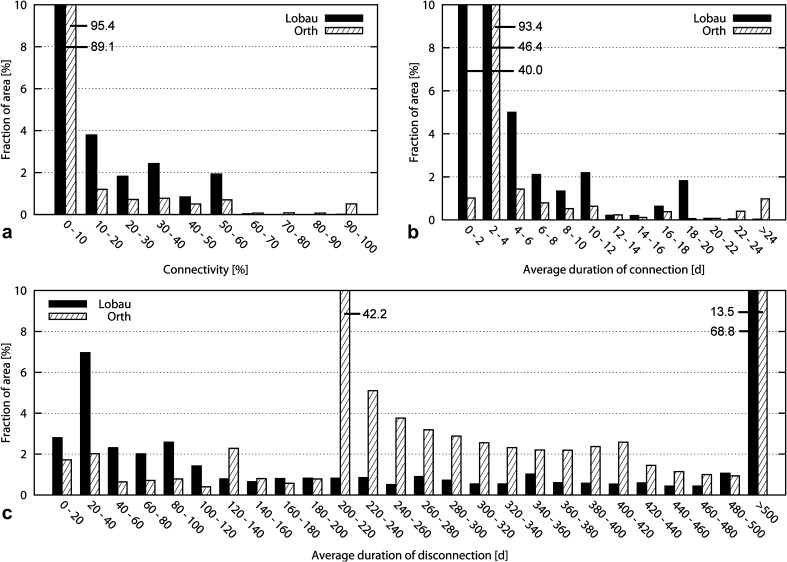
Histograms of the parameters connectivity, average connection duration and average disconnection duration, detailing the fractions of the total area occupied by classes of these parameters, are depicted in Fig. 9. Due to the distribution of terrain elevations, in both study areas a high proportion of around 90% of the total area were characterised by a low connectivity of less than 10% (Fig. 9a). However, while the Orth study area featured a more or less equal distribution of the remaining classes throughout the connectivity spectrum up to 50%, the corresponding values for the Lobau were subject to larger fluctuations between classes in that range. These fluctuations resulted from the geomorphic control of the Lobau due to its anthropogenic partitioning into several reservoir-like sections. Moreover, the Orth study site also encompassed areas in the range of 50% up to permanent connectivity (100%), while such areas were virtually nonexistent in the Lobau, which is another indicator of its underlying geomorphic control. A similar pattern was visible for the average duration of connection (Fig. 9b): around 90% of the total area were connected only for short periods of up to four days; while the Lobau exhibited peaks for some of the remaining classes – corresponding to the reservoir-like sections – and did not feature areas of a longer connection duration than 20 days, the study site near Orth showed a more uniform distribution of areas spread over a larger class spectrum, which indicated predominantly hydrologic control. When analysing the average duration of disconnection (Fig. 9c), a remarkably high fraction of 68.8% of the area within the Lobau study site was characterised by statistical average disconnection times longer than 500 days, while only 13.5% were in this class for the side arm system near Orth. This histogram revealed also an interesting feature of the Orth study site, where low variability of the bank elevations throughout the side arms led to sudden widespread inundations (42.2% of the area) on average every 200 days; while this feature is clearly of geomorphic nature, the general control is hydrologic, as indicated by the class distribution in the remaining spectrum.

Fig. 9.

Histograms of connectivity properties for both study sites, given as fraction of the total area: (a) connectivity in percent; (b) average duration of connection in days; (c) average duration of disconnection in days.

In the spatial distribution of the parameters connectivity, average connection duration and average disconnection duration the dominant influence of geomorphology – i.e. the conditioning of spatial parameter variability by morphological and retention structures – was visible for the Lobau. In contrast, hydrology was the prevailing factor in the Orth side arm system, as indicated by smooth patterns in the parameter distributions without major spatial discontinuities. This finding demonstrated the potential effects of restoration. A side-arm system restored through reconnection by lowering inlet elevations could be expected to exhibit generally higher connectivity values, while patterns of durations of connection or disconnection will be following the natural hydrographs of the main river rather than the discontinuities induced by anthropogenic structures. In general, this will be accompanied by an increase in the average connection duration and a decrease in disconnection duration, particularly for areas distant from the main river.

6.2. Potential microbial sediment respiration

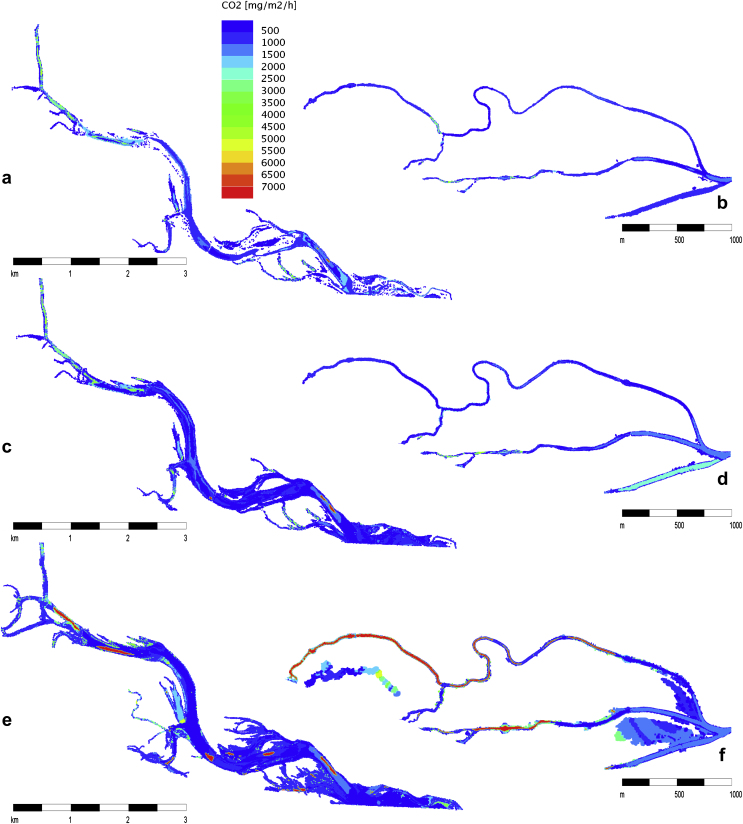
Following the approach outlined before, the output simulation module was run using the potential microbial respiration data and median sediment grain sizes determined from field samples as well as the modelled connectivity characteristics of the study regions. The modelled potential CO₂ emissions for the wetted regions of both floodplain systems are depicted in Fig. 10. The potential output took values of up to 7000 mg CO₂ m⁻² h⁻¹. While this is within the same range of observed data due to the underlying concept of the modelling framework, these values are far higher than actual respiration rates in the floodplain area previously found for a neighbouring side arm system by total respiration estimates (Preiner et al., 2008). However, the aim of the model was to identify areas of increased potential microbial respiration during different hydrological conditions, not to calculate exact rates. It was found that lower discharges in the main river generally resulted in a comparably lower potential CO₂ output irrespective of floodplain morphology (e.g. mean flow; Fig. 10a and b). However, areas with a lower connectivity such as the upper stages of the Lobau floodplain system at the same time presented higher potential CO₂ emission values (up to 3000 mg CO₂ m⁻² h⁻¹) than regions more frequently connected (overall less than 1000 mg CO₂ m⁻² h⁻¹ with a few exceptions). While this pattern remained consistent with rising main river discharge, the potential CO₂ output increased in absolute value (Fig. 10c and d). In the Lobau floodplain, regions characterised by comparably larger water depths of 4–8 metres exhibited a few hot spots with potential output values of up to 7000 mg CO₂ m⁻² h⁻¹ for main river discharges between mean flow and annual flood level; these hot spots were not present in the Orth sidearm system as water depths were generally lower. The existence of hot spots in areas characterised by larger water depths could be due to the increased carbon accumulation rate in sediments of deeper water bodies compared to shallow water areas (<0.5 m depth) (Reckendorfer et al., unpublished).

Fig. 10.

Potential CO₂ emission modelling results of the output simulation module in wetted regions: (a) Lobau at 1930 m³ s⁻¹ (mean flow, MQ); (b) Orth at 1930 m³ s⁻¹ (mean flow, MQ); (c) Lobau at 3500 m³ s⁻¹; (d) Orth at 3500 m³ s⁻¹; (e) Lobau at 5300 m³ s⁻¹ (annual flood, HQ₁); (f) Orth at 5300 m³ s⁻¹ (annual flood, HQ₁).

For annual flood stage however, hot spots were identified in both floodplains investigated (Fig. 10e and f), as overall water depths showed a significant increase. These hot spots with a potential CO₂ output of over 7000 mg CO₂ m⁻² h⁻¹ were mostly found in areas characterised by lower connectivity, such as the upper stages of the Lobau floodplain, but also in sections of the Orth floodplain system connected only a couple of days per year during higher main river discharges. As widespread inundation of the floodplain side arms started during annual flood, some normally dry areas exhibited lower water depths of less than 0.5–1.0 m and also presented higher potential CO₂ output, with rates in the middle range (2000 to 5000 mg CO₂ m⁻² h⁻¹). Environmental disturbances (i.e. flooding) have been shown to have a major impact on biogeochemical cycling in wetlands by increasing the substrate availability and stimulating bacterial activity (Song et al., 2010, Burns and Ryder, 2001). In general, the change between dry and wet phases was expected to impact the microbial activity and the oxygen availability and thus the processing of matter (Baldwin and Mitchell, 2000). These findings of the temporal and spatial distribution of potential rates underline the importance of connectivity patterns for the microbial processing and the sediment microbial activity. Yet, it should be remembered that in situ rates can deviate significantly from the measured potential rates. Changes in water temperature due to flooding and seasonality were not considered in this study; rather the relative changes occurring within the floodplain were compared. Therefore, the model output can only predict areas of potential hot spot activity in wetted areas under different flooding conditions.

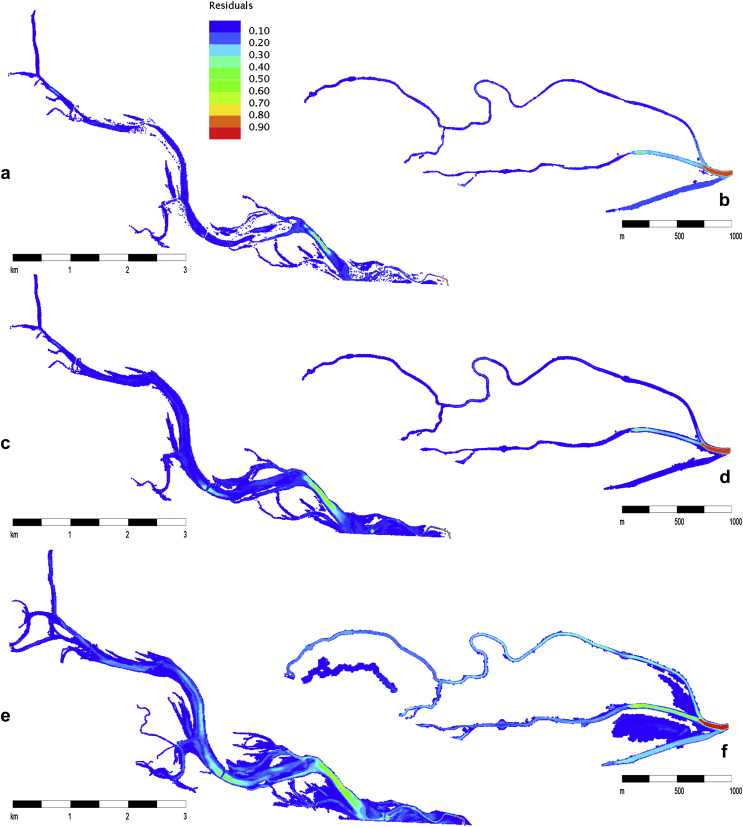
Since the prediction of potential CO₂ emissions was performed using a modelling approach based on least squares residuals, the method allowed for a calculation and interpretation of the uncertainty inherent to the results presented. The square root of the residuals corresponding to the results is plotted in Fig. 11, normalised to fit the range of 0.0 (zero residuals, exact match with conditions encountered during field sampling) to 1.0 (maximum residuals, basically unobserved natural state). At mean discharge in the main river (Fig. 11a and b), the residuals were generally low for both floodplain systems, with two notable exceptions near the inlet of the Lobau and the outlet of the Orth side arm system. These states of frequent (Lobau) or permanent connection (Orth) have not been covered by field sampling due to technical difficulty. Therefore, the predictions in these regions were characterised by a higher uncertainty than those in other regions of the floodplain systems. Higher residuals were also present in areas of comparable large water depths. Again, these situations were rarely sampled due to technical difficulties; however, some data comparable to the conditions encountered were available. This is why the residuals were not as high as for the inlet/outlet sections. With rising discharge (Fig. 11c and d), the issue of unobserved situations of frequent connection was still visible, while the increasing areas of large water depths led to larger regions of higher uncertainties. A significant increase in overall uncertainty was finally encountered during the annual flood stage (Fig. 11e and f), as the combination of water depth and connectivity present under these conditions in many regions, oxbows and side arms within both floodplain systems was never observed during the field sampling campaign. However, a large number of areas and particularly those identified as hot spots by the model were still characterised by comparably low residuals and therefore low modelling uncertainty, even under annual flood conditions.

Fig. 11.

Normalised residual maps of modelling in wetted regions: (a) Lobau at 1930 m³ s⁻¹ (mean flow, MQ); (b) Orth at 1930 m³ s⁻¹ (mean flow, MQ); (c) Lobau at 3500 m³ s⁻¹; (d) Orth at 3500 m³ s⁻¹; (e) Lobau at 5300 m³ s⁻¹ (annual flood, HQ₁); (f) Orth at 5300 m³ s⁻¹ (annual flood, HQ₁).

7. Conclusions

In this study a modelling framework capable of predicting patterns of potential microbial respiration in the aquatic compartment of complex floodplain landscapes has been derived. Hydrodynamics, hydrological connectivity and potential microbial respiration patterns were computed in a procedure performed in three modules. Based on the modelled water depths for characteristic discharges combined with a long-term hydrograph, flow events within the floodplain could be characterised regarding their frequency and duration at every point, eventually leading to the integrative parameters connectivity, average connection duration and average disconnection duration. These parameters were calculated for the corresponding locations of a statistically relevant number of field samples for which the potential biogeochemical output in terms of carbon had been measured. Subsequently a best-fit approach based on the method of least square errors was applied to every point within the floodplain in order to determine the sampling site that most closely resembles the environmental parameters encountered. The corresponding potential biogeochemical output was then assigned to the respective point, finally allowing for upscaling a limited number of samples to the entire floodplain and predicting potential microbial respiration patterns.

The modelling approach was used to evaluate the potential microbial respiration of the floodplain sediment under different river water discharges in two study sites at the Austrian Danube East of Vienna. Potential microbial respiration provided an assessment of the total heterotrophic respiration of the floodplain sediments and was tightly controlled by sediment aeration status, and in turn by water residence time. The spatial variability of the patterns obtained from connectivity calculations showed that a floodplain system strongly dominated by anthropogenic influences through the presence of retention structures (Lobau) was governed by geomorphology rather than hydrology, as opposed to a restored side arm system without human interference (Orth) which was mainly influenced by hydrology. The comparison of modelled and measured stage hydrographs for validation purposes exhibited good agreement, justifying the assumptions made in the design and implementation of the connectivity module.

By application of the output simulation module, patterns of potential microbial sediment respiration in the floodplains could be predicted. It was found that potential microbial respiration increases in aquatic regions of lower connectivity once they become connected during higher main river discharges. In addition, hot spots of potential CO₂ emissions were also found in areas characterised by larger water depths, which is credited to an increased carbon accumulation rate in sediments of deeper water bodies compared to shallow water areas. By plotting and analysing the residuals associated with the model output, the uncertainties corresponding to the results could be quantified. Regions of high connectivity and large water depths were found to exhibit larger uncertainties than those of low connectivity or water depth. This finding underlined that the transferability of these modelling results was given only to other floodplain systems of similar size, connectivity range and sediment properties, while the residuals and the associated uncertainty were assumed to increase if any of these parameters deviate significantly. While the modelling framework itself is invariant to the underlying hydrologic, geomorphic and sediment properties, a field sampling campaign would have to be conducted if the model was applied for floodplains differing significantly in size, connectivity or sediment quality.

The modelling framework presented here has shown to be a suitable tool to evaluate the consequences of river restoration and management on potential sediment microbial activities estimated by potential respiration. Furthermore, this modelling tool could be used to assess the effects of changing hydrology on microbial processing and to elucidate potential effects due to changed flow regimes at regional scales. Considerations for the future application of the approach include the availability of data in general, in particular regarding hydrologic and morphologic data sets, such as the length of time series observed at gauging stations or terrain elevations in reasonable accuracy. Moreover, a precondition for the applicability of the modelling framework is that hydrological connectivity between a river channel and its floodplain must be a primary driver for ecosystem processes. Future improvements of the modelling framework could be aimed towards the inclusion of actual instead of potential rates and the consideration of water temperature as additional variable; the model output could then be further enhanced by the conduction of a sampling campaign in non-saturated soils within the dry areas of the floodplain, thus eventually allowing for the calculation of actual respiration rates in the entire riverine landscape.