Fatigue failure of dentin-composite disks subjected to cyclic diametral compression

Abstract

Objective

Our aim was to establish the relationship between cyclic loading and fatigue life of the dentin-composite interface using the newly developed disk in diametral compression tests. The results were then used to estimate the fatigue life of restored teeth under occlusal loading.

Methods

Disk specimens (5mm dia. × 2mm thick) were prepared using bovine incisors and restored with either a methacrylate-based composite Z100™ with Adper Single Bond Plus (Z100) or silorane-based composite Filtek ™ LS with LS System adhesive (LS). The dentin-composite disks were tested under cyclic diametral compression to determine the number of cycles to failure (N_f) at three load levels (n = 3 per group). Finite element analysis (FEA) was used to calculate the interfacial stresses (σ) within the specimen, to establish the σ vs. N_f curves, and those within a restored tooth under normal chewing forces (15N maximum). These were then used to estimate the lifetime of the restored tooth for the two restorative systems.

Results

The disks restored with LS had a higher fatigue resistance than those restored with Z100. The maximum interfacial stress in the restored tooth determined by FEA was ∼0.5MPa. Based on the estimate of 300,000 cycles of chewing per year, the predicted lifetime under occlusal loading for teeth restored with LS and Z100 was 33 and 10 years, respectively.

Significance

The disk in cyclic diametral compression has been used successfully to provide fatigue data which allows the lifetime of composite-restored teeth under occlusal loading to be predicted using numerical simulation.

1. Introduction

Resin based dental composites are now widely used for both anterior and posterior restorations. Their comparable mechanical properties to dentin [1,2], ability to bond to tooth tissues and superior aesthetics make them more favorable than amalgam as a restorative material [3]. Adhesive systems are used to bond the composite to enamel and dentin. For the latter, the impregnation of the demineralized collagen fibrils with a bonding resin is a major factor in the formation of adhesion [4]. While the initial tooth-composite bonds may be adequate, continuous challenges from mastication [9], hydrolysis and biofilm attacks can degrade the interface, thus resulting in debonding. Secondary caries and fracture of the restoration or tooth, which are the major reasons for the replacement of resin composite restorations, may then follow.

Failures that occur over time as a result of cyclic and/or sustained loading are well recognized clinical problems associated with mineralized tissues [5-7]. A typical method for quantifying the fatigue behavior of a material is the stress-life approach which relates the number of cycles to failure (N_f) to the stress amplitude (σ). The measured fatigue lifetime represents the number of cycles to cause failure through unstable crack growth. Mineralized tissues such as dentin and enamel display typical σ-N_f curves in that N_f decreases with increasing σ [8,9]. Clinically, one of the main reasons for the failure of dental restorations is also cyclic fatigue associated with mastication. Being able to quantify the degradation of the tooth-restoration interface in the oral environment can therefore help to predict the lifetime of composite restorations. While the fatigue failure mechanisms of interfaces between composites and tooth tissues are expected to be different from those of the constituents, they display similar σ-N_f curves. There are relatively few investigations that focus on the cyclic fatigue of the tooth-composite interface [10-14], probably because they can be very expensive and time-consuming to perform, even using laboratory testing to simulate the occlusal load. A more efficient strategy, as widely used in engineering, would be to use numerical modeling, coupled with the σ-N_f data, to predict the lifetimes of dental restorations.

The aims of the present study were, therefore, to (1) determine the σ-N_f curve, i.e. the fatigue strength, for the composite-dentin interface using the newly developed composite-dentin disk specimen under diametral compression [15]; and (2) use this interfacial fatigue data to predict the lifetime of composite-restored teeth under physiological conditions. The composite-dentin disk in diametral compression has previously been used successfully to evaluate the static bond strength between these materials [15].

2. Materials and methods

2.1 Preparation of dentin-composite disks

Dentin-composite disks were prepared using the method reported previously [15]. Briefly, roots from bovine incisors were obtained by removing the crowns at the cemento-enamel junction. They were then trimmed into dentin cylinders of 5 mm in diameter, with the root canals enlarged concentrically to 2 mm in diameter. The dentin cylinders thus produced were randomly divided into two groups and restored with one of two composites (Z100™ and Filtek ™ LS, both from 3M ESPE, St. Paul, MN, USA) using the corresponding adhesives as per the manufacturer's instructions. These two composites were chosen because they have different polymerization chemistries and use different adhesive systems. Z100 is a conventional methacrylate-based composite and it uses a total etch and rinse adhesive system. It exhibits high volumetric shrinkage of over 2 % after curing [16]. In contrast, Filtek™ LS is a silorane-based composite with less than 1.0 % total volumetric shrinkage [17], and it uses a self-etch adhesive system. For specimens restored with the Z100 system, the inner dentin surface was etched with 35% phosphoric acid for 20s and then rinsed with deionized water. Two layers of adhesive (Adper™ Single Bond Plus, 3M ESPE) were applied to the etched surface and cured for 20s. To minimize shrinkage stress, Z100 composite was applied incrementally to fill the cylinders. Each increment, less than 2-mm thick, was cured for 40s to ensure adequate curing. For specimens restored with the LS system, a layer of Self-Etch Primer (LS System Adhesive, 3M ESPE) was first applied to the inner dentin surface and cured for 10s. This was followed by the application of a layer of Bond (LS System Adhesive, 3M ESPE) with 20s of curing. LS composite was then applied incrementally and cured in the same way as Z100. Finally, the composite-restored cylinders were transversely cut to produce 2-mm thick round disks. All restorative materials were cured using a LED light-curing unit (Elipar™ S10, 3M ESPE) with a power density of 1200 mW/cm². During curing, the tip of light guide was held as close as possible to the materials without touching them. The compositions and product information of the composites and adhesive bonding systems are described in Table 1.

Table 1. Product information of composites and adhesives used in the study.

Materials	Compositions	Lot #	Expiration date
Z100™	Bis-GMA, TEGDMA, silane treated microfiller (66vol%), initiator	N362979	2014-12
Filtek™ LS	Silorane resin, silane treated quartz filler (53vol%), yttrium floride, initiator, stabilizers	N554531	2015-05
Adper™ Single Bond Plus	Etch-and-rinse, conventional adhesive system; Bis-GMA; HEMA, Glycerol 1,3-dimethacrylate, copolymer of acrylic and itaconic acids, UDMA, initiator, ethanol, water	N437332	2015-10
LS System adhesive	Two-bottle self-etch adhesive system; Primer: Bis-GMA, HEMA, phosphorylated methacrylates, 1,6-hexanediol dimethacrylate, copolymer of acrylic and itaconic acid, silane-treated silica, initiators, stabilizers, water, ethanol. Bond: substituted dimethacrylate, TEGDMA, phosphorylated methacrylate, 1,6-hexanediol dimethacrylate, silane-treated silica filler, initiators, stabilizers	N522061	2015-05

2.2. Fatigue testing

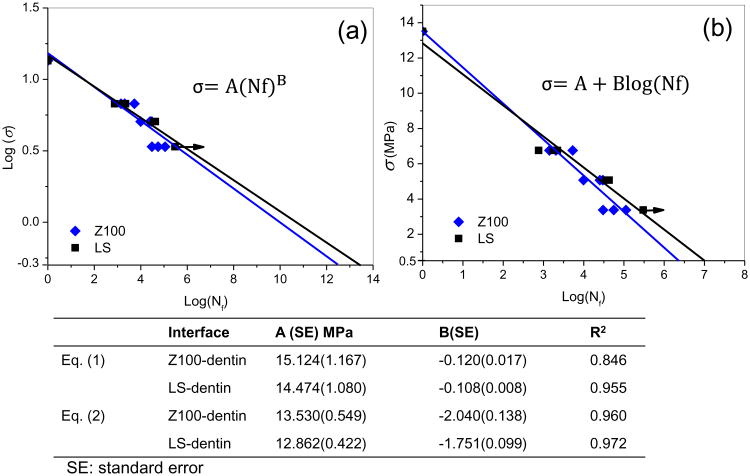
The prepared disks were loaded to failure in cyclic diametral compression using a universal testing system (MTS 858 Mini Bionix II, Eden Prairie, MN, USA) operated with load control (Fig. 1a). Cyclic diametral compression at 1 Hz with a square wave of zero minimum load was applied to the specimens in deionized water at room temperature. The load and displacement were monitored continuously throughout the whole cyclic loading process. The number of cycles to failure (N_f) was determined from a dramatic change in the displacement patterns (Fig. 1b). The static fracture load of both Z100- and LS-restored disks had previously been found to be approximately 400N [15]. For the current fatigue test, three load levels, with 50%, 37.5% and 25% of the static fracture load as the peak value, were applied, and three samples for each material group were evaluated at each load level. The use of such a small sample size was justified because the uncertainties in the parameters derived for the fatigue models were reasonably small (see standard errors in Fig. 6). The stress-life (σ-N_f) curves were constructed by first determining the maximum interfacial tensile stress within the disk using Finite Element Analysis (FEA, see later) with the peak load and then plotting the stress against the number of cycles to failure.

Fig. 1.

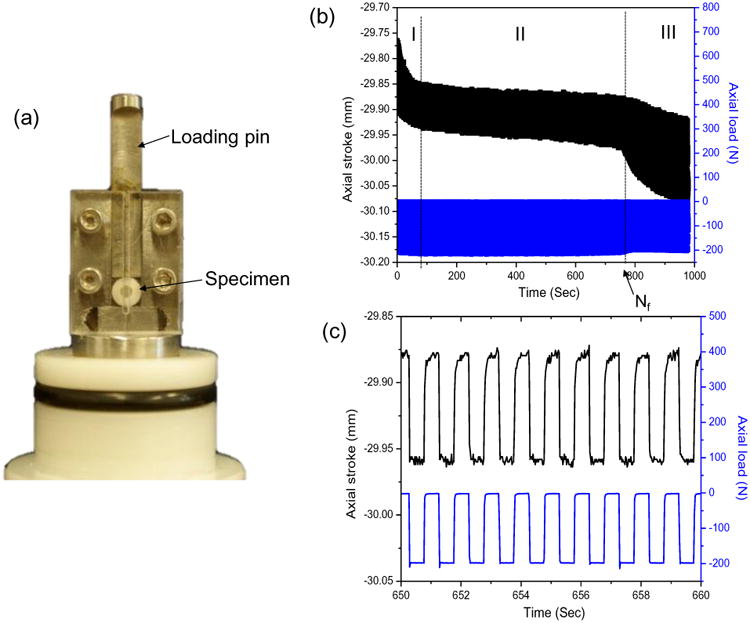
(a) Experimental set-up for the diametral compression fatigue test. (b) Typical patterns of axial stroke and axial load as a function of time. (c) Patterns of axial stroke and load from 650 s to 660 s of the test in (b) showing constant-amplitude cyclic loading and displacement.

Fig. 6.

Stress-life (σ-N_f) fatigue data for the dentin-composite disks fitted with the models of Equation 1 (a) and Equation 2 (b). The arrows indicate that the specimens survived the designated number of loading cycles. The power law constants (A, B) which describe the fatigue behavior according to Eq. (1) and Eq. (2) for each restorative system are listed in the table.

Linear regression was performed on the σ-N_f data using appropriate mathematical models for each restorative system. The quality of the linear regression and the uncertainties in the parameters for the fatigue models were then assessed using statistical analysis.

2.3. Scanning electron microscopy (SEM)

SEM was used to examine the morphology and fracture modes of the dentin-composite disks after fatigue testing. The fractured disks were air-dried overnight and mounted on aluminum stubs with carbon tapes. They were examined by a semi-environmental tabletop SEM (TM-3000, Hitachi, Japan) operated at a 15-kV accelerating voltage. No conductive coating was applied to the samples. To counteract the charging effect, the charge-up reduction mode was used for acquiring images. The working distance was in the range of 5-8 mm. The failure modes were classified as (1) cohesive failure in the resin composite; (2) interfacial failure between the adhesive and composite; (3) cohesive failure in the adhesive; or (4) interfacial failure between the adhesive and dentin.

2.4. Finite element analysis of interfacial stresses

Stresses at the dentin-composite interface of the disk under diametral compression were calculated with FEA for different load levels. The model of the specimen, together with the two horizontal steel plates for load application (Fig. 2a), was constructed using Hypermesh 11.0 (HyperWorks, Altair Engineering, USA). The frictional coefficient between the loading plates and the specimen was set as 0.3 [18]. Each component was assumed to be isotropic, homogeneous and linear elastic. Table 2 lists the elastic modulus and Poisson's ratio of dentin, enamel, steel, Z100 and LS. The disk model was analyzed using the FEA software ABAQUS 6.11 (SIMULIA, Providence, RI, USA). The maximum tensile interfacial stress was determined as a function of the applied load, which allowed the experimental data (load vs. N_f) to be presented as σ-N_f curves. In addition, the maximum tensile stress in the dentin was also calculated and compared with its reported fracture strength to assess the possibility that dentin cohesive fracture preceded interfacial fracture.

Fig. 2.

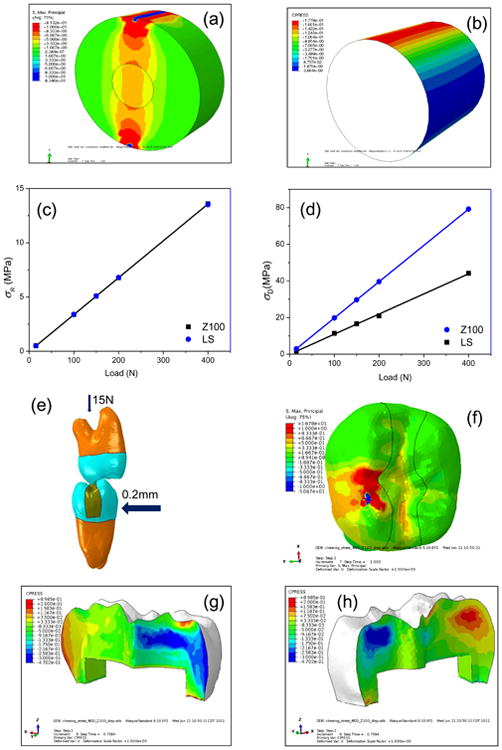
(a) Principal stress distribution in the dentin-composite disk. (b) Contact pressures at the disk composite-dentin bonding interface with blue-colored areas under tensile stresses (negative pressure) and red-colored areas under compressive stress. (c) Maximum interfacial tensile stresses in disks restored with LS and Z100 as a function of load. (d) The maximum tensile stress in the dentin near the loading point as a function of load. (e) Finite element model of two opposing molars. The mandibular molar was subjected to occlusal (vertical) force of 15 N and lateral (horizontal) displacement of 0.2 mm to simulate chewing movement. (f) Distribution of the maximum principal stress in the restored tooth. (g) and (h) Contact pressure at the tooth-restoration interface with the same color convention as in (b).

Table 2. Materials properties for finite elemental analysis.

Material	Elastic Modulus (GPa)	Poisson's ratio
Dentin[19]	18.6	0.31
Enamel[20]	84	0.3
Z100[21]	8.5	0.3
LS[22]	13.5	0.3
Steel[23]	210	0.3

As an example to demonstrate the application of an engineering approach to assessing the fatigue lifetime of composite restorations, the stresses of a tooth with a Mesial-Occlusal-Distal (MOD) restoration under normal chewing motions were also calculated using FEA (Fig. 2e). Failure of the restored tooth was assumed to be caused by debonding at the dentin-composite interface. A 2^nd mandibular molar and a 2^nd maxillary molar were scanned with an X-ray micro-computed tomography (micro-CT) machine (XT H 225, Nikon Metrology, United Kingdom) using the following operational parameters: 90kV, 90μA, 720 projections and 4 frames per projection. Reconstructions of the objects in 3D space were done with CT Pro 3D (Nikon Metrology, Brighton, MI, USA). The 3D CT images were used to build finite element models for the teeth. First, the surfaces of the dentin and enamel of each tooth were extracted using Amira (Mercury Computer Systems, Berlin, Germany). Solid tetrahedral elements were then created inside the volumes bounded by the surfaces using Hypermesh. A MOD restoration was introduced into the mandibular molar model, as shown in Fig. 2e. These two tooth models were first placed in the cusp-against-cusp position, simulating initial occlusion. The root of the maxillary molar was fully fixed, while the root of the mandibular molar was constrained in the mesial-distal direction and rotationally about all 3 axes, thus restricting its motions along the vertical and buccal-lingual directions only. A normal chewing or mastication cycle is composed of opening, closing and occlusion where the occlusal phase ends ∼0.5 mm from the maximum intercuspation position [24]. The chewing motion was thus simulated with 2 load steps. In the first load step, an upward occlusal force of 15N was applied to the mandibular molar. In the second load step, a lateral displacement of 0.2 mm was applied to the mandibular molar to bring it to centric occlusion. The model was again analyzed using ABAQUS to obtain the maximum interfacial tensile stress, which was then used, in conjunction with the experimental σ-N_f curves, to estimate the fatigue lifetime of the restored tooth under occlusal loads.

3. Results

3.1. Number of cycles to failure (N_f)

The number of cycles to failure (N_f) for the disk specimen was identified from significant changes in the axial stroke-time patterns. The axial stroke was the displacement of the loading plate required to maintain the load at the predetermined level and depended on the compliance of the disk: the more compliant the disk, the larger the axial stroke. The obtained axial stroke vs. time graphs (Fig. 1b) for the disk specimens demonstrated three distinct regions. Region I corresponded to the initial permanent deformation near the loading points due to the high but localized stress concentrations. Region II showed a steady, near constant axial stroke pattern corresponding to most of the fatigue challenge (Fig. 1b and 1c). Region III was characterized by a sharp increase in the axial stroke indicating the onset of failure. N_f was determined as the number of cycles separating region II and region III.

N_f for the two material groups at different loads is shown in Table 3. Our previous study had demonstrated that Z100- and LS-restored disks had similar fast fracture loads, which were approximately 400 N [15]. In the current study, with peak loads of 200 N and 150 N, which corresponded to 50% and 37.5% of the fast fracture load, the two groups of specimens also showed similar fatigue lifetimes (Z100: 2,924 ± 2,104 at 200N and 21,570 ± 10,383 at 150N; LS: 1,582 ± 755 at 200N and 39,454 ± 3,379 at 150N). With a peak load of 100 N, i.e., 25% of the fast fracture load, all three Z100-restored specimens failed at less than 150,000 load cycles (76,937 ± 41,695). In contrast, all three LS-restored disks survived after 300,000 cycles of loading.

Table 3.

Number of cycles to failure (N_f) for dentin-composite disks (n = 3) at different load levels.

	Nf mean (standard deviation)
Load (N)	Filtek™ LS	Z100™
200	1582(755)	2924(2104)
150	39454(3379)	21570(10383)
100	>300,000	76937(41695)

3.2. Failure analysis

As shown in Fig. 3, fatigue failure of the disks appeared to have initiated from one of the two positions where the horizontal diameter intersected with the circular composite-dentin interface. These positions had the highest interfacial tensile stress as determined by FEA (Fig. 2b). Once initiated, the fatigue crack grew along the interface and eventually resulted in dentin fracture. In disks restored with LS, most failures involved cohesive composite fracture near the interface (Fig. 4a) and adhesive (primer)-dentin interfacial debonding (Fig. 4b). In contrast, most of the failures in disks restored with Z100 were cohesive failure in the adhesive next to the hybrid layer. Resin tags pulled out from the dentinal tubules were consistently observed in the specimens from this group (Fig. 5a). Incomplete coverage of the etched dentin surface by the adhesive was also noticeable on the fractured surfaces (Fig. 5c and 5d).

Fig. 3.

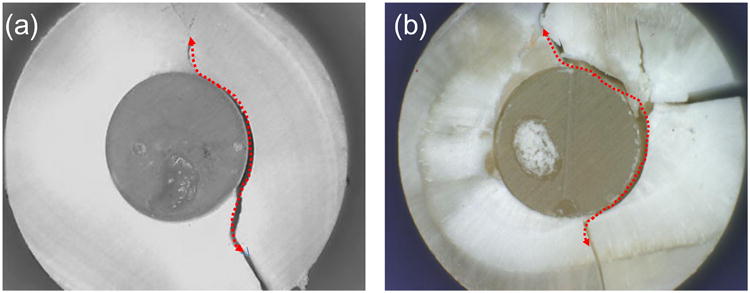
Fatigue-failed dentin-composite disks restored with LS (a) and Z100 (b). The fatigue load was 150 N. Red dotted arrows show the directions of crack propagation.

Fig. 4.

SEM images of disks restored with the LS system after fatigue failure. (a) and (b) Front views of the fractured disks showing cohesive composite fracture (left) and adhesive-dentin interfacial debonding (right). D: dentin, A+P: adhesive + primer, C: composite. Red arrows show the cracks caused by fatigue failure.

Fig. 5.

SEM images of disks restored with the Z100 system after fatigue failure. (a) and (b) Front views of fractured disks showing cohesive failure in the adhesive next to the hybrid layer. Note the resin tags pulled out from the hybrid layer in (a). (c) and (d) Images of the fractured surface on the dentin side showing incomplete adhesive coverage. D: dentin, A: adhesive, H: hybrid layer, C: composite.

3.3. Interfacial stresses predicted by FEA

The maximum principal stress distribution of the dentin-composite disks under 400 N of loading is shown in Fig. 2a. High tensile stresses in the horizontal direction occurred within a narrow vertical column between the two loading points. In particular, high stress concentrations were found in the dentin around the two loading points. The pressure distribution at the dentin-composite interface of the composite-restored disk is shown in Fig. 2b. In Fig. 2b, g and h, blue corresponds to areas under tensile stress (negative pressure), and red corresponds to areas under compressive stress (positive pressure). High tensile interfacial stresses were found at the two positions where the horizontal diameter intersected with the circular resin-dentin interface. These were the places where debonding was expected to take place. As shown in Fig. 2c and d, both the maximum tensile interfacial stress in the radial direction (σ_R) and the maximum tensile stress in the circumferential direction (σ_D) in the dentin were proportional to the applied load. Also, even though the elastic moduli of the Z100 and LS composites were different, they showed almost identical radial tensile stresses at the interface (Fig. 2c). However, the dentin stresses of Z100-restored disks were higher than the ones restored with LS (Fig. 2d).

The maximum tensile stress at the tooth-composite interface of the mandibular molar with a MOD restoration was calculated to be 0.47 MPa under a clinically representative occlusal load of 15N (Fig. 2f, g and h).

3.4. Fatigue lifetime prediction for restored teeth

A preliminary attempt at estimating the fatigue lifetime of restored teeth was made based on the interfacial stresses predicted by FEA and the σ-N_f curves obtained experimentally for the two restorative systems considered in this study (Fig. 6). It was conservatively assumed that all the LS disk specimens failed at 300,000 cycles with a peak load of 100 N. The maximum interfacial stress in the restored molar under a chewing force of 15N was predicted to be 0.47 MPa, and the number of chewing cycles per year was estimated to be around 300,000 [25]. Using a Basquin-type model [26] of the form:

$$\sigma =A{N}_f^B$$ (1)

where A and B are constants, the predicted fatigue life for a restored molar under the assumed chewing forces only is over 10 million years.

A more conservative model [27] is provided by Equation (2) below:

$$\sigma =A+B\cdot log{N}_f$$ (2)

where A and B are, again, constants. Even though this exponential model does not satisfy the condition that N_f should be infinite when σ is zero, it fits the fatigue data better with higher R² values (see table in Fig. 6). By using Equation (2) and the best estimates for the parameters, the predicted fatigue lifetime of a LS- and Z100-restored molar under the same loading condition is 33 and 10 years, respectively. When considering the standard errors of the parameters, the predicted lifetime would lie in the range of 2-47 years for Z100 and 28-58 years for LS.

4. Discussion

The mechanical fatigue of the dentin-composite interface was studied using the disk in cyclic diametral compression. The specimens were composed of dentin rings restored with composites and the corresponding adhesive systems, replicating the typical bonding structure of restored teeth [28,29]. Under vertical diametral compression, maximum radial tensile stresses were created at the two positions where the horizontal diameter intersected with the circular resin-dentin interface. Our results indicated that dentin-composite interfaces formed with the LS system were more durable than those formed with the Z100 system under cyclic loading, even though they had very similar fast fracture loads. The static bond strength is therefore not sufficient as a predictor of the clinical performance of these dental restorative systems; fatigue data for lower load levels is also required.

This study represented the first attempt at applying cyclic diametral compression tests to evaluate the durability of the dentin-composite interface. Diametral compression is commonly used on homogeneous disks of brittle materials to test their tensile strength. In previous studies, disks of composite-restored dentin rings were successfully used to measure the composite-dentin interfacial bond strength [15,30,31] There was concern that the localized high tensile and shear stresses produced at the contact points between the flat compression plates and the round disk could induce dentin fracture. At the fast fracture load of 400 N, the predicted maximum tensile stress in the dentin of disks restored with Z100 is ∼80 MPa, which is similar to the tensile strength of dentin [31]. It is therefore possible that failure of the disks was caused by dentin fracture. The previous study demonstrated that some disks did fracture near the point of loading [31]. However, as shown in Fig. 2d, the disks restored with LS showed much lower tensile stresses in the dentin than the ones restored with Z100. Yet, the two groups of specimens had very similar fast fracture loads and fatigue lifetimes with peak loads at 50% and 37.5% of the fast fracture load. This strongly suggested that dentin fracture was not responsible for their failures. To illustrate this point further, if the Basquin-type model was representative, a 50% reduction in stress, as seen in the dentin of the LS specimens, would produce an increase in lifetime of a few hundred folds for the dentin-composite disks. This large difference in fatigue lifetime between the two groups was not observed in our experiments. On the other hand, given that the maximum tensile stress (σ_R) at the composite-dentin interface was similar for both groups, it is more likely that fracture was initiated from this position for all specimens.

Fatigue failure is the result of cumulative damage leading to crack initiation and propagation. A defect can act as a stress raiser for crack nucleation during the fatigue process [13,32]. Indeed, the majority of the fatigue lifetime is spent in initiating a small crack from the most highly stressed area; and the inherent flaws at the stress concentrated area strongly affect the fatigue lifetime [8]. In disks restored with LS, the prevailing fatigue fracture modes were cohesive composite fracture and debonding at the dentin-primer interface. In disks restored with Z100, the prevailing fracture mode was cohesive failure in the adhesive. These results were consistent with our previous study on the fast fracture of composite-dentin disks prepared with the same restorative systems [15]. The bonding procedure for Z100 consisted of etching, rinsing and application of two consecutive adhesive layers; whereas that for LS consisted of the application of a self-etching primer and then a single layer of adhesive. Although the adhesive used for Z100 was easier to apply, due mainly to its lower viscosity, than the one used for LS, it produced inadequate coverage of the dentin surface [15], leading to a defective hybrid layer (Fig. 5c and d). Similarly, inadequate coverage of the first layer by the second was also noticeable. These discontinuities within and between the adhesive layers could act as stress concentrators for fatigue crack initiation, and might be the reason that Z100-restored disks had lower fatigue resistance than the ones restored with LS at the low load level. Fig. 5a and b confirm that failure of the Z100-restored disks was predominantly cohesive in the adhesive next to the hybrid layer. In contrast, the adhesive system of LS consisted of a self-etching primer and a layer of more viscous adhesive. This thick layer of adhesive provided a better coverage of the dentin surface and may have increased the strain capacity of the restoration by acting as an elastic buffer [33,34]. Note that no delamination between the primer and adhesive layer was observed, indicating there was good integration between the two components.

Incremental filling was used to restore the dentin disks in order to minimize shrinkage stress. According to the manufacturer's reports [35,36], Adper™ Single Bond Plus and LS System Adhesive have similar microtensile bond strength: ∼18MPa and ∼20MPa respectively - the presence of shrinkage stress is not expected in the microtensile specimens. The diametral compression test used in this study also gave similar static bond strength for these two adhesive systems: albeit of a lower value (13.5 MPa). This indicated that the level of shrinkage stress in the disk, if any, was low, at least not sufficient to affect the fast fracture loads. Nevertheless, some shrinkage stress may still have been created in the disk specimens, in particular for Z100, due to its high polymerization shrinkage. This may have contributed to its lower fatigue resistance at lower loads. It is worth pointing out that, in a longevity study of posterior Class II restorations, those restored with Z100 failed significantly more often than those restored with other resin composites (Tetricceram, Herculite XRV and Filtek Z250) and over 40% of them failed within five years of clinical service [37].

Since in the oral environment most restored teeth are subjected to cyclic fatigue with loadings much lower than the fast fracture load, it is important to investigate their fatigue behavior in addition to measuring the bond strength. Using numerical simulation and fatigue data derived from laboratory testing on simple specimens allows the lifetime of whole dental restorations to be predicted without actually testing them, which can be expensive and time-consuming. There are a few models in the literature that relate the fatigue lifetime of materials to the stress amplitude. The most commonly used one is the Basquin-type model given by Equation (1). This model is usually used for materials that are homogeneous, isotropic and linearly elastic. With this model, the predicted fatigue lifetime for molars restored with LS or Z100 under normal chewing forces was unrealistically high. When the more conservative exponential model, Equation (2), was used instead, the predicted fatigue lifetime for molars restored with LS and Z100 was 33 and 10 years, respectively. While these predictions are more reasonable, they are still longer than the reported average longevity of composite-resin restorations of 5.7 years [38]. In addition to the limitations of the models themselves, the difference between predictions and clinical observations could be attributed to other challenges not considered in this study, namely, shrinkage stress [16,39,40], varying temperatures and pH values, reactive biochemical species, and biofilms, which can all compromise the tooth-composite interface [41,42]. It should be noted that in the case of real restorations, both the enamel and dentin are bonded to the composite resin. However, the enamel-composite interface is small in area compared to the dentin-composite interface. Therefore, even though the enamel-composite interface appears to have a lower fatigue resistance than the dentin-composite interface [10,13], it is reasonable to assume that the fatigue life of dental restorations is mostly determined by the integrity of the dentin-composite interface.

Several methods have been used to examine the influence of cyclic loading on the degradation of composite-dentin interfaces. Examples include micro-rotary fatigue test [13], cyclic shear and push-out tests [43], as well as cyclic four-point flexure test [11,14,44]. The present study proposed an alternative test method for assessing the fatigue resistance of the dentin-composite interface. This testing method required relatively simple specimen preparation and loading configuration. Pretest failure was limited and no special jig was required for specimen fixation or loading. However, the method proposed here does have some disadvantages. For example, the dentin-composite interfacial stress cannot be calculated readily as in the simple tensile or shear test - the interfacial stress distribution in the shear test specimen is actually far from uniform [45,46]. Also, the localized contacts between the flat loading plates and the round disk produce high tensile and shear stresses that can induce dentin deformation or even fracture before interfacial debonding can take place. However, as explained above, failure initiated by dentin fracture did not seem to have occurred in our fatigue tests. Compared to the results from the four-point flexure test [11], the disk in diametral compression produced lower bond strength and a slightly higher rate of reduction in fatigue life with increasing stress. These are reflected in the lower values for A and slightly higher absolute values for B in Equation (1), respectively. The difference in bond strength can be attributed to the difference in specimen size and mode of loading between the two methods. It is well known that a material's flexural strength is higher than its tensile strength, and a material's strength decreases with increasing specimen size [47].

Secondary caries is a primary cause for the replacement of composite restorations [48,49]. The biofilm accumulated on the tooth surfaces produces acids and other biochemical molecules that can cause degradation of the tooth tissues and the tooth-composite interface. Our previous study demonstrated that the interfacial bond strength was significantly reduced by biofilm fed with sucrose [15]. In a study of the fatigue behavior of dentin-composite bonds exposed to S. mutans using the cyclic four-point flexure test, a significant reduction in fatigue resistance of the interface was also found [10]. Our future studies will combine the methodology presented here for mechanical loading with the biofilm challenge used in [15] to study composite-dentin interfacial degradation under more representative physiological conditions.

5. Conclusions

A new method based on cyclic diametral compression tests of dentin disks restored with dental composites has been developed to evaluate the composite-dentin interfacial integrity under cyclic loading. FEA and failure analysis verified that the dentin-composite disks preferentially failed at the interfacial locations where the tensile stress was highest. The results showed that the LS-restored disks had higher fatigue resistance than the Z100-restored ones. They also indicated the possibility that the dentin-composite disks had a fatigue limit, i.e. a stress level below which no fatigue failure could occur. The more conservative exponential model (σ = A + B · logN_f) provided more reasonable lifetime predictions for full composite restorations than the Basquin-type model.

Highlights.

• Dentin-composite interfaces were evaluated using cyclic diametral compression

• Silorane-based systems had higher fatigue resistance than methacrylate-based ones

• Reasonable lifetime of restored teeth was predicted by finite element simulation