Abstract
We evaluated the psychometric properties of the Cambridge face memory test (CFMT; Duchaine & Nakayama, 2006). First, we assessed the dimensionality of the test with a bi-factor exploratory factor analysis (EFA). This EFA analysis revealed a general factor and three specific factors clustered by targets of CFMT. However, the three specific factors appeared to be minor factors that can be ignored. Second, we fit a unidimensional item response model. This item response model showed that the CFMT items could discriminate individuals at different ability levels and covered a wide range of the ability continuum. We found the CFMT to be particularly precise for a wide range of ability levels. Third, we implemented item response theory (IRT) differential item functioning (DIF) analyses for each gender group and two age groups (Age ≤ 20 versus Age > 21). This DIF analysis suggested little evidence of consequential differential functioning on the CFMT for these groups, supporting the use of the test to compare older to younger, or male to female, individuals. Fourth, we tested for a gender difference on the latent facial recognition ability with an explanatory item response model. We found a significant but small gender difference on the latent ability for face recognition, which was higher for women than men by 0.184, at age mean 23.2, controlling for linear and quadratic age effects. Finally, we discuss the practical considerations of the use of total scores versus IRT scale scores in applications of the CFMT.
Keywords: Cambridge face memory test, differential item functioning, dimensionality, group difference, item response theory
Introduction
The task of recognizing faces is pervasive in our daily social interactions but the systematic study of individual differences in face recognition ability is relatively young. To study face recognition in the normal population, different labs often use their own set of idiosyncratically developed measures to suit their research questions. While sometimes the variability on these tasks is examined and related to other variables, it is rarely preceded by evaluation of the reliability and validity of test scores (e.g., Konar, Bennett, & Sekuler, 2010; Richler, Cheung, & Gauthier, 2011). In contrast, neuropsychological studies of face processing have relied on standardized tests since the early 80’s (Benton et al., 1983, Warrington, 1984), but more recent work has questioned the construct validity of performance on these tests: in particular, a normal score on these instruments can be obtained even when the internal face features are deleted, with only the hair or eyebrows available, suggesting that these tests allow a number of possible strategies, may not measure a unidimensional construct, and may be unsuitable for comparing different groups (e.g. patients versus controls) on the same scale (Duchaine & Weidenfeld, 2003; Duchaine & Nakayama, 2004).
These shortcomings motivated the creation of a measure specifically designed to reduce the usefulness of a feature-based strategy and to quantify face recognition ability across the entire range found in the normal and abnormal population: the Cambridge Face Memory Test (CFMT; Duchaine & Nakayama, 2006). It is currently the main standardized test of face recognition ability that is broadly used in face recognition research. The CFMT successfully discriminates individuals over a wide range of performance (Bowles et al., 2009; Germine, Duchaine, & Nakayama, 2011; Russell, Duchaine, & Nakayama, 2009). Consistent with other measures of face recognition (Holdnack & Dellis, 2004; Wilhelm et al., 2010), CFMT scores are not linearly correlated with verbal memory (Bowles et al., 2009; Wilmer et al., 2010, 2012) and IQ (Davis et al., 2011). Performance on the CFMT has also been found to be highly heritable, which is rare for an ability that dissociates from IQ (Wilmer et al., 2010). The CFMT has several applications both in the evaluation of acquired and congenital face recognition deficits (Bowles et al., 2009) for which it was originally created, but also in studying face recognition ability in the normal population (Germine et al., 2011; Wilmer et al., 2012). Researchers have used the CFMT to address basic questions about face recognition, such as whether this ability depends on holistic processing mechanisms (Richler et al., 2011; McGugin et al., 2012; DeGutis et al., 2013; Dennett et al., 2012), whether it shares mechanisms with non-face visual recognition (Wilmer et al., 2010; Wilmer et al., 2012; McGugin et al., 2012; Gauthier et al., submitted), and whether it can predict performance in applied situations such as eyewitness testimony (e.g., Morgan et al., 2007).
Here, our goal is to test two critical but untested assumptions of past uses of the CFMT, hopefully providing a stronger footing for its use in addressing a variety of theoretical questions as mentioned above. First is the assumption of unidimensionality1: the assumption that the CFMT measures one source of individual differences. Second is the assumption of measurement invariance across groups: the assumption that CFMT measures the same ability in different groups (males versus females, younger versus older individuals). Next, we explain why one might question either assumption, the consequences should they fail to hold, and what statistical techniques we used to test this.
Use of the CFMT implicitly assumes unidimensionality as soon as it computes a single score and calls it a measure of face recognition ability. There are, however, a few possible reasons why this assumption could not hold. First, the CFMT relies on multiple subsets of items related to 6 initial studied targets. There is no principled reason why 6 targets are used, apart from striving to present a reasonable challenge for visual learning, but this also creates subsets of items that could produce multidimensionality in the test. For example, visual short-term memory is limited for objects as complex as faces (Curby & Gauthier, 2007), and different subjects could distribute their study efforts differently over the 6 targets. It is also possible that the CFMT items with added noise (the most difficult items by design) measure something different than the other items on the test, relying more on global processing and less on featural processing. Another more speculative source of multidimensionality is that face recognition could depend on distinct abilities for different face parts (i.e., some people could be better than others in recognizing eyes, others at mouths, etc.), and different CFMT items could tap into such differences. Regardless of the reason, a lack of unidimensionality complicates interpretation and challenge the assumptions of most mathematical measurement models, including item response theory (IRT) (see below).
Use of the CFMT also implicitly assumes that it can measure the same ability in different groups or situations. But it is always possible that qualitative differences in processing exist between groups. Here we focused on gender and age because these factors have been found to affect performance on face recognition tasks, including the CFMT, and the correct interpretation of such effects depend on the validity of comparing these individuals on the same scale. Gender differences have sometimes been reported to be particularly large for female faces (Lovén et al., 2011; Lewin & Herlitz, 2002), but a small 0.15 SD difference favoring females was also found for the CFMT, which was developed using only male faces to minimize this gender difference (Wilmer et al., 2012). So far, gender effects have been interpreted as reflecting quantitative differences on the same unidimensional construct, but the sort of analyses required to test this assumption have not been conducted. The same can be said for age, which was found to have a curvilinear effect on face recognition performance, peaking shortly after age 30 (Germine et al., 2011). In fact, regardless of whether there is a difference in performance as a function of gender or age group, comparing them on the same scale assumes the instrument measures the same construct in both groups (e.g., that men and women are not using different strategies to obtain the same scores). To ask whether the CFMT produces qualitatively comparable scores in different genders or age ranges, we use IRT differential item functioning (DIF) analysis on the CFMT as a function of gender and age. We also briefly examine another grouping of potential importance: web-tested versus lab-tested participants (see Methods). In all cases, the aim was to ensure that individuals across these groups can be validly compared on a common scale.
Finally, a third goal of the current study was to facilitate the extraction of the most useful information from the 72 individual items on the CFMT, based on IRT. A unique virtue of IRT is its ability to calculate the precision of each individual person’s score. Such precision information (aka measurement error) is valuable in contexts where one wants to say something meaningful about an individual, such as when making educational/hiring decisions or when evaluating patients or exceptional performers (see Wilmer et al., 2012). Here, we compare different item response models to select the best performing model and explore characteristics of the CFMT using the model.
The application of IRT to cognitive and neuropsychological assessment is rare, but there has already been one application of IRT to the CFMT (Wilmer et al., 2012). That paper used a large (N=1471) item-by-item CFMT data set (which we use here as the web-tested portion of our data). The three key aims of this paper – testing the unidimensionality assumption, evaluating DIF for some of the most meaningful groupings likely to arise in research (gender and age), and choosing and exploring the best-performing item response model – each go beyond the analysis by Wilmer and colleagues (2012) in important ways.
Methods
Description of the data
Measures
The CFMT was designed as a test of the ability to learn to recognize novel faces across different views and illumination, based on facial features and without any other cues such as hair, make-up, or jewelry. Details of the test procedure are described in Duchaine and Nakayama (2006). The CFMT uses a three-alternative forced choice recognition paradigm so that a correct response probability by chance is 0.33. The CFMT begins with the study of 6 unfamiliar target faces, and their recognition is tested over the course of 72 items where one of the 6 target faces must be selected among two distractors. There are three blocks of trials shown sequentially. The first eighteen test items (6 target faces × 3 presentations) show the faces in a view that is identical to that which was studied in an introduction block (Block 1); the next 30 items (6 target faces × 5 presentations) use novel views (Block 2); and the last 24 items (6 target faces × 4 presentations) use novel views with the addition of Gaussian noise to keep performance off ceiling (Block 3). Each item was scored as 0 (incorrect) or 1 (correct).
Participants
Using an integrative data analysis approach (Curran & Hussong, 2009), several studies were combined to create two large samples and to investigate possible differences in online versus laboratory testing. The online sample consisted of the 1,471-participant data set used in Wilmer et al. (2012), collected on the website, Testmybrain.org. To create a comparable size sample of subjects tested in the laboratory on the same test, we combined data from three laboratories (see Table 1), totaling 1,075 participants.
Table 1. Descriptive statistics of samples for two studies (N=2,497).
| Lab testing | Online testing | |||
|---|---|---|---|---|
| Variable | Mean (SD) | Percent | Mean (SD) | Percent |
| Demographic Information | ||||
| Gender | ||||
| Female | 53.80 | 67.64 | ||
| Male | 46.20 | 32.36 | ||
| Age | 22.63(4.42) | 23.58(10.13) | ||
| <18 | 0.00 | 18.23 | ||
| 18 | 14.72 | 17.74 | ||
| 19 | 12.77 | 13.80 | ||
| 20 | 12.77 | 8.57 | ||
| 21 | 12.77 | 5.30 | ||
| 22 | 9.16 | 3.54 | ||
| 23 | 5.07 | 3.67 | ||
| 24 | 4.78 | 3.06 | ||
| 25 | 5.07 | 1.63 | ||
| 26 | 4.19 | 1.84 | ||
| 27 | 4.09 | 2.04 | ||
| 28 | 3.02 | 1.29 | ||
| 29 | 1.85 | 1.16 | ||
| 30 | 3.12 | 1.50 | ||
| >30 | 6.64 | 16.67 | ||
| Descriptive Statistics of Total Scores Ranged from 0 to 72 | ||||
| By Gender | ||||
| Female | 56.59(8.51) | 53.92(9.61) | ||
| Male | 54.29(9.16) | 52.42(10.27) | ||
| By Age Group | ||||
| Age <= 20 | 55.19(8.95) | 52.20(9.54) | ||
| Age > 21 | 55.76(8.85) | 55.16(10.02) | ||
The total number of subjects from the two test settings is 2,546. There were no missing data in item responses from 2,546 subjects. Subjects missing either gender or age information were excluded (49, from the Gauthier laboratory), yielding 2,497 subjects for analysis (see Table 1). The raw data are available at (URL provided by journal).
Dimensionality of CFMT (Step 0)
The three main analyses in the current study include an IRT analysis (including dimensionality analysis using IRT by comparing a unidimensional item response model to a multidimensional item response model), an IRT DIF analysis, and a group (gender) difference analysis. For theses analyses, it is important to select an item response model with appropriate assumptions (i.e., dimensionality and local independence) and dimensionality structure. To this end, our preliminary data analyses examined the number of dimensions and the dimensionality structure of the CFMT using eigenvalues of the sample tetrachoric correlation matrix2 and an exploratory factor analysis (EFA).
A series of EFAs using tetrachoric correlations (specifically, weighted least square with adjusted means and variance [WLSMV]3 with BI-GEOMIN rotation) were conducted using Mplus version 7.11 (Muthén & Muthén, 1998-2013), extracting 1-10 factors. When there is an evidence of a dominant general factor based on eigenvalues (i.e., the ratio of the first to second eigenvalue > 3.0), bi-factor EFA is considered instead of a regular EFA (Reise, Moore, & Haviland, 2010; Reise et al., 2011). Bi-factor EFA with 1 general and m-1 specific factors has the same model fit as regular EFA with m factors (same log-likelihood and number of parameters); it is effectively another rotation of the factors (Jennrich & Bentler, 2011, 2012).
Fit indices were compared across models having different number of factors. According to empirically supported guidelines, a model fits well if the root-mean-square error of approximation index (RMSEA; Steiger & Lind, 1980) is less than .06, root mean square residual (RMSR) is less than .08, and the comparative fit index (CFI; Bentler, 1990) and Tucker-Lewis index (TLI; Tucker & Lewis, 1973) are larger than .95 (Hu & Bentler, 1999; Yu, 2002).
Analysis outline
Based on findings on multidimensionality of CFMT (Step 0), we followed a set of best-practice sequential analysis steps for the three analyses: Step 1. IRT analysis; Step 2. IRT DIF analysis; and Step 3. Gender group difference analysis. Figure 1 presents the summary of these steps, with the dimensionality analysis labeled as Step 0 because it is a preliminary analysis for Steps 1-3. Results of Step 0 are required for Step 1 as indicated in Figure 1.
Figure 1.
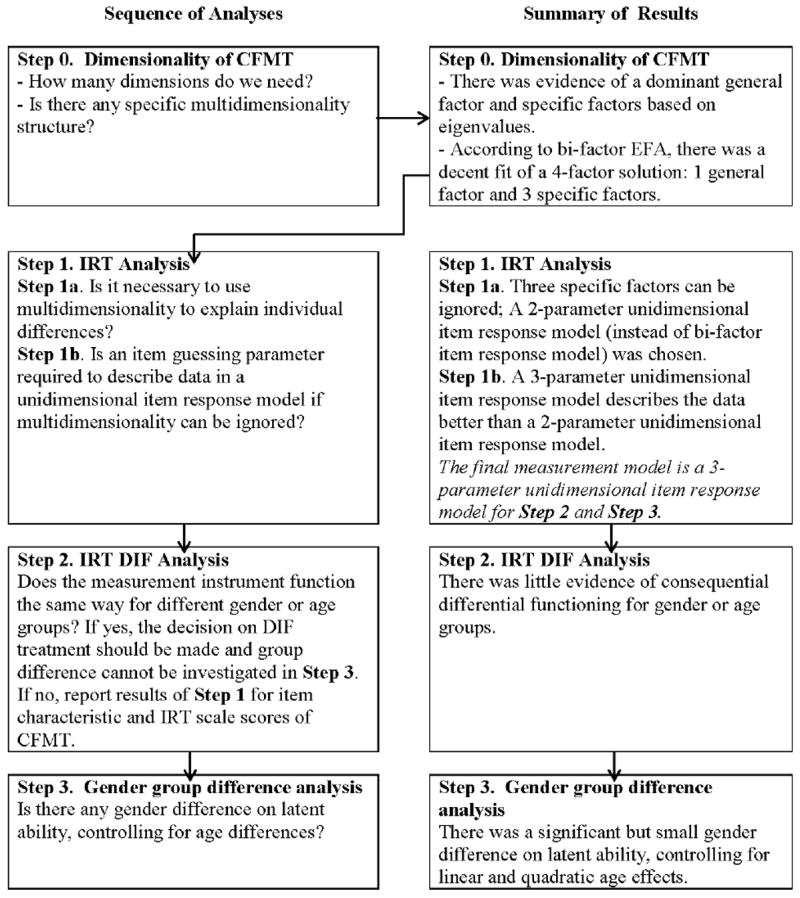
Sequence of analyses and summary of results
Based on findings in Step 0, an item response model was selected in Step 1 for IRT DIF analysis and group difference analysis in Steps 2 and 3, respectively. In Step 1, we checked whether it was necessary to consider multidimensionality in the CFMT and item guessing parameters to adequately describe the data. In Step 1a, we investigated whether multidimensionality needs to be considered to explain individual differences of CFMT by comparing an exploratory 2-parameter bi-factor item response model and a 2-parameter unidimensional item response model. When the findings from Step 1a suggest the use of unidimensional item response models, we then verified that the 3rd item parameter, representing item guessing, was required to describe data adequately (as used in Wilmer et al. [2012] for CFMT) as Step 1b.4 Once established that there was no concern about DIF in Step 2, the IRT analyses from the finalized item response model in Step 1 serve to extract information about the CFMT item characteristics, IRT scale scores, and their precision. Because group mean comparisons are not meaningful when DIF items exist, DIF analyses are first shown with respect to gender and age, respectively, using a multiple-group item response model. Accordingly, the group mean comparison with respect to gender, controlling for age differences, is presented in Step 3 after the IRT DIF analysis is implemented in Step 2. For an introduction to IRT and IRT DIF analyses, see Embretson and Reise (2000) and Millsap and Everson (1993), respectively.
Step 1. IRT analyses
Step 1a Comparisons between unidimensional and bi-factor (multidimensional) item response models
Because there was evidence for a dominant factor based on eigenvalues and (bi-factor) EFA analyses, we initially chose a bi-factor item response model (Gibbons & Hedeker, 1992) with one general dimension and several specific dimensions to investigate the psychometric properties of CFMT. The general dimension reflects what is common among items, and specific dimensions (orthogonal to the general dimension) explain item response variance that is not accounted for by the general dimension. Thus, item discriminations for the general dimension can be considered as discriminations for the ‘purified’ dimension (controlling for specific dimensions). Therefore, discrepancy between item discriminations of the general dimension in a bi-factor item response model and those of a dimension in a unidimensional item response models indicates misspecification of the unidimensional model parameter estimates in the presence of multidimensionality (e.g., Reise, Moore, & Haviland, 2010). The discrepancy also indicates whether specific dimensions can be ignored. In addition, unidimensional parameter estimates and latent variable scores tend to be only slightly affected by the other dimensions when there is a dominant dimension (e.g., Ansley & Forsyth, 1985; Reckase, 1979; Way, Ansley, & Forsyth, 1988). We therefore investigated item characteristics and IRT scale score properties obtained from two different item response models: an exploratory 2-parameter bi-factor model (or multidimensional item response model) for the general dimension, and a 2-parameter unidimensional item response model. In addition to item characteristics, we also compared IRT scale scores from the general dimension in an exploratory 2-parameter bi-factor model and from a 2-parameter unidimensional item response model. Mplus version 7.11 was used to fit the exploratory 2-parameter bi-factor model with WLSMV. The irtoys R package (Ivailo, 2013) was used to fit the unidimensional item response model with marginal maximum likelihood estimation (MLE).
Step 1b Comparison between 2-parameter and 3-parameter unidimensional item response models
If we find in Step 1a that one dominant dimension is sufficient to explain individual differences, we will then need to check whether the 3rd item parameter, representing item guessing, is required to describe the data. To this end we will compare a 2-parameter unidimensional item response model with a 3-parameter unidimensional item response model using a likelihood ratio test (LRT) (based on results of a marginal MLE). In addition, item fit and person fit statistics can be used to judge how well an item response model represents each test item and each person. Standardized residuals (Spiegelhapter, Thomas, Best, & Gilks, 1996) were used as a discrepancy measure. Item fit was calculated as the mean of the standard residuals over persons (Sinharay, 2005) and person fit was calculated as the mean of the standard residuals over items (Glas & Meijer, 2003). We consider posterior predictive p-values that are smaller than .025 or larger than .975 extreme values and indicative of misfit at 5% level.
In addition to item fit and person fit, we evaluated the adequacy of the model-data fit of the unidimensional item response model chosen based on item fit and person fit results by comparing observed total scores and posterior predictive score frequencies with a posterior predictive model checking procedure (Rubin, 1984). A new dataset was generated using the current draws of the parameters and then a posterior moment for each possible total score was calculated after convergence checking. WinBUGS 1.4.3 (Spiegelhalter, Thomas, Best, & Lunn, 2003) was used to obtain the posterior predictive score frequencies and posterior predictive p-values5. For IRT model-data fit analysis using Bayesian analysis, see Fox (2010) as an example.
Step 2. IRT DIF analysis
Based on the selected item response model from Step 1, we used IRT DIF analyses to identify differences in item parameters or item response functions (IRFs) after controlling for differences in levels of performance on the latent traits. Because there is no clear “best” DIF analysis method (e.g., Cohen & Kim, 1993), we chose to use, in parallel, three common IRT DIF detection methods: Lord’s Chi-square test (Lord, 1980), Raju’s z-statistics (Raju, 1990), and LRT method (Thissen, Steinberg, & Wainer, 1988). A 5% significance level was used for all three methods: 7.815 critical value of Chi-square distribution with df=3 for Lord’s Chi-square statistic, -1.96 and 1.96 critical values for Raju’s z-statistics, and 3.85 critical value of the Chi-square distribution with df=1. We considered items with significance on at least two of the three methods as detected DIF items.
DIF testing based on the Chi-square statistic is highly sensitive to sample size (e.g., Kim, Cohen, Alagoz, & Kim, 2007). When sample size is large, statistical significance can emerge even when DIF is actually quite small. Typically, examination of DIF effect sizes addresses this concern. In such cases, the magnitude of DIF is considered negligible for binary responses (Raju, van der Linden, & Fleer, 1995; Bolt, 2002; Flowers, Oshima, & Raju, 1999) when the noncompensatory DIF index (NCDIF) value (level index similar to Raju’s [1990] unsigned area index) is less than 0.006.
Before implementation of the DIF detection methods, the dimensionality and item fit under the item response model chosen based on IRT analyses were investigated in each group (laboratory versus online sample, males versus females, older versus younger group) to verify the adequacy of the model. The difR R package (Magis, 2013) was used to implement Lord’s Chi-square test and Raju’s area method6, and IRTLR DIF software (Thissen, 2001)7 was used for the LRT method. All three software packages use a marginal MLE approach to estimate item parameters for DIF detection. For each DIF analysis, an iterative purification procedure (Lord, 1980, p. 220) was first used to identify anchor items (i.e., non-DIF items).
Step 3. Gender group differences
An explanatory item response model (De Boeck & Wilson, 2004), a combination of the selected item response model from Step 1 and a regression model, was applied to investigate the effects of covariates (age, gender, and their interaction) on the latent ability scale. The possible nonlinear relationship between age and the latent ability scale was investigated graphically. The regression model is the same as the (polynominal) multiple regression model, except that the response variable is the latent ability. The analysis was done in a single-stage approach with all item parameters, coefficients of age, gender, and their interaction effects (on the latent ability scale), and population parameters of a random residual across persons estimated simultaneously in 3-parameter unidimensional item response model using WinBUGS 1.4.38. The single-stage approach has an advantage over a two-stage approach9 because uncertainty of the estimated parameters is taken into account when the effects of covariates on parameters are estimated (Fox, 2010).
Results
Figure 1 provides a summary of the results of each step. Below, we report the detailed results.
Step 0. Dimensionality of CFMT
Eigenvalues suggested one general factor and several specific factors: the eigenvalues for the first 10 factors were 18.558, 4.804, 2.559, 2.290, 2.075, 2.018, 1.638, 1.583, 1.505, and 1.398, respectively. The ratio of the first to second eigenvalue was 3.863, indicating a dominant general factor. Results of fit indices shown in Table 2 suggested a decent fit of a 4-factor solution based on all indices considered. Based on fit indices, and because the resulting factor structure lent itself to coherent theoretical interpretation, the 4-factor solution (1 general factor [F1] and 3 specific factors [F2-F4]) was selected. Table 3 presents the test design and the BI-GEOMIN rotated standardized loading (significantly different from 0 at 5% level in bold) to interpret specific factors, F2-F4. In Table 3, the first 18 items coded as 1 in the “Block” column indicate introductory learning phase, the subsequent 30 items coded as 2 are forced-choice test displays without noise, and the remaining 24 items coded as 3 are forced-choice test displays with noise. Significant specific factor correlations were found between F2 and F3 and between F2 and F4 (0.119 and 0.270, respectively).
Table 2. Results of fit indices.
| EFA solution | RMSEA (95% CI) | CFI | TLI |
|---|---|---|---|
| 1-factor | 0.023 (0.022, 0.024) | 0.902 | 0.899 |
| 2-factor bi-factor | 0.019 (0.019, 0.020) | 0.933 | 0.929 |
| 3-factor bi-factor | 0.017 (0.016, 0.018) | 0.940 | 0.942 |
| 4-factor bi-factor | 0.015 (0.014, 0.015) | 0.964 | 0.960 |
| 5-factor bi-factor | 0.012 (0.011, 0.013) | 0.975 | 0.972 |
Table 3. Test design and the BI-GEOMIN rotated standardized loading of a 4-factor solution.
| Item | Block | Target | F1 | F2 | F3 | F4 | Item | Block | Target | F1 | F2 | F3 | F4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 0.45 | -0.41 | -0.07 | -0.13 | 37 | 2 | 2 | 0.22 | -0.07 | 0.00 | 0.52 |
| 2 | 1 | 1 | 0.56 | -0.26 | -0.10 | -0.10 | 38 | 2 | 5 | 0.57 | -0.14 | 0.25 | -0.02 |
| 3 | 1 | 1 | 0.59 | -0.18 | -0.03 | 0.04 | 39 | 2 | 1 | 0.41 | 0.56 | -0.08 | -0.02 |
| 4 | 1 | 2 | 0.58 | -0.30 | -0.12 | 0.06 | 40 | 2 | 6 | 0.62 | -0.06 | 0.16 | -0.15 |
| 5 | 1 | 2 | 0.50 | -0.23 | 0.03 | 0.09 | 41 | 2 | 3 | 0.58 | 0.01 | -0.08 | 0.09 |
| 6 | 1 | 2 | 0.52 | -0.21 | -0.04 | -0.01 | 42 | 2 | 1 | 0.61 | 0.46 | -0.02 | 0.05 |
| 7 | 1 | 3 | 0.47 | -0.28 | -0.17 | -0.18 | 43 | 2 | 4 | 0.48 | -0.01 | 0.28 | 0.25 |
| 8 | 1 | 3 | 0.48 | -0.34 | 0.00 | -0.02 | 44 | 2 | 3 | 0.67 | 0.13 | -0.26 | 0.16 |
| 9 | 1 | 3 | 0.66 | -0.30 | 0.02 | -0.18 | 45 | 2 | 6 | 0.48 | -0.02 | 0.08 | -0.19 |
| 10 | 1 | 4 | 0.61 | -0.32 | -0.02 | -0.06 | 46 | 2 | 2 | 0.41 | 0.06 | -0.04 | 0.35 |
| 11 | 1 | 4 | 0.54 | -0.26 | 0.02 | -0.01 | 47 | 2 | 5 | 0.45 | 0.01 | 0.22 | 0.04 |
| 12 | 1 | 4 | 0.58 | -0.29 | -0.07 | -0.01 | 48 | 2 | 1 | 0.59 | 0.47 | 0.06 | -0.13 |
| 13 | 1 | 5 | 0.58 | -0.18 | -0.01 | 0.03 | 49 | 3 | 6 | 0.33 | 0.01 | -0.01 | -0.05 |
| 14 | 1 | 5 | 0.58 | -0.39 | -0.04 | 0.05 | 50 | 3 | 4 | 0.37 | 0.10 | 0.29 | 0.13 |
| 15 | 1 | 5 | 0.59 | -0.42 | 0.08 | -0.01 | 51 | 3 | 2 | 0.20 | -0.07 | 0.02 | 0.51 |
| 16 | 1 | 6 | 0.63 | -0.13 | -0.09 | -0.25 | 52 | 3 | 3 | 0.59 | -0.02 | -0.29 | 0.17 |
| 17 | 1 | 6 | 0.58 | -0.08 | -0.02 | -0.13 | 53 | 3 | 3 | 0.47 | 0.01 | -0.22 | 0.21 |
| 18 | 1 | 6 | 0.67 | -0.15 | -0.13 | -0.11 | 54 | 3 | 5 | 0.48 | 0.03 | 0.28 | 0.15 |
| 19 | 2 | 4 | 0.66 | -0.25 | 0.14 | -0.13 | 55 | 3 | 1 | 0.54 | 0.43 | -0.01 | 0.07 |
| 20 | 2 | 5 | 0.57 | -0.03 | 0.21 | -0.02 | 56 | 3 | 4 | 0.44 | 0.09 | 0.32 | 0.25 |
| 21 | 2 | 6 | 0.53 | 0.03 | 0.04 | -0.19 | 57 | 3 | 2 | 0.19 | 0.04 | 0.04 | 0.22 |
| 22 | 2 | 2 | 0.52 | 0.02 | -0.05 | 0.13 | 58 | 3 | 6 | 0.42 | 0.07 | 0.10 | -0.28 |
| 23 | 2 | 1 | 0.51 | 0.49 | -0.01 | -0.09 | 59 | 3 | 5 | 0.37 | 0.02 | 0.14 | 0.22 |
| 24 | 2 | 3 | 0.53 | 0.11 | -0.25 | 0.00 | 60 | 3 | 1 | 0.54 | 0.40 | 0.02 | 0.05 |
| 25 | 2 | 2 | 0.49 | 0.00 | -0.02 | 0.19 | 61 | 3 | 4 | 0.39 | 0.15 | 0.21 | 0.21 |
| 26 | 2 | 6 | 0.63 | -0.07 | 0.14 | -0.28 | 62 | 3 | 3 | 0.40 | 0.04 | -0.15 | -0.06 |
| 27 | 2 | 4 | 0.55 | 0.04 | 0.31 | -0.03 | 63 | 3 | 5 | 0.55 | 0.01 | 0.23 | 0.00 |
| 28 | 2 | 3 | 0.44 | 0.04 | -0.17 | 0.07 | 64 | 3 | 1 | 0.49 | 0.45 | 0.01 | 0.01 |
| 29 | 2 | 5 | 0.53 | 0.03 | 0.28 | -0.02 | 65 | 3 | 5 | 0.41 | 0.00 | 0.24 | 0.01 |
| 30 | 2 | 4 | 0.55 | 0.02 | 0.26 | 0.07 | 66 | 3 | 3 | 0.53 | 0.03 | -0.15 | 0.29 |
| 31 | 2 | 3 | 0.61 | 0.05 | -0.29 | 0.11 | 67 | 3 | 6 | 0.44 | 0.07 | -0.05 | -0.18 |
| 32 | 2 | 5 | 0.39 | -0.04 | 0.38 | -0.04 | 68 | 3 | 2 | 0.33 | 0.04 | 0.00 | 0.26 |
| 33 | 2 | 6 | 0.58 | 0.00 | 0.18 | -0.26 | 69 | 3 | 4 | 0.26 | -0.01 | 0.20 | 0.14 |
| 34 | 2 | 2 | 0.18 | 0.03 | 0.17 | 0.27 | 70 | 3 | 6 | 0.33 | 0.04 | 0.03 | -0.03 |
| 35 | 2 | 4 | 0.42 | 0.04 | 0.30 | -0.03 | 71 | 3 | 1 | 0.54 | 0.46 | -0.02 | 0.10 |
| 36 | 2 | 1 | 0.45 | 0.55 | -0.01 | -0.18 | 72 | 3 | 2 | 0.26 | 0.13 | -0.02 | -0.03 |
Note. Significantly different from 0 at 5% level in bold
To interpret the extracted four factors, we investigated how each item loaded on them. All items loaded significantly on a general factor (F1 in Table 3). Specific factors, F2 and F4, appear to be mainly clustered by targets. Specifically, 13 Target 1 items loaded on F2 significantly and saliently (loadings >|.32|)10 and 3 Target 2 items loaded on F4 significantly and saliently (loadings >|.32|). Subgroups of items might measure something in common beyond the main trait measured by the test as a whole, presumably the quality of encoding of a specific target by each subject, which could be related to relative attention to different targets or a target similarity to a known face. Regardless of the specific explanation for these effects, the results of the bi-factor EFA provide evidence of multidimensionality in CFMT.
Step 1. IRT analyses
Step 1a Comparisons between unidimensional and bi-factor (multidimensional) item response models
Our results yield a correlation coefficient of 0.90 between item discriminations from a general dimension extracted from an exploratory 2-parameter bi-factor model (or multidimensional item response model)11 and those from a unidimensional 2-parameter item response model. This implies that the strength of the relation between an item and a (unidimensional) construct is similar between the two models. Similarly, the correlation coefficient was 0.97 between the IRT scale scores from the two models. This suggests that the relative ordering of persons on the latent continuum did not substantially differ between models. Precision of the IRT scale scores was also similar across the models. Thus, we can conclude that a primary dimension was not distorted by multidimensionality (i.e., specific dimensions), and therefore a unidimensional model is sufficient to capture face recognition ability on the CFMT.
Step 1b Comparison between 2-parameter and 3-parameter unidimensional item response models
The LRT result indicates that the 3-parameter unidimensional item response model fits better than the 2-parameter unidimensional model (Chi-square value=737.38, df=72, p-value < 0.0001). Based on posterior predictive p-values, a 2-parameter unidimensional model yields a 7-item (10% of items) misfit, whereas a 3-parameter unidimensional model yields a 0-item misfit. Forty-two subjects (1.7 % of subjects) had larger than 0.975 posterior predictive p-values with the 2-parameter unidimensional model, indicating misfit. Only 2 subjects had posterior predictive p-values larger than 0.975 with the 3-parameter unidimensional model. Accordingly, a 3-parameter unidimensional item response model was chosen as a final item response model for subsequent analyses. Figure 2 shows the model-data fit analysis result by comparing the observed total scores (ranged from 0 to 72) and median expected scores (calculated based on the 3-parameter unidimensional model) with 95% posterior intervals to present uncertainty about the expected scores. All 95% posterior intervals include the observed data, indicating that the 3-parameter item response model is appropriate for the data.
Figure 2.
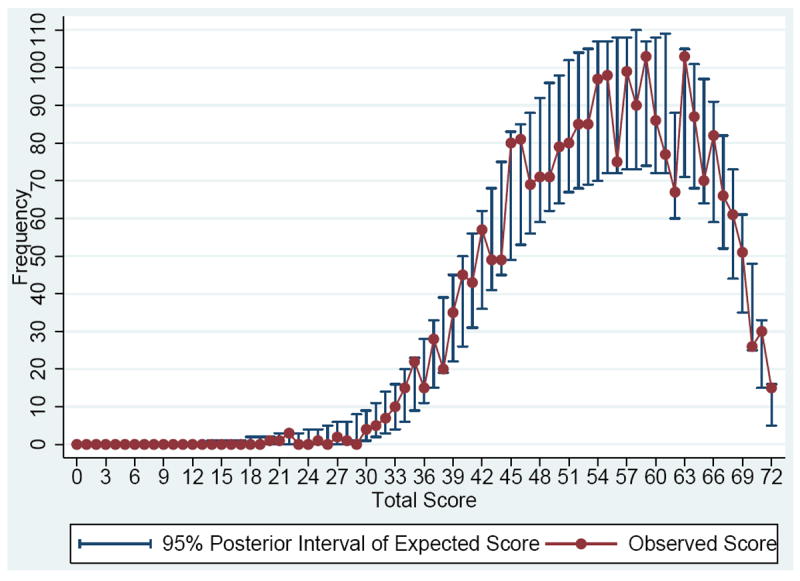
Posterior predictive plots for frequencies of 95% posterior interval of expected scores and observed scores
In summary, we found that a unidimensional model is sufficient to explain the dependency in item responses in the presence of multidimensionality, and that a 3-parameter model describes the data better than a 2-parameter model. In the following section, the results of the 3-parameter unidimensional item response model are shown.
Item characteristics
Table 4 reports the item parameter estimates and their standard errors for the 3-parameter unidimensional item response model12. Standard errors (SEs) of these item parameter estimates were acceptable except for the difficulty of Items 1, 6, 7, and 16 (standard error [SE] > 0.75 as a rule of thumb), located at the extreme of the lower level ability. Item discrimination parameter estimates were between 0.72 and 2.98 on the logit scale (i.e., log[probability of a correct response/probability of an incorrect response]), which are medium (values from 0.63 to 1.34) to large (values over 2.98) in magnitude13 (Baker, 2001). Item difficulty estimates were distributed from -5.67 to 1.58 on the logit scale14. These results indicate that the CFMT was satisfactory in terms of the quality of items to discriminate between individuals of lower and higher ability levels, and in terms of construct level coverage (i.e., wide range of item difficulty, [-5.67,1.58]).
Table 4. Item parameter estimates (SEs) of a 3-parameter unidimensional item response model.
| Item | Target | a (SE) | b (SE) | c (SE) | Item | Target | a (SE) | b (SE) | c (SE) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1.01(0.24) | -5.67(1.12) | 0.00(0.07) | 37 | 2 | 2.24(0.43) | -1.94(0.30) | 0.30(0.02) |
| 2 | 1 | 1.30(0.16) | -3.65(0.32) | 0.00(0.01) | 38 | 5 | 1.23(0.12) | 0.64(0.06) | 0.00(0.18) |
| 3 | 1 | 1.43(0.19) | -3.04(0.50) | 0.15(0.32) | 39 | 1 | 2.11(0.20) | -1.13(0.22) | 0.23(0.02) |
| 4 | 2 | 1.36(0.16) | -3.55(0.30) | 0.00(0.01) | 40 | 6 | 1.93(0.25) | -0.68(0.13) | 0.40(0.10) |
| 5 | 2 | 1.13(0.13) | -3.49(0.42) | 0.00(0.21) | 41 | 3 | 1.91(0.20) | 0.17(0.05) | 0.40(0.06) |
| 6 | 2 | 1.19(0.19) | -3.34(0.97) | 0.19(0.57) | 42 | 1 | 2.81(0.25) | -0.17(0.16) | 0.19(0.02) |
| 7 | 3 | 1.04(0.21) | -5.18(0.83) | 0.00(0.05) | 43 | 4 | 1.38(0.16) | -0.35(0.07) | 0.26(0.06) |
| 8 | 3 | 1.08(0.15) | -4.24(0.47) | 0.00(0.01) | 44 | 3 | 2.35(0.21) | -1.39(0.41) | 0.27(0.04) |
| 9 | 3 | 1.69(0.20) | -3.38(0.26) | 0.00(0.01) | 45 | 6 | 1.29(0.19) | 0.59(0.07) | 0.50(0.13) |
| 10 | 4 | 1.55(0.19) | -3.47(0.28) | 0.00(0.00) | 46 | 2 | 1.98(0.24) | -0.76(0.26) | 0.32(0.03) |
| 11 | 4 | 1.18(0.13) | -3.39(0.27) | 0.00(0.00) | 47 | 5 | 1.17(0.14) | -0.18(0.07) | 0.31(0.09) |
| 12 | 4 | 1.37(0.18) | -3.39(0.59) | 0.01(0.44) | 48 | 1 | 2.88(0.29) | -0.67(0.90) | 0.33(0.03) |
| 13 | 5 | 1.24(0.11) | -2.64(0.17) | 0.00(0.01) | 49 | 6 | 0.72(0.18) | 0.34(0.13) | 0.35(0.20) |
| 14 | 5 | 1.24(0.12) | -3.04(0.22) | 0.00(0.00) | 50 | 4 | 1.44(0.19) | 1.58(0.09) | 0.35(0.04) |
| 15 | 5 | 1.43(0.17) | -3.49(0.29) | 0.00(0.01) | 51 | 2 | 1.89(0.34) | -0.60(0.17) | 0.27(0.02) |
| 16 | 6 | 1.50(0.24) | -3.44(0.75) | 0.01(0.61) | 52 | 3 | 1.38(0.14) | -0.11(0.16) | 0.23(0.07) |
| 17 | 6 | 1.34(0.17) | -2.69(0.51) | 0.08(0.34) | 53 | 3 | 1.47(0.19) | -0.14(0.14) | 0.40(0.05) |
| 18 | 6 | 2.25(0.36) | -2.23(0.33) | 0.49(0.18) | 54 | 5 | 1.60(0.19) | 0.15(0.05) | 0.33(0.05) |
| 19 | 4 | 1.92(0.27) | -2.76(0.36) | 0.12(0.27) | 55 | 1 | 2.94(0.29) | 0.53(0.08) | 0.30(0.02) |
| 20 | 5 | 1.72(0.16) | -1.01(0.16) | 0.35(0.07) | 56 | 4 | 1.52(0.16) | 1.54(0.10) | 0.18(0.03) |
| 21 | 6 | 1.43(0.16) | -1.17(0.26) | 0.40(0.10) | 57 | 2 | 1.95(0.42) | -1.25(0.61) | 0.34(0.02) |
| 22 | 2 | 1.25(0.20) | -0.91(0.38) | 0.25(0.16) | 58 | 6 | 0.88(0.15) | 0.66(0.12) | 0.30(0.18) |
| 23 | 1 | 2.35(0.23) | 0.17(0.06) | 0.28(0.03) | 59 | 5 | 1.23(0.16) | 0.05(0.06) | 0.24(0.04) |
| 24 | 3 | 1.32(0.15) | -0.86(0.24) | 0.30(0.10) | 60 | 1 | 2.98(0.31) | 0.63(0.08) | 0.35(0.03) |
| 25 | 2 | 1.66(0.24) | -0.36(0.20) | 0.47(0.06) | 61 | 4 | 1.68(0.20) | -0.21(0.31) | 0.27(0.03) |
| 26 | 6 | 1.98(0.24) | -1.64(0.23) | 0.41(0.12) | 62 | 3 | 1.28(0.24) | -0.67(0.17) | 0.57(0.07) |
| 27 | 4 | 1.67(0.19) | -1.05(0.21) | 0.36(0.09) | 63 | 5 | 1.71(0.20) | 0.20(0.06) | 0.38(0.07) |
| 28 | 3 | 1.14(0.16) | -0.40(0.27) | 0.38(0.08) | 64 | 1 | 2.32(0.20) | -0.34(0.29) | 0.27(0.02) |
| 29 | 5 | 1.36(0.14) | -0.86(0.19) | 0.24(0.08) | 65 | 5 | 1.25(0.21) | 0.11(0.09) | 0.44(0.08) |
| 30 | 4 | 1.35(0.13) | -1.11(0.20) | 0.15(0.10) | 66 | 3 | 1.54(0.15) | -0.29(0.33) | 0.21(0.04) |
| 31 | 3 | 1.34(0.13) | -0.48(0.16) | 0.14(0.07) | 67 | 6 | 1.34(0.27) | 1.25(0.07) | 0.50(0.09) |
| 32 | 5 | 1.05(0.16) | -0.35(0.31) | 0.34(0.09) | 68 | 2 | 1.85(0.28) | 1.19(0.30) | 0.22(0.02) |
| 33 | 6 | 1.54(0.17) | -1.06(0.21) | 0.29(0.10) | 69 | 4 | 0.72(0.19) | 0.63(0.16) | 0.19(0.09) |
| 34 | 2 | 2.02(0.35) | 1.36(0.09) | 0.37(0.02) | 70 | 6 | 1.34(0.25) | 0.21(0.04) | 0.45(0.04) |
| 35 | 4 | 1.28(0.20) | -0.81(0.35) | 0.47(0.10) | 71 | 1 | 2.98(0.26) | 1.14(0.16) | 0.25(0.02) |
| 36 | 1 | 1.62(0.15) | 0.34(0.07) | 0.20(0.03) | 72 | 2 | 1.06(0.21) | -1.94(0.30) | 0.35(0.04) |
Note.
“a”, “b”, and “c” indicate an item discrimination, difficulty, and guessing parameter, respectively.
The 3-parameter unidimensional item response model produced item guessing parameter estimates (i.e., the probability of a correct response for a person with an infinitely low ability) ranging from 0 to 0.57. There were 27 items (38% of the test) with an item guessing parameter estimate higher than a random guessing probability (0.33 in a three-alternate forced recognition paradigm with the assumption that all alternatives are equally attractive.) A possible explanation for these items is that some of the distractors may be particularly obvious as incorrect options. Such high guess rates may lead to a negative skew of IRT true scores (i.e., test response function at the estimated ability). In addition, when item guessing parameter estimates are high, maximum information is provided at higher ability levels and the maximum amount of information that is provided decreases (Birnbaum, 1968).
The CFMT contains three blocks of trials shown sequentially: an introductory block (block 1), a novel image block (block 2), and a novel image with noise block (block 3). Average IRT item difficulties ascended by block: Block 1 was: -3.52, Block 2 was -0.56, and Block 3 was 0.25. Average item discrimination and guessing parameter estimates also ascended by block. Average item discrimination estimates across items in blocks were 1.35, 1.63, and 1.71 for Block 1 (i.e., items 1-18), Block 2 (i.e., items 19-48), and Block 3 (i.e., items 49-71), respectively. Average item guessing parameter estimates across items in blocks were 0.05, 0.30, and 0.32 for Block 1, Block 2, and Block 3, respectively. Variation in item discriminations (across items) increased as item difficulties increase, which means that items were endorsed in Blocks 2 and 3 mattered more for determining IRT scale scores than in Block 1. Finally, there was high item guessing parameter estimate (> 0.33) for items with difficulties between -2 and 1. IRT scale scores and reliability of test scores. Figure 315 shows the ability scores and their matched standard errors from the 3-parameter unidimensional item response model16. The ability score can be interpreted as a standardized z-score. The standard errors ranged from 0.23 to 0.55; the mean and SD of standard errors were 0.30 and 0.05, respectively. The CFMT gives particularly precise estimates of ability (i.e., smaller standard errors) for the ability level range between -3.5 and 1.5. Marginalized IRT reliability (Green, Bock, Humphreys, Linn, & Reckase, 1984) for CFMT performance was 0.91 (ranged from 0 to 1), which can be considered high.
Figure 3.
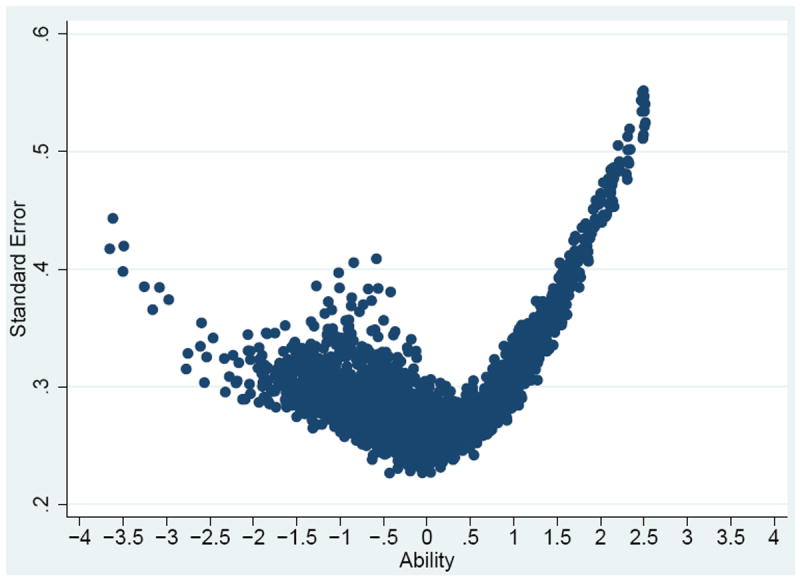
Ability scores (x-axis) and their standard errors (y-axis)
Step 2. IRT DIF analysis
A multiple-group 3-parameter unidimensional item response model was chosen for IRT DIF analyses because the analyses reported above of the dimensionality analysis and model comparisons (i.e., bi-factor [multidimensional] model vs. unidimensional model) suggested a unidimensional model, and a 3-parameter model fit the data better than a 2-parameter model.
Lab versus online testing DIF
We investigated if data collected in the lab and online could be justifiably combined for our analyses using IRT DIF analyses. Four items (Items 32, 36, 56, and 64) were detected as DIF items between the online and lab datasets. The NCDIF values for these four DIF items are less than 0.05, indicating that the magnitude of DIF was not large (Bolt, 2002; Flowers et al., 1999). Given these results, we concluded that DIF was negligible; in other words, there is no compelling evidence that CFMT functions qualitatively differently in the lab versus the web. We thus concluded that the datasets could be combined.
Gender DIF
DIF analysis was carried out to answer the question: “Does the measurement instrument function the same way for men and women?” The 3-parameter (unidimensional) item response model fit well for each gender group data. Table 5 shows DIF results per item for men (M; reference group; N=950) and women (F; focal group; N=1547). Thirteen items (Items 7, 12, 21, 31, 33, 42, 45, 46, 52, 54, 63, 67, and 69) were detected as DIF items between the gender groups based on two methods among the three IRT DIF detection methods we chose. Two items (Items 35 and 48) were detected as DIF items based on all three methods. No systematic pattern by blocks or targets was found in DIF items. Despite the significance of the results, the NCDIF index values for the 15 DIF items were less than 0.006 indicating that the magnitude of DIF was not large.
Table 5. DIF results.
| Item | Target | Gender | Age | Item | Target | Gender | Age | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lord | Raju | LRT | Lord | Raju | LRT | Lord | Raju | LRT | Lord | Raju | LRT | ||||
| 1 | 1 | 2.44 | 37 | 2 | 8.89 | ||||||||||
| 2 | 1 | 38 | 5 | 79.04 | 43.38 | ||||||||||
| 3 | 1 | 74.59 | 39 | 1 | |||||||||||
| 4 | 2 | 28.36 | 6.20 | 40 | 6 | 35.18 | |||||||||
| 5 | 2 | 17.5 | 85.59 | -2.26 | 41 | 3 | 34.71 | ||||||||
| 6 | 2 | 52.85 | 189.95 | 42 | 1 | 18.25 | 8.00 | ||||||||
| 7 | 3 | 16.22 | -3.12 | 71.53 | -5.30 | 43 | 4 | 18.40 | |||||||
| 8 | 3 | 8.35 | 3.29 | 44 | 3 | ||||||||||
| 9 | 3 | 11.83 | 45 | 6 | -2.56 | 5.00 | 40.42 | 2.36 | |||||||
| 10 | 4 | 46 | 2 | 12.62 | 6.30 | ||||||||||
| 11 | 4 | 6.70 | 47 | 5 | 42.90 | ||||||||||
| 12 | 4 | 10.42 | 10.10 | 58.25 | 48 | 1 | 10.92 | 2.23 | 13.70 | ||||||
| 13 | 5 | 16.31 | 92.72 | 5.90 | 49 | 6 | 140.97 | 4.00 | |||||||
| 14 | 5 | 50 | 4 | ||||||||||||
| 15 | 5 | 4.30 | 51 | 2 | |||||||||||
| 16 | 6 | 21.17 | 52 | 3 | 22.15 | 6.40 | |||||||||
| 17 | 6 | 92.04 | 177.48 | 53 | 3 | 29.61 | |||||||||
| 18 | 6 | 8.96 | 54 | 5 | 86.64 | 4.70 | 25.57 | 20.40 | |||||||
| 19 | 4 | 55 | 1 | ||||||||||||
| 20 | 5 | 56 | 4 | 24.25 | |||||||||||
| 21 | 6 | 29.67 | 4.40 | 33.79 | 3.31 | 57 | 2 | 68.49 | -2.93 | 10.90 | |||||
| 22 | 2 | 7.00 | 369.70 | 2.48 | 18.50 | 58 | 6 | 117.47 | 2.31 | ||||||
| 23 | 1 | 12.34 | 59 | 5 | |||||||||||
| 24 | 3 | 60 | 1 | 18.84 | -2.62 | ||||||||||
| 25 | 2 | 25.80 | -3.95 | 5.20 | 61 | 4 | |||||||||
| 26 | 6 | 62 | 3 | 39.28 | |||||||||||
| 27 | 4 | 63 | 5 | 11.59 | 4.10 | ||||||||||
| 28 | 3 | 43.76 | 66.16 | 2.06 | 64 | 1 | 8.90 | 10.21 | -2.23 | 10.30 | |||||
| 29 | 5 | 103.73 | 15.50 | 65 | 5 | 2.24 | 149.08 | ||||||||
| 30 | 4 | 14.91 | 66 | 3 | |||||||||||
| 31 | 3 | 11.63 | 7.00 | 51.51 | 15.50 | 67 | 6 | 37.16 | 3.90 | 176.01 | |||||
| 32 | 5 | 159.37 | 359.83 | 3.37 | 4.60 | 68 | 2 | 48.43 | |||||||
| 33 | 6 | 32.32 | 9.60 | 39.50 | 2.69 | 3.90 | 69 | 4 | 78.37 | 12.40 | 14.71 | 2.14 | |||
| 34 | 2 | 51.86 | 70 | 6 | 22.03 | 70.14 | |||||||||
| 35 | 4 | 27.12 | 2.3 | 9.30 | 15.24 | -3.00 | 71 | 1 | 5.60 | 21.83 | |||||
| 36 | 1 | 7.96 | 72 | 2 | |||||||||||
Note. Blank cells indicate that DIF results are not statistically significant at the 5% level.
Whether men and women can be scored and compared on the same scale in the presence of DIF items depends on two considerations (Smith & Reise, 1998). The first is the impact of removing DIF items on mean standardized latent scores. The mean score of the male group (coded as 1) was 0.173 (SE=0.044, z=-3.927, p-value=0.000) points lower than the mean of the female group (coded as 0) on the standardized latent trait continuum when using all 72 items (including DIF items), while the mean score of the male group was 0.177 (SE=0.045, z=-3.917, p-value=0.000) points lower than the mean of the female group on the scale using 57 non-DIF items17. Therefore, DIF items do not distort the scale score much at the gender group level. The second consideration is the correlation between scores using a calibration by gender group and a calibration with all subjects: here, these were highly correlated (Pearson’s correlation=0.997; Kendall’s tau-a=0.953). This indicates that the relative ordering of person’s scores does not change when using a separate scaling for men and women.
Age DIF
Age DIF analysis was used to answer the question: “Does the measurement instrument function the same way for different age groups?” We identified two age groups for DIF analysis (younger: age ≤ 20 years; older: age > 21 years). This particular split of the data was chosen for two reasons, one statistical and one theoretical. Statistically, it broke our sample roughly in half, which provided the greatest power for identifying DIF items. Theoretically, it allowed us to conduct the broadest test of the hypothesis that some qualitative change might happen over the adult age span.
The 3-parameter (unidimensional) item response model fit well for each age group’s data. Table 5 presents DIF results for the younger group (G1; reference group; N=1,271) and the older group (G2; focal group; N=1,226) and DIF detection results. Fourteen items (Items 4, 5, 6, 7, 13, 21, 28, 29, 31, 35, 45, 49, 58, and 69) were detected as DIF items with the two detection methods and 6 items (Items 22, 25, 32, 33, 57, and 64) were detected as DIF items with the three detection methods. There were six items with a large DIF magnitude (Items 5, 22, 32, 49, 54, and 57), based on NCDIF.
To ask if the two age groups can be scored and compared on the same scale in the presence of DIF items, we again considered that the mean score of the older age group (coded as 1) was 0.240 (SE=0.043, z=5.554, p-value=0.000) points higher than the mean of the younger age group (coded as 0) on the standardized latent trait continuum using all 72 items (including DIF items), and the mean score of the older age group was 0.277 (SE=0.044, z=6.309, p-value=0.000) points higher that of the younger age group using only the 52 non-DIF items18. The scale distortion by DIF items was negligible. Second, scores calibrated separately by age group and scores calibrated with all persons were highly correlated (Pearson’s correlation=0.99; Kendall’s tau-a=0.90). This indicates that relative ordering of persons’ scores changes little using a separate scaling for the two age groups.
Step 3. Gender group differences
Polynomial regression was applied because there is a nonlinear relationship between age and the total scores graphically. A polynomial in age centered on a mean age (23.2), gender, and their interactions were included as covariates on the latent ability variable in the explanatory item response model. A dummy variable was created for the gender group (female=0 and male=1). The best-fit model has the intercept estimate (0.159, 95% CI=[0.108,0.211]), the linear age effect estimate (0.037, 95% CI=[0.029,0.044]), the quadratic age effect estimate (-0.001, 95% CI=[-0.002,-0.001]), and the gender effect estimate (-0.184, 95% CI=[-0.259,-0.108]). Thus, the level on the latent ability scale for women was higher (0.184) than for men at the mean age 23.2, controlling for linear and quadratic age effects. This difference is on the standardized latent trait continuum and can be considered a small latent effect (Hancock, 2001).
Summary and Discussion
We explored the psychometric properties of CFMT to verify the important and untested assumptions of unidimensionality and equivalent functioning across various typical groups, and to draw inferences as to the circumstances in which this test can be used to investigate individual differences in face recognition ability. Several main findings emerged. First, we found evidence of multidimensionality due to item clustering by targets, but this multidimensionality did not distort the primary dimension. A unidimensional model was therefore sufficient to describe face recognition ability, as measured by the CFMT. Second, CFMT items proved to have desirable characteristics in that they cover a wide range of ability levels. Difficulty and discrimination ascended by blocks, as expected according to the test design. However, there were items with item guessing parameter estimates higher than random guessing probability (.33). This combination of broad ability coverage and high item guessing suggest that while the CFMT is, overall, an effective and efficient measurement instrument, it could be possible to ultimately develop a shorter, more efficient test of face recognition ability. Third, the CFMT was more informative (or precise) for the ability level range between -3.5 and 1.5 (on a standardized score scale with a mean 0 and a variance 1) than for ability levels at the extremes (though as pointed out by Wilmer et al. [2012], percentile ranks of IRT scale scores on CFMT will still be precise up through the extreme high and low performers). Similarly related to the precision of measurement, reliability for CFMT performance was high. These results suggest that CFMT may be particularly efficient and effective for diagnosing clinically poor performance. Fourth, there were a substantial number of DIF items between gender and age groups. However, the magnitude of these effects was very low, indicating that the CFMT was not seriously biased toward/against any subgroups. Our results with IRT scale scores did confirm, however, the previously reported higher face recognition ability for women than men (Wilmer et al., 2012) and differences in recognition performance across the age span (Germine et al., 2011). Overall, our results show that the CFMT stands up to rigorous evaluation of its assumptions and effectiveness, and suggest that the test can be broadly used to measure individual, clinical, and group differences.
Overall, these findings suggest that it is reasonable to use a single continuum of individual differences in facial recognition ability on the CFMT, and that this holds regardless of gender and age groups, as well as online versus laboratory settings.
Does using IRT versus total scores make any practical difference?
In practice, total scores are often used to generate standardized z-scores or percentile ranks of performance (e.g., Bowles et al., 2009). Percentile ranks and standardized z-scores are calculated based on total scores. IRT scale scores, unlike total scores, are calculated based on the estimation of a measurement model where item responses are indicators of the person’s level on the construct (or latent variable). IRT scale scores can be interpreted directly as standardized z-scores. One may be interested in the practical difference of deriving scores (e.g., standardized z-scores or percentile ranks) from each of these different theoretical frameworks. Toward this end, we evaluate the loss of information that occurs when IRT scale scores of CFMT performance are compared to the simpler total score.
In our data, there was a strong linear relationship between IRT scale scores from the (one-group) 3-parameter unidimensional item response model and the standardized z-scores of raw CFMT total scores (Pearson correlation = 0.98; Kendall’s tau-a= 0.92). Thus, little information is lost using raw scores, whether standardized z-scored or percentile-ranked. Further, there was little difference in using total scores versus the IRT scale scores to detect gender differences controlling for linear and quadratic age effects, given the score properties and high reliability: females scored 0.192 better on the standardized total score scale and 0.184 better on the standardized latent score scale. Critically, more information would be lost for a test that produced less unidimensional, less reliable scores, or had larger-magnitude DIF items; in such cases, raw scores may be a poor substitute for IRT scale scores.
Further, IRT scale scores may differentiate individuals who have the same total scores (something that tends to happen more frequently for higher than lower total scores on the CFMT, given its negative skew). Using the sum score assumes that all items are equally related to the construct. However, items can have different weights on the construct (Lord & Novick, 1968); people who score correctly on items with higher item discriminations have higher IRT scale scores than those who score correctly on items with lower item discriminations. In this regard, the IRT scale scores are based on item response pattern scoring. This is why there is variability in IRT scale scores given the same standardized z-score or percentile ranks (this is shown in Figure 4). The standardized z-scores and the percentile ranks are within 0.18 standard units of the IRT scale scores because the differences in item discriminations are relatively small across items in this dataset (SD=0.6). The differences between weighted and unweighted scores would be more noticeable in a test where item discriminations are more varied across items than on the CFMT.
Figure 4.
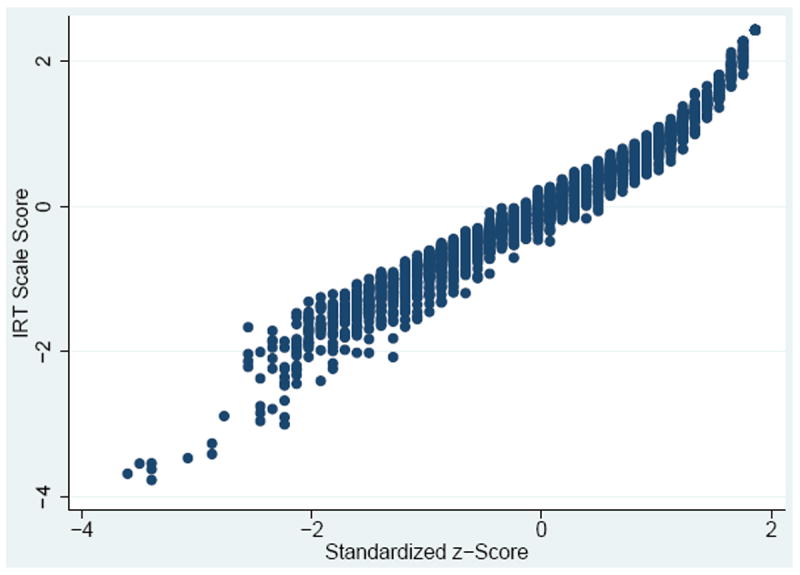
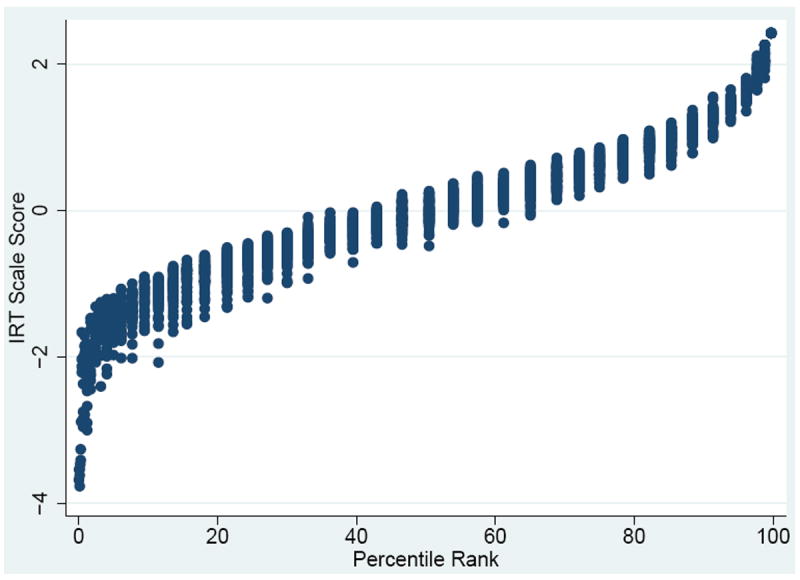
IRT scale scores vs z-scores (top) and IRT scale scores vs. percentile ranks (bottom)
In sum, our results suggest that IRT scale scores for the CFMT are not substantively different from raw scores in many respects; this is mainly attributable to the limited variation of item discrimination across items on the CFMT. Yet despite these similarities among scales, IRT scale scores have distinct properties and provide added information relative to total scores. First, as mentioned above, item response models produce an individualized standard error measurement for each individual’s IRT scale score (see Figure 3). Total scores, on the other hand, are amenable only to the computation of a mean standard error of measurement (SEM) across all individual scores, which may poorly reflect the error in some or many individual scores. These individualized errors enable more accurate inferences about individuals, a virtue, for example, in the evaluation of clinically poor (Duchaine & Nakayama, 2006) or exceptionally good (Russell et al., 2009) individuals.
Second, IRT can provide interval-level measurement scales.19 Thus, the difference between a score of -2 and a score of -1 is the same as the difference between a score of 1 and a score of 2 on the IRT scale. In contrast, this interpretation does not hold for the total scores or percentile rank scale, as those are ordinal-level measurement scales.
Third, IRT may provide results with fewer scaling artifacts than total scores (e.g., Thissen & Wainer, 2001). For example, in some cases, the difference between IRT scale scores and total scores may stem from a ceiling effect or a floor effect. This scaling artifact can be reduced on IRT scale scores because IRT scale scores are a nonlinear (e.g., logistic), weighted transformation of raw item scores.
Fourth, it is possible to use data from a one large study (such as the data provided here or by Wilmer et al., 2012) to compute IRT scale scores for other samples. This can be particularly valuable for small-scale studies (such as case studies of exceptionally good or bad performers). This can be done simply (i.e. without needing to fit a new item response model) via the estimated item parameters in our current large samples (reported in Table 4)20. IRT scoring for other samples rests on the (frequently plausible) assumptions that the same dimensionality structure holds and that the 3-parameter item response model is the best-fit to the small scale data (e.g., Kang & Cohen, 2007).
In sum, our analyses verify that even raw total scores on the CFMT provide a highly informative measure of clinical, individual, and group differences. IRT scale scores nevertheless provide significant additional advantages. Importantly, the large data set that we provide enables IRT scores (and standard errors) to be computed even for individual (e.g. clinical) case studies in future work, a helpful aid to diagnostic procedures. In recent years, the CFMT has become a widely-used and influential measure of face recognition ability. It is, among other uses, the de facto standard clinical instrument used to diagnose developmental and acquired prosopagnosia (Bowles et al., 2009; Wilmer et al., 2012). Our analyses remove several critical caveats that have necessarily qualified past work on clinical face recognition deficits. Moreover, our results suggest that IRT can be used to further enhance the CFMT’s utility as both a clinical and non-clinical measure.
Limitations
There are several methodological caveats to the present study. First, for the first time, we have examined whether the basic measurement properties of the CFMT hold across ages, across gender, and across whether the test was administered in the lab or via the web. These are major steps forward in terms of determining whether the test is measuring the same construct in the same way across demographic groups. This study does not, however, cover all demographic variables of interest. Future work will be required, for example, to test if these properties hold across ethnicities and socioeconomic variables.
Second, there are various ways to check if multidimensionality is necessary to explain individual differences (e.g., Reckase, 2009). In Step 1, for justification of unidimensionality, only correlation coefficients were calculated between item discrimination estimates from exploratory 2-parameter bi-factor item response model (or multidimensional) and unidimensional item response models and also for IRT scale scores. The two models were not compared using model selection methods because a different estimation method for each model was used. Namely, limited information estimation method, WLSMV, was used for the exploratory bi-factor item response model and full information estimation method, MLE, was used for the unidimensional item response model.
Third, it is ideal to have the same estimation method for model parameter estimation and for model evaluation. We used marginal MLE for the model parameter estimation because the DIF detection methods we used were developed mainly within a MLE framework. We chose a Bayesian model evaluation approach instead of a MLE model evaluation approach, because the latter lacks a test statistic of person and item fit measures. Though the estimation methods are different, item parameter estimates and person scores are highly similar between a marginal MLE and Bayesian approach when the same priors on all parameters are used in BILOG-MG (Zimowski, Muraki, Mislevy, & Bock, 1996). Thus, we can expect that the results of the Bayesian model evaluation approach are similar to those of the MLE model evaluation approach.
Fourth, the main purpose of the DIF analyses in this study was to detect DIF items and to investigate whether those DIF items contaminated a primary dimension (measured with a sensitivity analysis). We did not find systematic patterns in DIF items with respect to the test design by blocks and targets. Explaining why there were DIF items in a test is a different task from detecting DIF items (De Boeck, Cho, & Wilson, 2011), one we did not take on here because DIF levels were negligible.
Fifth, we created two age groups for age DIF analysis based, in part, on practical requirements. While a continuous analysis – analogous to our continuous regression analyses – would be of interest for a variable like age that has demonstrated a curvilinear relationship to CFMT performance (Germine et al., 2011), multiple-group analysis procedures for examining DIF as a function of a continuous variable have not yet been developed.
Sixth, we found evidence that some items have guessing parameter estimates higher than the .33 expected for a three-alternative forced choice test of this sort, evidence that distractors in these items may not function well (e.g. these distractors may be too easy to reject). A future distractor analysis (Haladyna, 2004) could be used to identify the reasons for these high guessing parameter estimates. Such an analysis requires a record of which distractor was chosen for each incorrect answer, however, information which was not available for most of the participants in the present dataset. The facial attributes that may render a particular foil easier or more difficult to reject are difficult to specify. This would require a model of what features (e.g., smaller local features and/or larger features) are used by subjects in the CFMT. Such a model does not currently exist. Some studies have suggested that CFMT scores are associated with holistic processing (e.g., Richler et al., 2011; Degutis et al., 2013), but recent work using a more reliable measure of holistic processing found that the degree of holistic processing was not related to performance on the CFMT (e.g., Richler et al., in press). Inspection of the trials in CFMT with high guessing parameter estimates suggests that some have one distractor with a feature (age, eyebrow shape) that is distinctive relative to the group of 6 targets. However, these are conjectures that would need to be verified in an experimental design.
Acknowledgments
The authors thank Jackie Floyd for her help in data collection. The research was supported by Brachman Hoffman Fellowship to J.W., NSF Grant SBE-0542013, NEI Grants P30-EY008126 and NEI R01 EY013441 to I.G., as well as NIH Grants MH64812 and MH096698 to G.H., and a grant from NSERC to D.F.
Footnotes
The assumption of local independence for the case when a latent trait is unidimensional and the assumption of a unidimensional latent space are equivalent (Lord & Novick, 1968).
Use of the Pearson correlation with binary data underestimates the strength of the relationships among variables (Olsson, 1979). In this situation, use of the tetrachoric correlation is recommended because it produces unbiased estimates of the relationships among the latent continuous variables thought to underlie the observed categories (Olsson, 1979).
For details about WLSMV, see Muthén, du Toit, and Spisic (1997).
It would be ideal to compare an exploratory 3-parameter bi-factor item response model to a 3-parameter unidimensional item response model. However, we could not compare these models for two reasons. First, to our knowledge, there is no software to fit an exploratory 3-parameter bi-factor item response model. Second, it is not desirable to compare item discriminations of the general dimension in an exploratory 2-parameter bi-factor item response model with item discriminations of a dimension in a 3-parameter unidimensional item response model. When ability level is equal to the item difficulty, the item discrimination in the 3-parameter (logistic) unidimensional item response model is at its maximum value, 0.426*discrimination*(1-guessing) (Baker & Kim, 2004).
The code is available from the first author upon request.
R code for Lord’s Chi square test and Raju’s area method is as follows: library(difR)
LORD <- difLord(data, group=“gender”, focal.name=0, model=“3PL”, c=NULL, engine=“ltm”, purify=TRUE) Raju <- difRaju(data, group=“gender”, focal.name=0, model=“3PL”, engine=“ltm”, signed=TRUE)
Software and its manual can be downloaded from http://www.unc.edu/~dthissen/dl.html.
Codes are available from the first author upon request.
In the two-stage procedure, IRT scale scores are obtained first from item response models and then use a (polynomial) multiple regression model to estimate the effects of covariates.
Tabachnick and Fidell (2001) cited .32 as a good rule of thumb for the minimum loading of an item in order to consider it important/salient,, which equates to approximately 10% (0.32ˆ2 × 100) overlapping variance with the other items in that factor in exploratory factor analysis. It should be noted that this criterion, although commonly used, is arbitrary and does not have any statistical foundation.
Exploratory analysis with WLSMV allows the probit link only in Mplus version 7.11. Thus, item discriminations of the exploratory bi-factor models were transformed to those on the logit scale for the comparison with item discriminations of unidimensional item response models using the ltm R package.
R code to obtain item parameter estimates and their standard errors is as follows: library(irtoys)
p.3pl <- est(data, model=“3PL”, engine=“ltm”, nqp = 30)
In a 3-parameter logistic model, discrimination is proportional to the slope at the inflexion point. The slope for the model is 0.426*discrimination*(1-guessing). See Baker and Kim (2004) for the detail.
In a 3-parameter logistic model, the probability of a correct response at item difficulty level is (guessing parameter estimate + 1)/2, which is always greater than 0.5.
Results shown in Figure 3 are different from those of Figure 8 (a) in Wilmer et al. (2012) because of differences in item discrimination estimates, different sample sizes receiving IRT scale scores (due to the limitation of ltm in R used in Wilmer et al., [2012]), and different IRT scoring estimation methods for standard errors.
R code to obtain ability estimate and its standard error for each individual person is as follows. Note that this can be done after item parameters are estimated or item parameters are provided as known values: library(irtoys)
th.eap <- eap(resp=data, ip=p.3pl$est, qu=normal.qu(n = 100))
For the results of 57 non-DIF items, item parameters of a 3-parameter unidimensional item response model were estimated using 57 non-DIF items and then IRT scale scores were calculated based on the estimated item parameters for the mean score calculation.
For the results of 52 non-DIF items, item parameters of a 3-parameter unidimensional item response model were estimated using 52 non-DIF items and then IRT scale scores were calculated based on the estimated item parameters for the mean score calculation.
Not all psychometricians agree with this point (e.g., Perline, Wright, & Wainer, 1979).
Using item parameter estimated reported in Table 4, IRT scale scores for other samples can be calculated using the following R code: library(irtoys)
data <- read.table(“C:/data.txt”, header=T, fill=T) #data.txt: new item response data
item <- read.table(“C:/item.txt”, header=T, fill=T) #values in Table 4; also provided as a supplementary data
item <- as.matrix(item) #covert the data file to matrix
th.eap <- eap(resp=data, ip=item, qu=normal.qu(n = 100))
scores <- write.table(th.eap, file=“C:/score.txt”, sep=“\t”) # IRT scale scores will be saved as “score.txt” in the #specified directory, c:\.
References
- Ansley TM, Forsyth RA. An examination of the characteristics of unidimensional IRT parameter estimates derived from two dimensional data. Applied Psychological Measurement. 1985;9:37–48. [Google Scholar]
- Baker F. ERIC Clearinghouse on Assessment and Evaluation. University of Maryland; College Park, MD: 2001. The basics of item response theory. [Google Scholar]
- Baker FB, Kim S-H. Item response theory: parameter estimation techniques. 2. New York: Dekker; 2004. [Google Scholar]
- Bentler PM. Significance tests and goodness of fit in the analysis of covariance structures. Psychological Bulletin. 1990;107:238–246. [Google Scholar]
- Benton AL, Sivan AB, Hamsher K, Varney NR, Spreen O. Benton facial recognition test. New York: Oxford University Press; 1983. [Google Scholar]
- Birnbaum A. Some latent trait models and their use in inferring an examinee’s ability. In: Lord FM, Novick MR, editors. Statistical theories of mental test scores. Reading, MA: Addison–Wesley; 1968. [Google Scholar]
- Bolt DM. A Monte Carlo Comparison of parametric and nonparametric polytomous DIF detection methods. Applied Measurement in Education. 2002;15:123–141. [Google Scholar]
- Bowles DC, McKone E, Dawel A, Duchaine B, Palermo R, Schmalzl L, Rivolta D, Wilson CE, Yovel G. Diagnosing prosopagnosia: Effects of ageing, sex, and participant–stimulus ethnic match on the Cambridge Face Memory Test and Cambridge Face Perception Test. Cognitive Neuropsychology. 2009;26(5):423–455. doi: 10.1080/02643290903343149. [DOI] [PubMed] [Google Scholar]
- Cohen AS, Kim S-H. A comparison of Lord’s Chi-square and Raju’s area measures in detection of DIF. Applied Psychological Measurement. 1993;17:39–52. [Google Scholar]
- Curby KM, Gauthier I. A visual short-term memory advantage for faces. Psychonomic Bulletin & Review. 2007;14(4):620–628. doi: 10.3758/bf03196811. [DOI] [PubMed] [Google Scholar]
- Curran PJ, Hussong AM. Integrative data analysis: The simultaneous analysis of multiple data sets. Psychological Methods. 2009;14:81–100. doi: 10.1037/a0015914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis JM, McKone E, Dennett H, O’Connor KB, O’Kearney R, Palermo R. Individual differences in the ability to recognise facial identity are associated with social anxiety. PloS one. 2011;6(12):e28800. doi: 10.1371/journal.pone.0028800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Boeck P, Wilson M. Explanatory item response models: A generalized linear and nonlinear approach. New York, NY: Springer; 2004. [Google Scholar]
- De Boeck P, Cho S-J, Wilson M. Explanatory secondary dimension modelling of latent DIF. Applied Psychological Measurement. 2011;35:583–603. [Google Scholar]
- DeGutis J, Wilmer J, Mercado RJ, Cohan S. Using regression to measure holistic face processing reveals a strong link with face recognition ability. Cognition. 2013;126(1):87–100. doi: 10.1016/j.cognition.2012.09.004. [DOI] [PubMed] [Google Scholar]
- Dennett HW, McKone E, Tavashmi R, Hall A, Pidcock M, Edwards M, Duchaine B. The Cambridge Car Memory Test: A task matched in format to the Cambridge Face Memory Test, with norms, reliability, sex differences, dissociations from face memory, and expertise effects. Behavior Research Methods. 2012;44(2):587–605. doi: 10.3758/s13428-011-0160-2. [DOI] [PubMed] [Google Scholar]
- Duchaine BC, Weidenfeld A. An evaluation of two commonly used tests of unfamiliar face recognition. Neuropsychologia. 2003;41(6):713–720. doi: 10.1016/s0028-3932(02)00222-1. [DOI] [PubMed] [Google Scholar]
- Duchaine BC, Nakayama K. Developmental prosopagnosia and the Benton Facial Recognition test. Neurology. 2004;62(7):1219–1220. doi: 10.1212/01.wnl.0000118297.03161.b3. [DOI] [PubMed] [Google Scholar]
- Duchaine B, Nakayama K. The Cambridge Face Memory Test: Results for neurologically intact individuals and an investigation of its validity using inverted face stimuli and prosopagnosic participants. Neuropsychologia. 2006;44(4):576–585. doi: 10.1016/j.neuropsychologia.2005.07.001. [DOI] [PubMed] [Google Scholar]
- Embretson SE, Reise SP. Item response theory for psychologists. Mahwah, NJ: Lawrence-Erlbaum; 2000. [Google Scholar]
- Flowers CP, Oshima TC, Raju NS. A description and demonstration of the polytomous-DFIT framework. Applied Psychological Measurement. 1999;23:309–326. [Google Scholar]
- Fox J-P. Bayesian item response modeling: Theory and applications. New York: Springer; 2010. [Google Scholar]
- Gauthier I, McGugin RW, Richler JJ, Herzmann G, Speegle M, Van Gulick AE. Experience moderates overlap between object and face recognition, suggesting a common ability. doi: 10.1167/14.8.7. submitted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Germine LT, Duchaine B, Nakayama K. Where cognitive development and aging meet: Face learning ability peaks after age 30. Cognition. 2011;118(2):201–210. doi: 10.1016/j.cognition.2010.11.002. [DOI] [PubMed] [Google Scholar]
- Gibbons RD, Hedeker DR. Full-information item bi-factor analysis. Psychometrika. 1992;57:423–436. [Google Scholar]
- Glas CAW, Meijer RR. A Bayesian approach to person fit analysis in item response theory models. Applied Psychological Measurement. 2003;27:217–233. [Google Scholar]
- Green BF, Bock RD, Humphreys LG, Linn RL, Reckase MD. Technical guidelines for assessing computerized adaptive tests. Journal of Educational Measurement. 1984;21:347–360. [Google Scholar]
- Haladyna TM. Developing and validating multiple-choice test items. 3. Mahwah, NJ: Lawrence Erlbaum; 2004. [Google Scholar]
- Hancock GR. Effect size, power, and sample size determination for structured means modeling and MIMIC approaches to between-groups hypothesis testing of means on a single latent construct. Psychometrika. 2001;66:373–388. [Google Scholar]
- Holdnack JA, Delis DC. Parsing the recognition memory components of the WMS-III face memory subtest: Normative data and clinical findings in dementia groups. Journal of Clinical and Experimental Neuropsychology. 2004;26(4):459–483. doi: 10.1080/13803390490496687. [DOI] [PubMed] [Google Scholar]
- Hu L, Bentler PM. Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modeling. 1999;6:1–55. [Google Scholar]
- Ivailo I. Simple interface to the estimation and plotting of IRT models. 2013 Retrieved from http://cran.r-project.org/web/packages/irtoys/irtoys.pdf.
- Jennrich RI, Bentler PM. Exploratory bi-factor analysis. Psychometrika. 2011;76:537–549. doi: 10.1007/s11336-011-9218-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jennrich RI, Bentler PM. Exploratory bi-factor analysis: The oblique case. Psychometrika. 2012;77:442–454. doi: 10.1007/s11336-012-9269-1. [DOI] [PubMed] [Google Scholar]
- Kang T-H, Cohen AS. IRT model selection methods for dichotomous items. Applied Psychological Measurement. 2007;31:331–358. [Google Scholar]
- Kim S-H, Cohen AS, Alagoz C, Kim S. DIF detection and effect size measures for polytomously scored items. Journal of Educational Measurement. 2007;44:93–116. [Google Scholar]
- Konar Y, Bennett PJ, Sekuler AB. Holistic processing is not correlated with face-identification accuracy. Psychological Science. 2010;21(1):38, 43. doi: 10.1177/0956797609356508. [DOI] [PubMed] [Google Scholar]
- Lewin C, Herlitz A. Sex differences in face recognition—Women’s faces make the difference. Brain and cognition. 2002;50(1):121–128. doi: 10.1016/s0278-2626(02)00016-7. [DOI] [PubMed] [Google Scholar]
- Lord FM. Applications of item response theory to practical testing problems. Lawrence Erlbaum; Hillside, NJ: 1980. [Google Scholar]
- Lord FM, Novick MR. Statistical theories of mental test scores. Addison-Wesley; Reading: MA: 1968. [Google Scholar]
- Lovén J, Herlitz A, Rehnman J. Women’s own-gender bias in face recognition memory: The role of attention at encoding. Experimental psychology. 2011;58(4):333. doi: 10.1027/1618-3169/a000100. [DOI] [PubMed] [Google Scholar]
- Magis D. Collection of methods to detect dichotomous differential item functioning (DIF) in psychometrics. 2013 Retrieved from http://cran.rproject.org/web/packages/difR/difR.pdf.
- McGugin RW, Richler JJ, Herzmann G, Speegle M, Gauthier I. The Vanderbilt Expertise Test reveals domain-general and domain-specific sex effects in object recognition. Vision Research. 2012;69:10–22. doi: 10.1016/j.visres.2012.07.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Millsap RE, Everson HT. Methodology review: Statistical approaches for assessing measurement bias. Applied Psychological Measurement. 1993;17:297–334. [Google Scholar]
- Morgan CA, III, Hazlett G, Baranoski M, Doran A, Southwick S, Loftus E. Accuracy of eyewitness identification is significantly associated with performance on a standardized test of face recognition. International Journal of Law and Psychiatry. 2007;30(3):213–223. doi: 10.1016/j.ijlp.2007.03.005. [DOI] [PubMed] [Google Scholar]
- Muthén B, du Toit SHC, Spisic D. Robust inference using weighted least squares and quadratic estimating equations in latent variable modeling with categorical and continuous outcomes. 1997 Unpublished manuscript retrieved from http://pages.gseis.ucla.edu/faculty/muthen/articles/Article_075.pdf.
- Muthén LK, Muthén BO. Mplus 7.1 [Computer program] Los Angeles, CA: Muthén & Muthén; 1998-2013. [Google Scholar]
- Olsson U. Maximum likelihood estimation of the polychoric correlation coefficient. Psychometrika. 1979;44:443–460. [Google Scholar]
- Perline R, Wright BD, Wainer H. The Rasch model as additive conjoint measurement. Applied Psychological Measurement. 1979;3:237–255. [Google Scholar]
- Raju NS. Determining the significance of estimated signed and unsigned areas between two item response functions. Applied Psychological Measurement. 1990;14:197–207. [Google Scholar]
- Raju NS, van der Linden WJ, Fleer PF. IRT-based internal measures of differential functioning of items and tests. Applied Psychological Measurement. 1995;19:353–368. [Google Scholar]
- Reckase MD. Unidimensional latent trait models applied to multifactor tests: Results and implications. Journal of Educational Statistics. 1979;4:207–230. [Google Scholar]
- Reckase MD. Multidimensional item response theory. New York, NY: Springer; 2009. [Google Scholar]
- Reise SP. The rediscovery of bifactor measurement models. Multivariate Behavioral Research. 2012;47:667–696. doi: 10.1080/00273171.2012.715555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reise SP, Moore TM, Haviland MG. Bifactor models and rotations: Exploring the extent to which multidimensional data yield univocal scale scores. Journal of Personality Assessment. 2010;92:544–549. doi: 10.1080/00223891.2010.496477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reise SP, Ventura JP, Keefe R, Baade LE, Gold JM, Green MF, Kern RS, Mesholam-Gately R, Nuechterlein KH, Seidman LJ, Bilder R. Bifactor and item response theory analyses of interviewer report scales of cognitive functioning in schizophrenia. Psychological Assessment. 2011;23:245–261. doi: 10.1037/a0021501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubin DB. Bayesianly justifiable and relevant frequency calculations for the applied statistician. Annals of Statistics. 1984;12:1151–1172. [Google Scholar]
- Richler JJ, Cheung OS, Gauthier I. Holistic processing predicts face recognition. Psychological Science. 2011;22(4):464–471. doi: 10.1177/0956797611401753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richler JJ, Floyd RJ, Gauthier I. The Vanderbilt Holistic Face Processing Test: a short and reliable measure of holistic face processing. Journal of Vision. doi: 10.1167/14.11.10. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Russell R, Duchaine B, Nakayama K. Super-recognizers: People with extraordinary face recognition ability. Psychonomic Bulletin & Review. 2009;16(2):252–257. doi: 10.3758/PBR.16.2.252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sinharay S. Assessing fit of unidimensional item response models using a Bayesian approach. Journal of Educational Measurement. 2005;42:375–394. [Google Scholar]
- Smith LL, Reise SP. Gender differences on negative affectivity: An IRT study of differential item functioning on the multidimensional personality questionnaire stress reaction scale. Journal of Personality and Social Psychology. 1998;75:1350–1362. doi: 10.1037//0022-3514.75.5.1350. [DOI] [PubMed] [Google Scholar]
- Spiegelhalter DJ, Thomas A, Best NG, Gilks WR. Version 0.5, (version ii) MRC Biostatistics Unit; Cambridge: 1996. BUGS: Bayesian inference Using Gibbs Sampling. [Google Scholar]
- Spiegelhalter DJ, Thomas A, Best NG, Lunn D. WinBUGS user manual. Cambridge, UK: MRC Biostatistics Unit, Institute of Public Health. 2003 Retrieved from http://www.mrc-bsu.cam.ac.uk/bugs/winbugs/manual14.pdf.
- Steiger JH, Lind J. Statistically-based tests for the number of common factors; Paper presented at the Annual Spring Meeting of the Psychometric Society; Iowa City. 1980. [Google Scholar]
- Tabachnick BG, Fidell LS. Using multivariate statistics. Boston: Allyn and Bacon; 2001. [Google Scholar]
- Thissen D. IRTLRDIF v.2.0b: Software for the computation of the statistics involved in item response theory likelihood-ratio tests for differential item functioning. Chapel Hill, NC: L. L. Thurstone Psychometric Laboratory; 2001. [Google Scholar]
- Thissen D, Steinberg L, Wainer H. Use of item response theory in the study of group differences in trace lines. In: Wainer H, Braun HI, editors. Test validity. Hillsdale, NJ: Lawrence Erlbaum; 1988. pp. 147–169. [Google Scholar]
- Thissen D, Wainer H, editors. Test Scoring. Hillsdale, NJ: Lawrence Erlbaum; 2001. [Google Scholar]
- Tucker LR, Lewis C. A reliability coefficient for maximum likelihood factor analysis. Psychometrika. 1973;38:1–10. [Google Scholar]
- Warrington EK. Recognition Memory Test. Windsor, England: NFER-Nelson; 1984. [Google Scholar]
- Way WD, Ansley TN, Forsyth RA. The comparative effects of compensatory and non-compensatory two dimensional data on unidimensional IRT estimates. Applied Psychological Measurement. 1988;12:239–252. [Google Scholar]
- Wilhelm O, Herzmann G, Kunina O, Danthiir V, Schacht A, Sommer W. Individual differences in perceiving and recognizing faces—One element of social cognition. Journal of Personality and Social Psychology. 2010;99(3):530. doi: 10.1037/a0019972. [DOI] [PubMed] [Google Scholar]
- Wilmer JB, Germine L, Chabris CF, Chatterjee G, Gerbasi M, Nakayama K. Capturing specific abilities as a window into human individuality: The example of face recognition. Cognitive Neuropsychology. 2012;29(5-6):360–392. doi: 10.1080/02643294.2012.753433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilmer JB, Germine L, Chabris CF, Chatterjee G, Williams M, Loken E, Nakayama K, Duchaine B. Human face recognition ability is specific and highly heritable. Proceedings of the National Academy of Sciences. 2010;107(11):5238–5241. doi: 10.1073/pnas.0913053107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu CY. Unpublished doctoral dissertation. University of California; Los Angeles, CA: 2002. Evaluating cutoff criteria of model fit indices for latent variable models with binary and continuous outcomes. [Google Scholar]
- Zimowski MF, Muraki E, Mislevy RJ, Bock RD. BILOG-MG: Multiple-group IRT analysis and test maintenance for binary items. Scientific Software International; Chicago, IL: 1996. Computer Program. [Google Scholar]


