A computational atlas of the hippocampal formation using ex vivo, ultra-high resolution MRI: Application to adaptive segmentation of in vivo MRI

Abstract

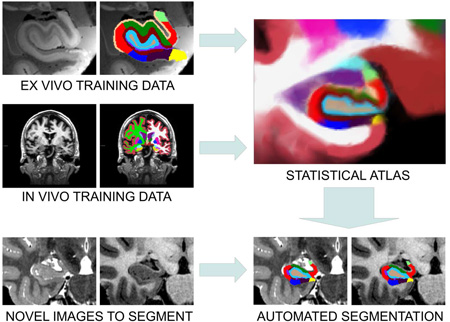
Automated analysis of MRI data of the subregions of the hippocampus requires computational atlases built at a higher resolution than those that are typically used in current neuroimaging studies. Here we describe the construction of a statistical atlas of the hippocampal formation at the subregion level using ultra-high resolution, ex vivo MRI. Fifteen autopsy samples were scanned at 0.13 mm isotropic resolution (on average) using customized hardware. The images were manually segmented into 13 different hippocampal substructures using a protocol specifically designed for this study; precise delineations were made possible by the extraordinary resolution of the scans. In addition to the subregions, manual annotations for neighboring structures (e.g., amygdala, cortex) were obtained from a separate dataset of in vivo, T1-weighted MRI scans of the whole brain (1 mm resolution). The manual labels from the in vivo and ex vivo data were combined into a single computational atlas of the hippocampal formation with a novel atlas building algorithm based on Bayesian inference. The resulting atlas can be used to automatically segment the hippocampal subregions in structural MRI images, using an algorithm that can analyze multimodal data and adapt to variations in MRI contrast due to differences in acquisition hardware or pulse sequences. The applicability of the atlas, which we will release as part of FreeSurfer (version 6.0), is demonstrated with experiments on three different publicly available datasets with different types of MRI contrast. The results show that the atlas and companion segmentation method: 1) can segment T1 and T2 images, as well as their combination, 2) replicate findings on mild cognitive impairment based on high-resolution T2 data, and 3) can discriminate between Alzheimer’s disease subjects and elderly controls with 88% accuracy in standard resolution (1 mm) T1 data, significantly outperforming the atlas in FreeSurfer version 5.3 (86% accuracy) and classification based on whole hippocampal volume (82% accuracy).

Graphical abstract

1 Introduction

The hippocampal formation is a brain region with a critical role in declarative and episodic memory (Scoville & Milner, 1957) (Eldridge, Knowlton, Furmanski, Bookheimer, Engel, & others, 2000), as well as a focus of structural change in normal aging (Petersen, et al., 2000) (Frisoni, et al., 2008) and diseases such as epilepsy (Cendes, et al., 1993) and, most notably, Alzheimer’s disease (AD) (Laakso, et al., 1998) (Du, et al., 2001) (Apostolova, et al., 2006). The hippocampal formation consists of a number of distinct, interacting subregions, which comprise a complex, heterogeneous structure. Despite its internal complexity, limits in MRI resolution have traditionally forced researchers to model the hippocampus as a single, homogeneous structure in neuroimaging studies of aging and AD (Boccardi, et al., 2011) (Chupin, et al., 2009). Even though these studies have shown that whole hippocampal volumes derived from automatically or manually segmented MRI scans are powerful biomarkers for AD (Convit, et al., 1997) (Jack, et al., 1999) (Frisoni, et al., 1999) (De Toleto-Morrell, Goncharova, Dickerson, Wilson, & Bennett, 2000) (den Heijer, Geerlings, Hoebeek, Hofman, Koudstaal, & Breteler, 2006) (Wang, et al., 2003) (Fischl, et al., 2002), treating the hippocampus as a single entity disregards potentially useful information about its subregions. In animal studies, these subregions have been shown to have different memory functions (Acsády & Káli, 2007) (Hunsaker, Lee, & Kesner, 2008) (Kesner, 2007) (Rolls, 2010) (Schmidt, Marrone, & Markus, 2012). In humans, they are also thought to play different roles in memory and learning (Gabrieli, Brewer, Desmond, & Glover, 1997) (Acsády & Káli, 2007) (Knierim, Lee, & Hargreaves, 2006) (Kesner, 2013) (Kesner, 2007) (Reagh et al., 2014) (Yassa & Stark, 2011), and to be affected differently by AD and normal aging – as indicated by ex vivo, histological studies (Braak & Braak, 1991) (Braak & Braak, 1997) (Arnold, Hyman, Flory, Damasio, & Van Hoesen, 1991) (Thal, et al., 2000) (Brady & Mufson, 1991) (Simic, Kostovic, Winblad, & Bogdanovic, 1997) (Harding, Halliday, & Kril, 1998).

Findings from histological studies on hippocampal samples have sparked interest in studying the hippocampal subregions in vivo with MRI, which has been made possible by recent advances in MRI acquisition. Neuroimaging studies that have characterized the subregions in normal aging and AD with in vivo MRI include (Mueller, et al., 2007) (Wang, et al., 2009) (Mueller, Schuff, Yaffe, Madison, Miller, & Weiner, 2010) (Small, Schobel, Buxton, Witter, & Barnes, 2011) (Kerchner, Deutsch, Zeineh, Dougherty, Saranathan, & Rutt, 2012) (Wisse, et al., 2012) (Wisse, et al., 2014) (Burggren, et al., 2008). Most of these studies rely on manual segmentations made on T2-weighted MRI data of the hippocampal formation. The T2 images are often acquired anisotropically, such that resolution along the direction of the major axis of the hippocampus is reduced in exchange for higher in-plane resolution within each coronal slice. This design choice is motivated by the internal structure of the hippocampus: resembling a Swiss roll, its spiral structure changes less rapidly along its major axis, which is almost parallel to the anterior-posterior direction. In in vivo T2-weighted data, part of this spiral becomes visible as a hypointense band that corresponds to the stratum radiatum, lacunosum moleculare, hippocampal sulcus and molecular layer of the dentate gyrus. These layers separate the hippocampus from the dentate gyrus. Henceforth, for simplicity in writing, we will refer to this band as the “molecular layer”ⁱ.

Manual segmentation protocols of high resolution, in vivo MRI data of the hippocampal subfieldsⁱ often rely heavily on this molecular layer, which is the most prominent feature of the internal region of the hippocampus that is visible in MRI. However, manual delineation of the subregions in these high-resolution images is extremely labor-intensive – approximately fifty hours per case. Few laboratories currently possess the resources in neuroanatomical expertise and staffing that are required to carry out such studies. Even within those laboratories, the number of cases that can be used in a study is limited by how time-consuming manually tracing the subregions is, which in turns limits the statistical power of the analysis.

These limitations can be overcome with the use of automated algorithms. Two major methods have been proposed for automated and semi-automated hippocampal subregion segmentation so far. In (Yushkevich, et al., 2010) – further validated in (Pluta, Yushkevich, Das, & Wolk, 2012) – Yushkevich and colleagues combined multi-atlas segmentation, similarity-weighted voting, and a learning-based label bias correction technique to estimate the subregion segmentation in a nearly automated fashion. The user needs to provide an initial partitioning of MRI slices into hippocampal head, body and tail. In (Van Leemput, et al., 2009), our group introduced a fully automated method based on a statistical atlas of hippocampal anatomy and a generative model of MRI data.

These two methods approach the segmentation problem from different perspectives – parametric and non-parametric. The algorithm we developed – which follows a generative, parametric approach – focuses on modeling the spatial distribution of the hippocampal subregions and surrounding brain structures (i.e., the underlying segmentation), which is learned from labeled training data. The segmentation, which is a hidden variable in the model, is connected to the observed image data through a generative process of image formation that does not make any assumptions about the MRI acquisition. This is indeed the strongest point of the algorithm, since it makes it adaptive to any MRI pulse sequence and resolution that might have been used to acquire the data - even if multimodal (Puonti, Iglesias, & Van Leemput, 2013). Conversely, the algorithm developed by Yushkevich and co-workers relies on a combination of a registration-based, multi-atlas algorithm (a non-parametric method) and machine learning techniques. Both components of their method effectively exploit prior knowledge about the distribution of image intensities derived from training data – information which our parametric method disregards. While the use of prior knowledge about the image intensities is advantageous when the MRI pulse sequence of the test scan matches that of the training data, segmentation of MRI images with different contrast properties is not possible with such an approach. Nonetheless, both Yushkevich’s method and ours have successfully been used to carry out subregion studies on large populations (Teicher, Anderson, & Polcari, 2012) (Das, et al., 2012) (Iglesias, Sabuncu, & Van Leemput, 2013).

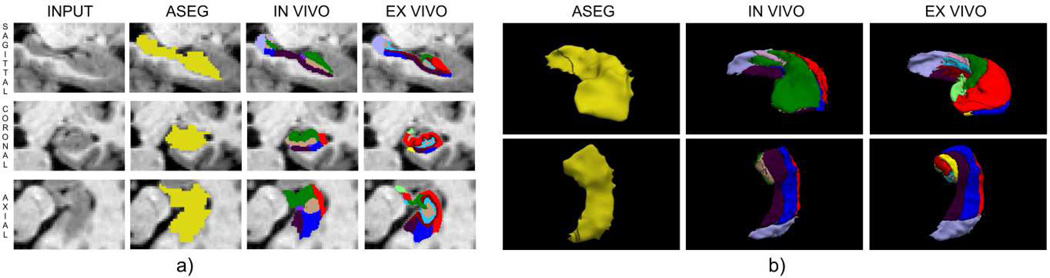
Our original subfield segmentation method, which is publicly available as part of the FreeSurfer open-source software package (Fischl, FreeSurfer, 2012) (version 5.3), is based on a probabilistic atlas that was built from in vivo MRI data acquired at 0.38×0.38×0.8mm resolution (Van Leemput, et al., 2009). Henceforth, we refer to this atlas as the “in vivo atlas” (FreeSurfer v5.3). The resolution of this atlas is only sufficient to produce a coarse segmentation of the subregions in standard-resolution MRI (i.e., 1 mm); a more accurate model of anatomy is necessary to analyze newer, higher resolution data where the hippocampal substructures are more clearly visualized. Specifically, the in vivo atlas in FreeSurfer v5.3 suffers from three shortcomings. First, the image resolution of the in vivo training data was insufficient for the human labelers to completely distinguish the subregions, forcing them to heavily rely on geometric criteria to trace boundaries, which affected the accuracy of their annotations. In particular, a problematic consequence is that the molecular layer was not labeled, compromising the ability of the atlas to segment high-resolution in vivo data. A second issue is that the delineation protocol was designed for the hippocampal body and did not translate well to the hippocampal head or tail. Due to the second issue, a third problem is that the volumes of the subregions did not agree well with those from histological studies (Simic, Kostovic, Winblad, & Bogdanovic, 1997) (Harding, Halliday, & Kril, 1998), as pointed out by (Schoene-Bake, et al.).

In this study, we address these shortcomings by replacing the hippocampal atlas in FreeSurfer v5.3 with a new version (FreeSurfer v6.0) built with a novel atlasing algorithm and ex vivo MRI data from autopsy brains. Since motion effects are eliminated, much longer MRI acquisitions are possible when imaging post-mortem samples. Our ex vivo imaging protocol yields images with extremely high resolution and signal-to-noise ratio, dramatically higher than is possible in vivo, which allows us to accurately identify more subregions with a delineation protocol specifically designed for this study. To the best of our knowledge, there is only one ex vivo atlas of the hippocampus, presented in (Yushkevich, et al., 2009); Adler et al. (2014) have presented promising work towards an atlas based on both ex vivo MRI and histology, but they only labeled one case. Compared with Yushkevich’s atlas (henceforth “UPenn atlas”), our atlas (FreeSurfer v6.0) has the following advantages: 1. it is built at a higher resolution (0.13 mm isotropic, on average, vs. 0.2 mm); 2. it models a larger number of structures (15 vs. 5); 3. it is built upon a larger number of cases (15 vs. 5); and 4. in addition to the hippocampal subregions, it also models the surrounding structures, which enables its use in a generative modeling framework to directly segment in vivo MRI data of varying contrast properties. To include the neighboring structures in the atlas, we have developed a novel atlas construction algorithm that combines the dedicated ex vivo data with a standard resolution dataset of in vivo scans of the whole brain, for which manual labels of the surrounding tissue are already available; this algorithm eliminates the need to delineate the neighboring structures at ultra-high resolution, which would be extremely time consuming. Throughout this article, we will refer to the hippocampal atlas resulting from these delineations as the “ex vivo atlas” (FreeSurfer v6.0) – even though, as explained above, in vivo data were used to build the model of the structures around the hippocampus.

In addition to the atlas, we also present in this study a segmentation algorithm for analyzing in vivo MRI scans with the ex vivo atlas. The method is largely based on (Van Leemput, et al., 2009). It is important to stress that a procedure that can adapt to different intensity distributions is required for using ex vivo data to infer in vivo structures. The ex vivo scans are acquired on fixed tissue with dramatically different contrast properties than in vivo tissue. The fixation process cross-links proteins, significantly shortening T1 and leaving little remaining T1-contrast. As a result, the ex vivo scans that we acquire are largely T2* weighted. Thus, even if one was to match acquisition protocols in vivo and ex vivo, the resulting images would have dramatically different intensity characteristics due to the changes in the intrinsic tissue properties that give rise to MRI contrast. Therefore, to take advantage of the ultra-high resolution images that can only be obtained ex vivo, one must use a procedure that does not require the same intensity characteristics in the atlas as in the in vivo scans to be segmented.

The rest of the paper is organized as follows. Section 2 describes the MRI data, delineation protocol and mathematical framework that were used to build the statistical atlas, shows the resulting atlas, and compares the subregion volumes that it yields with those from the UPenn atlas and from two histological studies. Section 3 details an algorithm to use the atlas to segment in vivo MRI data, and presents results on three datasets with different resolutions and types of MRI contrast. Finally, Section 4 concludes the article.

2 Atlas construction

The statistical atlas that we propose is built from a combination of ex vivo and in vivo MRI training data. Here we first describe the acquisition (Section 2.1) and manual labeling (Section 2.2) of the ex vivo data. Next, we introduce the in vivo training data we used (Section 2.3). The algorithm to build the atlas is described in Section 2.4, and the resulting atlas presented in Section 2.5.

2.1 Autopsy brain samples and ex vivo MRI acquisition

The ex vivo data consists of fifteen autopsied brain hemispheres from two different sources. Eight of the samples were from the Framingham Heart Study and Boston University Alzheimer’s Disease Center (Veterans Administration Medical Center, Bedford, VA). The other seven samples were from the Massachusetts General Hospital Autopsy Service (Massachusetts General Hospital, Boston, MA). The samples consisted of whole brain hemispheres (left n=8, right n=7) from 15 different subjects. Ten of the subjects did not have any neurological conditions, whereas four of them had mild AD and one had mild cognitive impairment (MCI). Eight samples were fixed with periodate-lysine-paraformaldehyde (PLP), and the other seven were fixed with 10% formalin. The demographics of the ex vivo samples were the following: age at death was 78.6± 11.9 years, 35.7% were females, 53.3% were left hemispheres and the post-mortem interval was less than 24 hours in all cases for which this information was available. The demographics are detailed in Table 1.

Table 1.

Demographics of the subjects whose hippocampi were used in this study. PMI stands for post-mortem interval. The resolution was isotropic in all cases. N/A represents unavailability of that demographic datum for that subject.

Case #	Age	Gender	Laterality	Resolution	Diagnosis	PMI
1	N/A	Male	Left	100 µm	AD	N/A
2	N/A	Female	Left	120 µm	AD	21 hours
3	91	Female	Right	120 µm	Control	16 hours
4	83	Female	Left	150 µm	AD	5.5 hours
5	89	Female	Right	120 µm	AD	N/A
6	82	Male	Right	120 µm	Control	N/A
7	63	Male	Left	120 µm	Control	N/A
8	87	Male	Left	120 µm	MCI	21 hours
9	67	Male	Right	150 µm	Control	12 hours
10	N/A	Male	Left	150 µm	Control	6.5 hours
11	N/A	Male	Right	150 µm	Control	N/A
12	N/A	Male	Left	150 µm	Control	N/A
13	60	Male	Right	120 µm	Control	< 24 hours
14	86	Female	Left	100 µm	Control	12–24 hours
15	N/A	N/A	Right	200 µm	Control	N/A

A block of tissue including the hippocampus was excised from each ex vivo sample. Depending on its size, the block was placed in either a plastic cylindrical centrifuge tube (60 ml, 3 cm diameter) or, if it did not fit, inside a bag filled with PLP and sealed. In the latter case, air was pumped out using a needle and a vacuum pump in order to minimize the number and size of air bubbles in the samples. Two different pumps were used in the process: a DV-185N-250 Platinum 10 CFM by JB (Aurora, IL), and a S413801 by Fisher Scientific (Hampton, NH).

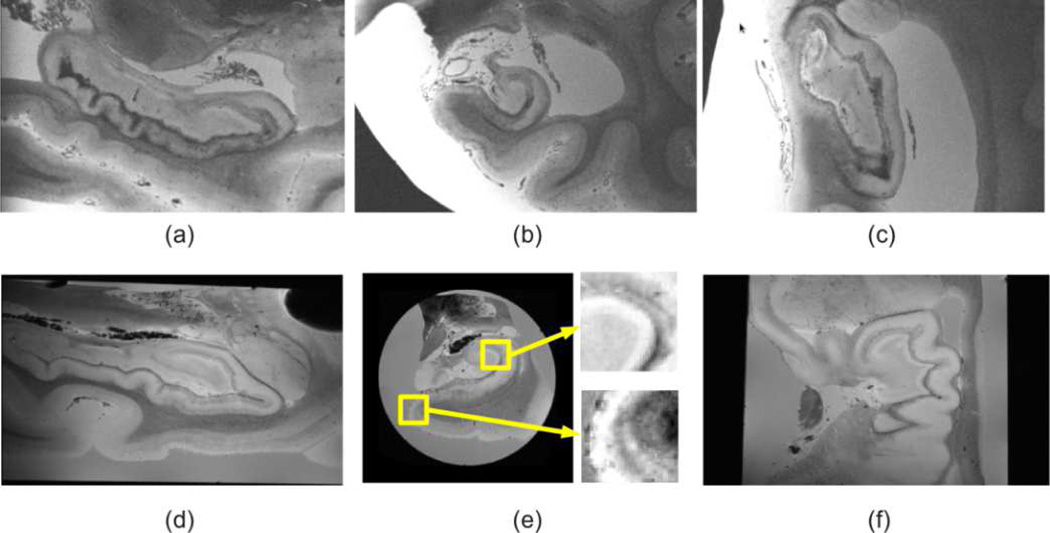
The tissue block was subsequently scanned in a 7 T Siemens scanner using a 3D FLASH sequence with TR = 50 msec, TE = 25 msec, α=20°. Two of the samples were scanned at 0.1 mm isotropic resolution, seven at 0.12 mm, five at 0.15 mm and one at 0.2 mm (see Table 1). Three different coils were used in the acquisition, accommodating variations in sample size: a 4-turn solenoid coil (28.5 mm inner diameter, 44 mm length), a 4-channel phased-array (a linear array of loop coil elements each with 5 cm coil diameter, 1.5 cm overlap between adjacent elements, 16 cm in length) and a small birdcage (24 rings, outer diameter = 19.7 cm, inner diameter = 19.3 cm, length = 12 cm). Despite the fact that different coils were used to scan the different samples, the output images were comparable in quality. The whole procedure received IRB approval before its execution by the Partners Human Research Committee. Figure 1 displays some sample slices of the data.

Figure 1.

sample sagittal (a), coronal (b) and axial (c) slices from the ex vivo data of Case 8. Sample sagittal (d), coronal (e) and axial (f) slices from the ex vivo MRI data of Case 14. In (e), two regions of the slice are zoomed in to better appreciate the level of resolution of the scan (0.1 mm). Note that the acquisition of Case 8 was carried out in a bag, whereas Case 14 was scanned in a tube.

2.2 Manual segmentation of ex vivo MRI data: anatomical definitions

In this section we describe the protocol for manually labeling the hippocampal subregions in the ex vivo data. The protocol was specifically designed for this study, and is largely based on the histology and morphometry from (Rosene & Van Hoesen, 1987), and partly also on (Lorente de No, 1934) (Insausti & Amaral, 2011) (Green & Mesulam, 1988). The Duvernoy atlas (Duvernoy, 1988) was also used as an aid in the delineation process. The set of annotated labels, along with the protocol for their annotation, is described in Table 2. The descriptions in the table are based on ex vivo contrast, not histological data. Given the excellent resolution of the ex vivo MRI data (100 µm), most of the subregion boundaries were visible in the images, but subtle transitions were still difficult to distinguish. Another source of differences between our ex vivo MRI labels and histology is that many boundaries are oblique (rather than perpendicular) to the imaging planes. Nonetheless, we used previously published anatomical contrast to guide us (Augustinack, et al., 2005) (Fischl, et al., 2009) (Augustinack, et al., 2010) (Augustinack, et al., 2013). We also used neuroanatomical knowledge of particular layers to help us identify boundaries.

Table 2.

Protocol for manual segmentation of the ex vivo MRI data.

STRUCTURE	DEFINITION
Alveus (beige)	The alveus, a white matter structure, covers the hippocampus on the superior rim. It is the white matter directly adjacent to the cornu ammonis, not extending separately (such as fimbria). The alveus borders the amygdala at the anterior end and fuses with the fimbria/fornix at the posterior end. The alveus extends from the floor of the inferior horn of the lateral ventricle until it meets the cerebral white matter where the ventricle ends laterally. The alveus is present throughout the rostrocaudal regions of the hippocampus (head, body, and tail). The alveus appears dark in FLASH MRI.
Parasubiculum (yellow)	The parasubiculum is Brodmann’s area 49. Parasubiculum is considered periallocortex (~5–6 layers) and lies on the lower bank of the hippocampal fissure. Parasubiculum is the medial-most of the subicular cortices, with presubiculum laterally and entorhinal cortex medially. The parasubiculum is relatively small compared to the subiculum and presubiculum. Parasubiculum displays less lamination than presubiculum and entorhinal cortex in ex vivo MRI (i.e. superficial layers about the same size, thickness, and contrast as infragranular layers).
Presubiculum (dark purple)	The presubiculum is Brodmann’s area 27. The presubiculum is periallocortex and has distinct superficial layers with a heavily myelinated molecular layer. The presubiculum makes up a large portion of territory on the lower bank of the hippocampal fissure in the human brain and extends posteriorly to the retrosplenial region. The presubiculum lies between the parasubiculum (medially) and the subiculum (laterally). The contrast in presubiculum is heterogeneous, with light and dark contrast in its superficial layer (the lamina principalis externa), making it a particularly distinctive pattern in ex vivo MRI. The lamina principalis externa of the presubiculum ends at the subiculum.
Subiculum (blue)	The subiculum belongs to the allocortex group – three layered cortex with a molecular layer, a pyramidal layer and a polymorphic layer. As the light and dark contrast of the presubiculum ends, the subiculum begins laterally. The boundary between presubiculum and subiculum is distinct because the subiculum has a well-defined pyramidal layer in ex vivo MRI. The pyramidal layer in the subiculum widens (compared to presubiculum) and ramps up from a narrow wedge to full-fledged allocortex. The molecular layer appears directly superior to the subiculum. It is between presubiculum and subiculum that the cortex simplifies to a three-layered cortex. We did not segment the prosubiculum.
CA1 (red)	The subiculum transitions into CA1 laterally. CA1 displays light homogeneous contrast for the pyramidal layer, similar to the subiculum and other CA fields. The subiculum/CA1 boundary occurs approximately where the hippocampus turns upward (at 7 o’clock using the letter C as a representation for the hippocampus and radiologic convention for the right side). We labeled the hippocampal molecular layer separately from CA1 pyramidal layer because we could distinguish the difference. CA1 continues until the top of the first hippocampal fold, where it meets CA2. CA1 dominates at the hippocampal head and lessens in the hippocampal body. The uncal (medial) portion of CA1 was included in the CA1 label.
CA2/3 (green)	We combined subfields CA2 and CA3 due to lack of distinguishing contrast in MRI and variability among our labelers in preliminary experiments. We encountered great variability particularly with the angle of the original CA2 label. CA2/3 showed a light intensity and homogeneous contrast as the pyramidal layer in CA1 but the pyramidal layer of CA2/3 appeared thinner than in CA1. The thickness change between CA1 and CA2/3 was a distinguishing feature to delineate these two subfields. When this change was gradual, the boundary was placed approximately in the center of the region of varying thickness. CA2/3 extended from the posterior half of the hippocampal head to the tail. CA2/3 was typically superior to the dentate gyrus but also weaved throughout hippocampal folds. Here, we also labeled the molecular layer in CA2/3 separately from the CA2/3 pyramidal layer.
CA4 (light brown)	CA4 is also known as the hilar region of the dentate gyrus. Topographically, the CA4 subfield lies within the dentate gyrus. Thus, CA4 fills the interior of the GC-DG label. The limit between CA2/3 and CA4 is at the entrance of the hilus. The contrast of CA4 has a similar contrast to CA1–3 but lighter contrast for the polymorphic layer. Thus, in ex vivo MRI with a FLASH sequence, it appears slightly darker intensity in the inner-most portion (i.e. the modified pyramidal area of CA4), but lighter outside of that (i.e. the polymorphic cell layer of the dentate gyrus). The ability to distinguish these particular strata depended on the brain quality and resolution. We included the polymorphic layer in our CA4 label.
GC-DG: granule cell layer of dentate gyrus (cyan)	The dentate gyrus is another three layered structure. The dentate gyrus consists of a molecular layer, a granule cell layer and a polymorphic layer. The granule cell layer shows a bright white intensity with a FLASH sequence in ex vivo MRI, the intense contrast likely due to the high packing density of the granule cells. The molecular layer of the dentate gyrus has dark contrast and was included in the CA4 label because we could not always distinguish the stratum. The dentate gyrus begins about one third to halfway through the hippocampal head from the rostral-most slices. The shape of the dentate gyrus varies depending on the cut plane.
HATA (ligh green)	The hippocampus-amygdala-transition-area (HATA) lies in the medial region of the hippocampus and is superior to the other subfields. The HATA shows a dark intensity compared to the CA subfields. Its base forms the medial and slightly dorsal border of the hippocampus, but this may depend on orientation. We consistently observed that the top of the hippocampal folds (i.e. the superior-most folds) were a tangential landmark to delineate the HATA inferior boundary. The inferior horn of the lateral ventricle borders the medial side of the HATA and the alveus borders the HATA laterally.
Fimbria (violet)	The fimbria is a white matter structure that extends from the alveus and eventually forms the fornix. The fimbria exits posteriorly the mid-body level of the hippocampus and has the same dark intensity as the alveus.
Molecular layer (brown)	This label consists of two parts, molecular layer for subiculum or molecular layer for CA fields. The molecular layer appears as dark contrast that lies directly underneath the hippocampal fissure and above the subiculum. The molecular layer of the hippocampus continues as dark contrast that forms between the CA regions and the GC-DG as well as the hippocampal fissure. The molecular layer follows the shape of the hippocampal folds.
Hippocampal Fissure (purple)	The hippocampal fissure opens up medially and extends laterally until it is a vestigial space between the molecular layers of the hippocampus and dentate gyrus. In ex vivo MRI, our scanning liquid (paraformaldehyde solution) fills the ventricle as cerebrospinal fluid would in the living brain. Air bubbles frequently appear as artifacts in this kind of imaging.
Tail (bright green)	The hippocampal tail has not been extensively studied in the neuroanatomical literature yet, so it is difficult to make reliable annotations in this region. Instead, we identified the first coronal slice (anterior to posterior) where the fornix is fully connected to the hippocampus, and labeled the whole hippocampus with this “umbrella” label in the remaining slices (approximately 40).

Distinguishing the boundaries between subiculum, CA1, CA2 and CA3 was more difficult due to the lack of image contrast between those subfields, but we used the pyramidal layer thickness and pyramidal layer intensity for this. We also combined the knowledge of location and pyramidal layer thickness to determine the subregions: the subiculum is widest, CA1 is thinner than subiculum, CA2 is thinner than CA1, and finally CA3 is the thinnest of the subfields. To distinguish the subicular boundaries, we used neighboring neuronal groupings such as entorhinal layer II islands (Augustinack, et al., 2005), presubicular clouds (Green & Mesulam, 1988), and reduced lamination in parasubiculum (compared with presubiculum and entorhinal cortex) (Green & Mesulam, 1988). A full description of the histologic architecture is beyond the scope of this work because the atlas described here is based on ex vivo contrast. Nonetheless, our ex vivo MRI delineations represent a significant improvement over the previous FreeSurfer hippocampal segmentation (that only used geometric properties), and are much closer to the underlying subregion boundaries.

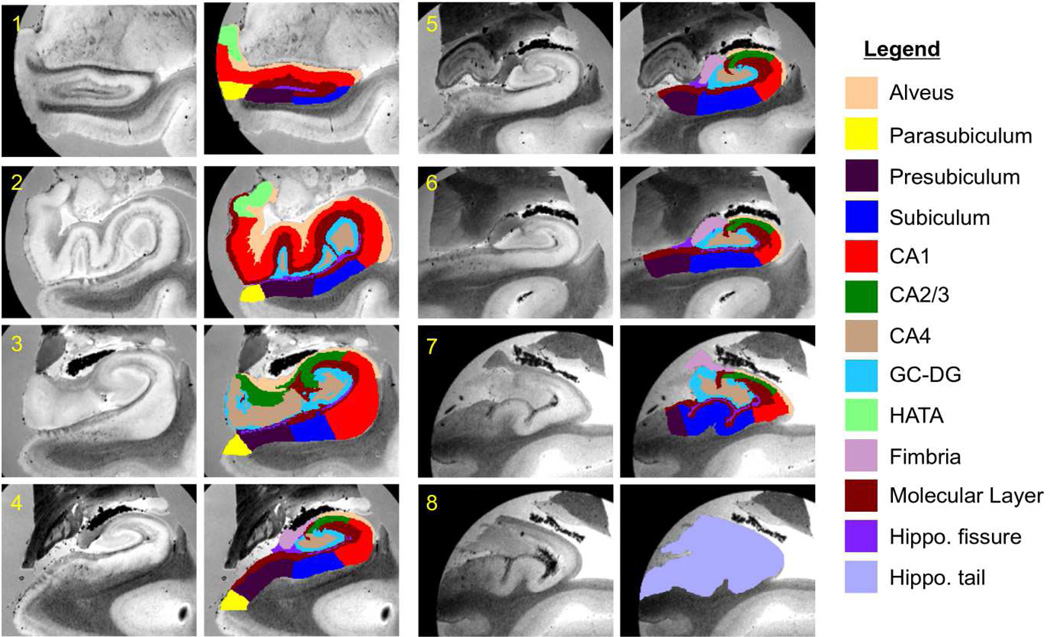
Seven manual labelers that were supervised by J.C.A. used the protocol described in Table 2 to annotate the subregions in the 15 ex vivo scans. Annotating each scan took approximately 60 hours; a single hippocampus at this resolution contains more voxels than an in vivo scan of an entire brain. The annotations were made using Freeview, a visualization tool that is included in FreeSurfer. The first step in the protocol was to rotate the MRI volume to align the major axis of the hippocampus with the perpendicular direction to the coronal view. Then, assuming a left hippocampus (in right hemispheres, the image was flipped for delineation), the subregions were labeled using the definitions in Table 2. When bubbles were present in the images, the labelers filled them with the label of the structure they believe would be under the bubble. Since this introduces noise in the manual labels, minimizing the number and size of air bubbles in the sample prior to acquisition is crucial. The delineations were made in coronal view, while using information from the other two views (sagittal and axial) to guide the tracing; even though this might lead to slightly jagged boundaries in sagittal and axial view, this roughness is averaged out when the manual segmentations are downsampled and combined into the probabilistic atlas (see Section 2.5). In order to ensure the consistency between the manual labelers, J.E.I and J.C.A. evaluated their delineations and served as quality control for each case, refining the segmentations where necessary. Sample manual tracings, along with the color coding of the subregions (for visualization purposes), are shown in Figure 2.

Figure 2.

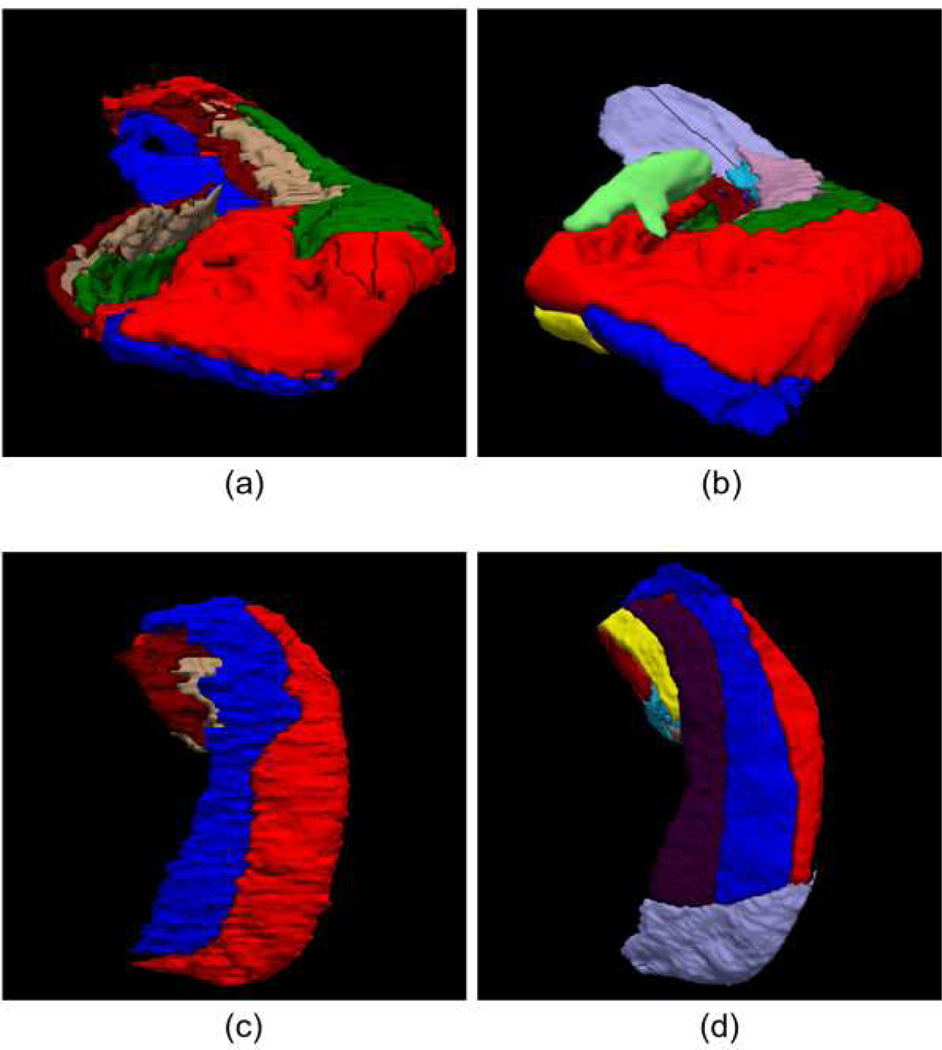
Eight coronal slices from Case 14 and corresponding manual annotations. The slices are ordered from anterior to posterior. Sagittal and axial slices, as well as 3D renderings of the manual segmentation are shown in the supplementary material (Figure 15, Figure 16 and Figure 17).

2.3 In vivo training MRI data

Learning the spatial distribution of labels surrounding the hippocampus from the ex vivo data requires manual delineation of its neighboring structures. Even though it would be possible to trace these structures on ultra-high resolution, ex vivo MRI data, such approach would represent an unnecessary labeling effort for two reasons. First, the neighboring structures only need to provide a course context to assist the subregion segmentation, and therefore do not require labeling at ultra-high resolution, which is extremely time consuming; delineation at standard resolution (i.e., ~1 mm) is sufficient. And second, there is already a number of publicly available and proprietary in vivo datasets for which such structures have already been manually labeled.

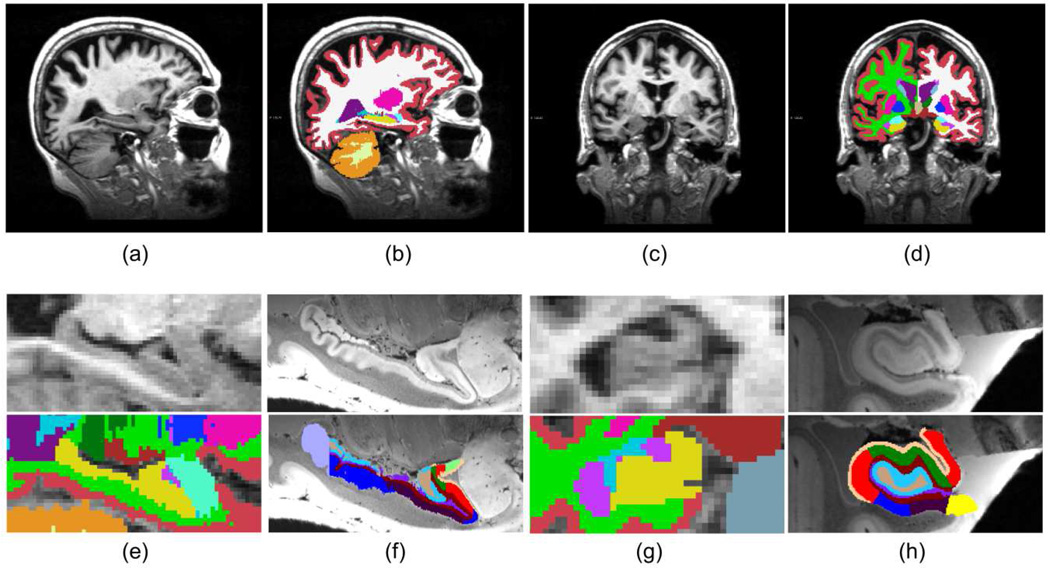
These are the motivations for using an additional training dataset consisting of in vivo, whole brain MRI scans. The dataset consists of T1-weighted scans from 39 subjects (19 males, 20 females, mean age: 56.3 years, 29 controls, 10 mildly demented) acquired with a MP-RAGE sequence in a 1.5T scanner with the following parameters: TR=9.7ms, TE=4.ms, TI=20ms, flip angle = 10°, 1 mm. isotropic resolution. Thirty-six brain structures, including the whole left and right hippocampi, were manually delineated using the protocol described in (Caviness, Filipek, & Kennedy, 1989); see sample slices, as well as a qualitative comparison with the ex vivo delineation protocol, in Figure 3. Note that these are the same subjects that are used to construct the probabilistic atlas in the software package FreeSurfer.

Figure 3.

In vivo dataset and comparison with ex vivo images. (a) Sagittal slice in vivo. (b) Corresponding manual delineation of brain structures; note that the hippocampus (in yellow) is labeled as a single entity. (c) Coronal slice in vivo. (d) Corresponding manual delineation. e) Close-up of the hippocampus (in yellow) on a sagittal slice in vivo. f) An approximately corresponding slice from Case 12 of the ex vivo dataset. (g) Close-up of the hippocampus on a coronal slice in vivo. (h) An approximately corresponding slice from Case 12 (ex vivo).

2.4 Algorithm for atlas construction

Here we describe the procedure to build our probabilistic atlas from in vivo and ex vivo data. We will first describe the underlying model, which is based on a tetrahedral mesh representation. Then, we will use Bayesian inference to learn the parameters of the mesh from manual annotations, assuming that its topology is fixed. Finally, we introduce a Bayesian algorithm to optimize the topology of the mesh, which is a model selection problem. Throughout the rest of this section, we will assume that all the training samples correspond to left hippocampi; samples from right hippocampi are simply flipped before being fed to the algorithm.

Underlying model

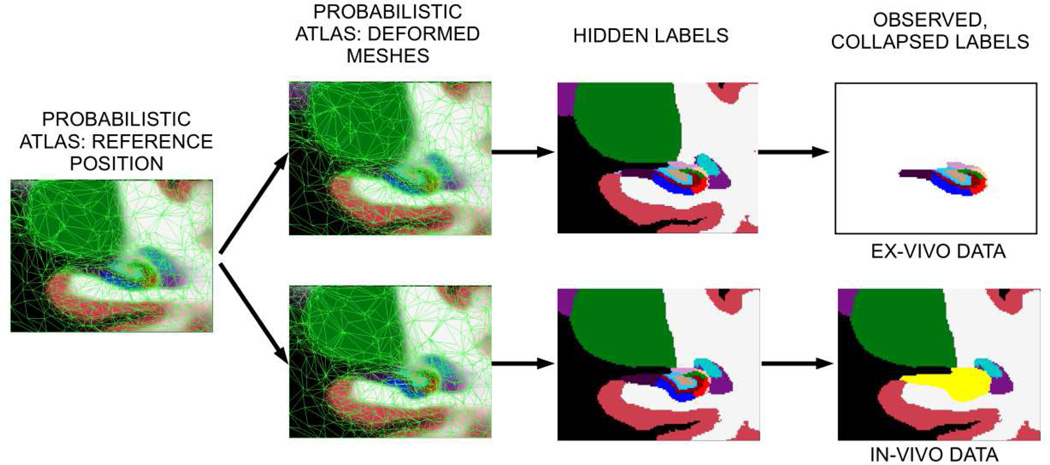
To build our probabilistic atlas of the hippocampal formation from ex vivo and in vivo data, we developed a generalization of our previous method (Van Leemput K., 2009) that can deal with partial information. The algorithm aims to produce a compact tetrahedral mesh representation of the atlas, in which each vertex has an associated vector of probabilities for the different hippocampal subregions and surrounding structures. The topology and resolution of the mesh are locally adaptive to the shape of each anatomical region i.e., coarse in uniform regions and fine around convoluted areas. The difference with respect to the original method is that we no longer assume that all the labels of the training dataset are readily available: for the ex vivo data, the labels for the surrounding structures are not given, and for the in vivo data, the hippocampal subregions are not available. Instead, we observe a modified version in which some sets of labels have been collapsed into more general labels in a deterministic fashion. The function that collapses the labels is different for each training dataset: for the ex vivo samples, it collapses all the non-hippocampal structures into a single, generic background label. For the in vivo data, the function collapses all the hippocampal subregions into a single label corresponding to the whole hippocampus.

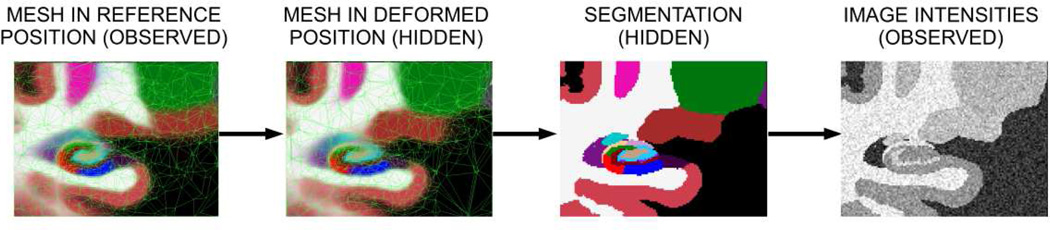
Specifically, let there be M label volumes C_m, m = 1,2, …, M, derived from in vivo or ex vivo data. Each label volume ${\mathbf{C}}_m=\{{\mathrm{c}}_{\mathit{i}}^m,i=1,2,\dots ,I\}$ has I voxels, where each voxel has a manual label belonging to one of P possible collapsed classes: ${\mathrm{c}}_i^m\in \{1,2,\dots ,P\}$. We model these label images as having been generated by the following process (illustrated in Figure 4):

1. A tetrahedral mesh covering the image domain is defined. This mesh is described by the position of its N vertices ${\mathit{x}}^r=\{{\mathit{x}}_n^r,n=1,2,\dots ,N\}$ and their connectivity 𝒦. Henceforth, we will refer to x^r as the reference position of the mesh. Each mesh node has an assigned vector of label probabilities ${\mathit{\alpha }}_n=({\alpha }_n^1,{\alpha }_n^2,\dots ,{\alpha }_n^L)$, where {1,2, …, L} is the set of labels before collapsing. The probabilities satisfy ${\alpha }_n^k\ge 0,{\sum }_{k=1}^K{\alpha }_n^k=1$.

2. M deformed meshes are obtained by sampling M times from the following probability distribution:

   $$p({\mathit{x}}^m|\beta ,{\mathit{x}}^r,𝒦)\propto \text{exp}[-\frac{U({\mathit{x}}^m|{\mathit{x}}^r,𝒦)}{\beta }]=\text{exp}[-\frac{{\sum }_{t=1}^T{U}_t^{𝒦}({\mathit{x}}^m|{\mathit{x}}^r)}{\beta }],$$

   where x^m is the deformed mesh position, T is the number of tetrahedra in the mesh, β is a mesh flexibility parameter, and $U_t^{𝒦}(\mathit{x}|{\mathit{x}}^r)$ is a penalty that goes to infinity if the Jacobian determinant of the t^th tetrahedron’s deformation becomes zero (Ashburner, Andersson, & Friston, 2000). This deformation model allows the mesh to describe a broad spectrum of hippocampal shapes, while preventing the Jacobian determinant of the deformation of each tetrahedron from becoming zero (which is equivalent to collapsing it) or negative (which is equivalent to reversing its orientation). By avoiding collapses and orientation reversals of the tetrahedra, we ensure that the topology of the mesh is preserved. Throughout the rest of this paper, we will assume that β is a known constant.
3. From each deformed mesh x^m, a latent label ${\mathrm{l}}_i^m\in \{1,2,\dots ,L\}$ is generated for each voxel i by sampling from the label probabilities given by the mesh. At non-vertex locations, these probabilities are computed using barycentric interpolation: $p_i(k|\mathit{\alpha },{\mathit{x}}^m,𝒦)={\sum }_{n=1}^N{\alpha }_n^k{\varphi }_n^m({\mathit{x}}_i)$, where p_i is the prior probability at voxel i, x_i is the spatial location of voxel i, and ${\varphi }_n^m(·)$ is an interpolation basis function attached to node n of mesh m – see details in (Van Leemput K., 2009). Assuming conditional independence of the labels between voxels given the deformed mesh position x^m, we have that:

   $$p({\mathit{L}}_m|\mathit{\alpha },{\mathit{x}}^m,𝒦)={\prod }_{i=1}^I{p}_i({\mathrm{l}}_i^m|\mathit{\alpha },{\mathit{x}}^m,𝒦),$$

   where ${\mathit{L}}_m=\{l_1^m,\dots ,l_I^m\}$ is the m-th latent label volume.
4. Finally, the observed label volumes are given by ${\mathrm{c}}_i^m=f_{\mathit{\text{in}}}({\mathrm{l}}_i^m)$ (for in vivo volumes) and ${\mathrm{c}}_i^m=f_{\mathit{\text{ex}}}({\mathrm{l}}_i^m)$ (for ex vivo volumes). The function f_in collapses all the hippocampal subregion labels into a single, global hippocampal label, whereas f_ex collapses all the non-hippocampal labels into a single, generic background label. Therefore, we can write:

   $$p_i({\mathrm{c}}_i^m|\mathit{\alpha },{\mathit{x}}^m,𝒦)={\sum }_{k\in {\mathrm{c}}_i^m}{p}_i(\mathrm{k}|\mathit{\alpha },{\mathit{x}}^m,𝒦),$$ Equation 1

   where $k\in {\mathrm{c}}_i^m$ denotes looping over the labels such that $f_{(·)}({\mathrm{l}}_i^m)={\mathrm{c}}_i^m$. If the mapping from L to C is bijective (i.e., no labels are collapsed), the generative model is the same as in (Van Leemput K., Encoding probabilistic brain atlases using bayesian inference, 2009).

Figure 4.

Illustration of the generative model of the manual labels for ex vivo (top) and in vivo (bottom) MRI.

Given this probabilistic model, the construction of the atlas is equivalent to solving the following inverse problem: given a set of (collapsed) label volumes (i.e., manual segmentations), we search for the atlas that most likely generated them according to the model. We use Bayesian inference to find the answer, as detailed below.

Optimization of model parameters – mesh deformations and atlas probabilities

Assuming that the mesh connectivity 𝒦 and reference position x^r are known, the problem to solve is:

$$\{\hat{\mathbf{\alpha }},\{{\hat{\mathbf{x}}}^{\mathrm{m}}\}\}={\text{argmax}}_{\mathbf{\alpha },\{{\mathbf{x}}^{\mathrm{m}}\}}p(\mathbf{\alpha },\{{\mathbf{x}}^{\mathrm{m}}\}|\{{\mathbf{C}}_{\mathit{m}}\},{\mathbf{x}}^{\mathrm{r}},𝒦,\mathrm{\beta }),$$

where α̂ and {x̂^m} represent the most likely atlas probabilities and atlas deformations, respectively. Using Bayes’s rule, we have:

$$\{\hat{\mathbf{\alpha }},\{{\hat{\mathbf{x}}}^{\mathrm{m}}\}\}={\text{argmax}}_{\mathbf{\alpha },\{{\mathbf{x}}^{\mathrm{m}}\}}p(\{{\mathbf{C}}_m\}|\mathbf{\alpha },\{{\mathbf{x}}^{\mathrm{m}}\},𝒦)p(\{{\mathit{x}}^m\}|\beta ,{\mathit{x}}^r,𝒦)={\text{argmax}}_{\mathbf{\alpha },\{{\mathbf{x}}^{\mathrm{m}}\}}{\prod }_{m=1}^{M}p({\mathbf{C}}_{\mathrm{m}}|\mathbf{\alpha },{\mathbf{x}}^{\mathrm{m}},𝒦)p({\mathit{x}}^m|\beta ,{\mathit{x}}^r,𝒦),$$ Equation 2

where we have assumed a flat prior for α, i.e., p(α) ∝ 1. Now, taking the logarithm of Equation 2, and expanding the sum over voxels and hidden labels (Equation 1), we have:

$$\{\hat{\mathbf{\alpha }},\{{\hat{\mathbf{x}}}^{\mathrm{m}}\}\}=\underset{\mathbf{\alpha },\{{\mathbf{x}}^{\mathrm{m}}\}}{\text{argmax}}ℒ(\mathbf{\alpha },\{{\mathbf{x}}^{\mathrm{m}}\};{\mathbf{C}}_{\mathrm{m}},{\mathbf{x}}^{\mathrm{r}},\beta ,𝒦),\text{with}$$ Equation 3: target function for atlas building

$$ℒ(\mathbf{\alpha },\{{\mathbf{x}}^{\mathrm{m}}\};{\mathbf{C}}_{\mathrm{m}},{\mathbf{x}}^{\mathrm{r}},\beta ,𝒦)=\sum _{m=1}^M\{\text{log}p({\mathit{x}}^m|\beta ,{\mathit{x}}^r,𝒦)+\sum _{i=1}^I\text{log}\sum _{k\in {\mathrm{c}}_i^m}{p}_i(\mathrm{k}|\mathit{\alpha },{\mathit{x}}^m,𝒦)\}.$$

The first term in ℒ in Equation 3 represents the (negated) cost of warping the mesh according to the deformation model we have borrowed from (Ashburner, Andersson, & Friston, 2000), whereas the second term represents the data fidelity. We solve Equation 3 by optimizing α with {x^m} fixed and vice versa until convergence. Updating α amounts to re-estimating the label probabilities at each spatial location, whereas the optimization of {x^m} with α fixed represents a group-wise, nonrigid registration process. As shown below, the update equations are analogous to those from the original method (Van Leemput K., Encoding probabilistic brain atlases using bayesian inference, 2009).

Update of {x^m}

We perform the optimization of Equation 3 with respect to {x^m} one dataset index m at the time. We use a conjugate gradient algorithm to numerically optimize the expression. The gradients are given in analytical form by:

$$\frac{\partial ℒ(\mathbf{\alpha },\{{\mathbf{x}}^{\mathrm{m}}\};{\mathbf{C}}_{\mathrm{m}},{\mathbf{x}}^{\mathrm{r}},\beta ,\mathit{𝒦}}{\partial {\mathbf{x}}^{\mathrm{m}}}=-\frac{1}{\beta }\sum _{t=1}^T\frac{\partial U_t^{𝒦}({\mathit{x}}^m|{\mathit{x}}^r)}{\partial {\mathit{x}}^m}+\sum _{i=1}^I\frac{{\sum }_{k\in C_{m,i}}\frac{\partial p_i(\mathrm{k}|\mathit{\alpha },{\mathit{x}}^m,𝒦)}{\partial {\mathit{x}}^m}}{{\sum }_{k\in C_{m,i}}{p}_i(\mathrm{k}|\mathit{\alpha },{\mathit{x}}^m,𝒦)}=-\frac{1}{\beta }\sum _{t=1}^T\frac{\partial U_t^{𝒦}({\mathit{x}}^m|{\mathit{x}}^r)}{\partial {\mathit{x}}^m}+\sum _{i=1}^I\frac{{\sum }_{k\in C_{m,i}}{\sum }_{n=1}^N{\alpha }_n^k\frac{\partial {\varphi }_n^m({\mathit{x}}_{\mathit{i}})}{\partial {\mathit{x}}^m}}{{\sum }_{k\in C_{m,i}}{\sum }_{n=1}^N{\alpha }_n^k{\varphi }_n^m({\mathit{x}}_i)}.$$

Update of α

We carry out the optimization of Equation 3 with respect to α with an expectation maximization (EM) algorithm (Dempster, Laird, & Rubin, 1977) as follows. Leaving aside the term that is independent of α, we iteratively build a lower bound to the target function ℒ(α,{x^m};C_m, x^r, β, 𝒦) that touches it a the current value of α (“E step”) and subsequently optimize this bound with respect to α (“M step”). This procedure is guaranteed to always improve the value of the original target function (or leave it unchanged when convergence has been achieved). If α̃ is the current estimate of α, the bound is:

$$Q(\mathbf{\alpha };\tilde{\mathbf{\alpha }})=\sum _{m=1}^M\sum _{i=1}^I\sum _{n=1}^N\sum _k{W}_{i,n}^{m,k}\text{log}[{\mathrm{\alpha }}_n^k{\varphi }_n^m(x_i)\delta (k\in {\mathrm{c}}_i^m)]-W_{i,n}^{m,k}\text{log}{W}_{i,n}^{m,k}\le \sum _{m=1}^M\sum _{i=1}^I\text{log}\sum _k\sum _{n=1}^N{\alpha }_n^k{\varphi }_n^m(x_i)\delta (k\in {\mathrm{c}}_i^m)=\sum _{m=1}^M\sum _{i=1}^I\text{log}\sum _{k\in {\mathrm{c}}_i^m}{p}_i(\mathrm{k}|\mathit{\alpha },{\mathit{x}}^m,𝒦),$$

where $W_{i,n}^{m,k}$ is given by:

$$W_{i,n}^{m,k}=\frac{{\tilde{\alpha }}_n^k{\varphi }_n^m({\mathit{x}}_{\mathit{i}})\delta (k\in {\mathrm{c}}_i^m)}{{\sum }_{n\prime }{\sum }_{k\prime }{\tilde{\alpha }}_{n\prime }^{k\prime },{\varphi }_{n\prime }^m({\mathit{x}}_{\mathit{i}})\delta (k\prime \in {\mathrm{c}}_i^m)}.$$ Equation 4: E step

It can easily be shown that the maximum of, Q(α; α̃) is attained at:

$${\mathrm{\alpha }}_n^k=\frac{{\sum }_{m=1}^M{\sum }_{i=1}^I{W}_{i,n}^{m,k}}{{\sum }_{m\prime =1}^M{\sum }_{i\prime =1}^I{\sum }_k,W_{i\prime ,n}^{m\prime ,k\prime }}$$ Equation 5: M step

As mentioned previously, the optimization scheme in (Van Leemput K., Encoding probabilistic brain atlases using bayesian inference, 2009) is recovered when the mapping from L to C is bijective.

Optimization of mesh topology – model selection

So far we have assumed that the mesh connectivity and reference position were fixed. Optimizing the mesh topology is important to avoid overfitting to the training data due to the large variability in neuroanatomy across subjects. For instance, at a given spatial location, an atlas built upon a small training dataset could incorrectly assign a zero probability for a given label, if it was not present in any of the training volumes. This problem can be partly overcome by smoothing the atlas (Ashburner & Friston, 2001). As shown in (Van Leemput K., Encoding probabilistic brain atlases using bayesian inference, 2009), the mesh topology can be optimized such that an automatically estimated amount of blurring is introduced in the atlas, allowing it to generalize well to previously unseen data. Following Van Leemput’s framework, we compare meshes with different topologies by evaluating their so-called evidence, which expresses how probable the observed training data is for each mesh topology. To compute the model evidence, we follow (Van Leemput K., 2009), with the difference that we replace $p_i({\mathrm{l}}_i^m|\mathit{\alpha },{\mathit{x}}^m,𝒦)$ by $p_i({\mathrm{c}}_i^m|\mathit{\alpha },{\mathit{x}}^m,𝒦)={\sum }_{k\in {\mathrm{c}}_i^m}{p}_i(\mathrm{k}|\mathit{\alpha },{\mathit{x}}^m,𝒦)$ – recovering our previous algorithm if f_(·)(l) is bijective. The evidence is given by:

$$p(\{C_m\}|\mathrm{\beta },{\mathbf{x}}^{\mathrm{r}},𝒦)\approx \frac{1}{Z}(\prod _{n=1}^N{[({\hat{N}}_n+1)({\hat{N}}_n+2)]}^{-1}\left)\right(\prod _{m=1}^{M}p(C_m|\hat{\mathbf{\alpha }},{\hat{\mathit{x}}}^m,𝒦)),$$ Equation 6: model selection

where ${\hat{N}}_n={\sum }_{m=1}^M{\sum }_k{\sum }_{i=1}^I{W}_{i,n}^{m,k}$, α̂, x̂^m are the minimizers of Equation 3, and where the constant Z includes a number of factors that only depend significantly on β (which is kept fixed in this work).

In order to compute the most likely connectivity 𝒦 and reference position x^r using Equation 6, these variables are first initialized with a high-resolution, regular mesh. Then, the mesh parameters {α̂, {x̂^m}} are optimized by solving the problem in Equation 3. Finally, the mesh is simplified by repeatedly visiting each edge (in random order), comparing the effect on the evidence of either keeping the edge while optimizing the reference position of the two nodes at its ends, or collapsing the edge into a single node and optimizing its reference position; the details can be found in (Van Leemput K., Encoding probabilistic brain atlases using bayesian inference, 2009).

Data preprocessing

To build the atlas, all the training label volumes must be in the same coordinate space. For this purpose, we carried out the following preprocessing steps: 1. manually rotating the FreeSurfer whole brain atlas – described in (Fischl, et al., 2002) – so that the major axis of the left hippocampus was aligned with the anterior-posterior axis; 2. extracting from the atlas a binary mask corresponding to the voxels for which the left hippocampus is the most likely label; 3. left-right flipping all right hippocampi in the training data; 4. affine co-registration of the training data (using binary hippocampal masks) to the left hippocampus of the rotated FreeSurfer atlas, using sum of squares as metric; 5. resampling to 0.25 mm resolution (which is above the limit that can currently be achieved with in vivo brain MRI scanning); and 6. cropping a bounding box around the hippocampi, leaving a 10 mm margin with respect to the boundary as defined by the FreeSurfer atlas – which yielded volumes of dimension 131×241×99 voxels. The resampling of label volumes was carried out by resampling binary masks for each label separately using cubic interpolation, and picking the label with the maximum value at each voxel. This approach mitigates the block effect caused by nearest neighbor interpolation. This preprocessing pipeline yielded 93 (78 in vivo, 15 ex vivo) volumes with the same size and resolution, in which the hippocampi were affinely aligned, and which were then fed to the algorithm described above. The mesh flexibility parameter was set to β = 0.15; visual inspection of the results of pilot segmentation experiments using the algorithm proposed in Section 3.4 below and 10 T1 scans of the OASIS datasetⁱ showed that this value of β provided a good compromise compromise between specificity and generalization ability.

2.5 Statistical atlas: volumes of subregions and sample slices

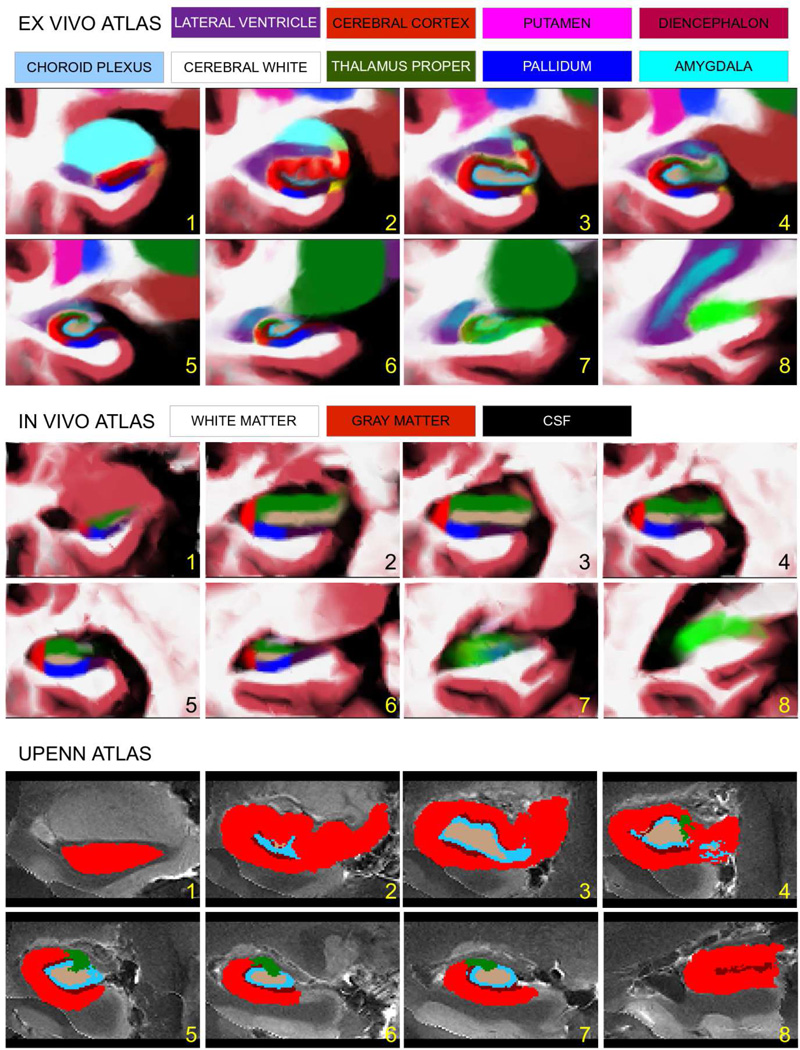
Coronal slices from the resulting statistical atlas are displayed in Figure 5. The atlas has a total of 18,417 vertices, so the dimensionality of x – which is equal to the number of degrees of freedom of the nonlinear deformation – is approximately three times this value, i.e., ca. 55,000. Figure 5 also displays the original in vivo atlas currently distributed with FreeSurfer for comparison. Both atlases show similar levels of blurring in the label probabilities that allow them to avoid overfitting the training data and generalize well to test images. However, the ex vivo atlas follows the internal structures of the hippocampus with much more accuracy than the in vivo version, which relies much more on geometric features – see for instance the vertical boundary of CA1 (in red) in Figure 5. In fact, the in vivo atlas does not describe the molecular layer (dark brown), which is the main feature that will allow the atlas to segment high-resolution MRI data of the hippocampus. The figure also displays the UPenn atlas from (Yushkevich, et al., 2009), which has lower resolution than the presented ex vivo atlas, has fewer subregions, and does not model additional surrounding (extrahippocampal) structures.

Figure 5.

corresponding coronal slices (from anterior to posterior) of the label probabilities derived from the proposed ex vivo (top two rows) and original in vivo (middle two rows) atlases, as well as the UPenn atlas (Yushkevich, et al., 2009) (bottom two rows). For the FreeSurfer atlases, the color at each voxel is a linear combination of the colors assigned to the substructures, weighted by the corresponding probabilities. For the UPenn atlas, the color corresponds to the label with highest probability at each location. The color legend for the hippocampal subregions is the same as in Figure 2. The color code for the surrounding structures is displayed in the figure – note that the in vivo atlas uses generic labels for the gray matter, white matter and cerebrospinal fluid structures. Sagittal and axial slices of the atlases are provided as part of the supplementary material (Figure 18 and Figure 19).

The improved accuracy of the ex vivo atlas is also reflected on the volumes of the subregions. Table 3 shows the average subregion volumes for the in vivo (FreeSurfer v5.3) and ex vivo atlases (FreeSurfer v6.0), for the UPenn atlas (Yushkevich, et al., 2009), and for two different previous histological studies: (Simic, Kostovic, Winblad, & Bogdanovic, 1997) and (Harding, Halliday, & Kril, 1998). Compared with the in vivo atlas, the ex vivo counterpart models a larger number of subregions and also yields volumes for CA1 and (especially) CA2/3 that are much closer to those reported by the referenced histological studies. The UPenn atlas yields accurate volumes for CA4 (for which it agrees well with our ex vivo atlas), but underestimates the volume of CA2/3 and largely overestimates the volume of CA1. Both our ex vivo atlas and the UPenn atlas overestimate the volume of the dentate gyrus, compared with the histological studies.

Table 3.

Mean hippocampal volumes derived from the proposed ex vivo atlas (FreeSurfer v6.0), the in vivo atlas (FreeSurfer v5.3), the UPenn atlas (Yushkevich, et al., 2009), and two histological studies of the hippocampus (Simic, Kostovic, Winblad, & Bogdanovic, 1997) (Harding, Halliday, & Kril, 1998). All the volumes are in cubic millimeters. The UPenn atlas is available at http://www.nitrc.org/projects/pennhippoatlas/; we computed its volumes from the most likely labels.

Method	AGE	PARA.	PRE.	SUB.	CA1	CA2/3	CA4	DG	TAIL	ML	HATA	FIM.	ALV.
Ex vivo atlas	78.6	51	254	337	520	179	211	244	465	466	50	92	320
In vivo atlas	22–89		420	521	330	906	496 (CA4+DG)		350			83
UPenn	N/A				1574	86	201	167		127
Simicii	80.2			404	591	139	197	59
Harding	69		321	529	731	138	169	50

3 Segmentation of in vivo MRI data

In this section, we first introduce an algorithm to segment in vivo MRI data using the proposed statistical atlas (Section 3.1). Subsequently, Sections 3.2 through 3.4 present segmentation results on three different publicly available datasets with different resolutions and MRI contrasts, in order to demonstrate the ability of the algorithm to adapt to monomodal and multimodal data acquired with different MRI protocols and different hardware platforms. In Section 3.2, the algorithm is applied to high resolution (0.6 mm isotropic) T1/T2 data, segmenting the T1 and T2 channels both independently and simultaneously. In Section 3.3, we use 1 mm isotropic T1 data and corresponding high-resolution T2 images (0.4 mm in-plane, 2 mm slice thickness) to find group differences in subregion volumes between MCI subjects and elderly controls. Finally, in Section 3.4 we automatically segment 1 mm isotropic T1 scans of AD subjects and elderly controls to compute volumes that are used as feature in classification experiments.

3.1 Algorithm for segmenting an in vivo scan

Here we describe the algorithm to segment an in vivo MRI scan given the atlas built in Section 2. We first describe the underlying generative model, which builds on that of Section 2.4, and then detail an algorithm to estimate the segmentation using Bayesian inference. As in the previous section, we will assume that we are segmenting a left hippocampus. If we wish to segment the right hippocampus, we simply flip the atlas in the left-right direction.

Generative model

The built atlas can be used to segment a previously unseen MRI scan acquired with any type of MRI contrast (monomodal or multimodal), using the generative model displayed in Figure 6. The first layers of the model are the same as in Figure 4: the atlas, which defines prior probabilities of label occurrences in space, is first deformed according to the model proposed in (Ashburner, Andersson, & Friston, 2000), and then labels are sampled at each voxel location to obtain a segmentation L. The difference is that now this segmentation is connected to image intensities through a likelihood term, for which we assume that a Gaussian distribution is associated with each label.

Figure 6.

Illustration of the generative model of MRI images (monomodal data).

In order to reflect the fact that there is very little contrast between different white matter structures in structural MR images of the brain, we assume that the fimbria and the cerebral white matter belong to a global white matter class, described by a single Gaussian distribution. Likewise, the cerebral cortex, amygdala and hippocampal gray matter structures (para-, pre-, and subiculum, CA1–4, GC-DG, HATA) also are assumed to be part of a global gray matter class. The cerebrospinal fluid (CSF) structures (ventricles, hippocampal fissure) share a class as well. The diencephalon, thalamus, pallidum, putamen and choroid plexus each have independent intensity classes. The alveus and molecular layer could in principle be part of the global white matter class; however, due to their thin shape, they are often affected by partial voluming, so we allow them to have their own Gaussian parameters as well.

The observed MRI intensity image Y is assumed to have been generated by sampling a Gaussian distribution at each voxel i, parameterized by the mean and covariance corresponding to its global class:

$$p(\mathit{Y}|\mathit{L})=\prod _{i=1}^I{p}_i({\mathit{y}}_i|{\mathit{\mu }}_{G(l_i)},{\mathbf{\Sigma }}_{G(l_i)})=\prod _{i=1}^I𝒩({\mathit{y}}_i;{\mathit{\mu }}_{G(l_i)},{\mathbf{\Sigma }}_{G(l_i)}),$$

where G(l_i) represents the global class corresponding to label l_i, μ_G and Σ_G) are the mean and covariance of the global tissue class G, 𝒩(·;μ, Σ) represents the (possibly multivariate) Gaussian distribution with mean μ and covariance Σ, and y_i denotes the intensity in voxel i.

The generative model is completed by a prior distribution on the Gaussian parameters {μ_G}, {Σ_G}. We use a normal-inverse-Wishart distribution for each class – which is the conjugate prior for a multivariate Gaussian distribution with unknown mean and covariance – with covariance-related hyperparameters set to zero (i.e., uninformative prior on the covariance structure):

$$p(\{{\mathit{\mu }}_G\},\{{\mathbf{\Sigma }}_G\})={\prod }_{G}p({\mathit{\mu }}_G,{\mathbf{\Sigma }}_G)={\prod }_{G}NIW({\mathit{\mu }}_G,{\mathbf{\Sigma }}_G;{\mathbf{M}}_G,{\nu }_G,0,0)\propto {\prod }_G𝒩({\mathit{\mu }}_G;{\mathbf{M}}_G,{{\nu }_G}^{-1}{\mathbf{\Sigma }}_G).$$

Here {M_G} and {ν_G} are the remaining hyperparameters of the normal-inverse-Wishart distribution. Their interpretation is that prior to observing any image data, we have an initial guess M_G of the mean of tissue class G, which is assumed to have been obtained as the sample mean of ν_G observations (note that for ν_G = 0 a uniform prior is obtained).

Segmentation as Bayesian inference

Using the described generative model, segmentation is cast as an optimization problem in a Bayesian framework – we search for the most likely labeling given the probabilistic atlas and the observed image intensities. Exact inference would require marginalizing over the model parameters x (the mesh deformation) and {μ_G, Σ_G}, which leads to an intractable integral. Therefore, we make the approximation that the posterior distribution of such parameters in light of the atlas and observed image intensities is heavily peaked. This allows us to first find the maximum-a-posteriori (MAP) estimates of the parameters, and then use these values to derive the segmentation:

$$\hat{\mathit{L}}=\underset{\mathbf{L}}{\text{argmax}}p(\mathit{L}|\mathit{Y},\mathit{\alpha },{\mathit{x}}^r,\beta ,𝒦)\approx \underset{\mathbf{L}}{\text{argmax}}p(\mathit{L}|\hat{\mathit{x}},\{{\hat{\mathit{\mu }}}_G\},\{{\hat{\mathbf{\Sigma }}}_G\},\mathit{Y},\mathit{\alpha },{\mathit{x}}^r,\beta ,𝒦),$$

where the most likely model parameters are given by:

$$\{\hat{\mathit{x}},\{{\hat{\mathit{\mu }}}_G\},\{{\hat{\mathbf{\Sigma }}}_G\}\}=\underset{\mathit{x},\{{\mathit{\mu }}_G\},\{{\mathbf{\Sigma }}_G\}}{\text{argmax}}p(\mathit{x},\{{\mathit{\mu }}_G\},\{{\mathbf{\Sigma }}_G\}|\mathit{Y},\mathit{\alpha },{\mathit{x}}^r,\beta ,𝒦)$$ Equation 7: model parameter estimation

Using Bayes rule, the problem in Equation 7 can be rewritten as:

$$\{\hat{\mathit{x}},\{{\hat{\mathit{\mu }}}_G\},\{{\hat{\mathbf{\Sigma }}}_G\}\}=\underset{\mathit{x},\{{\mathit{\mu }}_G\},\{{\mathbf{\Sigma }}_G\}}{\text{argmax}}p(\mathit{Y}|\mathit{\alpha },\mathit{x},𝒦,\{{\mathit{\mu }}_G\},\{{\mathbf{\Sigma }}_G\})p(\mathit{x}|\beta ,{\mathit{x}}^r,𝒦)p(\{{\mathit{\mu }}_G\},\{{\mathbf{\Sigma }}_G\})=\underset{\mathit{x},\{{\mathit{\mu }}_G\},\{{\mathbf{\Sigma }}_G\}}{\text{argmax}}\text{log}p(\mathit{x}|\beta ,{\mathit{x}}^r,𝒦)+{\sum }_{i=1}^I\text{log}[{\sum }_G{p}_i(y_i|{\mathit{\mu }}_G,{\mathbf{\Sigma }}_G)p_i(G|\mathit{\alpha },\mathit{x},𝒦)]+{\sum }_G\text{log}p({\mathit{\mu }}_G,{\mathbf{\Sigma }}_G),$$ Equation 8: target function for parameter estimation

where we have introduced the prior for global tissue class G as: p_i(G|α, x, 𝒦) = Σ_k∈G p_i(k|α, x, 𝒦). We solve Equation 8 by alternately optimizing for the mesh deformation x and the Gaussian parameters {μ_G}, {Σ_G}. We update the mesh deformation x by optimizing Equation 8 directly with a conjugate gradient algorithm, and the Gaussian parameters with an EM algorithm. In the E step, we perform a probabilistic label classification for each voxel:

$${\mathrm{\Omega }}_i^G=\frac{p_i({\mathit{y}}_i|{\mathit{\mu }}_G,{\mathbf{\Sigma }}_G)p_i(G|\mathit{\alpha },\mathit{x},𝒦)}{{\sum }_{G\prime }{p}_i({\mathit{y}}_i|{\mathit{\mu }}_{G\prime },{\mathbf{\Sigma }}_{G\prime })p_i(G\prime |\mathit{\alpha },\mathit{x},𝒦)},$$

and in the M step, the Gaussian parameters are updated as follows:

$${\mathit{\mu }}_G\leftarrow \frac{{\nu }_G{\mathbf{M}}_G+{\sum }_{i=1}^I{\mathrm{\Omega }}_i^G{\mathit{y}}_i}{{\nu }_G+{\sum }_{i=1}^I{\mathrm{\Omega }}_i^G},$$

$${\mathbf{\Sigma }}_G\leftarrow \frac{{\sum }_{i=1}^I{\mathrm{\Omega }}_i^G({\mathit{y}}_i-{\mathit{\mu }}_G){({\mathit{y}}_i-{\mathit{\mu }}_G)}^t+{\nu }_G({\mathit{\mu }}_G-{\mathbf{M}}_G){({\mathit{\mu }}_G-{\mathbf{M}}_G)}^t}{{\sum }_{i=1}^I{\mathrm{\Omega }}_i^G}$$

Once the optimal parameters x, {μ̂_G}, {Σ̂_G}, have been estimated, the (approximately) optimal segmentation $\underset{\mathbf{L}}{\text{argmax}}p(\mathit{L}|\hat{\mathit{x}},\{{\hat{\mathit{\mu }}}_G\},\{{\hat{\mathbf{\Sigma }}}_G\},\mathit{Y},\mathit{\alpha },{\mathit{x}}^r,\beta ,𝒦)$ can be computed voxel by voxel as:

$${\hat{l}}_i\approx \underset{\mathrm{k}}{\text{argmax}}{p}_i({\mathit{y}}_i|{\mathit{\mu }}_{G(k)},{\mathbf{\Sigma }}_{G(k)})p_i(k|\mathit{\alpha },\mathit{x},𝒦).$$

If we are interested in the volumes of the different structures, their expected values are given by:

$$V_k={\sum }_{i=1}^I\frac{p_i({\mathit{y}}_i|{\mathit{\mu }}_{G(k)},{\mathbf{\Sigma }}_{G(k)})p_i(k|\mathit{\alpha },\mathit{x},𝒦)}{{\sum }_{k\prime }{p}_i({\mathit{y}}_i|{\mathit{\mu }}_{G(k\prime )},{\mathbf{\Sigma }}_{G(k\prime )})p_i(k\prime |\mathit{\alpha },\mathit{x},𝒦)}.$$ Equation 9: estimation of volume

Image preprocessing, algorithm initialization and computation of hyperparameters

To initialize the segmentation algorithm and compute the hyperparameters {M_G, ν_G}, we use the output from the standard FreeSurfer pipeline (“recon-all”), which operates on whole brain T1 data at 1 mm resolution. FreeSurfer produces a skull-stripped, bias field corrected volume that we use as T1 component of the input to the hippocampal segmentation algorithm. It also produces a segmentation of this whole brain volume into 36 structures. If additional channels (e.g., high-resolution T2) are available, they are first rigidly coregistered with the T1 scan with mutual information (FreeSurfer’s “mri_robust_register”), using the brain mask provided by FreeSurfer to eliminate the influence of non-brain tissue on the alignment. The resulting transform is used to map the (skull-stripped, bias field corrected) T1 data and its automated segmentation to the space of the additional scan. The mapped segmentation is used to skull strip the additional channels. The preprocessed data from all the available channels is then resampled to the voxel size at which we desire to compute the segmentation, which is equal to the resolution at which the atlas will be rasterizedⁱ.

We position the cuboid region that the atlas models by mapping it to the image to be segmented with an affine, sum of squares based registration algorithm (implemented in “mri_robust_register”). The algorithm uses the binary hippocampal segmentation from FreeSurfer as target image, and a soft probability map for the whole hippocampus – computed from the mesh in reference position – as source image for the registration. Henceforth, we refer to the region covered by the mapped atlas cuboid as “atlas region of interest (ROI)”. The voxels outside the atlas ROI are not considered by the segmentation algorithm.

In addition to preprocessing the input data and computing the atlas ROI, the segmentation of the brain into 36 structures generated by FreeSurfer is also used compute the hyperparameters {M_G, ν_G} as follows: for each global class G, we first find all the voxels segmented as such structure by FreeSurfer. Next, we set M_G to the modality-wise median intensity of that structure. Then, we set ν_G to the number of voxels used in the estimation of the median. Using the FreeSurfer segmentation from the whole brain improves the estimate of the Gaussian parameters, especially when the number of voxels for a given class is small within the atlas ROI. For instance, it is not always easy to estimate the Gaussian parameters of the CSF from the atlas ROI, partly due to the presence of the choroid plexus. However, if we look at the whole brain, such parameters can be easily estimated from the full ventricles.

There are however four classes for which the hyperparameters are computed in a different manner: gray matter, white matter, alveus and molecular layer. For the gray and white matter, since there are so many voxels labeled as such in the whole brain, we only use those from the hippocampus and neighboring regions in the FreeSurfer parcellation of each hemisphere. This way, we take advantage of a relatively large number of voxels to inform the model while eliminating the drift in the hypermeans {M_G} that could be caused by voxels far away from the hippocampus due to the MRI bias field. For the white matter, we use the superior occipital gyrus, the orbital part of inferior frontal gyrus and the opercular part of the inferior frontal gyrus of the corresponding hemisphere. For the gray matter, we use the parahippocampal, entorhinal and fusiform cortices, as well as the whole hippocampus and amygdala from the corresponding hemisphere.

The hyperparameters of the alveus and molecular layer are computed in a different way because, due to their thin shapes, they are more severely affected by the partial volume effect, such that the global white tissue class does not model their intensity distribution correctly (despite the fact that they are white matter structures). We compute the hyperparameters of these structures by mimicking the partial volume effect as follows. First, we rasterize the mesh at the initial position x at the native resolution (0.25 mm isotropic). Next, we sample a label l_i at each voxel i from l_i ~ p_i (k|α, x^m, 𝒦) to generate a sample segmentation L. Then, we assign to each voxel the mean intensity of its corresponding label, while assuming that the alveus and molecular layer belong to the global white matter class. Then, we blur this image with a Gaussian kernel that matches the resolution of this synthetic image to that of the test scan to segment, by setting its FHWM (in voxels) in each direction to the voxel size of the test scan in that direction divided by the native voxel size of the atlas (0.25 mm). Finally, M_alv and M_ML are set to the median intensity of the fimbria and molecular layer in the synthetic image, whereas we set ν_alv and ν_ML to the volume of these two structures provided by the atlas (see Section 2.5).

3.2 Qualitative segmentation results on high resolution T1/T2 data from Winterburn et al. (2013)

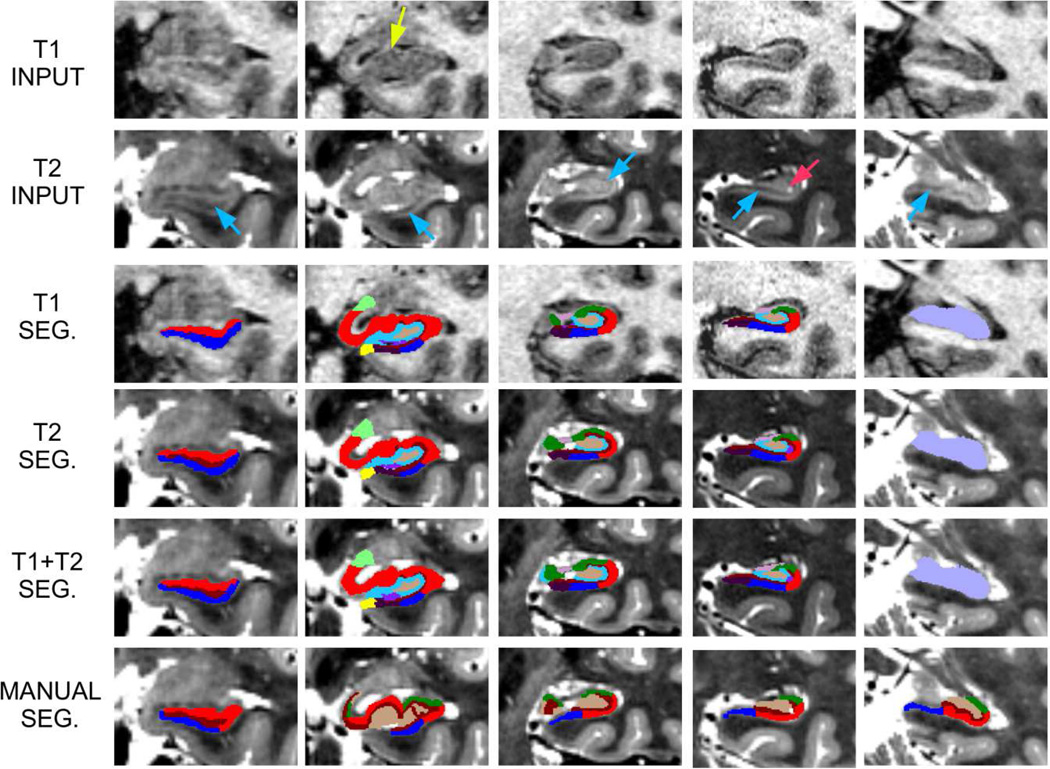
In this section, we show qualitative results on a publicly available dataset of high resolution T1/T2 data. The dataset (Winterburn, et al., 2013) is a public repository of T1 and T2-weighted scans of five subjects (two males, three females, ages 29–57) acquired on a 3T GE scanner with an 8-channel head coil. Both the T1 and the T2 scans were acquired at 0.6 mm isotropic resolution, and then super-sampled to 0.3 mm isotropic. Manual delineations of five subregions are also available as part of the repository: CA1, CA2/3, dentate gyrus, molecular layer and subiculum. Note, however, that a direct evaluation through comparison of manual and automated segmentations (e.g., with Dice scores) is not possible due to the differences between our subregion labeling protocol (described in Section 2.2) and theirs. Instead, we present qualitative results: since high resolution images are available for both the T1 and T2 channels (see sample slices in Figure 7), we can compare the outputs produced by the segmentation algorithm on the T1 data, the T2 data, and both combined. When using a single channel in the segmentation, y_i is a scalar with the T1 (or T2) intensity, and {μ_G, Σ_G} are also scalars with the means and variances of the tissue types. When we segment both channels simultaneously, y_i is a 2 × 1 vector with the T1 and T2 intensities at spatial location i, while the means {μ_G} are 2 × 1 vectors and the covariances Σ_G are 2 × 2 matrices. In this experiment, the work resolution is set to 0.3 mm – equal to the voxel size of the input scans.

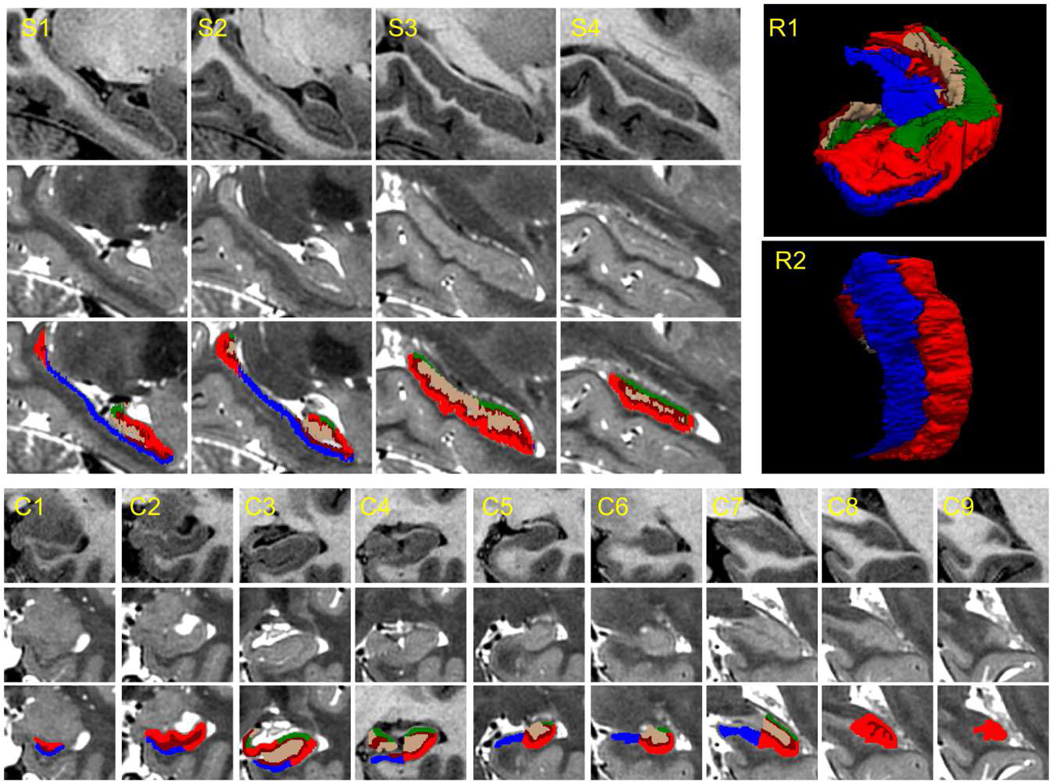
Figure 7.

Sample images (T1 and T2 weighted) and manual segmentations of “subject 1” from (Winterburn, et al., 2013). (S1–S4) Sagittal slices, from medial to lateral. (C1–C9) Coronal slices, from anterior to posterior. (R1) 3D rendering of manual segmentation, anterior view. (R2) 3D rendering, inferior view.

Figure 8 and Figure 9 show sample segmentations from “subject 3” in the dataset using the T1 scan alone, the T2 scan alone, and both scans simultaneously; segmentations from the other four subjects in the dataset are provided in the supplementary material (Figure 20 and Figure 21). Note that we have removed from the final segmentation the neighboring structures of the hippocampus, as well as the alveus; showing very little contrast in in vivo MRI due to its thin shape, its automated segmentation is often unreliable. The method effectively adapts to the MRI contrast in each case, successfully segmenting the hippocampus in all three scenarios. The segmentation based solely on the T1 image accurately captures the global shape of the hippocampus, but often under-segments the molecular layer (marked with blue arrows in the figures) and CSF pockets (red arrows), which are hardly visible in T1. These features are correctly segmented in the T2 image, which, on the other hand, captures the global shape of the hippocampus less accurately than the T1 scan, due to its poorer contrast between gray and white matter (see regions marked with yellow arrows in the figures). The output based on multimodal MRI data takes advantage of the information from both channels to produce a smoother, more accurate segmentation that combines the advantages of the T1 and T2 MRI contrasts.

Figure 8.

Sample coronal slices of “subject 3” from (Winterburn, et al., 2013), from anterior (left) to posterior (right). Top row: T1 image. Second row: T2 image. Third row: segmentation computed with the T1 scan. Fourth row: segmentation computed with T2 scan. Fifth row: segmentation computed with T1 and T2 scans simultaneously, overlaid on the T2 images. Bottom row: manual segmentation from the original study. The red arrow marks a CSF pocket, the blue arrows mark the molecular layer, and the yellow arrow marks the medial digitation.

Figure 9.

Sample sagittal slices of “subject 3” from (Winterburn, et al., 2013), from medial (left) to lateral (right). See caption of Figure 8 for an explanation of the different rows. The red arrow marks a CSF pocket, the blue arrows mark the molecular layer, and the yellow arrows mark segmentation errors in the whole hippocampal shape.

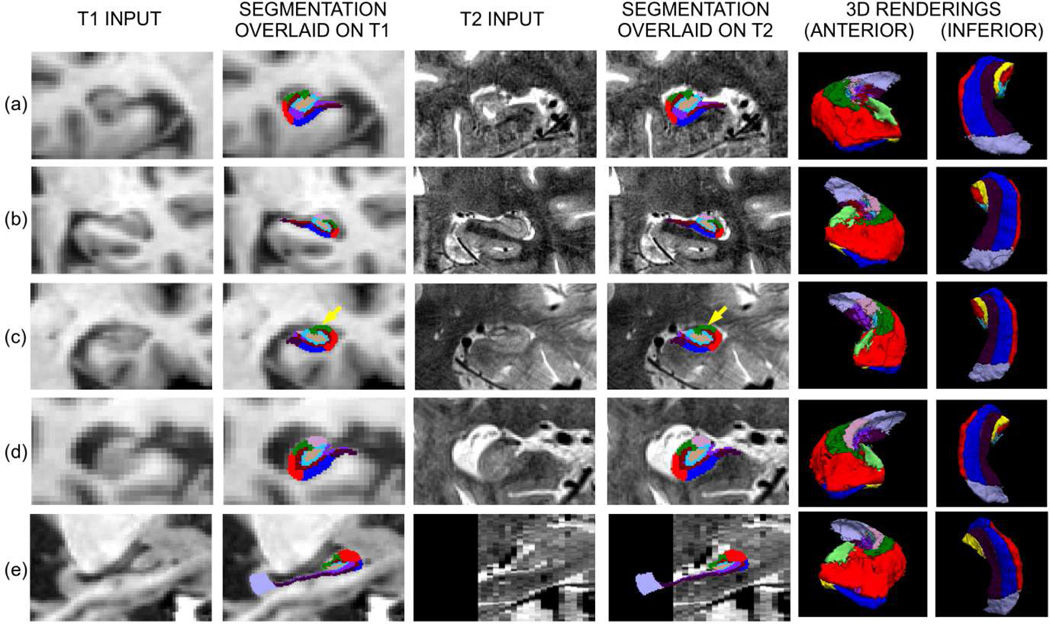
Figure 8 and Figure 9 also show the corresponding manual segmentations from the original article (Winterburn, et al., 2013). The agreement between the manual and automated segmentations is fair in general, but some differences can be found in the areas where the segmentation is poorly supported by the image contrast (e.g., the medial digitation in Figure 8) and also in the hippocampal regions where our definitions of the subregions and theirs disagree. First, some of the labels of our protocol do not exist in their labeling scheme: tail, fimbria, GC-DG, HATA, parasubiculum and presubiculum. Second, even though the agreement of the protocols is good in the superior part of the hippocampus (see 3D renderings in Figure 10), large differences in the definition of the subregions can be generally observed in the inferior part: our subiculum is largely part of their CA1, while our presubiculum and parasubiculum correspond approximately to their subiculum.

Figure 10.

3D renderings of segmentations of the high-resolution T1/T2 data. (a) Manual segmentation from (Winterburn, et al., 2013), anterior view. (b) Automated segmentation using T1 and T2 volume simultaneously, anterior view. (c–d) Inferior view of (a–b).

3.3 Quantitative results on ADNI T1/T2 data

In this section, we present segmentation results on a dataset of 30 T2 MRI scans from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (adni.loni.usc.edu). The ADNI was launched in 2003 by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, the Food and Drug Administration, private pharmaceutical companies and non-profit organizations, as a $60 million, 5-year public-private partnership. The main goal of ADNI is to test whether MRI, positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to analyze the progression of MCI and early AD. Markers of early AD progression can aid researchers and clinicians to develop new treatments and monitor their effectiveness, as well as decrease the time and cost of clinical trials. The Principal Investigator of this initiative is Michael W. Weiner, MD, VA Medical Center and University of California - San Francisco. ADNI is a joint effort by co-investigators from industry and academia. Subjects have been recruited from over 50 sites across the U.S. and Canada. The initial goal of ADNI was to recruit 800 subjects but ADNI has been followed by ADNI-GO and ADNI-2. These three protocols have recruited over 1,500 adults (ages 55–90) to participate in the study, consisting of cognitively normal older individuals, people with early or late MCI, and people with early AD. The follow up duration of each group is specified in the corresponding protocols for ADNI-1, ADNI-2 and ADNI-GO. Subjects originally recruited for ADNI-1 and ADNI-GO had the option to be followed in ADNI-2. For up-to-date information, see http://www.adni-info.org.

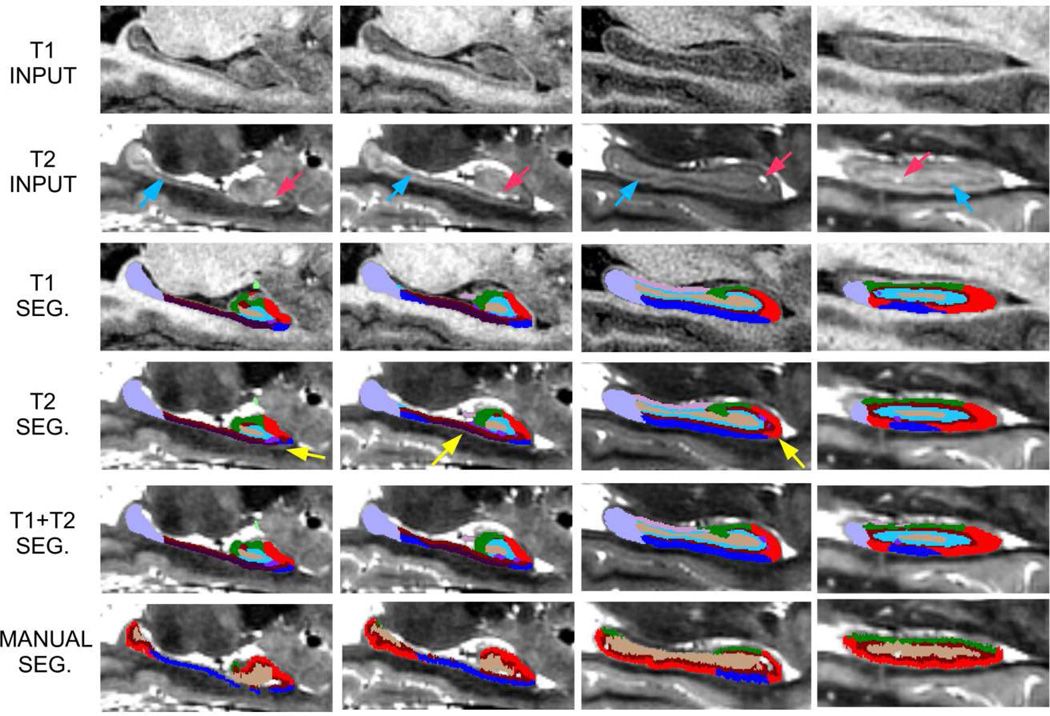
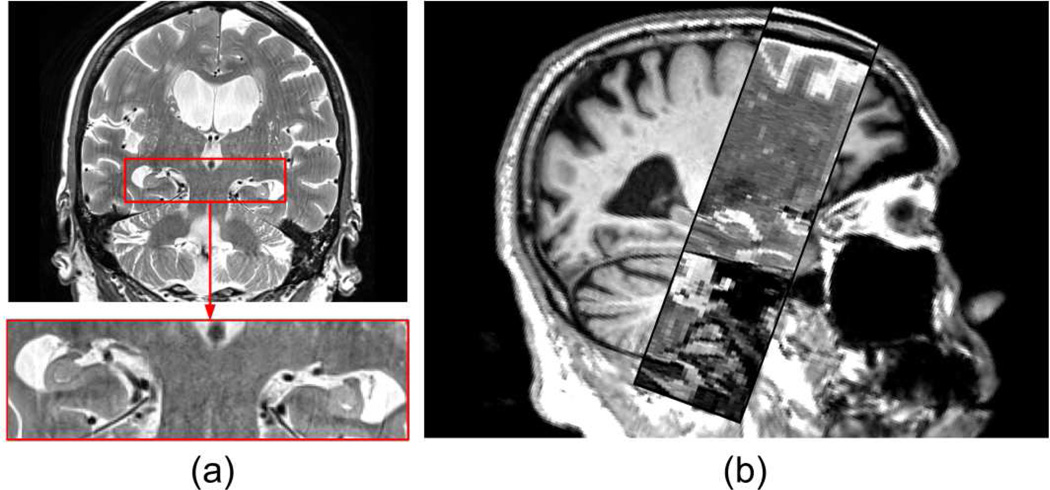
The choice of the subset of ADNI scans for this analysis was motivated by the fact that these are the exact same images that were used in (Mueller, et al., 2013), which includes MCI classification results derived from segmentations produced by a number of automated and semi-automated methods, as well as a manual delineation protocol that only considers five coronal slices in the body of the hippocampus (Mueller, Schuff, Yaffe, Madison, Miller, & Weiner, 2010). Using this dataset enables direct comparison of our results with those from (Mueller, et al., 2013). The 30 scans correspond to an acquisition protocol that has recently been added to the ADNI study, with the following parameters: TR = 8,020 ms, TE = 50 ms, resolution 0.4×0.4×2.0 mm (coronal), 24–30 slices, acquisition time 8 minutes. Of the 30 scans, 16 correspond to subjects with early MCI (ages 74.3±7.6), and the other 14 to age-matched healthy controls (ages 70.8±7.2). Since these scans are part of the ADNI, the corresponding T1-weighted images (sagittal 3D MPRAGE scans at 1 mm resolution) are also available. A sample coronal slice of a T2 scan from ADNI is shown in Figure 11a, and a sagittal slice (overlaid on the corresponding T1-weighted scan) in Figure 11b. The sagittal slice shows how narrow the field of view of these scans sometimes is, failing to cover the whole hippocampus.

Figure 11.

(a) Coronal slice from T2 scan from ADNI, and close-up of the hippocampi. (b) Sagittal slice from a T2 scan from ADNI, overlaid on the corresponding T1 volume. This view illustrates the limited field of view of the T2 scans in ADNI. The in-plane resolution of the T2 scans is 0.4 mm, and the slice separation is 2 mm. The T1 scans are 1 mm isotropic.

To segment these ADNI data, we take advantage of not only the high-resolution T2 images, but also the 1 mm isotropic T1 scans, which provide complementary information. On the one hand, the T2 data have good contrast between subregions, but large slice separation and a narrow field of view. On the other hand, the T1 scans provide isotropic data throughout the whole brain – though with little information on the subregions. Therefore, we segment both channels simultaneously, i.e., {y_i} and {μ_G} are a 2 × 1 vectors and the covariances {Σ_G} are a 2 × 2 matrices. The information of the T1 scan is particularly important when the T2 intensities are missing for some hippocampal voxels due to the limited field of view of the T2 scan (as in Figure 11b, where the hippocampal tail is only visible in the T1 scan). In that case, the equations for Gaussian parameter optimization in Section 3.1 needs to be modified in order to account for this missing information – see details in Appendix A. In this experiment, the work resolution is 0.4 mm isotropic – equal to the in-plane resolution of the T2 images.

Figure 12 shows slices from automated segmentations of some representative cases in the ADNI T1/T2 dataset. When the quality of the scan is good and the molecular layer is visible (as in Figure 12b), the model generally produces a good segmentation. However, mistakes occur sometimes due to image artifacts. In Figure 12c, CSF and white matter mix in the same voxel, making it resemble gray matter (partial volume effect) and thus misleading the segmentation algorithm. In Figure 12d, motion artifacts render the molecular layer invisible. In such cases, the internal boundaries of the hippocampus are mostly determined by the statistical atlas (rather than image intensities), and to a lesser extent by other features such as cysts or the hippocampal fissure. Finally, Figure 12e shows an example of when the lower-resolution T1 is most useful, which is when the field of view of the T2 scan does not cover the whole hippocampus. In that case, the algorithm can still produce a seamless, smooth segmentation of the whole hippocampal formation.

Figure 12.

Inputs (T1, T2) and segmentations for five representative cases of the ADNI T1/T2 dataset. The resolution of the T1 scans is 1 mm isotropic, whereas the T2 scans have 0.4 mm in-plane resolution (coronal) and 2 mm slice separation. (a) A cyst being segmented as hippocampal fissure. (b) A case with good contrast, well-segmented. (c) A case where the partial volume effect has misguided the segmentation, such that part of the lateral ventricle (marked by the arrow) is labeled as CA2/3. (d) A case with poor contrast; the internal segmentation of the hippocampus is largely determined by the prior. (e) A case in which the field of view of the T2 scan does not cover the whole hippocampus; the segmentation of the tail relies solely on the T1 data. All slices are coronal except for (e), which is sagittal. More slices are displayed in the supplementary material (Figure 22).

Direct evaluation of the produced segmentations would require manual delineations for the T2 data made with the ex vivo protocol from Section 2.2, which are not available (and would be extremely difficult to make due to the lack of resolution). Therefore, we use indirect evaluation methods instead, based on assessing the ability of the automatically estimated subregion volumes to discriminate two populations (MCI and elderly controls) in a group analysis framework. First, we compute the subregion volumes from the soft segmentations with Equation 9. Then, we correct these estimates for age and intracranial volume (ICV) by regressing them out with a general linear model. This step is important because the subregion volumes are strongly correlated with these two variables, which can easily confound the analysis – subjects with large ICV and/or of younger age are expected to have larger hippocampi; see for instance (Mueller, Schuff, Yaffe, Madison, Miller, & Weiner, 2010). Moreover, such correction was used in (Mueller, et al., 2013), so we used this correction as well in order to directly compare the results.

Once the corrected volumes have been computed, we compare the volumes of the two groups for each subregion independently with unpaired, two-sample t-tests. Since we have a strong hypothesis that the volume of the subregions does not increase in MCI or AD (except for the fissure, which tends to increase in AD), we can conduct one-tailed tests – for the fissure, we just invert the sign of the test. In addition, we also conduct a power analysis in which we compute the sample size required by the test to have a powerⁱ of 0.50 – which was the value used in (Mueller, et al., 2013) – as well as the power provided by the actual sample size of the dataset.

The group analysis of the subregion volumes is summarized in Table 4. The table also includes two sets of results reported in (Mueller, et al., 2013): a group analysis for subregion volumes derived from the manual segmentation protocol, and another group analysis for the volumes given by the semiautomated algorithm from (Yushkevich, et al., 2010). Our algorithm finds differences in the left and right CA1, molecular layer, dentate gyrus, CA4 and whole hippocampus, as well as the left fimbria and CA2/3 region. The manual annotations (for which the volumes were left-right averaged) show differences in CA1 and dentate gyrus, whereas Yushkevich’s semi-automated method yields significant differences in CA1–3 and CA4-DG – also with left-right averaged volumes. Our results are quite consistent with theirs, given that their methods do not consider the smaller subregions contained in our protocol. In addition, our results show strong consistency with prior work using manual and semi-automated segmentation procedures on the same type of images: even if direct comparison across studies is not possible due to differences in labeling protocols, the differences in CA1, CA4-DG and whole hippocampus have been previously described in (Pluta, Yushkevich, Das, & Wolk, 2012), which is based on the method from (Yushkevich, et al., 2010). In addition, our algorithm also finds statistically significant differences in the molecular layer and fimbria; a decline of the former, which shows great discrimination power in both the left and right hippocampus, has been previously described in the literature (Kerchner, et al., 2010) (Kerchner, Deutsch, Zeineh, Dougherty, Saranathan, & Rutt, 2012).

Table 4.

Group analysis for the hippocampal subregion volumes of MCI subjects (n=14) and elderly controls (n = 16) in the ADNI T1/T2 data. The samples sizes correspond to significance criterion = α = 0.05, power = 1-β = 0.50 - which were the values used in (Mueller, et al., 2013). The p-values correspond to unpaired, one-tailed, two-sample t-tests, and are not corrected for multiple comparisons. Significant values (α < 0.05) are marked in bold. For Mueller et al. and Yushkevich et al., some of the definitions of the subregions are different from ours (Section 2.2). In these cases, their definitions are shown in parentheses. Note that the ex vivo atlas does not include the entorhinal and perirhinal cortices; these are already analyzed by FreeSurfer (Fischl, et al., 2009) (Augustinack, et al., 2013).

STRUCTURES	LEFT (this study)			RIGHT (this study)			L/R AVERAGE (Mueller et al., manual)		L/R AVERAGE (Yushk evich et al.)
	p value	Sample size	Power	p value	Sample size	Power	Sample size	Power	Sample size	Power
Parasubiculum	0.15	73	0.27	0.22	134	0.19
Presubiculum	0.21	121	0.20	0.08	41	0.40
Subiculum	0.14	66	0.29	0.18	95	0.23	25	0.57	59	0.27
CA1	0.03	24	0.58	0.02	18	0.69	11	0.95	10 (CA1/2/3)	0.99
CA2/3	0.02	18	0.71	0.10	47	0.36	27 (CA1/2)	0.55
CA4	0.03	23	0.59	0.04	25	0.57			26 (CA4/DG)	0.42
GC-ML-DG	0.02	20	0.65	0.01	16	0.75	14 (CA3/DG)	0.88
Molec. layer	0.02	20	0.67	0.05	28	0.52
Fimbria	0.02	19	0.68	0.04	26	0.55
Hippo. fissure	0.45	>1000	0.10	0.26	187	0.17
HATA	0.20	111	0.21	0.07	36	0.43
Hippo. tail	0.45	>1000	0.10	0.49	>1000	0.10
Whole hippo.	0.04	27	0.54	0.04	25	0.56
Entorhinal							500	0.07	96	0.18
Perirhinal									223	0.10

In order to quantify the impact of the high-resolution T2 scan in the segmentation, we also compare the ability of the subregion volumes to discriminate the two groups when they are measured with the combined T1/T2 data and when they are derived from the T1 images alone. Table 5 displays the p-values of the corresponding t-tests, which show that the measurements using both modalities better capture the differences in the subregions between the two groups. When only the T1 scans are used, the resolution is insufficient to distinguish the molecular layer. In this case, the volumes of the subregions depend largely on the volume and shape of the whole hippocampus, which reduces the ability of the individual subregions to separate the two groups. Only the fimbria, which is visible at 1 mm resolution, seems to provide comparable discrimination power after the high-resolution T2 scan is removed from the analysis.

Table 5.

Comparing subregion volume measurements from different modalities (only T1 vs. combined T1/T2) through their ability to discriminate MCI subjects from elderly controls in the ADNI T1/T2 data (measured with p-values of unpaired, one-tailed, two-sample t-tests, without correction for multiple comparisons).

Side	Modality	Parasu.	Presub.	Sub.	CA1	CA2/3	CA4	GC- DG	Mol. Lay.	Fimb.	Hipp. Fiss.	HATA	Tail	Whole hippo.
Left	T1	0.10	0.47	0.23	0.08	0.12	0.08	0.11	0.09	0.04	0.30	0.30	0.44	0.08
	T1+T2	0.15	0.21	0.14	0.03	0.02	0.03	0.02	0.02	0.02	0.45	0.20	0.45	0.04
Right	T1	0,34	0.47	0.32	0.10	0.25	0.08	0.06	0.12	0.07	0.35	0.21	0.28	0.10
	T1+T2	0.22	0.08	0.18	0.02	0.10	0.04	0.01	0.05	0.04	0.26	0.07	0.49	0.04

3.4 Quantitative results on standard resolution ADNI T1 data

Here we present results on a dataset of standard resolution scans from the ADNI. The dataset consists of 400 baseline T1 scans from the study, for which high-resolution T2 data are not available. These scans were acquired with MPRAGE sequences at 1 mm isotropic resolution. The MRI data were processed through the standard FreeSurfer pipeline, including the current hippocampal subfield module, which is useful to compare the segmentations yielded by the in vivo atlas with those produced by the ex vivo atlas we are introducing in this study. This hippocampal subfield processing did not complete successfully for 17 scans (due to software crashes), which were removed from the analysis. The demographics of the remaining 383 subjects are as follows: 56.2% elderly controls (age 76.1±5.6 years), 43.8% AD patients (age 75.5±7.6); 53.6% males (ages 76.1±5.6), 46.4% females (ages 75.9±6.8). The resolution at which we rasterized the atlas and computed the segmentation in this experiment was 1/3 mm.

As in Section 3.3, we use the performance in a group analysis as a surrogate for segmentation quality. In this case, we validate the segmentation by comparing the subregion volumes of AD patients and elderly controls. As in the previous section, the resolution of the ADNI T1 scans is insufficient to distinguish the molecular layer, making the segmentation much less reliable. Therefore, the volumes of the subregions are largely determined by the whole hippocampal volume, such that most subregions show large discriminative power, but little differentiation between the subregions is observed. This is illustrated by the results in Table 6, which displays effect sizes for each subregion – for both the in vivo and ex vivo atlases – measured with Cohen’s d, i.e., the difference between two means divided by the standard deviation of the data. We used effect sizes rather than p-values in this experiment because, due to the large sample size and strong effect, all p-values were very small and the differences between the effects on the subregions were harder to appreciate. Large or very large effect sizes are observed for all subregions, except for the hippocampal fissure. The effect sizes given by the segmentations based on the in vivo and ex vivo atlases are quite similar, even though they are – on average – slightly larger for the ex vivo atlas. The main difference between the results of the two atlases is the effect for CA1, which is smaller in the in vivo version.

Table 6.

Effect sizes (Cohen’s d) of the group analysis for the hippocampal subregion volumes in the AD discrimination task. Larger effect sizes correspond to larger differences between the two groups.

STRUCTURES	LEFT		RIGHT
	Ex vivo	In vivo	Ex vivo	In vivo
Parasubiculum	1.37		1.06
Presubiculum	1.99	1.94	1.80	1.48
Subiculum	1.89	1.78	1.89	1.54
CA1	1.99	0.90	1.82	0.67
CA2/3	1.58	1.39	1.59	1.24
CA4	1.79	1.53	1.80
GC-ML-DG	1.81		1.84
Molecular layer	2.09		2.03
Fimbria	0.60	0.70	0.39	0.67
Hippocampal fissure	0.13	0.15	0.21	0.17
HATA	1.45		1.51
Hippocampal tail	1.71	1.45	1.64	1.24
Whole hippocampus	2.11	1.82	2.08	1.49

For the reason mentioned above, (i.e., the lack of internal contrast of the hippocampus at 1 mm resolution), the results in Table 6 must be interpreted with caution. Therefore, we use another method to separate the two populations, based on a statistical classifier that discriminates the groups using all the subregion volumes simultaneously. The process is the following. First, we average the subregion volumes from the left and right hippocampi, as this boosts the power of the analysis without compromising the generalization ability of the classifier by increasing the dimensionality of the data. Subsequently, we perform a correction for age and ICV, for each subregion independently, in the same way as described in Section 3.3. Then, we concatenate all the subregion volumes of each subject into a vector, and use it as input to a linear discriminant analysis (LDA) classifier (Fisher, 1936). The use of a simple, linear classifier such as LDA ensures that the classification accuracy is mainly determined by the quality of the input data (i.e., the subregion volumes) rather than stochastic variations in the classifier.

We compared the performance of the segmentations given by the new ex vivo atlas with those produced by the in vivo atlas in FreeSurfer v5.3 (we used the “off-the-shelf” implementation of the segmentation algorithm). We used two metrics in the comparison: the area under the receiver operating characteristic (AUROC) of the classifiers and their maximum classification accuracy. The latter is given by the threshold corresponding to the “elbow” of the receiver operating characteristic (ROC) curve, i.e., the point closest to FPR=0, TPR=1. We used leave-one-out cross-validation to compute the ROC. Significance in the difference in AUROCs was assessed with a non-parametric test (DeLong, DeLong, & Clarke-Pearson, 1988). In addition, we also compared a classifier based solely on whole hippocampal volume, which allows us to quantify the benefit of using the subregion volumes with respect to the whole hippocampus. We used two different estimates of the volume: the sum of the subregion volumes given by the ex vivo atlas (except for the fissure) and the whole hippocampus estimate provided by FreeSurfer’s automated segmentation (“aseg”).

The ROC curves for the AD vs. elderly controls discrimination task are shown in Figure 13, whereas the areas under the curves and accuracies are displayed in Table 7. The ex vivo atlas outperforms the in vivo counterpart, especially around the elbow of the ROC, which is the region where a classifier typically operates. The increment in the AUROC is moderate (1.4%), but statistically significant (p < 0.02). This indicates that the segmentations based on the ex vivo atlas provides more informative estimates of the volumes than those based on the in vivo version. Both the in vivo and the ex vivo atlas outperform the whole hippocampal segmentations, which yields 82% (“aseg”) and 84% (sum of subregions) classification accuracy. The difference in AUROC between the ex vivo atlas and the whole hippocampal segmentations is considerable (5.9% and 4.0%, respectively) and statistically significant (p < 0.01 in both cases). These results indicate that the subregion volumes carry useful information, even when the images display limited contrast on the internal subregion boundaries. Automated segmentations of a test scan are shown in Figure 14.

Figure 13.

ROC curves for the AD discrimination task using a LDA classifier on the hippocampal subregion volumes estimated by our ex vivo atlas (FreeSurfer v6.0) and the in vivo atlas (FreeSurfer v5.3 and earlier), as well as for discrimination based on whole hippocampal volume as estimated by FreeSurfer (“aseg”) and by the ex vivo atlas (adding up the volumes of the subregions).

Table 7.

Accuracy and area under the curve for the AD discrimination task.

Atlas	Accuracy at elbow	AUROC
Whole hippocampus (“aseg”, FreeSurfer v5.3)	82.1%	0.887
Whole hippocampus (adding up the volumes of the subregions)	84.0%	0.901
In vivo (FreeSurfer v5.3)	86.3%	0.917
Ex vivo (this study and FreeSurfer v6.0)	88.0%	0.931

Figure 14.

Automated segmentation of the hippocampal subregions of a sample case from the ADNI T1 dataset (T1-weighted, 1mm isotropic) using FreeSurfer automated segmentation (“aseg”), as well as the in vivo and ex vivo atlases. a) Slices of the segmentation. b) 3D renderings of their shape. The color map is the same as in Figure 2 and Figure 5.

4 Discussion and Conclusion

In this paper we have presented the construction of a statistical atlas of the hippocampus at the substructure level using a combination of ex vivo and in vivo MRI data. Manual annotations of the hippocampal subregions (on ex vivo images) and of the neighboring structures (on in vivo data) were combined into a single atlas using a novel algorithm. Using Bayesian inference, the constructed atlas can be used to automatically segment the hippocampal subregions in in vivo MRI scans. Given thethe generative nature of the framework, the segmentation method is adaptive to MRI contrast and can naturally handle multi-contrast inputs. The segmentation algorithm was validated on three publicly available datasets with varying MRI contrast and resolution (Winterburn, ADNI T1/T2, and ADNI T1). We plan to release the atlas as part of the next release of FreeSurfer, replacing the in vivo atlas of the hippocampal subfield module in the current version of the package (v5.3).

The presented atlas improves previous high-resolution atlases of the hippocampus in several directions. Compared with the in vivo version, the ex vivo atlas was built upon data of much higher resolution, which allowed us to accurately trace the molecular layer with very little dependence on geometric criteria. As a consequence, the atlas yields subregion volumes that better matched values to previously reported histological studies (Simic, Kostovic, Winblad, & Bogdanovic, 1997) (Harding, Halliday, & Kril, 1998). Compared to the ex vivo UPenn atlas presented in (Yushkevich, et al., 2009), we have extended their work in four directions. First, we have scanned the samples at .13mm isotropic resolution on average, which yields voxels four times smaller than those in their atlas. Second, we have modeled a larger number of hippocampal structures (13 vs. 5). Third, we have used a greater number of cases (15 vs. 5). And fourth, our ex vivo atlas models not only the hippocampal formation but also the surrounding structures. This is a critical difference, since it enables us to use the atlas in a Bayesian framework to directly segment in vivo MRI data of arbitrary contrast properties.

We have tested the ability of the volumes derived from automated segmentations given by the atlas to find differences between controls and subjects with MCI and AD. Using high-resolution T2 data, we can reliably fit the atlas to the internal structure to the hippocampus; this was not possible with the previous atlas in FreeSurfer (v5.3 or earlier), which did not model the molecular layer. In a group experiment with MCI subjects and controls, our method reproduced the results of previous manual and semi-automated methods. Moreover, we found differences in the molecular layer and the fimbria, which the aforementioned methods do not segment. Since the molecular layer is a thin structure, it is possible that the lower volume estimates are due to motion artifacts, to which the MCI group is more susceptible. Regarding the fimbria, visual inspection of the images reveals that the appearance of this subregion tends to shift towards that of gray matter in aging and AD. It is important to note that we cannot conclude from our volumetric analysis whether this is a true biological process or the result of motion artifacts.

We also used the atlas to segment standard resolution (1 mm) T1 data. In this case, the molecular layer is not visible, and the fitting of the internal structure of the atlas mostly relies on the prior information encoded in it. Therefore, volumetric results from individual subregions must be interpreted with caution. Still, we hypothesize that the segmentations will be very useful as seed and target regions in functional and diffusion MRI studies, in which the large voxel sizes make the analysis less sensitive to small segmentation errors. Moreover, we have shown that the subregion segmentation carries, despite the lack of internal contrast of the hippocampus, useful information that is not conveyed by its whole segmentation: the ex vivo atlas significantly outperforms the in vivo atlas in the AD classification task, which in turns significantly outperforms the segmentation of the whole hippocampus.

The segmentation algorithm runs in approximately 20 minutes on a desktop computer – approximately twice as long when the input consists of two MRI modalities. This is in contrast with multi-atlas methods which are currently used in hippocampal subregion segmentation – such as (Yushkevich, et al., 2010) – which are intrinsically slow (typically 10–20 hours) due to the need to nonlinearly register a number of atlases to the test scan. On the other hand, our algorithm requires at this point that the data have been processed with the standard FreeSurfer pipeline, which takes approximately 10 hours on a single core.

A limitation of the atlas presented in this study is that, even with ultra-high resolution MRI, there are boundaries that cannot be seen in the training data, e.g., the interfaces between the CA fields along the pyramidal layer of the hippocampus or the CA4/GC-DG interface. This remains an open problem in the hippocampal subregion MRI literature, in which the discrepancy and variability in subregion definitions remains rather large (Yushkevich, et al., 2015). This effect can be immediately noticed by comparing the heterogeneous manual annotations used in works such as (Yushkevich, et al., 2009) (Yushkevich, et al., 2010) (Winterburn, et al., 2013) (Mueller, et al., 2007) (Mueller, Schuff, Yaffe, Madison, Miller, & Weiner, 2010) (Van Leemput, et al., 2009) (Wisse, et al., 2012). Another potential limitation of the proposed atlas is that it was built from manual delineations in elderly subjects only. Therefore, the atlas might include slight hippocampal atrophy that could decrease its applicability to studies of younger populations.

Future work will follow three main directions. First, we will evaluate the usefulness of the segmentations on 1 mm data as seed and target regions on diffusion and functional MRI studies. Second, we plan to extend the atlas to include the hippocampal tail – which will require a careful histologic analysis of the autopsy samples – and also other subcortical structures of interest, such as the thalamic and amygdaloid nuclei. Due to the generative nature of the segmentation framework, we are not constrained to derive the manual delineations from MRI data: histology or optical coherence tomography can be used, too (Augustinack, Magnain, Reuter, van der Kouve, Boas, & Fischl, 2014) (Magnain, et al., 2014). And third, we would like to include explicit models of the partial volume effect, as partial voluming makes it very challenging to accurately describe thin white matter structures such as fimbria, and the molecular layer. In this study, we tackled this problem by guiding the image intensity distributions of these structures with hyperparameters derived from subject-specific simulations of partial voluming. However, we believe that explicitly incorporating the partial volume effect in the model, for instance as in (Van Leemput, Maes, Vandereulen, & Suetens, 2003), will further increase the accuracy of our segmentations.

Highlights.

A highly detailed computational atlas of the human hippocampus built upon ex vivo MRI

Volumes of hippocampal subregions agree well with prior histological studies

Application to Bayesian segmentation of hippocampal subregions from in vivo MRI

The segmentation method is adaptive to MRI contrast and resolution

The atlas and segmentation code will be released as part of FreeSurfer 6.0

Appendix 1

Estimation of Gaussian parameters with missing data

In the segmentation of a multimodal test scan, it can happen that the MRI data for some channels are missing at a given voxel (as in Figure 11b or Figure 12e). In that case, the M step of the Gaussian parameter estimation (Section 3.1) becomes complicated. Instead, we use a generalization of the EM algorithm called “Expectation Conditional Maximization” (ECM) (Meng & Rubin, 1993), in which the M step is replaced by two iterative conditional maximization (CM) steps that update the means and covariance matrices, respectively. Let ${\mathit{y}}_i^o$ and ${\mathit{y}}_i^m$ represent the observed and missing parts of vector y_i, respectively; let ${\mathbf{\mu }}_G^{o(i)}$ and ${\mathbf{\mu }}_G^{m(i)}$ represent the corresponding parts of the mean μ_G; let ${\mathbf{\Sigma }}_G^{o(i)},{\mathbf{\Sigma }}_G^{m(i)}$ represent the corresponding parts of the covariance matrix Σ_G; and let ${\mathbf{\Sigma }}_G^{m,o(i)}$ be the part of the covariance matrix describing the cross-correlation between the observed and missing components of y_i. The update of the mean is then:

$${\mathit{\mu }}_G\leftarrow \frac{{\nu }_G{\mathbf{M}}_G+{\sum }_{i=1}^I{\mathrm{\Omega }}_i^G{\tilde{\mathit{y}}}_i}{{\nu }_G+{\sum }_{i=1}^I{\mathrm{\Omega }}_i^G},\mathit{\text{where}}{\tilde{\mathit{y}}}_i^o={\mathit{y}}_i^o,{\tilde{\mathit{y}}}_i^m={\mathbf{\mu }}_G^{m(i)}+{\mathbf{\Sigma }}_G^{m,o(i)}{\left[{\mathbf{\Sigma }}_G^{o(i)}\right]}^{-1}({\mathit{y}}_i^o-{\mathbf{\mu }}_G^{o(i)}),$$

and the update of the covariance is:

$${\mathbf{\Sigma }}_G\leftarrow \frac{{\sum }_{i=1}^I{\mathrm{\Omega }}_i^G[({\tilde{\mathit{y}}}_i-{\mathit{\mu }}_G){({\tilde{\mathit{y}}}_i-{\mathit{\mu }}_G)}^t+{\tilde{\mathbf{\Psi }}}_i]+{\nu }_G({\mathit{\mu }}_G-{\mathbf{M}}_G){({\mathit{\mu }}_G-{\mathbf{M}}_G)}^t}{{\sum }_{i=1}^I{\mathrm{\Omega }}_i^G},$$

where ỹ_i is defined the same way as above, and the matrix Ψ̃_i has observed and missing parts ${\tilde{\mathbf{\Psi }}}_i^o=0$ and ${\tilde{\mathbf{\Psi }}}_i^m={\mathbf{\Sigma }}_G^{m(i)}-{\mathbf{\Sigma }}_G^{m,o(i)}{\left[{\mathbf{\Sigma }}_G^{o(i)}\right]}^{-1}{\left[{\mathbf{\Sigma }}_G^{m,o(i)}\right]}^t$ (with the part describing their cross correlation equal to zero). The E step of the ECM algorithm is the same as in the EM counterpart, with the difference that the likelihood term is now evaluated as: $p_i({\mathit{y}}_i|\{{\mathit{\mu }}_G,{\mathbf{\Sigma }}_G\})=𝒩[{\mathit{y}}_{\mathit{i}}^{\mathit{o}};{\mathit{\mu }}_{\mathit{G}(l_i)}^{o(i)},{\mathbf{\Sigma }}_{\mathit{G}(l_i)}^{o(i)}]$.

In the specific case that the test has two channels and one of them is always observed – which is the case of the experiments of the ADNI T1/T2 data in Section 3.3, it can be shown (Provost, 1990) that the M step is closed form, which leads to faster convergence of the algorithm. In our implementation of the presented Bayesian segmentation algorithm, we use these update equations whenever it is possible – including the experiments with the ADNI T1/T2 data in this paper.