A Histogram Approach to the Quality of Fit in Sedimentation Velocity Analyses

Abstract

The quality of fit of sedimentation velocity data is critical to judge the veracity of the sedimentation model and accuracy of the derived macromolecular parameters. Absolute statistical measures are usually complicated by the presence of characteristic systematic errors and run-to-run variation in the stochastic noise of data acquisition. We present a new graphical approach to visualize systematic deviations between data and model in the form of a histogram of residuals. In comparison with the ideally expected Gaussian distribution it can provide a robust measure of fit quality and be used to flag poor models.

Sedimentation velocity (SV) analytical ultracentrifugation has re-emerged in the last decade as a popular and powerful physical tool for characterizing nanoscopic particles in a wide range of fields, including the study of biological macromolecules and their interactions [1–5]. This was contributed to, among other factors, by new instrumentation and extended detection limits [6–8], theoretical advances in the sedimentation of interacting systems [9,10], new sedimentation data analysis approaches [11–16], and new computational methods for hydrodynamic modeling [17–19]. Analysis strategies for the global analysis of hydrodynamic data and those of other techniques are expected to further enhance the utility of SV [20–22].

A critical step in the renaissance of SV has been an advance in the mathematical data analysis enabling the direct fitting of raw sedimentation velocity data with explicit models based on solutions of the Lamm equation [23], where macromolecular sedimentation parameters and/or distributions of parameters are calculated and/or refined in non-linear optimization. An obvious criterion for the quality of fit, and the primary optimization objective, is the root-mean-square deviation (rmsd) between experimental data and model.

However, it is not always trivial to judge whether the final best-fit adequately describes the data, or whether extended models should be tested. One of the problems is that the rmsd (or χ²) of the fit, is not necessarily a reliable absolute measure for the quality of fit, due to the common (and sometimes considerable) run-to-run variations in the level of stochastic noise of the data. The noise level can depend, for example, on the lamp emission intensity and buffer absorption properties at the acquisition wavelength when using the absorbance optical system, or on changes in the fringe contrast in the interference optical system, respectively. Thus, an important additional criterion for a satisfactory fit is the lack of systematicity of the residuals. Ideally they should be completely random; this has been quantified rigorously with a runs test [24], where the Z-value reports the number of standard deviations by which the runs of positive or negative residuals differ from the expectation for normally distributed residuals [24]. This is implemented as a default output of SV analyses in the software SEDFIT (https://sedfitsedphat.nibib.nih.gov/software/). But, unfortunately, when applied to SV, the Z-value is overly sensitive in practice. Here, it is useful only as a qualitative comparative measure of fit quality, since SV data are typically subject to considerably systematic errors from data acquisition. For example, even though algebraic noise decomposition techniques [25,26] can account explicitly for time-invariant and radial-invariant signal offsets, respectively, when using the interference optics, fluctuations in the radial baseline profiles can occur from vibrational modes or thermal distortions of the optical path that are not captured in this baseline model. Although the signals from these imperfections in the data acquisition are typically small compared to the macromolecular signal, they can still dominate the residuals in conjunction with a good model of the sedimentation process. This poses the question which criterion of goodness of fit can be used in practice, in addition to the overall rmsd, to examine in a robust way the quality of the sedimentation boundary model.

To this end, we have previously introduced and implemented in SEDFIT a picture representation of the residuals [27], where the time and radial dimension of the SV data are mapped to the row and column number of pixels, respectively, and the magnitude of the residual is mapped onto its grey scale (Figure 1C and G). This takes advantage of the superb sensitivity of the human eye to recognize patterns, and allows systematic misfits of the sedimentation boundary to be identified as diagonal features in a picture that would ideally be neutral grey, distinct from vertical and horizontal features that indicate imperfections in the TI and RI noise model, respectively [27,28]. Mapping residual values onto the color scale in bitmaps solves the problem that a simple overlay of the many radial residual curves for all scans at all times will conceal critical systematic misfits of the sedimentation boundary, even more so when modeling difference curves [14]. This bitmap representation was widely adopted and subsequently utilized also by the software SEDANAL [29] and ULTRASCAN [30].

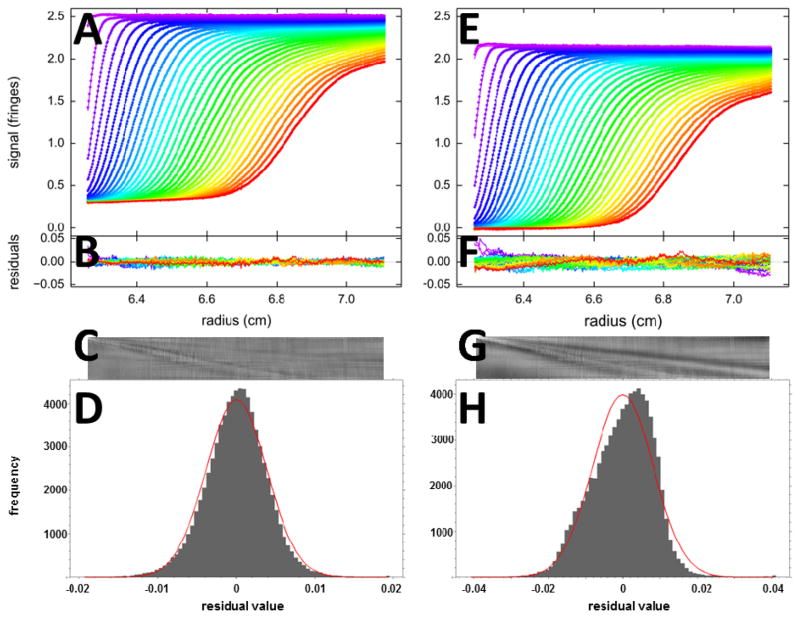
Figure 1.

Fits with two different models for SV data of BSA sedimenting at 50,000 rpm: (A – D) A c(s) analysis leads to a good fit with rmsd of 0.0039 fringes (Z-value 160); (E – H) a two discrete species model leads to an inadequate fit with rmsd of 0.0081 fringes (Z-value 224). The top panels (A, E) show the raw data (points, only every 2^nd scan shown) and best-fit profiles (lines). Panels B and F are an overlay of the residuals, and C and G are the corresponding residual bitmaps (with time indicated by row number, and radius by column number of pixel). The residuals histogram is shown in panels D and H, with the grey bins indicating the frequency of residuals of a certain magnitude, and the red solid line the ideally expected distribution of residuals for normally distributed noise with the same rmsd, leading the H-numbers of 0.6% and 3.2%, respectively.

Yet, even though the complete visual inspection of residuals with the bitmap overview is extremely useful and provides detailed insight in the origin of misfit, its interpretation is entirely qualitative and requires some degree of familiarity with the technique of SV for empirical assessment. It would be desirable to achieve a simpler description that reduces the dimensionality of the residuals into a single curve or a single number that reflects in a robust way on their systematicity. Therefore, we have developed a residuals histogram, where the magnitude of deviation between best-fit model and data, usually comprising 10⁴ – 10⁵ data points, are binned (aiming for ~ 10² – 10³ data points per bin) and compared to the frequency expected for normally distributed noise with the same rmsd (Figure 1D and H). The comparison with a normal distribution is further condensed into a number ‘H’, which is calculated as the sum of square differences between obtained and ideally expected frequencies for a normal distribution, normalized by the sum of squares of the ideal frequencies. These measures are complementary to the bitmap and overall rmsd in that they display the amplitude of residuals and frequency of larger than average deviations, which will be more than normally expected for boundary misfits.

As an illustration, Figure 1 shows two alternative fits of sedimentation velocity profiles of a bovine serum albumin sample. The c(s) model (left panels) results in a sedimentation coefficient distribution where the BSA monomer and dimer represents 95% of all signal, but there are also traces of higher order oligomers and smaller breakdown products (not shown). The rmsd is 0.0039 fringes, which is ~ 0.15% of the total signal, in our experience representing an excellent fit. However, there is a low level of remaining systematicity in the residuals, which may be recognized by a faint diagonal feature in the residuals bitmap (C), in addition to weak vertical and horizontal features indicating instabilities in the fringe pattern. With the 76,000 data points, the low level of systematicity causes the runs of residuals to be already 160 standard deviations removed from the expectation of a normal distribution. The residuals histogram is less detailed and shows frequencies deviating only little from the normal expectation with H = 0.6%.

For comparison, shown in the right panels is an alternative fit from modeling the data with only monomer and dimer species, not accounting for the remaining 5% of trace higher oligomers and breakdown products. (Similar simplified descriptions are often required to enable direct fits the coupled Lamm equations of interacting systems, which are intrinsically discrete models, as opposed to fits with sedimentation coefficient distributions followed by boundary structure analysis [31].) Even though the rmsd is more than twofold that of the good fit, the poor fit cannot be recognized either directly from inspection of the data fit (E) or the residuals overlay (F). The bitmap (G) clearly shows diagonal features corresponding to misfits co-localized with the data points of the moving boundary. In the residual histogram (H), these misfits are clearly highlighted as the substantial deviation from normalcy with an H-value of 3.2%.

We have added the residuals histogram and report of H-values in the default display after fits of SV data in the SEDFIT software. When modeling interference data, we found H-values > 1% to correlate well with inadequate fits. In particular, this value can highlight the effect of unaccounted low amplitude boundaries, such as of trace aggregates. However, in conjunction with data of lower signal/noise ratio it will be less sensitive to imperfections in the model and rather highlight statistical properties of the data acquisition. This, too, can offer useful insights in properties of SV data that are otherwise obscured. For example, in the application to fluorescence optical data the underlying noise distribution is sometimes not Gaussian but exhibits tails. This makes the quantification by the H-value not as useful, but the symmetry and monotonicity of the residual distribution is still a good indicator for the quality of fit. In the meantime, the histogram has to be considered in the context of other measures for the quality of fit, such as the rmsd.

In conclusion, we found the residuals histogram to provide a useful tool to effectively evaluate statistical aspects of data acquisition and fit in a simpler way than bitmaps, robust to common instrumental imperfections, and requiring less technical experience.