Two ways to save a newly learned motor pattern

Abstract

Savings, or faster relearning after initial learning, demonstrates humans' remarkable ability to retain learned movements amid changing environments. This is important within the context of locomotion, as the ability of the nervous system to “remember” how to walk in specific environments enables us to navigate changing terrains and progressively improve gait patterns with rehabilitation. Here, we used a split-belt treadmill to study precisely how people save newly learned walking patterns. In Experiment 1, we investigated savings by systematically varying the learning and unlearning environments. Savings was predominantly influenced by 1) previous exposure to similar abrupt changes in the environment and 2) the amount of exposure to the new environment. Relearning was fastest when these two factors coincided, and we did not observe savings after the environment was introduced gradually during initial learning. In Experiment 2, we then studied whether people store explicit information about different walking environments that mirrors savings of a new walking pattern. Like savings, we found that previous exposure to abrupt changes in the environment also drove the ability to recall a previously experienced walking environment accurately. Crucially, the information recalled was extrinsic information about the learning environment (i.e., treadmill speeds) and not intrinsic information about the walking pattern itself. We conclude that simply learning a new walking pattern is not enough for long-term savings; rather, savings of a learned walking pattern involves recall of the environment or extended training at the learned state.

through experience, we develop a rich repertoire of movements tailored for different environments and situations. This ability requires the capacity to learn new motor patterns and form memories of them that can be quickly called on when reexperiencing the same situation. Many studies have shown that movement patterns acquired via error-based learning or “adaptation” are remembered and retained over time (Kitago et al. 2013; Klassen et al. 2005; Malone et al. 2011; Martin et al. 1996). Importantly, such motor memories are also recalled even after participants unlearn the new motor pattern and return to baseline performance (Caithness et al. 2004; Kitago et al. 2013; Kojima et al. 2004; Krakauer et al. 2005; Malone et al. 2011; Shadmehr and Brashers-Krug 1997). Evidence for motor memory recall is the fact that adaptation occurs faster when participants readapt to a previously experienced situation, a phenomenon commonly referred to as savings.

Savings has been observed robustly in adaptation of reaching movements, walking, and oculomotor control (Burdet et al. 2013; Kojima et al. 2004; Krakauer et al. 2005; Malone et al. 2011; Shadmehr and Brashers-Krug 1997). The ability to save what is learned over time is particularly important within the context of walking, as rehabilitation specialists aim to build on what has been learned previously with repeated therapy sessions. However, the underlying mechanisms for savings remain controversial. Studies using multistate linear time-invariant models explain savings after a brief unlearning session as an interaction between fast and slow learning processes, with the slower process posited to be the basis of savings (Smith et al. 2006). However, these models cannot explain savings observed after prolonged washout (Zarahn et al. 2008). Savings has also been suggested to rely on “model-free” processes, where repetition of a fully adapted movement facilitates faster relearning (Huang et al. 2011). There, the important factors were thought to be use-dependent learning and operant reinforcement of the repeated motor pattern. Still, other findings demonstrate that the training schedule impacts savings (Malone et al. 2011). Repeated, short adaptations alternated with short unlearning sessions lead to greater savings compared with one longer adaptation in which participants spent more time repeating the fully adapted movement. These findings suggested that repeated information about the nature of the environment driving learning seemed essential. Given these conflicting ideas, it is unclear what factors drive savings.

Here, we studied a protocol where people learn, unlearn, and relearn a novel split-belt walking pattern. We systematically varied the learning and unlearning environments to demonstrate that savings is driven by previous exposure to similar abrupt changes in the environment and by the amount of exposure to the new environment. We then demonstrate that humans store explicit information about previously experienced walking environments. Mirroring savings, this information is also affected by prior exposure to abrupt changes in the environment. Our findings indicate that savings of a learned walking pattern is influenced by the environment in which the pattern is learned and is likely dependent on the ability to recognize that a particular environment has been previously encountered.

MATERIALS AND METHODS

Participants

One hundred thirty young persons participated in this study (Experiment 1: n = 70, 23 males, 47 females; mean age ± SD: 22 ± 4 yr; Experiment 2: n = 60, 16 males, 44 females; mean age ± SD: 23 ± 3 yr). No participants were included in both experiments. All participants provided written, informed consent before participating, and protocols were approved by the Johns Hopkins Medicine Institutional Review Board. They were free of any neurological, musculoskeletal, or cardiovascular conditions. Leg dominance was determined by asking the participants which leg they would use to kick a soccer ball.

Protocol

During Experiments 1 and 2, participants walked on a custom-built split-belt treadmill (Woodway USA, Waukesha, WI) with two separate belts, each driven by independently controlled motors. The belt motors were controlled using custom-written MATLAB code (The Mathworks, Natick, MA). Participants began by standing in the middle of the treadmill with one foot on each belt. A thin partition approximately 12 in. tall was placed lengthwise between the belts. This prohibited stepping on both belts simultaneously but did not otherwise interfere with walking. Participants also wore a safety harness that did not provide body weight support. They were informed as to when the treadmill was about to start or stop; however, they were told neither the speed of the belts nor whether changes would occur to the belt speeds during the experiment. The treadmill was stopped briefly (<5 min) between testing sessions (e.g., baseline, adaptation 1, deadaptation, etc.).

Experiment 1.

During Experiment 1, the participants were allowed to hold onto a horizontal handrail in front of them as the belts began moving although they were asked to release the rail and cross their arms as soon as possible (this occurred within the first few seconds after the treadmill was started). While walking, the participants watched a television placed directly in front of them to discourage them from looking downward at the treadmill belts.

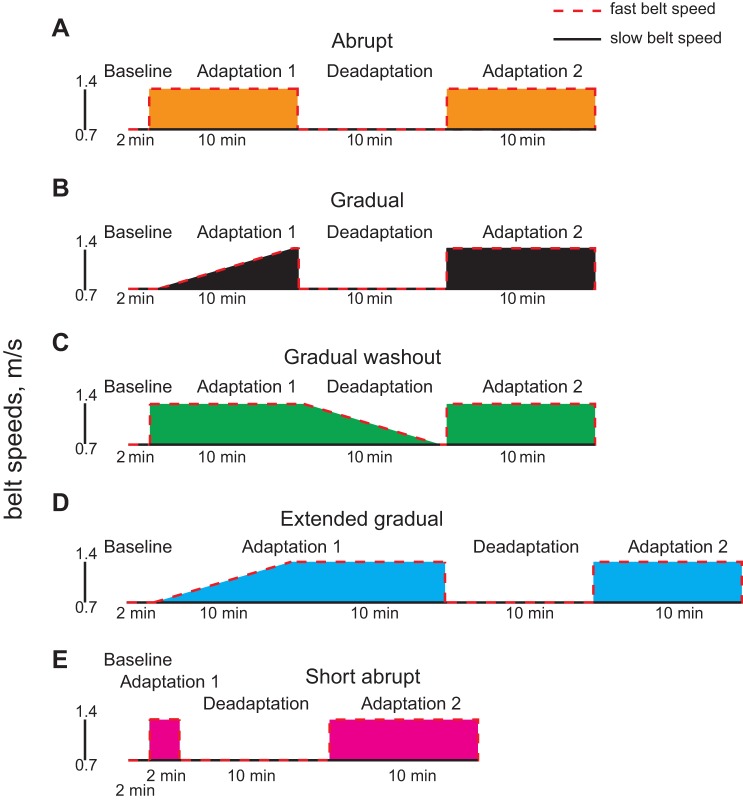
The goal of Experiment 1 was to understand how the ways in which we learn and unlearn new walking patterns influence savings. First, we aimed to examine whether gradually or abruptly introduced environments influence savings. In other words, is simply learning a new walking pattern enough to save or must participants experience an immediate, abrupt change in the environment? We randomly assigned participants into one of two groups: Abrupt (n = 14) or Gradual (n = 14). The protocols are shown in Fig. 1, A and B, respectively. Both groups walked at baseline with the belt speeds tied at 0.7 m/s for 2 min, followed by the 10-min learning session (adaptation 1), the 10-min unlearning session (deadaptation), and the 10-min relearning session (adaptation 2). The lone difference between the groups was that the Abrupt group was exposed to the full 2:1 split in the belt speeds immediately during adaptation 1 (1.4 m/s nondominant limb, 0.7 m/s dominant limb), whereas the Gradual group was exposed to the 2:1 split gradually in a linear fashion over 9 min (with the treadmill speeds updating every second). In the Gradual group, the belts were tied during the first 30 s and moved at the full 2:1 split for the last 30 s. The baseline, deadaptation, and adaptation 2 sessions were identical between the two groups. Baseline consisted of 2 min of walking with both belts moving at 0.7 m/s; deadaptation consisted of 10 min of walking with both belts moving at 0.7 m/s; and adaptation 2 consisted of 10 min of walking with the belts under the nondominant and dominant limbs moving at 1.4 and 0.7 m/s, respectively. Importantly, the environment for adaptation 2 was abrupt and identical across all groups in Experiment 1.

Fig. 1.

Experiment 1 protocol diagrams are shown for the Abrupt (A), Gradual (B), Gradual Washout (C), Extended Gradual (D), and Short Abrupt (E) groups. Dashed and solid lines indicate the speeds of the fast and slow belts, respectively. Colors assigned to each group will remain consistent throughout the figures.

Because we saw markedly better savings in the Abrupt vs. Gradual group (see results), we then tested whether this was attributable to the number of abrupt contextual switches, as the Abrupt participants had more practice making abrupt changes in their gait pattern. Specifically, they experienced three abrupt contextual switches (from baseline to adaptation 1, adaptation 1 to deadaptation, and deadaptation to adaptation 2), whereas the Gradual group experienced only two (from adaptation 1 to deadaptation and deadaptation to adaptation 2). We controlled for the number of abrupt contextual switches by devising a gradual washout protocol (n = 14; Fig. 1C). The participants in the Gradual Washout group experienced the same baseline, adaptation 1, and adaptation 2 sessions as the Abrupt group; the only difference between the two groups was that deadaptation was gradual (i.e., mirroring adaptation 1 in the Gradual group).

We also tested the possibility that the difference in savings between the Abrupt and Gradual groups was attributable to the differing amounts of time that each group experienced the full perturbation during adaptation 1. The Abrupt group experienced the full 2:1 split for 10 min, whereas the Gradual group experienced the full 2:1 split for only the final 30 s. We studied an Extended Gradual group to control for this discrepancy (n = 14; Fig. 1D). The participants in Extended Gradual group adapted gradually over 9 min and were then held at the full 2:1 perturbation for an additional 10 min.

Finally, we designed another group to investigate whether savings in the Abrupt group required the full 10 min or whether simply previously experiencing the abrupt environment was enough. The Short Abrupt group (n = 14; Fig. 1E) experienced the same baseline, deadaptation, and adaptation 2 sessions as the Abrupt group; the only difference between the two groups was that we truncated adaptation 1 from 10 min to 2 min, allowing enough time for the participants to adapt to reach adaptation plateau but limiting the time for reinforcement of the adapted gait pattern.

Experiment 2.

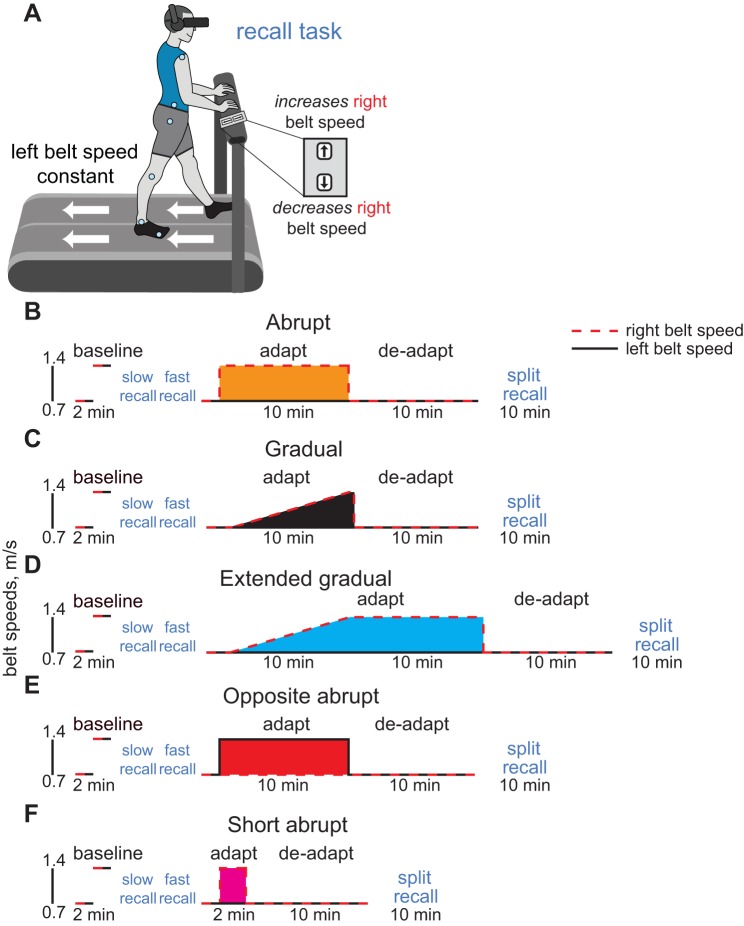
The goal of Experiment 2 was to examine how well participants could explicitly recall the environment experienced during adaptation, as explicit recall could be important for perceiving whether the current environment is similar to a previously experienced environment during relearning. We tested whether people could use a handheld button box to reproduce the adaptation belt speeds after washout. We also tested how the explicit recall of the environment was influenced by the learning environment and whether the participants recalled information about the environment or the resulting gait pattern.

Similar to Experiment 1, participants were randomly assigned to one of two groups: Abrupt (n = 12) or Gradual (n = 12). They were allowed to hold onto the horizontal handrail in front of them throughout the duration of testing and used a button box to change the right belt speed during the recall tasks. First, we asked how well they could recall normal, tied-belt walking patterns after baseline exposures at 0.7 m/s and 1.4 m/s (order randomized). During baseline sessions, a television screen displayed the session number (i.e., Session 1 and Session 2). Immediately following the two baseline sessions, participants performed recall tasks for each session. During the recall tasks, the participants used a handheld button box to make the treadmill move as it did first during Session 1 and then during Session 2 while wearing blinders and noise-canceling headphones to eliminate visual and auditory information about the treadmill (Fig. 2A). The left belt moved at the baseline belt speed (0.7 m/s for the slow recall task, 1.4 m/s for the fast recall task), and the right belt was initially stationary. Participants pushed the “up” button to increase the right belt speed and the “down” button to decrease it. They were informed that they could change the right belt speed as frequently as they liked over the duration of the 2-min task with the goal to make the treadmill belts move as they had during each baseline session.

Fig. 2.

A: general experimental setup for the Experiment 2 baseline and split recall tasks. Participants wore noise-canceling headphones and blinders while using a handheld button box to control the right belt speed of the treadmill. Experiment 2 protocol diagrams are also shown for the Abrupt (B), Gradual (C), Extended Gradual (D), Opposite Abrupt (E), and Short Abrupt (F) groups. The dashed red line indicates the speed of the right belt, whereas the solid black line indicates the speed of the left belt. Blue text indicates that the participant performed a recall task (slow and fast baseline recall tasks were performed in a randomized order across participants within each group).

Following the baseline recall tasks, we tested adaptation. First, participants walked for 2 min with the belts tied at 0.7 m/s to washout any adaptation that may have occurred if they had selected asymmetric speeds during the baseline recall tasks. Participants then adapted for 10 min to a split-belt environment introduced abruptly or gradually (adaptation, or Session 3), deadapted for 10 min (deadaptation, or Session 4), and then performed a 10-min split recall task. During the split recall task, participants in the Abrupt group were asked to make the treadmill move as it did at the “beginning of Session 3.” Participants in the Gradual group were asked to make the treadmill move as it did during “the end of Session 3” to ensure that all participants would attempt to recall how the treadmill was moving when they experienced the full perturbation.

We tested three additional groups (all group protocols shown in Fig. 2, B–F). The Extended Gradual group (n = 12) was used to determine whether differences in speed recall error between the Abrupt and Gradual groups were attributable to the differing amounts of time that each group experienced the full perturbation during adaptation. The Opposite Abrupt group (n = 12) was used to determine whether participants remembered a specific walking pattern or the treadmill speeds regardless of which leg was moving faster. The Opposite Abrupt group adapted to the opposite 2:1 split-belt perturbation compared with the Abrupt group (left fast, right slow). Then, during the recall task, participants were asked to use the button box to make the treadmill move as it did “at the beginning of Session 3, but with the belts switched” (i.e., they should make the right belt move at 1.4 m/s while the left belt moves at 0.7 m/s). We hypothesized that the Opposite Abrupt group should struggle during the split recall task if they attempted to recall a specific walking pattern, because they had not previously walked with the right belt going twice as fast as the left, but should perform well if they attempted to recreate the treadmill speeds irrespective of which leg was on the fast belt. The Short Abrupt group (n = 12) was used to confirm that previous exposure to an abrupt perturbation leads to greater explicit recall during the split recall task irrespective of the length of exposure to the perturbation.

Data Collection

All participants wore comfortable walking shoes and form-fitting clothing to reduce marker movement artifacts. Kinematic data were collected at 100 Hz using Optotrak Certus motion capture hardware (Northern Digital, Waterloo, Ontario, Canada). Active markers were placed bilaterally over the toe (5th metatarsal head), ankle, knee, hip, pelvis, and shoulder. All participants remained on the treadmill throughout the duration of the testing sessions.

Data Analysis

Experiment 1.

During Experiment 1, we calculated one primary measure and two secondary measures. Our primary measure is step length asymmetry, which has previously been shown to adapt robustly to split-belt walking perturbations (Reisman et al. 2005). It is the difference between the lengths of the “fast” and “slow” steps normalized by the sum of the two step lengths as follows: step length asymmetry = [(fast step length − slow step length)/(fast step length + slow step length)]. Fast and slow refer to the nondominant and dominant limbs, respectively. Step length is defined as the distance between the ankle markers along the walking axis at heel strike of each leg.

Step length is a spatiotemporal parameter during treadmill walking (i.e., it relies not only on where the feet land, but also when they land). We calculated two secondary measures, center of oscillation and phasing, to identify the spatial and temporal characteristics of stepping, respectively. These measures are based on the angular movement of the foot relative to the hip, which we define as a limb angle. The center of oscillation is calculated as the limb angle exactly halfway between heel strike and toe-off for each leg (i.e., the limb angle at 50% of stance). A positive center of oscillation value indicates that the limb oscillates about a flexed axis, whereas a negative value indicates that the limb oscillates about an extended axis (a value of 0 indicates that the limb is oscillating about the vertical axis). We then calculated the center of oscillation difference between the two limbs by subtracting the center of oscillation of the slow limb from that of the fast limb (a value of 0 indicates spatial symmetry). Phasing indicates the temporal shift in the movement of one limb relative to the other. We calculated phasing by determining the lag at peak cross correlation of the limb angle trajectories over one stride cycle with the slow limb designated as the reference limb (Choi and Bastian 2007). Phasing values can range from 0 to 1 (0.5 indicates symmetric, out-of-phase walking).

For each of the three measures, we analyzed the data from adaptation 1, deadaptation, and adaptation 2 across three distinct time epochs: the initial perturbation (mean of the first 5 strides), early change (mean of strides 6–30), and plateau (mean of the last 30 strides, with one exception; we calculated the plateau during adaptation 1 in Short Abrupt as the mean of the last 5 strides because only 2 min of data were collected). During adaptation 2, these time epochs allow us to investigate savings by quantifying how the groups differed in initial recall (initial perturbation), accelerated adaptation (early change), and success of adaptation (plateau). It is important to remember that, in this walking task, we assess step length asymmetry by calculating the difference between two consecutive steps. Therefore, unlike reaching, the first stride (i.e., two steps) in adaptation 2 must not necessarily overlay that of adaptation 1. This is because online corrections can be made from the first step to the second to immediately reduce asymmetry. For each measure, we also calculated the mean of all strides collected during baseline.

Experiment 2.

During Experiment 2, we assessed the final right belt speed that the participants selected and the speed recall error (absolute difference between the target and final selected speed) during each of the three recall tasks. Speed recall error removes directional information from the data, thus avoiding issues with calculating mean responses (i.e., 2 participants could select final right belt speeds of 1.0 and 1.8 m/s, and the mean of these data would be equal to the target speed of 1.4 m/s, which would falsely suggest that the participants performed the task accurately).

Statistical Analysis

Experiment 1.

To confirm that no differences existed in baseline walking among the five groups, we first performed one-way ANOVAs to compare baseline performance in all three measures (step length asymmetry, center of oscillation difference, and phasing). To investigate differences among groups during learning, unlearning, and relearning, we looked at three epochs (initial perturbation, early change, and plateau) during each session of the experiment (adaptation 1, deadaptation, and adaptation 2) using separate one-way ANOVAs. Note that we were not able to compare adaptation 1 to adaptation 2 within each group because some participants received gradual perturbations in adaptation 1 (thus savings could not be assessed using that comparison). The α-level for the ANOVAs was set at P = 0.05.

Given that each group experienced different belt speed configurations during adaptation 1 and deadaptation (i.e., some adapted or deadapted abruptly, others gradually), there was no reasonable null hypothesis that all groups should perform similarly during these testing sessions. For this reason, we used Tukey's honest significant difference tests as post hoc analyses to compare the performance of each group to all other groups during adaptation 1 and deadaptation. However, all participants experienced the same belt speed configuration (abrupt adaptation) during adaptation 2. Here, we used Dunnett's tests as post hoc analyses to test each group's performance against the null hypothesis that savings did not occur (as we observed in the Gradual group). In other words, a significant difference compared with the Gradual group during adaptation 2 indicated that savings occurred.

We were also interested in knowing whether the behavior at the end of adaptation 1 and deadaptation (i.e., plateaus) predicted savings during adaptation 2. We performed a linear regression to determine whether group membership or plateaus during adaptation 1 and deadaptation predicted the initial perturbation during adaptation 2. Dummy variables were used for each group, with the Gradual group treated as the reference because these participants exhibited no savings.

Finally, we performed Pearson's correlations to investigate relationships between step length asymmetry and both center of oscillation difference and phasing during initial perturbation of adaptation 2 to understand whether savings of step length asymmetry was associated with savings of spatial or temporal gait parameters, respectively. The α-level for both analyses was set at P = 0.05. SPSS 17.0 (IBM, Armonk, NY) was used for all statistical analyses.

Experiment 2.

A Shapiro-Wilk test indicated that the final right belt speed and speed recall error data were not normally distributed; thus, we performed a series of Kruskal-Wallis H-tests to investigate differences among groups in the final right belt speed and speed recall error at the end of each of the three recall tasks. The α-level was set at P = 0.05, and post hoc analyses were performed using Mann-Whitney U-tests.

RESULTS

Experiment 1

All participants performed the walking tasks without difficulty. All groups walked similarly at baseline; we did not observe main effects of group on step length asymmetry [F_(4,65) = 0.92, P = 0.46], center of oscillation difference [F_(4,65) = 0.26, P = 0.90], or phasing [F_(4,65) = 0.63, P = 0.65].

We then checked to see whether there were differences in adaptation 2 across the groups because this is the session of most interest. We observed significant differences in savings among groups during the initial perturbation [step length asymmetry (F_(4,65) = 7.63, P < 0.001), center of oscillation difference (F_(4,65) = 2.93, P = 0.03), and phasing (F_(4,65) = 4.5, P = 0.003)]. This difference persisted during the early change epoch as well as for step length asymmetry [F_(4,65) = 5. 68, P = 0.0006] and center of oscillation difference [F_(4,65) = 4.4, P = 0.003] but not phasing [F_(4,65) = 0.7, P = 0.59]. Finally, all groups eventually reached the same plateau, indicating that they were able to successfully reduce errors to a similar extent (all P > 0.15). We now describe specific results and comparisons among the groups.

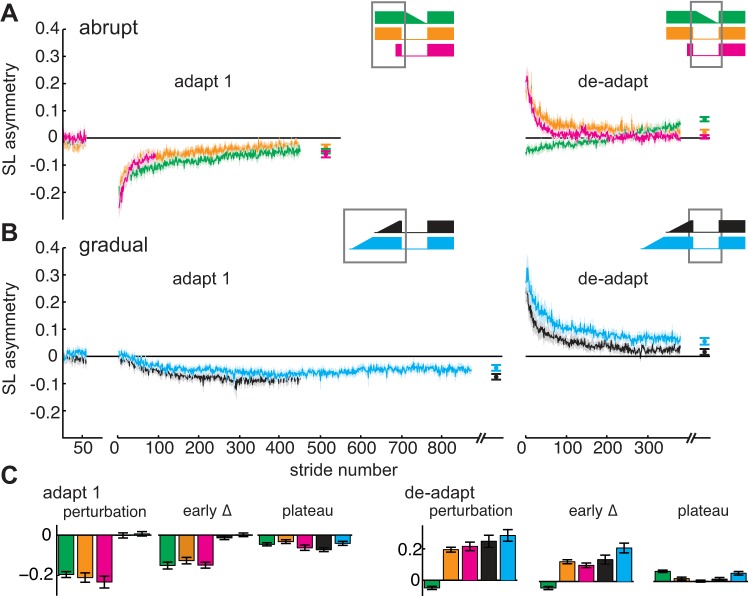
The Abrupt group demonstrated significantly larger step length asymmetry than the Gradual group during the initial perturbation (P < 0.001) and the early change (P < 0.001) of adaptation 1 (Fig. 3, A and B, orange and black lines, respectively). This was not surprising considering that gradual adaptation resulted in small errors, whereas abrupt adaptation resulted in large errors. ANOVA revealed a nonsignificant trend toward a main effect of group on the plateau of adaptation 1 [F_(4,65) = 2.31, P = 0.07] that was driven largely by the comparison between the Abrupt and Gradual groups. The Gradual group exhibited larger residual step length asymmetry at the end of adaptation 1, suggesting that they did not fully compensate for the perturbation. This finding was also not unexpected, as similar results were observed during an upper extremity gradual adaptation task (Klassen et al. 2005).

Fig. 3.

Comparison of step length (SL) asymmetry during baseline, adaptation 1, and deadaptation among groups that adapted abruptly (Abrupt, orange; Gradual Washout, green; Short Abrupt, pink) (A) and adapted gradually (Gradual, black; Extended Gradual, blue) (B). Mean curves across participants within each group ± SE are shown. The curves are truncated in length to match the participant that took the fewest strides during each condition. Data points immediately following each adaptation 1 and deadaptation curve show the step length asymmetry during plateau (mean ± SE of the last 30 strides) for each group. Note that the adaptation 1 plateau for the Short Abrupt group was calculated as the mean of the last 5 strides. C: column graphs are shown indicating step length asymmetry during initial perturbation (mean of the first 5 strides), early change (mean of strides 6–30), and plateau of adaptation 1 (left) and deadaptation (right) for each group (mean ± SE). Gray boxes around the protocol diagrams included on the top right of each set of curves outline the portions of the protocol from which the data are presented. The statistical analyses are included in results.

Interestingly, we observed that the Abrupt and Gradual groups exhibited similar step length asymmetry patterns during deadaptation (Fig. 3, A and B, orange and black lines); there were no significant differences between the groups in initial perturbation, early change, or plateau (all P > 0.05). These findings indicate that, although the Abrupt group experienced the full 2:1 split for 10 min, whereas the Gradual group experienced the full perturbation for only 30 s, both groups stored the walking pattern similarly into deadaptation.

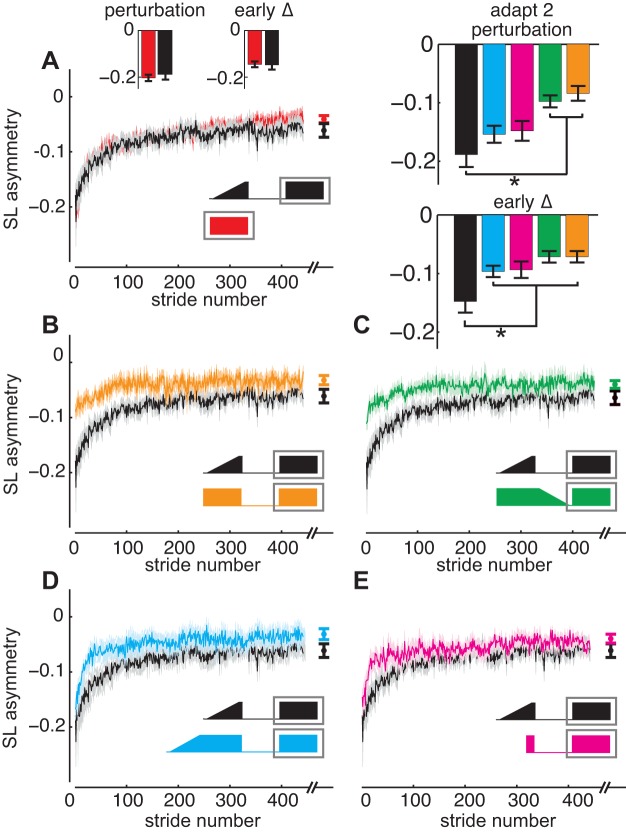
Conversely, the Gradual and Abrupt groups exhibited markedly different patterns during adaptation 2 (Fig. 4B). The Gradual group exhibited significantly lesser savings, as evidenced by the larger step length asymmetry observed during initial perturbation (P < 0.001) and early change (P < 0.001) compared with the Abrupt group. To investigate whether the Gradual group showed savings of the adapted walking pattern at all during adaptation 2, we also compared this data to naïve adaptation data (i.e., the adaptation 1 data from the 28 participants in the Abrupt and Gradual Washout groups; Fig. 4A). We found that savings did not occur in the Gradual group, as we did not observe significant differences in step length asymmetry during initial perturbation, early change, or plateau between naïve performance and the Gradual group during adaptation 2 (Fig. 4A; all P > 0.05).

Fig. 4.

Comparison of step length asymmetry during adaptation 2 (i.e., savings). Mean curves across participants within each group ± SE are shown. Note that the curves are truncated in length to match the participant that took the fewest strides during adaptation 2. Rows of plots are organized to indicate groups exhibiting no savings (top), savings during both initial perturbation and early change (middle), and savings during early change but not initial perturbation (bottom). Differences among groups during initial perturbation and early change are shown in the column graphs in the top right. A: Gradual (black) is compared with naïve abrupt adaptation data from the 28 participants in Abrupt and Gradual Washout during adaptation 1 (red). Embedded above the curves are column graphs indicating step length asymmetry during initial perturbation and early change. As Gradual performed similarly to naïve adaptation (i.e., no savings), we show all other groups relative to Gradual in B–E to demonstrate savings. Gray outlines behind the protocol diagrams included on the top right of each set of curves outline the portion of the protocol from which the data are presented. B: Abrupt (orange) is compared with Gradual (black). C: Gradual Washout (green) is compared with Gradual (black). D: Extended Gradual (blue) is compared with Gradual (black). E: Short Abrupt (pink) is compared with Gradual (black). Mean ± SE plateau values are plotted after each curve. There were no significant differences among groups in plateau during adaptation 2. *P < 0.05.

We next addressed the possibility that the differences in savings we observed between the Abrupt and Gradual groups were influenced by the number of abrupt contextual switches each group experienced. The Abrupt group experienced three abrupt switches (baseline to adaptation 1, adaptation 1 to deadaptation, deadaptation to adaptation 2), whereas the Gradual group experienced only two (adaptation 1 to deadaptation, deadaptation to adaptation 2). We did not observe any significant differences in initial perturbation, early change, or plateau step length asymmetry during adaptation 1 between the Abrupt and Gradual Washout groups (Fig. 3A, orange and green lines, respectively; all P > 0.05). Not surprisingly, we did observe significantly smaller step length asymmetry during initial perturbation and early change during deadaptation in the Gradual Washout group compared with the Abrupt group (both P < 0.001). However, the Gradual Washout group deadapted slightly beyond baseline compared with the Abrupt group (P = 0.006).

During adaptation 2, the Gradual Washout group exhibited savings similar to the Abrupt group. We observed significant differences in initial perturbation and early change step length asymmetry when comparing the Gradual Washout and Gradual groups (Fig. 4C; both P < 0.001). These findings suggest that previous experience making abrupt contextual switches alone does not affect savings, but rather keeping the introduction of the perturbation consistent between adaptation sessions (e.g., adapting abruptly from tied belts to split belts during the transitions from both baseline to adaptation 1 and deadaptation to adaptation 2) increases savings.

We then addressed the possibility that the differences in savings we observed between the Abrupt and Gradual groups were influenced by the amount of time each group experienced the full perturbation (i.e., the Abrupt group experienced the full 2:1 ratio for 10 min during adaptation 1, whereas the Gradual group experienced the full 2:1 ratio for only the final 30 s of adaptation 1). The Extended Gradual group performed similarly to the Gradual group during adaptation 1; there were no differences in step length asymmetry during initial perturbation, early change, or plateau (Fig. 3B, blue and black lines, respectively; all P > 0.05). During deadaptation, there was larger step length asymmetry during initial perturbation in the Extended Gradual group compared with the Gradual Washout groups (P < 0.001) but not the Abrupt or Gradual group (P = 0.16 and P = 0.88, respectively). The early change was larger in the Extended Gradual group compared with the Gradual, Abrupt, and Gradual Washout groups (all P < 0.05). Step length asymmetry during plateau in the Extended Gradual group was larger compared with the Gradual group (P = 0.04) but similar to the Abrupt and Gradual Washout groups (P = 0.08 and P = 0.87, respectively).

During adaptation 2, the Extended Gradual group showed intermediate savings. Step length asymmetry in the Extended Gradual group was similar to the Gradual group during initial perturbation (Fig. 4D; P = 0.332) but smaller during early change (Fig. 4D; P = 0.03). Thus the Extended Gradual group did not immediately adapt to the perturbation during adaptation 2 but adapted quickly during early change. Accordingly, we postulated that introducing the perturbation similarly in adaptation 1 and adaptation 2 (e.g., perturbation introduced abruptly during both) facilitates recall of the initial perturbation, whereas reinforcement facilitates faster adaptation during adaptation 2 (as evidenced by the differences among groups in early change).

However, it remained unclear whether introducing the perturbation similarly during adaptation 1 and adaptation 2 facilitated recall of the initial perturbation only if the perturbation was followed by reinforcement during adaptation 1 (i.e., the Abrupt and Gradual Washout groups were introduced to the perturbation abruptly during adaptation 1 and adaptation 2, but both also experienced reinforcement following the perturbation during adaptation 1 in the form of 10 min of split-belt walking). Thus we devised the Short Abrupt group to address the question of whether reinforcement must follow the perturbation during adaptation 1 to facilitate savings, even if the perturbations are introduced abruptly during both adaptation 1 and adaptation 2.

During adaptation 1, there were no significant differences in step length asymmetry during initial perturbation, early change, or plateau among the Abrupt, Gradual Washout, and Short Abrupt groups (all P > 0.05; note that the plateau session was truncated to the last five strides of adaptation 1 for the Short Abrupt group as opposed to last 30 strides in the Abrupt and Gradual Washout groups). These findings indicate that all three groups that experienced an abrupt perturbation during adaptation 1 adapted similarly (Fig. 3A, orange, green, and pink lines), and, importantly, the Short Abrupt group reached the same plateau as the Abrupt and Gradual Washout groups. During deadaptation, step length asymmetry during initial perturbation in the Short Abrupt groups was similar to the Abrupt, Gradual, and Extended Gradual groups (all P > 0.05). Step length asymmetry during early change and plateau was smaller in the Short Abrupt group compared with the Extended Gradual group (P = 0.004 and P = 0.002, respectively) but not the Abrupt or Gradual groups (all P > 0.05).

During adaptation 2, the Short Abrupt group surprisingly also exhibited intermediate savings. In the Short Abrupt group, step length asymmetry was similar to the Gradual group during initial perturbation (P = 0.21, Fig. 4E) but smaller than the Gradual group during early change (P = 0.02). Thus the Short Abrupt group showed savings that was similar to the Extended Gradual group.

These findings confirm that neither introducing the perturbation abruptly during adaptation 1 and adaptation 2 nor providing sufficient reinforcement during adaptation 1 are alone sufficient for greatest savings. Rather, greatest savings is observed when the perturbation is introduced abruptly during adaptation 1 and adaptation 2 and the learned walking pattern is reinforced during adaptation 1.

Looking Beyond Group Effects: What Other Factors Influence Initial Perturbation During Adaptation 2?

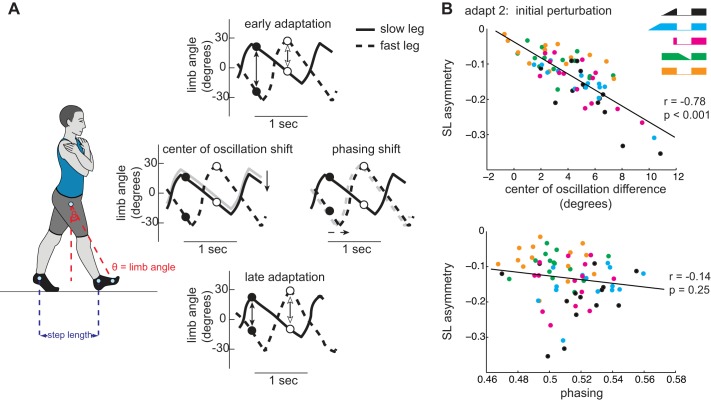
As many of our findings indicated differences among groups in initial perturbation during adaptation 2, we wondered whether factors beyond group assignment contributed to these differences. We performed a pair of Pearson's correlations to investigate how savings in spatial and temporal parameters relate to savings in step length asymmetry. Figure 5A shows example limb angles plotted as a function of time to demonstrate how spatial (e.g., center of oscillation difference) and temporal (e.g., phasing) gait parameters contribute to step length asymmetry and change over the course of split-belt adaptation (Malone and Bastian 2010). When correlating initial perturbation of step length asymmetry with initial perturbation of center of oscillation difference and phasing during adaptation 2 across the participants in all five groups, we observed a significant relationship between step length asymmetry and center of oscillation difference (Fig. 5B, top; r = −0.78, P < 0.0001) but not between step length and phasing (Fig. 5B, bottom; r = −0.14, P = 0.25). Hence, savings of step length asymmetry was related to savings of spatial not temporal information.

Fig. 5.

A: visual example for step length and limb angle calculations (far left) and example limb angles plotted as a function of time to demonstrate how spatial (e.g., center of oscillation difference) and temporal (e.g., phasing) gait parameters change from early adaptation (top) to late adaptation (bottom). Middle left shows a spatial shift, and middle right shows a temporal shift, with the gray lines indicating the original limb angle traces shown in the top diagram and the black lines indicating the limb angle traces after either a spatial (left) or temporal (right) shift. Black and white circles indicate the limb angles at slow leg heel strike and fast leg heel strike, respectively. Black and white arrows represent angular spread at heel strike of the slow and fast leg, which is analogous to step length. Note how the relative asymmetry in the size of the arrows during early adaptation is reduced by altering the spatial and temporal relationships between the 2 limbs. B: center of oscillation (top) and phasing (bottom) plotted against step length asymmetry during initial perturbation of adaptation 2. Pearson's correlation coefficients and corresponding P values are also presented for each comparison.

We also performed a linear regression to evaluate whether plateau during adaptation 1 and deadaptation predicted step length asymmetry during initial perturbation of adaptation 2 independently of group assignment (i.e., does step length asymmetry at the end of adaptation 1 or deadaptation predict step length asymmetry at the beginning of adaptation 2?). We treated the Gradual group as the reference group (adaptation 2 in this group was not significantly different from naïve adaptation). The full regression model is shown as follows: adaptation 2 initial perturbation = β₁ (adaptation 1 plateau) + β₂ (deadaptation plateau) + β₃ (Abrupt group) + β₄ (Extended Gradual group) + β₅ (Gradual Washout group) + β₆ (Short Abrupt group), with all group variables holding values of either 1 or 0.

When plateau during adaptation 1 and plateau during deadaptation were both included with group assignment as predictors, we observed that step length asymmetry during plateau of adaptation 1 (but not deadaptation) was a significant predictor of step length asymmetry during initial perturbation of adaptation 2 (β₁ = 0.599, P = 0.002). Importantly, dummy variables for assignment to the Abrupt and Gradual Washout groups were significant predictors in the same model (β₃ = 0.080 and β₅ = 0.072, P = 0.001 and P = 0.002, respectively). In other words, these groups exhibited step length asymmetry during initial perturbation of adaptation 2 that was significantly different from the reference group, Gradual, even after controlling for step length asymmetry during plateau of adaptation 1 and deadaptation. A subsequent stepwise regression revealed the same three significant predictors. Thus the differences we observed in savings among groups are influenced by both group assignment and step length asymmetry during plateau of adaptation 1.

Experiment 2

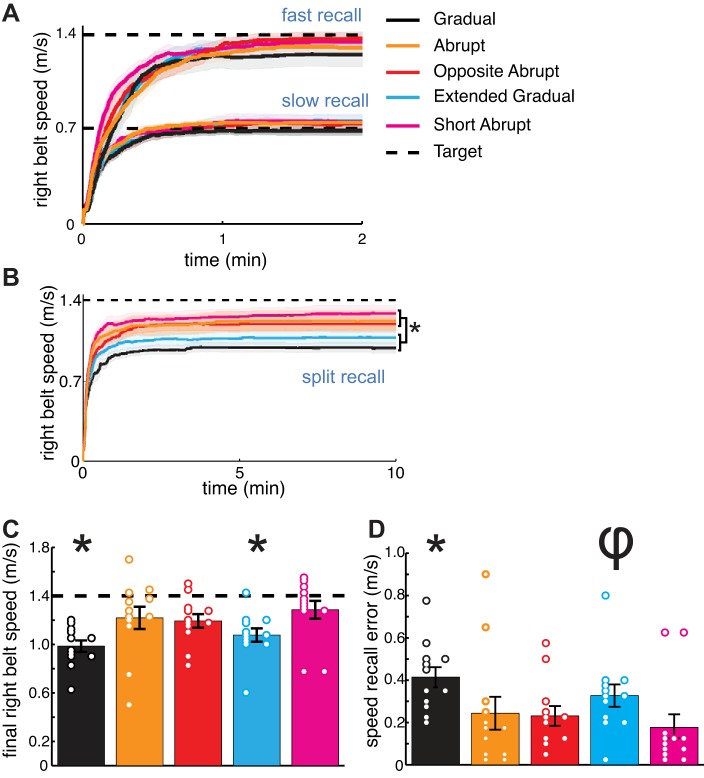
In Experiment 2, we investigated how well the participants could explicitly recall the environment experienced during adaptation 1 after the learned gait pattern was washed out. The Kruskal-Wallis H-tests revealed significant effects of group on speed [χ²(4) = 16.7, P = 0.002] and speed recall error [χ²(4) = 15.2, P = 0.004] during the split recall task. However, we did not observe significant group effects during the slow [speed: χ²(4) = 2.01, P = 0.73, speed recall error: χ²(4) = 3.27, P = 0.51; Fig. 6A, bottom] or fast [speed: χ²(4) = 0.89, P = 0.93, speed recall error: χ²(4) = 1.78, P = 0.78; Fig. 6A, top] recall tasks. During the split recall task, the Abrupt group demonstrated faster speeds (P < 0.01, Fig. 6, B and C) and smaller speed recall error (P = 0.01, Fig. 6D) compared with the Gradual group. The Abrupt group also demonstrated faster speeds (P = 0.03) and marginally smaller speed recall error (P = 0.06) compared with the Extended Gradual group. Interestingly, speed and speed recall error were similar between the Abrupt, Opposite Abrupt, and Short Abrupt groups (all P > 0.13; the Opposite Abrupt and Short Abrupt groups also showed faster speeds and smaller speed recall error compared with the Gradual group, with all P < 0.05). Speed and speed recall error were also similar between the Gradual and Extended Gradual groups (both P = 0.19).

Fig. 6.

A: right belt speed data for each group during the fast and slow baseline recall tasks (curves show group mean ± SE). We did not observe differences among groups in the right belt speed selected during either baseline recall task. B: right belt speed data for each group across the entire time course of the split recall task. At the end of the task, we observed that the Gradual (black) and Extended Gradual (blue) groups selected significantly slower right belt speeds compared with the Abrupt (orange), Opposite Abrupt (red), and Short Abrupt (pink) groups (*P < 0.05). C: columns indicate the final right belt speeds selected during the split recall task for each group (mean ± SE). These data are equivalent to the data at the 10-min mark in B. Open circles show individual participant data. Note that all but 1 of the participants in the Gradual and Extended Gradual groups underestimated the target speed. *Significant difference from the Abrupt, Opposite Abrupt, and Short Abrupt groups with P < 0.05. D: Columns indicate the speed recall error during the split recall task for each group (mean ± SE). *Significant difference from the Abrupt, Opposite Abrupt, and Short Abrupt groups with P < 0.05; φtrend level difference from the Abrupt, Opposite Abrupt, and Short Abrupt groups with P = 0.06.

These findings indicate quite clearly that the Abrupt and Short Abrupt groups more accurately recalled the environment that they had walked in during adaptation compared with the Gradual and Extended Gradual groups. Thus participants in the Gradual and Extended Gradual groups more drastically underestimated the difference in belt speeds during adaptation, recalling a perturbation that was smaller than the actual perturbation during split-belt adaptation. We think that this inaccurate perception of the environment contributed to the reduced savings we observed in these groups during the initial perturbation of adaptation 2 in Experiment 1. In other words, it seems likely that relearning was slower in the Gradual and Extended Gradual groups because these participants did not immediately perceive that the environments experienced during adaptation 1 and adaptation 2 were similar. On the other hand, previous exposure to an abrupt perturbation leads to a lasting, more accurate perception of the learning environment (as observed in the Abrupt and Short Abrupt groups). The results from the Opposite Abrupt group provide further evidence that people, not only learn a new walking pattern during split-belt adaptation, but also acquire and store information about the learning environment itself.

DISCUSSION

The human nervous system is remarkably adept at learning, storing, and recalling walking patterns for use in a diverse range of environments. These processes not only orchestrate our ability to safely and efficiently explore and navigate constantly changing surroundings, but also are crucial to making progressive improvements in dysfunctional gait patterns with rehabilitation. Here, we provide new information about how long-term motor memories of new walking patterns are formed. We first uncovered two key factors that drive savings of a learned walking pattern, 1) exposure to abrupt changes in the environment and 2) the amount of exposure to the new environment. These two factors also led to savings independently of one another although relearning was slower when they did not coincide (e.g., the Extended Gradual and Short Abrupt groups). All groups saved primarily spatial (e.g., center of oscillation) but not temporal (e.g., phasing) information about the new gait pattern. We next revealed that humans store explicit information about walking environments that can be used to facilitate faster recall of appropriate gait patterns. Critically, exposure to abrupt changes in the environment led to greater accuracy of this explicit information, whereas the amount of exposure to the new environment did not. Our collective findings suggest that savings of a learned walking pattern is dependent on multiple interactive yet distinct processes, including the ability to perceive that a given environment has been experienced previously and repetition of the new gait pattern.

We first showed that gradual learning without repetition does not result in savings of an adapted gait pattern. As the Gradual and Abrupt groups learned the gait pattern similarly (i.e., they showed similar aftereffects during deadaptation), why doesn't the Gradual group exhibit savings? We found that an abrupt (2:1 speed difference) change in the walking environment engages neural processes to acquire and store explicit knowledge about the new environment. This allows the nervous system to quickly recall an appropriate gait pattern if it immediately detects that the walking environment has been experienced previously; if not, it must start from scratch and learn to walk in the new environment. This idea explains the diminished savings observed in the Extended Gradual and Gradual groups quite well, as these groups failed to store accurate information about the initial learning environment and subsequently relearned the gait pattern at a slower rate. Our hypothesis also explains why our results are not consistent with previous studies that have shown certain learning phenomena (e.g., aftereffects and retention) to be similar following gradual and abrupt adaptation (Hussain and Morton 2014; Klassen et al. 2005; Kluzik et al. 2008; Sawers et al. 2013; Torres-Oviedo and Bastian 2012). These previously reported phenomena notably do not involve two identical exposures to a novel environment (as the environment simply returns to a familiar baseline during unlearning and does not change at all during retention). However, abrupt adaptation results in greater interlimb transfer (Malfait and Ostry 2004), a process that does involve two identical exposures to a novel environment (the same perturbation is applied across limbs). Thus learned movement patterns are saved and transferred within the context of a specific perceived environment; simply having previously learned the pattern is not enough to readily recall it.

We also demonstrated that savings during split-belt treadmill walking can be facilitated by prolonged repetition of the adapted gait pattern once performance has plateaued. It seems obvious that the ability of the nervous system to detect a previously experienced environment is of little use unless a learned walking pattern is associated with the environment. Thus we hypothesize that repetition at plateau affects savings by strengthening the association between the adapted walking pattern and the perceived environment. For instance, the participants that had previously experienced repetition but not an abrupt perturbation (i.e., the Extended Gradual group) exhibited savings but only after sufficient information was obtained during the second adaptation session to conclude that the environments were indeed similar. Likewise, participants that initially adapted abruptly but with limited repetition (i.e., the Short Abrupt group) likely recognized that the environments were similar during both adaptation sessions (as supported by the results of Experiment 2) but did not immediately recall the adapted walking pattern, as it had not yet been reinforced for the specific environment through repetition.

Our findings from Experiment 2 show that abrupt and gradual adaptation result in different internal representations of the learning environment. These results are consistent with previous notions that learning from abrupt or gradual perturbations is driven by fundamentally different processes. For instance, in upper extremity motor learning, it is thought that adaptation to an abrupt perturbation is driven by feedforward motor planning, whereas adaptation to a gradual perturbation is more reliant on feedback control (Saijo and Gomi 2010). This idea that abrupt adaptation is more cognitively demanding is also substantiated within the gait adaptation literature (Sawers et al. 2013). Here, our results offer an explanation as to why abrupt adaptation should indeed be more cognitively challenging. We have shown that, during abrupt adaptation, the nervous system acquires explicit information about the change in the environment that is used not only to adapt to the new environment, but also to remember the environment in case it reappears in the future. However, the acquisition of explicit information about the walking environment occurs to a much lesser extent during gradual adaptation.

To our knowledge, the findings presented in this study cannot be explained by existing computational models of motor adaptation. It is clear that multistate linear time-invariant models are not sufficient, as they are only able of accounting for savings following very short washout sessions (Smith et al. 2006; Zarahn et al. 2008). Furthermore, models that utilize estimations of the sources of errors (e.g., body or world) and their relevance predict savings after gradual adaptation (Berniker and Kording 2011). This finding was not observed in the present study. Finally, current multistate linear time-varying models would predict that, as long as performance has returned to baseline by the end of washout, all groups should exhibit the same initial perturbation during the second adaptation session (Mawase et al. 2014; Zarahn et al. 2008). This prediction is also not supported by our results.

It is likely that the two ways to save a walking pattern identified here are influenced by multiple neural structures. First, we think that the prefrontal cortex and cerebellum may be important for detecting that two environments are identical and triggering recall of the adapted gait pattern. The cerebellum is necessary for updating a forward model to drive locomotor adaptation (Jayaram et al. 2011, 2012; Morton and Bastian 2006). It also plays a role in savings, as anodal stimulation of the cerebellum during initial adaptation accelerates both learning and relearning during visuomotor adaptation (Galea et al. 2011). On the other hand, we suspect that the prefrontal cortex could be important for detecting a change in the environment and identifying it as being either similar or dissimilar to a previously experienced environment. Studies of visuomotor adaptation support this hypothesis, as the prefrontal cortex is important for perturbation detection and early adaptation (Anguera et al. 2010; Seidler and Noll 2008; Slachevsky et al. 2001, 2003). Furthermore, the prefrontal cortex plays a role in explicit learning, and adaptation has been recently suggested to have a more profound explicit component than previously thought, particularly early on (Taylor et al. 2014). However, it should be noted that walking is more automatic compared with upper extremity movements; thus, the exact role of the prefrontal cortex in locomotor adaptation and learning has yet to be elucidated.

We suspect that the basal ganglia could also contribute to savings of a learned gait pattern, particularly when repetition of the adapted gait pattern is provided. These nuclei are widely assumed to play a role in reinforcement learning (Ito and Doya 2011), and repetition-dependent mechanisms appear crucial for savings here and following visuomotor adaptation (Huang et al. 2011). Indeed, persons with basal ganglia disorders have demonstrated impairments in savings of adapted upper extremity movements (Bédard and Sanes 2011; Marinelli et al. 2009). However, persons with Parkinson's disease recently demonstrated at least partial savings during split-belt treadmill walking even when withdrawn from dopaminergic medication (Roemmich et al. 2014a, 2014b). Thus it is unclear whether the basal ganglia play a differential role in locomotor and visuomotor adaptive learning.

Our study is not without limitations. First, the Gradual Washout group did not experience the same 10-min tied-belt washout period that the other groups experienced. Although the Gradual Washout group washed out to a plateau that was not significantly different from other groups studied (e.g., the Extended Gradual group) and our regression found that deadaptation plateau was not a significant predictor of savings, it is possible that the number of contextual switches might influence savings if the washout period were extended. Although our statistical analyses largely failed to detect differences among groups in adaptation 1 plateau, it also appears that there may be some subtle qualitative differences in these values. A study designed and powered to focus on the performance of these groups during adaptation 1 rather than on savings (as in the present study) may be of interest.

In this study, we demonstrated that savings of a learned gait pattern is driven by 1) previous exposure to similar abrupt changes in the environment and 2) the amount of exposure to the new environment. These two factors must cooccur for maximal savings although savings was present to a lesser degree when they occur independently of one another. We also showed that persons acquire and store explicit information about walking environments and may use this information to facilitate faster adaptation upon subsequent exposures to the same environment. Our future work will attempt to ascertain specific neural mechanisms involved in savings during split-belt treadmill walking. Ultimately, we aim to use this information to facilitate savings of learned walking patterns in populations characterized by gait disorders.

GRANTS

This work was supported by National Institutes of Health grant F32 NS090751 to R. T. Roemmich and National Institutes of Health grant R01 HD048741 to A. J. Bastian.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

Author contributions: R.T.R. and A.J.B. conception and design of research; R.T.R. performed experiments; R.T.R. analyzed data; R.T.R. and A.J.B. interpreted results of experiments; R.T.R. and A.J.B. prepared figures; R.T.R. and A.J.B. drafted manuscript; R.T.R. and A.J.B. edited and revised manuscript; R.T.R. and A.J.B. approved final version of manuscript.