Planning multiple movements within a fixed time limit: The cost of constrained time allocation in a visuo-motor task

Abstract

S.-W. Wu, M. F. Dal Martello, and L. T. Maloney (2009) evaluated subjects' performance in a visuo-motor task where subjects were asked to hit two targets in sequence within a fixed time limit. Hitting targets earned rewards and Wu et al. varied rewards associated with targets. They found that subjects failed to maximize expected gain; they failed to invest more time in the movement to the more valuable target. What could explain this lack of response to reward? We first considered the possibility that subjects require training in allocating time between two movements. In Experiment 1, we found that, after extensive training, subjects still failed: They did not vary time allocation with changes in payoff. However, their actual gains equaled or exceeded the expected gain of an ideal time allocator, indicating that constraining time itself has a cost for motor accuracy. In a second experiment, we found that movements made under externally imposed time limits were less accurate than movements made with the same timing freely selected by the mover. Constrained time allocation cost about 17% in expected gain. These results suggest that there is no single speed–accuracy tradeoff for movement in our task and that subjects pursued different motor strategies with distinct speed–accuracy tradeoffs in different conditions.

Introduction

Recently, Wu, Dal Martello, and Maloney (2009) investigated a visuo-motor task where subjects were required to plan not one but two movements in rapid succession within a fixed time limit. Examples of the sequential movement task of Wu et al. are diagrammed in Figures 1A and 1B. Before movement initiation, the subject has as much time as desired to view the targets and plan the movements. Once the subject has initiated movement, she must attempt to touch both targets within a fixed time limit. If she fails to complete both movements within the time limit, she receives no reward. Otherwise, she receives rewards for the targets she touched. In Figure 1A, the subject can earn 10 points for each target. In Figure 1B, in contrast, the second target is worth 50 points.

Figure 1.

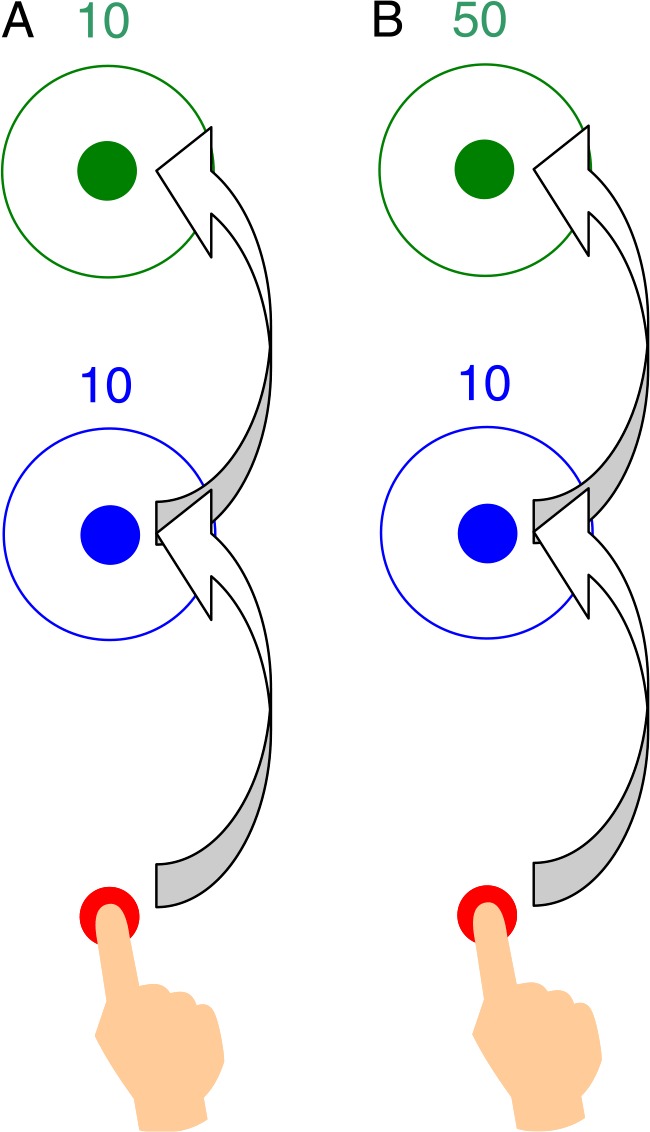
The sequential movement task in one condition of Wu et al. (2009). At the beginning of each trial, the subject placed her right index fingertip on a red starting circle. Once she began to move, the subject had 400 ms total time to attempt to touch two color-coded targets in a specified sequence (blue, then green). Subjects received rewards for each target they touched. They had as much time as desired to plan their movements. Timing began only when they moved away from the red start point. (A) The rewards are equal. (B) The reward for the second target is five times greater than that for the first.

Wu et al. (2009) developed and tested a model of speed–accuracy tradeoff (SAT) for each of the two movements and used it to predict how subjects should allocate time in order to maximize their expected gain. A key prediction of their model was that subjects should invest more of the available time in the movement to the more valuable target. Wu et al. found that subjects either did not vary their time allocation at all, or varied it in the wrong direction, even when one target was five times more valuable than the other.

Given past research, this outcome is surprising. People, for example, do trade off viewing time and movement time to maximize the probability of hitting targets (Battaglia & Schrater, 2007). People exhibit good knowledge of their own SAT (Augustyn & Rosenbaum, 2005) in single movements and they do vary their timing so as to nearly maximize expected gain in a single speeded reach task whose payoff declined with movement time (Dean, Wu, & Maloney, 2007). In a multi-target sequential movement with no strict time constraint, people move more slowly for targets that are smaller than others (Smiley-Oyen & Worringham, 1996).

In this article, we consider possible explanations for subjects' performance in Wu et al.'s (2009) study. One possibility is that people need practice in allocating time in order to learn how time allocation separately affects accuracy in the two movements. In Wu et al.'s experiment, subjects did practice the task extensively. However, during the practice session, the values of the targets never varied. As a consequence, subjects had no incentive to explore how spatial accuracy in the two movements varied with changes in time allocation.

In the first experiment of the present study, we explicitly trained subjects to vary their allocation of a fixed amount of time between the two movements before assessing how they varied time allocation when the rewards associated with the two targets varied.

The training also allowed us to evaluate the possibility that although people can arbitrarily and strategically vary the time they allocate to single movements, they are simply unable to allocate time arbitrarily in making two movements. Previous work indicates that people tend to apply the same proportion of time to parts of a sequence of movements no matter how long the total movement time is (Carter & Shapiro, 1984). Of course, this result does not show that people cannot vary time allocation, only that they do not do so in the absence of incentives.

The results of the first experiment will lead us to reject the explanation just advanced. The failure to maximize gain observed in Wu et al. (2009) is not simply due to a lack of training in time allocation. The results will motivate a second possible explanation, that constrained time allocation in itself might reduce accuracy of the sequential movements. If this were the case, it would challenge the idea that there is a simple tradeoff between time and accuracy embodied in an SAT function. We return to this point in the Discussion.

In a second experiment, we estimated the cost of constrained time allocation by comparing two conditions. In the first condition, subjects were free to allocate time as they wished in attempting to hit two targets in sequence (the task of Wu et al., 2009; Figures 1A and 1B). In the second condition, they were required to carry out the same task but allocating time as dictated by the experimenter. However, the time allocation imposed by the experimenter was set to be the same time allocation freely chosen by the subject in the first condition. The effect on the subject's performance will prove to be an additive increase in spatial uncertainty independent of the time spent on the movement.

Experiment 1: The effect of training

The experiment consisted of two sessions, training and test. The task in the test session was similar to that of Wu et al. (2009) just described. Before the test session, the subject completed a training session in which the subject was required to touch the first target within a specified time window and then to touch the second within second time window centered on 600 ms. Failing to hit within either time window resulted in a loss of all reward for that trial. We systematically varied the first time window from trial to trial. The subject effectively practiced allocating the total movement time available (600 ms) between the two movements.

We refer to the tasks in the training and test sessions as the constrained timing task and the choice timing task, respectively. We were interested in whether subjects who had received training in the constrained timing task would later vary their time allocation in the test condition so as to increase their expected reward.

Methods

Apparatus

A touch monitor (ELO IntelliTouch 17-in. LCD monitor) was mounted vertically on a framework (Structural Framing System, McMaster Carr Inc.). This framing system was specifically selected to minimize the vibration of the setup caused by the speeded reaching movements to the monitor. The experimental room was dimly lit. The experiment was run using the Psychophysics Toolbox (Brainard, 1997; Pelli, 1997) on a Pentium 4 Dell Optiplex GX280. To optimize the recording accuracy of endpoint, a touch screen calibration procedure was performed for each subject at the beginning of each session.

Stimuli

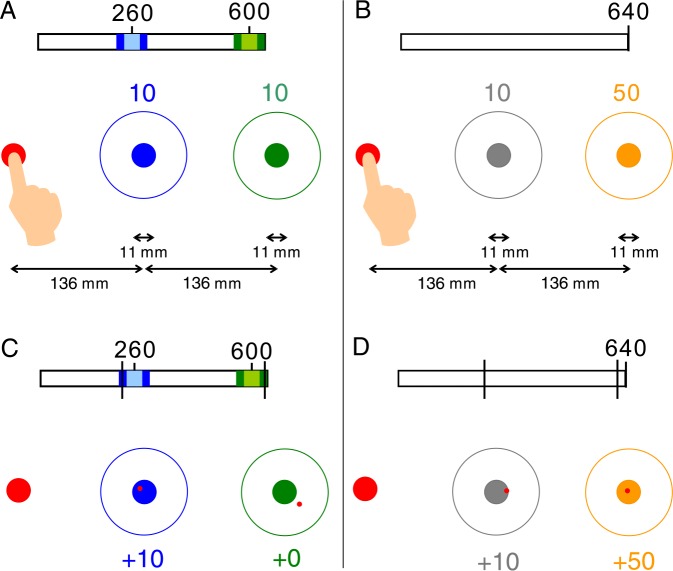
Figure 2 provides a schematic of the stimulus display during the training trials (Figures 2A and 2C) and during the test trials (Figures 2B and 2D). The starting position on each trial was marked by a red filled circle of 11-mm diameter on the left side of the screen. The first target was 136 mm to the right of the starting position. The second target was 136 mm right to the first target. Targets were colored filled circles of 11-mm diameter, each surrounded by a concentric ring four times larger. The purpose of these “outer circles” was to force the subject to attempt to hit both targets on every trial rather than, say, skipping the first target and moving directly to the second. If the endpoint of either movement fell outside the corresponding outer circle, the subject received no reward for the trial. The value (in points) of a target was shown numerically outside and above the outer ring. In the choice timing task, to emphasize the value differences, different values were rendered in different colors. All subjects knew they would receive US$1 for every 1000 points earned.

Figure 2.

An illustration of the sequential movement tasks. (A) The constrained timing task in the training session. Time windows marked on a timing bar specified the required movement durations. The colors of the first and second time windows corresponded to the colors of the first and second targets. (B) The choice timing task in the test session. The first and second targets were silver and golden, respectively. Silver targets were worth 10 points. Golden targets were worth 50 points. (C) Feedback for the constrained timing task. Vertical lines on the time bar marked the times when the subject hit each target. Dots (shown here in red to improve visibility) marked the subjects' spatial endpoints. (D) Feedback for the choice timing task for the last four subjects, similar to feedback of the constrained timing task. Feedback for the first four subjects consisted of a report of total winnings or written messages specifying that they had violated one of the conditions for a reward (e.g. “You were too slow”).

A horizontal time bar was presented near the top of the screen. Timing began only when the subject's finger left the starting position and consequently subjects could spend as much time as desired planning their movements before initiating the first.

In the constrained timing task, the time bar contained two color-filled rectangles, whose colors corresponded to those of the targets and whose positions and widths relative to the whole bar indicated the required time windows. The time values of their centers were also marked above in milliseconds. Each time window was 80 ms wide. To encourage accuracy in timing, hitting a target within the central 40 ms of its time window was triply rewarded for that target when all other reward requirements were met. In the choice timing task, only the right end of the time bar was marked with a number (Figures 2B and 2D), the time limit, which was identical to the upper limit of the second time window in the training session.

At the end of each trial, subjects received feedback on their performance (Figures 2C and 2D). A dot marked the endpoint of each of two reaches and a vertical line imposed on the time bar indicated the time of completion of each reach. If a trial was eligible for rewards, the subject received the specified rewards for each target hit.

The first four subjects in the choice timing task were given feedback consisting of a summary of the amount earned in the trial and whether the temporal or spatial requirement was violated, similar to the feedback of Wu et al. (2009). The remaining four subjects received additional graphical feedback specifying their errors in space and in time as described above.

Procedure

All subjects took part in the training session and the test session. A subject would participate in the two sessions on separate days but within 48 hours of each other. At the end of a session, subjects collected all they had earned in that session.

The subject started a trial by putting her finger on the starting position. Then the two targets, the reward values, and the time bar appeared. After the subject reached to the two targets, she received feedback. The whole display remained visible until the subject pressed the space bar on the keyboard to initiate the next trial. For each trial, we recorded the arrival and departure times of each reach (relative to the time the finger left the starting position), the endpoints of the movements, and the score.

The training session (constrained timing task) included four timing conditions. The second time window always ended at 600 ± 40 ms, while the first time window could end at 180, 260, 340, or 420 ± 40 ms. Thus, we asked subjects to divide 600 ms in the proportions 180:420, 260:340, 340:260, or 420:180. Each target was worth 10 points ($0.01). There were 10 experimental blocks of 80 trials for the constrained timing task, i.e., 10 blocks × 80 trials = 800 trials in total.

The first four blocks each contained a different timing condition, whose order was counterbalanced across subjects. To help the subject get a sense of timing, in these four blocks, beeps were sounded during the required time windows. The second four blocks were identical to the first four but with no auditory cues. The 9th and 10th block had 20 trials from each timing condition, randomly mixed. The 10th block was performed in the test session before the choice timing task, serving as a test of the stability of training effects.

At the beginning of the training session, subjects were introduced to the constrained timing task in a warm-up, no-reward block with looser timing requirements. Only after having completed at least 10 trials and scoring at least three successes could the subject begin the experimental blocks. The subject was encouraged to take breaks (3 min) between blocks and shorter breaks as needed (20 s) in between trials to minimize the impact of fatigue. The training session took approximately 60 min to complete.

In the test session, three value conditions were constructed to reveal subjects' timing strategies. The values of the first and second targets were (10 50), (10 10), or (50 10) points. The time limit to finish the two reaches was always 640 ms. The subject completed five experimental blocks. Each block included 20 trials from each value condition, randomly interleaved. In total there were 5 blocks × 60 trials = 300 experimental trials. A similar warm-up procedure was adopted as that in the training session. The test session took approximately 30 min to complete.

Subjects

Eight subjects, four female and four male, participated. Subjects, except subject S02, were unaware of the purpose of the experiment. S02 was aware of Wu et al.'s (2009) study and knew explicitly that the expected gain depends on the allocation of movement times.

All subjects were right handed and had normal or corrected-to-normal vision. Subjects gave informed consent prior to the experiment. The subjects each received US$24 for their time as well as a performance-related bonus based on points earned. Total payment, including any bonus, ranged from US$33 to US$47 across subjects.

Model of optimal sequential movement planning

Our interest is in the strategy people would use for the choice timing task. Based on statistical decision theory (Berger, 1985; Blackwell & Girshick, 1954; Trommershäuser, Maloney, & Landy, 2008), we modeled an ideal mover who selects a movement strategy that maximizes her expected gain and compared the subject's behavior with the ideal mover. This model is identical to that developed and tested by Wu et al. (2009).

The mover's expected gain in a trial could be formulized as the sum of her expected gain for each target:

$$\mathrm{E}\mathrm{G}\left(s\right)=\sum _{i=1}^{2}P(H_i\&C|s)R_i,s\in S,$$ (1)

where s is a motor strategy, S is the set of all possible strategies, R _i is the value of the ith target, H _i is the event of the ith target being hit, and C is the event that the trial is eligible for rewards. As described previously, a trial was eligible for rewards if both reaches fell within the outer rings of the targets and the second movement was completed before the time limit.

For our purposes, the choice of visuo-motor strategy s is equivalent to the selection of movement time in the sequential reach, more particularly, the ratio of the movement time for the first reach, t ₁, to the total movement time, T. The underlying basic idea is to trade off between the movement times of the two reaches. With the ideal mover reduced to an “ideal time allocator,” we fit the model of Wu et al. (2009) to the data after testing its assumptions.

First, we assume that the mover always aims for the center of the circular target. The subject could in principle aim for the nearer edge of the small target region and thereby reduce the distance traveled at the cost of increasing the likelihood of missing the target. However, as shown by Wu et al. (2009), such a strategy results in no benefit for such small targets separated by relatively large distances.

Second, we assume that whether the second target is hit is independent of whether the first target is hit conditional on the allocation of time. We tested and failed to reject this independence assumption in our data as did Wu et al. (2009). We describe this test below.

With these assumptions, we rewrite Equation 1 as:

$$\mathrm{E}\mathrm{G}(t_1|T)=P\left(V\right)\left[R_{1}P\right(H_1|t_1\left)P\right({\bar{O}}_2|t_2)+R_{2}P(H_2|t_2\left)P\right({\bar{O}}_1|t_1\left)\right],$$ (2)

where t _i is the planned movement time for the ith reach, T is the total movement time, P(V) is the probability of completing both movements before the time limit, P(H _i∣ t _i) is the probability to hit the ith target given the ith movement time is t _i, and P($\bar{O}$_i∣t_i) is the probability to hit within the outer ring of the ith target when the ith movement time is t _i. T, P(V), and R_i are constants. To express expected gain purely as a function of time allocation, t ₁/ T, we need to determine the nature of t ₂, P(H_i∣t_i), and P($\bar{O}$_i∣t_i).

The total time T of a sequential movement consists of three parts: the first movement time t ₁, the dwell time on the first endpoint t _dwell, the second movement time t ₂. We found that we could readily predict dwell time: the ratio of dwell time to total time is a linear function of T/ t ₁:

$$t_{\mathrm{d}\mathrm{w}\mathrm{e}\mathrm{l}\mathrm{l}}/T=m+kT/t_1,$$ (3)

where m and k are parameters estimated from the data separately for each subject. Assuming that the subject chooses the same timing across trials of a condition, we compute the mean t _dwell/ T and T/ t ₁ for each of the four timing conditions in the training session and three value conditions in the test session to estimate m and k. Then we could write t ₂ as:

$$t_2=T(1-t_1/T-m-kT/t_1),$$ (4)

For P(H_i∣t_i) and P($\bar{O}$_i∣t_i), we adopted the following steps. First, we obtained the relation of the standard deviation of a movement's endpoint to its movement time. We model the standard deviation of the ith movement separately for the directions parallel and perpendicular to the movement based on Schmidt, Zelaznik, Hawkins, Frank, and Quinn (1979):

$$\begin{array}{c}{\sigma }_{\parallel }\left(t_i\right)=b_{\parallel }\frac{d_i}{t_i}+c_{\parallel },\\ {\sigma }_{\perp }\left(t_i\right)=b_{\perp }\frac{d_i}{t_i}+c_{\perp },\end{array}$$ (5)

where d_i is the distance of the ith movement, and b_∥, b_⊥, c_∥, and c_⊥ are estimated parameters. We assume that the subject has the same timing plan throughout a condition and the first and second movements have the same parameters. We compute σ_∥, σ_⊥, and d_i/t_i for the four timing conditions in the training session to estimate the parameters.

Second, we assume that the endpoint of the ith reach, $\overrightarrow{v}$ _i, is distributed as a bivariate Gaussian random variable whose mean is the center of the target, $\overrightarrow{\mu }$, and whose covariance is

$${\sum }_i=\left(\begin{array}{cc}{\sigma }_{\parallel }^2\left(t_i\right)& 0\\ 0& {\sigma }_{\perp }^2\left(t_i\right)\end{array}\right),$$ (6)

so that the probability density function of endpoint distribution is,

$$f_i(\overrightarrow{v}|\overrightarrow{\mu },t_i)=\frac{1}{2\pi |{\sum }_i{|}^{1/2}}{e}^{-\frac{1}{2}(\overrightarrow{v}-\overrightarrow{\mu }{)}^T{\sum }_i^{-1}(\overrightarrow{v}-\overrightarrow{\mu })}.$$ (7)

Finally, the probability of hitting the target or outer circle can be computed as the integration of f _i($\overrightarrow{v}$∣$\overrightarrow{\mu }$, t_i) over the target or outer circle using the integration method of DiDonato and Jarnagin (1961):

$$\begin{array}{c}P\left(H_i|t_i\right)=\int \underset{B(0;r)}{\int }{f}_i(\overrightarrow{v}|\overrightarrow{\mu },t_i)d\overrightarrow{v}\\ P\left({\bar{O}}_i|t_i\right)=\int \underset{B(0;4r)}{\int }{f}_i(\overrightarrow{v}|\overrightarrow{\mu },t_i)d\overrightarrow{v},\end{array}$$ (8)

where r and 4r are respectively the radius of the target and outer circle. Although the subject is supposed to aim at the center of the target, there can be constant error in their movements as found in other studies (Wright & Meyer, 1983). We compute the constant errors for the first and second targets in the parallel and perpendicular directions as an average across all trials of the experiment. As noted above, this error had negligible effect on subjects' expected gain.

Results

Trials with either endpoint out of the outer circle or with a total movement time greater than 1000 ms were excluded from the analysis. No more than 2.5% trials were excluded for each subject.

The ability of constrained timing and the effect of training

The failure of effective time allocating in sequential movements as found in our previous study might indicate that people cannot divide time arbitrarily at all or cannot do so before necessary training. The training session allowed us to test for this possibility. For each subject, we computed the mean ratio of the first movement to the total movement time, t ₁/ T, for each timing condition and regressed it against the required ratio.

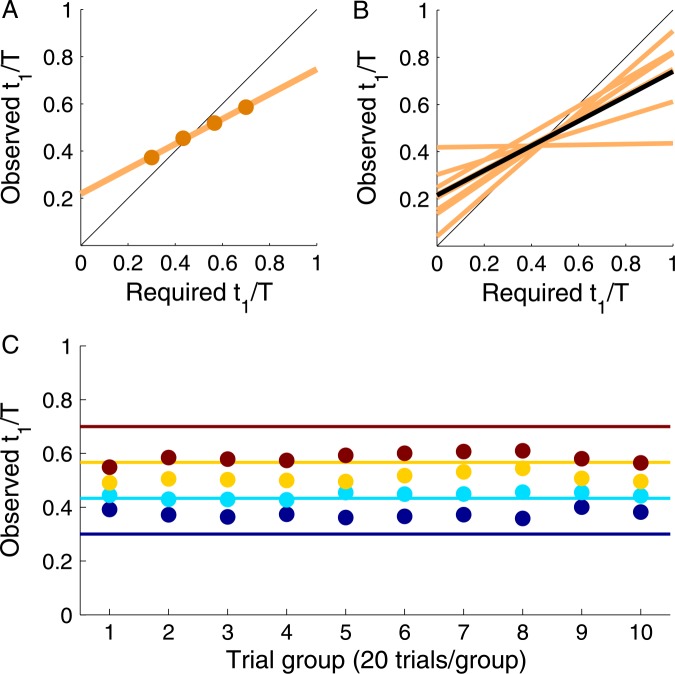
If people were not able to follow the timing requirement, the slope of the regression would be zero. In contrast, if people correctly executed every time allocation specified by the experimenter, the slope would be one. The data fell between these extremes. Figure 3A shows the results of our first subject S01. When the required t ₁/ T was 180/600, S01 spent a larger share of time on the first movement than required, while when required t ₁/ T was 340/600 or 420/600, the reverse. That is, mean observed t ₁/ T in both higher and lower required t ₁/ T conditions approached to a middle value. This pattern repeated itself with all subsequent subjects. Figure 3B shows the fitted regression line for all the eight subjects and the average across subjects.

Figure 3.

Timing performance in the training session. (A) Subject S01's observed mean t ₁/ T plotted against the required t ₁/ T in each of the four timing conditions with superimposed regression line. (B) Observed-required t ₁/ T regression lines for each of eight subjects. Only one slope was not significantly greater than zero (p > .05). All slopes were significantly less than one. A line whose slope is the mean of the slopes of the subjects is plotted in black. (C) The mean observed t ₁/ T across time averaged across subjects throughout the training session. Each trial group represents a cluster of 20 trials. The horizontal lines each denote the required t ₁/ T for one of the four timing conditions. Dots with the same color as a line mark mean observed t ₁/ T for each group in that timing condition.

For each subject, we computed a 95% confidence interval for the slope using a bootstrap method ¹ (Efron & Tibshirani, 1993), resampling the movement times for each timing condition with 10,000 runs. At the 95% confidence level, all the slopes were greater than zero except for one subject, demonstrating that subjects were able to voluntarily vary their timing in sequential movements. However, all slopes were lesser than one, implying that subjects did not do the constrained time division perfectly and instead contracted toward a preferred t₁/T ratio. The mean slope across subjects was 0.52. Consistent with the above individual analysis, the mean slope, by two-tailed Student's t-tests, was significantly greater than zero, t(7) = 5.72, p < .001, and significantly smaller than one, t(7) = −5.20, p = .001.

To examine whether training helped, we partitioned the 200 trials in each timing condition into 10 groups of 20 trials and computed the absolute difference of mean observed t ₁/ T ratio to required t ₁/ T ratio for each group. We examined the training effect by calculating the regressive slope of the abstract difference to the group number. The last group was not included, for it was performed immediately before the test session, typically on the next day of the training session. There was no evidence of improvement.

Figure 3C plots mean observed t ₁/ T across subjects against trial group for each timing condition. Improvement in timing performance should have resulted in a negative slope. At the 95% confidence level (Bonferroni corrected for four conditions), only one slope of one subject was significantly different from zero. Neither did the timing performance worsen after the interval between the training session and the test session. A one-tailed Student's t-test for each subject in each timing condition revealed few differences between the mean absolute deviation of the movement time of the 9th group and that of the 10th group. Averaged across all the eight subjects, only in 0.5 out of 4 conditions ² was the mean observed t ₁/ T of the 10th trial group further from the required t ₁/ T than that of the 9th trial group at the 95% confidence level (Bonferroni corrected for four conditions).

The independence of the two movements

For each subject, we made two analyses to test the spatial independence of movements for each timing or value condition. First, we computed the correlation between the coordinates of the first and second endpoints separately for the parallel and perpendicular directions. Second, we examined whether the probability of hitting or missing one target depended on whether the other target was hit.

At the 95% confidence level (Bonferroni corrected for seven conditions), there was little or no correlation between the two endpoints. Across the eight subjects, only 0.75 out of 7 conditions in the parallel direction and 0.63 out of 7 conditions in the perpendicular direction showed significant correlation and these correlations, though significant, were small (no more than 0.31).

For each timing and value condition, we computed the conditional probability of the second hit given the first target was hit or missed. P(hit2∣miss1) is plotted against P(hit2∣hit1) in Figure 4 for each subject (in a unique color). According to Pearson's χ ² test on the number of hits or misses, at the 95% confidence level (Bonferroni corrected for seven conditions), P(hit2∣miss1) differed from P(hit2∣hit1) only for two data points of two different subjects in two different conditions (circled in Figure 4). Put together, these two analyses demonstrate that the two movements within a sequential movement can be treated as independent, in agreement with the conclusions of Wu et al. (2009).

Figure 4.

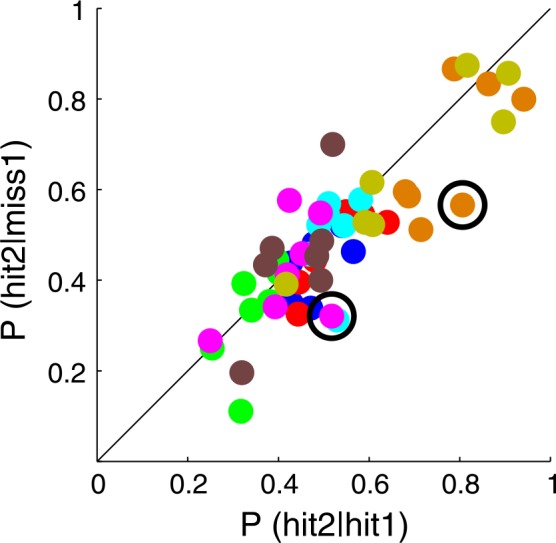
Movement independence. The probability of hitting the second target conditional on missing the first is plotted against the probability of hitting the second target conditional on hitting the first for each timing and value condition, for each subject. Each color denotes the results for one subject. If the two movements were independent, the data points should not depart significantly from the identity line. We tested equality of the two conditional probabilities using Pearson's χ ² test with Bonferroni correction for seven conditions (overall .05 significance level corresponds to corrected level .0071). Only two differences proved to be significant (circled).

Parameter estimation

We estimated the parameters in the dwell time (Equation 3) and SAT (Equation 5) functions for each subject. The subject was assumed to execute the same timing planning when faced a certain timing condition in the training session or a certain value condition in the test session. Thus, each condition provided a data point.

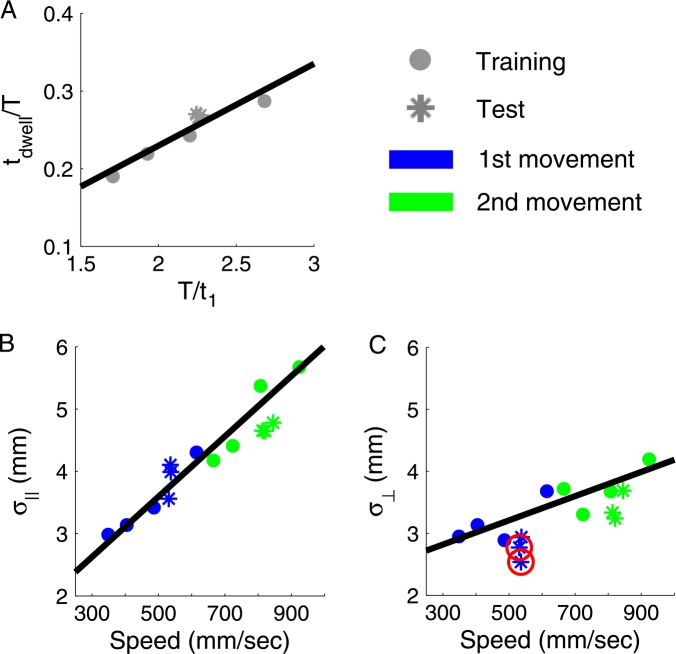
Figure 5A gives the t _dwell/ T − T/ t ₁ pairs and fitted line of subject S01. The R ² of the eight subjects (in descending order) were .95, .89, .86, .72, .67, .66, .64, and .61. The median across subjects was .70.

Figure 5.

Timing results for one subject (S01). (A) Mean observed ratio of dwell time to total time as a linear function of mean observed ratio of total time to the first movement time. Each dot denotes a timing condition in the training session. Each star denotes a value condition in the test session. (B) Standard deviation of the endpoint of a movement in the parallel directions (σ_∥) as a linear function of mean movement speed. Each data point is a movement of a timing or value condition. Blue denotes the first reach. Green denotes the second reach. Dots denote the training session. Stars denote the test session. We fit a line to the data of the training session. (C) Standard deviation of the endpoint of a movement in the perpendicular directions (σ_⊥) as a linear function of mean movement speed. Same format as Figure 5B. The test session standard deviations that are significantly smaller than those predicted by the fitted lines are circled.

For the SAT function, we used only data from the training session to fit the line. Figures 5B and 5C shows the results for subject S01. We noticed that, for most subjects, the standard deviations in most conditions of the test session were slightly smaller than what was predicted by the fitted SAT line. We tested whether they in fact were smaller by using a bootstrap method (Efron & Tibshirani, 1993) to resample each condition and estimating the SAT function in the same way for 10,000 runs. At the 95% confidence level (Bonferroni corrected for 14 data points), averaged across subjects, in the parallel direction, 1 out of 8 conditions in the training session had significantly smaller standard deviation than predicted, while 3.3 out of 6 conditions in the test session had significantly smaller standard deviations; in the perpendicular direction, 0.5 out of 8 conditions in the training session had significantly smaller standard deviation, while 4 out 6 conditions in the test session had significantly smaller standard deviations.

Given this discrepancy, we based the SAT estimation on the data of the constrained timing task rather than on the data of both tasks.

Model comparison

After obtaining the dwell and SAT functions of a subject, we searched for the maximum of the subject's expected gain function in each value condition. We compared the subject's observed t ₁/ T with the optimal t ₁/ T that led to maximal expected gain. We used a bootstrap method (Efron & Tibshirani, 1993) as follows to estimate the 95% confidence interval (Bonferroni corrected for three conditions) of the observed-optimal t₁/T difference. We ran a simulated experiment for 10,000 runs. In each run, we resampled data for each condition in each group, then estimated the parameters in the dwell time and SAT functions, and finally searched for the maximum of the subject's expected gain function and estimated the optimal t₁/T. We used bootstrap methods based on 10,000 simulations (Efron & Tibshirani, 1993) to calculate 95% confidence intervals for these estimates.

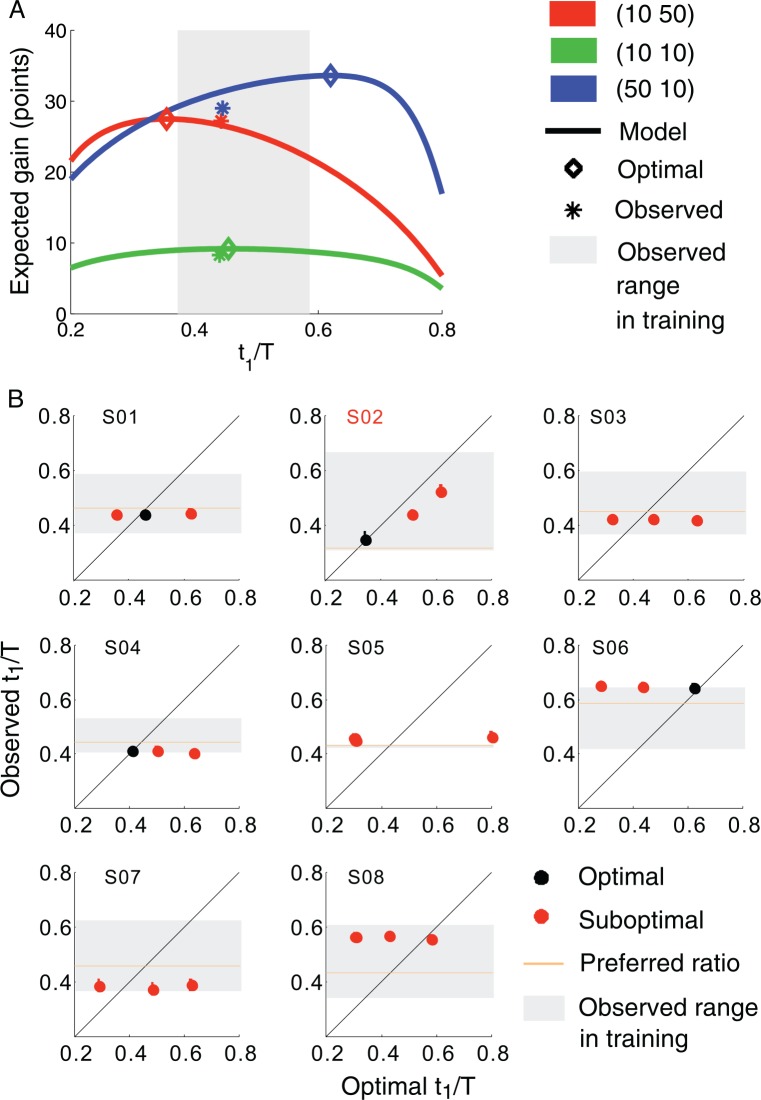
Subject S01's modeled expected gain functions and observed performance in each value condition are plotted in Figure 6A. The results for six additional subjects were similar to those of S01: they seemed not to vary their t ₁/ T ratio at all.

Figure 6.

Model comparison of the timing strategy. (A) The predicted expected gain functions compared with observed performance in each value condition for subject S01. Results for six of the other seven subjects resembled those for S01. None of these subjects varied their time allocation across value conditions as predicted by the model. See text. (B) Mean observed t ₁/ T plotted against optimal t ₁/ T in each value condition. Each panel corresponds to one subject. S02 was the subject who was partially aware of the hypothesis under test. The data points for which observed t ₁/ T did not significantly deviate from the optimal t ₁/ T that would maximize expected gain are colored black, otherwise, red. The error bars denoting the 95% confidence intervals (Bonferroni corrected for three conditions) are in most cases smaller than the plotting symbols. The range of t ₁/ T observed in training is marked in gray.

Each subject's mean observed t ₁/ T ratio in each value condition is plotted in Figure 6B against the subject's model-predicted optimal t ₁/ T ratio, with “optimal” data points in black and “suboptimal” ones in red. An observed t ₁/ T ratio is labeled ³ “optimal” if it did not significantly deviate from optimal t ₁/ T at the 95% confidence level (Bonferroni corrected for three conditions) according to the bootstrap test; otherwise, “suboptimal.”

The preferred ratio and available t ₁/ T range as shown in the training session are also presented. Two points should be highlighted for Figure 6B: First, all but one subject did not vary their time allocation (the three points fall on a horizontal line). Second, most subjects' observed t ₁/ T ratios were close to their preferred ratio in training. The remaining subject S02 (upper row, center) was the subject who was partially aware of the hypothesis under test. He did vary time allocation but two of his three time allocations are significantly different from optimal.

Efficiency

Efficiency was defined as the average score of a trial in a condition divided by the maximal expected gain of the condition. In the computation of expected gain (Equation 2), P(V) was computed for each subject and each value condition as the proportion of trials in the test session in which the time limit was not exceeded. For each subject, we computed the 95% confidence interval (Bonferroni corrected for three conditions) of efficiency using the method for computing observed-optimal t ₁/ T difference confidence interval as described earlier. Figure 7 shows the data. To our surprise, almost no efficiencies were significantly smaller than one, and some were even significantly larger than one.

Figure 7.

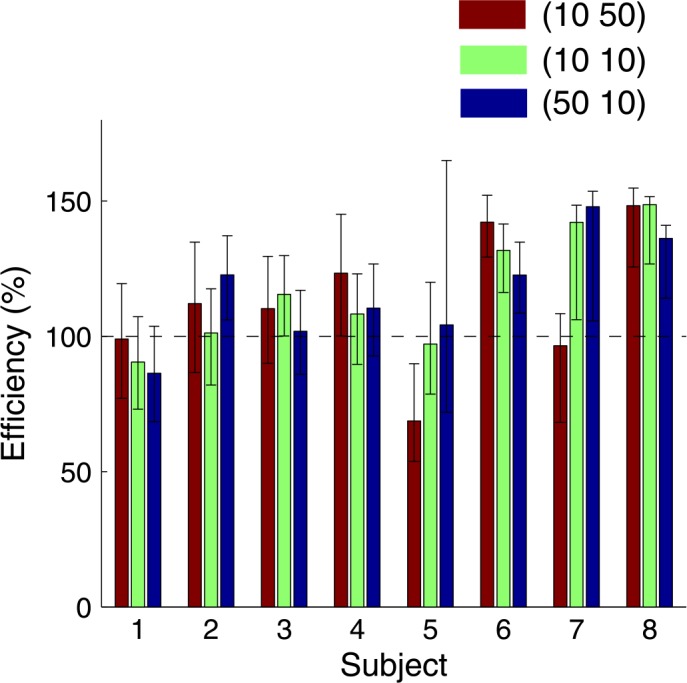
Efficiency. Efficiency for subjects in the test session. The error bars mark 95% confidence intervals (Bonferroni corrected for three conditions).

We considered the possibility that the benefit to subjects of varying timing was so small, in terms of reward, that subjects had little reason to vary timing. We used the SAT model to predict the expected gain that would result from the subject's actual choice of timing allocation and compared this to the predicted maximum expected gain (with optimal choice of timing allocation). We expressed the difference as a percentage of the predicted maximum expected gain.

The predicted costs of allocating time as the subjects did were a reduction of expected gain in at least one condition of 7%, 4%, 10%, 13%, 64%, 26%, 22%, and 10%, respectively, for S01–S08. S05, for example, chose an allocation of time in the (10, 50) condition that would result in a reduction of her winnings in that condition of 64% if the SAT model correctly predicted her expected gain. If we exclude S02 (who did vary timing and had a correspondingly low reduction of only 4%), the median percentage loss across subjects is 13%.

Thus, based on our SAT model, we predict that subjects' lack of variation in timing as we varied reward should have cost them about one dollar out of every eight. The actual results (Figure 7) suggest otherwise and this discrepancy is the focus of the remainder of the article.

An aside: We know of no general rule for deciding whether a difference such as 13% is large enough to affect behavior. “Flatness [of the reward function near the maximum] is not a mathematical but a psychological concept. 5% loss may be substantial for one decision maker and negligible for another” (von Winterfeldt & Edwards, 1973). However, the results in Figure 7 together with the results of Experiment 2 below will suggest that the outcome of Experiment 1 is not simply the result of an insensitivity to reward.

Experiment 2: The cost of constrained time allocation

In Experiment 1, subjects completed 800 trials in an constrained timing task before completing a decision task similar to that of Wu et al. (2009) in which they could pick whatever allocation of time they wished (choice timing task). The constrained timing task demonstrated subjects' ability to divide up movement time arbitrarily and should have given them opportunity to observe how their own accuracy varied with the duration of each movement. However, we found that, even after the 800 trials of training, subjects did not vary their timing in the choice timing decision task.

However, we hesitated to conclude people are suboptimal movers in sequential movements because of a puzzle that emerged in the results. Although subjects did not vary their time allocation, their winnings in the choice timing decision task were typically better than what we predicted given their performance in the constrained timing training task. The key deviation is visible in Figure 5C where the measured standard deviations in the choice timing decision task (“test”) are somewhat lower than predicted given the results of the constrained timing training trials by about 23%.

In Experiment 2, we tested the possibility that, when people try to actively divide up movement time, their spatial accuracy is thereby reduced. We asked subjects to complete a choice timing decision task essentially identical to that in Experiment 1. We then asked subjects to complete a constrained timing task where they were asked to allocate movement time in a pre-specified way. However, unlike the constrained timing task in Experiment 1, the required timing was not arbitrary but was the actual timing exhibited by the subject in the choice timing task.

Intuitively, in the constrained timing task, we are requiring subjects to allocate time as they freely chose to allocate it in the choice timing task. We are in effect constraining them to do what they would have done anyway. By comparing people's performance in the constrained timing task with that in the corresponding choice timing task, we can directly estimate the cost of constrained time allocation, if any.

Methods

Apparatus

The same as Experiment 1.

Stimuli

Stimuli in the choice timing task were the same as those in the choice timing task of Experiment 1. Stimuli in the constrained timing task were almost the same as those in the constrained timing task of Experiment 2, except that the widths of time windows were 40 ms and there were no central triple reward areas on the time bar.

Procedure

All subjects took part in two 40-min sessions run on two successive days. Each session consisted of eight blocks of 50 trials, i.e., 2 days × 8 blocks × 50 trials = 800 trials in total. There were, in order, two blocks of the choice timing task, two blocks of the constrained timing task, then two more blocks for the choice timing task, then two more blocks for the constrained timing task. In one session, the values of the targets were (10, 10) points; in the other, (10 50) points. The order of the two sessions was counterbalanced across subjects. As in Experiment 1, subjects received US$1 for every 1000 points they collected in a session.

The procedures of the choice timing and constrained timing tasks were essentially those of the choice timing and constrained timing tasks of Experiment 1. In the choice timing task, the subject was rewarded for hits only if she completed her movements before 640 ms. In the constrained timing task, the subject needed to arrive at the two targets within two specified time windows. The time windows of a trial in a constrained timing block were centered at the mean arrival times of the trials in the two immediately preceding choice timing blocks. Trials with total movement time longer than 1000 ms were excluded in computing these means.

At the beginning of each session, there were one choice timing and one constrained timing practice blocks, both of 50 trials, with the required timings of the latter taken from the recorded timings of the former.

Subjects

Four subjects, two female and two male, participated. All were unaware of the hypotheses under tests and none had participated in the previous experiment. All subjects were right-handed and had normal or corrected-to-normal vision. Informed consent was given by the subject prior to the experiment. The subject received US$20 for the time and a performance-related bonus. Total payment, including a bonus based on points earned, ranged from US$28 to US$34 across subjects.

Results

Trials with either endpoint out of the outer circle or with a total movement time greater than 1000 ms were excluded from the analysis. No more than 4.5% trials were excluded for any subject.

The expected gain ratio of choice timing to constrained timing

We wished to test whether the expected gain of a choice timing task is higher than the spatial accuracy of its matched constrained timing task and, if it is higher, to estimate how much higher. As a between-block design was used, we found it convenient to present the data in units of block or “super-block” (defined below) so that any systematic variation across time other than the manipulated variations would be readily visible.

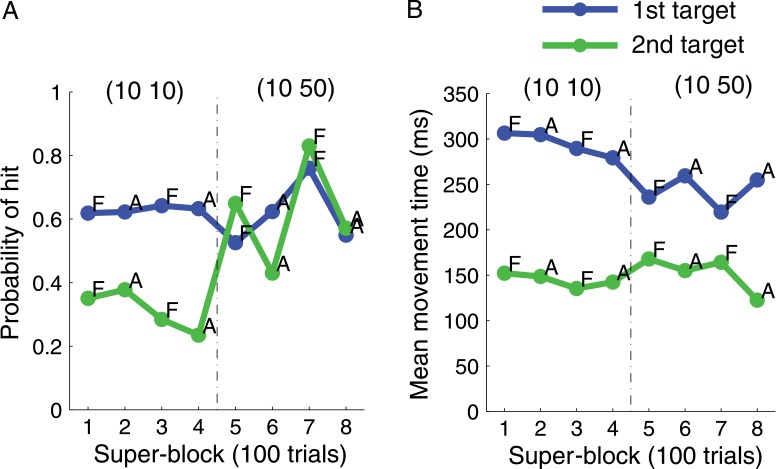
Figures 8A and 8B present the data of a typical subject, S03. Every two adjacent choice timing blocks or constrained timing blocks were grouped as a “super-block” and each data point has a label F(ree) or A(ctive). Figure 8A plots the probability of hit of the first and second targets against super-block index. We computed expected gain as the weighted sum of the probability of hit multiplied by the target value and computed the ratios of expected gain of choice timing to that for constrained timing in each value condition, which, for subject S03, were 1.02 and 1.40 in the (10 10) and (10 50) value conditions.

Figure 8.

Subject S03's data. (A) The mean probability of hitting each target separately for each super-block. (B) Mean movement time for each target by super-block. Legends (10 10) and (10 50) denote the two value conditions. F denotes the choice timing condition. A denotes the constrained timing condition.

However, before concluding that choice timing boosted S03's expected gain, we need to compensate for any differences in movement time in the choice timing and the constrained timing tasks, as shown in Figure 8B. These differences by themselves might lead to changes in spatial variation, accuracy and expected gain.

The way we compensated for the time difference was to fit the relationship between spatial variance and movement time, substitute the constrained timing movement times with their choice timing counterparts, and generate spatial variances for them from the model. Then, based on this spatial variance, we computed the predicted probability of hitting a target and the corresponding expected gain. As in Experiment 1, we took advantage of the linear relation between the standard deviation of endpoints and movement speed. We computed the linear function separately for each value and timing condition and separately for the parallel and perpendicular directions.

The corrected expected gain ratio of choice timing to constrained timing is shown in Figure 9. Its 95% confidence interval (Bonferroni corrected for two conditions) was obtained with a bootstrap method (Efron & Tibshirani, 1993) by simulating the experiment for 10,000 times and using the procedure described above to compute expected gain.

Figure 9.

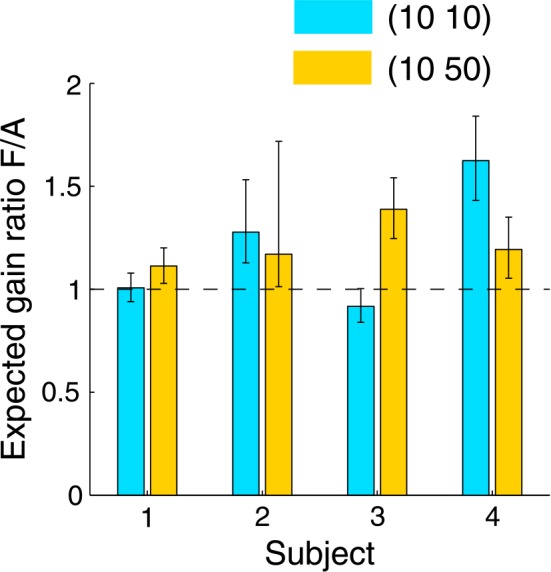
Cost of constrained time allocation for each subject. The dependent variable is the predicted ratio of expected gain in the choice timing condition to expected gain in the constrained timing condition when the movement times of the two are made equivalent. A value greater than one means that there is a cost in the constrained timing condition relative to the choice timing condition. In the (10 50) value condition, the expected gain ratio is significantly greater than one for all subjects. Error bars denote the 95% confidence interval, Bonferroni corrected for two conditions. Requiring the subjects to move with the same pattern of timings as they would otherwise have freely chosen reduced their performance by 5–28% (mean value 17%).

For the four subjects, 6 out of 8 expected gain ratios were significantly greater than one; none was significantly lesser than one; the mean values for (10 10) and (10 50) value conditions were 1.21 and 1.22, respectively. Thus, we find that the cost in expected gain of constrained time allocation is about 17% for the conditions in these experiments. The cost in movement error standard deviation was an increase of 18%.

In Experiment 1, the efficiency was the ratio of the expected gain of the choice timing task over the expected gain predicted by a model fitted with performances in the constrained timing task, a task with time constraints for both targets as the constrained timing task had. We can explain the superior efficiency in Experiment 1 as the result of an amplification factor similar to the expected gain ratio of choice timing to constrained timing.

The practice/fatigue effect

As described in the Procedure section, each session of the experiment was organized into eight blocks of a fixed sequence: First two choice timing blocks, then two constrained timing blocks, then two choice timing blocks, last two constrained timing blocks. That is, on average, constrained timing trials were two blocks behind choice timing trials. This leaves open the possibility that the greater-than-one expected gain ratio of choice timing to constrained timing might result from a fatigue effect, which would weaken our argument that it is the consequence of the cost of constrained time allocation.

To estimate the practice/fatigue effect, we computed the expected gain ratio of the four early blocks to the four late blocks in each session with the data of probability of hit. We used a bootstrap method (Efron & Tibshirani, 1993), resampling 10,000 times to estimate its 95% confidence interval (Bonferroni corrected for two conditions). Figure 10 shows the results. The fatigue effect, if any, was balanced or a little outweighed by the reverse practice effect. Among the eight ratios, none was significantly greater than one; three were significantly but slightly less than one. Therefore, the cost of constrained time allocation could not be attributed to fatigue.

Figure 10.

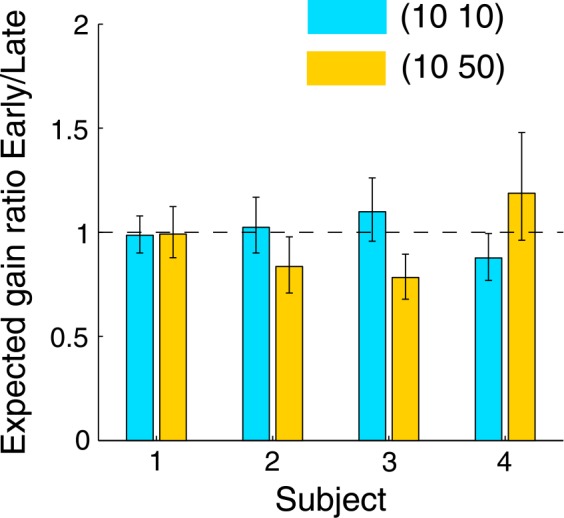
Practice/fatigue effect for each subject. The dependent variable is the expected gain ratio of the four early blocks to the four late blocks in each session. A value greater than one indicates a fatigue effect. Values less than one are consistent with a practice effect. Error bars denote the 95% confidence interval, Bonferroni corrected for two conditions.

Discussion

There is an intimate connection between action and reward. By systematically varying rewards and punishments in visuo-motor tasks, we pose problems to the movement planning system and, in doing so, we can potentially reveal aspects of movement planning not otherwise observable.

There are now several studies where experimenters impose rewards and punishments on possible outcomes in motor tasks and evaluate how close subjects come to maximizing expected gain (Hudson, Maloney, & Landy, 2008; Trommershäuser, Gepshtein, Maloney, Landy, & Banks, 2005; Trommershäuser, Landy, & Maloney, 2006; Trommershäuser, Maloney, & Landy, 2003a, 2003b). Overall, the results of these studies give the impression that people are nearly optimal movers even when they have little experience in a particular motor task. Consequently, the large, qualitative failures observed in Wu et al. (2009) are striking.

In that study, subjects were asked to allocate time between two successive reaching movements to targets as the experimenter varied the rewards associated with hitting the targets. Subjects either did not vary their allocation of time or varied it in the wrong direction even when one target was as much as five times more valuable than the other. In related experiments involving only a single reaching movement, subjects did vary the time allocated to the movement so as to maximize their performance (Battaglia & Schrater, 2007; Dean et al., 2007; Hudson et al., 2008).

In Experiment 1, we considered the possibility that the observed failures in allocating time were the consequence of a lack of experience with allocating time between movements. If so, a session of motor practice before the motor decision task should move human performance toward optimal performance, maximizing expected gain.

In the first part of the experiment, we trained subjects to divide up the total movement time in different ways (constrained timing task). They were able to do so (but see below) and in doing so they could observe the consequences of varying timing on their accuracy in both movements. However, in the second part of the experiment, when they were left to choose a timing strategy, they did not vary their allocation of time between targets. We observed a similar pattern of failures to that observed by Wu et al. (2009). Training with the constrained timing task did not lead to improved performance in the choice timing task.

One interesting finding of Experiment 1 was that when people attempt to divide the movement time of the sequential movements in a constrained ratio, their actual division regresses to a certain ratio that is very close to the ratio in their spontaneous time division. This outcome hinted that subjects resist varying time allocation away from a specific default value, their preferred ratio. A second interesting finding is that the dwell times (the time subjects spent in contact with the first target before initiating the second movement) had a simple reciprocal relation to the proportion of time allocated to the first movement.

A third intriguing phenomenon revealed by Experiment 1 is the unusually high efficiencies found. Even though subjects did not vary their time allocation between the two movements, their winnings were not reduced as much as we predicted they would be. Battaglia and Schrater (2007) reported a similar phenomenon. Their task was to reach a target within a time limit for monetary rewards. The exact position of the target was hidden, and the location of the hidden target was signaled to the observer by dots sampled from an isotropic bivariate Gaussian distribution whose mean was the hidden target location. Subjects viewed the distribution of the dots, judged the target position, and then made the reach. The number of dots increased at a fixed rate after a trial began until the reach was initiated. Given the limited total time, there was a tradeoff between viewing time and movement time. Subjects out-performed predicted maximal expected gain although their time tradeoff significantly deviated from the optimal one predicted by the model. Battaglia and Schrater attributed the unexpectedly good performance to “increased participant motivation” for the experimental task than the baseline task. But they were still puzzled with the larger movement time variability in the experimental task, which could not be the result of higher motivation.

In our case, a motivation-difference explanation is untenable because our subjects were rewarded in both the training and test sessions. We considered a second explanation, that constraining time allocation reduces spatial accuracy of movements. We confirmed this possibility in Experiment 2 by comparing the performance in two conditions that differed only in that time allocation was constrained in one but not in the other. In the constrained time condition we required subjects to carry out the movement with the timings that they would have freely chosen had the choice of time allocation been left up to them. We found that there was a cost of constraining time allocation that, in our task, was about a 17% reduction in expected gain.

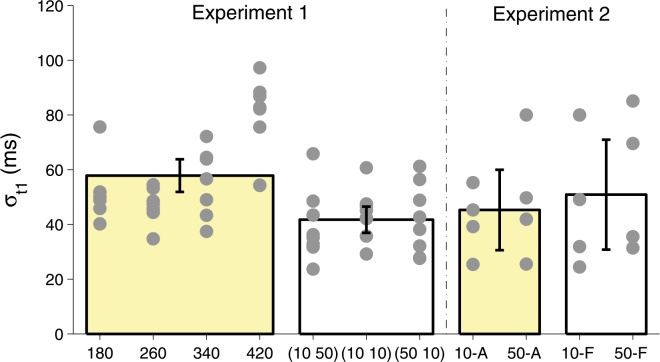
Based on previous work concerning single movements (Carlton, 1994; Zelaznik, Mone, McCabe, & Thaman, 1988), we might expect that smaller spatial variance comes only at a cost of larger temporal variance. As shown in Figure 11, this is not the case. In Figure 11, we plot the temporal standard deviation for subjects and conditions in both Experiments 1 and 2. For each experiment, we ran a repeated-measures one-way ANOVA for all its constrained timing and choice timing conditions. For Experiment 2, there is no significant difference among conditions, F(3, 9) = 0.56, p = .66. For Experiment 1, the effect of condition is significant, F(6, 42) = 15.12, p < .001, but as a Tukey's HSD test shows, the significant differences are either between two constrained timing conditions, or between choice and constrained conditions with the standard deviation of a choice timing condition significantly less than that of a constrained timing condition, exactly the reverse of what we might expect given previous work. Subjects achieve higher spatial accuracy without detectable decreases in temporal accuracy (Experiment 2) or even with increases in temporal accuracy (Experiment 1).

Figure 11.

Temporal movement uncertainty. The standard deviation of t ₁. The effort to constrain t ₁ to a specified time window, as in the constrained timing conditions of Experiment 1 or 2, did not lead to a smaller standard deviation than when there was no need to control t ₁. Each gray dot above a condition of Experiment 1 or 2 denotes the data of a subject under that condition. The bars shown serve to group conditions. The height of each bar is the mean across the conditions grouped. Yellow bars group the constrained timing conditions. White bars group the choice timing conditions. The error bars mark the 95% confidence intervals of the means.

We are left with two questions: Why does choice time allocation in sequential reaching movements improve the spatial accuracy of reaching without a concomitant decrease in temporal accuracy? And why do subjects not vary their time allocation as we vary reward? We address these two questions next.

Soechting and Flanders (1998) emphasized that imposing different constraints on motor dynamics may lead the motor system to adopt qualitatively different solutions for motor control. That is, the motor system can switch “motor strategies” in response to changes in task demands. In a recent paper, for example, Welchman, Stanley, Schomers, Miall, and Bülthoff (2010) found that movements made in reaction to an opponent's movements are faster than movements initiated voluntarily. They argue that different movement types have different neural bases.

While there may be a fixed relation between speed and accuracy for any one strategy, the relation between speed and spatial or temporal accuracy for movements generated by two different strategies is less clear.

Meyer, Smith, and Wright (1982) considered the different functional forms of speed–accuracy tradeoff found by Fitts (1954) and Schmidt, Zelaznik, and Frank (1978; Schmidt et al., 1979). Fitts constrained spatial accuracy and asked subjects to maximize speed. He found that the relation between speed and accuracy was logarithmic in form, a relationship known as Fitts' Law. Schmidt et al. constrained speed and asked subjects to be as spatially accurate as possible. They found an SAT that was linear in form, not logarithmic.

Meyer et al. (1982) conjecture that the different forms of SAT, linear and logarithmic, resulted from the use of different motor strategies (models): the symmetric impulse variability model and the overlapping impulse model.

The symmetric impulse variability model assumes that a reaching movement is produced by generating a single force pulse whose cycle runs from the start to the end of the movement. Both spatial and temporal uncertainty are determined by the choice of force pulse and increase linearly.

The overlapping impulse model assumes that a reach is the result of a series of small, overlapping force pulses. The model allows for the possibility of multiple spatial corrections during the reach and a consequent reduction of spatial uncertainty. Meyer et al. (1982) show that the logarithmic SAT (Fitts' Law) is a consequence of adopting this model.

Similarly, Bye and Neilson (2008) proposed their BUMP model of motor control which includes two motor control strategies: fixed horizon control and receding horizon control. The basic assumption of the BUMP model is that movement control is a discrete-time process consisting of multiple intervals. In each interval, typically 100–200 ms, motor commands for the incoming movement stage are computed. When a movement is close to its end, the fixed horizon control and the receding horizon control differ in whether the motor commands generated in each interval are supposed to end at a specific time. The fixed horizon control allows more accurate control of timing but poses a more difficult computational problem than the receding horizon control. Interpreting our results by the BUMP model, we conjecture that choice time allocation in sequential movements induces receding horizon control while constrained time allocation leads to fixed horizon control.

Todorov and Jordan (2002; Todorov, 2004) and others (Diedrichsen & Gush, 2009) conjecture that the motor system could minimize the effort of motor control by allowing variances in task-irrelevant dimensions to increase. It implies an effective switch of motor control strategy in the face of different task situations.

In the constrained timing trials, we were able to model the SATs for two successive movements as we changed the constraints on timing. But when the timing constraint was removed altogether, subjects reached with greater spatial accuracy than we would expect based on their performance in the constrained task. We conjecture that this change in SAT corresponds to a shift in motor strategy, a shift in how the reaching movement is generated and controlled.

What is unusual about the observed speed and accuracy in the choice timing conditions is that subjects (with one exception) do not vary mean timing as we vary the rewards associated with successful completion of the first or second reaching movement. We conjecture that they cannot. That is, the movement they adopt for the choice timing task is generated by a privileged motor strategy that, given the conditions of our experiment, can divide time between the two movements in only one ratio, the one observed.

That is, the privileged timing strategy achieves a higher spatial accuracy for the same speed as the constrained timing strategy, but, with this strategy, the motor system has no freedom in allocating time between the two movements. Only one time division is possible. We further conjecture that the privileged time allocation corresponds to the preferred time durations identified in analyzing the constrained timing data of Experiment 1.

If our conjecture concerning two strategies is valid, then we may schematize the possible speed–accuracy tradeoffs available to the subject: a range of SATs available through constrained timing where accuracy smoothly increases with increased time duration of each of two movements and an isolated point, corresponding to the privileged timing strategy with only one possible allocation of times between the two movements.

If the privileged strategy leads to higher spatial accuracy than the constrained at every speed across the range employed in the experiment, then it is always the strategy to employ in order to maximize expected gain in Experiment 1. The subject maximizing expected gain should not vary timing as we vary reward over the range of rewards employed and speeds evoked and that is what (with one exception) they did.

If this analysis is correct, then subjects did err but in only one respect. In the constrained timing task in Experiment 2, they should have employed the same movement strategy as they did in the choice timing task. It may be that subjects knew that the privileged motor strategy led to greater spatial accuracy than the constrained but incorrectly believed that it led to lower temporal accuracy as well. Thus, when the instructions put an emphasis on time, subjects used the constrained motor strategy, intending to sacrifice spatial accuracy for temporal accuracy. They did not know the sacrifice was in vain.