Abstract
The gating of Kir channels depends critically on phosphatidylinositol 4,5-bisphosphate (PIP2), but the detailed mechanism by which PIP2 regulates Kir channels remains obscure. Here, we performed a series of Targeted molecular dynamics simulations on the full-length Kir2.1 channel and, for the first time, were able to achieve the transition from the closed to the open state. Our data show that with the upward motion of the cytoplasmic domain (CTD) the structure of the C-Linker changes from a loop to a helix. The twisting of the C-linker triggers the rotation of the CTD, which induces a small downward movement of the CTD and an upward motion of the slide helix toward the membrane that pulls the inner helix gate open. At the same time, the rotation of the CTD breaks the interaction between the CD- and G-loops thus releasing the G-loop. The G-loop then bounces away from the CD-loop, which leads to the opening of the G-loop gate and the full opening of the pore. We identified a series of interaction networks, between the N-terminus, CD loop, C linker and G loop one by one, which exquisitely regulates the global conformational changes during the opening of Kir channels by PIP2.
Inwardly rectifying potassium (Kir) channels allow greater K+ influx at membrane voltages more negative rather than efflux at voltages more positive than the potassium equilibrium potential. Kir channels are involved in a wide range of physiological processes, such as maintaining stable resting membrane potentials, controlling cell excitability, shaping the initial depolarization, regulating cardiac rhythm, vascular tone, insulin release, and salt flow across epithelia1,2,3, as well as the final repolarization of action potentials in many cell types, including heart cells4,5,6,7,8.
There are 16 members in the Kir family belonging to seven subfamilies (Kir1-7). Kir channels are homo- or hetero- tetramers of four subunits. Each subunit has a simple transmembrane domain (TMD), containing an outer transmembrane helix (M1), an ion-selective P loop (selectivity filter - SF), and an inner transmembrane helix (M2). Besides the M1-P-M2 motif, there exist a cytoplasmic domain (CTD), which is composed of N- and C- termini located on the intracellular side of the membrane forming a large ‘cytoplasmic pore’ structure. The C-linker, containing a dozen amino acids, connects the TMD and CTD9,10. The extension of the transmembrane permeation pathway to the cytoplasm is one unique characteristic feature of Kir family members11.
Kir channels are regulated by several different cellular factors, such as G-proteins, ATP, pH, some of which act specifically on specific subfamily members (nucleotides-Kir6, G-protein-Kir3, intracellular Na+-Kir3.2, 3.4, and extracellular K+ and Mg2+-Kir2)12,13,14. The anionic lipid phosphatidylinositol 4,5-bisphosphate (PI(4,5)P2, known as PIP2) on the other hand is needed to activate all members of eukaryotic Kir channels13. Kir channel regulation is accomplished by a conformational change that allows the protein to switch between two alternative (closed vs. open) conformations, a process known as gating. The cytosolic domain is highly conserved among the Kir subfamilies and forms the cytosolic vestibule15,16,17, which, together with the transmembrane pore, generates a long ion conduction pore18. There are three gates along the long central pore of Kir channels: the selectivity filter gate, the inner helix gate (both in the transmembrane pore) and the G-loop gate (in the cytoplasmic pore)13. Functional studies and mutagenesis data have suggested that positively charged residues in the N- and C-termini determine sensitivity of Kir channels to PIP2 activation19,20,21,22,23,24,25,26. These positively charged residues of the C-linker are capable of forming electrostatic interactions with the negatively charged head group of PIP2. Recently, atomic structures of Kir2.210 and Kir3.2 bound to PIP227 have been solved identifying residues that bind PIP2 directly. On the basis of static crystallographic structures, two possible gating models have been described as follows. The first model named “twist model”, which was proposed by Bavro and colleagues, was based on the structure of KirBac3.1 S129R (PDB code: 3ZRS)9. The hypothesis is that the rotation of the cytoplasmic domain (CTD) prepares the C-linker and brings the slide helix into register with the CD loop to open the inner helix gate9. The second model, named “upward motion model”, was proposed by Hansen and colleagues based on the structure of cKir2.2 (PDB code: 3SPI)10. This model suggested that an upward motion of the CTD translates towards and becomes tethered to the transmembrane domain (TMD), the G-loop first inserts into the TMD and then opens the inner helix gate10. However, the detailed gating mechanism of Kir channels induced by PIP2 remains obscure.
Among Kir channels, Kir2.1 channel is activated by PIP2 alone, serving as an excellent model with which to understand the detailed gating mechanism induced by PIP2. Here, we have combined molecular dynamics (MD) with targeted MD simulations to address the conformational transition pathway in the gating of the Kir2.1 channel. Our data show that Kir2.1 channel gating unfolds in a step-by-step process as follows. First, with the upward motion of the CTD, the C-linker forms a new helix and the Kir2.1 channel achieves an “activated” state but the pore remains in the closed state. Second, the kink of the C-linker triggers the rotation of the CTD which pulls the pore open. Moreover, we identified a series of interaction networks that controls the PIP2-induced conformational changes during Kir channel gating. Based on the data, a brand new gating model is proposed which will shed light on understanding the molecular mechanism of PIP2 gating of Kir channels.
Methods
Homology Modeling
Homology models of the full-length mouse Kir2.1 channel were performed using the SWISS-MODEL server28,29,30. The target sequences were taken from Genbank (http://www.ncbi.nlm.nih.gov/Genbank/). The template structures were the chicken Kir2.2 (PDB code: 3JYC31 and 3SPI), and the mouse Kir3.2 (PDB code: 3SYQ). These homology models were based on chain A of the template structures, in which the two missing loops, one that connects the N-terminal beta-strand and the slide helix, and one that connects the two transmembrane alpha-helices, were completed. All the models were evaluated with QMEAN (The QMEAN4 score is a composite score consisting of a linear combination of 4 statistical potential terms (estimated model reliability between 0–1)32. The pseudo-energies of the contributing terms are given their Z-scores with respect to scores obtained for high-resolution experimental structures of similar size solved by X-ray crystallography. The members of the inwardly rectifying K+ channel family exhibit high degree of sequence similarity. Due to high sequence homology (about 78%, 77% and 53% sequence identity to chicken Kir2.2 and mouse Kir3.2 respectively), the QMEAN4 score was 0.79, 0.566 and 0.545 respectively and QMEAN Z-score was −4.54, −3.36 and −3.66 respectively. Each model was compared to its template to verify that the modeling step had not significantly altered backbone and side chain conformation.
Conventional Molecular Dynamics
For the full-length Kir2.1 channels simulation, the channels were immersed in an explicit palmitoyloleoyl-phosphatidylcholine (POPC) bilayer generated by the VMD membrane package33. The whole system was then solvated, and K+ and Cl− of ~150 mM were positioned randomly among the solvent to neutralize the system. We built three systems (Closed, Activated, and Open states). Each system involved ~140,000 atoms in the MD simulation. Full three-dimensional periodic boundary conditions were used. Each system was in a rectangular box with the size of 101 × 98 × 156 Å3 (Closed state), 101 × 99 × 156 Å3 (Activated state), and 104 × 105 × 153 Å3 (Open state), respectively. The solvated systems then underwent four equilibration steps: (i) 4 ns of equilibration with melting of lipid tails, (ii) the entire protein was fixed for 5 ns, enabling reorganization of the lipid and solution (iii) 5-ns extensive equilibration with protein released, (iv) finally letting the system relax freely for over 10–20 ns until reaching equilibrium. Each Targeted Molecular Dynamic is performed on the equilibrated system.
ALL MD simulations were performed in with the NAMD2 program (http://www.ks.uiuc.edu/Research/namd/)34 and the CHARMM 27 force filed35. A scaling factor for 1–4 interactions of 1.0 was applied in all simulations. Langevin dynamics and the Langevin piston were used to maintain the temperature at 310 K and a pressure of 1 atm with a damping coefficient of 1 ps–1. The barostat oscillation and damping time scale for the Langevin piston method36,37 were set to 200 fs and 50 fs, respectively. The van der Waals interactions were modeled using the Lennard-Jones potential. Short-range interactions was smoothed at 10 Å and truncated at 12 Å. Long-range electrostatic forces were taken into account using the Particle Mesh Ewald (PME) method (120 × 120 × 180 grid points)38,39. Non-bonded and PME calculations were performed on every time step. The time step employed was 2 fs, and pair lists were updated every 20 iterations. The coordinates were saved every 4 ps for analysis. Pore dimensions were evaluated using HOLE40. For molecular visualization and structural diagrams we used VMD. Simulations were carried out on a 64-processor Linux cluster.
Targeted Molecular Dynamics (Targeted MD)
In Targeted MD41, a subset of atoms in the simulation is guided towards a final ‘target’ structure by means of steering forces. The force on each atom is given by the gradient of the potential:
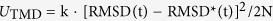 |
where k is the force constant, RMSD(t) is the instantaneous best-fit RMSD of the current coordinates to the target coordinates, RMSD*(t) is the preset RMSD value for the current time step, and N is the number of targeted atoms. The number of atoms used to calculate the RMSD from the target structure was set to be the same as the number of restrained atoms. The targeted RMSD value was decreased monotonically from the initial RMSD to the target structure until it reached near 0 Å at the end of the Targeted MD simulation. The Targeted MD method generates the trajectory of the conformational transition by using an external force between the starting and the target molecular conformation42,43,44,45,46.
Results
Constructing 3D structural models in different conformational states of Kir2.1
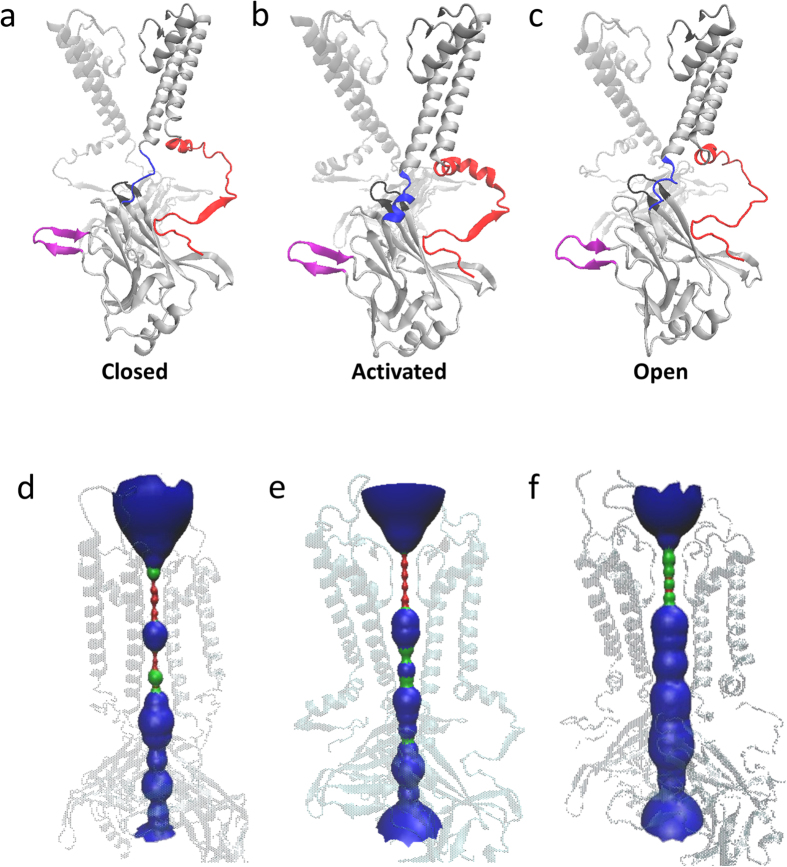
As shown in Fig. 1a–c, we constructed three 3-dimentional structures of Kir2.1 channels. The crystal structure of chicken Kir2.2 and mouse Kir3.2 with PDB ID 3JYC31, 3SPI and 3SYQ are chosen as the templates. The sequences identities are 78%, 77% and 53%, respectively. Based on the radius of the pore (Fig. 1d–f), we named them closed, activated and open states of Kir2.1, respectively. During 10–20 ns free MD simulations, these three structures reach their equilibration states whose RMSD values are 3 Å or less (Fig. 2). Comparing the three structures, we identified the main conformational difference which is the C-linker. Electrophysiological experiments and crystallographic data show that there are PIP2 binding sites at the C-linker.
Figure 1. Schematic diagrams of the structures of Kir2.1 in closed.
(a), activated (b) and open (c) states. C-linker, N-terminal and G-loop are highlighted as blue, red and black, respectively. (d–f) are the pore lining of closed, activated and open channel, respectively. The pore lining generated using HOLE is shown as a red (radius < size of water), green (radius ≈ size of water) and blue (radius > size of water). All the structures are generated using VMD.
Figure 2. RMSD variations for three systems.
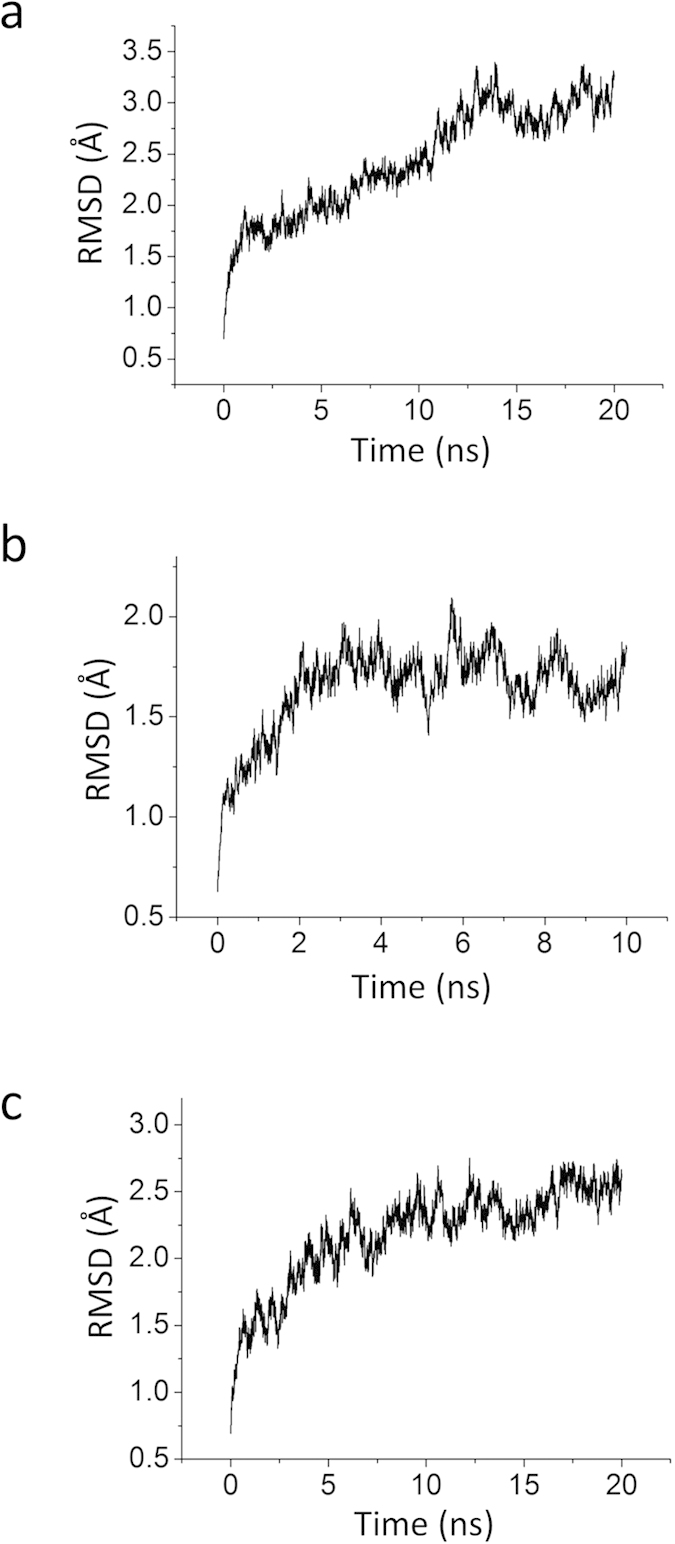
(a, Closed. b, Activated. c, Open.) throughout the simulation. RMSDs were calculated based on all the Cα atoms of the channel.
Next, we proceeded to perform a series of Targeted MD simulations on the C-linker to confirm the conformational pathway involved in the gating of Kir channels.
Formation of a helix of the C-linker induces a 5 Å upward motion of the CTD pushing the pore to the activated state
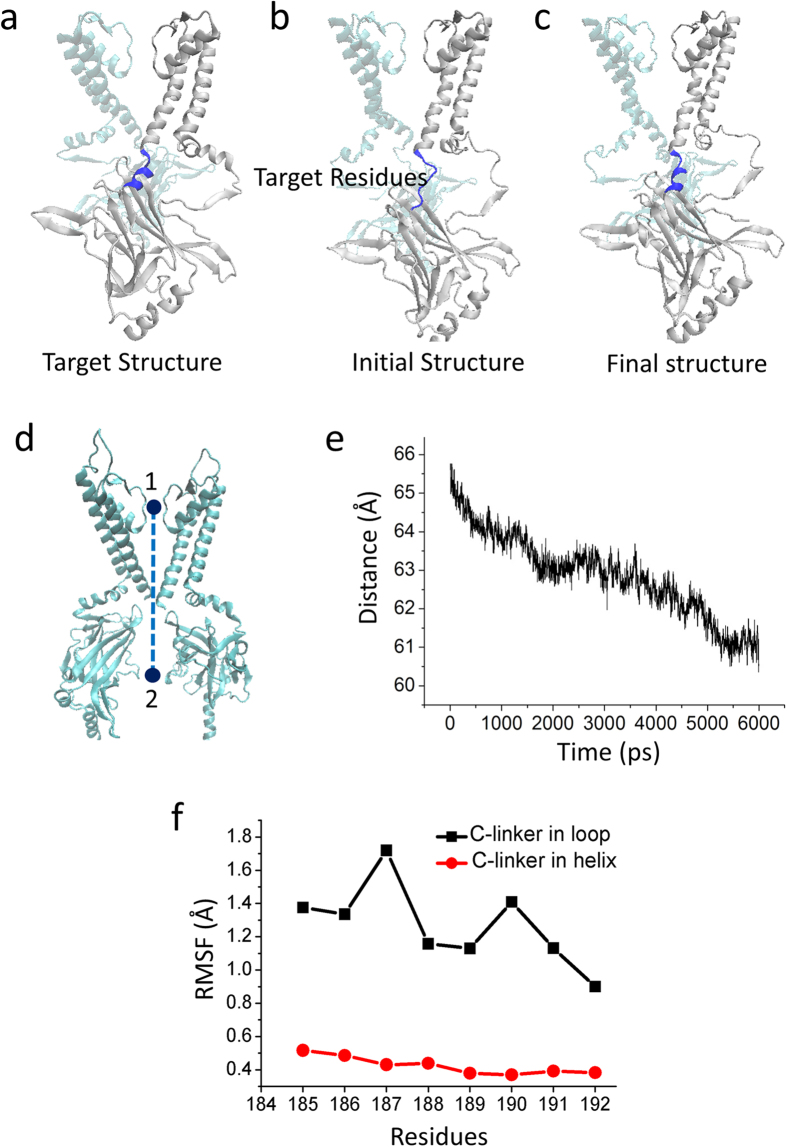
To test whether the conformational change of the C linker could open the channel, we first performed Targeted MD simulation at the C-Linker of Kir2.1 which are highlighted in blue in Fig. 3a–c. The C-Linker at the helical state in the activated Kir2.1 channel was set as the target structure (Fig. 3a, the blue helix). During the Targeted MD simulation, an external force was applied to the backbone atoms of the C-linker residues (Lys185 to Thr192) with a force constant of 500 kcal/mol/Å2, which pushed the C-Linker to change from a loop to a helix. After 6 ns Targeted MD, the final structure of the C-Linker changed from loop to helix (Fig. 3c). During this process, the distance R (the R is the distance from the center of the selectivity filter to the center of the CTD) decreased from 65.6 Å to 60.8 Å, showing about 5 Å upward movement of the CTD toward the membrane (Fig. 3d, e). The RMSF (root mean squared fluctuation) shows that the transition from a loop to a helical structure produced a more rigid C-linker (Fig. 3f), which enhanced the connection between the TMD and CTD. Thus the pore reached the activated state.
Figure 3. The CTD transfers 5 Å towards the TMD during the first Targeted MD simulation which focuses on the C-linker (blue).
(a) The schematic diagram of the targeted structure, which is in the activation state. (b) The schematic diagram of the initial structure, which is in the closed state. The target residues, to which the targeted force is applied (residues Lys185-Thr192), are colored blue. (c) The schematic diagram of the final conformation, which is achieved by the Targeted MD simulation. (d) Definition of the distance (R) which is from the center of the selectivity filter (the upper sphere) to the center of the C-terminal domain (CTD) (the lower sphere). (e) Evolution of the distance R vs. time. (f) RMSFs of the residues in C-linker, when the conformation of the C-linker is in the helical (black) and in the loop states (red).
The rotation of the CTD pulls the pore to the open state
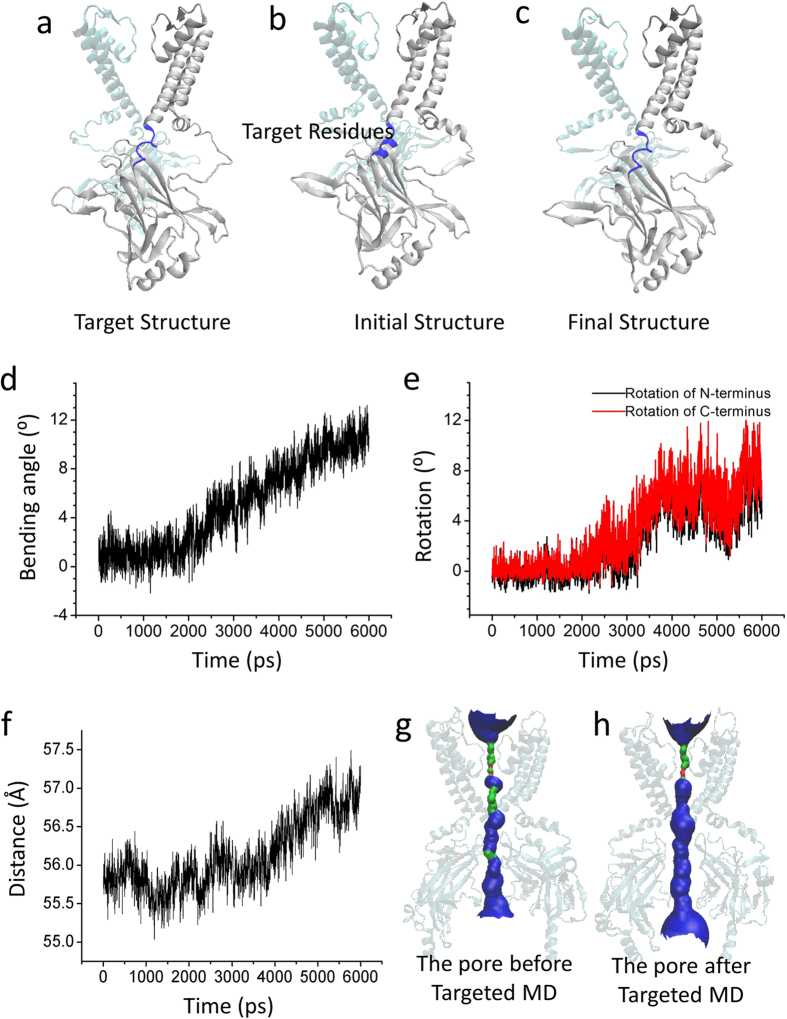
We next performed a Targeted MD simulation, which started with the activated state targeting the structure at the open state (Fig. 4a, b). The final structure is shown in Fig. 4c. During this simulation, an external force was applied to the backbone atoms of the C-linker (Lys185 to Thr192) (blue) and the PIP2 binding sites (Arg80, Trp81, Arg82, Lys182, Lys185, Pro186, Lys187, Lys188, Arg189 and Arg218) with a force constant of 500 kcal/mol/Å2, which made the C-linker start to bend at 2 ns, by up to about 12° (Fig. 4d). At the same time, the N/C-termini also started to rotate at 2.5 ns, by up to about 8° around the channel axis in an anticlockwise direction (viewed from the membrane) (Fig. 4e)47. The C-linker transitioned from a helical to a semi-helical state (Fig. 4c). The CTD showed a small downward movement at 3.6 ns (Fig. 4f) with the pore achieving the full open state (Fig. 4g, h).
Figure 4. The rotation of CTD pulls the channel to the open state.
(a) The schematic diagram of targeted structure, which is in the open state. (b) The schematic diagram of the initial structure, which is in the activated state. The target residues, to which the targeted force is applied (residues Lys185-Thr192 and PIP2 binding sites), are colored blue. (c) The schematic diagram of the final conformation, which is achieved by our last Targeted MD simulation. (d) The time course of the kinking of the C-linker. (e) The time course of the rotation of the N- (black) and C-termini (red). There is an 8° rotation-angle of the CTD the during Targeted MD simulation. (f) The distance, R, vs. the simulation time. (g) and (h) show the schematic pore lining by Kir2.1 (generated using HOLE) for the initial-activated state and the final conformations achieved by the simulations, respectively. The pore lining generated using HOLE is shown as a red (radius < size of water), green (radius ≈ size of water) and blue (radius > size of water).
The twisting of the C-linker induces a kink of the M2 which opens the inner helix gate
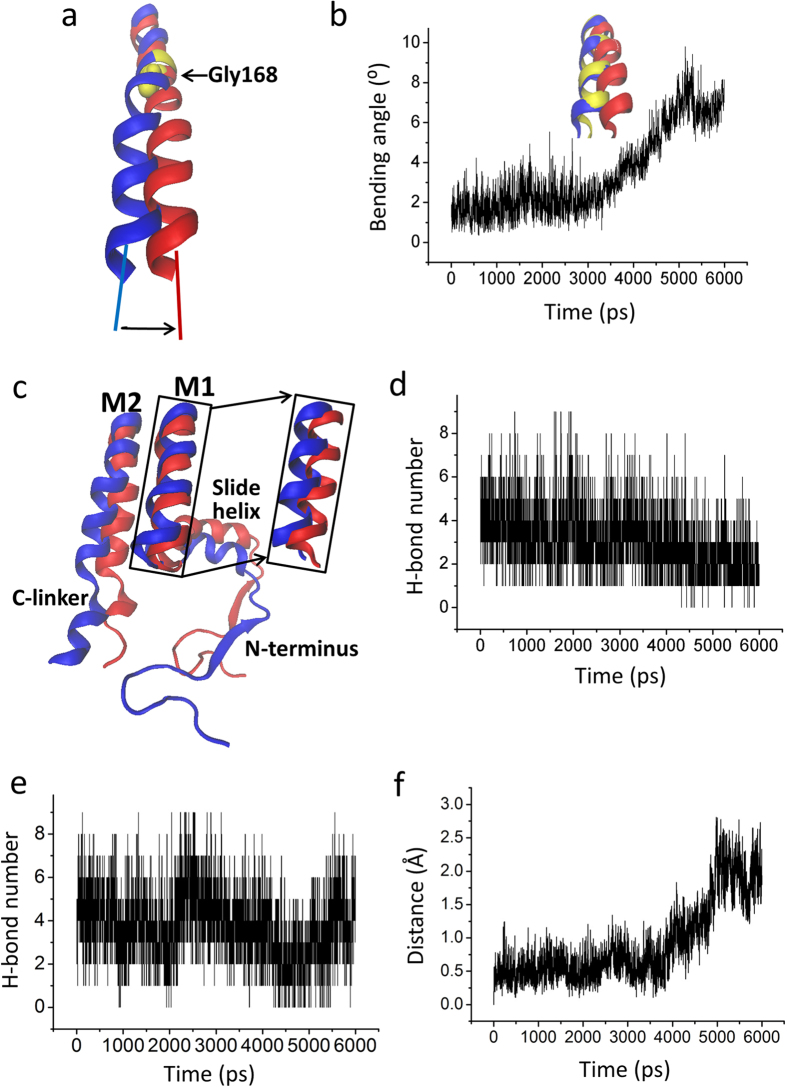
More generally, the mechanistic details of opening of the inner helix and G-loop gates are far from clear. Compared to the activated state, the lower part of the M2 bends at a highly conserved glycine, the hinge residue48,49,50, whereas the structure above the conserved glycine remains relatively rigid. The M2 helix starts to bend at approximately 3.6 ns, by up to about 8° (Fig. 5a, b)9,51. As shown in Fig. 4a–c, the C-linker connects the inner helix M2 and the CTD. The C-linker in a helical state shows high rigidity, which strengthens the connection between M2 and the CTD (Fig. 3f). Our data show that there are two parts that contribute to bending the M2 helix. First, the bending of the C-linker contributes to the kink of the M2 helix (Figs 4d and 5c). The upward motion of the slide helix starting at 3.6 ns facilitates the bending of the M2 helix (Fig. 5c, f). Second, the Interactions between the M1 and M2 helices and between the slide helix and between M1 helix contribute to a conformation change of M1 making the M2 helix bend (Fig. 5d, e).
Figure 5. Bending of inner M2 helix opens the bundle-crossing gate.
(a) The kink of M2 helix at the conserved glycine hinge (Gly 168) from the closed state (blue) to the conformation (red). (b) Evolution of the bending angle of M2 vs. the simulation time. Inside panel shows the conformation of the inner M2 helix at 0 ns (blue), 3 ns (yellow), and 6 ns (red) during the Targeted MD simulation. (c) Partial structure in the final Targeted MD conformation (red) compared to the initial conformation (blue). (d) and (e) are the time courses of the H-bond forming between outer M1 and inner M2 helix, and between slide helix and M1 helix, respectively. (f) The time courses of the distance of the center of slide helix upward movement to the membrane.
The G-loop bounces away from the CD loop, which opens the G-loop gate
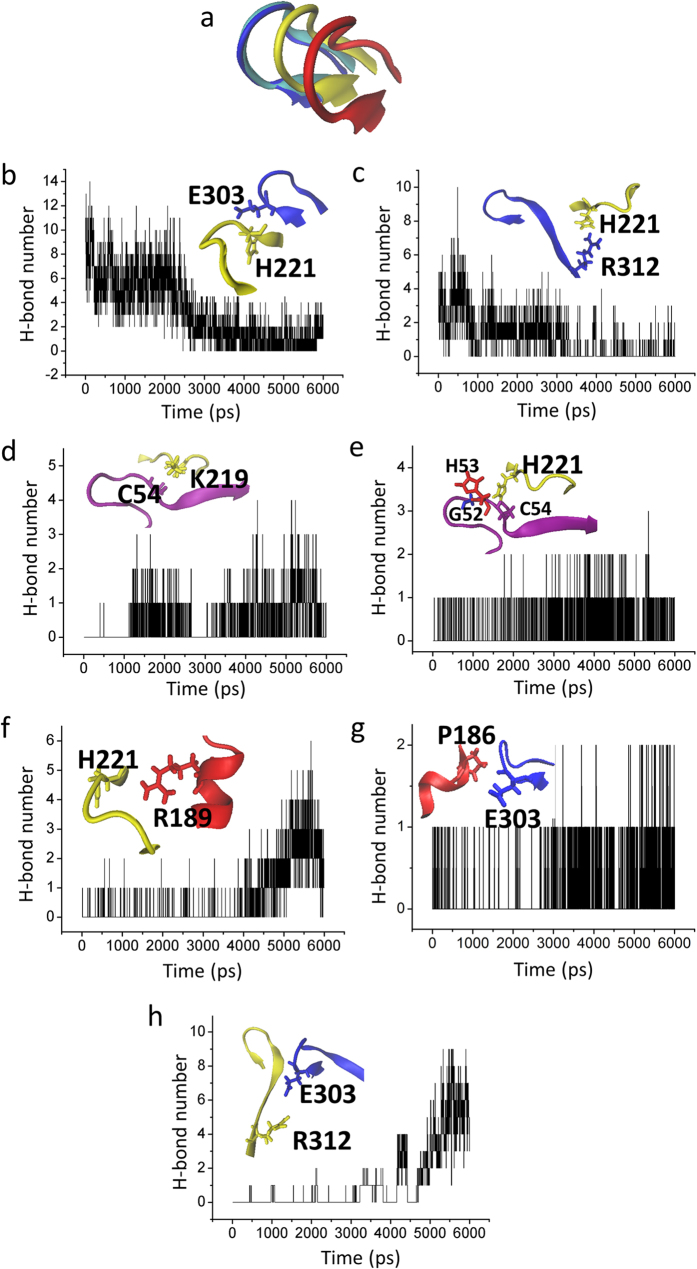
Besides the inner helix gate located near the inner leaflet of the bilayer, the G-loop gate is located at the CTD along the pore. As shown in Fig. 6a, the G-loop moves significantly as the channel achieves its open state. In this Targeted MD simulation, we identified three interaction-networks. The interactions between G loop and CD loop (E303-H221 and R312-H221) are weakened (Fig. 6b, c), which destabilizes the closed state of the G-loop gate. The intrasubunit interactions between the N-terminus and the CD loop are strengthened, namely C54 with K219 and G52, H53, C54 with H221 (Fig. 6d, e) which enhances the connections between the N terminus and the C terminus. The intersubunit interactions between the CD loop and the C-linker (H221-R189), between the C-linker and the G loop (P186-E303) and between the adjacent G loops (E303-R312) are strengthened (Fig. 6f–h), which enhances the connections between the C terminal, C-linker and G loop. We speculate that these interactions between N-terminus, CD loop, C linker and G loop are gradually strengthened, which will stabilize the G loop in the open state.
Figure 6. The interaction network that opens the G-loop gate.
(a) The distinct conformations of G loop at 0 ns (blue), 2 ns (silver), 3 ns (yellow), and 6 ns (red) during the Targeted MD simulation. (b) and (c) show the time course of the interaction between G-loop (blue) and CD-loop (yellow) through intrasubunit E303-H221 (b) and intersubunit R312–H221 (c). (d) and (e) show the time course of interactions between N-terminus (purple) and CD-loop (yellow) through C54–K219 (d) and G52/H53/C54-H221 (e). (f–h) show the strengthened interactions between CD-loop (yellow) and C-linker (red) through H221–R189 (f), between C-linker (red) and G-loop (blue) through P186–E303 (g) and between adjacent G-loops through E303–R312 (h).
Gating model of Kir channels
The data obtained in this study now allow us to propose a more detailed model of PIP2-induced gating of Kir channels. The first conformational change of the CTD is a 5 Å upward translocation towards the TMD which is pushed by the C-linker to change from a loop to a helical structure. The pore of the Kir channel is still closed. But the kink of the C linker, which is involved in interactions with PIP2 triggers the rotation of the CTD (Fig. 4d, e). The rotation of the CTD causes the C-linker to partially uncoil because of the same direction of the rotation of the CTD and the uncoiling of C-linker (Figs 4e and 5c). The C-linker switches from a helix to a semi-helix, which engages the further rotation of the N/C-terminus (Fig. 4e) which triggers a small downward movement of the CTD (Fig. 4f) and the upward movement of the slide helix (Fig. 5f)52,53. The two movements cause the kink of the M2 helix (Fig. 5b), ultimately opening the inner helix gate (Fig. 5h)9,51. The rotational movement or twist of the CTD could therefore conceivably promote opening of the inner helix gate16,47,54. With rotation of the N-terminus, the interaction between G loop and CD loop is broken and then the bouncing away of the G loop leads to the opening of the G loop gate (Fig. 6a–c). The strengthened interaction between N-terminus, CD loop, C-linker and G loop not only stabilize the G loop gate in the open state (Fig. 6d–h), but also can stabilize the inner helix gate (Fig. 6f, g). The gating model we propose here is similar to previous gating models52,53,55, but our current model provides greater details than the former ones leading to channel full opening.
Discussion
PIP2-induced gating of Kir channel is an intrinsically dynamic process and difficult to understand by the few available static crystal structures that are missing the key transition steps connecting them. There have been various studies aiming to understand the molecular mechanism of Kir channel gating51,56,57,58,59,60,61,62. However, since allosteric conformational changes, such as the PIP2-driven gating of Kir channels, take place on the microsecond time scale, it is not possible to capture the transfer of a closed channel to an open one even through 100 ns-long MD56 or 500 ns-long Coarse-Grained MD58 simulations. To accomplish the transition from the closed to the open state of full-length Kir channels, we performed Targeted MD simulations, which was developed by Schlitter et al.41,63 and has been used to study a variety of allosteric transitions in large proteins42,43,44,45,46,64,65,66,67.
Here we applied Targeted MD to study the gating of Kir2 channels. We have focused on the gating changes induced by the C-linker (a domain at the C-terminus of the inner helix). We performed a two step-targeted MD on a modeled mouse full-length Kir2.1 channel. To the best of our knowledge, this is the first time Targeted MD simulations have been utilized aiming to understand the detailed gating mechanism of Kir channels.
Comparing available crystal structures of Kir channels, we noticed that the C-linker can change conformation from a loop to a helix in a PIP2-dependent manner. If PIP2 is replaced by PPA, which contains as a head group only phosphoric acid, the head group does not interact with the CTD and cannot maintain the helical structure of the C-linker. This suggests that to keep the C-linker in a helical structure PIP2 is needed10. This is compatible with a recent functional study showing that small head group anionic lipids failed to activate Kir channels in the absence of PIP268. PIP2 facilitated the cytoplasmic domain movement toward the membrane. A vertical motion of the Kir domains seems to be a critical step for channel opening13,69,70. So the C-linker changes conformation from a loop to a helix, which is the first step toward Kir channel pore opening. The best-characterized lipid modulator of Kir channel activity is the anionic membrane phospholipid, PIP2, only 1% of the acidic lipid in the whole cell71,72,73. PIP2 mainly binds to the N-terminal end of the slide helix, at the domain connecting the TMD and CTD (C-linker)10,22,74,75. The channel-PIP2 interaction providing a tangential force may facilitate the bending of the C-linker which causes the rotation of the CTD, and then the C-linker uncoils. Limited by the methods, there is no PIP2 in our Targeted MD simulations. During the simulation, we applied force on the PIP2 binding residues and hoped that the applied forces, in somehow, mimic the channel-PIP2 interactions. Following this idea, we propose that the same direction of the uncoiling of C-linker and the rotation of the CTD causes a further counterclockwise rotation of CTD (Fig. 4e) to trigger a small downward movement of CTD (Fig. 4f) and an upward movement of the slide helix (Fig. 5f) driving the kinking of the M2 helix (Fig. 5b) to open the inner helix gate. The secondary anionic phospholipids including PG, PA, PS, PI, and CL can potentiate the high PIP2 sensitivity68. The synergistic PL(-) can pull the N-terminal Slide Helix towards the membrane to increase the PIP2 affinity. Our results are consistent with the conformational effect, which can stabilize the open state47. The Slide Helix is important for channel gating. For example, Slide Helix mutations were reported to cause Barter’s syndrome (in Kir1.1)76,77, neonatal diabetes (in Kir6.2)78 and Andersen-Tawil (in Kir2.1)79.
Following our previous notion57 which was that the interaction networks between the N termini, CD-G loops and C-linker play a critical role in the PIP2-induced gating of Kir channels, we focused on the interactions between these residues. Our data show that the rotation of CTD of Kir2.1 alters interactions between the G-loop and CD-loop, thus breaking interactions between H221 of the CD-loop and the tip (H221-E303) (Fig. 6b) or the base of the G-loop (H221-R312) (Fig. 6c). Liberation of the two residues allowed the G-loop to “bounce back” and open wide enough for K+ ion passage. Three new interactions are then formed, namely E303 interacts both with intersubunit P186 and R312, H221 interacts both with R189 and N-terminus, and the N-terminus interacts with the CD-loop (C54-K219) (Fig. 6d–h). These interactions stabilize the G-loop in the open state. Moreover, the crystal structures of Kir channels also show that the opening of the G-loop is PIP2 independent, for example Kir2.2-apo (PDB code: 3JYC) and Kir2.2-holo (PDB code: 3SPI), have open and closed G-loop, respectively. The counterclockwise rotation of CTD leads to the kinking of the M2 helix and the opening of the G-loop gate. As has been shown for the X-ray structure of Kir3.2 channel47, rotation of the CTD facilitates the gating of Kir channels.
Our data show that the opening of the G-loop gate precedes the opening of the inner helix gate (Figs 5a, b and 6a). However, there is still an open question: is the G-loop gate coupled to the inner helix gate? Undoubtedly, more experiments will be needed to answer these questions.
Additional Information
How to cite this article: Li, J. et al. Identification of the Conformational transition pathway in PIP2 Opening Kir Channels. Sci. Rep. 5, 11289; doi: 10.1038/srep11289 (2015).
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Grant No. 11247010 to HA, 11175055 and 11475053 to YZ, 11347017 to SZ), NIH R01 grant HL059949 to DEL and the Natural Science Foundation of the Hebei Province of China (Grant No. C2012202079 and C2015202340 to HA). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Footnotes
Author Contributions J.L., Y.Z. and H.A. designed the project and wrote the main manuscript text. J.L. and H.A. did most computation and data analysis and prepared all figures. S.L., C.P. and S.Z. did most of the computational work and data analysis. Y.L., Y.C. and H.Y. helped with the preparation of some figures. D.E.L., H.Z., M.L., Y.Z. and H.A. revised the manuscript. All authors reviewed the manuscript.
References
- Lopatin A. N., Makhina E. N. & Nichols C. G. Potassium channel block by cytoplasmic polyamines as the mechanism of intrinsic rectification. Nature 372, 366–9 (1994). [DOI] [PubMed] [Google Scholar]
- Nichols C. G., Makhina E. N., Pearson W. L., Sha Q. & Lopatin A. N. Inward rectification and implications for cardiac excitability. Circ Res 78, 1–7 (1996). [DOI] [PubMed] [Google Scholar]
- Nichols C. G. & Lopatin A. N. Inward rectifier potassium channels. Annu Rev Physiol 59, 171–91 (1997). [DOI] [PubMed] [Google Scholar]
- Hagiwara S., Miyazaki S. & Rosenthal N. P. Potassium current and the effect of cesium on this current during anomalous rectification of the egg cell membrane of a starfish. J Gen Physiol 67, 621–38 (1976). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ishihara K., Mitsuiye T., Noma A. & Takano M. The Mg2+ block and intrinsic gating underlying inward rectification of the K+ current in guinea-pig cardiac myocytes. J Physiol 419, 297–320 (1989). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ishihara K. & Hiraoka M. Gating mechanism of the cloned inward rectifier potassium channel from mouse heart. J Membr Biol 142, 55–64 (1994). [DOI] [PubMed] [Google Scholar]
- Stanfield P. R. et al. The intrinsic gating of inward rectifier K+ channels expressed from the murine IRK1 gene depends on voltage, K+ and Mg2+. J Physiol 475, 1–7 (1994). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kubo Y. Effects of extracellular cations and mutations in the pore region on the inward rectifier K+ channel IRK1. Receptors Channels 4, 73–83 (1996). [PubMed] [Google Scholar]
- Bavro V. N. et al. Structure of a KirBac potassium channel with an open bundle crossing indicates a mechanism of channel gating. Nat Struct Mol Biol 19, 158–63 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansen S. B., Tao X. & MacKinnon R. Structural basis of PIP2 activation of the classical inward rectifier K+ channel Kir2.2. Nature 477, 495–8 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nishida M. & MacKinnon R. Structural basis of inward rectification: cytoplasmic pore of the G protein-gated inward rectifier GIRK1 at 1.8 A resolution. Cell 111, 957–65 (2002). [DOI] [PubMed] [Google Scholar]
- Hibino H. et al. Inwardly rectifying potassium channels: their structure, function, and physiological roles. Physiol Rev 90, 291–366 (2010). [DOI] [PubMed] [Google Scholar]
- Xie L. H., John S. A., Ribalet B. & Weiss J. N. Activation of inwardly rectifying potassium (Kir) channels by phosphatidylinosital-4,5-bisphosphate (PIP2): interaction with other regulatory ligands. Prog Biophys Mol Biol 94, 320–35 (2007). [DOI] [PubMed] [Google Scholar]
- Li J. et al. Lack of negatively charged residues at the external mouth of kir2.2 channels enable the voltage-dependent block by external mg2+. PLoS One 9, e111372 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuo A., Domene C., Johnson L. N., Doyle D. A. & Venien-Bryan C. Two different conformational states of the KirBac3.1 potassium channel revealed by electron crystallography. Structure 13, 1463–72 (2005). [DOI] [PubMed] [Google Scholar]
- Pegan S. et al. Cytoplasmic domain structures of Kir2.1 and Kir3.1 show sites for modulating gating and rectification. Nat Neurosci 8, 279–87 (2005). [DOI] [PubMed] [Google Scholar]
- Nishida M., Cadene M., Chait B. T. & MacKinnon R. Crystal structure of a Kir3.1-prokaryotic Kir channel chimera. EMBO J 26, 4005–15 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuo A. et al. Crystal structure of the potassium channel KirBac1.1 in the closed state. Science 300, 1922–6 (2003). [DOI] [PubMed] [Google Scholar]
- Huang C. L., Feng S. & Hilgemann D. W. Direct activation of inward rectifier potassium channels by PIP2 and its stabilization by Gbetagamma. Nature 391, 803–6 (1998). [DOI] [PubMed] [Google Scholar]
- Rohacs T., Chen J., Prestwich G. D. & Logothetis D. E. Distinct specificities of inwardly rectifying K(+) channels for phosphoinositides. J Biol Chem 274, 36065–72 (1999). [DOI] [PubMed] [Google Scholar]
- Zhang H., He C., Yan X., Mirshahi T. & Logothetis D. E. Activation of inwardly rectifying K+ channels by distinct PtdIns(4,5)P2 interactions. Nat Cell Biol 1, 183–8 (1999). [DOI] [PubMed] [Google Scholar]
- Lopes C. M. et al. Alterations in conserved Kir channel-PIP2 interactions underlie channelopathies. Neuron 34, 933–44 (2002). [DOI] [PubMed] [Google Scholar]
- Donaldson M. R. et al. PIP2 binding residues of Kir2.1 are common targets of mutations causing Andersen syndrome. Neurology 60, 1811–6 (2003). [DOI] [PubMed] [Google Scholar]
- Pegan S., Arrabit C., Slesinger P. A. & Choe S. Andersen’s syndrome mutation effects on the structure and assembly of the cytoplasmic domains of Kir2.1. Biochemistry 45, 8599–606 (2006). [DOI] [PubMed] [Google Scholar]
- Xie L. H., John S. A., Ribalet B. & Weiss J. N. Phosphatidylinositol-4,5-bisphosphate (PIP2) regulation of strong inward rectifier Kir2.1 channels: multilevel positive cooperativity. J Physiol 586, 1833–48 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soom M. et al. Multiple PIP2 binding sites in Kir2.1 inwardly rectifying potassium channels. FEBS Lett 490, 49–53 (2001). [DOI] [PubMed] [Google Scholar]
- Whorton M. R. & MacKinnon R. Crystal structure of the mammalian GIRK2 K+ channel and gating regulation by G proteins, PIP2, and sodium. Cell 147, 199–208 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guex N. & Peitsch M. C. SWISS-MODEL and the Swiss-PdbViewer: an environment for comparative protein modeling. Electrophoresis 18, 2714–23 (1997). [DOI] [PubMed] [Google Scholar]
- Schwede T., Kopp J., Guex N. & Peitsch M. C. SWISS-MODEL: An automated protein homology-modeling server. Nucleic Acids Res 31, 3381–5 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arnold K., Bordoli L., Kopp J. & Schwede T. The SWISS-MODEL workspace: a web-based environment for protein structure homology modelling. Bioinformatics 22, 195–201 (2006). [DOI] [PubMed] [Google Scholar]
- Tao X., Avalos J. L., Chen J. & MacKinnon R. Crystal structure of the eukaryotic strong inward-rectifier K+ channel Kir2.2 at 3.1 A resolution. Science 326, 1668–74 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benkert P., Biasini M. & Schwede T. Toward the estimation of the absolute quality of individual protein structure models. Bioinformatics 27, 343–50 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Humphrey W., Dalke A. & Schulten K. VMD: visual molecular dynamics. J Mol Graph 14, 33–8, 27-8 (1996). [DOI] [PubMed] [Google Scholar]
- Phillips J. C. et al. Scalable molecular dynamics with NAMD. J Comput Chem 26, 1781–802 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKerell A. D. et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J Phys Chem B 102, 3586–3616 (1998). [DOI] [PubMed] [Google Scholar]
- Feller S. E., Zhang Y., Pastor R. W. & Brooks B. R. Constant pressure molecular dynamics simulation: the Langevin piston method. J Chem Phys 103, 4613 (1995). [Google Scholar]
- Martyna G. J., Tobias D. J. & Klein M. L. Constant pressure molecular dynamics algorithms. J Chem Phys 101, 4177 (1994). [Google Scholar]
- Essmann U. et al. A smooth particle mesh Ewald method. J Chem Phys 103, 8577–8593 (1995). [Google Scholar]
- Darden T., York D. & Pedersen L. Particle mesh Ewald: An N⋅ log (N) method for Ewald sums in large systems. J Chem Phys 98, 10089 (1993). [Google Scholar]
- Smart O. S., Neduvelil J. G., Wang X., Wallace B. A. & Sansom M. S. HOLE: a program for the analysis of the pore dimensions of ion channel structural models. J Mol Graph 14, 354–60, 376 (1996). [DOI] [PubMed] [Google Scholar]
- Schlitter J., Engels M. & Kruger P. Targeted molecular dynamics: a new approach for searching pathways of conformational transitions. J Mol Graph 12, 84–9 (1994). [DOI] [PubMed] [Google Scholar]
- Li Y., Barbault F., Delamar M., Zhang R. & Hu R. Targeted molecular dynamics (TMD) of the full-length KcsA potassium channel: on the role of the cytoplasmic domain in the opening process. J Mol Model 19, 1651–66 (2013). [DOI] [PubMed] [Google Scholar]
- Weng J., Fan K. & Wang W. The conformational transition pathways of ATP-binding cassette transporter BtuCD revealed by targeted molecular dynamics simulation. PLoS One 7, e30465 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perdih A., Kotnik M., Hodoscek M. & Solmajer T. Targeted molecular dynamics simulation studies of binding and conformational changes in E. coli MurD. Proteins 68, 243–54 (2007). [DOI] [PubMed] [Google Scholar]
- Lee H. S. et al. Targeted molecular dynamics simulation studies of calcium binding and conformational change in the C-terminal half of gelsolin. Biochem Biophys Res Commun 342, 702–9 (2006). [DOI] [PubMed] [Google Scholar]
- Cheng X., Wang H., Grant B., Sine S. M. & McCammon J. A. Targeted molecular dynamics study of C-loop closure and channel gating in nicotinic receptors. PLoS Comput Biol 2, e134 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whorton M. R. & MacKinnon R. X-ray structure of the mammalian GIRK2-betagamma G-protein complex. Nature 498, 190–7 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magidovich E. & Yifrach O. Conserved gating hinge in ligand-and voltage-dependent K+ channels. Biochemistry 43, 13242–13247 (2004). [DOI] [PubMed] [Google Scholar]
- Jin T. et al. The βγ Subunits of G Proteins Gate a K+ Channel by Pivoted Bending of a Transmembrane Segment. Mol cell 10, 469–481 (2002). [DOI] [PubMed] [Google Scholar]
- Jiang Y. et al. The open pore conformation of potassium channels. Nature 417, 523–526 (2002). [DOI] [PubMed] [Google Scholar]
- Grottesi A., Domene C., Hall B. & Sansom M. S. Conformational dynamics of M2 helices in KirBac channels: helix flexibility in relation to gating via molecular dynamics simulations. Biochemistry 44, 14586–94 (2005). [DOI] [PubMed] [Google Scholar]
- Logothetis D. E., Jin T., Lupyan D. & Rosenhouse-Dantsker A. Phosphoinositide-mediated gating of inwardly rectifying K(+) channels. Pflugers Arch 455, 83–95 (2007). [DOI] [PubMed] [Google Scholar]
- Enkvetchakul D., Jeliazkova I., Bhattacharyya J. & Nichols C. G. Control of inward rectifier K channel activity by lipid tethering of cytoplasmic domains. J Gen Physiol 130, 329–34 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clarke O. B. et al. Domain reorientation and rotation of an intracellular assembly regulate conduction in Kir potassium channels. Cell 141, 1018–29 (2010). [DOI] [PubMed] [Google Scholar]
- Lee S. J. et al. Secondary anionic phospholipid binding site and gating mechanism in Kir2.1 inward rectifier channels. Nat Commun 4, 2786 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meng X. Y., Zhang H. X., Logothetis D. E. & Cui M. The molecular mechanism by which PIP(2) opens the intracellular G-loop gate of a Kir3.1 channel. Biophys J 102, 2049–59 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- An H. L. et al. The cytosolic GH loop regulates the phosphatidylinositol 4,5-bisphosphate-induced gating kinetics of Kir2 channels. J Biol Chem 287, 42278–87 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stansfeld P. J., Hopkinson R., Ashcroft F. M. & Sansom M. S. PIP(2)-binding site in Kir channels: definition by multiscale biomolecular simulations. Biochemistry 48, 10926–33 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haider S., Tarasov A. I., Craig T. J., Sansom M. S. & Ashcroft F. M. Identification of the PIP2-binding site on Kir6.2 by molecular modelling and functional analysis. EMBO J 26, 3749–59 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haider S., Khalid S., Tucker S. J., Ashcroft F. M. & Sansom M. S. Molecular dynamics simulations of inwardly rectifying (Kir) potassium channels: a comparative study. Biochemistry 46, 3643–52 (2007). [DOI] [PubMed] [Google Scholar]
- Domene C., Grottesi A. & Sansom M. S. Filter flexibility and distortion in a bacterial inward rectifier K+ channel: simulation studies of KirBac1.1. Biophys J 87, 256–67 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Capener C. E., Proks P., Ashcroft F. M. & Sansom M. S. Filter flexibility in a mammalian K channel: models and simulations of Kir6.2 mutants. Biophys J 84, 2345–56 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schlitter J., Engels M., Krüger P., Jacoby E. & Wollmer A. Targeted molecular dynamics simulation of conformational change-application to the T↔ R transition in insulin. Mol Simulat 10, 291–308 (1993). [Google Scholar]
- Ovchinnikov V., Trout B. L. & Karplus M. Mechanical coupling in myosin V: a simulation study. J Mol Biol 395, 815–33 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madhusoodanan M. & Lazaridis T. Investigation of pathways for the low-pH conformational transition in influenza hemagglutinin. Biophys J 84, 1926–39 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma J. et al. A dynamic analysis of the rotation mechanism for conformational change in F(1)-ATPase. Structure 10, 921–31 (2002). [DOI] [PubMed] [Google Scholar]
- Ma J., Sigler P. B., Xu Z. & Karplus M. A dynamic model for the allosteric mechanism of GroEL. J Mol Biol 302, 303–13 (2000). [DOI] [PubMed] [Google Scholar]
- Cheng W. W., D’Avanzo N., Doyle D. A. & Nichols C. G. Dual-mode phospholipid regulation of human inward rectifying potassium channels. Biophys J 100, 620–8 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Enkvetchakul D. & Nichols C. G. Gating mechanism of KATP channels: function fits form. J Gen Physiol 122, 471–80 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- D’Avanzo N., Cheng W. W., Wang S., Enkvetchakul D. & Nichols C. G. Lipids driving protein structure? Evolutionary adaptations in Kir channels. Channels (Austin) 4, 139–41 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu C., Watras J. & Loew L. M. Kinetic analysis of receptor-activated phosphoinositide turnover. J Cell Biol 161, 779–91 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- McLaughlin S. & Murray D. Plasma membrane phosphoinositide organization by protein electrostatics. Nature 438, 605–11 (2005). [DOI] [PubMed] [Google Scholar]
- Hilgemann D. W. Local P. I. P.(2) signals: when, where, and how? Pflugers Arch 455, 55–67 (2007). [DOI] [PubMed] [Google Scholar]
- Schmidt M. R., Stansfeld P. J., Tucker S. J. & Sansom M. S. Simulation-based prediction of phosphatidylinositol 4,5-bisphosphate binding to an ion channel. Biochemistry 52, 279–81 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- D’Avanzo N., Lee S. J., Cheng W. W. & Nichols C. G. Energetics and location of phosphoinositide binding in human Kir2.1 channels. J Biol Chem 288, 16726–37 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Konrad M., Leonhardt A., Hensen P., Seyberth H. W. & Kockerling A. Prenatal and postnatal management of hyperprostaglandin E syndrome after genetic diagnosis from amniocytes. Pediatrics 103, 678–83 (1999). [DOI] [PubMed] [Google Scholar]
- Peters M. et al. Classification and rescue of ROMK mutations underlying hyperprostaglandin E syndrome/antenatal Bartter syndrome. Kidney Int 64, 923–32 (2003). [DOI] [PubMed] [Google Scholar]
- Nichols C. G. KATP channels as molecular sensors of cellular metabolism. Nature 440, 470–6 (2006). [DOI] [PubMed] [Google Scholar]
- Decher N. et al. Impaired interaction between the slide helix and the C-terminus of Kir2.1: a novel mechanism of Andersen syndrome. Cardiovasc Res 75, 748–57 (2007). [DOI] [PubMed] [Google Scholar]