Level set method for segmentation of infrared breast thermograms

Abstract

Breast thermography is a physiological test that provides information based on the temperature changes in breast. It records the temperature distribution of a body using the infrared radiation emitted by the surface of that body. Precancerous tissue and the area around a cancerous tumor have higher temperature due to angiogenesis, and higher chemical and blood vessel activity than a normal breast; hence breast thermography has potential to detect early abnormal changes in breast tissues. It can detect the first sign of forming up cancer before mammography can detect. The thermal information can be shown in a pseudo colored image where each color represents a specific range of temperature. Various methods can be applied to extract hot regions for detecting suspected regions of interests in the breast infrared images and potentially suspicious tissues. Image segmentation techniques can play an important role to segment and extract these regions in the breast infrared images. Shape, size and borders of the hottest regions of the images can help to determine features which are used to detect abnormalities. In this paper, three image segmentation methods: k-means, fuzzy c-means and level set are discussed and compared. These three methods are tested for different cases such as fibrocystic, inflammatory cancer cases. The hottest regions of thermal breast images in all cases are extracted and compared to the original images. According to the results, level set method is a more accurate approach and has potential to extract almost exact shape of tumors.

1. Introduction

All objects with temperature above absolute zero (0 K) radiate specific intensity of thermal energy and the amount of this radiation increases with temperature (EtehadTavakol et al., 2010[11]). The radiation emitted by an object causes infrared energy (Griffith et al., 2001[13]), but it is invisible to the human eye. Thermography is a method which helps to display thermal energy and one of its applications is Digital Infrared Thermal Imaging (DITI). It is a noninvasive, non-contact method of detecting the heat coming from human body (Arora et al., 2008[4]).

Breast thermography (Kennedy et al., 2009[15]) is a physiological test that displays information on temperature changes in breast tissues. The thermal information can be shown in a pseudo colored image where each color represents a specific range of temperature (EtehadTavakol et al., 2010[11]). This method has high portability and real time imaging capability. It is non-invasive (Ng, 2008[19]), passive, pain free, fast, low cost, sensitive and safe with no compression (EtehadTavakol et al., 2010[11]). Breast thermography can be utilized for women of all ages, with any breast size and density, for young, pregnant or nursing women. It is also effective for fibrocystic breasts and breasts with implants (EtehadTavakol et al., 2010[11]; Kennedy et al., 2009[15]). The procedure is based on the principle that precancerous tissue and the area around a cancerous tumor have higher temperature due to angiogenesis, and higher chemical and blood vessel activity than a normal breast (Ng and Kee, 2008[22]; EtehadTavakol et al., 2011[10]).

Studies support thermography's potential for early detection of breast abnormalities (Kennedy et al., 2009[15]), because it is based on detecting chemical changes and new blood vessels caused by tumor. In the other hand, mammography is an anatomical test that can find signs of cancer later than thermography. Various types of image segmentation (EtehadTavakol et al., 2010[11]; Gonzales and Woods, 2001[12]; Sowmya and Bhattacharya, 2005[28]; EtehadTavakol and Ng, 2013[9]; Pakhira, 2009[25]; Ng and Chen, 2006[21]; Ng et al., 2001[21]) methods can be applied to extract hot regions for detecting breast abnormalities and potentially suspicious tissues. Shape and size of tumor region that has been diagnosed with cancer can specify some tumor characteristics. For example it can determine how serious the tumor is and classifies its type. Unlike benign growth tumor which is encapsulated and has a smooth boundary, malignant tumor has an irregular shape (Healthhype, 2013[14]). These facts help to distinguish the type of detected tumor from thermal image but it requires an accurate regional division.

This paper is organized as follows: Three image segmentation methods are reviewed in section 2. K-means algorithm in Section 2A, Fuzzy c-means in 2B, and Level set in Section 2C. Experimental results are explained in Section 3. Section 4 concludes the results.

2. Methodology

Image segmentation (EtehadTavakol et al., 2011[10]) is the process by which an original image is segmented into multiple regions. The classification is based on some characteristic, such as color, intensity, texture, etc. In this paper three algorithms are described: k-means, fuzzy c-means and level set.

2A. K-means clustering

K-means clustering (MacQueen, 1967[17]) is a simple, fast and unsupervised method to classify data to a specified number of clusters (Pakhira, 2009[25]). The main idea is to define a centroid for each cluster in a way that all centroids are as far away from each other as possible, and then assign each data point to the nearest centroid. In each cycle K new centroids are re-calculated for the clusters resulting from previous step, and then data sets are categorized by minimizing the sum of squares of distances between data and the corresponding cluster centroid. As a result, k centroids change their location in each cycle until no further changes are done.

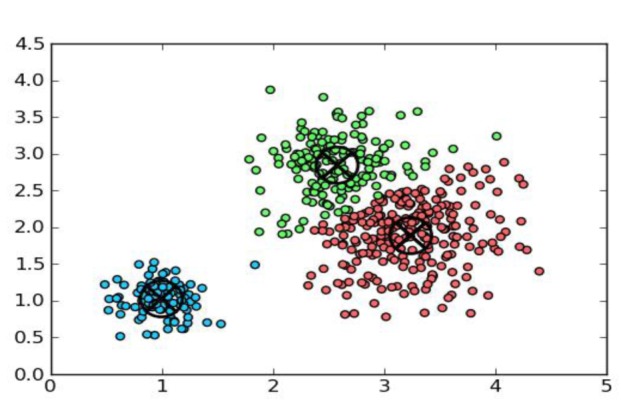
Figure 1(Fig. 1) shows a set of data which is divided into three clusters, and each cluster is represented by a specific color. Each data point is assigned to the nearest cluster center, such that the squared distances from the cluster are minimized.

Figure 1. K-means clustering.

In summary, this algorithm attempts to minimize the objective function J which is the sum of the squared error.

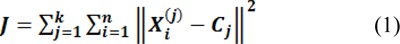
where X_i^(j) is a vector of points in cluster j and C_j is the cluster mean.

In summary, this clustering method follows these steps (EtehadTavakol et al., 2010[11]):

1. Choose the number of clusters (k)

2. Selects k points as the initial cluster centers randomly (initialization)

3. Assign each point to the closed cluster, based upon the Euclidean distance between each point and each cluster center

4. Re-calculate the mean of each cluster as the average of the points in that cluster

5. Iterate over steps 3 and 4 until the clusters converge. Convergence may be defined differently depending upon the implementation, but it normally means that no data point change clusters when these steps are repeated, and the function J reaches its minimum value.

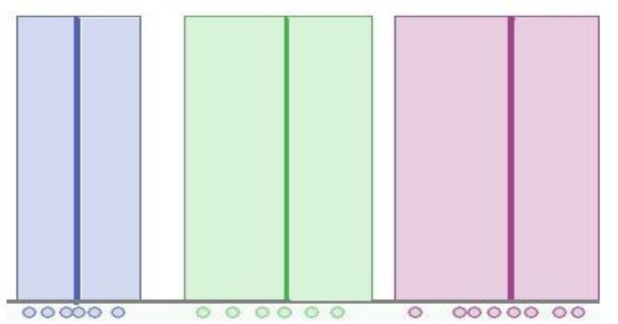
Figure 2(Fig. 2) shows the result of K-means clustering. It shows that each data element belongs to exactly one cluster, and consequently the membership function is a step function. It means that the allocation of data points is hard (all or nothing).

Figure 2. Membership function in K-means clustering.

2B. Fuzzy c-means clustering (FCM)

Fuzzy c-means clustering (developed by Dunn (1973[8]) and improved by Bezdek (1981[5])) is a class of algorithms for cluster analysis in which the allocation of data points to clusters is not hard (0 or 1) but allows one piece of data to belong to more than one cluster with a degree of membership between 0 and 1. This algorithm assigns membership to each data point corresponding to each cluster center on the basis of distance between the cluster center and the data point. The more the data is near to the cluster center more is its membership towards the particular cluster center. Clearly, summation of membership of each data point should be equal to one. Fuzzy c-means is frequently used in pattern recognition (Zhang and Chena, 2004[33]). This algorithm attains to minimize the objective function J_m (Chuang et al., 2006[7])

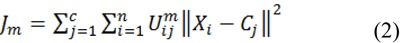
where m is any real number greater than one and controls the fuzziness of the membership function, X_i is a d-dimensional point, C_j is the d-dimension centers vector of the cluster, each element of matrix

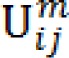
is a weight factor between 0 and 1 and shows the degree of membership of X_i in the cluster j, such that

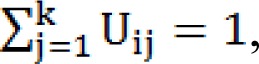
and ||*|| is any norm expressing the similarity between any measured data and its corresponding cluster center (EtehadTavakol et al., 2010[11]). It is an approach, where the data points have their membership values with the cluster centers, which will be updated iteratively. The FCM algorithm consists of the following steps:

1. Choose the number of clusters, c, exponent weight, m, and initialize the matrix U.

2. Calculate the centers vector C.

3. Update matrix U.

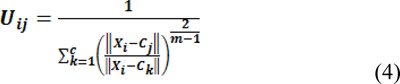
4. Iterate over steps 2 and 3 and update membership and cluster centers until the minimum value of J_m is achieved or change in any element of matrix U is below a specific threshold, ε.

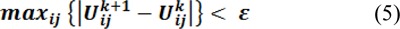
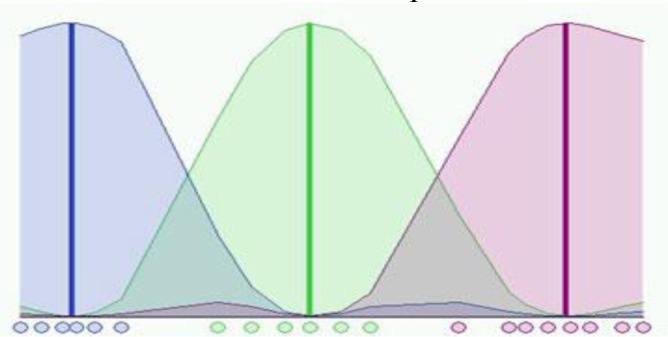
In Figure 3(Fig. 3), twenty data and three clusters are used to initialize the algorithm and to compute the U matrix. It shows the membership value for each datum and for each cluster. The color of the data is that of the nearest cluster according to the membership function. In this figure, each data point does not belong exactly to a cluster, but it can be placed in a middle way. In this case, the membership function follows a smooth line to indicate that every data point may belong to several clusters with different values of the membership coefficient.

Figure 3. Membership function in Fuzzy c-means clustering.

2C. Level set

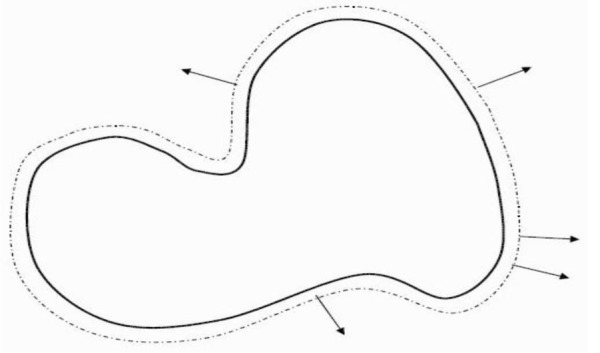
Active contour or snake is an energy minimizing, deformable spline influenced by constraint and image forces. They are often used in image analysis and computer vision to detect object boundaries, and to describe their shape. The main idea is to move the curve within an image under the speed F toward features of interest such as lines and edges. But the process become very complicated and hard if the snakes try to cross over themselves, or if the shape tries to break into two (Figure 4(Fig. 4)).

Figure 4. Active contour evolves under influence of forces.

Osher and Sethian (1988[24]) introduced the level set method for tracking interfaces and shapes. The central idea of this method is to represent the implicit contour as the zero level set of a higher dimensional function, referred as the level set function (LSF), and to approximate the motion equations of the level set function (Osher and Sethian, 1988[24]). This method provides a new framework for active contour models to overcome the problems associated with energy minimization, and instead of moving the position of contour only value of points change. As a consequence, this approach presents a major desirable feature for level set method which is the ability to handle topological merging and splitting naturally. In addition, this method works in any number of space dimensions, and is easy to program for many medical image analysis and applications of computer vision.

If the level set function, φ, moves in the normal direction with a speed function F, it satisfies the Partial Differential Equation (PDE):

This Hamilton-Jacobi equation is called level set evolution equation and guides the motion of the LSF. Segmentation with Level Set consists of:

1. Initialize the level set function based on the initial contour C₀. The function can be anything as long as its zero level set gives the contour.

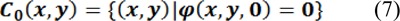
2. Update the function φ(x, y, t) in the narrow band, based on Hamilton-Jacobi equation.

3. The simulation iterates over step 2 until predefined number of iteration is reached or a desired object has been extracted.

LSF is assumed as a signed distance function (SDF) that is negative for inside the contour and positive for outside. However, the level set evolution equation does not guarantee to preserve the LSF as a signed distance function which cause instability and numerical errors during the implementation. In references (Sethian, 1996[26], 1999[27]; Osher and Fedkiw, 2002[23]), some available methods such as fast marching algorithm periodically reinitialize the LSF to reshape the surf as a signed distance function and to reduce numerical errors. Unfortunately, reinitialization may evolve the contour to an incorrect position (Sethian, 1999[27]; Osher and Fedkiw, 2002[23]), so reinitialization should be avoided as much as possible (Xu et al., 2010[32]). In Xu et al. (2010[32]) and Li et al. (2011[16]), a new type of level set evolution called distance regularized level set evolution (DRLSE) is able to maintain the desired shape of LSF near the zero level set and to eliminate the reinitialization procedure (Xu et al., 2010[32]).

Conventional level set algorithms compute the SDF in the whole domain which is very time consuming. In order to improve the computational efficiency, the Narrow Band implementation (Adalsteinsson and Sethian, 1995[1]) can be applied to update only a few points close to the zero level set.

For image segmentation, the speed term formulation is based on different features; accordingly, two main categories exist for level set method: edge-based models and region-based models. Edge-based models propagate the contour based on the information provided by image gradients and object boundaries, and the speed function attain zero value as it gets closer to the object boundaries. These models are adequate for images with intensity inhomogeneity, but they are sensitive to noise, dependent on initial curve placement and inaccurate for images with weak object boundaries (Li et al., 2011[16]).

The region-based models evolve the contour based on information provided by the entire region such as intensity, color or texture. Mumford and Shah (1989[18]) introduced a function which is used to segment an image into sub-regions. Methods aiming to find an optimal segmentation of the image I by minimizing the functional energy:

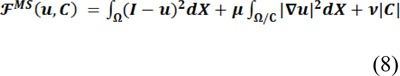
The methods aiming to minimize this energy are called piecewise smooth (PS). The first term is the data term, which forces u to be close to the image I, and the second term is the smoothing term, which forces u to be smooth within each of the regions separated by the contour C. The third term is introduced to regularize the contour C. |C| is the length of the contour C which separates the image domain Ω into disjoint regions Ω₁, ..., Ω_N. u is a piecewise smooth function that approximates the image I and is smooth inside the each region Ω_i. They have ability to segment images with intensity inhomogeneities; however, sensitivity to initialization and also expensive computation are their weaknesses (Li et al., 2011[16]).

Chan and Vese (1999[6]) proposed a simpler formulation to segment image I by finding the level set function ϕ and constants c₁ ^and c₂ that minimize the energy:

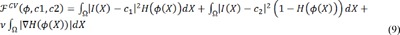
where H is Heaviside function, and ϕ segments the image domain Ω into two disjoint regions Ω₁ = {X:ϕ (X) > 0} and Ω₂ = {X:ϕ (X) > 0}. These models are termed piecewise constant (PC), and are inappropriate for images with intensity inhomogeneities. The first two terms in Eq. (9) are the data fitting terms. While the third term, with the weight parameter ν > 0, can regularize the zero level contour. Image segmentation is therefore achieved by finding the level set function ϕ and the constants c₁ and c₂ that minimize the energy.

The following model of intensity inhomogeneity for image I is proposed by Li et al. (2011[16]):

n is additive noise, J is true image, and b is referred to as a bias field (or shading image) for the intensity inhomogeneity that can be considered approximately constant in a neighborhood of

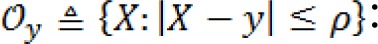
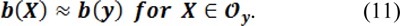
The true image J approximately takes N distinct constant values c₁, ..., c_N in disjoint regions Ω₁, ..., Ω_N, where

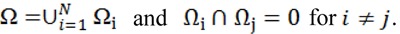
Therefore, the intensity of points in a neighborhood of each point can be approximated as follow:

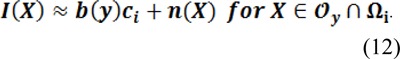
Note that the radius ρ of the neighborhood should be selected appropriately according to the intensity degree of inhomogeneity. The bias field varies faster for more localized intensity inhomogeneity, and therefore the approximation in Eq. (12) is valid only in a smaller neighborhood.

Based on the assumption of zero-mean additive Gaussian noise with small variance, intensities in the neighborhood can be classified into N distinct clusters with centers m_i ≈ b(y)c_i:

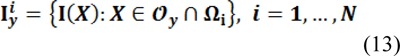
In Li et al. (2011[16]), the K-means algorithm is applied to classify the local intensities. It minimizes the clustering criterion function that is described by:

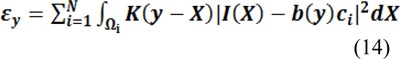
K(y - X) is named kernel function which is zero for

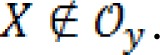
This function is chosen as a truncated Gaussian function:

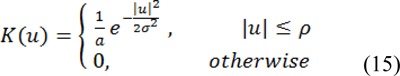
where a is a normalization constant such that ∫ K(u) = 1, σ is the standard deviation (or the scale parameter) of the Gaussian function, and ρ is the radius of the neighborhood which should be selected according to the degree of the intensity. Local clustering criterion function has to be minimized for all y in Ω. Therefore, energy, ε, is defined in the following form:

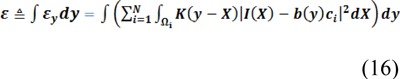
The energy formulation is expressed in terms of N disjoint regions which makes the energy minimization difficult. Therefore, ε is converted to a level set formulation with a number of level set functions and the energy minimization can be solved by using well-established variational methods. Level set formulation is called two-phase for N=2 and called multiphase formulation for N>2. In general, the energy ε, can be written as the function of ϕ = (φ₁, ..., φ_k), c = c₁, ... c_N) and the bias field b:

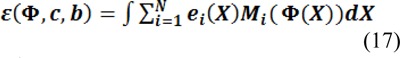
where

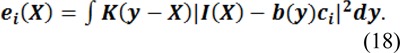
and the membership functions are defined by:

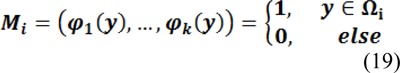
For the case of two-phase the level set function φ represents the two regions Ω₁ and Ω₂, therefore the energy ε is a function of φ and the membership functions are defined by M₁(φ) = H(φ) and M₂(φ) = 1 - H(φ).

The energy functional in two-phase level set formulation is defined by:

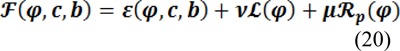
and for the multiphase:

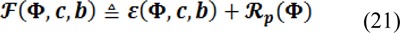
where

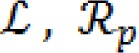
are the regularization terms (Li et al., 2011[16]). The energy minimization with respect to each variable can be achieved (Li et al., 2011[16]). More detail can be found in (Li et al., 2011[16]; Xu et al., 2010[32]).

3. Experimental results

In this paper, thirty thermal images are taken from Ann Arbor Thermography (2008[3]), Thermal imaging lab in the San Francisco Bay Area (2008[30]), American College of Clinical Thermology (2008[2]), Thermography of Iowa (2008[31]) and Sunstate Thermal Imaging Center in Australia (2009[29]). In this section, some experimental results for comparing segmentation performance of the three different algorithms are presented. The three methods are implemented for different cases; one fibrocystic case and four malignant cancer cases. Cases are as follows:

In Figure 5(Fig. 5), the image belongs to a patient who had Fibrocystic changes in left breast (Sunstate Thermal Imaging, 2009[29]). The patient in Figure 6(Fig. 6) had a thermography test. She had inflammatory cancer in right breast, although it was asymptomatic and unsuspected. Inflammatory breast cancer (IBC) is a rare and very aggressive disease in which cancer cells block lymph vessels in the skin of the breast. This type of breast cancer is called “inflammatory” because the breast often looks swollen and red, or "inflamed" (Ann Arbor Thermography, 2008[3]). In Figure 7(Fig. 7), the image shows a significant increase in temperature and vascularity (angiogenesis) in the right breast. The patient in Figure 8(Fig. 8) had a thermography test with a recent mammogram that was considered watchful for an area in the left breast. A follow-up ultrasound of the left breast was also watchful for the same area. The report recommended a follow-up mammogram in 6 months to monitor the finding in the left breast. The image to the left indeed shows a noticeable increase in heat and blood vessel activity (angiogenesis) in the left breast when compared to the right (Thermography of Iowa, 2008[31]). Figure 9(Fig. 9) shows a thermography test of a patient after having a normal mammogram and a watchful ultrasound of the left breast. The report recommended follow-up imaging in 6 months. Her doctor was concerned over a thickening of the left breast. The image to the left also shows a significant increase in temperature of the entire left breast along with noticeable vascularity (angiogenesis) (Thermography of Iowa, 2008[31]).

Figure 5. (a) Fibrocystic case, (b) hottest region extracted by K-means, (c) fuzzy C-means, (d) level set.

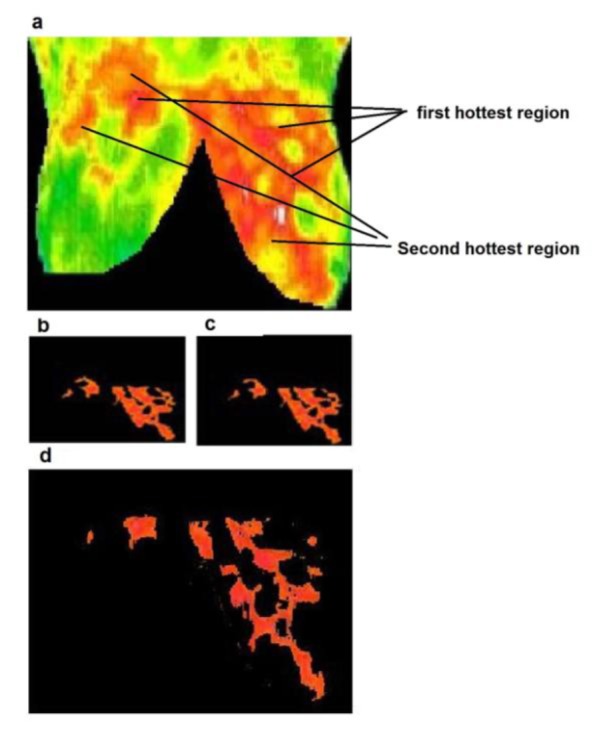
Figure 6. (a) Inflammatory cancer case, (b) hottest region extracted by K-means, (c) fuzzy C-means, (d) level set.

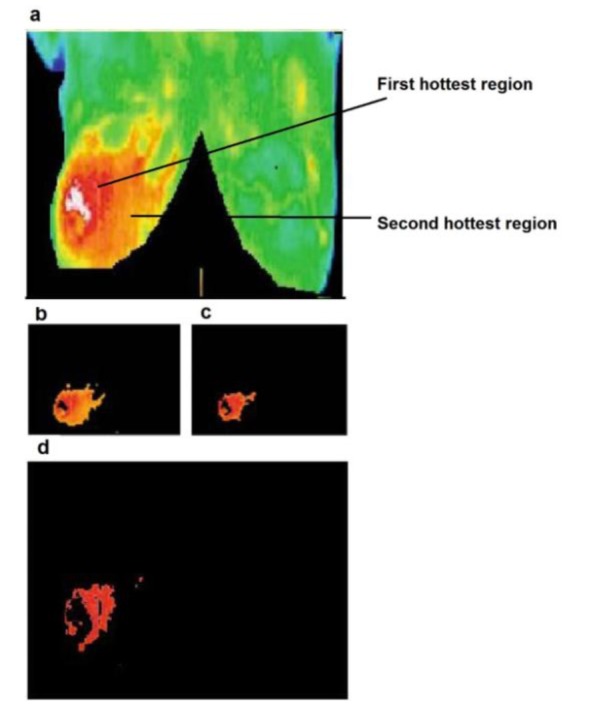
Figure 7. (a) Cancer case 2, (b) hottest region extracted by K-means, (c) fuzzy C-means, (d) level set.

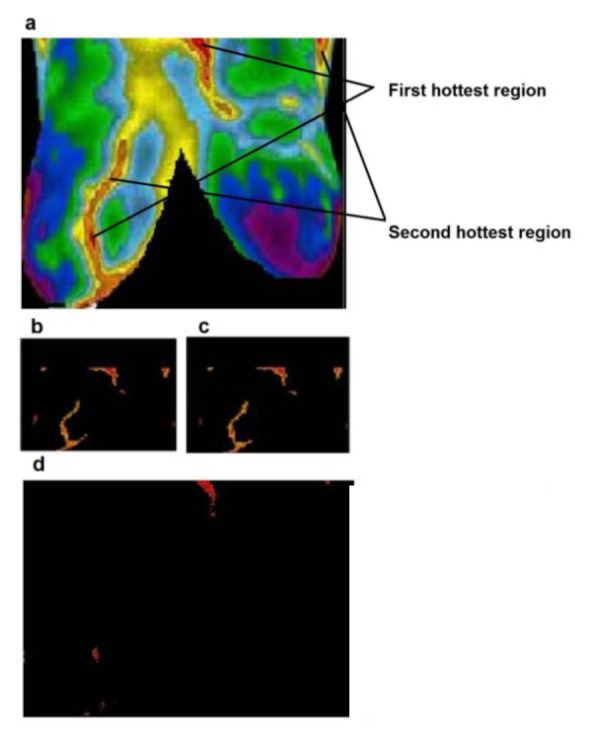
Figure 8. (a) Cancer case 3, (b) hottest region extracted by K-means, (c) fuzzy C-means, (d) level set.

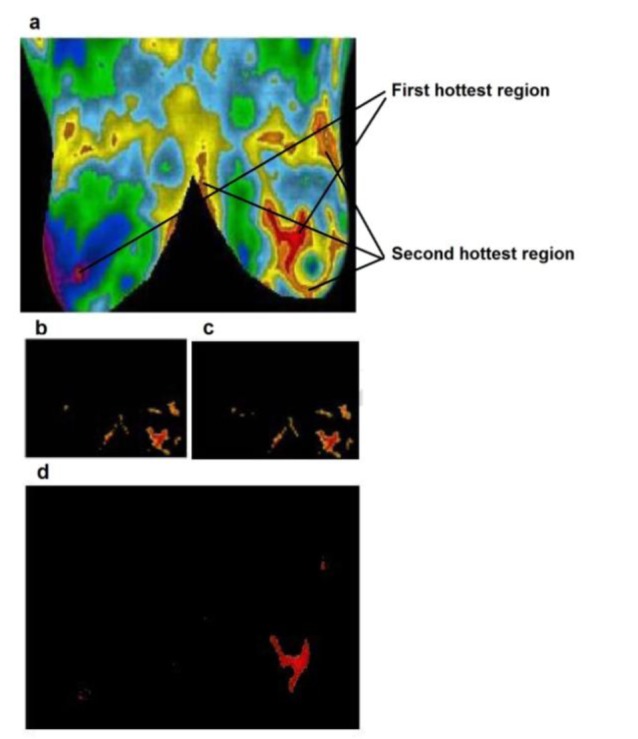
Figure 9. (a) Cancer case 4, (b) hottest region extracted by K-means, (c) fuzzy C-means, (d) level set.

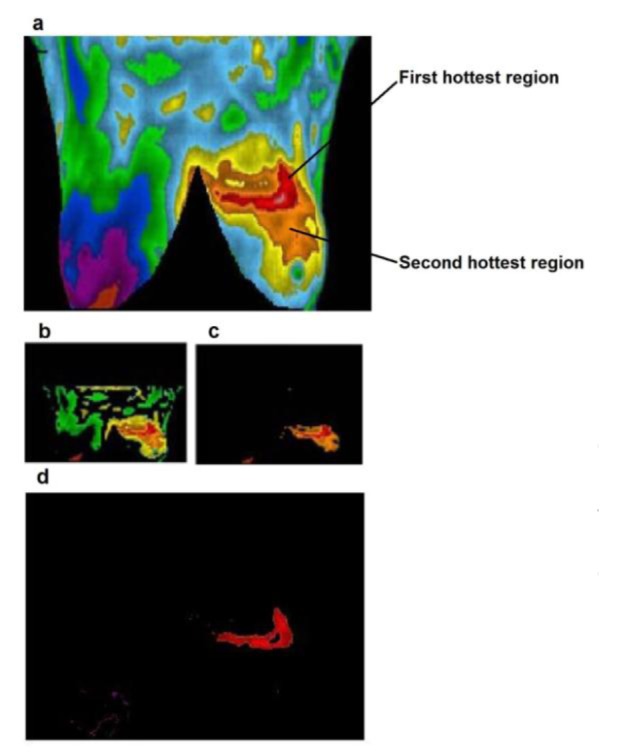
In this study, three different segmentation algorithms: k-means, fuzzy c-means and level set were applied. The hottest regions of three different approaches for each case are extracted and compared. The implementations results of K-means algorithm are shown in part b/s of each figure. Also the implementation results of fuzzy c-means algorithm are shown in part c/s (EtehadTavakol et al., 2010[11]). Level set algorithm as proposed in this paper (Li et al., 2011[16]) is a region-based segmentation method. By minimizing the energy, it is able to segment the image and estimate the bias field that can be applied for bias correction. In this implementation, all parameters are set to the default values as mentioned in Li et al. (2011[16]), only "timestep" parameter varies in the range of [0.001-0.1]. The implementation results of level set algorithm are shown in part d/s of figures.

Figure 5(Fig. 5) shows a comparison of segmentation results between k-means, fuzzy c-means, and level set, for a fibrocystic case. As shown in Figure 5b-c(Fig. 5) the exact shape of borders is not achieved by both the k-means and fuzzy c-means implementation. By using the level set, we are however able to elicit the exact borders where some useful features could be extracted from them. As shown in Figure 5d(Fig. 5) the borders are more similar and matching to the borders of the hottest region in original image. Figures 6-9(Fig. 6)(Fig. 7)(Fig. 8)(Fig. 9) present comparison of segmentation results between k-means, fuzzy c-means, and level set, when applied on malignant cancer cases. As we can see in the figures, neither K-means nor fuzzy c-means can separate the first hottest region from the second hottest region; while level set is completely succeed in segmentation and extraction of the first hottest regions.

There are several drawbacks of color segmentation of thermal infrared breast images by K and fuzzy c-means. In practice, where clusters are not disjoint and a pixel may belong to different clusters K-means clustering does not have a suitable performance. Moreover, poor initial partitions can result in empty clusters (EtehadTavakol et al., 2010[11]). In K and fuzzy c means, prior specification of the number of clusters is required. In this paper, level set technique gives more accurate result for segmentation of IR images. It has preferable efficiency, accuracy, and much more robustness for initialization (Li et al., 2011[16]). The hottest regions extracted by this method are more similar and matching to their respective original images than the k and fuzzy c-means. Regarding to the suspicious region, we would be able to extract some useful information.

4. Conclusion

Image segmentation plays an important role in many medical imaging applications. In this paper, we present three image segmentation methods: k-means, fuzzy c-means (FCM) and a region-based level set for segmentation of various breast thermograms. The improved level set algorithm (energy functional formulation) used in this paper has preferable efficiency, accuracy, and much more robustness for initialization than the conventional level set methods. These methods have been applied to the abnormal thermal images, and the hottest regions of three different algorithms for each case are extracted and compared. Some useful features can be extracted from them. Experimental results have demonstrated the superior performance of level set in terms of accuracy, efficiency, and robustness. The hottest regions extracted by the level set are more similar to the original image than the other segmentation methods.