Chemical Interactions of Polyethylene Glycols (PEG) and Glycerol with Protein Functional Groups: Applications to PEG, Glycerol Effects on Protein Processes

Abstract

Here we obtain the data needed to predict chemical interactions of polyethylene glycols (PEGs) and glycerol with proteins and related organic compounds, and thereby interpret or predict chemical effects of PEGs on protein processes. To accomplish this we determine interactions of glycerol and tetraEG with >30 model compounds displaying the major C, N, and O functional groups of proteins. Analysis of these data yields coefficients (α-values) quantifying interactions of glycerol, tetraEG and PEG end (-CH₂OH) and interior (-CH₂OCH₂-) groups with these groups, relative to interactions with water. TetraEG (strongly) and glycerol (weakly) interact favorably with aromatic C, amide N, and cationic N, but unfavorably with amide O, carboxylate O and salt ions. Strongly unfavorable O and salt anion interactions help make both small and large PEGs effective protein precipitants. Interactions of tetraEG and PEG interior groups with aliphatic C are quite favorable, while interactions of glycerol and PEG end groups with aliphatic C are not. Hence tetraEG and PEG 300 favor unfolding of the DNA-binding domain of lac repressor (lacDBD) while glycerol, di- and mono-ethylene glycol are stabilizers. Favorable interactions with aromatic and aliphatic C explain why PEG400 greatly increases the solubility of aromatic hydrocarbons and steroids. PEG400-steroid interactions are unusually favorable, presumably because of simultaneous interactions of multiple PEG interior groups with the fused ring system of the steroid. Using α-values reported here, chemical contributions to PEG m-values can be predicted or interpreted in terms of changes in water-accessible surface area (ΔASA), and separated from excluded volume effects.

Polyethylene glycols (PEGs) are widely used in biochemistry, structural biology, and medicine, as well as in the pharmaceutical and chemical industries. Applications include protein crystallization¹ and stabilization, protein separation² and boosting osmotic pressure^{3, 4}, as well as use as an excipient in medications⁵, an anticancer agent⁶, and a stabilizer of organs for transplants^{7, 8}. Other recent and significant applications include pressure control in biomedical devices⁹, drug delivery^{10, 11}, an intelligent biomaterial for treating injures in membranes¹², and antifouling coating in biomedical devices¹³. Properties of PEGs relevant for these applications include their high solubility or complete miscibility with water, their chemical interactions with molecular and macroscopic biosurfaces, and excluded volume effects. Here, by quantifying the interactions of glycerol and tetraEG with model compounds displaying functional groups of proteins, we deduce the chemical interactions of PEG with protein and other functional groups, relative to interactions with water. From this information, we predict and/or interpret the chemical component of PEG-protein interactions and PEG m-values for protein processes in terms of structural information, and thereby separate chemical from excluded volume effects. We also address the question of how the different interactions of PEG with different types of molecular surface make both small and large PEGs effective protein precipitants while solubilizing drugs and other aromatic compounds.

Glycerol and PEG are routinely used to perturb biopolymer processes. Glycerol modestly stabilizes globular proteins ^14–17, beta-hairpins ^{18, 19}, protein assemblies^20–23 and protein-DNA complexes²⁴, but modestly destabilizes nucleic acid duplexes^25–27, and can stabilize or destabilize RNA tertiary structure²⁷. Tetraethylene glycol (tetraEG) is a weak destabilizer of nucleic acid duplexes^{26, 28}, and larger PEGs destabilize proteins ^29–32. Oligo ethylene glycols and polymeric PEGs are common protein crystallization agents ¹, stabilize protein-DNA complexes^{24, 33, 34} and perturb their kinetics^{24, 35}. Effects of PEGs on stability of these assemblies have been variously interpreted as osmotic effects (effects primarily on water activity), excluded volume effects, and as combinations of preferential (chemical) interactions (including osmotic effects) and excluded volume effects ²⁸.

Previously we quantified the chemical noncovalent interactions of urea^{36, 37}, glycine betaine (GB), proline)^{37, 38} and the spectrum of protein-stabilizing and -destabilizing Hofmeister salts^{39, 40} with sets of model compounds selected to display various combinations of the functional groups of proteins and (for urea) nucleic acids. These chemical interactions are preferential interactions, i.e. interactions relative to interactions with water; an unfavorable interaction between solute and model compound means that both species prefer to interact with water than with each other. Analysis of these data reveals that solute-model compound interactions can be dissected into independent, additive interactions of the solute with functional groups of the model compound. Dissection by functional groups provides a more chemical interpretation of solute interaction data than the backbone-sidechain interpretation of amino acid and dipeptide transfer free energies ^{17, 41}, involves many fewer parameters (7 vs. 20 for applications to protein processes at pH 7) and eliminate ambiguities in interpretation or prediction when only part of a sidechain or backbone unit is buried or exposed in a processes. The two approaches have been compared recently ³⁷.

Large areas of biopolymer surface are buried in interfaces and coupled conformational changes in the steps of biopolymer self-assembly and function. Chemical effects of solutes and Hofmeister salts on a biopolymer processes (as distinct from excluded volume effects of large solutes and/or coulombic effects of salts) are well interpreted or predicted as additive interactions of the solute or salt ions with the functional groups on the biopolymer that are buried (or exposed) in the process. For example, proline and GB stabilize proteins against unfolding because of the unfavorable chemical interactions of these solutes with the aliphatic hydrocarbon surface and amide oxygens buried in folding, while urea destabilizes in large part because of its favorable interactions with these groups^36–38. Many of the chemical interactions between two solutes or between solute and biopolymer in water, including hydrogen bonding and hydrophobic interactions, are the same as those of biopolymer self-assembly. Quantitative information about solute-solute interactions is needed to develop the use of solutes as probes of changes in biopolymer surface area in the key intermediates and transition states in the mechanisms of self- assembly and function, as well as to quantify the contributions of noncovalent interactions to biopolymer stability.

Here we determine the interactions of tetraEG and glycerol with a large set of model compounds chosen to display various combinations of the functional groups of proteins, and interpret these measurements in terms of chemical interactions (α-values) of these solutes and of the terminal -CH₂OH and interior -CH₂OCH₂- groups of PEG with the chemically-distinct types of protein functional groups (designated aliphatic (sp³) C, aromatic (sp²) C, amide N, cationic N, amide O, carboxylate O, carboxylic acid O, hydroxyl O) and with four inorganic ions (Na⁺, K⁺, Cl⁻, HPO₄ ²⁻). In principle an excluded volume (EV) contribution to these interactions of two small solutes may also be present. Because the solutes are of similar size to one another and are probably also similar in size to the average cluster size of water molecules, we expect that EV interactions are not significant. SPT calculations including water find that the EV contribution to small-solute effects on protein folding is negligible when the solute is of same size as water ⁴². Both chemical and EV effects are generally significant for interactions of two polymeric solutes. Quantitative analyses of polymeric PEG-protein interactions ⁴³ and effects of polymeric PEG on DNA helix formation ²⁸ (see discussion below) have recently been presented.

We apply α-values analysis to predict and interpret the chemical interactions of glycerol, tetraEG and other PEG oligomers with proteins and effects of these solutes on protein solubility, folding, and subunit assembly, including new results quantifying effects of the series from diEG to PEG 300 and the polyols EG and glycerol on folding of the lac repressor DNA binding domain (lacDBD). Our analysis explains why polyols like EG and glycerol are protein stabilizers while tetraEG and larger PEG oligomers are destabilizers, and (in the companion paper⁴³) why both small and large PEGs can be effective protein precipitants. For these larger PEGs (flexible coils), both excluded volume and shielding of chemical interactions must be considered. Good agreement with literature data quantifying favorable interactions of PEG 400 with aromatic compounds and unfavorable interactions of small and large PEGs with native proteins ⁴³ is obtained.

Materials and Methods

Details about measurements of µ₂₃ by vapor pressure osmometry and solubility and of m-values of lacDBD unfolding are provided in Supplemental Materials. Calculations of ASA of model compounds (Table S1), PEG oligomers (Table S3), aromatic compounds (Table S6), and change in ASA of proteins processes (Table S5) are performed as described in SM. Analysis of experimental data including uncertainty estimations with Eqs of Table 1 were performed as described in SM.

Table 1.

Quantifying Solute (Glycerol, tetraEG, PEG) Interactions with Model Compounds and Effect on Processes: Chemical Potential Derivatives μ₂₃

Determination of μ23 by Osmometry	$$\text{Osmolality difference}\mathrm{\Delta }\text{Osm}\text{Osm}({\mathrm{m}}_2,{\mathrm{m}}_3)-\text{Osm}({\mathrm{m}}_2,0)-\text{Osm}(0,{\mathrm{m}}_3)=({\mu }_{23}/\mathit{\text{RT}})m_2{m}_3$$		Eq.1
Determination of μ23 by Solubility	$$\mathit{\text{solubility m}}-\mathit{\text{valve}}\equiv -\mathit{\text{RT}}\left(\frac{d\text{ln}{m}_2^{\mathit{\text{ss}}}}{{\mathit{\text{dm}}}_3}\right)=-\mathit{\text{RT}}{\left(\frac{\partial \text{ln}{m}_2}{\partial m_3}\right)}_{{\mu }_2}\cong {\mu }_{23}$$		Eq.2
Group ASA-based Interpretation of μ23	$${\mu }_{23}={\left(\frac{\partial {\mu }_2}{\partial m_3}\right)}_{P,T}=\sum _i{\alpha }_{\mathit{\text{solute}},i}{\mathit{\text{ASA}}}_i^{\mathit{\text{model compound}}}+\sum _k{\beta }_{\mathit{\text{solute}},k}{\nu }_k^{\mathit{\text{ion}}}$$		Eq.3
SPM Interpretation of αsolute,i	$${\alpha }_{\mathit{\text{solute}},i}=-\mathit{\text{RT}}(K_{p,i}-1)b_{1,i}(1+{\epsilon }_3)/m_1^{•}$$		Eq.4
m-Value, Relation to μ23	$$\mathrm{m}-\text{value}\equiv \frac{\partial \mathrm{\Delta }{\mathrm{G}}_{\text{obs}}}{\partial {\mathrm{m}}_3}=-\text{RT}\frac{\partial \text{ln}{K}_{\mathit{\text{obs}}}}{\partial {\mathrm{m}}_3}=\mathrm{\Delta }{\mu }_{23}$$		Eq.5
Predicting m-value	$$\mathrm{m}-\text{value}=\mathrm{\Delta }{\mu }_{23}=\sum _i{\alpha }_{\mathit{\text{solute}},i}\mathrm{\Delta }{\mathit{\text{ASA}}}_i^{\mathit{\text{biopolymer}}}+\sum _k{\beta }_{\mathit{\text{solute}},k}\mathrm{\Delta }{\nu }_k^{\mathit{\text{ion}}}$$		Eq.6
Predicting PEG μ23 values	$${\mu }_{23}=\sum _i[{\alpha }_{2E,i}+(N_3-1){\alpha }_{I,i}]{\mathit{\text{ASA}}}_i+\sum _k[{\beta }_{2E,k}+(N_3-1){\beta }_{I,k}]{\nu }_k^{\mathit{\text{ion}}}$$		Eq.7
Predicting PEG m- values	$$m-\mathit{\text{value}}=\sum _i[{\alpha }_{2E,i}+(N_3-1){\alpha }_{I,i}]\mathrm{\Delta }{\mathit{\text{ASA}}}_i^{\mathit{\text{biopolymer}}}+\sum _k[{\beta }_{2E,k}+(N_3-1){\beta }_{I,k}]\mathrm{\Delta }{\nu }_k^{\mathit{\text{ion}}}$$		Eq.8
Definitions:	Kp,i = m3i,loc/m3i,bulk	${\epsilon }_i=\frac{d\mathit{\text{ln}}{\gamma }_i}{d\text{ln}{m}_i}$

Background and proposed analysis of PEG interactions

Chemical potential derivatives µ₂₃ quantifying chemical (preferential) interactions

Our strategy, as in previous studies, is to determine chemical interactions of tetraEG and glycerol (each designated component 3) with large sets of model compounds (designated component 2) displaying the most common functional groups of proteins. These interactions are quantified by chemical potential derivatives (∂µ₂/∂m₃)_m2 = µ₂₃, model-independent thermodynamic quantities which characterize solution nonideality arising from interactions of two solutes. When independent of solute concentration between 0 and 1 molal, µ₂₃ is numerically equal to the transfer free energy for the process of transferring the model compound from a dilute solution in water to a solution with the same low concentration of model compound that is 1 molal in solute ^{17, 37, 41}. Values of µ₂₃ can be interpreted using Kirkwood-Buff (KB) statistical mechanics ⁴⁴ or molecular thermodynamic analysis of the solute partitioning model (SPM) ^36–38,45 to obtain the local concentration of one solute in the vicinity of another, and by simulations⁴⁶.

A negative µ₂₃ indicates a favorable solute-model compound interaction relative to interactions with water. A positive µ₂₃ indicates an unfavorable interaction, i.e. that components 2 and 3 prefer to interact with water rather than with one another. Higher molecular weight PEGs, as well as other polymers (e.g. dextran, Ficoll) also exert physical (excluded volume) effects ^{43, 47–52} (see ^{53, 54} for reviews). One goal of determining chemical interactions of tetraEG and glycerol with protein groups is to predict interactions of PEG end and interior residues with these groups, and thereby predict chemical contributions to any PEG-protein interaction. In this way, chemical and excluded volume contributions to effects of large PEGs on protein processes can be dissected ^{28, 43}.

Measurement of µ₂₃ for interactions of glycerol and tetraEG with soluble model compounds by vapor pressure osmometry

To quantify preferential interactions of tetraEG and glycerol with protein functional groups, vapor pressure osmometry (VPO) is used to measure the excess osmolality ΔOsm of each of a series of 3-component solutions with varying concentrations of component 3 (either tetraEG or glycerol) and component 2 (one of a set of more than 30 small, nonvolatile model compounds displaying functional groups of proteins (or inorganic ions) to the solution. Ethylene glycol and the smallest PEG oligomers (diEG, triEG) are too volatile to investigate by VPO. The excess osmolality of a 3-component solution, ΔOsm, is defined in Eq. 1 (Table 1) as the difference between the osmolality of the 3-component solution Osm(m₂, m₃) and the sum of the osmolalities of the corresponding 2-component solutions (Osm(m₂, 0) + Osm(0, m₃)).

Excess osmolality (ΔOsm) data is analyzed to obtain values of µ₂₃, the chemical potential derivative quantifying solute-model compound interactions. Multicomponent solution theory ⁵⁵ shows that analysis of ΔOsm as a function of m₂m₃, the product of the molal concentrations of model compound (component 2) and solute (3), yields µ₂₃ (see Eq. 1, Table 1). The m₂m₃ product quantifies the probability of an interaction between solutes 2 and 3, and µ₂₃ quantifies the strength of this interaction.

Measurement of µ₂₃ for interactions of glycerol and tetraEG with low–solubility model compounds by solubility assays

Chemical interactions (µ₂₃) of glycerol and tetraEG with sparingly soluble model compounds are quantified from the effect of these solutes on the solubility of the model compound. Provided that the concentration of model compound (component 2) in a saturated solution is small enough that self-interactions of the model compound are negligible (i.e. provided that the saturated solution is an ideal dilute solution), then the solubility m-value (-RTdlnm₂ ^ss/dm₃, where m₂ ^ss is the molal concentration of model compound in the saturated solution) is equal to µ₂₃ (see Eq. 2, Table 1). If self-interactions of the model compound in the saturated solution are non-negligible, another method such as osmometry (Eq. 1) should be used at lower concentrations to determine µ₂₃.

Quantifying interactions of solutes like glycerol and tetraEG with protein functional groups and salt ions

Values of µ₂₃ for the interactions of the small solutes investigated to date (urea, GB, proline and the series of Hofmeister salts^36–38) with model compounds and biopolymers are found to be well-described as a sum of independent short-range interactions of these solutes with the individual functional groups on the model compounds or biopolymers and the inorganic salt ion(s) of the electroneutral component (see Table 1, Eq. 3). In Eq. 3, the chemical interaction coefficient α_solute,i (in cal·mol⁻¹·molal⁻¹·Å⁻²) quantifies the interaction of the solute (here tetraEG or glycerol) with 1 Ų of protein functional group type i, relative to interactions with hydration water, and the β_solute,i (in cal·mol⁻¹·molal⁻¹) quantify the interaction of these solutes with inorganic ions. In Eq 3, ASA_i is the amount of water accessible surface (in Ų) of functional group type i. To interpret a value of α_solute,i, one must consider not only the interaction between the solute and this functional group but also the solute-water and functional group-water interactions that are disrupted when this solute-group interaction occurs.

The SPM (^{36–38, 45}) provides a molecular interpretation of preferential interactions of a small solute with a chemically homogeneous surface, like the macroscopic air-water interface or the molecular surface of an aromatic or aliphatic hydrocarbon. For interactions of a small solute with a molecular surface with a hydration b₁ (molecules of water per unit area of surface), the SPM predicts the observed proportionality of µ₂₃ to surface area and interprets the proportionality constant (α_solute) in terms of the accumulation or exclusion of the solute in the vicinity of the surface, as quantified by a microscopic local-bulk partition coefficient K_p. This relationship is given as Eq. 4 (Table 1). In Eq. 4, K_p = m₃ ^loc/m₃ ^bulk, where m₃ ^loc and m₃ ^bulk are local and bulk solute molalities; K_p is a microscopic analog of an equilibrium constant for the process of transferring the solute from bulk solution to the vicinity of the surface, and as such is relatively independent of bulk solute concentration.Eq. 4 has been extended to interpret interactions of a small solute with individual functional groups (i) on the surface of a model compound^36–38. A negative (favorable) α_solute,i means that K_p,i > 1 and that the solute accumulates in the vicinity of functional group of type i to a concentration that is higher than its bulk concentration (by the factor K_p,i). Conversely, a positive (unfavorable) α_solute,i means that K_p,i < 1 and the solute is excluded from the water of hydration of the functional group, so the local solute concentration is less than its bulk concentration (by the factor K_p,i). Also in Eq. 4, ε₃ = (∂ ln γ₃/∂ ln m₃)m2 is a solute-solute self-nonideality correction, typically small in magnitude and not very concentration-dependent below 1 molal, and m₁ ^● is the molality of pure water (55.5 mol/Kg).

Predicting, interpreting effects of solutes like glycerol and tetraEG on biopolymer processes

Experimentally, the effect of a solute on folding, precipitation and other biopolymer processes is quantified by an m-value, the derivative of the observed standard free energy change for the process (ΔG^o _obs) with respect to solute concentration (here expressed on the molal scale). Thermodynamically, the m-value is the difference in chemical potential derivatives µ₂₃ quantifying the preferential interaction of the solute with the final (product) and initial (reactant) species in the process⁵⁶ (see Eq 5, Table 1). Using Eq. 3 and the hypothesis of additivity, the quantity Δµ₂₃ in Eq.5 is interpreted as the interaction of the solute with the ASA exposed or buried in the process (Eq. 6). In Eq. 6 (Table 1), $\Delta {\mathit{\text{ASA}}}_i^{\mathit{\text{biopolymer}}}$ is the difference in ASA of functional group i between product and reactant species in the process, and $\Delta v_k^{\mathit{\text{ion}}}$ is the corresponding difference in the number of free ions. For precipitation and crystallization, the $\Delta v_k^{\mathit{\text{ion}}}$ terms are expected to be significant. For biopolymer processes in solution, including folding, subunit assembly and ligand binding, these salt ion terms generally are negligible and $\Delta v_k^{\mathit{\text{ion}}}=0$. We test these predictions by comparisons with available data at or near 25 °C, including glycerol m-values for conversion of ConA dimers to tetramers²¹ and glycerol and tetraEG m-values for unfolding lacDBD.

Predicting, interpreting effects of PEG oligomers on folding, assembly and other protein processes

By extension of Eq. 3, we propose that the preferential interaction (µ₂₃ value) of any PEG oligomer (degree of polymerization N₃) with any model compound or biopolymer can be dissected into interactions of the end groups and interior repeats with the functional groups on the biopolymer and with the ions of the biopolymer component. Assigning interaction potentials α_2E and α_I for the interactions of the two end groups (E, -CH₂OH) and the interior group (I, -CH₂OCH₂-) with 1 A² of ASA of each type of functional group on the biopolymer, and values β_2E and β_I for the interactions of end and interior groups of PEG with inorganic ions of the biopolymer component, we obtain Eq. 7 (Table 1). Likewise m-values = Δµ₂₃ quantifying chemical effects of any PEG oligomer on these processes are predicted or interpreted using Eqs. 8 (Table 1). For processes in solution where inorganic ions are not stoichiometric participants, $\Delta v_k^{\mathit{\text{ion}}}=0$.

When α- and β-values for interactions of other PEG oligomers with protein functional groups are determined, analysis of these α- and β-values as a function of the number of interior - CH₂OCH₂- repeats will yield α- and β-values for interactions of end and interior repeat groups of PEG with protein groups, from which the chemical interactions of any PEG with any protein surface can be predicted. Such predictions are needed to separate chemical (soft) and excluded volume (hard) contributions to the interaction of any PEG with proteins, as well as PEG effects on protein solubility and other protein processes (see below). However, PEG oligomers shorter than tetraEG are found to be unsuitable for osmometric studies by VPO, and chemically homogeneous longer PEG oligomers are not readily available.

Here, as a practical alternative, we obtain the necessary interaction potentials α_2E (also β_2E) and α_I (also β_I) for interactions of end and interior groups of any PEG (from diEG to PEG20000 or larger) with protein groups (also salt ions) from analysis of glycerol and tetraEG α- and β-values for interactions with these groups, assuming addivitity. TetraEG α- and β-values are composed of contributions from interactions with three interior –CH₂OCH₂- groups and two –CH₂OH end groups. Because of the chemical analogy between PEG end groups and glycerol, scaling of glycerol α- and β-values is used to obtain PEG end group α_2E and β_2E values. These are approximate because of the difference in composition (aliphatic C: hydroxyl O ASA ratios) of glycerol and PEG end groups. (EG would be a closer, though also approximate, model for PEG end groups, but is found to be unsuitable for VPO studies.) As an empirical correction, we use the experimentally-determined contribution of PEG end groups to the m-value data for unfolding of lacDBD (for which 65% of the ΔASA is aliphatic C) to set the α-value for the interaction of PEG end group with aliphatic C. We test these PEG α- and β-values by predicting the incremental effect of additional interior residues in the PEG series from diEG to PEG300 on the lacDBD stability m-value, and by comparisons with literature data quantifying effects of PEG400 on solubility of 28 aromatic compounds with the same or similar functional groups to those investigated here.

Results and Interpretations

Preferential interactions of tetraEG with model compounds displaying protein groups

VPO determinations of µ₂₃ values quantifying preferential interactions of tetraEG with 34 nonvolatile, soluble model compounds, each displaying one or more protein functional groups and/or inorganic ions, are shown in the panels of Figure 1. Excess osmolalities ΔOsm (Eq 1) are plotted as a function of the concentration product m₂m₃, where m₂ is the molal concentration of model compound and m₃ is the molal concentration of tetraEG. These plots are linear within uncertainty over the concentration ranges studied here (< 0.6 m in each component); values of µ₂₃ for each tetraEG-model compound preferential interaction, obtained from the slope, are reported in Table S1.

Fig. 1. Interactions of TetraEG with Salts and Compounds Displaying Protein Groups.

Determination of µ₂₃ quantifying tetraEG -model compound preferential interactions by vapor pressure osmometry. Excess osmolality ΔOsm plotted against m₂m₃, the product of the molal concentrations of the two solutes (tetraEG, component 3; model compound, component 2). From Eq. 1 (Table 1), slopes are µ₂₃/RT. (A) inorganic salts, (B) amino acids, zwitterions and derivatives, (C) amides, (D) carboxylate salts and carboxylic acids, (E) amino acid salts, (F) other model compounds. Abbreviations for model compounds are defined in the footnote to Table S1.

For solutions of tetraEG and an amino acid, polyol or carboxylate salt, Fig. 1 shows that ΔOsm increases with increasing concentration of either component (plotted as the m₂m₃ product). Hence preferential interactions of tetraEG with these model compounds are unfavorable, with positive values of µ₂₃. TetraEG and these model compounds prefer to interact with water than with one another, causing the local concentration of tetraEG in the vicinity of these model compounds to be less than its bulk concentration. By contrast, Fig. 1 shows that interactions of tetraEG with all aromatic compounds and carboxylic acids studied, as well as with compounds with primarily amide N or cationic N functional groups (urea, GuHCl) are favorable. For these solutes, ΔOsm decreases with increasing m₂m₃, indicating negative µ₂₃ values and local accumulation of tetraEG in the vicinity of these model compounds.

Solubility data characterizing the favorable preferential interactions of tetraEG with two low-solubility model compounds (butylhydroxytoluene and phenylacetic acid) are shown in Fig S1; µ₂₃ values obtained from these data (Eq. 2) are negative (cf. Table S1) indicating accumulation of tetraEG in the vicinity of these aromatic solutes.

Though the chemical compositions of tetraEG and glycine betaine (GB) are very different, signs and in some cases magnitudes of µ₂₃ for interactions with the same model compound often agree. For example, values of µ₂₃ for interactions of GB and tetraEG with amino acids, carboxylate salts and polyols are positive (unfavorable) and similar in magnitude, while µ₂₃ values for interactions of GB and tetraEG with urea and Na benzoate are both negative (favorable).

Preferential interactions of glycerol with model compounds displaying protein groups

Preferential interactions of glycerol with 34 soluble model compounds (in most cases the same as those investigated with tetraEG) are quantified by VPO; a solubility assay is used with an additional model compound. Figures 2 (osmometry) and S1 (solubility) summarize the results of these experiments. As observed for tetraEG (Fig. 1), values of ΔOsm of solutions of glycerol and an amino acid, polyol or carboxylate salt increase with increasing concentration of either solute (corresponding to unfavorable preferential interactions; µ₂₃ > 0) while values of ΔOsm of solutions of glycerol and aromatics or compounds with primarily amide N or cationic N functional groups decrease with increasing concentration of either solute (corresponding to favorable preferential interactions; µ₂₃ < 0).

Results for glycerol-model compound interactions (Fig. 2) in general parallel those obtained for tetraEG. For all compounds investigated except citric acid, values of µ₂₃ have the same sign but are approximately one-third to one-tenth as large in magnitude for glycerol as for tetraEG. (The glycerol-citric acid interaction is unfavorable while the tetraEG-citric acid interaction is favorable.) In many cases, values of µ₂₃ for glycerol-model compound interactions are of opposite sign but similar magnitude to those reported previously for urea³⁶. Exceptions are GuHCl and carboxylate salts (sodium propionate, trisodium and tripotassium citrate, potassium glutamate, sodium benzoate), for which µ₂₃ values for both glycerol and urea have the same sign.

Fig. 2. Interactions of Glycerol with Salts and Compounds Displaying Protein Groups.

Determination of µ₂₃ quantifying glycerol-model compound preferential interactions by vapor pressure osmometry. Excess osmolality ΔOsm plotted against m₂m₃, the product of the molal concentrations of the two solutes (glycerol, component 3; model compound, component 2). From Eq. 1 (Table 1), slopes are µ₂₃/RT. (A) inorganic salts, (B) amino acids, zwitterions and derivatives, (C) amides, (D) carboxylate salts and carboxylic acids, (E) amino acid salts, (F) other model compounds. Abbreviations for model compounds are defined in the footnote to Table S1.

Chemical interaction coefficients (α values) for interactions of tetraEG and glycerol with functional groups of proteins

Model compounds investigated here were selected to display one or more of the eight (coarse-grained) principal functional groups of proteins (aliphatic and aromatic C; amide, hydroxyl, carboxylate and carboxylic acid O; amide and cationic N). All these functional groups are defined to include their covalently-bonded proton or protons (one proton on carboxylic acid and hydroxyl O, and on secondary amide N; two protons on primary amide N; one, two or three protons on cationic N of guanidinium and ammonium groups). This definition is consistent with the unified atom analysis of the surface areas of these model compounds⁵⁷.

To interpret the interactions (µ₂₃ values) of tetraEG and glycerol with these model compounds in terms of interactions with individual functional groups, numerical values of µ₂₃ (Table S1) and water accessible surface areas (ASA) of the model compounds (Table S2) are used as inputs to Eq. 3, and the resulting over-determined linear systems of 36 (tetraEG) and 35 (glycerol) equations are solved to obtain eight chemical interaction coefficients (α values) quantifying the preferential interactions of tetraEG and glycerol with unit surface area of these functional groups, as well as four β-values quantifying interactions of tetraEG and glycerol with the inorganic ions present in the model compound set. This analysis assumes that chemical interactions of functional groups determine these small solute – small solute µ₂₃ values and that excluded volume contributions are negligible. In these analyses, β-values for all inorganic ion are individually floated. β-values for interactions of glycerol and tetraEG with the anions investigated (Cl⁻, HPO₄ ²⁻) are large and positive, with small relative uncertainties, while β-values for the salt cations (Na⁺, K⁺) are smaller in magnitude with larger relative uncertainties. Since β-values for interactions of Na⁺ with glycerol and of K⁺ with tetraEG are approximately zero given these uncertainties, we also tested fits assigning these values to zero. These fits gave α values (and β-values for the other ions) that are not significantly different from those reported in Table 2.

Table 2.

Interactions of tetraEG, glycerol, End and Interior Groups of PEG with Protein Groups, Salt Ions

A) Group Interaction Potentials (αsolute,i, cal·mol−1·molal−1 Å−2)
Group (i)	αtetraEG,i	αglycerol,i	α2E,i	αI,i
Aliphatic C	−0.349 ± 0.029	0.0548 ± 0.011	−0.00268 ± 0.020	−0.115 ± 0.012
Aromatic C	−2.66 ± 0.028	−0.431 ± 0.011	−0.364 ± 0.0094	−0.765 ± 0.01
Hydroxyl O	0.843 ± 0.025	0.0305 ± 0.0079	0.0258 ± 0.0067	0.272 ± 0.0085
Amide O	2.94 ± 0.11	0.826 ± 0.059	0.698 ± 0.050	0.747 ± 0.041
Carboxylate O	3.59 ± 0.06	0.467 ± 0.024	0.395 ± 0.021	1.07 ± 0.021
Carboxylic Acid O	−0.41 ± 0.039	0.0446 ± 0.0086	0.0377 ± 0.0072	−0.149 ± 0.013
Amide N	−1.67 ± 0.056	−0.491 ± 0.034	−0.415 ± 0.029	−0.418 ± 0.021
Cationic N	−0.805 ± 0.041	−0.245 ± 0.017	−0.207 ± 0.015	−0.199 ± 0.014
B) Ion Interactions (βsolute,k, cal·mol−1·molal−1 ion−1)
Ion (k)	βtetraEG,k	βglycerol,k	β2E,k	βI,k
HPO42−	780 ± 16	93.9 ± 6.3	79.3 ± 5.3	234 ± 5.5
Cl−	132 ± 6.8	22.8 ± 2.9	19.3 ± 2.5	37.6 ± 2.4
K+	6.19 ± 10	−4.11 ± 3.1	−3.47 ± 2.6	3.22 ± 3.4
Na+	18.5 ± 5.2	5.34 ± 3.2	4.51 ± 2.7	4.66 ± 2

Consistent with comparisons of µ₂₃ values, α-values for interactions of tetraEG and glycerol with individual functional groups are found to differ greatly in magnitude but to have the same sign for most groups; important exceptions include aliphatic C and carboxylic acid O. Table 2 shows that, except for hydroxyl O where the magnitude of the glycerol α-value is very small, tetra EG α- values for tetra EG are 3 to 7 times larger than the corresponding glycerol α-values. Many glycerol α-values are comparable in magnitude (and in some important cases opposite in sign) to urea³⁶. For tetraEG, many α-values are comparable in magnitude and of the same sign as for GB³⁸.

To test additivity (Eq. 3) and the ability of these eight α-values and four β-values to describe the preferential interactions of tetraEG and glycerol with the three-fold larger number of model compounds, Fig. 3 compares experimental values of µ₂₃ for tetraEG (panel A) and glycerol (panel B) to values of µ₂₃ predicted from the interaction potentials of Table 2. The good agreement for the large majority of the model compounds studied, especially in the case of tetraEG, supports the assumption of additivity, the neglect of excluded volume, and the use of ASA as the weighting factor for the solute-group interaction potentials α_solute,i in Eq. 3. The observed additivity and context-independence of these solute- model compound preferential interactions indicates that interactions of water with solute and model compound functional groups are also well-approximated as additive and context-independent. Relative (%) deviations between predicted and observed µ₂₃ values for glycerol interactions are larger than for tetraEG because glycerol interactions are weaker and therefore more difficult to determine by VPO, as comparison of Figs. 1 and 2 reveals. Uncertainties in µ₂₃ values are estimated as described in Supplemental Materials. Applications of these glycerol and tetra EG α-values (Table 2) are provided below.

Fig. 3. Comparison of Predicted and Observed Preferential interactions µ₂₃.

Predicted µ₂₃ (cal mol⁻¹ molal⁻¹; Table S1) for interactions of (A) tetraEG and (B) glycerol with model compounds plotted against the observed (experimental) value. Predictions are generated using Eq. 3, ASA information from Table S2, and interaction potentials α_i and β_k (Table 2) obtained from analysis of these model compound datasets. The line indicates equality of predicted and observed µ₂₃. Error bars are one standard deviation of fitting uncertainty for observed values and determined as described in Supplemental Materials for predicted values.

Determination of lacDBD unfolding m-values for glycerol and small PEGs (EG to PEG 300)

For comparison with α-value predictions, equilibrium constants K_obs for two-state, reversible unfolding of marginally-stable lacDBD, the operator binding domain of lac repressor^{58, 59}, were determined as a function of concentration of glycerol, ethylene glycol and a series of PEG oligomers including tetraEG, to concentrations of at least 3 monomolal. Values of ΔΔG^o _obs = -RTln(K_obs/K_obs ^o) for unfolding lacDBD at 40 °C are plotted vs. solute molality in Figure 4A; slopes obtained from these plots are unfolding m-values, listed in Table 3. A temperature of 40 °C was chosen because it is within the transition region and does not require extrapolation of the thermodynamic data for unfolding. Glycerol is stabilizing, with a m-value about half as large in magnitude and opposite in sign to that of urea ⁵⁹, while ethylene glycol and diEG are marginally stabilizing, triEG is neutral within the uncertainty, and tetraEG and PEG 300 are destabilizing.

Fig. 4. Effects of Glycerol and Small PEGs on Unfolding lacDBD.

(A) Standard free energy differences ΔΔG^o _{obs, 313} (kcal mol⁻¹) of unfolding of lac repressor DNA binding domain (lacDBD) at 313 K, expressed relative to unfolding in the absence of the solute, are plotted as a function of molality of glycerol, EG, diEG, triEG, tetraEG and PEG 300. Slopes of lines are m-values (Δµ₂₃; Eq. 5, Table 1) for these solutes. B) Contribution from each surface type to the ΔASA of unfolding lacDBD to an extended polypeptide chain (ref Guinn 2011). Predicted contribution (kcal mol⁻¹·\molal⁻¹) from solute interactions with each surface type (from α-values (Table 2)) to the tetraEG (C) and glycerol (D) m-values. Color coding is as in B. The sum of the bars is equal to the m-value. Purple bars represent the experimental tetraEG and glycerol m-values in panel (A).

Table 3.

m-Values Quantifying Effects of Polyols, Small PEGs, Other Solutes on LacDBD Unfolding and Dissociation of ConA Tetramer

	Lac DBD unfolding m-value (cal·mol−1·molal−1)		concanavalinA tetramer-dimer m-value (cal·mol−1·molal−1)
Solute	Experiment a	Predicted b	Experiment c,d	Predicted b
EG	56.9 ± 11	--
Glycerol	203 ± 18	276 ± 34	170 ± 260	227 ± 37
DiEG	67.0 ± 34	53.8 ± 54		239 ± 53
TriEG	−21.0 ± 29	−14.4 ± 73		411 ± 72
TetraEG	−111 ± 41	−82.6 ± 98 e		583 ± 88 f
PEG300	−253 ± 64	−253 ± 170		1010 ± 180
urea	−440 ± 10 d,g	−512 ± 84	−855 ± 69	−547 ± 120
proline		773 ± 210	598 ± 41	694 ± 310
GB	820 ± 110 d,h	631 ± 470	2160 ± 76	724 ± 520
GuHCl	−747 ± 60 i	−895 ± 170

^aDetermined at 40 °C.

^bPredicted at 25 °C using α-values from Table 2 for glycerol and for PEG end and interior groups, α-values from Diehl et al ³⁷ for urea, proline and GB, and α-values from Pegram et al ³⁹ for GuHCl. In all cases, ASA information is from Table S5; for lacDBD unfolding, an extended-chain model of unfolded lac DBD is used. ³⁶

^cDetermined at 20 °C ²¹

^dExperimental m-values are reported in cal mol⁻¹ M⁻¹. Values in cal mol⁻¹ m⁻¹ will be somewhat smaller in magnitude (except for initial slopes at low solute concentration); differences do not exceed the uncertainties listed.

^ePrediction from 25 °C tetraEG α values in Table 2 is −82.2 ± 79 cal·mol^−1·molal⁻¹

^fPrediction from 25 °C tetraEG α values in Table 2 is 581 ± 91 cal·mol⁻¹·molal⁻¹

^gUrea m-value at 25 °C is −449 ± 11 cal mol⁻¹ M^{−1 59}

^hGB m-value at 25 °C is 780 ± 110 cal mol⁻¹ M^{−1 58}

ⁱExperimental data and α-values are from Pegram et al ³⁹.

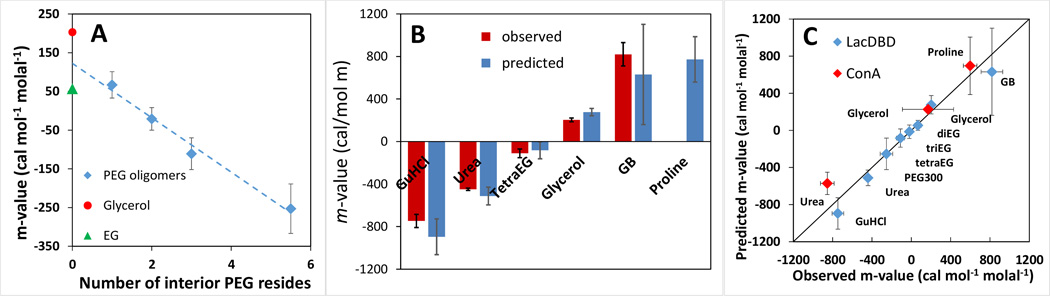
Di-, tri-, and tetraEG and PEG 300 form a series with the same end group ASA and composition (2 -CH₂OH groups), and an increasing number of -CH₂OCH₂- interior repeats. Fig. 6A reveals that PEG-lacDBD unfolding m-values decrease linearly with the number of -CH₂OCH₂- interior repeats. The intercept (122 ± 40 cal mol⁻¹molal⁻¹) and slope (−70.2 ± 16 cal mol⁻¹ molal⁻¹) are the experimentally-determined contributions of the two -CH₂OH end groups and each -CH₂OCH₂- PEG repeat to these lacDBD m-values.

Fig. 6. Effects of Glycerol, Small PEGs and Other Solutes on lacDBD Unfolding; Comparison of Predicted and Observed m-Values.

(A) Experimental lacDBD unfolding m-values (Fig.4A) for PEG oligomers diEG-PEG 300 (diamonds) are plotted vs. the number of interior -CH₂OCH₂- PEG units. Glycerol and EG m-values are shown for comparison; these were not used in obtaining the best-fit line. (B) Comparison of tetraEG and glycerol m-values for lacDBD unfolding with previously-determined lacDBD unfolding m-values for destabilizers (GuHCl; ³⁹; urea; ⁵⁹ ) and a stabilizer (GB, ⁵⁸). Predicted m-values (Table 3) for these solutes and for the stabilizer proline are also plotted. (C) Comparison of predicted and observed m-values for lacDBD unfolding (blue symbols) and dissociation of ConA tetramers into dimers (red symbols). (See Table 3.) Predictions are at 298K while observed lacDBD m-values are at 313K and ConA m-values are at 293 K. ²¹

The contribution of two PEG end groups to the lacDBD m-value obtained from this analysis (122 ± 40 cal mol⁻¹molal⁻¹) is twice as large as the EG m-value (56.9 ± 11 cal mol⁻¹ molal⁻¹) even though the functional groups are the same and the ASA of EG (212 A²) is almost the same as that of two PEG end groups (214 A²; Table 3 and S3). What differs is the composition of the ASA: EG is 47.5% hydroxyl O while PEG end groups are 49.7% hydroxyl O. Glycerol (55.6% hydroxyl O, only 20% larger ASA than EG (253 vs 212 A²) exhibits a lacDBD m-value (203 ± 18 cal mol⁻¹ molal⁻¹) that is almost four times as large as the EG m-value. From these results, we propose that the % hydroxyl O ASA of a polyol determines whether it is stabilizing or destabilizing, and that, for a given % hydroxyl O, the total amount of hydroxyl O ASA determines the magnitude of the protein-stabilizing effect. Tests of this proposal are in progress. These effects indicate a delicate balance between the favorable interaction of polyol aliphatic C and unfavorable interaction of polyol hydroxyl O with the largely (65%) aliphatic C surface exposed in unfolding lacDBD.

Chemical interaction coefficients (α values) for interactions of PEG end (-CH₂OH) and interior (-CH₂OCH₂-) groups with functional groups of proteins

Since no direct experimental route is available to determine α- and β-values for interactions of end and interior repeat groups of PEG with protein groups, we propose to use α- and β-values for interactions of tetraEG and glycerol with protein functional groups and ions to obtain the corresponding α- and β-values for interior and end groups of PEG. α- and β-Values for glycerol, scaled by the ratio of ASA of two PEG end groups to glycerol (214/253 = 0.845), provide approximate α- and β-values for two PEG end groups. These are approximate because of the small but significant difference in aliphatic C: hydroxyl O ASA ratio between glycerol and PEG end groups discussed above. Therefore, because the surface exposed in unfolding lacDBD is 65% aliphatic C, we correct the α-value for interaction of two PEG end groups with aliphatic C in order to obtain the experiment-based (extrapolated) lacDBD m-value (122 cal mol⁻¹ molal⁻¹). Given the dominance of interactions of the interior groups of PEG over end group interactions (see below), any inaccuracy introduced by this approximation is not expected to have a significant effect on predictions of chemical interactions of PEGs with protein surfaces. Resulting α and β values for interactions of two PEG end groups with protein functional groups (α_2E,i) and inorganic ions (β_2E,i) are listed in Table 2.

To obtain α and β values for the interactions of interior -CH₂OCH₂- groups of tetraEG with functional groups of proteins (α_I,i) and inorganic ions (β_I,i), we interpret tetraEG α-values (Table 2) as additive contributions from end-group and interior-group interactions: α_tetraEG,i = α_2E,i +3 α_I,i. TetraEG β-values are analyzed similarly to obtain β_I,i; values of α_I,i and β_I,i are listed in Table 2. Tests of the predictive ability of these PEG end group and interior group α-values are provided in Discussion.

Table 2 reveals that α- and β-values quantifying chemical interactions of the interior -CH₂OCH₂- group of PEG with protein functional groups and inorganic ions are as large or larger in magnitude as those of two end -CH₂OH groups. Indeed interactions of the interior group are at least as important as those of the two end groups even for diEG, and become progressively more dominant with increasing number of interior groups in larger PEGs. Although the two -CH₂OH end groups contribute more than half the ASA of tetraEG, they contribute less than a third of the interaction of tetraEG with most protein functional groups and inorganic ions. Interactions of the three interior -CH₂OCH₂- repeats make the dominant contribution to tetraEG α- and β-values for all groups and ions except cationic N.

Discussion

Comparisons of Chemical Interactions (α values) of Protein Groups with Glycerol (also PEG End Groups) and with tetraEG (also PEG Interior Groups)

Key Differences in Sign of Interactions with Protein Groups

Because aliphatic C makes by far the largest contribution to the ASA of both folded and unfolded proteins and to the ΔASA of unfolding, interactions of glycerol, tetraEG and PEG groups with aliphatic C are very important determinants of effects of these solutes on protein processes even though α-values (Table 2) and K_p values (Table S4) for interactions with aliphatic C are relatively small in magnitude. TetraEG and PEG interior residues interact moderately favorably with aliphatic C while glycerol and PEG end groups exhibit small unfavorable interactions, relative to interactions with water. This difference is a major reason why glycerol is a protein stabilizer while tetraEG and larger PEGs are destabilizers.

At acidic pH (<pH 3), carboxylates of proteins are protonated and hence the relevant interactions of solutes are with carboxylic acid oxygens (i.e. =O and –OH) instead of with carboxylate oxygens (both –O^0.5−) present at neutral or alkaline pH. Table 2 shows that tetraEG and PEG interior residues interact moderately favorably with carboxylic acid O, while glycerol and PEG end groups exhibit a small unfavorable interaction with carboxylic acid O. The favorable interaction of PEG interior residues with carboxylic acid O indicates that the carboxylic acid -OH group is a good hydrogen bond donor to the ether O of PEG, relative to interactions with water.

Similarities in Sign of Interactions with Most Protein Groups

α- and β-Values (Table 2) reveal that preferential interactions of tetraEG and PEG interior -CH₂OCH₂- groups with amide O and anionic carboxylate O, as well as with dianionic phosphate, are strongly unfavorable. Interactions of glycerol and PEG –CH₂OH end groups with these functional groups are weakly unfavorable. Strongly unfavorable interactions of PEG -CH₂OCH₂- moieties with these oxygens are expected, as discussed above, because -CH₂OCH₂- lacks the hydrogen bond donor capability necessary to compete effectively with water to interact with these oxygens.

Preferential interactions of tetraEG, PEG end and interior residues, and glycerol with hydroxyl O are also unfavorable, though for glycerol this preferential interaction is very small. The relatively small magnitude (compared to tetraEG and PEG interior residues) of glycerol and PEG end group α-values for interactions with both hydrogen bond donor and acceptor groups means that these hydrogen bonding interactions are nearly equivalent in free energy to the corresponding hydrogen bonding interactions with water.

α-Values (Table 2) also reveal that interactions of glycerol and PEG end groups with amide and cationic N are weakly favorable while interactions of PEG -CH₂OCH₂- repeats and therefore of tetraEG with amide and cationic N are strongly favorable. Amide and cationic N groups are good hydrogen bond donors, allowing them to compete with water to interact with the ether oxygen of PEG interior groups.

Interactions of glycerol, tetraEG and PEG end and interior groups with aromatic C are all very favorable. Studies of the interactions of alcohols, polyols and small PEGs with aromatic hydrocarbons and nucleobases are in progress to determine the contributions of individual –HO, -O- and hydrocarbon functional groups to the interaction of these solutes with aromatic C, and the differences in interactions with aromatic and aliphatic C.

Comparisons of PEG and Glycerol Interactions with Other Osmolytes

Interactions of PEG interior groups and of tetraEG with protein functional groups, quantified by α-values (Table 2), are a mixture of strong favorable and unfavorable interactions, resulting in predictions of PEG-protein µ₂₃ values and of m-values for protein processes that are small differences between large offsetting contributions, and as such are quite sensitive to the details of the composition of the protein surface with which PEG is interacting. This situation parallels what is observed for glycine betaine and proline^{37, 38}, and indeed PEG interior group α- values in many cases are of the same sign and in some cases similar in magnitude to the interactions of glycine betaine (GB) and proline with these groups. For interactions with amide and carboxylate O, this parallel has a straightforward explanation. PEG interior groups and GB (also, but to a lesser extent, proline and tetraEG) lack the hydrogen bond donor capability necessary to compete with water to interact with amide and carboxylate O of proteins. Therefore these solutes interact unfavorably with these groups and are strongly excluded from them. Figure 5A uses local-bulk partitioning coefficient K_p (Table S4), derived from α-values using Eq. 4 (Table 1) to predict the extent of accumulation or exclusion of the PEG interior -CH₂OCH₂- repeat at each functional group of a FS (phe-ser) dipeptide, and compares these predictions with those for GB. These predictions can be made for any amino acid, peptide or protein. The FS dipeptide is chosen for purposes of illustration because it displays all but one of the major protein functional groups. Colors represent the gradation from strong accumulation (red, corresponding to K_p > 1.4 (see Table S4) to strong exclusion (violet, corresponding to K_p < 0.5).

Fig. 5. Predicted Interactions of Glycerol, PEG Interior Groups, Urea and Glycine Betaine with the Ser-Phe Model Dipeptide.

Predicted extent of accumulation and exclusion of solutes from functional groups of the arbitrarily chosen model peptide Ser-Phe from K_p values (Table S4) using a color “heat map”³⁷. Comparison of (A) glycerol and (B) PEG interior group with each other and with (C) urea^{36, 37}, and (D) glycine betaine^{37, 38}. Analogous predictions can be made for any other peptide or other compound with these functional groups using this set of K_p values (Table S4).

Interactions of glycerol and PEG -CH₂OH end groups with the functional groups of proteins are also a mixture of favorable and unfavorable interactions, all of which are relatively weak by comparison with the analogous interactions of PEG interior groups or tetraEG. Comparison with results for other solutes investigated to date shows that interactions of glycerol and PEG end groups with functional groups of proteins are most similar in magnitude, though not in sign, to urea. Interactions of glycerol and urea with two of the most significant functional groups for protein unfolding (aliphatic C, amide O) are opposite in sign, making glycerol a protein stabilizer (unfavorable interactions with the functional groups exposed in unfolding) while urea is a destabilizer (favorable interactions). Glycerol and urea exhibit the same sign of interaction with aromatic C and amide N (both favorable), but opposite signs of interaction with hydroxyl and carboxylate O (urea favorable, glycerol unfavorable) and with cationic N (urea unfavorable, glycerol favorable). Figure 5B compares the extent of accumulation or exclusion of glycerol and urea at each functional group of the FS (phe-ser) dipeptide, showing the extent to which glycerol is an “anti-urea”. This comparison is based on K_p values for glycerol (Table S-4) and urea^{36, 37}.

Predicting LacDBD Unfolding m–Values for Glycerol, tetraEG and other PEGs; Comparison with Experiment and with Results for Other Solutes

From α-values quantifying interactions of glycerol, tetraEG, and PEG end and interior groups with unit area of each major functional group of proteins (Table 2) and the amount and composition of the ΔASA of unfolding lac DBD to an extended chain (Fig 4B, Supp. Table 5), unfolding m-values are readily predicted. Aliphatic C makes the dominant contribution (65%) to the ΔASA of unfolding, with amide O (11%) the next largest contributor. Figure 4C shows the predicted contribution of each type of surface to the glycerol and tetraEG m-values. Table 3 compares predicted (25 °C) and observed (40 °C) m-values: for both glycerol and tetraEG these agree within the uncertainty. For tetraEG, analysis of the contributions of different surface types to the predicted m-value shows substantial compensation between moderately large stabilizing and destabilizing interactions, resulting in the small magnitude of the m-value. The uncertainty in the predicted m-value is relatively large because propagation of error does not exhibit this compensation. Any effect of the temperature difference between observed and predicted m-values is likely to be much smaller than this uncertainty. LacDBD unfolding m-values for urea ⁵⁹ and GB ⁵⁸ are not significantly temperature dependent in this range (Table 3).

From the PEG end and interior group α values of Table 3 and the ΔASA of unfolding lacDBD, m-values for the chemical effect of any small PEG on unfolding of lac DBD are readily predicted. For larger PEGS, shielding of chemical interactions (χ effect) and excluded volume effects also need to be considered ⁴³. The contribution of the PEG end group to these predictions is fixed as described in Results, using the intercept of the plot (Fig 6A) of the diEG-PEG 300 m-values vs. the number of interior residues. Here we examine whether the PEG interior-residue α- values in Table 2 can predict the slope of this plot (i.e. the increment in PEG m-value per interior residue). From Fig 6A the experimental m-value increment is −70.2 ± 16 cal mol⁻¹ molal⁻¹ at 25 °C which agrees well with the prediction from the α-values of Table 2 (−68.2 ± 31 cal mol⁻¹ molal⁻¹ at 40 °C). Predictions of di-, tri-, tetraEG and PEG 300 m-values from these α-values are also in agreement with the experimental values within uncertainty, as shown in Table 3. The EG m-value cannot be predicted at this time because α- values for interactions of EG with all the different functional groups exposed in unfolding lacDBD are not yet available. For some predictions the % uncertainty is large because the propagation of the uncertainty does not exhibit the compensation between large opposing contributions that m-values do.

Currently the experimental uncertainty in the van’t Hoff analysis of lacDBD thermal unfolding as a function of glycerol and PEG concentration is too large to test this. For urea and glycine betaine, examples where the entropy m-value either small or much larger in magnitude than the enthalpy m-value ^{58, 59}, m-values are similar at 40°C and 25°C and the extrapolated 25°C experimental m-value agrees well with the 25°C prediction. Figure 6B compares experimentally-determined LacDBD unfolding m-values for glycerol and tetraEG with previously-determined results for denaturants (GuHCl, urea) and osmolyte-stabilizers (GB, proline). These m-values give the destabilization (negative) or stabilization (positive) ΔΔG^o _obs at 1 molal solute concentration. TetraEG and glycerol are less perturbing than these other solutes.

The destabilizing effect of tetraEG arises from favorable preferential interactions with the aliphatic C, aromatic C, and amide and cationic N surface exposed in unfolding, partially compensated by unfavorable interactions with amide and carboxylate O. As noted above, parallels exist with GB, which also has favorable interactions with aromatic C and amide and cationic N surface exposed in unfolding, partially compensated by unfavorable interactions with amide and carboxylate O. What makes GB a stabilizer while tetraEG is a destabilizer is the sign of the small-magnitude interaction with aliphatic C surface, which is favorable for tetraEG but unfavorable for GB. For tetraEG, aliphatic C makes a large (destabilizing) contribution despite a relatively small aliphatic C α-value, because aliphatic C accounts for the majority of the ΔASA of unfolding (65%). In contrast, though aromatic C accounts for only about 6% of the total ΔASA, it makes a large (destabilizing) contribution because preferential interactions of tetraEG with aromatic C are highly favorable. This parallels the situation for urea, where weak favorable interactions of urea with aliphatic C and strong favorable interactions of urea with aromatic C are deduced to make similar significant contributions to the m-value for unfolding of a typical globular protein³⁶. The protein-stabilizing effect of glycerol arises from its unfavorable preferential interactions with amide O and aliphatic C; favorable interactions with amide N and aromatic C only partially offset these stabilizing contributions.

Predicting solute m-values for association of ConA dimers into tetramers; comparison with experiment

Effects of solutes and Hofmeister salts on the association of two concanavalin A dimers to form a tetramer have been determined at room temperature^{21, 22}. Glycerol modestly favors tetramerization (m-value = 170 ± 260 cal mol⁻¹ molal^{−1 21}; Table 3). Structural analysis reveals a large dimer-tetramer interface (ΔASA = − 4900 Ų ; Table S5), differing somewhat in composition from that buried in protein folding, with smaller proportions of aliphatic C and amide O, N and larger proportions of both cationic N and anionic O. Using the ASA information in conjunction with the glycerol α-values in Table 2, we predict a small stabilizing glycerol m-value (Table 3) which is completely consistent with the experimental value (see Figure 6C). m-Values were also determined for urea, proline, GB and other solutes;^{21, 22}). Predicted m-values for urea and proline (Table 3) are comparable to the experimental values. For all other cases, Figure 6C summarizes the generally good agreement of observed solute m-values for lacDBD unfolding and ConA tetramer dimer dissociation with those predicted from solute α-values and ASA information (Table 3).

Predicting Effects of PEG400 on Solubility of Aromatic Compounds; Comparison with Experiment

Selection of Aromatics for Analysis

Rytting et al (’05) determined solubilities of more than 100 aromatic compounds at PEG400 volume fractions of 0, 0.25, 0.5, 0.75, and 1⁶⁰. Functional groups on 28 of these compounds (see Table S6 for names and structures) are sufficiently similar to the protein groups investigated here to warrant comparing predicted and observed µ₂₃. These include biphenyl and naphthalene as well as derivatives of benzene, naphthalene, biphenyl and other aromatic or fused aromatic-aliphatic (steroid) ring systems. Nucleobases and other heterocyclic aromatics, as well as those with halogens and/or ether oxygens are omitted from the present analysis. In addition to aromatic (sp²) C, these 28 model compounds also display aliphatic (sp³) C, amide and carbonyl O, amide and amino N, and hydroxyl and carboxylic acid O groups.

Solubilities of these 28 uncharged aromatic compounds in the absence of PEG400 are in the range 10⁻⁵ – 10⁻¹ M. Figs. S3A,B show the dramatic increases in solubility with increasing PEG400 concentration, by factors of up 10⁴ in 75% PEG 400. Qualitatively, these large solubility increases result from the very favorable interactions (large negative alpha values) of the interior (and end) groups of PEG 400 with the aromatic C surface of these model compounds (as quantified by the α-values in Table 2). Interactions with aliphatic C, amide (and amino) N and carboxylic acid O are also predicted to be favorable and contribute to these solubility increases, while interactions with amide (and carbonyl) O are predicted to be unfavorable. Table 2 lists α- values for the interactions of end and interior groups of any PEG with these groups in a non-aromatic context. The effect on interactions with PEG400 of placing these groups in an aromatic context can be assessed from analysis of these data. The other two groups present on these aromatic model compounds (carbonyl O and amino N) should be similar in hydrogen bonding interactions to amide O and N. Indeed interactions of urea with carbonyl O and amino N functional groups on the heterocyclic aromatic rings of nucleobases are found to be similar to interactions with amide O and N⁶¹. On the other hand, interactions of urea with nucleobase methyl groups are found to be more favorable than those with other aliphatic C⁶¹.

Plots of the experimental data (the logarithm of the molar solubility of the aromatic as a function of PEG400 volume fraction for these 28 compounds are shown in Figure S3, together with fits of these data to quadratic functions of PEG400 concentration. These data are converted to molal scale solubilities (m₂ ^ss) as a function of PEG400 molality using the equations of Table S8, plotted as in Fig. S4 and fitted as either a quadratic or linear (first two or three points only) function of PEG400 molality. Values of µ₂₃ obtained from the initial slopes are reported in Table S10. The uncertainties in the initial slopes are relatively large, especially where curvature is pronounced, because of the small data sets and the lack of data at low PEG 400 concentrations. In addition, for the higher-solubility compounds (S > 0.1 M), µ₂₃ values estimated from these initial slopes have an additional uncertainty resulting from the neglect of self interactions in Eq. 2.

The α-values for the interaction of PEG400 with the aromatic C of these compounds is predicted by additivity to be a linear combination of α-values from Table 2 for aromatic interactions of its two end groups and 7.7 interior groups (α_PEG400,aroC = α_2E,aroC + 7.7α_I,aroC). α-Values for interactions of PEG400 with unit area of the other functional groups and types of surface of these aromatic compounds are predicted analogously. Many of these functional groups are the same as those present on model compound studied here (alkyl, amide, carboxylic acid, hydroxyl groups; Table S1), though the context of these groups on an aromatic ring may in principle alter their interaction with PEG400. Other functional groups are different (carbonyl O of ketone or quinone groups, amino N).

Predicted µ₂₃ values obtained from these PEG400 α-values (Table S9) and ASA information (Table S7) are listed in Table S10. For these predictions, carbonyl O, phenolic hydroxyl O and amino N of the aromatic compounds are treated as amide O, hydroxyl O and amide N, respectively. α -Values for interactions of urea with carbonyl O and amino N of nucleobases are similar though not identical to α-values for interactions of urea with amide O and amide N of protein model compounds⁶¹. For the 16 non-steroid compounds (derivatives of benzene, naphthalene and biphenyl) agreement between predicted and observed µ₂₃ values is generally within ±25%, and is not significantly different for the ten compounds with carbonyl O, phenolic hydroxyl O, and/or amino N than for the six compounds lacking these groups. These sixteen comparisons largely validate the approach developed here for predicting interactions and m-values for any PEG from the data for glycerol- and tetraEG-model compound interactions developed here, and also show that context (aromatic vs nonaromatic) in general is not of primary significance as a determinant of PEG-functional group α –values.

For the twelve steroids with a fused ring system, experimental values of µ₂₃ are systematically more favorable than predicted values by approximately −1.5 kcal mol⁻¹ molal⁻¹, giving rise to the offset in the predicted-observed comparison shown in Figure 7. This offset is most simply interpreted as a favorable concerted (context dependent) interaction involving multiple residues of the PEG400 chain molecule and the fused ring system of the steroids.

Fig. 7. Comparison of Predicted and Observed Interactions of PEG 400 with Aromatic Compounds and Steroids.

Predicted vs observed µ₂₃ values determined by solubility ⁶⁰ for interactions of PEG400 with 28 aromatic compounds (Table S6) with functional groups that are the same or similar to those of the model compound set investigated here. Predictions are obtained from α-values for interactions of PEG 400 with functional groups of proteins given in Table S9, using ASA information from Table S7. Experimental uncertainty is calculated as described in Supplemental Materials. Blue symbols are µ₂₃ values for 16 compounds without a steroid fused-ring system; red symbols are µ₂₃ values for 12 steroid compounds with fused ring systems. For all 12 steroids, observed µ₂₃ values are systematically more favorable (more negative) than predicted µ₂₃ values by ~1.5 kcal mol⁻¹ molal⁻¹.

Conclusions

We develop the ability to predict or interpret effects of glycerol and any low molecular weight PEG on protein processes and solubility of organic compounds in terms of the change in water-accessible surface area (ASA) of the protein or organic compound in these processes. Relatively small differences between interactions of protein aliphatic carbon surface with -CH₂OH groups (unfavorable) and -CH₂OCH₂- groups (favorable), relative to interactions with water, explain the opposite effects of glycerol and tetraEG on protein stability. We demonstrate the ability to predict the concentration-dependent effects of any PEG oligomer on solubility of any organic compound with protein-like functional groups; this should be of practical significance. Current research is focused on expanding the groups of solutes and model compounds characterized to include interactions of nucleobases and sugars with glycerol and other polyols of different ratios of aliphatic C to hydroxyl O ASA and small PEGs, dissecting contributions of unfavorable chemical interactions and unfavorable excluded volume interactions to the interactions of low and high molecular weight PEGs with native proteins, relevant for understanding PEG effects on protein solubility, protein folding and other protein processes.