Preliminary Clinical Evaluation of a 4D-CBCT Estimation Technique using Prior Information and Limited-angle Projections

Abstract

Background and Purpose

A new technique has been previously reported to estimate high-quality 4D-CBCT using prior information and limited-angle projections. This study is to investigate its clinical feasibility through both phantom and patient studies.

Materials and Methods

The new technique used to estimate 4D-CBCT is called MMFD-NCC. It is based on the previously reported motion-modeling and free-form deformation (MMFD) method, with the introduction of normalized-cross-correlation (NCC) as a new similarity metric. The clinical feasibility of this technique was evaluated by assessing the accuracy of estimated anatomical structures in comparison to those in the ‘ground-truth’ reference 4D-CBCT, using data obtained from a physical phantom and three lung cancer patients. Both volume percentage error (VPE) and center-of-mass error (COME) of the estimated tumor volume were used as the evaluation metrics.

Results

The average VPE/COME of the tumor in the prior image was 257.1%/10.1 mm for the phantom study and 55.6%/3.8 mm for the patient study. Using only orthogonal-view 30° projections, the MMFD-NCC has reduced the corresponding values to 7.7% /1.2 mm and 9.6%/1.1 mm, respectively.

Conclusions

The MMFD-NCC technique is able to estimate 4D-CBCT images with geometrical accuracy of the tumor within 10% VPE and 2 mm COME, which can be used to improve the localization accuracy of radiotherapy.

I. INTRODUCTION

Accurate tumor localization is critical for radiation therapy, especially for treating moving tumors such as lung tumors [1–3]. Emerging hypo-fractionated treatment regimens such as lung stereotactic body radiation therapy [4–6] deliver a much higher radiation dose per fraction, which further necessitates accurate tumor localization. 4D on-board imaging techniques such as 4D cone-beam CT (CBCT) [7–10] and 4D digital tomosynthesis (DTS) [11–14] have found wider clinical interest recently to improve the localization accuracy of moving tumors. Compared with 3D imaging techniques, the 4D capacity of these techniques enables the trajectory of moving tumors to be captured, which can lead to better alignment of the target volume. 4D-CBCT is also potentially useful for treatment dose verification and accumulation [15]. However, using the current clinical ‘gold-standard’ Feldkamp-Davis-Kress (FDK) [16] algorithm, 4D-CBCT reconstruction requires full-angle projection data, leading to an excessive amount of scanning time and imaging dose. In contrast, 4D-DTS reconstruction uses only limited-angle projection data, requiring less scanning time and imaging dose [11, 12]. However, 4D-DTS is limited by its degraded resolution along the plane-to-plane direction without full volumetric information, which may impair the tumor localization accuracy [17, 18].

Recently we have developed a new technique entitled-motion modeling and free-form deformation (MMFD) to estimate high-quality 4D-CBCT images using a priori information and only limited-angle projections from 4D-DTS acquisition [19]. A simulation study using digital anthropomorphic phantoms demonstrated the feasibility of this method. However, that study was limited to simulated idealized, scatter-free imaging data from perfectly matched CT and CBCT imaging systems of monochromatic energy. The MMFD technique is less robust to the real clinical imaging data, which contains scatter, beam-hardening effects and energy spectrum mismatches between CT and CBCT. In this study, we developed a normalized-cross-correlation based MMFD method (MMFD-NCC) to improve its robustness for real clinical data and evaluated its accuracy through both phantom and patient studies.

II. MATERIALS AND METHODS

II.A. MMFD-NCC method

In the MMFD-NCC method, each phase of the new on-board 4D-CBCT (CBCT_new) is considered as a deformation of the CT volume (CT_prior) acquired previously for treatment planning. The CBCT_new at each phase is generated by deforming CT_prior using a deformation vector field DVF. To solve for the optimal DVF, we used the data fidelity constraint, which requires the DRRs of CBCT_new to match with the acquired on-board projections. For real clinical images, the data fidelity constraint based on the sum of squared difference (SSD) [19] between DRRs and the on-board projections may not hold due to errors caused by the gray level mismatches between CT and CBCT. To solve this problem, we introduce the normalized cross-correlation (NCC) [20] metric in the data fidelity constraint to measure the similarity between the DRRs and the on-board projections. Defining DRR image as f(x, y) and the corresponding onboard projection as t(x, y), NCC is calculated as following:

$$\mathit{NCC}[f,t]=\frac{{\mathrm{\sum }}_{x,y}(f(x,y)-\overline{f(x,y)})\ast (t(x,y)-\overline{t(x,y)})}{\sqrt{{\mathrm{\sum }}_{x,y}{(f(x,y)-\overline{f(x,y)})}^2}\ast \sqrt{{\mathrm{\sum }}_{x,y}{(t(x,y)-\overline{t(x,y)})}^2}}$$ (1)

x and y represent the pixel coordinates on the DRR and the on-board projection image. As shown in Eq. (1), NCC measures the linear correlation between the DRR and the on-board projection, which is more robust against intensity mismatches.

Besides the NCC based data fidelity constraint, the MMFD-NCC method uses two deformation models to solve DVF: motion-modeling and free-form deformation. A stepwise explanation of the MMFD-NCC method is described below.

First, the end-expiration phase of an n-phase 4D-CT previously acquired for planning is selected as CT_prior in this study due to its relative stability [21]. All of the other (n−1) phases of 4D-CT are deformed to CT_prior using Velocity AI (Varian Medical Systems, Palo Alto, CA) to obtain (n−1) deformation fields. A principal component analysis (PCA)-driven motion model [22–24] is then built based on the (n−1) deformation fields to extract the PCA eigenvectors, which represent both the common features and unique variance in the (n−1) deformation fields. Correspondingly, the deformation field DVF can be represented as a linear combination of the 3 most prominent PCA eigenvectors, as shown in previous studies [25, 26]. A gradient-descent optimizer is adopted to derive the weightings of these PCA eigenvectors based on the data fidelity constraint.

The above PCA-based DVF optimization is the motion-modeling (MM) part of MMFD-NCC, which builds the DVF based on motion models derived from 4D-CT images. However, in real clinical practice, the motion models derived from 4D-CT can be outdated due to anatomical variations and motion pattern changes. Thus, the MM can only provide a quick coarse estimation of DVF.

Following MM, the free-form deformation (FD) [27, 28] process fine-tunes the coarse estimation from MM by allowing each voxel to move independently without any assumption of the motion model. The FD process minimizes a deformation energy cost function while reducing the data fidelity error to fine-tune the DVF. Compared to motion modeling, the free-form deformation process has many more variables to optimize and is easy to be trapped at a local optimum. After motion modeling generates a starting DVF that is closer to the global optimum, the following free-form deformation is able to converge to the global optimum faster without being trapped at a local optimum. After FD, final 4D-CBCTs were estimated by deforming CT_prior using the fine-tuned DVF for each phase.

As a summary, the MMFD-NCC method uses motion modeling to quickly derive a coarse DVF, followed by free-form deformation to correct the residual errors in the DVF.

II.B. Evaluation study

Studies using one phantom and three patients’ data [9] were conducted to evaluate the clinical feasibility of using MMFD-NCC technique to estimate 4D-CBCT.

II.B.1. Phantom study

An anthropomorphic lung phantom (CIRS 008A, Computerized Imaging Reference Systems, Norfolk, VA) was used for the study. During the 10-phase prior 4D-CT acquisition, a 3 cm-diameter and soft tissue-equivalent (density: 1.06 g/cc) spherical insert was placed inside the phantom to simulate a tumor and was programmed to move based on a cos⁴(x) curve in longitudinal direction with 4 seconds (s) cycle and 2 cm amplitude. The 4D-CT was acquired by a PET-CT scanner (Siemens Biograph mCT, Siemens Medical Solutions, Malvern, PA) in helical mode using 120 kVp and 40 mAs per rotation.

After the 4D-CT scan, the phantom was positioned on a LINAC (Truebeam, Varian Medical Systems, Palo Alto, CA) treatment couch for 4D-CBCT imaging. To simulate anatomical variation and motion pattern change from 4D-CT to 4D-CBCT acquisition, the 3 cm insert was replaced by a 2 cm insert, and its motion amplitude was increased to 3 cm. Although 3 cm tumor motion is rare in clinical cases, this study aims to simulate a difficult scenario with large tumor motion to evaluate the accuracy of the estimation method under extreme conditions. The onboard 4D-CBCT projections were acquired by a slow-gantry technique using TrueBeam developer mode, which runs the LINAC using preset ‘control points’ defining the machine accessories’ parameters. The in-house developed slow-gantry technique was able to run the gantry to acquire full-fan projections with varying speeds. The acquisition frame rate was 7 frames per second (fps), using 120 kVp, 20 mA and 16 ms for each projection. The details of the five acquisitions with different gantry rotation speeds are listed in Table 1.

Table 1.

Five imaging sets acquired with varying gantry rotation speeds for the phantom.

Acquisition Set	Scan Angle	GRS (°/s)	No. of Projections	Sampling Interval (°/prj)	Imaging Time (s)	mAs
1	−15°~15° & 75°~105°	0.25	1671	0.4 ± 0.4	240 + 10	535
2		0.5	834	0.7 ± 0.9	120 + 10	267
3		1	416	1.4 ± 1.7	60 + 10	133
4		2	207	2.8 ± 3.5	30 + 10	66
5		4	103	5.5 ± 6.8	15 + 10	33

^*GRS: gantry rotation speed; No. of projections: total number of 4D projections acquired; Sampling Interval: average sampling interval (± standard deviation) of phase-binned projections. °/prj: degree per projection.

In Table 1, the imaging time for MMFD-NCC was calculated based on a limited orthogonal-view 30° scan angle, comprising 30° (−15°~15°, by IEC 1217 Varian scale convention) around the anterior-posterior (AP) direction and 30° (75°~105°) around the left-lateral (LLAT) direction. The additional 10 s imaging time accounted for the gantry rotation time between the two scan directions, using a gantry rotation speed of 6°/s. The mAs values were calculated based on the total number of projections acquired. From acquisition sets 1 to 5, both the scan time and dose were reduced as the gantry rotation speed increased. However, the projections became more sparsely sampled, with the average sampling interval increased.

In Table 1, the average sampling interval (± standard deviation) was calculated as the mean and standard deviation of the interspacings between phase-binned adjacent projections. The standard deviations are non-negligible compared to the average sampling interval, which are caused by the ‘clustering’ and ‘gap’ [29] seen in the phase-binned slow-gantry projections. The step-and-shoot technique [11], which acquires fluoroscopy for over a respiratory cycle at preselected scan angles, is an acquisition technique that can avoid the ‘clustering’ and ‘gap’ to achieve evenly spaced projections. More-evenly spaced projections offer more effective sampling, as suggested in another study [30]. However, step-and-shoot technique is not used in this study, because the current developer mode of Varian TrueBeam machines does not support very low frame rate acquisition (below 3 fps), which makes the dose of step-and-shoot technique much higher than the slow-gantry technique. Besides the step-and-shoot technique, recently developed active acquisition technique triggered by tracked tumor motion [29–31] can also achieve more evenly-spaced projections through adjusting gantry rotation speed/acquisition frame rate or dropping excessive projections. Due to the lack of supporting hardware and software, they were not used in this study either.

The 4D projections of different acquisition sets were individually post-processed and sorted into 10 phases by manually identifying the projections with tumor motion peaks and then dividing the projections in-between into equally distributed phase bins. The effects of the projection average sampling interval on the estimation accuracy were evaluated by comparing the estimation results for acquisition sets 1–5.

To evaluate the effects of the scan direction, 4D projections from the orthogonal-view-oblique 30° scan angles, i.e. 30°–60° at left-anterior-oblique (LAO) direction and 120°–150° at left-posterior-oblique (LPO) direction were also acquired with the same gantry rotation speeds as in acquisition sets 1–5 for image estimation.

To provide the ‘ground-truth’ on-board reference 4D-CBCT image, fully-sampled 4D projections covering a 200° scan angle were acquired in the full-fan mode with a gantry rotation speed at 0.25°/s. The projections were then manually sorted through identifying projections with tumor motion peaks and reconstructed by the conventional FDK algorithm to obtain a 10-phase reference 4D-CBCT. Note that the gantry rotation speed of 0.25°/s led to an average sampling interval of 0.4° per projection (0.4°/prj) for each phase, which is sufficient for FDK reconstruction.

II.B.2. Patient study

The patient imaging data were acquired under an IRB-approved protocol. The 4D-CTs of three patients were acquired on a CT scanner (LightSpeed, GE Healthcare, Milwaukee, WI) in cine mode [9]. Scan parameters were set at 120 kVp, 100 mA, 0.5 s cine time, and cine duration of average breathing cycle plus 1 s. For 4D-CBCT acquisition, 200° on-board full-fan projections of each patient were acquired within two weeks from 4D-CT acquisition, using an adaptive-speed slow-gantry rotation setting [9] using 120 kVp, 80 mA and 25 ms. The projections were phase-sorted using an in-house developed Fourier-transform based method [32, 33]. The average sampling intervals (± standard deviations) of phase-binned projections for patient 1, 2 and 3 are 0.9 ± 1.0°/prj, 0.9 ± 0.9°/prj and 1.1 ± 1.2°/prj, respectively. Similar to the phantom study, full 200° projections were used to reconstruct the reference 4D-CBCT and orthogonal-view 30° projections around the posterior-anterior (PA) (150°~180°) and the right-lateral (RL) (240°~270°) directions were used for MMFD-NCC estimation.

II.C. Evaluation metrics

To evaluate the estimation results, the tumors in both the estimated and the reference images were contoured for comparison. For the phantom images, the tumors were automatically contoured in Eclipse (Varian Medical Systems, Palo Alto, CA) using HU threshold. For the patient cases, the tumors were manually contoured and cross-validated by two clinicians. Furthermore, internal target volumes (ITV) of the patients were generated by combining the tumor contours from all 10 phases. For target localization of lung cancer patients, ITV captures the entire motion range of the tumor. Therefore, accurate estimation of ITV is the key for localizing the moving tumor. Eq. (2) and Eq. (3) define the metrics to quantify the geometric accuracy of the tumor volumes:

$$\mathit{VPE}=\frac{\mid V\cup V_0-V\cap V_0\mid }{V_0}\ast 100\%$$ (2)

$$\mathit{COME}=\sqrt{\mathrm{\Delta }{x}^2+\mathrm{\Delta }{y}^2+\mathrm{\Delta }{z}^2}$$ (3)

VPE calculates the volume percentage error between V (estimated or prior tumor volume) and V_o (reference tumor volume) and indicates tumor shape accuracy. COME calculates the center-of-mass error between V and V_o and indicates tumor location accuracy. Δx, Δy and Δz are center-of-mass distances from V to V_o in each of the three canonical directions.

III. RESULTS

III.A. Phantom study

III.A.1. Image comparison between different techniques

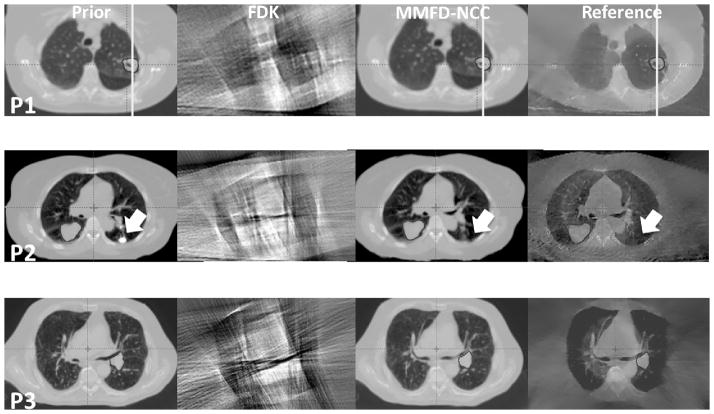
Fig. 1 shows the slice cuts of different images. The prior image differed from the ‘ground-truth’ reference image as the latter had a smaller tumor with shift along the longitudinal direction. The FDK image displayed excessive streak artifacts and distortions in the axial view due to lack of information from only orthogonal-view 30° projections. The MMFD-SSD image was very noisy and the tumor was not well deformed, due to the intensity mismatches between CT and CBCT systems. Compared with the FDK image, the MMFD-NCC image was free from streak artifacts by using the information from high quality prior image. Compared with the MMFD-SSD image, the MMFD-NCC image largely removed the noise and estimated the tumor volume more accurately due to the introduction of the NCC, which is a more robust similarity metric to handle intensity mismatches between CT and CBCT. Note that the peripheral phantom surface appeared slightly distorted in the MMFD-NCC images. It is mainly due to the limited field-of-view of full-fan projections, which cannot fully cover the peripheral parts of the phantom.

Figure 1.

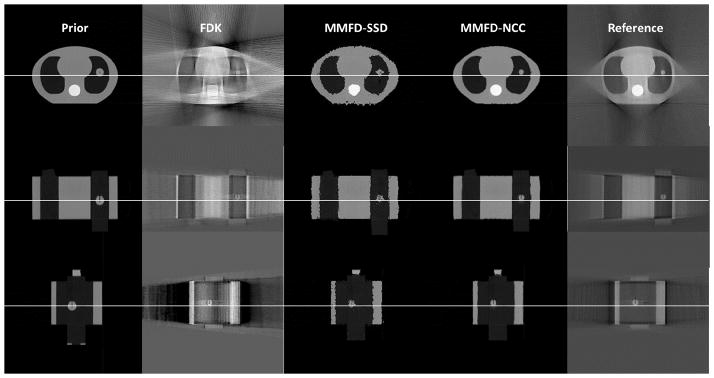
Slice cuts from the prior CT image, the image reconstructed by FDK, the image estimated by MMFD-SSD, the image estimated by MMFD-NCC and the reference CBCT image of the CIRS phantom at the end-expiration (50%) phase. The FDK reconstruction, MMFD-SSD estimation and MMFD-NCC estimation all used orthogonal-view 30° projections around anterior-posterior and left-lateral directions from acquisition set 2 (Table 1). The ‘ground-truth’ on-board reference image was reconstructed by FDK algorithm using 200° fully-sampled projections.

III.A.2. Geometric accuracy of the estimated tumor (VPE and COME)

Table 2 compares the VPE and COME values of the tumor in the prior image to those of the estimated tumors by MMFD-NCC. The average (±standard deviation) VPE for the tumor in the prior image and the MMFD-NCC estimated tumors was 257.1% (±60.2%) and 7.7% (±1.2%), respectively. The corresponding COME was 10.1 mm (±4.5 mm) and 1.2 mm (±0.2 mm), respectively. The MMFD-NCC greatly reduced the VPE and COME by deforming the tumor in the prior image to the correct locations and size for each 4D-CBCT phase.

Table 2.

VPE and COME values of the tumor in the prior volume and the MMFD-NCC estimated tumors for all ten 4D-CBCT phases. All image estimations used orthogonal-view 30° projections around anterior-posterior and left-lateral directions from acquisition set 2 (Table 1).

	Phase	Peak-insp (0%)	10%	20%	30%	40%	Peak-exp (50%)	60%	70%	80%	90%
VPE/%	Prior	357.7	220.8	183.0	254.4	268.1	268.5	252.1	183.2	230.0	353.1
	MMFD-NCC	6.8	8.4	7.1	9.8	5.8	7.2	8.8	7.1	6.9	8.9
COME/mm	Prior	17.4	7.7	4.1	10.0	11.2	11.2	10.0	4.0	8.5	16.8
	MMFD-NCC	1.5	1.4	1.0	1.2	1.1	1.4	1.4	1.3	1.0	1.0

^*Abbreviations: VPE: volume percentage error. COME: center-of-mass error.

III.A.3. Effects of scan directions and sampling intervals

Table 3 shows the results of different projection scan directions and sampling intervals. For the scan direction test, the estimation using projections around anterior-posterior and left-lateral directions achieved similar accuracy as using projections around left-anterior-oblique and left-posterior-oblique directions. For the sampling interval test, the estimation accuracy was similar between acquisition sets 1–3, which corresponds to average sampling intervals ranging from 0.4°/prj to 1.4°/prj. The estimation accuracy was slightly degraded for acquisition set 4 (2.8°/prj), and more for acquisition set 5 (5.5°/prj). The above results suggest the MMFD-NCC is relatively robust except for very large average sampling intervals.

Table 3.

Evaluation of projections’ scan direction and sampling interval on the estimation accuracy. The VPE and COME values were calculated as the average (± standard deviation of all 10 phases.

	Acquisition Set	1	2	3	4	5
VPE/%	AP&LLAT	6.9 ± 1.2	7.7 ± 1.2	7.7 ± 2.1	9.7 ± 2.4	13.4 ± 2.5
	LAO&LPO	6.2 ± 2.5	6.6 ± 2.0	8.0 ± 3.7	9.8 ± 4.1	10.0 ± 4.8
COME/mm	AP&LLAT	1.1 ± 0.1	1.2 ± 0.2	1.0 ± 0.2	1.1 ± 0.3	0.9 ± 0.2
	LAO&LPO	1.2 ± 0.2	1.3 ± 0.2	1.2 ± 0.3	1.3 ± 0.3	1.1 ± 0.3

Abbreviations: VPE: volume percentage error. COME: center-of-mass error. AP&LLAT: anterior-posterior and left-lateral. LAO&LPO: left-anterior-oblique and left-posterior-oblique.

^†All estimations were based on orthogonal-view 30° projections from either AP&LLAT directions or LAO&LPO directions (listed in rows). AP&LLAT indicates the estimation was based on 30° (−15°~15°) projections around the anterior-posterior direction and 30° (75°~105°) projections around the left-lateral direction. LAO&LPO indicates the estimation was based on 30° (30°~60°) projections around the left-anterior-oblique direction and 30° (120°~150°) projections around the left-posterior-oblique direction.

^††The projection average sampling intervals were determined by the different gantry rotation speeds used for different acquisition sets (listed in columns) in Table 1. From acquisition set 1 to 5, the corresponding average projection sampling interval (± standard deviation was 0.4 ± 0.4°/prj, 0.7 ± 0.9°/prj, 1.4 ± 1.7°/prj, 2.8 ± 3.5°/prj and 5.5 ± 6.8°/prj, respectively.

III.B. Patient study

III.B.1. Image comparison between different techniques

Fig. 2 shows the axial slice cuts from the prior images, FDK images, MMFD-NCC estimated images and reference images of different patients. The FDK images of all three patients displayed excessive streak artifacts and distortions due to the lack of information, which prohibited tumor contouring. For patient 1, the vertical lines were placed at the same horizontal location in each subfigure. The tumor in the prior image was deviated from that in the reference on-board image in both shape and location. The MMFD-NCC estimated the new tumor shape and location accurately. For patient 2, there were two tumors, with one in each side of the lung. The tumor in the left lung existed in the axial slice of the prior image, but not in the on-board reference image (pointed to by arrows) in this slice due to shift of the tumor location. The MMFD-NCC successfully estimated the tumor location change. Similarly for patient 3, the MMFD-NCC estimated the tumor location and shape, which matched well with the reference image.

Figure 2.

Slice cuts from the prior images, FDK images, MMFD-NCC estimated images and reference images of different patients (P1-Patient 1; P2-Patient 2; P3-Patient 3) at the end-expiration (50%) phase. Both FDK reconstructions and MMFD-NCC estimations used orthogonal-view 30° projections around posterior-anterior and right-lateral directions. The onboard reference images were reconstructed using fully-sampled 200° projections.

III.B.2. Geometric accuracy of the estimated tumor (VPE and COME)

Fig. 3 shows the plots of VPE and COME values for prior and MMFD-NCC estimated tumors of different patients. Considering all three patients, the average (±standard deviation) VPE for tumors in the prior images and tumors estimated by MMFD-NCC was 55.6% (± 45.9%) and 9.6% (±6.1%), respectively. The corresponding COME was 3.8 mm (±1.9 mm) and 1.1 mm (±0.5 mm), respectively. MMFD-NCC method greatly reduced the VPE and COME errors when comparing to the ‘ground-truth’ on-board reference tumors.

Figure 3.

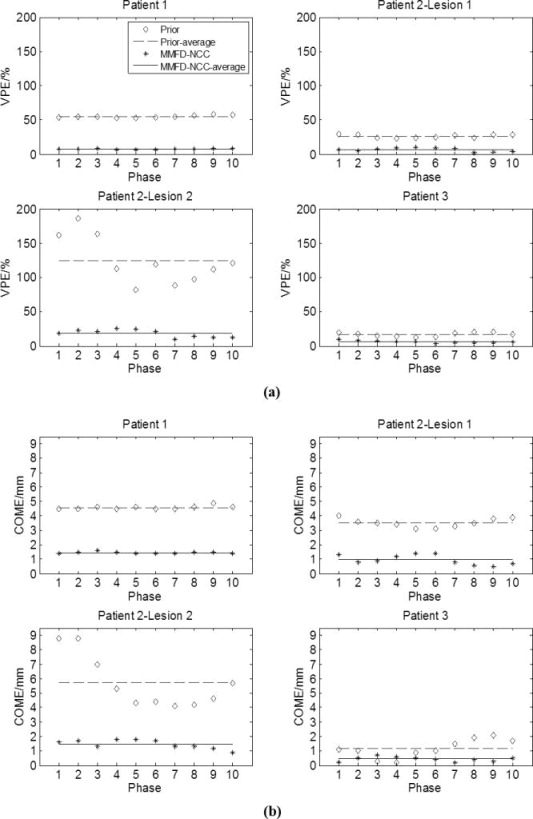
Plots of (a) VPE and (b) COME values for prior and MMFD-NCC estimated tumors using the patients’ data. The x-axis indicates different phase bins of the 4D-CBCT. All estimations used orthogonal-view 30° projections around posterior-anterior and right-lateral directions.

Besides the results for each individual phase, the VPE of the ITVs estimated by MMFD-NCC for patient 1, patient 2-tumor 1, patient 2-tumor 2 and patient 3 was 7.5%, 5.3%, 18.3% and 4.3%, respectively. The corresponding COME was 1.3 mm, 0.6 mm, 1.7 mm and 0.4 mm. The MMFD-NCC correctly estimated the ITV shapes and positions.

IV. DISCUSSIONS

IV.1. Clinical Implementation of MMFD-NCC

In this study, limited-angle projections were used for MMFD-NCC estimation, instead of full-angle projections. This scan angle arrangement allows substantial scan time/dose reduction and better mechanical clearance [34] than full-angle scan. Results in Table 3 showed that the MMFD-NCC could provide accurate imaging estimation results with only ~1/5 of the scan time/dose (40 s/67 mAs, acquisition set 4) of a commercial 4D-CBCT system (180 s/320 mAs).

In this study, orthogonal-view projections were acquired for image estimation, which provides more effective angular sampling than single-view projections [19]. In clinical practice, the orthogonal-view projections can be acquired consecutively using the kV on-board imager, which was done in this work. A potentially more interesting acquisition protocol may be to acquire images from orthogonal directions concurrently, either using a dual-source kV system [35] or the combined kV/MV acquisition [36]. Using the concurrent imaging approach, the imaging time can be further reduced by half to allow even faster imaging. The combined kV/MV acquisition also enables intra-treatment verification. However, the cross-scatter from the orthogonal kV-kV or kV-MV sources can potentially affect the image quality and needs to be addressed [37].

In this study, slow-gantry rotation technique is used to acquire 4D-CBCT projections. The resulting ‘clustering’ and ‘gap’ in phase-binned projections may degrade the image quality. In the future, other acquisition techniques like the step-and-shoot technique and the actively triggered acquisition technique will be evaluated for potential improvements in image quality and resulting further scan time and dose reduction.

In the patient study, we used a Fourier-transform based automatic sorting method [32] to sort the projections. The sorting method is more robust when the intensity of a large portion of the projection changes with respiratory motion, which is true for lung cancer patient data. Alternatively, the projections can also be sorted using external respiration surrogates used in the clinics, such as the Varian RPM system [38], the Anzai Belt [39] etc. For the phantom study, only the inserted tumor area was moving, which would have made the Fourier-transform based sorting method less robust. Instead of using the Fourier-transform method for the phantom study, we manually sorted the projections using the motion peaks of the tumor observed in projections.

IV.2. MMFD-NCC vs. other reconstruction methods

Many other methods have been developed in recent years to reconstruct 4D-CBCT images with fewer projections, e.g. the ‘volume-of-interest’ method [40] based on FDK algorithm, or the iterative methods based on total variation [41] or temporal nonlocal means regularizations [42]. Although these methods can reduce the image noise or streak artifacts in 4D-CBCT, they cannot remove the structure distortion or reconstruct full volumetric images when only limited-angle projections are used for reconstruction due to the missing of information. Compared with these methods, MMFD-NCC utilizes prior volumetric/motion information from 4D-CT images to estimate high quality volumetric images using limited-angle projections. Compared with other prior knowledge based methods [23–25, 43], MMFD-NCC provides better image estimation accuracy as it combines the advantages of motion modeling and free-form deformation. Compared to our previous MMFD-SSD method, the MMFD-NCC uses the NCC as the similarity metric in the data fidelity constraint, which is more robust against the intensity mismatches between CT and CBCT (Fig. 1). To our knowledge, MMFD-NCC is the first reported method that can use clinically acquired limited-angle projections to generate high-quality 4D-CBCT images (Figs. 1–3, Tables 2–3).

IV.3. Limitations of this study

In this study, the end-expiration phase of 4D-CT is chosen as the prior CT volume due to its relative stability. Though not seen in the cases of this study, tumor hysteresis, other large motion irregularities and large intra-phase motion can all potentially contribute to the artifacts in the 4D-CT images, even in the most stable end-expiration phase, and can potentially affect the accuracy of MMFD-NCC estimation. Future studies are warranted to further evaluate these effects.

4D-CBCT images reconstructed from fully-sampled on-board projections were used as reference images in our study, which generate high imaging dose to the patient. As a result, only very limited number of patients were enrolled in the study. Future investigation is warranted when a larger patient cohort is available.

The reference 4D-CBCT may have its own limitations, such as the phase binning and breathing irregularities issues and it may not serve as the perfect ‘ground-truth’, especially for the patient studies. However, the 4D-CBCT reconstructed from the fully sampled projections is the current standard image for localization, and is the only image available to be used as a reference to evaluate our method. By comparing to the ‘ground-truth’ 4D-CBCT, our study showed that our method achieved similar accuracy while using only limited-angle projections to reduce scan time, dose and improve mechanical clearance.

Ideally, we would like to evaluate patient projections with lower mAs values to study the potential of MMFD-NCC for further dose reduction. However, the limited patient data we have only contain projections acquired using 80 mA and 25 ms. Alternatively, we acquired the phantom scan with lower mAs (20 mA and 16 ms per projection) and validated the performance of MMFD-NCC for low mAs scans in this study.

Another limitation of this study is that the estimated 4D-CBCTs can only capture inter-treatment tumor variations as they were acquired prior to treatment. The intra-treatment tumor variations cannot be captured, which can also affect the treatment accuracy. In light of this issue, we are currently investigating a 4D-CBCT estimation method using aggregated intra-treatment 4D kV and MV projections [36] to capture the intra-treatment tumor variations for real-time tumor localization.

Currently, the image estimation time of MMFD-NCC method is approximately 3–4 hours for ~100 projections at each phase (the image estimations are independent among different phases, which can be executed in parallel). The acceleration of the optimization speed through software-based restructuring and hardware-based GPU [44, 45] computation is under progress. A preliminary version of the accelerated code has already achieved a computation speed of around 70 times faster [46].