Automated AFM force curve analysis for determining elastic modulus of biomaterials and biological samples

Abstract

The analysis of atomic force microscopy (AFM) force data requires the selection of a contact point (CP) and is often time consuming and subjective due to influence from intermolecular forces and low signal-to-noise ratios (SNR). In this report, we present an automated algorithm for the selection of CPs in AFM force data and the evaluation of elastic moduli. We propose that the CP may be algorithmically easier to detect by identifying a linear elastic indentation region of data (high SNR) rather than the contact point itself (low SNR). Utilizing Hertzian mechanics, the data are fitted for the CP. We first detail the algorithm and then evaluate it on sample polymeric and biological materials. As a demonstration of automation, 64 x 64 force maps were analyzed to yield spatially varying topographical and mechanical information of cells. Finally, we compared manually selected CPs to automatically identified CPs and demonstrated that our automated approach is both accurate (< 10 nm difference between manual and automatic) and precise for non-interacting polymeric materials. Our data show the algorithm is useful for analysis of both biomaterials and biological samples.

Graphical Abstract

1. Introduction

The influence of mechanical properties of the extracellular matrix or underlying substrate on cellular stiffness (Tee et al., 2011), cytoskeletal dynamics (Smith et al., 2003), cell migration (Lo et al., 2000; Pelham and Wang, 1997; Wong et al., 2003), differentiation (Discher et al., 2005; Engler et al., 2006) and drug response (McKee et al., 2011b) has been widely reported. Consequently, the characterization of mechanical properties of biomaterials and biological samples and the analysis of large data-sets has become increasingly important. The atomic force microscope (AFM) (Binnig et al., 1986) is a powerful tool that can characterize the localized mechanical properties of both cell culture substrates (Markert et al., 2013; Vinckier and Semenza, 1998) and biological samples (Radmacher, 1997) (see Supplementary Fig. 1). Models for contact mechanics such as Hertz (Hertz, 1882), JRK (Johnson et al., 1971) and DMT (Derjaguin et al., 1975) are used to determine the elastic modulus (E) of a sample and rely on force versus indentation relationships obtained from the AFM. However, the AFM does not directly measure force or indentation. Instead, force and indentation (a force curve) are calculated from the deflection and vertical position of the AFM cantilever, respectively. The former is easily and commonly calculated by application of Hooke’s law, while the latter requires the selection of a “contact point” (CP), the vertical position of the cantilever where the AFM tip first makes contact with the sample. Establishing the CP is critical for correct assessment of mechanical properties. However, the CP is not known a priori and must be inferred from the deflection and vertical position of the cantilever. Intermolecular forces (hydrostatic, van der Waals, electrostatic attraction and repulsion, etc.) and low signal-to-noise ratios (SNR) in the contact region of AFM data make identification of the CP extremely difficult, time consuming and subjective. Therefore, there is a need for analytical techniques that accurately and precisely identify the CP, reduce iterative data processing and remove user bias. Such methods have important consequences for the design and characterization of biomaterials.

The simplest method of identifying the CP is by visual inspection of the data and determining the point where the deflection begins to increase (Supplementary Fig. 1B). Several researchers (Benitez et al., 2013; Crick and Yin, 2007; Dimitriadis et al., 2002; Gergely et al., 2000; Jaasma et al., 2006; Lin et al., 2007a, b; Melzak et al., 2010; Monclus et al., 2010; Nyland and Maughan, 2000; Polyakov et al., 2011; Radmacher, 2002; Roduit et al., 2012) have utilized analytical techniques aimed to automate CP selection and AFM force curve analysis for a variety of types of samples. While each method has its own strengths and weaknesses, AFM data is still plagued by low SNR at the contact point, making analysis difficult. To circumvent this problem, we propose that the contact point can be obtained by fitting a linear elastic indentation region of data to a Hertz-like equation. An indentation region of data has a higher SNR than data near the CP and will therefore be algorithmically easier to identify.

In this work, we present a new automated analytical technique for AFM force curve CP determination (CPD) that provides consistent and accurate CP selection and we directly compare it to manually selected CPs. In the described algorithm, a force curve is searched for a linear-elastic region of data and fitted to a Hertz-like model to determine the CP. We first show how the CPD algorithm is applied to determine E of a sample. The CPD algorithm was evaluated and verified by implementing the algorithm on experimental force curves on soft materials commonly used for cell culture substrates (polyacrylamide (PA) hydrogels and poly(ethylene glycol) (PEG) films). As a demonstration of the high-throughput of the CPD algorithm, it was applied to 64 x 64 two-dimensional arrays of force curves (force map or force volume (Dufrene et al., 2013; Gaboriaud et al., 2008; Heinz and Hoh, 1999; Radmacher et al., 1994)) of cells and was used to construct resolved topographical and mechanical properties of the biological sample. Finally, inter- vs intra- user variability in manual CP detection was established in order to directly compare the CPD to manually selected CP and verify the CPD technique.

2. Materials and methods

2.1. Materials fabrication

Sample materials used in this study included PA hydrogels of approximately 1 mm in thickness and swellable PEG films with molded nano-topographical ridges and grooves. Briefly, PA hydrogels fabrication methods are the following. A mixture of 1.7 mL of 40% w/v ready-made 29:1 mole ratio of Acrylamido to N,N′-Methylenebisacryalmide (Fisher Scientific), 400 μL of (3-Acrylamidopropyl)trimethylammonium chloride 75% wt solution (Sigma Aldrich) and 7.9 mL of ultrapure deionized water (Millipore, Milli-Q) was combined in a 50 mL conical tube. This mixture was gently swirled to mix and allowed to equilibrate for 30 min. A freshly prepared 10% w/v solution of ammonium persulfate (APS, Fisher Scientific) in ultrapure deionized water was added (200 μL) to the acrylamide mixture and gently swirled. Tetramethylethylenediamine (Sigma Aldrich) was immediately added (12 μL) and the solution gently swirled (approx. 20–30 sec) before casting in a 10 mL Criterion cassette (Bio-Rad). The gel was removed after 1 hour, cut into 2 cm dia. circles and rinsed thrice with phosphate buffered saline (PBS, HyClone). Hydrogels were sterilized by 30 min of UV irradiation and a final rinse with sterile PBS. Hydrogels were first incubated at 37°C for 24 hours in PBS, then placed on a glass bottom petri dish (World Precision Instruments, Inc) and incubated for an additional 24 hours in DMEM low glucose media (HyClone). Prior to AFM force measurements, media was aspirated and replaced with Dulbecco’s PBS (DPBS, HyClone).

Swellable PEG films were fabricated as follows. A 3 μL volume of prepolymer solution made up of 20% w/v poly(ethylene glycol) diacrylate (PEG, 6,000 g/mol MW, Sigma Aldrich) and 0.15% w/v Irgacure 2959 (Ciba) was placed on a glass slide silanated with 3-acryloxypropyl trichlorosilane (Gelest) and sandwiched with a Sylgard 184 (PDMS, Dow Corning) mold (previously described in (Teixeira et al., 2003)) with nano-topographical features. Samples were enclosed in a container with pure nitrogen gas and equilibrated for 2 hours. Samples were then crosslinked in the nitrogen container by UV (365 nm, approx. 35 mW/cm²) irradiation for 20 min and PDMS stamps were removed. The resulting thin PEG films were swelled by immersion in ultrapure ethanol overnight. Swelling resulted in a cell culture substrate that has both topographical features and biologically relevant stiffness.

2.2. Cell culture methods

Canine iridocorneal angle cells (CICACs) were isolated from canine eyes. Briefly, the corneoscleral rim was dissected from the eye and washed in sterile PBS. Using a scalpel, the iris and ciliary body were detached from the corneoscleral rim, revealing the angle. The trabecular meshwork and attached tissue was then dissected out of the corneoscleral tissue in 1–2 mm segments and placed with 0.2% Cytodex beads (Sigma Aldrich) in Dulbecco’s Modified Eagle Medium/Nutrient Mixture F-12 (50:50; DMEM/F12) supplemented with 10% fetal bovine serum (FBS) and 1% penicillin/streptomycin/fungizone (Life Technologies). Cells which migrated out of the tissue were maintained in supplemented DMEM/F12 and passaged with 0.25% Trypsin-EDTA (Life Technologies). For AFM analysis, cells were plated at a concentration of 30,000 cells per AFM dish (Fluorodish, World Precision Instruments) and allowed to attach overnight. Shortly before AFM measurements media was discarded, cells were washed in PBS and incubated in Hank’s Balanced Salt Solution (HBSS, Life Technologies). Immortalized human (hTERT) corneal fibroblasts (htHCF) were similarly cultured in DMEM/High Glucose media supplemented with 10% FBS and 1% Pen/Strep and plated at a concentration of 25,000 cells per AFM dish and allowed to attach overnight. htHCFs were also washed and equilibrated in HBSS prior to AFM measurements.

2.3. Hertzian mechanics

The Hertz model describes the deformation behavior of purely linear elastic materials (Johnson et al., 1971); therefore, a fit of any linear elastic region of data to the Hertz model for E, will yield the same E for any other linear elastic region. Hertzian mechanics for conical tip geometry (to approximate pyramidal AFM tip geometry) was considered in this study. The Hertz model in this case is

$$F=\frac{2}{\pi }tan(\alpha )\frac{E}{1-{\nu }^2}{\delta }^2$$ (1)

where F is force, α is the half-angle opening of the AFM tip, ν is Poisson’s ratio and δ is indentation (Love, 1939). We assumed a Poisson’s ratio of 0.5 (incompressible material) for all samples (Anseth et al., 1996; Dimitriadis et al., 2002; Vinckier and Semenza, 1998).

A fit of any linear elastic region to the modified Hertz-like model (equation (2)) for CP will yield the same “best fit” CP for any other linear elastic region.

$$F=\frac{2}{\pi }tan(\alpha )\frac{E^{\ast }}{1-{\nu }^2}{(S-CP)}^2$$ (2)

The definition of indentation in terms of separation (S) and CP is utilized in equation (2) (δ = S – CP). Identifying a linear elastic region may be easier than identifying the CP through search algorithms as the region that contains the CP has a high noise background. The approach of the CPD algorithm is to determine the CP by first identifying a linear elastic fit region where SNR is high and then fitting for CP rather than initially trying to identify the CP initially in a low SNR region.

The underlying assumption of the CPD method is that the region of selected data is still within the linearly elastic deformation range. To check the linearity of the indentation range, the Hertz model (equation (1)) can be re-arranged to yield E as a function of force and indentation (equation (3)).

$$E=\frac{\pi }{2}\frac{F\left(1-{\nu }^2\right)}{tan(\alpha ){\delta }^2}$$ (3)

A plot of E vs indentation would demonstrate that E oscillates at very short indentations (order of ~10 nm), stabilizes at a value (this is the apparent E of the sample) and finally deviates. This deviation of E from a stable value represents a deviation from linear elastic deformation and can be used to help verify linear elasticity of the algorithm fit region.

2.4. Algorithm description

Fig. 1 highlights major steps in the CPD algorithm. Raw deflection and Z sensor data are first converted into nanometers for convenience. The data is then separated into approach and retract curves. The retract curve is discarded by splitting the data at the point of maximum deflection. Noise and thermal drift may result in a non-zero deflection reading in the pre-contact region. Therefore, the deflection is zeroed by fitting a line to the initial 40% of the data and subtracting this line from the entire deflection curve. Deflection and Z sensor data are then transformed into force (Hooke’s Law) and separation data by the following formulas:

$$F=k+D$$ (4)

$$S=-(D+Z)$$ (5)

where k is the spring constant, D is deflection, S is separation and Z is the Z sensor position.

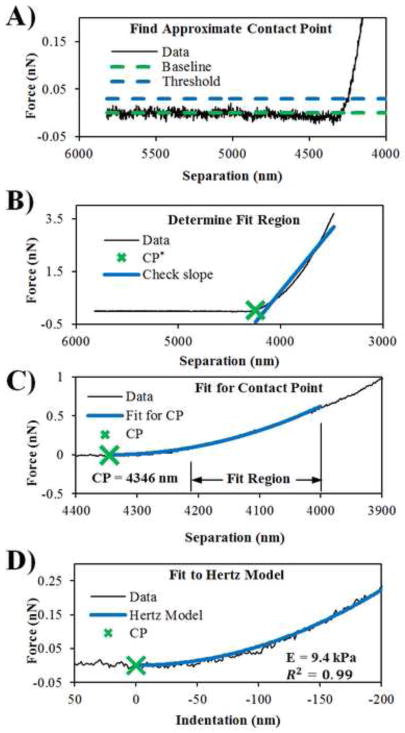
Fig. 1.

Highlighted steps in the CPD algorithm. (A) An approximate contact point is found by finding the point above the threshold level (dashed blue line); (B) The slope of the line fitted through the data from the approximate contact point is determined and heuristics are used to determine a fit region; (C) A non-linear regression is performed on the fit region where the contact point is a fit parameter; (D) The Hertz model is fitted to the data for the elastic modulus.

A fit region is determined by first finding an approximate CP (CP^*). A baseline force value in the pre-contact region (Fig. 1A, dashed green line) is established in the force versus separation data (Fig. 1A, solid line) by taking the average of the force values in the initial 40% of the data. A measure of the noise level in the pre-contact region is determined by taking the standard deviation of the force values in the initial 40% of the data. CP^* is found by following along the force curve until the force value exceeds a threshold level (Fig. 1A, dashed blue line) by five standard deviations above the baseline. Five standard deviations was empirically determined and consistently results in CP^* being in the indentation region. CP^* is the start of the fit region.

For an ideal linear elastic material, this fit region could practically be any region well into the contact region, any part of the force curve significantly above the baseline. Unfortunately, polymeric materials and biological samples of interest to biomedical scientists are never perfectly linear elastic materials, but instead are typically viscoelastic with a short range of linear elasticity (McKee et al., 2011a). Therefore, only a short indentation depth is taken and used for analysis to capture only the elastic region. Since this elastic region is inversely proportional to the apparent stiffness, the CPD algorithm selects an indentation depth (empirically ~ 50 – 200 nm, see Supplementary Material for more details) based on a measure of how stiff the force curve appears to be (Fig. 1B). This measure is made by approximating the force curve over the entire indentation range with a line (the greater the slope, the greater the apparent elastic modulus).

The data from the CP^* to the end of the fit region are then fit to a Hertz-like equation (equation (2), Fig. 1C) for CP while E^* remains as a free parameter. The resulting value of CP is then the best-fit CP for the selected region of data. Once the CP has been obtained, the data are easily transformed into force versus indentation data and fitted to the Hertz model (Fig. 1D) for the same indentation depth determined previously. The E from this second non-linear regression is then the reported elastic modulus. The CPD algorithm was implemented in custom MATLAB (MathWorks, Natick, MA) script and the code is detailed in Supplementary Material.

2.5. AFM force measurements

All force measurements were made using an Asylum Research MFP-3D-BIO (Santa Barbara, CA) atomic force microscope and PNP-TR-50 silicon nitride cantilevers (NanoWorld, Switzerland) with nominal spring constants of 0.32 N/m and 35° half-angle openings. All cantilevers were first calibrated for the deflection inverse optical lever sensitivity (Defl InvOLS) by indentation in DPBS on glass and then calibrated for the spring constant by the thermal method using the Asylum Research software. The authors would like to emphasize that proper calibration of the Defl InvOLS is critical for accurate force measurements. All force measurements were made at a scan velocity of 1.98 μm/s. Five force measurements were taken at five different locations for each sample. For PEG samples, the surface was briefly imaged in AFM contact mode to identify ridges and grooves in the surface topography. Force measurements were taken on top of the ridges.

Due to the ease of automation, the CPD algorithm can be used to analyze large force maps and extract topographical and mechanical information. A 64 x 64 force map was taken on live canine iridocorneal angle cells (CICACs) and human telomerase reverse transcriptase (hTERT) immortalized corneal fibroblasts (htHCF) in HBSS. A cell was first identified with phase microscopy on a 40x objective, the AFM cantilever was then positioned over the cell and a force map was taken. The CPD algorithm was used to calculate a height map and an E map from the data. The calculated height map was obtained by first generating a CP map with the Z sensor position at the CP. The CP map was then converted to a height map by subtracting the average Z value of the glass substrate areas from the entire map. The E map was generated directly from the CPD algorithm generated E values.

2.6. Algorithm evaluation

Automated CPs were verified by comparing to manually selected CPs. Ten force curves from three different tested materials (PA, PEG and CICA cells; 30 curves total) were triplicated, shuffled, masked and presented one at a time to three individuals with experience in AFM force curve analysis. The individual was asked to select, based solely on visual inspection of the data, the “best” CP. Results were recorded, unmasked and compared. The CP was averaged for each data set and for each user and subtracted from the CP determined by the CPD algorithm to find the average difference (AD). The standard deviation (SD) of the CP position for each force curve and for each user was also computed.

3. Results and Discussion

3.1. Algorithm validation and contact point selection analysis

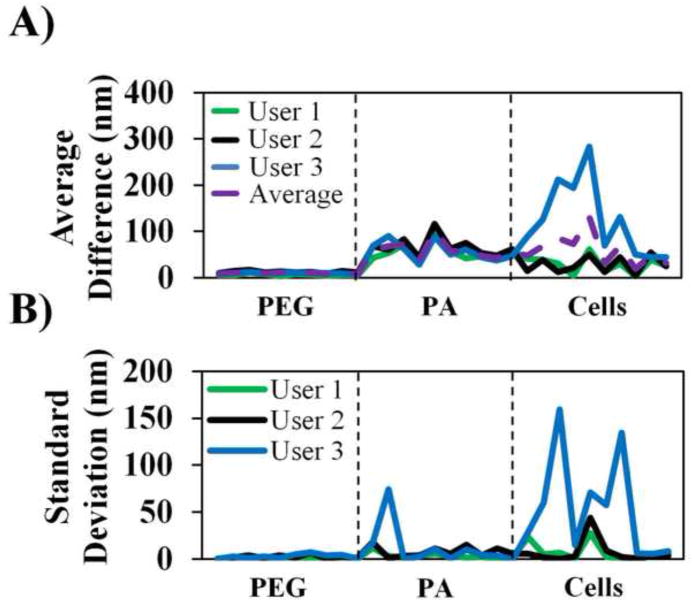
CPs were selected manually for randomly selected force curves and compared to automated CPs. Fig. 2A–B demonstrates that the CPD algorithm picked a CP very close to a manually selected CP (AD < 20 nm) for stiffer samples such as PEG. Automated CPs and manual CPs were reasonably similar for the softer PA samples, although the differences were consistently greater across all users (AD 50 – 100 nm). Force curves for PA and cells may be more difficult to analyze since they both are significantly softer than PEG. In addition, the heterogeneity and porosity of the PA surface may cause complex tip-surface interactions that make CP selection more difficult. This issue was likely exacerbated in the analysis of the force curves from the CICA cells, as significant differences were observed between manual and automated CP selection. Despite this, averaged across all users, AD between manually selected CPs and automatically selected CPs does not generally exceed 100 nm which still results in accurate material property assessment (Crick and Yin, 2007).

Figure 2. Validation of CPD algorithm contact point selection.

(A) Average difference (AD) of the manually selected contact point from the CPD contact point for three users. AD was calculated by first averaging the manually selected CP then subtracting it from the automatic CP value. The horizontal axis represents an index of the individual force curves analyzed; (B) Standard deviation of manually selected contact points for the same force curve of three users.

The CPD algorithm is more consistent in selecting the CP than human users. As a comparison, the SD of the CP position selected by each user was calculated (shown in Fig. 2B) and demonstrated the intra-user variability and subjectivity. Consistency was very good for stiffer PEG samples (average SD for PEG < 5 nm but still rarely zero). Consistency became increasingly worse for samples with complex surfaces (PA and cells). This highlights the need for automated CP selection as well-designed algorithms will more predictably select the same CP for a given force curve, eliminate significant inter-user variability and subjectivity, and provide more confidence in a value than manual selection.

3.2. Algorithm performance on polymeric materials

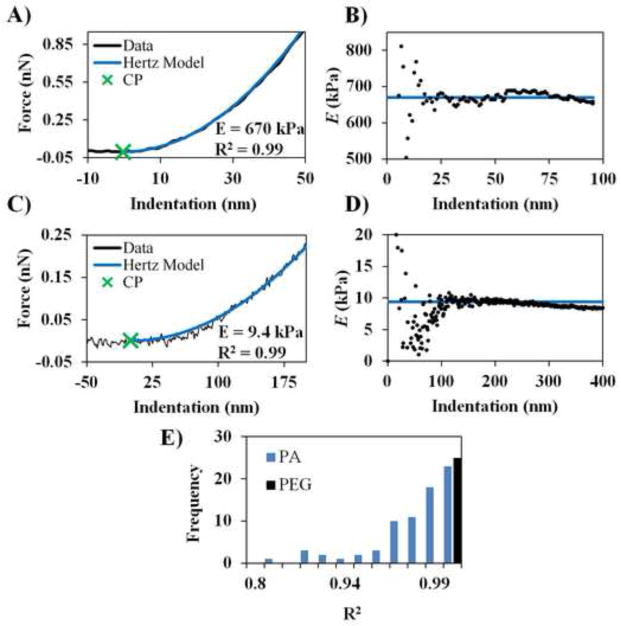
In analyzing the CP selection, we first evaluated qualitatively how well the CPD algorithm performed by visual inspection and goodness of fit (R²). A total of 100 force curves were obtained for stiff PEG films (E = 420 ± 70 kPa) and soft PA hydrogels (E = 10 ± 3 kPa). Representative fitting results for PEG and PA are shown in Fig. 3A and 3C, respectively and provide CPs that fit the selected data well. Fig. 3B and 3D are the corresponding E vs indentation plots for the representative PEG and PA data respectively. To re-iterate, E vs indentation plots typically show that E initially oscillates and tends towards a stable value in a linear elastic range. E is stable for up to ~50 nm of indentation for PEG and ~200 nm for PA. This demonstrates that the CPD algorithm does select fit regions that are still in the linear elastic indentation range.

Fig. 3.

Representative results from the CPD algorithm. (A) Representative force curve, CP and Hertz model fit for PEG. (B) Corresponding E vs indentation plot for data in (A). (C) Representative force, CP and Hertz model fit for PA. (D) Corresponding E vs indentation plot for data in (C). E vs indentation plots illustrates a region of linear elastic indentation. (E) Histogram of R² values for all sample curves. The vertical axis represents the number of occurances. One force curve exhibited random fluctuations in the baseline and was excluded as poor data and Hertz model fit. See Supplementary Material for the excluded force curve.

Of the analyzed force curves, only one data set yielded a poor CP selection and poor fit (see Supplementary Fig. 3). This force curve exhibits abnormal fluctuations in the baseline that cause a premature CP identification. After these data were discarded a robust data set still remained for evaluating algorithm performance. A histogram of the R² values is shown in Fig. 3E and demonstrates good Hertz model fits for the data. These data establish that the algorithm behaves predictably and yields consistent and reasonable results.

3.3. Cell force mapping application

The algorithm was then tested on CICACs and htHCFs to evaluate the CPD’s performance on complex biological materials. Fig. 4 demonstrates the application of the CPD algorithm to a 64 x 64 resolution force map of a live CICA cell (htHCF data in Supplementary Fig. 2). Fig. 4A and 4B are phase and AFM deflection images of a selected cell, respectively; both images are commonly obtained from integrated optical AFMs. Fig. 4C is a height map based on CP selections. Comparison of the AFM image and the height map from CP selection yields complimentary results which support the veracity of the CP selection by the automated CPD algorithm. The CP-derived height map shows cell morphological and topographical information that are consistent with the phase and AFM deflection images. The cell outline is consistent among phase, AFM deflection and force map images. This indicates that the CPD algorithm differentiates between CPs for soft force curves (cell body) and stiff force curves (glass substrate) accurately. Spatial distribution of stress fibers in the CP height map are also consistent with prominent stress fibers found in the AFM deflection image and the nuclear position between height and phase images is consistent.

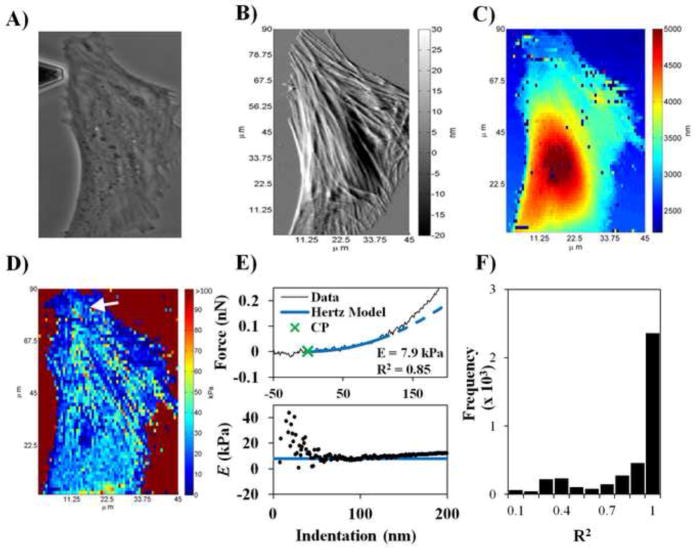
Fig. 4.

Demonstration of force mapping with CPD algorithm. (A) A 40x phase image of selected CICAC cell. (B) AFM deflection image of cell. (C) 64 x 64 calculated height map of the cell from the CPD algorithm. Force curves with significant baseline fluctuations were not considered for analysis and identified by basic error handling in the code. For these curves, the height and E were set to zero and do not represent the actual cell height and stiffness, respectively. (D) 64 x 64 E map of the cell from the CPD algorithm. (E) Representative force curve (from arrow position in E map), Hertz model fit and corresponding E vs indentation plot. The dashed line is an extrapolation of the Hertz model beyond the indentation range selected by the CPD algorithm. The solid line in the E vs indentation plot is E value determined by the CPD algorithm. (F) Histogram of R² values for Hertz model fits of the entire force map. The vertical axis represents the number of occurances.

Fig. 4D shows that the elastic modulus of the cell ranges from 10 kPa to 40 kPa, which is within the range of previously reported stiffnesses of cells (Mathur et al., 2001; Radmacher et al., 1996; Weisenhorn et al., 1993). We hypothesize that the high density of stress fibers, as seen in the AFM deflection image, may have contributed to a higher apparent E. Prominent stress fibers can still be discerned as stiff (higher E) lines across the cell body compared to the softer (lower E) region over the cell nucleus and line up with stress fibers seen in the AFM deflection and recalculated height images. A histogram of the R² values of the Hertz model fits for the force map is shown in Fig. 4E. The range of R² values for the cell map is greater than the range of R² values for polymeric materials as cells are much more complex.

The threshold level of five standard deviations (step in Fig. 1A) and a dynamic fitting range (step in Fig. 1B) were necessary in order for the CPD algorithm to distinguish features in stiff force curves (e.g. indentation on glass) and soft force curves (e.g. indentation on cells). In the cell force map application, substratum effects and deviations from non-linearity may influence force curve analysis. As highlighted in Fig. 4E, it is evident that the Hertz model fit (dashed line is an extrapolation of the Hertz fit) for a sample force curve on the body of the cell deviates from the data at around 100 nm of indentation. This deviation may be due to the composite nature of cells (e.g. the nucleus, organelles, etc. directly under the cytoskeleton) or increased contributions of the viscous component of cellular deformation. The E vs indentation plot in Fig. 4E illustrates that E tends towards a stable value at ~100 nm of indentation. This supports the fit region determined by the CPD algorithm for the selected force curve. The CP^* detection step, threshold level and the dynamic indentation range features specified in the CPD algorithm assist the CPD algorithm in limiting the CP selection and Hertz model fit region to a linear elastic region.

The E map in Fig. 5A is the same data in Fig. 4D but analyzed at a set indentation range. The CP selection in this case was based on a fit to the entire indentation region of data. In the case of thin samples where the AFM indentation measurement distance is significant compared to the layer thickness, substratum effects may become more influential. Force curves such as the one presented in Fig. 5B have two (or more) clear stiffness regions. First, there is a soft force curve which may represent the cell surface and then there is a stiff force curve that may be due to the glass substrate. Fig. 5B and 5C show the same force curve located near the periphery of the cell for a set fit region and dynamic fit region, respectively. The set fit region yielded a high stiffness (E = 113.7 kPa) and an E vs indentation plot that does not demonstrate linear elasticity for the fit region. The threshold level and dynamic indentation range work in tandem to limit analysis in the initial, softer region and avoid significant contributions of the substrate. This is most prominently demonstrated in Fig. 5A where the fit range is set as the entire indentation range of the data. In this case, the thin, soft cell membrane near the cell periphery is lost and considered as glass.

Fig. 5.

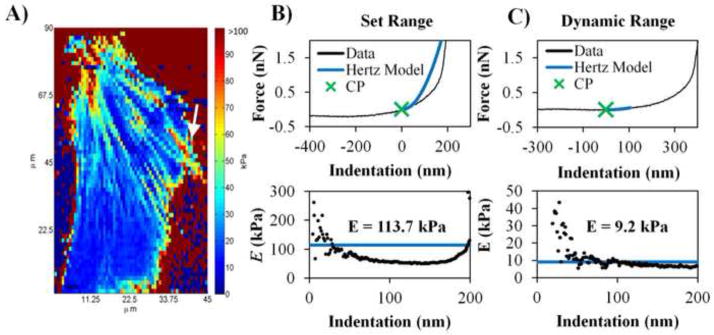
Comparison of indentation ranges used in CPD algorithm. (A) Same force map data from Figure 3D but analyzed with the CPD algorithm using the entire indentation length of collected data (set indentation range). Regions of E = 0 kPa on glass substrate regions are a result of error handling processes in the code (i.e. E is set to 0 kPa when there is an abnormal force curve). (B) A sample force curve from force map in (A; indicated by white arrow) and CP selection based on a set indentation range along with the corresponding E vs indentation plot. (C) Same location of selected force as (B) but CP selection was based on the dynamic indentation range specified in the CPD algorithm and the corresponding E vs indentation plot.

3.4. Comparison of automated AFM analysis algorithms

Several automated AFM force curve analysis algorithms are available commercially and in the literature. In Table 1, we briefly describe selected methods for automated force curve analysis for comparison. Monclus et al. describe the simplest method of automatically selecting CPs and analyzing AFM force data for the elastic modulus (Monclus et al., 2010). CP selection is based on a single threshold level above the pre-contact deflection signal. While this method is effective for stiff materials (E ~ MPa to GPa), it becomes less so for soft polymeric materials and biological samples (E ~ kPa) due to low SNR. This drawback is mitigated in the method developed by Benitez et al. Benitez and coworkers implemented a “double alarm” system to detect the CP and demonstrated that the algorithm may be accurately applied to biological samples (Benitez et al., 2013). Alternative, Lin et al. presented a comprehensive approach for determining the CP and analyzing the elastic modulus for either non-adhesive or adhesive cases ((Lin et al., 2007a), (Lin et al., 2007b)). Also, Roduit et al. introduced open source software for the semi-automated analysis of AFM force mapping (Roduit et al., 2012). The CP detection is based on linear fits to the pre-contact region of data. Open source software may provide ease and standardization of analysis for groups of researchers in the future as the software is further developed.

Table 1.

Comparison of select previously published and commercially available methods of determining contact point and elastic modulus from AFM force curves.

Source	Brief description
Asylum Research	Commercially available software (Igor Pro, WaveMetrics Inc., with Asylum Research add-on).
Benitez et al. 2013	Contact point detection system based on “double alarm” system. Requires selection of parameters. Does not analyze for elastic modulus.
Monclus et al. 2010	Simple procedure selecting the CP based on a single threshold level above pre-contact region.
Lin et al. 2007	Comprehensive approach for analyzing AFM force curves using a Golden Section search.
Roduit et al. 2012	Open source software for analysis of AFM force curves. CP is determined by linear fits to portions of the pre-contact region of data.
Present Work	Fits for contact point by searching for a linear elastic region rather than CP. Assumes linearity of selected data. Features dynamic indentation range selection to distinguish between stiff and soft force curves.

It is instructive to compare the presented CPD algorithm to two selected methods in Table 1. Of particular interest is (1) the Asylum Research software, which is commercially available and distributed with Asylum Research AFMs and (2) the Benitez algorithm, which was robustly verified by multiple comparisons to previously published methods (Benitez et al., 2013). In Supplementary Fig. 4, we show a force map analyzed with Asylum Research software for a Hertz model fit for a set indentation length of 100 nm (Supplementary Fig. 4A) and for a fit for the entire indentation length (Supplementary Fig. 4B). In both cases, the software produces artifacts in areas of the force map due to inclusion of data that violates the linear elastic assumption in Hertzian analysis. This again highlights the function of the dynamic indentation fit length in the CPD algorithm. In Supplementary Fig. 5, we examine a CP height map determined by the method presented by Benitez and coworkers with the CP height map from the present algorithm. Comparison of the CP based height maps reveals qualitatively similar CP maps. Quantitatively, we found that the CP based height maps differed by a relative % difference of approximately 5%. These comparisons further support the validity of the presented CPD algorithm.

The common thread that runs through these methods is that the algorithms directly search for the CP, a singular point in the dataset. Detection of the CP for soft polymeric materials and biological samples becomes difficult due to low SNR in the contact region of AFM force data. In such cases, methods based on threshold detection may fail due to the low SNR. Comprehensive strategies may be employed to overcome this problem but these methods may be algorithmically more complex. The CPD algorithm presented here is unique in that it identifies a linear elastic region of data which inherently has higher SNRs rather than distinctly locating the CP in the contact region.

Given the diversity of biomaterials utilized in research, it is unrealistic for any single algorithm to thoroughly handle all AFM force spectroscopy data sets. We speculate that the CPD algorithm may therefore fail to select accurate CPs in the case of extremely soft materials (E ~ 1 kPa), materials with strong surface-tip interactions (i.e. van der Waals or electrostatic interactions), non-linear strain or viscoelastic (time-dependent) behavior. Several of these issues are addressed through application of more appropriate models such as the JRK model for adhesive samples and the Kelvin-Voigt model for viscoelastic materials. The extent to which the empirical parameters specified in the CPD algorithm may result in failure is not completely known. However, in this study, the robustness of the algorithm in determining the contact point accurately and subsequent elastic modulus has been tested for polyacrylamide hydrogels, PEG films and cells. Our results demonstrate that the empirical parameters allow the CPD algorithm to perform well for these data sets. Application of the CPD algorithm to a wide variety of biomaterials may require new sets of empirically determined parameters. Nevertheless, we foresee that the CPD algorithm can be a useful tool in the characterization of the mechanical properties of biologically inspired materials.

4. Conclusions

We have developed and tested a novel algorithm for automated contact point detection in AFM force curve analysis. We have demonstrated that the algorithm can reproducibly select CPs that agree well with manual CP selection (average difference < 10 nm) for PEG. For force curves exhibiting more complex surface-tip interactions, the automated method provided significantly more consistent CP values than manual methods. We have also demonstrated the utility of automated analysis and the CPD algorithm through a 64 x 64 pixel force mapping application where topographical and mechanical data may be obtained from a single AFM force scan. Automated AFM analysis methods can significantly decrease analysis time for large data-sets. These methods have consequences for the screening and design of biomaterials and the analysis of large cell populations for representative assessment. We would like to emphasize that the currently presented work was done using strictly Hertzian mechanics. As researchers begin looking at more complex biomaterials or biological samples that may exhibit extreme non-linear elastic behaviors and heterogeneity, more complex automated analytical techniques must be developed to more carefully handle such data where linear elastic assumptions no longer apply.

Highlights.

• We report an algorithm for contact point detection for atomic force microscopy data

• We demonstrate accuracy of the algorithm on commonly used biomaterials

• A force mapping application yielded spatially varying topographical and mechanical data

• Automated analysis was more consistent and accurate compared to manual analysis