Multimodal Registration via Mutual Information Incorporating Geometric and Spatial Context

Abstract

Multimodal image registration is a class of algorithms to find correspondence from different modalities. Since different modalities do not exhibit the same characteristics, finding accurate correspondence still remains a challenge. In order to deal with this, mutual information (MI) based registration has been a preferred choice as MI is based on the statistical relationship between both volumes to be registered. However, MI has some limitations. First, MI based registration often fails when there are local intensity variations in the volumes. Second, MI only considers the statistical intensity relationships between both volumes and ignores the spatial and geometric information about the voxel. In this work, we propose to address these limitations by incorporating spatial and geometric information via a 3D Harris operator. Specifically, we focus on the registration between a high-resolution image and a low-resolution image. The MI cost function is computed in the regions where there are large spatial variations such as corner or edge. In addition, the MI cost function is augmented with geometric information derived from the 3D Harris operator applied to the high-resolution image. The robustness and accuracy of the proposed method were demonstrated using experiments on synthetic and clinical data including the brain and the tongue. The proposed method provided accurate registration and yielded better performance over standard registration methods.

I. Introduction

Multimodal image registration is a basic yet important operation for many applications. Clinical research studies often involve large numbers of volumes taken from multiple modalities. Different modalities provide diverse features, which can be used in a variety of theoretical and practical applications, such as relating function to anatomy or image guided surgery [1], [2].

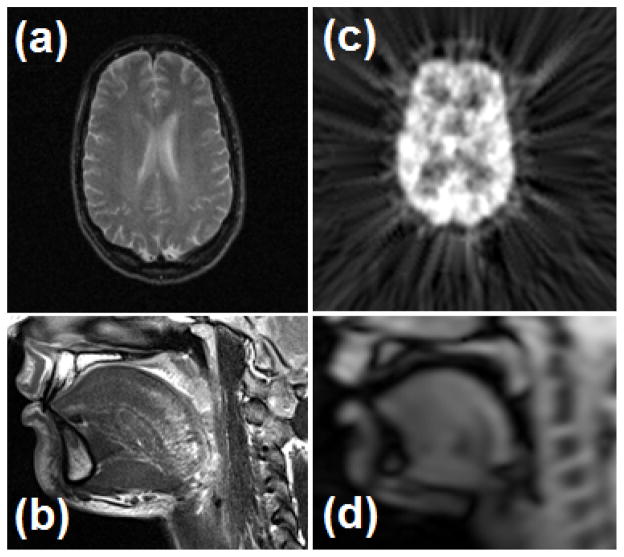
Multimodal image registration still remains a challenge partly because different modalities to be registered exhibit different characteristics. For instance, the widely used modalities, structural imaging, such as Computed Tomography (CT), and high-resolution magnetic resonance imaging (MRI) (see Fig. 1(a, b)) depict detailed anatomical information. Functional or dynamic imaging, such as Positron Emission Tomography (PET) (see Fig. 1(c)), Single Photon Emission Computed Tomography (SPECT), functional MRI (fMRI) contain information about changes in blood flow, metabolism, and regional chemical composition. Cine-MRI (see Fig. 1(d)) provides surface motion of anatomical structures. The benefits of using multimodal data have created a need for the development of highly accurate and robust multimodal image registration. In particular, multimodal image registration of high-resolution images (e.g., high-resolution MRI) with low-resolution images (e.g., PET) is often needed. Such registration is the main interest of this paper, as our method specifically exploits geometric information in the higher resolution image in the computation of the similarity measure.

Fig. 1.

Examples of multimodal images: (a) an MR-T2 image of the brain, (b) a high-resolution MRI (hMRI) of the tongue that was acquired at rest, (c) a PET image of the brain, and (d) the first time frame of cine-MRI of the tongue. These images differ considerably in spatial resolution.

Multimodal image registration is a class of algorithms to find correspondences between multiple datasets from the same subject, acquired using different imaging modalities [3]. The task of aligning two images is cast as an optimization problem: a common approach to registration is to deform one of the images so as to maximize its similarity to the other image while maintaining a “smoothness” in the estimated deformation field. Most of the similarity measures can be classified into two categories [4]: feature-based and intensity-based. The former usually requires four steps: (1) feature detection, (2) feature matching, (3) transform model estimation, and (4) resampling. In general, feature-based methods are computationally efficient compared to intensity-based methods; but manual intervention is often required to improve accuracy and efficiency.

Intensity-based methods have been shown to be more accurate than feature-based methods [5], but special assumptions on the intensities of the images are often required in order to achieve successful registration. For instance, while unimodal image registration is based on the assumption that corresponding pixels have similar intensity values, the same assumption does not hold in multimodal registration problems. This is because the two modalities may assign different intensities to the same structure. Mutual information (MI), therefore, has become the established intensity similarity measure in multimodal registration because it accommodates different intensities between the modalities provided that they are relatively consistent within each modality [6], [7]. MI has been extensively used for many applications including diagnosis [8], surgical planning [9], and radiation therapy [10].

Although MI is considered to be the gold standard similarity measure for multimodal image registration, there are two problems with the traditional method. First, the performance of MI degrades when there are local intensity variations; this happens because the joint histogram computation is adversely affected [11], [12]. Second, the conventional similarity measure only incorporates intensity information, which means that the spatial information that may provide additional cues about the optimal registration is entirely ignored [13]. Fig. 2 illustrates the problem with local intensity variations and demonstrates the improvement provided by our proposed approach.

Fig. 2.

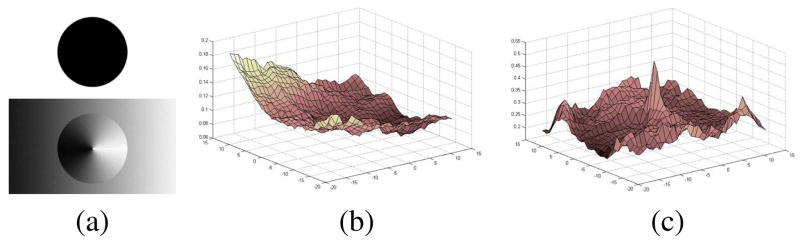
When the two circles in (a) are to be aligned, the conventional MI objective function in (b) fails to show a peak at the correct point of alignment, whereas the proposed method in (c) has the desired peak. Note that the values in (b) and (c) are plotted with respect to the x and y translation of the dark circle (top (a)) against the gray circle (bottom (a)).

Several previous methods incorporated spatial information in the computation of MI. Pluim et al. [13] combined spatial information by multiplying the MI with an external local gradient, and both gradient magnitude and orientation were incorporated into the calculation of MI. Rueckert et al. [14] proposed second-order MI to the problem of 2D registration by using a 4D joint histogram that considered the six nearest neighbors of each voxel to calculate MI. However, Rueckert et al. [14] required a large number of samples to compute the high-dimensional histogram, and therefore is not easily extended to 3D for computational reasons. As an extension of the second-order MI, Russakoff et al. [15] performed regional MI taking into account both corresponding pixels and their neighbors. This method also used a high-dimensional histogram, which may not be reliable when the number of samples is small. Yi et al. [16] proposed the inclusion of spatial variability via a weighted combination of normalized mutual information (NMI) and local matching statistics. Loeckx et al. [17] introduced conditional MI, which incorporates both intensity and spatial dimensions to express the location of the joint intensity pair. Zhuang et al. [18] proposed to unify spatial information into the computation of the joint histogram. This method used a hierarchical weighting scheme to differentiate the contribution of sample points to a set of entropy measures, which are associated to spatial variable values. In related developments, Myronenko et al. [19] presented a novel similarity measure, the residual complexity, that accounts for complex spatially-varying intensity distortions in mono-modal settings. However, this approach may not work well in multi-modal settings.

Our work shares the spirit of these past works in the sense that we include spatial information in the computation of MI, thereby incorporating both spatial and geometric information. However, one of the main contributions of this work is that our method involves a new approach that specifically exploits the higher resolution image. Specifically, we compute a structure matrix at each voxel and use the 3D Harris operator to decompose the image into three disjoint and geometrically distinct regions. These classes were then used to determine the relative contribution of each voxel’s intensity in the computation of the joint histogram. In this way, geometric structure from the high-resolution image influences the matching computation between the two images. A preliminary version [20] of this method was reported. Here we report the completed algorithm design and provide new validations on both synthetic and in vivo data including the tongue and the brain.

The remainder of this paper is organized as follows. Section II provides a background about maximization of MI and Harris corner detector. The proposed registration method with the 3D Harris operator is described in Sec. III, followed by experimental results presented in Sec. IV. Finally, a discussion and concluding remarks are given in Secs. V and VI, respectively.

II. Preliminaries

A. Maximization of Mutual Information

In this section, we describe the maximization of MI for multimodal image registration. We first define terms and notation used in this work. The images I₁: Ω₁ ⊂ ℝ³ → ℝ and I₂: Ω₂ ⊂ ℝ³ → ℝ, defined on the open and bounded domains Ω₁ and Ω₂, are the template and target images, respectively. Given two images, a deformation field is defined by the mapping u(x;μ): Ω₂ ↦ Ω₁. In our work, u is a B-spline transformation with associated parameters μ = (μ₁, μ₂, μ₃, ···), containing the B-spline coefficients. The goal of registration is to find a deformation field at each pixel location x such that the deformed template I₁(u(x)) aligns the underlying anatomy as closely as possible with I₂(x) satisfying the given criterion. Since I₁ and I₂ are considered to be different modalities, we focus on the MI criterion. The main idea is to find the deformation field û that maximizes the mutual information contained in the distribution of paired image intensities of the aligned images. Accordingly,

$$\widehat{u}=arg\underset{u}{max}(\mathcal{M}(I_1(u(\mathbf{x})),I_2(\mathbf{x}))),$$ (1)

where

$$\mathcal{M}(I_1(u(\mathbf{x})),I_2(\mathbf{x}))=\int \int p_u(i_1,i_2)log\frac{p_u(i_1,i_2)}{p_{I_1}(i_1)p_{I_2}(i_2)}d{i}_{1}d{i}_2.$$ (2)

Here, i₁ and i₂ are the image intensity values in I₁(u(x)) and I₂(x), respectively, and p_I1 (i₁) and p_I2 (i₂) are their marginal probability distributions while p_u(i₁, i₂) is their joint probability distribution. All densities are computed using a Parzen window approximation [21] and the joint density is computed only over the overlap region.

B. Harris corner detector

The Harris corner detector [22] was first introduced to detect corner features that contain high intensity changes in both the horizontal and vertical directions. The Harris corner detector is a well established technique using linear filtering of an image. Given an image I, the autocorrelation matrix of the point l = (x, y) in the neighborhood N of l is given by

$$\mathcal{N}(l)=\left(\begin{array}{cc}\sum _{m\in N}{I}_x^2(m)& \sum _{m\in N}{I}_x(m)I_y(m)\\ \sum _{m\in N}{I}_x(m)I_y(m)& \sum _{m\in N}{I}_y^2(m),\end{array}\right)$$ (3)

where I_x and I_y denote the partial derivatives of I in the x and y directions, respectively.

The Harris corner indicator H₂ is then given by

$$H_2=det(\mathcal{N})-r{(\text{trace}(\mathcal{N}))}^2,$$ (4)

where r is an arbitrary constant.

III. Proposed Approach

In this section, we describe our proposed method. Our method is based on an iterative framework of computing MI incorporating spatial information and geometric cues. The underlying idea is to split the image into a set of non-overlapping regions using the 3D Harris operator derived from the higher resolution image and to perform registration on spatially meaningful regions. Additionally, we exploit structural information describing the gradient of the local neighborhood of each voxel to define structural similarity for MI computation.

A. Volume Labeling Using 3D Harris Operator

In this work, we extend the 2D Harris detector to three dimensions so that it can be used to define regions over which MI is more heavily weighted. The Harris operator is derived from the local autocorrelation function of the intensity. The autocorrelation function at a point (x, y, z) is defined as

$$f(x,y,z)=\sum _p\sum _q\sum _{r}w(p,q,r){[I(p+x,q+y,r+z)-I(p,q,r)]}^2,$$ (5)

where I(·, ·, ·) is the 3D image, (p, q, r) denote a neighborhood of (x, y, z) in the Gaussian function w(·, ·, ·) centered on (x, y, z). Using a first-order Taylor expansion, I(p + x, q + y, r + z) is approximated by

$$I(p+x,q+y,r+z)\approx I(p,q,r)+x{I}_x(p,q,r)+y{I}_y(p,q,r)+z{I}_z(p,q,r).$$ (6)

f(x, y, z) can then be given by

$$f(x,y,z)=\sum _p\sum _q\sum _{r}w(p,q,r){[x{I}_x(p,q,r)+y{I}_y(p,q,r)+z{I}_z(p,q,r)]}^2$$ (7)

$$\begin{array}{l}f(x,y,z)\approx \sum _p\sum _q\sum _{r}w(p,q,r){\left\{\left[I_x(p,q,r)I_y(p,q,r)I_z(p,q,r)\left[\begin{array}{c}x\\ y\\ z\end{array}\right]\right]\right\}}^2\\ =[\begin{array}{ccc}x& y& z\end{array}]\mathcal{C}(x,y,z)\left[\begin{array}{c}x\\ y\\ z\end{array}\right].\end{array}$$ (8)

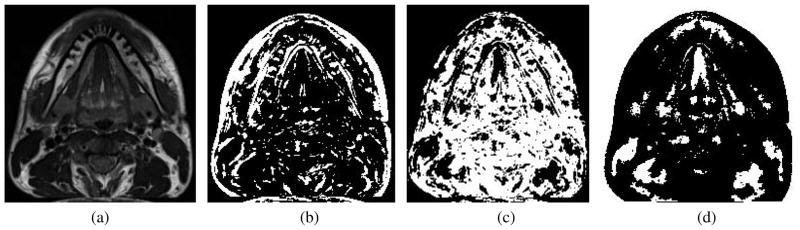
Here the local structure matrix 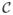(x, y, z), which captures the intensity structure of the local neighborhood, is defined as

$$\mathcal{C}(x,y,z)=\sum _p\sum _q\sum _{r}w(p,q,r)\left(\begin{array}{ccc}{I}_x^2& I_x{I}_y& I_x{I}_z\\ I_x{I}_y& I_y^2& I_y{I}_z\\ I_x{I}_z& I_y{I}_z& I_z^2\end{array}\right)$$ (9)

where I_x, I_y, and I_z denote the partial derivatives of I in the x, y, and z directions, respectively. In analogy to the 2D Harris operator [22], we define the 3D Harris operator as

$$H_3=det(\mathcal{C})-k{(\text{trace}(\mathcal{C}))}^3,$$ (10)

where k is an arbitrary constant. Each voxel can then be classified as one of three types using a threshold T and the following definitions

• Type 1: H₃ ≥ T, voxel has significant local variation

• Type 2: H₃ ≤ −T, voxel has moderate local variation

• Type 3: −T ≤ H₃ ≤ T, voxel has small local variation

We assume that Type 1 and Type 2 regions have more structural and characteristic information compared to Type 3 (homogeneous) region to calculate local statistics. Thus we use Type 1 and Type 2 regions to calculate MI. One example result of the voxel labeling is shown in Fig. 3. It is worth noting that we perform the 3D Harris operator on higher resolution volumes such as hMRI only because the higher resolution image has more detailed anatomical information.

Fig. 3.

Examples of voxel labeling using the 3D Harris operator. (a) An axial image of hMRI. In (b–d), white voxels represent (b) Type 1 - high variability, (c) Type 2 - moderate variability, and (d) Type 3 - small variability.

B. Mutual Information Using the Local Structure Matrix

As shown in Eq. (2), MI provides a measure of image similarity using only the marginal and joint probability densities of the image intensities. Here, we incorporate spatial and geometric information into the calculation of MI by computing a weighted joint distribution similar to the work by Luan et al. [23] as follows

$$p_u^{\mathcal{C}}(i_1,i_2)=\frac{1}{\mid V\mid }{\int }_V\gamma (\mathbf{x})\phi \left(\frac{i_1-I_1(u(\mathbf{x}))}{\rho }\right)\phi \left(\frac{i_2-I_2(\mathbf{x})}{\rho }\right)d\mathbf{x},$$ (11)

where φ is a Gaussian kernel, the overlap region V = Ω₂ ∩ u⁻¹(Ω₁), ρ controls the width of window, and γ(x) is a weighting function that is large when local structure matrices are similar and is small otherwise. Specifically, we define this weighting function as

$$\gamma (\mathbf{x})=exp(-\frac{\mathrm{\Delta }({\mathcal{C}}_{i_1}(\mathbf{x}),{\mathcal{C}}_{i_2}(\mathbf{x}))}{m}),$$ (12)

where Δ( 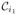(x), 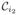(x)) is a distance between two matrices, m is a normalization constant, and 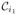(x) and 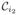(x) are the local structure matrices of the corresponding pixels in I₁(u(x)) and I₂(x), respectively.

Since local structure matrices do not live in a vector space, the distance function Δ cannot be defined by a conventional Euclidean metric. The matrices are symmetric and positive semidefinite (like covariance matrices), however, and therefore belong to a connected Riemannian manifold that is locally Euclidean [24]. Accordingly, we can define the distance between two structure matrices as

$$\mathrm{\Delta }({\mathcal{C}}_{i_1}(\mathbf{x}),{\mathcal{C}}_{i_2}(\mathbf{x}))=\sqrt{\sum _{n=1}^N{(ln{\lambda }_n({\mathcal{C}}_{i_1}(\mathbf{x}),{\mathcal{C}}_{i_2}(\mathbf{x})))}^2},$$ (13)

where N is the number of rows and columns in each matrix and λ_n are the generalized eigenvalues of 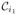(x) and 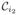(x) defined by

$${\lambda }_n{\mathcal{C}}_{i_1}{x}_n={\mathcal{C}}_{i_2}{x}_n,n=1,\dots ,N,$$ (14)

where x_n, n = 1, …, N, are the corresponding generalized eigenvectors. This definition of distance satisfies the metric properties including symmetry, positivity, and the triangle inequality. An example of this distance, computed between aligned 2D cine-MRI and hMRI images, is shown in Fig. 4(c). This shows that the distance metric is small when there are regions of high geometric similarity, such as edges.

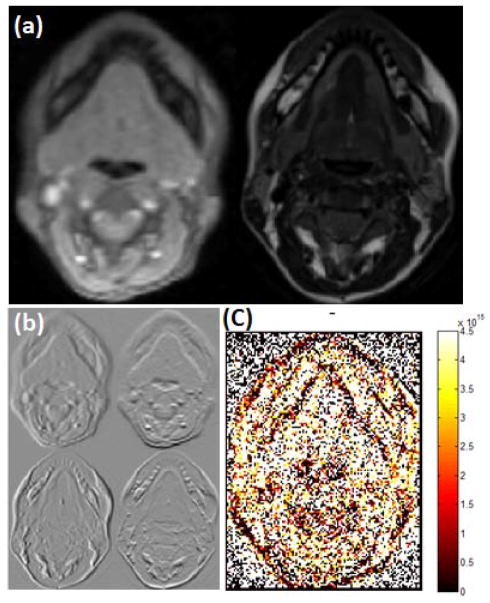
Fig. 4.

Distance calculated between structure matrices in hMRI and cine-MRI. (a) 2D slice of cine (left) and high-resolution (right) MR images. (b) First order derivatives with respect to x and y axes of 2D cine (top) and high-resolution (bottom) MR slices. (c) Distance between structure matrices defined in Eq. (13).

We write a modified MI criterion using the above weighting scheme as follows

$${\mathcal{M}}^{\mathcal{C}}(I_1(u(\mathbf{x})),I_2(\mathbf{x}))=\int \int p_u^{\mathcal{C}}(i_1,i_2)log\frac{p_u^{\mathcal{C}}(i_1,i_2)}{{\widehat{p}}_{I_1}(i_1){\widehat{p}}_{I_2}(i_2)}d{i}_{1}d{i}_2,$$ (15)

where p̂_I1 (i₁) and p̂_I2 (i₂) are recomputed based on $p_u^{\mathcal{C}}(i_1,i_2)$ as in [25]. Using this modified MI, the local structure matrices provide a geometric similarity measure while the image intensities continue to provide an appearance measure, thereby allowing us to find correspondence more reliably and address the limitation of the traditional MI-based registration. In summary, our registration approach seeks to maximize the image similarity given By

$$\mathcal{D}(I_1(u(\mathbf{x})),I_2(\mathbf{x}))={\mathcal{M}}^{\mathcal{C}}(I_1(u(\mathbf{x}))),I_2(\mathbf{x})),\mathbf{x}\in M(\mathbf{x}),$$ (16)

where M(x) is a mask comprising only the Type 1 and Type 2 voxels in the higher resolution image.

C. Transformation Model

Having defined an image similarity, we must now define a model for the spatial transformation that we will use. Here we follow a standard model [26],

$$h(\mathbf{x})=h_1(\mathbf{x})+h_2(\mathbf{x}),$$ (17)

where h₁(x) and h₂(x) are affine and deformable registrations, respectively. Affine registration accounts for large displacements including rotations, translations, and scalings. Deformable registration accounts for the finer details at a local level. We use free-form deformations (FFD) based on uniform cubic B-splines [26] to implement deformable registration. Therefore h₂(x) can be written as the 3D tensor product of 1D cubic B-splines,

$$h_2(\mathbf{x})=\sum _{l=0}^3\sum _{m=0}^3\sum _{n=0}^3{B}_l(u)B_m(v)B_n(w)c_{i+l,j+m,k+n},$$ (18)

where c denotes the control points and i, j, and k represent the index of the control point.

The B-spline transformation model has three desirable properties for the present application. First, estimated deformation field is easily regularized by controlling the control point separation [26]. We use this property to balance accuracy versus smoothness of the resulting deformation field. Second, B-splines are separable in multiple dimensions, providing computational efficiency. We refer the reader to [25], [27] for implementation details. Finally, optimization is inherently local, since changing the location of a single control point modifies only a local neighborhood of control point [28]. This permits additional computational efficiency since regions that have converged do not need further updating.

D. Optimization

The energy functional is minimized using a gradient descent method [29] defined by

$${\mathit{\mu }}_{k+1}={\mathit{\mu }}_k-a_{k}g({\mathit{\mu }}_k),$$ (19)

where g(μ_k) is the derivative of the cost function evaluated at the current position μ_k. From our weighted joint distribution, we first re-compute the marginal probability distribution, p̂_I1 (i₁). In calculating the gradient of the modified MI, we follow the work [25], [27]. We first derive a Taylor expansion of the modified MI as given by

$${\mathcal{M}}^{\mathcal{C}}(\mathit{\mu })={\mathcal{M}}^{\mathcal{C}}(\mathit{\nu })+\sum _i\frac{\partial {\mathcal{M}}^{\mathcal{C}}(\mathit{\nu })}{\partial {\mu }_i}({\mu }_i-{\nu }_i)+\frac{1}{2}\sum _{i,j}\frac{{\partial }^2{\mathcal{M}}^{\mathcal{C}}(\mathit{\nu })}{\partial {\mu }_i\partial {\mu }_j}\partial {\mu }_j({\mu }_i-{\nu }_i)({\mu }_j-{\nu }_j)+\cdots .$$ (20)

We simplify the above equation by ignoring all terms above second-order as in [25]. Here the quadratic model yields the optimal solution when the Parzen window is a B-spline of degree m ≥ 3 [25].

We then calculate the gradient of the cost function, which is necessary for its efficient minimization. The gradient of the modified MI with respect to the parameter μ is given by

$$\nabla {\mathcal{M}}^{\mathcal{C}}=\left[\frac{\partial {\mathcal{M}}^{\mathcal{C}}}{\partial {\mu }_1},\frac{\partial {\mathcal{M}}^{\mathcal{C}}}{\partial {\mu }_2},\cdots \right].$$ (21)

A single component of the gradient is found by

$$\frac{\partial {\mathcal{M}}^{\mathcal{C}}}{\partial \mu }=-\int \int \frac{\partial p_u^{\mathcal{C}}(i_1,i_2)}{\partial \mu }log\frac{p_u^{\mathcal{C}}(i_1,i_2)}{{\widehat{p}}_{I_1}(i_1)}d{i}_{1}d{i}_2.$$ (22)

Additionally, a multi-resolution scheme is used to represent coarse-to-fine details of both volumes for fast and robust registration [30].

IV. Experiments and Results

In this section, we present results of experiments on synthetic data, the brain data, and the tongue data, which together demonstrate the performance of the proposed method. Software was implemented using C++ with the Insight Segmentation and Registration Toolkit (ITK) [31], an open source library. For comparison, we used the MI registration algorithm described in Mattes et al. [25], which was also implemented in ITK. All experiments were performed on an Intel i7 CPU with a clock speed of 1.74 GHz and 8 GB memory.

A. Synthetic Data

In this experiment, we compared the performance of the proposed method to the conventional MI method on a pair of synthetic images at different noise levels, similar to the work by Fan et al. [32]. The synthetic images are shown in Figs. 5(a) and 5(b). The images in Figs. 5(c) and 5(d) are generated to test robustness of the methods against noise and spatial variation. In Fig. 5(c) the object is noisy and spatially variant; the background is spatially variant. The pattern is reversed in Fig. 5(d).

Fig. 5.

Synthetic images: (a) and (b) are original images and backgrounds. (c) and (d) show spatial gradient or gradient plus noise imposed on the figure or on the background (Image size is 210×300).

Fig. 6 shows the cost values of MI for the proposed method as a function of horizontal and vertical shifts ranging from −20 to 20 pixels. When Figs. 5(a) and 5(b) were used as template and target images, respectively, both methods found correct alignments as illustrated in Figs. 6(a) and 6(d). However, the MI failed to register as shown in Fig. 6(b) when Figs. 5(c) and 5(d) were used as template and target images, respectively. This is shown more clearly from Figs. 6(c) and 6(f) that the proposed method provided less dispersion of joint histogram compared to the MI after registration of Figs. 5(c) and 5(d) with initial misalignments of 5 and 5 pixels in x and y axes, respectively. The proposed method has good performance on both the noisy images as well as on the noiseless pair. It is observed from these examples that the proposed method provided robust and accurate results in the presence of noise and spatial variation. Although the intensity values inside the object are worsened due to the noise and spatial variance, the proposed method exploited the information from spatially salient regions, enabling the proposed method to find correct alignment and locating the peak value in the center as illustrated in Fig. 6(e). In these experiments, the number of histograms were set to 50 and 80% of the sample size in order to calculate MI. In this case, the 2D Harris operator was used to extract corner and edge information by setting k=0.05 and T=800.

Fig. 6.

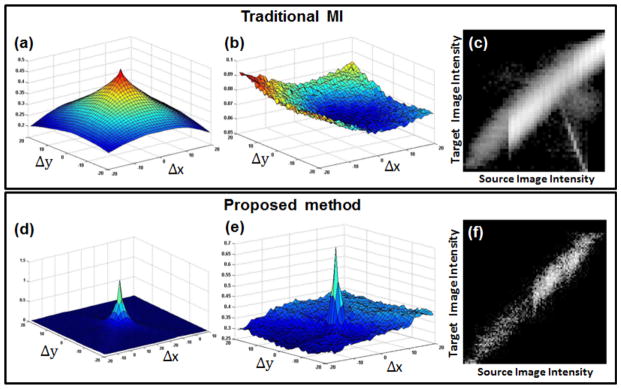
Comparison between MI (top row) and proposed method (bottom row) on synthetic datasets. (a) and (d) represent the cost value plots between Figs. 5(a) and 5(b) as a function of horizontal and vertical shifts. (b) and (e) show the cost value plots between Figs. 5(c) and 5(d). (e) and (f) show the joint histograms plotted after performing registration with initial misalignments of 5 and 5 pixels in x and y axes.

Additional experiments were carried out to test robustness against different noise levels (see Figs. 6(c) and 6(d)) and different spatial variations inside the object and background (see Fig 7), respectively. To generate the noise, we used Gaussian noise with standard deviation varied from 10% to 50% of the pixel value. Multiple registrations were performed with different initial positions ranging from −6 to 6 pixels in steps of 3 pixels in x and y directions (25 combinations in total per one noise level). A translation spatial transformation was used in these experiments and the root-mean-square (RMS) errors between corrected displacements and initial positions were used as a metric to measure the accuracy of the registration. Registration was considered to be a success if the RMS error was less than 3 pixels. Table I and Table II list the percentage of successful registrations for each method with different noise levels; Table III and Table IV show statistics of RMS error after registration for each method. The performance of the registration using the MI deteriorated as the noise or spatial variation were added whereas the proposed method demonstrated more robust and superior performance in these experiments.

Fig. 7.

Synthetic images with different spatial variations: (a) low spatial variation, (b) intermediate spatial variation, and (c) high spatial variation (Image size is 210×300).

TABLE I.

Success rate for both methods on synthetic data (noise)

Noise Level	MI	Proposed method
0%	90%	100%
10%	72%	100%
20%	40%	100%
30%	32%	100%
40%	28%	92%
50%	32%	92%

TABLE II.

Success rate for both methods on synthetic data (spatial variation)

Spatial Variation	MI	Proposed method
Low	90%	90%
Intermediate	24%	68%
High	16%	52%

TABLE III.

RMS error (pixel) after registration for both methods on synthetic data (noise)

Noise level	MI		Proposed method
	Mean±SD	Max	Mean±SD	Max
0%	2.28±1.23	6.45	0.06±0.01	0.06
10%	2.48±1.48	7.34	0.07±0.01	0.07
20%	3.42±1.79	6.64	0.20±0.01	0.21
30%	4.07±1.70	6.65	0.24±0.01	0.24
40%	3.87±1.45	6.61	0.69±1.32	5.54
50%	3.73±1.53	6.49	0.79±1.58	6.47

TABLE IV.

RMS error (pixel) after registration for both methods on synthetic data (spatial variation)

Spatial Variation	MI		Proposed method
	Mean±SD	Max	Mean±SD	Max
Low	2.16±0.46	3.25	1.40±1.52	5.90
Intermediate	3.42±0.63	4.82	1.98±1.95	8.10
High	3.69±1.42	9.88	3.31±2.94	11.45

B. In Vivo Brain Data

1) RIRE data

We used the publicly available brain data from the Retrospective Image Registration Evaluation (RIRE) project [34] to objectively evaluate the performance of the proposed method. The RIRE project provides ground truth transformation to evaluate rigid registration. In our experiments, we focus on the registration between (rectified) MR-T2 and PET datasets similar to [33]. The RIRE project provides one training data and seven testing data, five of which only have PET images. Thus we use five datasets for PET-MR registration (i.e., patient 001, patient 002, patient 005, patient 006, and patient 007). The voxel size is 1.25×1.25×4 mm³ for MR, and 2.59×2.59×8 mm³ for PET images.

2) Evaluation

In order to compare different statistical similarity measures, we used the results reported in [33] as they used the same data. Our method was compared with several entropy-based measures, including MI, normalized MI (NMI), entropy correlation coefficient (ECC), cumulative residual entropy correlation coefficient (CRECC), their modified overlap invariant measures (MMI, MECC, MCRECC) [35], and a learning based method [33]. Please note that we did not reimplement these algorithms but used the results in [33]. The accuracy of the registration was evaluated using target registration error (TRE) [36] provided by the RIRE project website. To obtain TRE, the physical coordinates of the transformed points were uploaded to the RIRE website, thus automatically computing and posting TRE on the website¹. In our experiments, we set the number of histograms to 50, and used the entire volume as the sample size in order to calculate the modified MI. In addition, the 3D Harris operator was used to label the voxels by setting k=0.01 and T=50,000,000. These parameters were set empirically, but the same parameters were used throughout experiments using the RIRE data. The TRE results are shown in Table V. Our proposed method outperformed the other methods in terms of mean TRE. However, the worst case TRE of the learning based method provided a better result compared to the proposed method.

TABLE V.

PET-MR registration errors using the RIRE data

TRE (mm)	MI	MMI	NMI	ECC	MECC	CRECC	MCRECC	Learning-based Method [33]	Proposed Method
Mean	8.19	3.00	3.20	3.10	2.96	3.34	3.29	2.60	2.44
Median	5.16	2.37	2.64	2.54	2.40	3.01	2.95	2.52	1.81
Max	37.18	7.71	7.57	7.65	7.50	7.53	7.47	4.81	5.81

C. In Vivo Tongue Data

By using hMRI when the tongue is at rest, one can visualize details of this muscle anatomy (see Fig. 1(c)). The motion of the tongue during speech can be fast and quite complex, however, and unlike the heart, it is not periodic by default. These facts make tongue motion imaging during speech quite challenging. As a consequence, cine magnetic resonance images (cine-MRIs), are captured at movie frame rates but with low spatial resolution (see Fig. 1(d)). Since hMRI captures the structure of the tongue and cine-MRI captures the motion of the tongue, these two MRI “modalities” offer complementary information about the tongue. Our approach allows to further enhance their utility by registering the hMRI data, captured in a resting position, to the cine-MRI data.

1) Subjects and Task

Nine normal native American English speakers were subjects in this experiment. The speech task was “a geese”. The word was chosen because the motion is complex. The tongue moves from a neutral tongue shape in “a” to a high back tongue position for “g” which is followed by forward motion into “ee” and tongue body lowering for “s”. In addition, this word does not involve jaw opening, which would assist tongue motion. Therefore the functional load, creation of different vocal tract configurations, is placed entirely on the tongue.

2) Recording and Procedure

Both types of MRI datasets—hMRI and cine-MRI—were recorded in the same session using a head and neck coil. Cine-MRI datasets were collected with a 6 mm slice thickness and had an in-plane resolution of 1.875 mm/pixel. 14 axial slices were acquired. hMRI datasets were 3 mm thick with an in-plane resolution of 0.94 mm/pixel. 24 axial slices were acquired. The subjects were required to remain still from 1.5 to 3 minutes for each plane. The datasets were aligned such that one cine slice contained two hMRI slices. University of Maryland MRI facilities have an MRI trigger system that uses acoustic cues to synchronize speech utterance repetitions with MRI acquisition. The protocol for synchronized auditory cueing is based on the method of Masaki and colleagues [37]. Cine-MRI datasets were collected in multiple planes, while the subject repeated speech tasks (“a geese”) to the beat of the auditory rhythm cue. To collect the datasets, the subject repeated the speech task 4 times per slice. A 15-minute training protocol, with feedback from the experimenter, was developed using the subjects. Due to the training, excellent cine images are obtained for naive subjects and patients even with long repetition sets. Recording time can take up to 1 hour and 15 minutes.

3) Evaluation on Simulated Tongue Data

We first validated the accuracy of the proposed method on simulated tongue MR images. Low-resolution MR images were generated by downsampling the hMRI by a factor of 2. Low-resolution MR images were then deformed artificially using randomly generated transformations by setting maximum displacements from 5 to 15 mm. In order to ensure regularity, the transformations were smoothed by a Gaussian kernel with standard deviation σ=2. Fig. 9 shows an example of the pair of hMRI and a deformed low-resolution MR image, and the ground truth deformation, respectively.

Fig. 9.

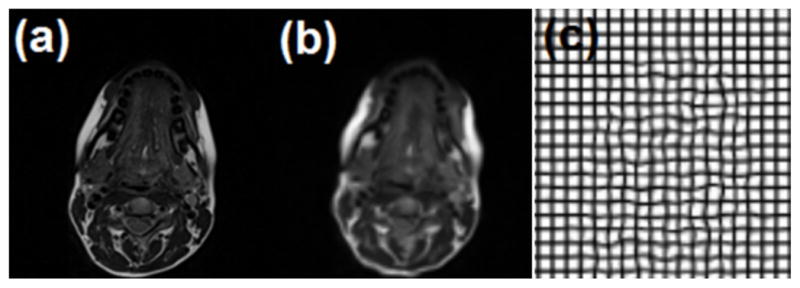
Synthetic simulation using tongue data. (a) high-resolution MRI, (b) artificially deformed downsampled hMRI, and (c) the ground truth deformation. The maximum displacement of the ground truth deformation is 15 mm in this case.

Registration of hMRI (template) with the low-resolution MR image (target) was then performed using MI-based registration and the proposed method. The obtained deformations were compared with the ground truth deformations using the RMS error. We tested the two methods on three subjects and the results are shown in Table VI. It is clearly observed from the results that the proposed approach offers more accurate registration than the MI-based method in all three cases.

TABLE VI.

RMS error (mm) between ground truth and recovered deformations using synthetic tongue simulation.

Max	Sub 1		Sub 2		Sub 3
	MI	Proposed	MI	Proposed	MI	Proposed
15	1.167	0.959	1.275	1.230	1.361	1.190
14	1.134	0.939	1.223	1.175	1.380	1.199
13	1.102	0.904	1.194	1.122	1.285	1.112
12	1.080	0.869	1.153	1.086	1.257	1.061
11	1.035	0.826	1.089	1.013	1.189	0.986
10	1.027	0.785	1.066	0.971	1.154	0.934
9	1.003	0.745	1.038	0.956	1.127	0.901
8	0.984	0.719	0.994	0.884	1.118	0.852
7	0.968	0.682	0.980	0.876	1.058	0.800
6	0.947	0.651	0.963	0.829	1.036	0.770
5	0.952	0.635	0.940	0.802	0.997	0.731

4) Evaluation on Real Data

Registration was performed on the two static volumes: (1) the first time frame of the axial cine-MRI that was acquired during speech task of “a geese” and (2) the axial hMRI volume that was acquired at rest. We used first time frame of cine-MRI and hMRI for our registration since first frame of cine-MRI is neutral (schwa position) and therefore the position is close to the resting tongue position found in the hMRI data. The registration methods used affine registration as an initialization, followed by the deformable registration using the proposed and MI-based method using FFD. In our experiments, we set the number of histograms to 30, and used 80% of the entire volume as the sample size. We used control point spacings of 16 mm in each axis. For the 3D Harris operator, we set k = 0.001 and T = 50, 000, 000. The parameters were chosen empirically to provide the best registration performance. The method stops when the movement is less than 0.001 mm or iteration reaches the predefined iteration number 200 in both methods.

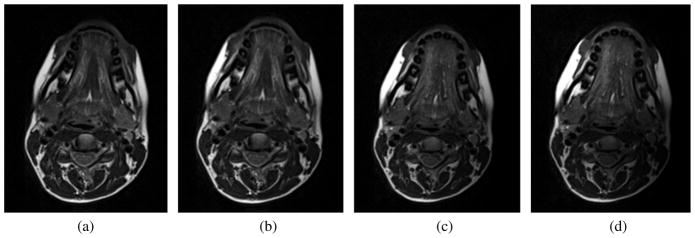
To evaluate the accuracy and robustness of the proposed method, we performed two experiments on the nine pairs of 3D axial MRI volumes described above. The first experiment assessed the accuracy of the registration method using TRE. Two expert observers independently selected three corresponding anatomical landmarks from each volume including tongue tip, lower lip, and posterior pharynx as illustrated in Fig. 8. Table VII lists the mean and standard deviation of TRE and inter-observer variability using both methods. In all cases, the original data misalignments were larger than 3.5 voxels. Affine registration and further deformable registration using MI and proposed method reduced the mean TRE to 2.7 and 2.1 voxels, respectively (p<0.05). The TRE results show that the proposed method provided accurate results compared to the traditional MI-based method. In addition, the TRE results obtained from the proposed method were not much different from the observer variability (p = NS). Fig. 10 shows one result of the first experiment. It is apparent in the figure that the proposed method has better alignment.

Fig. 8.

Anatomical landmarks used for validation shown in one example case with images from hMRI (top row) and images from a cine-MRI (bottom row). We have obtained independent sets of anatomical landmarks from two expert observers. Red crosses indicate the positions of landmarks, including tongue tip, lower lip, and posterior pharyns.

TABLE VII.

Registration errors and observer variability (voxel)

TRE (voxel)	Before Registration	Affine Registration	MI	Proposed method	Observer Variability
Tongue Tip	6.2±3.7	3.8±1.4	3.6±1.8	2.5±1.2	1.8±1.3
Lower Lip	3.9±1.8	2.8±1.1	2.6±1.4	1.8±1.2	2.7±1.7
Posterior pharynx	3.9±5.8	1.9±0.9	1.5±0.7	1.5±0.9	1.4±1.3
Average	4.7±4.0	3.1±2.8	2.7±2.6	2.1±1.2	2.0±1.4

Fig. 10.

One example of the results: (a) template image (hMRI) (b) volume labeling of the template image using the Harris operator, (c) a resulting image using MI-based registration, (d) a resulting image using the proposed method and (e) the target image (cine-MRI). The red arrows show that (d) and (e) are better aligned than (c) and (e) in terms of vocal tract edge.

The second experiment further demonstrated the performance of the registration method. Three different levels of intensity non-uniformity (bias) were generated including small (20%), medium (40%), and large (60%) bias fields (see Fig. 11). In these experiments, we also used TRE to measure the performance of the methods. As shown in Table VIII, the results of the proposed method were superior to the MI-based registration and were also robust against the bias fields.

Fig. 11.

Different non-uniformity fields: (a) original image (b) small bias field (20%), (c) medium bias field (40%), (d) large bias field (60%).

TABLE VIII.

Registration errors in different non-uniformity fields (voxel)

TRE (voxel)	Affine Registration	MI	Proposed method
Small bias field (20%)	3.8±1.6	3.5±2.6	2.3±1.2
Medium bias field (40%)	3.7±1.3	3.6±2.6	2.4±1.2
Large bias field (60%)	3.8±1.5	3.8±2.5	2.7±1.5

V. Discussion

We used a 3D Harris operator to characterize and label the tissue into three disjoint regions and the local structure matrix was used in the calculation of a modified MI image similarity criterion. It is possible to use other image descriptors to label the tissue. For example, scale invariant feature transform (SIFT) [38] or maximally stable extremal regions (MSER) [39] are likely to give similar pixel labeling results. However, the local structure matrix defined at each voxel offers information about the local geometry, which we were able to exploit in a new weighted MI image similarity computation. As demonstrated in the synthetic experiments, the capture range may not be wide, compared to the MI. However, in practice, we used affine registration as an initialization to further perform deformable registration and therefore the capture range did not affect the results greatly.

Multimodal image registration has been explored in great detail (see [3], [4], [11] and references therein); however, only a few methods have been proposed for tongue images. Yang and Stone [40] proposed to reconstruct 3D tongue motion by aligning temporal data from ultrasound images. Li et al. [41] performed tongue motion averaging to provide best representation of speech motion from several repetitions. Singh et al. [42] proposed to register multiple swallows for generating high temporal resolution in MRI videos. Aron et al. [43] investigated registration of multimodal data including ultrasound, and stereovision data within MRI.

The tongue has three orthogonal muscle fiber directions and extensive fiber inter-digitation and it has no bones or joints. Therefore MRI is an excellent tool because it images soft tissue very well; however, there are challenges. hMRI, collected when the tongue is at rest, can visualize the muscle anatomy in great detail, as shown in Fig. 1(b). Cine-MRI captures tongue motion at movie frame rates, providing good temporal resolution, but with low spatial resolution, as shown in Fig. 1(d). Moreover, these two modalities are different enough that their registration is more akin to multimodal registration than unimodal registration. Our three dimensional registration approach successfully registered the two datasets. A second challenge is that the motion of the tongue during speech can be fast and quite complex unlike the heart and it is not periodic by default. These facts make high quality tongue image analysis during speech quite challenging. Nonetheless, our method provided registered complementary information: temporal and spatial.

The current study registered cine-MRI to hMRI. This is useful for comparing multiple subjects in the same spatial coordinate space, such as, high-resolution atlas space [44]. In the future, registration from hMRI to cine-MRI is planned. The goal is to incorporate high-quality muscle definition into cine-MRI to better interpret tongue muscle motion from cine-MRI data.

To validate the proposed method, experiments with both synthetic and in vivo human datasets including the tongue and the brain were performed. Experiments with synthetic datasets allowed evaluation of the accuracy and robustness of the proposed method to different noise levels. Experiments with human tongue datasets allowed the evaluation of both accuracy and robustness in images with different magnitudes of intensity non-uniformity. Experiments with brain datasets allowed to comparisons of several entropy-based measures used in [33], [35] and allowed to objectively compare the similarity measure itself. This is because the evaluation focused on the rigid transformation and thus the TRE results were independent of the choice of the transformation models or different regularization methods. It was observed that the proposed method provided superior performance even when noise level or the intensity non-uniformity became stronger. Also the proposed method outperformed entropy-based similarity measures such as MMI, ECC, MECC, CRECC, MCRECC [35], and the learning based method [33].

In our method, the choice of T determines how much anatomical detail is included in the registration, which will be different from one application to another. In our case, anatomical details are captured in Type 1 and 2 regions and Type 3 captures a homogeneous region. In the registration process, Type 1 and 2 regions are combined; therefore we chose T based on the Type 3 homogeneous region. Once we set T, we used the same parameters within the same experiments as the anatomical details are similarly presented in the images. The choices of the associated weights of Type 1 and 2 and the parameters for the Harris operator are subject to modification. Although in this work we used spatially meaningful regions (i.e., Type 1 and 2) with the same weights, this can be improved by a mechanism to incorporate importance of each region in an adaptive manner such as the work by Yi et al. [16].

The choice of the width of the Parzen window in estimating MI could influence the registration performance. While a large width will over-smooth the density estimation and mask the structure of the data, a small width will yield a density estimation that is noisy. In our work, we used MI metric available in ITK, which used a third order B-spline function as the Parzen window [31]. The use of B-spline function satisfies the constraint for the partition of unity, while remaining positive, thus being an admissible Parzen window [25], [27]. In addition, in the ITK implementation, in calculating the probability density function, the image intensity values are linearly scaled between zero and one. Thus, in order to handle image data with varying magnitude and range, a fixed B-spline kernel bandwidth of one is used [31].

A challenge for the method to be applied in large population studies and routine clinical practice is the computational cost. It takes on average 1–2 hours for the in vivo tongue experiments on an Intel i7 CPU with a clock speed of 1.74 GHz. This could sped up by either implementing the method with GPU or using parallel computing. In addition, more sophisticated optimization schemes such as gradient descent with backtracking line search could be employed to improve the convergence speed.

Validation of any registration algorithm is a challenging task. Compared to brain registration, both tongue image registration and its validation are inherently more difficult due to the movement of tongue. Therefore, selecting anatomical landmarks is of great importance and, at the same time, a challenging task even for humans, in assessing the accuracy of the registration method. This is because there is no true gold standard other than visual judgment, which is marred by inter-observer variability. The chosen landmarks are soft tissue points that abut the pharyngeal airway. They were chosen because they are visible on both datasets; we did not choose other landmarks due to differences in spatial resolution of muscles, slice thickness, and T2-weighting. For example, the hinge point of the soft palate is not used as a landmark because the hinge point of the soft palate is not comparable in the two datasets and the high-resolution dataset captures quiet breathing and the soft palate is open. The cine dataset captures speech and the soft palate is closed. Therefore the hinge is not the same tissue point in the two datasets. The chosen landmarks are tongue tip, lower lip, and posterior pharynx. In the present study, the inter-observer variability was high especially in the lower lip but the overall TRE was comparable to inter-observer variability (p = NS).

The tongue moves during speech, therefore, different anatomical features including the tongue surface and velum move on cine time frames. As a result, there could be geometrical ambiguities in finding the correct features to match between hMRI and cine-MRI images. Thus, we aligned the hMRI data to the first time frame of the cine image because the tongue is in a relatively neutral position due to the “uh” speech sound being made. The position of the tongue and surrounding structures should be close to the resting tongue position found in hMRI data.

To our knowledge, this is the first report addressing registration of hMRI and cine-MRI in tongue images. These images are multimodal in a certain sense and a method to provide routine coregistration could yield a unique resource in the scientific research of speech science and speech-related disorders. The proposed work holds promise to bridge the two modalities, thereby enriching the information for further tongue image and motion analyses.

VI. Conclusion

In this work, we presented a novel multimodal image registration algorithm. In order to address limitations of the MI, we utilized structural information computed from the 3D Harris operator to encode spatial and geometric cues into the computation of MI. The proposed method was validated extensively on synthetic data, tongue and brain data to demonstrate the benefit of its novel features.