Abstract
We present a numerical study of the acoustophoretic motion of particles suspended in a liquid-filled PDMS microchannel on a lithium niobate substrate acoustically driven by surface acoustic waves. We employ a perturbation approach where the flow variables are divided into first- and second-order fields. We use impedance boundary conditions to model the PDMS microchannel walls and we model the acoustic actuation by a displacement function from the literature based on a numerical study of piezoelectric actuation. Consistent with the type of actuation, the obtained first-order field is a horizontal standing wave that travels vertically from the actuated wall towards the upper PDMS wall. This is in contrast to what is observed in bulk acoustic wave devices. The first-order fields drive the acoustic streaming, as well as the time-averaged acoustic radiation force acting on suspended particles. We analyze the motion of suspended particles driven by the acoustic streaming drag and the radiation force. We examine a range of particle diameters to demonstrate the transition from streaming-drag-dominated acoustophoresis to radiation-force-dominated acoustophoresis. Finally, as an application of our numerical model, we demonstrate the capability to tune the position of the vertical pressure node along the channel width by tuning the phase difference between two incoming surface acoustic waves.
1 Introduction
The emergence of lab-on-a-chip technologies has sparked a renewed interest in microfluidics. One of the requirements for the success of lab-on-a-chip systems is to precisely manipulate fluids and particles immersed in them at microscales. Here, surface acoustic wave (SAW) based systems, recently reviewed in Refs., 1–3 have shown great potential in recent years.
SAW based systems rely on piezoelectric actuation of surface acoustic waves in a solid substrate. These waves propagate along the substrate surface and, as they encounter a fluid interface, they radiate acoustic energy into the fluid. This drives acoustic streaming in the fluid itself as well as the motion of the immersed particles. The particles experience primarily two forces, the acoustic radiation force arising from the scattering of sound waves on the particles and the Stokes drag force from the induced acoustic streaming. However, while bulk acoustic wave (BAW) based systems have been heavily studied, 4–7 the theoretical and numerical work on SAW-driven systems is rather limited and so is the full understanding of the underlying physics. For example, the mechanisms underlying the vertical focusing of particles in polydimethylsiloxane (PDMS) channels, 8 the effect of using PDMS channels as opposed to silicon walls, the precise bulk acoustic fields and associated acoustic streaming, and the critical particle size for the transition between radiation-dominated and streaming-dominated acoustophoresis. The latter has been extensively studied within BAW-driven systems, 7,9,10 but it is yet to be examined in SAW-driven systems.
One of the primary reasons for the lack of a detailed theoretical understanding of the physical processes involved in SAW devices is the difficulty in the identification of precise boundary conditions. From a numerical viewpoint, the difference between BAW systems and SAW systems is limited to the differences in actuation and wall conditions, while the governing equations remain the same. While SAW-based systems with free boundaries in form of droplets have been heavily studied numerically, 11–13 SAW-driven systems with closed boundaries have received less attention. Using hard-wall boundary conditions, few studies have been reported for the acoustic streaming in a closed SAW-driven system. 14,15 However, while BAW systems utilize walls that are often made of hard material like glass or silicon making hard-wall boundary conditions appropiate, SAW-based systems often utilize soft materials such as PDMS leading to significant radiative energy losses.
In this work, we employ impedance boundary conditions to model the PDMS walls of a typical SAW-based device to setup a numerical model for investigating the acoustophoretic motion in SAW devices. In line with the work by Muller et al.7 we employ perturbation theory and use the solution of the first-order equations to calculate the time-averaged solutions, such as the acoustic streaming induced in the liquid and the acoustic radiation force acting on suspended particles. These are then used to determine the particle trajectories and to study the transition of dominance on particles’ motion between the two forces. The numerical method and the results presented in this work will be helpful in providing a better understanding of the physics in SAW-driven devices as well as to allow for future optimization and reliable control of SAW-based microfluidic devices.
2 Governing Equations
The mass and momentum balance laws governing the motion of a linear viscous compressible fluid are 16,17
| (1) |
where ρ is the mass density, v is the fluid velocity, p is the fluid pressure, and where μ and μb are the shear viscosity and bulk viscosity, respectively. Here, the fields ρ, p, and v are understood to be in Eulerian form, 17 i.e., functions of time t and spatial position r within a fixed volume. Furthermore, in order to describe the fluid motion, we need a constitutive relation linking the pressure and density. We assume a linear relation between p and ρ:
| (2) |
where c0 is the speed of sound in the fluid at rest. Combining Eqs (??)–(2) with appropriate boundary conditions, the system is fully determined. Nonetheless, the above-mentioned nonlinear system of equations is numerically challenging to solve via a direct numerical simulation due to the widely separated time scales (characteristic oscillation periods vs. characteristic times dictated by the streaming speed). 18 For example, a typical SAW device is operated at frequencies in the range of 1 – 100 MHz, while the streaming fields are characterized by time scales of the order of tenth of seconds to several minutes. Therefore we neglect the transient build-up of the acoustic fields and in this work we only consider time-harmonic forcing. However, because of viscous dissipation, the response of the fluid to a harmonic forcing is, in general, not harmonic. The fluid response can be understood to be comprised of two components: (i) a periodic component with period equal to the forcing period, and (ii) a remainder that can be viewed as being steady. It is this second component which is generally referred to as the streaming motion. 2 Following our recent model, 19 we employ Nyborg’s perturbation technique 20 in which fluid velocity, density, and pressure are assumed to have the following form
| (3a) |
| (3b) |
| (3c) |
where ε is a non-dimensional small parameter. Following Köster,14,21 we define ε as the ratio between the amplitude of the displacement of the boundary in contact with the piezoelectrically driven substrate (i.e., the amplitude of the boundary excitation) and a characteristic length. We take the zeroth order velocity field v0 to be equal to zero thus assuming the absence of an underlying net flow along the microchannel. Letting
| (4) |
substituting Eqs. (3) into Eqs. (??) and (1), and setting the sum of all the terms of order one in ε to zero, the following problem, referred to as the first-order problem, is obtained
| (5) |
| (6) |
Repeating the above procedure for the terms of order two in ε, and averaging the resulting equations over a period of oscillation, the following set of equations, referred to as the second-order problem, is obtained
| (9) |
where 〈A〉 denotes the time average of the quantity A over a full oscillation time period. As pointed out by Stuart, 22 inertial terms in Eq. (2) can be significant and must be retained in the formulation. Also, to fully account for viscous attenuation of the acoustic wave, both within and without the boundary layer, the last term in Eq. (2) associated with the bulk viscosity must also be retained.
3 Numerical Model
3.1 Model system and computational domain
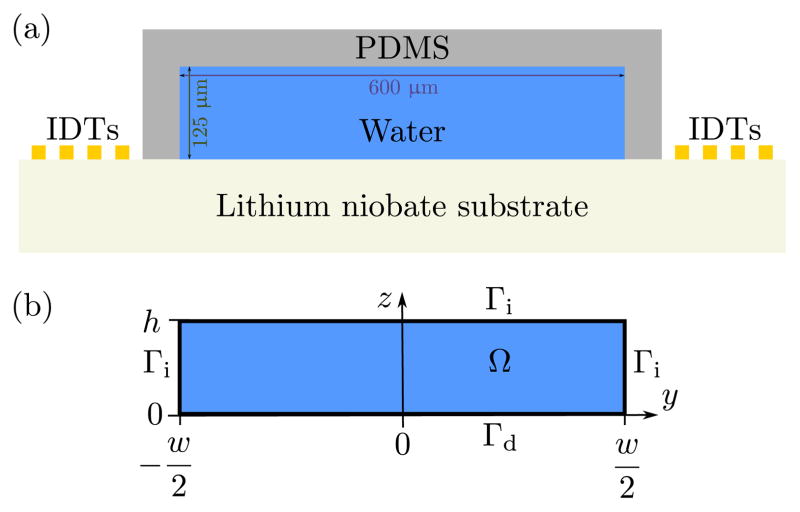
A typical standing SAW (SSAW) device for particle manipulation consists of a PDMS channel bonded on a piezoelectric substrate, see Fig. 1(a). The device employs a pair of metallic interdigitated transducers (IDTs) sitting on the surface of the piezoelectric substrate. A standing SAW is produced via the superposition of two counter-propagating traveling SAWs generated on the surface of the piezoelectric substrate by applying a harmonic electric signal to the IDTs. The full physical system is governed by coupling of elastic, electromagnetic, and hydrodynamic effects, which makes numerical modeling challenging. 14,21 Thus, we simplify the system by modeling the PDMS walls of the channel using impedance boundary conditions limiting this study to cases with PDMS walls of thickness 2 mm or greater, while the effect of piezoelectric substrate is modeled using a displacement function at the substrate boundary. As a result our computational domain Ω shown in Fig. 1(b) consists of a rectangular microchannel of width w = 600 μm and height h = 125 μm, where the boundaries subject to the impedance condition are denoted by Γi, while the actuated boundary is denoted by Γd. The boundary conditions are discussed in detail in Section 3.2. In this work we analyse the case where the piezoelectric substrate is made of lithium niobate actuated with a surface wave of wavelength λ = 600 μm and frequency f = 6.65 MHz, and where the channel is filled with water. The values for all the relevant properties of the piezoelectric substrate and water, as well as the typical operational parameters used in our numerical model, are listed in Table 1.
Fig. 1.
(a) Cross-sectional sketch of the SAW-driven device consisting of a lithium niobate substrate and liquid-filled PDMS channel (width w = 600 μm and height h = 125 μm). The substrate is acoustically actuated via two sets of interdigitated electrodes (IDTs). Note, the figure is not drawn to scale and that the PDMS channel walls are considered to be of thickness 2 mm or greater. (b) Sketch of the computational domain Ω with impedance boundaries Γi and Dirichlet actuation boundary Γd.
Table 1.
Material parameters at T = 25 °C.
| Water
| ||
| Density 23 | ρ0 | 997 kg m−3 |
| Speed of sound 23 | c0 | 1497 m s−1 |
| Shear viscosity 23 | μ | 0.890 mPa s |
| Bulk viscosity 24 | μb | 2.47 mPa s |
| Compressibility* | κ0 | 448 TPa−1 |
|
| ||
| Lithium niobate (LiNbO3)
| ||
| Speed of sound 25 | csub | 3994 m s−1 |
|
| ||
| Polydimethylsiloxane (PDMS, 10:1)
| ||
| Density 26 | ρwall | 920 kg m−3 |
| Speed of sound 27 | cwall | 1076.5 m s−1 |
| Attenuation coeff. (6.65 MHz) † 27 | 31 dB/cm | |
|
| ||
| Polystyrene
| ||
| Density 23 | ρp | 1050 kg m−3 |
| Speed of sound 28 (at 20 °C) | cp | 2350 m s−1 |
| Poisson’s ratio 29 | σp | 0.35 |
| Compressibility‡ | κp | 249 TPa−1 |
|
| ||
| Acoustic actuation parameters
| ||
| Wavelength (set by IDTs) | λ | 600 μm |
| Forcing frequency | f | 6.65 MHz |
| Displacement amplitude | u0 | 0.1 nm |
| Displacement decay coefficient | Cd | 116 m−1 |
3.2 Boundary Conditions
As the objective of this work is to study the fluid and particle motion inside the microfluidic channel shown in Fig. 1, we simplify the system considerably by modeling the effect of piezoelectric substrate via a displacement boundary condition while the PDMS walls are modeled using impedance boundary conditions.
The type of waves usually considered in SAW devices are the so-called Rayleigh waves. The amplitude of these waves decay exponentially with the depth into the substrate, thereby confining most of the energy to the surface. 31 The two wave motions in the y and z direction are known to be 90° out of phase in time, thereby resulting in elliptical displacements. Based on these considerations, it is possible to find displacement functions for waves which propagate along the y direction and decay exponentially in both y and z direction. Taking these considerations into account, Gantner et al.32,33 analyzed numerically the Rayleigh waves in piezoelectric substrates in great detail. We use the displacement results from his analysis, also used by Köster, 14,21 to describe the displacement profile due to a traveling SAW which takes the form
| (10) |
where uy and uz are the displacements along the y and z direction, respectively, Cd is the decay coefficient, and ω = 2πf is the angular frequency. The value of Cd employed by Köster 14,21 (8060 m−1) is appropriate for a SAW device loaded with an infinite layer of water at frequencies in the range of 100 MHz. Recently, Vanneste and Bühler 34 investigated streaming patterns using an attenuation coefficient of 2800 m−1 for a frequency of approximately 150 MHz. Using the leaky SAW dispersion relation employed by Vanneste and Bühler 34 for a frequency of 6.65 MHz, we get an attenuation coefficient of 116 m−1. However, we note that the dispersion relation employed by Vanneste and Bühler 34 is valid for a SAW propagating under an infinitely thick layer of water. A finite thickness might further reduce the attenuation coefficient. Noting this, for comparison purposes we considered a case with Cd = 0 (see ESI fig. 1). We observed that decreasing the value of Cd from 116 m−1 to zero does not change the solution significantly. With this in mind, we have used an attenuation coefficient of 116 m−1 for all the results presented in this article.
Using Eq.(10), we construct the standing SAW displacement profile over Γd by superimposing the displacement profile of two SAWs traveling in opposite directions with a phase difference of Δϕ:
| (11) |
This displacement function is then differentiated with respect to time to obtain the first-order velocity that we impose over Γd (Fig. 1(b)):
| (12) |
For the boundary condition on the channel walls, marked as Γi in Fig. 1(b), we use the so-called impedance or lossy-wall boundary condition given as 35
| (13) |
where i is the imaginary unit, and ρm and cm are the mass density and the speed of sound of the wall material, respectively. Note that this boundary condition is very different from the hard-wall condition, n·v1 = 0, used to model silicon or glass walls in BAW systems as the impedance boundary condition allows a non-zero first-order wall velocity. Futhermore, with this boundary condition, the model assumes all transmitted wave energy to be absorbed in the PDMS, i.e. no reflected waves, from a potential PDMS/air interface, are allowed to re-enter the water channel. The model therefore only applies to cases, where the PDMS walls are thick enough to attenuate waves transmitted from the channel. In commonly-used PDMS (10:1), the attenuation coefficient for frequencies of 5 MHz and 7 MHz are 21.30 dB/cm to 33.57 dB/cm, respectively, which translate to decay coefficients of 490 m−1 and 773 m−1. 27 For the specific frequency of 6.65 MHz used in this work, the attenuation coefficient is close to 31 dB/cm corresponding to a decay coefficient of 714 m−1. Therefore, if the channel walls are thicker than 2 mm, only a exp(−714 m−1 × 2 × 0.002 m) = 0.058 fraction of the transmitted waves at the water/PDMS interface will reach the PDMS/air interface and come back again. This corresponds to an absorption of more than 94 % and thus the assumption of total absorption of acoustic waves in the PDMS walls is reasonable for channel walls thicker than 2 mm. For higher actuation frequencies common in SAW devices (tens of MHz) the attenuation coefficient increases further (more than double at 11 MHz) thus making the assumption of total absorption even better.
For the second-order problem, Bradley 36 offered a careful analysis of the boundary conditions to be satisfied on the moving surfaces. Specifically, the no-slip boundary condition needs to be satisfied on the deformed positions of the moving surfaces, and not on the initial rest positions. However, the displacement amplitude in SAW devices is usually in sub-nanometer range, thus it is possible to neglect the minute difference between the initial and the deformed positions. Noting this, we employ the zero-velocity boundary condition on all the boundaries, similar to those used by Muller et al.: 7
| (14) |
3.3 Single-particle acoustophoretic trajectories
In order to be able to predict acoustophoretic particle trajectories of a typical microfluidic experiment using polystyrene tracer particles, we implement a particle tracking strategy. Such trajectories will also create the foundation for experimental verification of our numerical model by using three-dimensional particle tracking velocimetry. 7,37 We consider particles suspended in a suspension dilute enough to neglect particle-particle interactions, hydrodynamic as well as acoustic. The tracking strategy is predicated on the determination of the acoustic radiation force due to the scattering of waves on the particle as described by Settnes and Bruus. 38 Considering a particle of radius a much smaller than the wavelength λ, mass density ρp, and compressibility κp, the radiation force takes the form: 38
| (15) |
where is the compressibility of the fluid, Re(A) denotes the real part of quantity A, the asterisk denotes the complex conjugate of the quantity, and the coefficients f1 and f2 are given by
| (16) |
with
| (17) |
Note that we use the general expression for the radiation force without a priori assumption of whether we deal with traveling or standing waves.
In addition to the radiation force, a bead is assumed to be subject to a drag force proportional to vp − 〈v2〉, which is the velocity of the bead relative to the streaming velocity. When wall effects are negligible, the drag force is estimated via the simple formula Fdrag = 6πμa(〈v2〉 − vp). The motion of the bead is then predicted via the application of Newton’s second law
| (18) |
where mp is the mass of the bead. In many acoustofluidics problems the inertia of the bead can be neglected since the characterstic time of acceleration is small in comparison to the time scale of the motion of the particles. 39 Doing so, Eq. (18) can be solved for vp
| (19) |
For steady flows, we can identify the bead trajectories with the streamlines of the velocity field vp in Eq. (19).
3.4 Numerical Scheme
For the first-order problem we seek solutions of the following form
| (20a) |
| (20b) |
where v(r) is a vector-valued function of space while p(r) is a scalar function of space. For the second-order problem, we seek steady solutions. We also note that the second-order problem has pure Dirichlet boundary conditions on all sides and hence does not admit a unique solution unless we assign an additional pressure constraint. However, since the radiation force used here is completely dependent only on the first-order fields, we do not use the second-order pressure in any of our calculations. Combining information from the first- and the second-order solutions, it is then possible to estimate the mean trajectory of particles in the flow.
All the solutions discussed later are for two-dimensional problems. The numerical solution was obtained via the finite element software COMSOL Multiphysics 4.4.40 For both the first- and second-order problems we used Q2-Q1 elements for velocity and pressure, respectively, where Q1 and Q2 denote triangular elements supporting Lagrange polynomials of order one and two, respectively.
4 Results and Discussions
4.1 Mesh convergence analysis
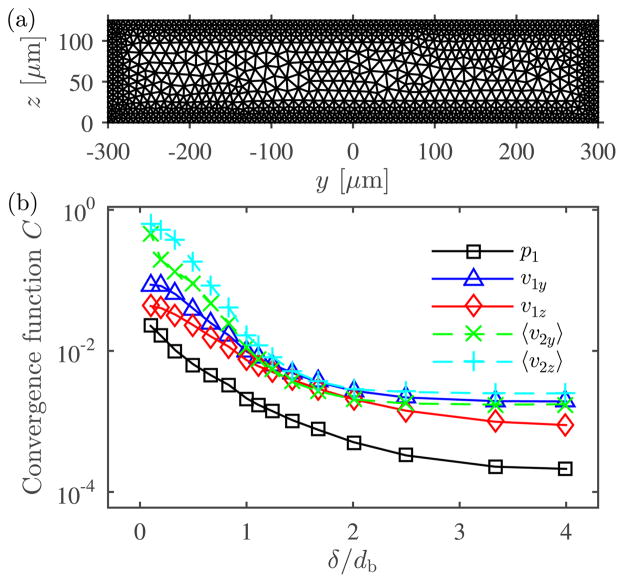
To capture the physics inside the boundary layers near the walls, we use a computational mesh with a maximum element size near the boundary, db while the maximum element size in the bulk of the domain was set to 2 μm. Fig. 3(a) shows an illustrative mesh with db = 30δ, where δ is the viscous boundary layer thickness given by Eq. (17). To check for mesh convergence, we investigate the behavior of the variables solved for on a series of meshes generated by progressively decreasing the mesh element size, db. We define a relative convergence function C(g) for a solution g with respect to a reference solution gref obtained on the finest mesh as
Fig. 3.
Mesh convergence analysis. (a) An illustrative computational mesh with 2478 triangular elements obtained with maximum element size near the boundary, db = 30δ, while the maximum element size in the bulk of the domain was set to 20 μm. (b) Semi-logarithmic plot of the relative convergence parameter C, as given in Eq. (21), for decreasing mesh element size near the boundaries, db.
| (21) |
where we use a reference solution g obtained for db = 0.2δ with approximately 5.6 × 105 elements. The results of the mesh convergence analysis are shown in Fig. 3(b) where the convergence function C is plotted as a function of δ /db. As the value of db reaches 0.3δ all the variables have reached sufficient convergence and throughout the rest of the work we use a mesh with db = 0.3δ.
4.2 Wall impedance sweep
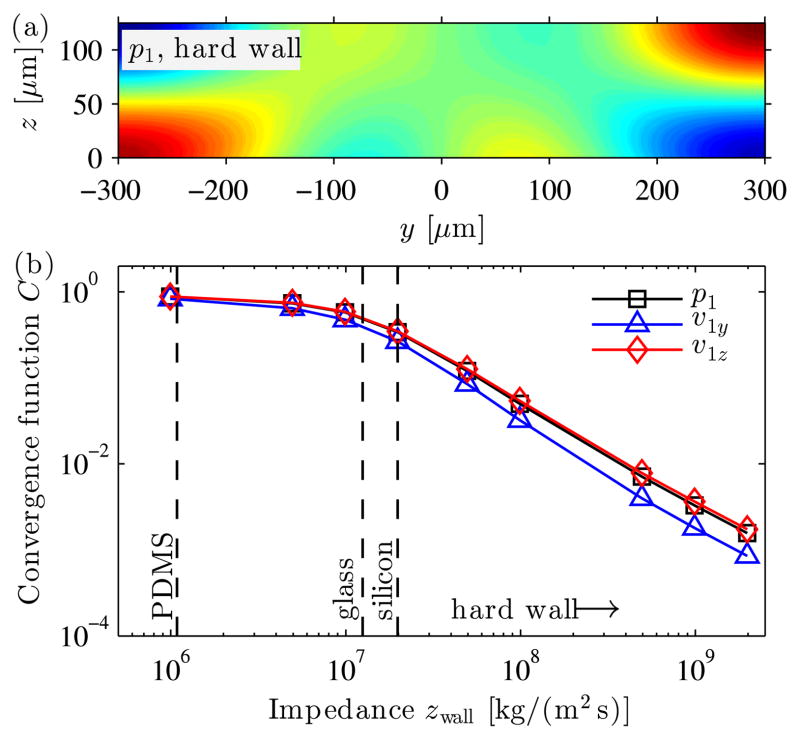
To study the effect of the wall material of the microfluidic channel, we perform a series of simulations with increasing value of wall impedance while the fluid impedance is kept constant. For each value of increasing impedance we compare the solution g to the solution gref obtained using hard-wall boundaries (i.e. n·v1 = 0 at Γi) by calculating the convergence function C(g) in Eq. (21). The first-order pressure field from the hard-wall solution is shown in Fig. 4(a) and features a resonance with no traveling waves as typically observed in BAW systems. The convergence function C(g) for the first-order pressure and velocity fields is plotted in Fig. 4(b) and it is seen that as the wall impedance increases, the solutions converge to the hard-wall solution. The values of the convergence function C for impedance values for those of glass (zgl = 1.3 ×107 kg m−2 s−1) and silicon (zsi = 2.0 × 107 kg m−2 s−1) were around 0.45 and 0.3, respectively, while C for PDMS is around 1. Thus, to a reasonable approximation, hard-wall boundary conditions can be used for BAW systems using typically silicon or glass walls, while it is an inaccurate condition for SAW systems using PDMS walls. This is in good agreement with the fact that PDMS, having an acoustic impedance similar to water, absorbs most of the incident waves with little reflections while silicon and glass, having very different acoustic impedances from water, reflect most of the incident waves leading to the building up of resonances inside the microchannel.
Fig. 4.
Impedance convergence analysis. (a) First-order pressure field p1 when using hard-wall conditions n·v1 = 0 at Γi boundaries [color plot ranging from −70.5 kPa (blue) to 70.5 kPa (red)]. (b) Semi-logarithmic plot of the relative convergence parameter C, as given in Eq. (21), as a function of the wall impedance zwall. The solution with hard-wall boundary conditions in panel (a) was chosen as the reference solution. As the impedance of the walls increases, the solution with impedance boundary conditions converges to the solution with the hard-wall boundary conditions.
4.3 Acoustic fields
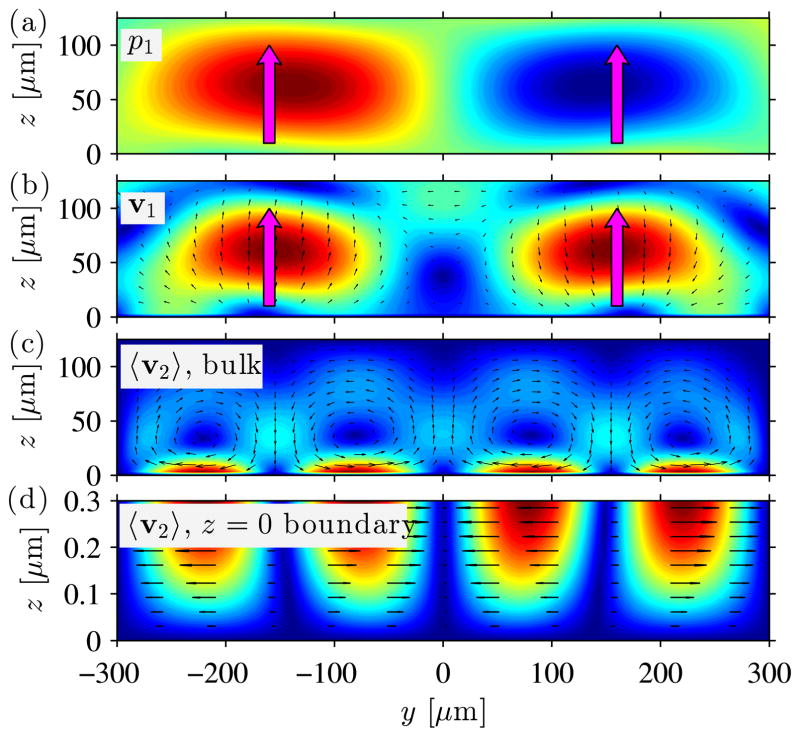
Having identified the proper mesh refinement level in Section 4.1 and that impedance boundary conditions are appropriate for modeling PDMS walls in Section 4.2, we investigate the acoustic fields that are set up inside the channel. In Fig. 5 we show the first-order pressure field p1, first-order velocity field v1, and the second-order velocity field 〈v2〉, where the plotted colors indicate the field magnitude (from blue minimum to red maximum) and the black arrows indicate the field vectors. For the first-order pressure field p1 and first-order velocity field v1 in Fig. 5(a) and (b), respectively, we observe a clear horizontal standing wave along y, but as indicated by the upwards-pointing magenta arrows, we observe that the first-order fields are traveling waves moving from the bottom wall towards the top wall along the z direction. The first-order pressure amplitude pa is observed to be 12.9 kPa as opposed to 70.5 kPa observed when using the hard-wall boundary conditions as shown in Fig. 4(a). This difference in pressure amplitude can be attributed to the fact that a resonance is set up in the channel when using the hard-wall boundary condition, leading to an increased pressure amplitude. Furthermore, we notice that the first-order velocity amplitude |va| is observed to be 5.3 mm/s. This amplitude is greater than the actual velocity amplitude |va| = ωu0 = 4.17 mm/s imposed via the actuation function described in Eq. (11), which indicates that the traveling wave is not completely transmitted through the PDMS walls and thus reflections occur from the channel walls due to the small but non-zero impedance mismatch between the PDMS and water.
Fig. 5.
Color plots of the first-order pressure p1 and velocity v1 fields as well as the time-averaged second-order velocity 〈v2〈. The first-order fields oscillate in time with a standing wave along y and a travelling wave along z indicated by the upwards-pointing magenta arrows. (a) Oscillating first-order pressure field p1 [colors ranging from −12.9 kPa (blue) to 12.9 kPa (red)]. (b) Oscillating first-order velocity field v1 [magnitude shown as colors ranging from zero (blue) to 5.3 mm s−1 (red), vectors shown as black arrows]. (c) Time-averaged second-order velocity field 〈v2〉 [magnitude shown as colors ranging from zero (blue) to 1.47 μm s−1 (red), vectors shown as black arrows]. (d) Zoom of the time-averaged second-order velocity field 〈v2〉 in (c) in a slab of 0.3 μm height from the bottom wall [magnitude shown as colors ranging from zero (blue) to 1.72 μm s−1 (red), vectors shown as black arrows].
Fig. 5(c) shows the second-order velocity field 〈v2〉, in which four streaming vortices are observed along the y direction with a maximum velocity of 1.47 μm s−1 close to the bottom wall. Fig. 5(d) shows a zoomed version of the second-order velocity near the bottom boundary and we note that no streaming rolls are observed within the viscous boundary layer of width , which were observed numerically by Muller et al.7 for a BAW system. The difference between the model by Muller et al. and our model, is that we use impedance boundary conditions instead of hard-wall conditions, which allow the first-order velocity to have a slip-velocity thus minimizing the velocity gradients near the walls. Furthermore, in contrast to the work by Muller and coworkers, we actuate the bottom wall from where the streaming is driven.
4.4 Particle trajectories
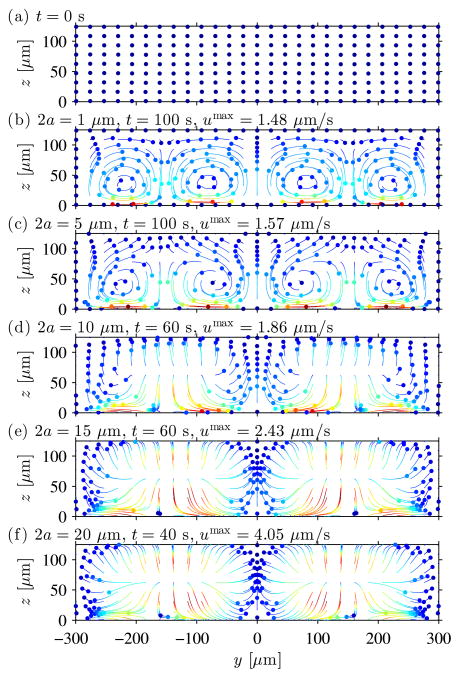
Based on the acoustic fields described in the former section and the theory described in Section 3.3 (see the radiation force field in ESI Fig. 2), we calculate the velocities and trajectories of polystyrene particles of diameters ranging from 1 μm to 20 μm. The trajectories are plotted in Fig. 6 for 243 particles with uniformly-distributed initial positions as shown in Fig. 6(a). The panels (b)-(f) show the trajectories of (b) 1 μm particles during 100 s, (c) 5 μm particles during 100 s, (d) 10 μm particles during 60 s, (e) 15 μm particles during 60 s, and (f) 20 μm particles during 40 s. For each particle trajectory the colors denote the particle velocity ranging from zero (blue) to its maximum (red), while the colored disks show the particles’ final positions and velocities. For the 1 μm and 5 μm particles in panel (b) and (c), respectively, we clearly see that their motion is governed by the viscous drag from the acoustic streaming as plotted in Fig. 5(c). The particles are carried around in the four horizontal streaming rolls and the maximum velocities of around 1.5 μm s−1 are very close to the maximum streaming velocity of 1.47 μm s−1. As the particle size increases, the acoustic radiation force becomes influential and for the motion of the 10 μm particles in panel (d) we observe that far from the strong streaming at the bottom wall, the acoustic radiation force pushes the particles out of the streaming vortices towards the top wall. This is even more evident for the 15 μm particles in panel (e), where the radiation force contribution is (15/10)2 ≈ 2.25 times larger, which is seen by an almost complete vanishing of the vortex motion as well as a maximum particle velocity of 2.43 μm s−1. In panel (f) for the 20 μm particles, the acoustic streaming pattern has completely vanished and the acoustic radiation is fully dominating the motion. We note that the radiation force carries the particles outwards from (±w/4, h/2) towards the channel walls consequently bringing the particles to the standing pressure nodes at y equal to −w/2, 0, and w/2. Furthermore, we notice that the 20 μm particles obtain velocities 4.05/2.43 ≈ 1.7 times larger than those of the 15 μm particles, which is close to the expected ratio of (20/15)2 = 1.8 if both the particles were fully dominated by the radiation force, see Eqs. (15) and (19). For the investigated system, the critical particle size for the transition between streaming-dominated and radiation-dominated motion is around 10 μm depending on the particle z-position as the acoustic streaming is strongest at the bottom wall. If we compare this to the BAW system studied by Muller et al.7,41 and Barnkob et al.9 where they found a transition diameter around 1 – 2 μm, it is clear that the acoustic streaming has a larger influence in the system studied in this work. However, typically SAW systems are driven at higher frequencies, which will increase the effect from the radiation force due to its linear dependence on the actuation frequency, Eq. (15). Finally, note that we have not taken into account the enhanced viscous drag force due to the presence of the channel walls, which would decrease the radiation force contribution for the large particles and for particles close to the channel walls. 42
Fig. 6.
Particle trajectories with particle velocities as colors from blue minimum to red maximum and colored disks denoting the final positions within the observation time. (a) Starting position of 243 particles distributed uniformly within the microchannel. The panels (b)-(f) show the trajectories of (b) 1 μm particles during 100 s, (c) 5 μm particles during 100 s, (d) 10 μm particles during 60 s, (e) 15 μm particles during 60 s, and (f) 20 μm particles during 40 s. The motion of the smaller particles is dominated by the viscous drag force from the acoustic streaming, while the larger particles are pushed to the pressure nodes by the acoustic radiation force.
We note that once the radiation force has pushed the particles to the pressure nodal lines, the acoustic streaming will carry the particles to the top wall. If we combine this behavior with a gravitational force in the negative y-direction (not considered in our simulations), this could explain the vertical focusing observed by Shi et al., 8 where they studied 1.9 μm particles in a microchannel of 50 μm width and 100 μm height actuated at around 40 MHz.
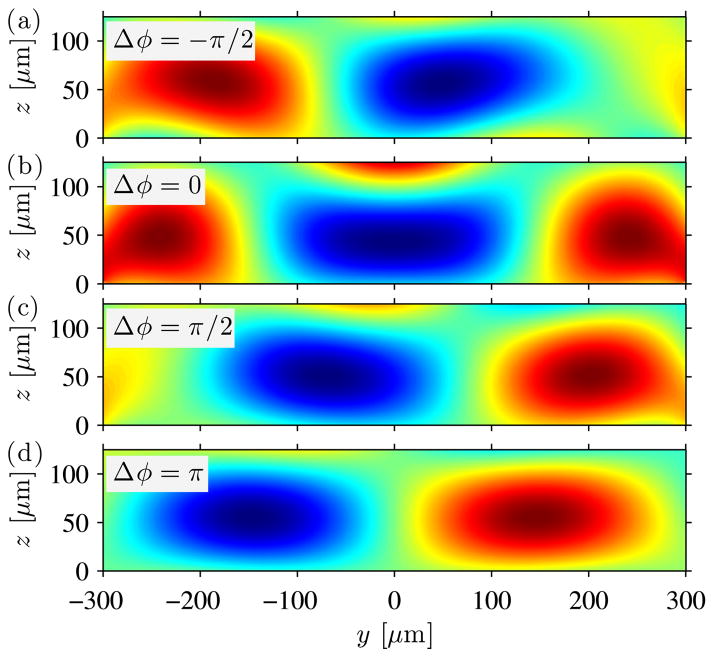
4.5 Phase sweeping
As an application of our numerical model, we investigate the effect of the phase difference between the two incoming SAWs by changing their relative phase Δϕ in Eq. (11). Fig. 7 shows the plots of the first-order pressure fields p1 for varying phase difference Δϕ. We see that the position of the pressure node along the y direction can be tuned by changing the phase difference between the two incoming SAWs. For a phase difference of π /2, the shift in the phase difference is λ/8. In other words, a phase difference of π results in an interchange in the position of the nodes and the antinodes. This is in agreement with the results obtained by Meng et al., 43 where they used the tuning of the pressure node to transport single cells or multiple bubbles. This principle has recently been utilized by Li et al.44 to study heterotypic cell-cell interaction by sequentially patterning different types of cells at different positions inside the microfluidic channel. Figure 7 also points to the fact that a minor shift in actuation does not affect the solution in a drastic manner, indicating the robustness of the solution with respect to minor perturbations in the applied actuation.
Fig. 7.
Color plots of the first-order pressure field for different values of phase difference Δϕ, as in Eq. (11), between the two incoming traveling waves. The position of the pressure node along the y direction can be tuned by changing the value of Δϕ. The pressure node moves by a distance of λ/8 for each phase difference of π /2.
5 Conclusions
We have successfully used a finite element scheme to model the acoustophoretic motion of particles inside an isentropic compressible liquid surrounded by PDMS walls. The system is acoustically actuated via two counter-propagating surface acoustic waves that form a standing wave in a piezoelectric material interfacing the liquid channel. Our model employs an actuation condition from the literature based on piezoelectric simulations as well as impedance boundary conditions to model the PDMS channel walls. Our model results in significantly different acoustic fields as those observed in bulk acoustic wave devices. Firstly, the first-order acoustic fields are travelling in the vertical direction away from the actuated boundary, while the horizontal standing wave feature remains. This results in a time-averaged second-order velocity field (the so-called acoustic streaming) driven by products of first-order fields with the characteristics of four horizontal streaming rolls per wavelength, which each decay vertically from the actuated boundary. In contrast to reported bulk acoustic wave cases, we do not observe any acoustic streaming rolls inside the viscous boundary, which we attribute to the differences in actuation condition as well as differences in the established first-order fields.
The motion of the particles is governed by the viscous drag force from the acoustic streaming as well as the direct acoustic radiation force due to scattering of sound waves on the particles. For our specific model parameters of 600 μm wavelength, 6.65-MHz actuation frequency, and polystyrene particles suspended in water, we obtain an approximate critical particle size of 4 – 8 μm for which the particle motion goes from being streaming-drag dominated to being radiation dominated. The critical particle size is only approximate due to the acoustic streaming decaying strongly along the height of the channel. Furthermore, our results do not take into account gravity, however, in combination with our vertically pushing streaming component, gravity could be responsible for the vertical focusing of particles in similar systems as reported by Shi et al.8
The next important step is to obtain direct experimental verification of our numerical results by use of 3D astigmatism particle tracking velocimetry capable of determining the three-dimensional three-component particle trajectories.37 Such experimental verification would pave the road for further enhancements of our numerical model to include wall-enhancement effects of the viscous drag force as well as the inclusion of the heat-transfer equation in the governing equations in order to account for temperature effects as recently studied by Muller and Bruus. 45
Fig. 2.
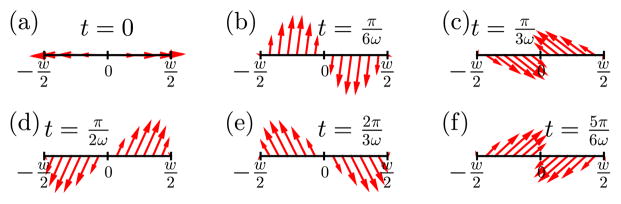
Plot of standing SAW displacement vectors along the interface of the channel and the piezoelectric substrate at z = 0 at (a) t = 0, (b) t = π /6ω, (c) t = π /3ω, (d) t = π /2ω, (e) t = 2π /3ω, and (f) t = 5π /6ω. The displacement function is obtained by superimposing two incoming traveling SAWs from the left and the right direction, see Eq. (11).
Acknowledgments
This work was supported by National Institutes of Health (1R01 GM112048-01A1, 1R33EB019785-01), National Science Foundation (CBET-1438126 and IIP-1346440), the Penn State Center for Nanoscale Science (MRSEC) under grant DMR-0820404, and the German Research Foundation (DFG), under the individual grants program KA 1808/16-1.
Contributor Information
Francesco Costanzo, Email: costanzo@engr.psu.edu.
Tony Jun Huang, Email: junhuang@psu.edu.
References
- 1.Gedge M, Hill M. Lab on a Chip. 2012;12:2998–3007. doi: 10.1039/c2lc40565b. [DOI] [PubMed] [Google Scholar]
- 2.Ding X, Li P, Lin S-CS, Stratton ZS, Nama N, Guo F, Slotcavage D, Mao X, Shi J, Costanzo F, Huang TJ. Lab on a Chip. 2013;13:3626–3649. doi: 10.1039/c3lc50361e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Yeo LY, Friend JR. Annual Review of Fluid Mechanics. 2014;46:379–406. doi: 10.1146/annurev-fluid-010313-141309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Neild A, Oberti S, Haake A, Dual J. Ultrasonics. 2006;44:455–460. doi: 10.1016/j.ultras.2006.05.168. [DOI] [PubMed] [Google Scholar]
- 5.Dual J, Hahn P, Leibacher I, Möller D, Schwarz T, Wang J. Lab on a Chip. 2012;12:4010–4021. doi: 10.1039/c2lc40733g. [DOI] [PubMed] [Google Scholar]
- 6.Lei J, Glynne-Jones P, Hill M. Lab on a Chip. 2013;13:2133–2143. doi: 10.1039/c3lc00010a. [DOI] [PubMed] [Google Scholar]
- 7.Muller PB, Barnkob R, Jensen MJH, Bruus H. Lab on a Chip. 2012;12:4617–4627. doi: 10.1039/c2lc40612h. [DOI] [PubMed] [Google Scholar]
- 8.Shi J, Yazdi S, Lin S-CS, Ding X, Chiang I-K, Sharp K, Huang TJ. Lab on a Chip. 2011;11:2319–2324. doi: 10.1039/c1lc20042a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Barnkob R, Augustsson P, Laurell T, Bruus H. Phys Rev E. 2012;86:056307. doi: 10.1103/PhysRevE.86.056307. [DOI] [PubMed] [Google Scholar]
- 10.Lei J, Hill M, Glynne-Jones P. Lab on a Chip. 2014;14:532–541. doi: 10.1039/c3lc50985k. [DOI] [PubMed] [Google Scholar]
- 11.Yeo LY, Friend JR. Biomicrofluidics. 2009;3:012002. doi: 10.1063/1.3056040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Shilton R, Tan MK, Yeo LY, Friend JR. Journal of Applied Physics. 2008;104:014910. [Google Scholar]
- 13.Alghane M, Chen B, Fu Y, Li Y, Desmulliez M, Mohammed M, Walton A. Physical Review E. 2012;86:056304. doi: 10.1103/PhysRevE.86.056304. [DOI] [PubMed] [Google Scholar]
- 14.Köster D. SIAM Journal on Scientific Computing. 2007;29:2352–2380. [Google Scholar]
- 15.Antil H, Glowinski R, Hoppe RH, Linsenmann C, Pan T-W, Wixforth A. J Comput Math. 2010;28:149–169. [Google Scholar]
- 16.Landau LD, Lifshitz EM. Fluid Mechanics. 2. Vol. 6. Pergamon Press; Oxford: 1993. Course of Theoretical Physics. [Google Scholar]
- 17.Gurtin ME, Fried E, Anand L. The Mechanics and Thermodynamics of Continua. Cambridge University Press; New York: 2010. [Google Scholar]
- 18.Frommelt T, Gogel D, Kostur M, Talkner P, Hanggi P, Wixforth A. Ultrasonics, Ferroelectrics and Frequency Control, IEEE Transactions on. 2008;55:2298–2305. doi: 10.1109/TUFFC.928. [DOI] [PubMed] [Google Scholar]
- 19.Nama N, Huang P-H, Huang TJ, Costanzo F. Lab on a Chip. 2014;14:2824–2836. doi: 10.1039/c4lc00191e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Nyborg WL. In: Nonlinear Acoustics. Hamilton MF, Blackstock DT, editors. Academic Press; San Diego, CA: 1998. pp. 207–231. [Google Scholar]
- 21.Köster D. PhD thesis. Universität Augsburg; Germany: 2006. [Google Scholar]
- 22.Stuart J. Journal of Fluid Mechanics. 1966;24:673–687. [Google Scholar]
- 23.CRCnetBASE Product. CRC Handbook of Chemistry and Physics. 92. Taylor and Francis Group; 2012. www.hbcpnetbase.com/ [Google Scholar]
- 24.Holmes MJ, Parker NG, Povey MJW. Journal of Physics: Conference Series. 2011;269:012011. [Google Scholar]
- 25.Sankaranarayanan S, Bhethanabotla VR. Ultrasonics, Ferroelectrics and Frequency Control, IEEE Transactions on. 2009;56:631–643. doi: 10.1109/TUFFC.2009.1079. [DOI] [PubMed] [Google Scholar]
- 26.Armani D, Liu C, Aluru N. Micro Electro Mechanical Systems, 1999. MEMS’99. Twelfth IEEE International Conference on; 1999; pp. 222–227. [Google Scholar]
- 27.Tsou JK, Liu J, Barakat AI, Insana MF. Ultrasound in medicine & biology. 2008;34:963–972. doi: 10.1016/j.ultrasmedbio.2007.11.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Bergmann L. In: Der Ultraschall und seine Anwendung in Wissenschaft und Technik. 6. Hirzel Verlag S, editor. Stuttgart: 1954. [Google Scholar]
- 29.Mott PH, Dorgan JR, Roland CM. J Sound Vibr. 2008;312:572–575. [Google Scholar]
- 30.Landau LD, Lifshitz EM. Theory of Elasticity. Course of Theoretical Physics. 3. Vol. 7 Pergamon Press; Oxford: 1986. [Google Scholar]
- 31.Farnell G. Surface wave filters. Wiley; New York: 1977. Elastic surface waves. [Google Scholar]
- 32.Gantner A. PhD thesis. Universität Augsburg; Germany: 2005. [Google Scholar]
- 33.Gantner A, Hoppe RH, Köster D, Siebert K, Wixforth A. Computing and Visualization in Science. 2007;10:145–161. [Google Scholar]
- 34.Vanneste J, Bühler O. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Science. 2011;467:1779–1800. [Google Scholar]
- 35.Bruus H. Lab on a Chip. 2012;12:20–28. doi: 10.1039/c1lc20770a. [DOI] [PubMed] [Google Scholar]
- 36.Bradley C. The Journal of the Acoustical Society of America. 1996;100:1399–1408. [Google Scholar]
- 37.Cierpka C, Rossi M, Segura R, Kaehler CJ. Meas Sci Technol. 2011;22:015401. [Google Scholar]
- 38.Settnes M, Bruus H. Phys Rev E. 2012;85:016327. doi: 10.1103/PhysRevE.85.016327. [DOI] [PubMed] [Google Scholar]
- 39.Barnkob R. PhD thesis. Danmarks Tekniske Universitet (DTU); Lyngby, Denmark: 2012. [Google Scholar]
- 40.COMSOL Multiphysics 4.4. 2013 www.comsol.com.
- 41.Muller PB, Rossi M, Marín AG, Barnkob R, Augustsson P, Laurell T, Kähler CJ, Bruus Phys Rev E. 2013;88:023006. doi: 10.1103/PhysRevE.88.023006. [DOI] [PubMed] [Google Scholar]
- 42.Faxén H. Ann Phys. 1922;68:89–119. [Google Scholar]
- 43.Meng L, Cai F, Zhang Z, Niu L, Jin Q, Yan F, Wu J, Wang Z, Zheng H. Biomicrofluidics. 2011;5:044104. doi: 10.1063/1.3652872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Li S, Guo F, Chen Y, Ding X, Li P, Wang L, Cameron CE, Huang TJ. Analytical Chemistry. 2014;86:9853–9859. doi: 10.1021/ac502453z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Muller PB, Bruus H. Phys Rev E. 2014;90:043016. doi: 10.1103/PhysRevE.90.043016. [DOI] [PubMed] [Google Scholar]