DECISION MAKING IN LIVING CELLS: LESSONSFROM A SIMPLE SYSTEM

Abstract

The life cycle of bacteriophage lambda serves as a simplified paradigm for cell-fate decisions. The ongoing quantitative, high-resolution experimental investigation of this life cycle has produced some important insights in recent years. These insights have to do with the way cells choose among alternative fates, how they maintain long-term memory of their gene-expression state, and how they switch from one stable state to another. The recent studies have also highlighted the role of spatiotemporal effects in cellular processes and the importance of distinguishing chemical stochasticity from possible “hidden variables” in cellular decision making.

INTRODUCTION

One of the most striking features exhibited by living cells is their ability to process information and make decisions (3, 16, 72). In response to signals from the environment and from other cells, a cell may modulate its behavior either continuously (e.g. changing the expression level of a gene) or in a “digital” manner, choosing between a discrete set of predefined behaviors. Once a cell has chosen a specific option, it can remember that decision and maintain its state even as the environment keeps changing and the original stimulus is gone. However, this stability in face of fluctuations does not come at the expense of the ability to switch to an alternative state when the proper signal is given(45, 72).

To a person trained in statistical physics, these properties are strongly reminiscent of the emergent states of multi-particle systems (38, 94). One is then tempted to emulate for living cells what has been done in azoic systems: create a narrative for the behavior of the system, which is quantitative, simple and universal all at the same time. This narrative would arise not from a molecular understanding of every detail, but from a coarse-grained (“systems level”) approach. As in the physics of nonliving systems, the way to construct this narrative is through the formulation of basic “laws” characterizing the process of cellular decision-making. Over the last decade or so, such an endeavor has been pursued by a growing number of researchers. It is arguably one of the greatest challenges to physics in this century.

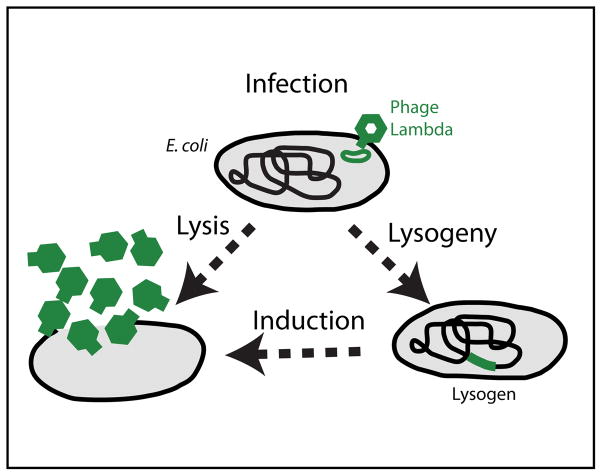
So where should one begin to study the process of cellular decision making? The answer is clear. The bacterium Escherichia coli (E. coli) has long served as the “hydrogen atom” of biology. The way E. coli modulates its swimming behavior (15, 16) and the expression of its genes (3, 71) has proven a fertile ground for studying cellular information processing. And when it comes to discrete cell-fate decisions and the long-term memory of cellular state, the system comprised of E. coli and one of its viruses, bacteriophage lambda, is a perfect place to start. The life cycle of phage lambda is depicted in FIGURE 1. Following infection of the bacterial cell, a decision is made between two alternative pathways: the invading phage can either replicate and lyse (kill) the host cell (“lytic pathway”), or it can integrate into the host chromosome—becoming a prophage—where it replicates as part of the bacterial genome while all lytic functions are repressed (“lysogenic pathway”). In response to cell damage, a switch back to the lytic pathway can be “induced”: The prophage exits the host chromosome, replicates, and lyses the bacterial cell (70, 72).

FIGURE 1. The life cycle of bacteriophage lambda.

Following infection, the bacteriophage can either replicate and kill the host cell (lysis), or it can integrate into the bacterial chromosome, where it replicates as part of the host genome (lysogeny). The lysogenic state is extremely stable, but a lysogen can be switched (induced) back to the lytic pathway, either spontaneously or in a directed manner. Adapted from (22).

Despite its relative simplicity, phage lambda already displays some of the intriguing features of cellular decision-making seen in higher systems; this is what makes it an ideal starting point in the endeavor to unveil universal principles in cellular decision making: (i) Noisy decision. When examined at the single-cell level, cellular decision-making often appears imprecise or “noisy”, in the sense that individual cells in a clonal population undergo different fates even when subject to identical conditions (6, 20, 52, 61, 62, 84, 86, 89, 93). This phenotype is commonly attributed to biochemical stochasticity (6, 20, 52, 61, 62, 84, 89). (ii) A self-regulating fate determining gene. Once a decision has been made towards lysogeny, the lysogenic state of an E. coli cell harboring a dormant bacteriophage serves as one of the simplest examples for a differentiated cellular state (70, 73, 74). Lysogenic stability is maintained by the activity of a single protein species, the lambda repressor (CI), which acts as a transcription factor to repress all lytic functions from the prophage, as well as to regulate its own production (73). This feature of auto-regulation by the fate-determining protein is also observed in higher systems displaying long-term cellular memory (28, 45, 57). (iii) Stability and switchability. The lambda lysogeny system exhibits extremely high stability: under the proper conditions, spontaneous switching events occur less than once per 10⁸ cell generations (59). Yet, fast and efficient switching can be observed in response to the appropriate stimulus, e.g. damage to the bacterial genome (70). Thus, the lysogenic state, like the differentiated state in higher systems, combines long-term stability with efficient state-switching (“reprogramming”) in response to the proper stimulus (45).

A verbal, non-quantitative narrative already exists for the lambda life cycle, based on half a century of genetics and biochemistry (49, 50, 72). In addition, considerable theoretical effort has been invested in forming a dynamical-systems picture for the lysis/lysogeny decision and the maintenance of lysogeny, based on the known biochemical players (see e.g. (1, 6, 10, 11, 64, 83, 92)). Earlier studies are phrased in deterministic terms (1, 64, 83); later ones often incorporate the effects of chemical stochasticity (6, 10, 11).

Though constituting important first steps towards the formation of a quantitative narrative, these theoretical works were limited by the fact that the kinetics characterizing the relevant cellular processes are largely unknown. Despite a small number of pioneering efforts to quantitatively phenotype the lambda system (4, 51, 55, 78), the kinetic assumptions and parameter values used in modeling typically arise from either (I) ad hoc choices made so as to reproduce the observed phenomena; (II) measurements made on whole populations, which average out much of the relevant dynamics in both space and time; or (III) in vitro measurements, far removed from actual physiological conditions (33). The bottom line is that a wide quantitative gap still exists between the vast genetic and biochemical knowledge on the one hand, and the observed phenotype on the other. In this regard phage lambda serves as an example of the inadequacy of our current comprehension of living systems—but it is also a system where this gap can arguably be bridged for the first time.

To begin this process, we have been endeavoring in my lab over the last few years to characterize the life cycle of phage lambda in a quantitative manner, in real time, at the resolution of individual phages and cells. By doing so, we are hoping to obtain a quantitative understanding of the lysis/lysogeny switch: from the initial cell-fate decision following infection; through the long-term maintenance of the lysogenic state; and the kinetics of switching from lysogeny to lysis during induction. Below I describe some of the insights that have emerged from this effort, as well as from parallel efforts by our colleagues.

THE LIFE CYCLE OF BACTERIOPHAGE LAMBDA

Target finding by the infecting phage: Rethinking spatiotemporal dynamics

The bacterial cell is traditionally considered a well mixed “sack of soup” where interactions are largely governed by diffusion kinetics. In recent years, however, this simple picture is being challenged by a wealth of new information regarding the complex organization and intricate spatiotemporal dynamics inside bacterial cells, which are reminiscent of those observed in eukaryotes. Specific cellular functions are performed at designated locations in the cell (60); active transport mechanisms are used to shuttle macromolecules to their destination (90). During our own studies of transcription in E. coli we found that mRNA molecules accumulate at the site of transcription to a larger degree than was previously believed (39). Furthermore, mRNA molecules moving randomly in the cytoplasm exhibit anomalous rather than normal (Fickian) diffusion, pointing to a unique interaction between the moving macromolecules and the medium surrounding them (40). All of these deviations from the ideal homogenous, diffusion-dominated picture may have a critical effect on the kinetics of intracellular processes, such as gene expression, by bringing closer together molecules which have to interact with each other while keeping apart those that should not. This intricacy should also remind us why biochemical parameters obtained in vitro should always be taken with a grain of salt.

The lambda life cycle offers an opportunity to characterize in a quantitative manner the spatiotemporal aspects of basic cellular processes, and examine the effects of spatial organization on the observed kinetics when compared to the naïve picture of diffusion-limited reactions. Here I discuss one such case, that of target finding by the infecting phage. The initial step in viral infection is the attachment of a virus to the surface of the host cell, followed by delivery of the viral genome into the cell (63, 85). This process involves a highly specific interaction between the virus and a receptor on the cell surface (63, 85). In the case of lambda, the target receptor (LamB) is originally used by the cell for uptaking maltose sugar, but has been “hijacked” by the phage (as is often done by viruses) for the purpose of injecting its DNA into the host. The number of LamB receptors on the cell surface varies depending on environmental conditions, typically a few hundreds under lab conditions (21, 68).

How does the phage “find” its target receptor? In other words, what are the spatiotemporal dynamics by which a phage, initially diffusing in bulk, arrives at a specific site on the cell surface and there inject its DNA? The classical biophysical picture of this process goes back to Adam and Delbruck, who introduced the concept of “reduction of dimensionality” as a means of minimizing target-finding time (2). According to this picture, the phage freely diffuses in three dimensions (3D) until it encounters the surface of the cell. The 3D motion is then replaced by a two-dimensional (2D) diffusion on the cell surface, until the target—a receptor—is found, the phage injects its DNA and the infection cycle ensues. The reduction in spatial dimension, from 3 to 2, is seen as a way to accelerate the process of target finding (2). Bulk infection experiments exhibit kinetics that are consistent with this 2-step picture (68, 81). However, in recent years a number of intriguing observations have been made, which suggested that our view of the target-finding process should be reexamined: A study of infection kinetics in bulk suggested that the presence of LamB receptors on the host cell is required not only for the final injection step, but also for the initial virus-host association (68). In another study, imaging of fluorescently-labeled phages on individual cells indicated that infecting viruses bind preferentially to the bacterial poles rather than cover the cell surface uniformly (31). Last, a time-varying, non-uniform spatial organization of the LamB receptors in live E. coli cells was revealed using fluorescently labeled tails of phage lambda (37).

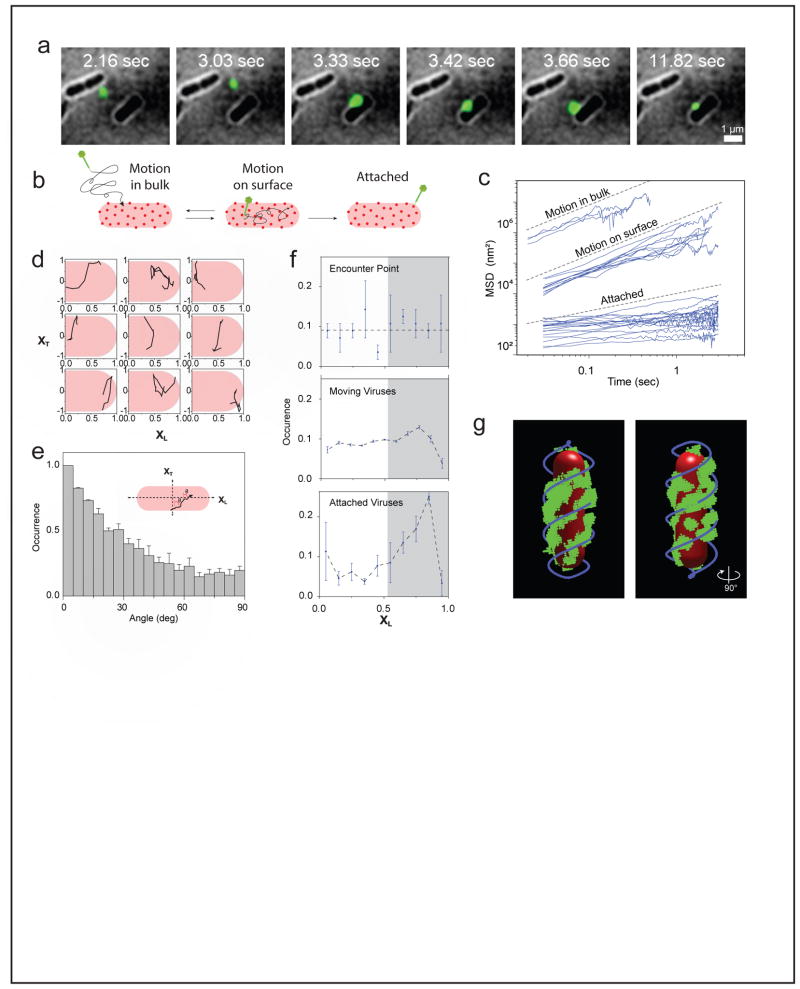
To examine the process by which the phage arrives at it final attachment site, we recently performed single-particle tracking of individual fluorescent phages on live bacterial cells during the early stages of infection, and quantified viral trajectories with nanometer accuracy and ~50 ms resolution (79) (FIGURE 2A). The inspection of hundreds of phage infection events at first suggested that the classical picture was appropriate: phages diffused in the bulk until randomly encountering the surface of a bacterial cell. A phage would then move randomly on the cell surface. The surface motion ended with either an attachment to a specific site on the cell, or—with a similar probability—with the phage falling off the cell and diffusing away (FIGURE 2B). The different modes of motion exhibited markedly different diffusion coefficients (FIGURE 2C).

FIGURE 2. Target finding by the infecting phage.

(A) Time lapse images of a lambda phage (green spot) moving near- and on the surface of an E. coli cell.

(B) Illustration of the different stages observed in the phage target-finding process. The phage first freely diffuses in bulk until it encounters a bacterial cell. The phage then moves on the cell surface, motion that ends in either falling off the cell (back to bulk motion) or attachment to a target receptor and cessation of movement.

(C) The calculated mean squared displacement (MSD) as a function of lag-time for individual viral trajectories during free diffusion in bulk (top cluster), motion on the cell surface (middle cluster) and attachment (bottom cluster). The different motion types form distinct clusters with more than an order of magnitude separation in MSD values.

(D) Typical phage trajectories on the cell surface, plotted in normalized coordinates along (X_L) and across (X_T) the bacterial cell.

(E) The distribution of instantaneous angles relative to the cell short axis, from >100 viral trajectories. The tendency to move along the short axis is evident.

(F) The distribution of phage positions along the cell length during the target-finding process. The initial points of encounter are uniformly distributed (top). Phages moving on the cell surface show an affinity towards the cell pole (middle). The final attachment sites show a pronounced polar localization (bottom). Gray shading highlights the area to which phages converge during the search process.

(G) Spatial organization of LamB receptors on the cell surface. One typical cell is shown. Quantum dots (green) were used to label the receptors, and a 3D reconstruction of the spatial structure was obtained by imaging multiple z-positions. The observed pattern is well described by two helices out of phase (blue). The cell outline is highlighted in red.

Adapted from (79).

We next examined closely the portion of viral motion that occurs on the cell surface prior to attachment. To our surprise, we found that phages exhibited an anisotropic motion pattern, with a tendency to move along the short axis of the cell (FIGURE 2D and E). Their motion was also inhomogeneous. Specifically, the viruses exhibited what we termed “spatial focusing” along the cell (FIGURE 2F): The initial virus-cell points of encounter were uniformly distributed along the cell, but subsequent virus trajectories showed an affinity to reside in specific regions along the cell, one of which is the cellular pole; eventually, bound viruses were “spatially focused”, showing a distinct preference for the cell poles.

These unique features of viral motion led us to ask whether they reflect an interaction of the moving viruses with an ordered pattern present on the surface of the cell; specifically, with the viral receptors, LamB. Fluorescently labeling the LamB receptors on the cell revealed striped patterns of receptors on the surface, reminiscent of rings and helices (FIGURE 2G). The spatial organization of the receptors—position along the cell and angles of receptor “bands”—suggested that the observed viral motion is largely influenced by the receptor network. Next, dual labeling experiments confirmed that phages moving on the surface spend the majority of their time in the vicinity of receptors (79). The presence of receptors was also shown to determine both the diffusion coefficient and the dwell time of phages on the cell surface. A control experiment demonstrated that when phages land on cells lacking LamB, they fall off almost instantaneously rather then spend time moving on the cell surface.

The emerging picture is that the interaction of phage lambda with the cell surface occurs exclusively through the LamB receptor. In other words, the receptor is not only the final “target” for the phage, the place where DNA injection will occur; it is also the element that guides the phage through the search process, on its way to the final attachment site. Though we have no clear molecular picture of this search process, it likely involves a weak, reversible interaction between the lambda tail and LamB (68). To examine the plausibility of this scenario, we have formulated a simple coarse-grained model of phage motion on the cell surface (79). In this model, the cell surface is divided into receptor-rich and receptor-free regions. The presence or absence of receptors in turn affects phage dynamics by determining the diffusion coefficient as well as the probabilities of attachment and of falling off the surface. By numerical simulations, we found that this simple model reproduces much of the observed dynamics (79), thus suggesting that it captures at least some of the essential features of the target-finding process.

Finally, it is interesting to speculate whether what we observed represents a reduction-of-dimensionality scheme, albeit different than the one originally envisioned: The interaction of phages with the network of LamB receptors on the cell surface limits their motion to a fraction of the surface, in effect rendering the motion “quasi 1D”, or possibly of a fractal dimension between 1 and 2. Thus, the reduction in dimensionality in the transition from bulk (3D) to cell surface is larger than previously assumed. The question of whether this scenario optimizes the search process—for example, by minimizing the time it takes the phage to arrive at the cell pole—is a promising avenue for further theoretical investigation.

The post-infection decision: Stochasticity versus hidden variables

Following infection by the bacteriophage, a decision is made between cell death (lysis) and viral dormancy (lysogeny) (72). During the decision process, the regulatory circuit encoded by viral genes (primarily cI, cII and cro) integrates multiple physiological and environmental signals, including the number of infecting viruses and the metabolic state of the cell, in order to reach a decision (55, 70, 92). This post-infection choice serves as a simple paradigm for decision-making between alternative cell-fates during development (26, 74, 88). It also serves as a test case for the role of stochasticity in cellular processes.

Our limited understanding of cellular decision-making is aptly demonstrated by the contradictory views of researchers towards the role of stochasticity in the lambda system. On one hand, the genetic circuitry of lambda serves as a paradigm for the intricacy and precision of gene regulation, as exemplified by the function of lysis/lysogeny switch (26, 72) and the timing of cell lysis by the phage (44, 91). At the same time, one of the first demonstrations of heterogeneity in cell phenotype within a clonal population was Ellis and Delbruck’s study of the wide distribution of phage burst sizes following lysis (32) (We have obtained similar results in the lambda system; data not shown). The cell-to-cell variability in event timing following induction was also recently quantified (4). Almost sixty years after Ellis and Delbruck’s work, Arkin and coworkers used a numerical study of the lambda lysis/lysogeny decision following infection to emphasize the role of chemical stochasticity in genetic circuits (6). Their work led to the emergence of the widely accepted picture of cell variability driven by spontaneous biochemical stochasticity, not only in lambda but in other systems as well (20, 61, 62, 84, 89). More recently, however, the pendulum has shown signs of swinging back to the deterministic direction. St-Pierre and Endy have shown that, at the single-cell level, cell size is correlated with cell-fate following infection. They thus demonstrated how previously-undetected “hidden variables” can explain away some of the observed cell-fate heterogeneity and reduce (though not eliminate) the expected role of biochemical stochasticity in the decision (88).

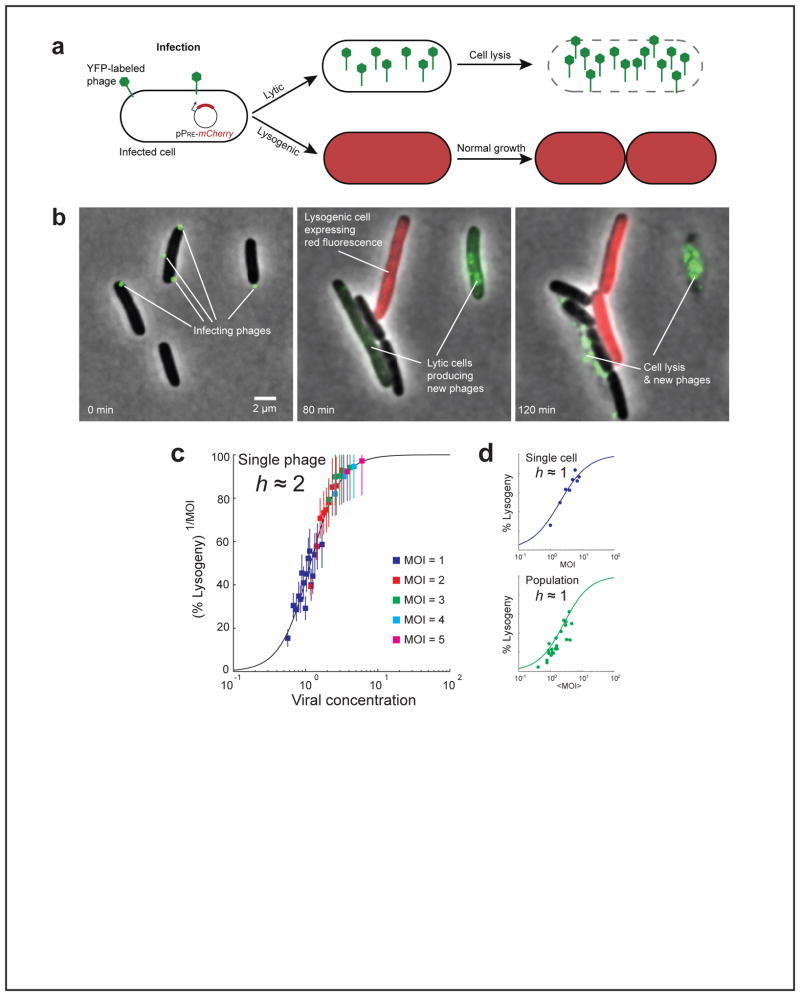
We recently developed an assay for following the post-infection decision under the microscope in real time, at the level of individual phages and cells (FIGURE 3A and B) (96). Examination of thousands of infection events showed that the probability of lysogenization f increases with the number of infecting phages (multiplicity-of-infection, m) and decreases with the cell length l. Both these observations were in agreement with earlier studies (56, 88). A simple theoretical model of the lysis/lysogeny decision circuit predicts that the probability of lysogenization should scale like (m/l), approximating the concentration of viral genomes in the cell, since this concentration determines the dosage of the fate-determining genes (92). However, we found that plotting f(m/l) failed to collapse the data from different multiplicities of infection (96). In trying to understand the failure of this model, we asked: What if each individual phage makes an independent decision? We hypothesized that the decision by each infecting phage depends only on the viral concentration (m/l) as predicted by the simple model. However, as an added feature, we assumed that the individual decisions by all infecting phages have to be considered when deciding the fate of the cell. Based on the known genetic circuitry, we assumed that lysis is the default route (27, 70), and thus only if all phages independently “vote” for lysogeny, that fate will be chosen and the cell will survive. The new model predicted a different scaling for the probability of lysogeny: f(m, l) = [f₁(m/l)]^m, where f₁ is the probability of choosing lysogeny by an individual phage, when m phages infect a cell of length l. The exponent m arises from the requirement of unanimous vote by all phages for producing lysogeny. As seen in FIGURE 3C, this scaling successfully collapsed the data from all experiments. Additional experiments using fluorescent reporters for lysogenic and lytic genes supported the hypothesis of individual decisions by infecting phages and the requirement of unanimous vote for obtaining lysogeny (96).

FIGURE 3. Cell-fate decision following infection.

(A) A schematic description of our cell-fate assay. Multiple fluorescently-labeled phages (green) simultaneously infect individual cells of E. coli. The post-infection fate can be detected in each infected cell. Choice of the lytic pathway is indicated by the intracellular production of new fluorescent phages (green), followed by cell lysis. Choice of the lysogenic pathway is indicated by the production of red fluorescence from the P_RE promoter, followed by resumed growth and cell division. The three stages of the process correspond to the three images seen in panel (B) below.

(B) Frames from a time-lapse movie depicting infection events. At time t = 0 (left), two cells are seen each infected by a single phage (green spots), and one cell is infected by three phages. At t = 80 min (middle), the two cells infected by single phages have each gone into the lytic pathway, as indicated by the intracellular production of new phages (green). The cell infected by three phages has gone into the lysogenic pathway, as indicated by the production of red fluorescence from P_RE (red). At t = 2 hr (right), the lytic pathway has resulted in cell lysis, whereas the lysogenic cell has divided.

(C) Scaled probability of lysogeny [f(m, l)]^1/m as a function of viral concentration (m/l). Data from different MOIs (filled squares, different colors) collapse into a single curve, representing the probability of lysogeny for each individual infecting phage (f₁), in a cell of length l infected by a total of m phages. f₁ can be fitted to a Hill function, f₁(m/l) = (m/l)^h/(K^h+(m/l)^h), with h ≈ 2.

(D) The probability of lysogeny as a function of the relevant input parameter, at the single-cell (top, blue; input is MOI of the individual cell) and population-average (bottom, green; input is the average MOI over all cells) levels. Circles: experimental data. Solid lines: theoretical prediction, fitted to a Hill function. The decision becomes more “noisy” (lower Hill coefficient, h ≈ 1) when moving from the single-phage (panel C) to the single cell level. Moving from the single cell to the population average does not decrease the Hill coefficient further.

Reprinted from (96), with permission from Elsevier.

Having quantified the “decision curve” of the individual phage, f₁(m/l), we next reversed the process and reconstructed the observed decision-making phenotype at the level of the whole cell and the whole population (FIGURE 3D). This was done by integrating over the different degrees of freedom that remained hidden in the lower-resolution (“coarse-grained”) experiments. Thus, when going from individual phages to the whole cell, we integrated over the spatial positions of phage infections and their effect on infection efficiency, as well as the length distribution of cells in the population, obtaining the predicted single-cell response curve f(m). We then integrated further over the random phage-bacterium collision probabilities (68) to obtain the predicted population-averaged response, f(M). When comparing the decision curves at the different resolution levels (FIGURE 3C and D), we found that most of the apparent noise in the decision arises at the transition from the single-phage to the single-cell level, when integrating over individual phage decisions and the distribution of cell-ages in the population. Moving further from individual cells to the population average did not add significantly to the observed imprecision of the decision. In other words, measurements at the single-cell level mask as much of the critical degrees of freedom as measurements made in bulk—counter to the widely-accepted view (6, 84).

The concept of decision-making at the sub-cellular level may at first appear counter intuitive: presumably, all of the relevant regulatory proteins produced from the individual viral genomes achieve perfect mixing in the bacterial cytoplasm within seconds of their production, due to diffusion (34). How viral individuality is maintained inside the cell is an open question. The answer may lie in the discreteness of viral genomes and of the gene-expression events underlying the decision-making process (19, 41, 55, 95). Another possibility is that sub-cellular decision-making is enabled by spatial separation of key players in the process (60). It is intriguing to contemplate the possibility of sub-cellular decision making by individual genomes at the other end of the complexity spectrum, in higher eukaryotic systems. In those systems, multiple copies of a gene-circuit often exist, and copy-number variations play a critical role in health and disease (25). Sub-cellular decision making may thus have a profound effect if present.

Maintenance of lysogeny: A simple model for cell-state stability

The ability of cells to maintain an inheritable memory of their gene-expression state is key to cellular differentiation (69). A differentiated cellular state may be maintained for a long time, while at the same time allowing efficient state-switching (“reprogramming”) in response to the proper stimulus (45). However, even in the absence of external perturbation, cell-state may not be “infinitely stable” (irreversible)(57). Stochastic fluctuations may switch a cell from one state to another. A natural question then arises: How stable is a cell’s gene-expression state, in the absence of an external perturbation? In other words, how long will a differentiated cell stay in the same state before spontaneously switching to an alternative one? What features of the underlying gene-regulatory network determine this stability?

The lambda lysogen serves as one of the simplest examples for a stable cellular state (70, 73, 74). Lysogenic stability is maintained by the activity of the lambda repressor (CI), which acts as a transcription factor to repress all lytic functions from the prophage in the bacterial cell, as well as to regulate its own production (FIGURE 4A) (73). As mentioned above, auto-regulation by the fate-determining protein is also observed in higher systems displaying long-term cellular memory (28, 45, 57). The resulting lysogenic state is extremely stable: spontaneous switching events occur less than once per 10⁸cell generations in the absence of cellular RecA activity (59).

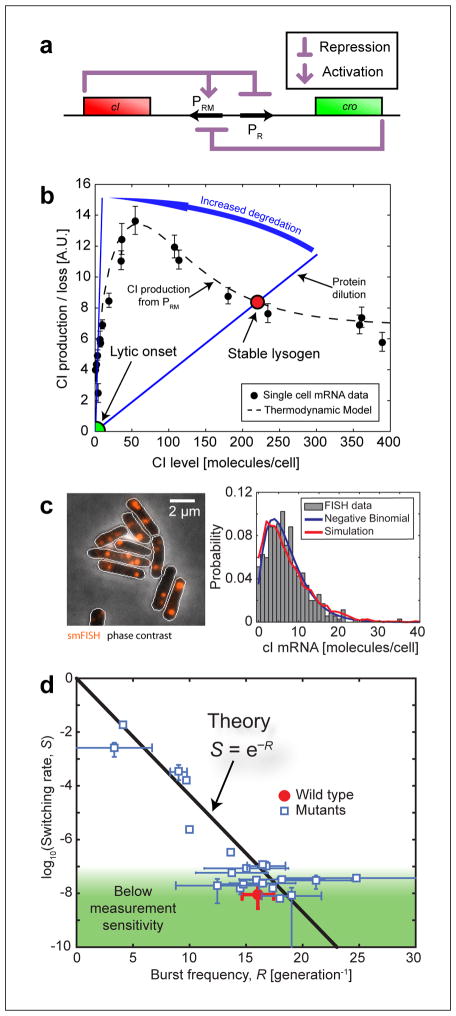
FIGURE 4. Maintenance of the lysogenic state.

(A) The lysis/lysogeny switch is governed (to a first approximation) by a mutual repression loop between two genes: the lambda repressor cI and the “anti-repressor” cro. cI also regulates its own production. Adapted from (18), with permission from Elsevier.

(B) According to the standard theoretical picture, the stable lysogenic state is defined by the balance between CI production (from the P_RM promoter) and elimination. P_RM activity was measured in individual cells (solid black circles), and can also be reproduced using a thermodynamic model for promoter occupancy (dashed black line)(97). In wild type lysogens, CI elimination is dominated by cell growth and division (solid blue line). During forced induction, CI degradation is increased (blue arrow), shifting the steady state from [CI]≫ 0 (lysogeny) to [CI] ≈ 0 (lytic onset).

(C) Left: cI mRNA in lysogens, labeled using single-molecule fluorescence in situ hybridization (smFISH). Fluorescent foci (red) indicate the presence of cI mRNA molecules. The photon count from these foci was used to estimate the number of mRNA molecules in each cell. The resulting cI mRNA copy-number distribution is shown on the right. The experimental histogram (bars) was fitted to a negative binomial distribution (blue curve) whose parameters were used to calculate the transcriptional burst frequency and burst size. The results of a stochastic simulation of the gene circuit (red curve) are also shown for comparison. Adapted from (97).

(D) The relation between lysogen stability and P_RM activity. The measured switching rate (S) is plotted as a function of the number of activity bursts from P_RM in one cell generation (R), for the wild type lysogen (red circle), and mutants in cI and P_RM (blue squares). The points fall close to the theoretical prediction given by S = exp (−R) (solid blackline). Adapted from (97).

To understand what determines cell-state stability, one first needs to define the “steady state” of the system—the gene-expression level, averaged over time and over cells in the population. The lambda system has been well characterized in terms of the regulatory circuitry that creates the stable lysogenic state. The regulation of the two key promoters, P_RM (producing CI) and P_R (which produces the “anti-repressor” Cro that initiates the lytic cascade at low repressor levels) has been mapped as a function of CI and Cro concentrations (30, 73, 97)(FIGURE 4B). A thermodynamic model using grand-canonical ensemble has been used to describe the occupancy of the six operator sites controlling promoter activities (O_R1-3, O_L1-3) and the resulting protein levels (5, 29, 83).

In the resulting theoretical picture, the lysogenic state is seen as the stable attractor of a dynamical system, or the point of minimum potential. Taking this analogy further, the event of spontaneous induction, when prophage escapes lysogenic repression and initiates lytic development, is (somewhat loosely) mapped to the thermally-driven escape of a particle from a potential well—a so called “Kramers problem” (11, 17, 46). A significant degree of complexity is added by the properties of the effective “temperature”, given in this case by the stochasticity of gene expression (17). Thus, characterization of the steady state has to be accompanied by quantification of the stochastic dynamics of gene activity, which shift individual cells away from the “average state”, and may switch a cell from lysogeny to lysis. It is now known that both transcription (41) and translation (19, 95) exhibit intermittent, non-Poissonian kinetics. Such “bursty” gene activity has been previously suggested to affect cell-state switching (24, 42, 53, 65).

To try and predict the stability of the lysogenic state, we recently formulated, and then tested experimentally, a very simple model for the maintenance of lysogeny (97). We assumed that CI molecules are produced in discrete bursts, and that the occurrence of these bursty activity events obeys Poissonian statistics (35, 41). We denote that average frequency of activity bursts as r. For a switch from lysogeny to lysis to occur, a cell needs to lose most of its repressor molecules. This will happen if no P_RM activity occurs for one generation time τ, since this is the typical protein lifetime (due to cell growth and dilution). Under the assumption that transcription-burst occurrence follows Poisson statistics, the probability of a cell not producing cI mRNA (and therefore repressor proteins) for duration τ is P₀ = exp(−rτ). Thus, the probability of switching from lysogeny to lysis during one cell generation is approximately equal to the exponent of the number of activity bursts from P_RM during the same time (a number we denote as R= rτ).

Note that the model above is extremely simple. We have neglected some of the features which are considered essential in the maintenance of lysogeny: First, the fact that CI regulates its own production—see the P_RM([CI]) curve in FIGURE 4B, whose properties supposedly determine the stable lysogenic state at [CI] > 0. In our case, we approximated P_RM as a constitutive promoter, whose activity does not vary as CI levels change. Second, the attractor at [CI] ≈ 0 (the lytic onset) was described simply using an “absorbing wall” at [CI] = 0, instead of explicitly modeling the gradual de-repression of the P_R promoter (producing Cro) as CI numbers decrease (80).

Our model is thus very simple. The important question is, of course, is it too simple? To test the prediction of lysogen stability, we had to first measure the frequency of transcription bursts from P_RM (97). We used single-molecule fluorescence in situ hybridization (smFISH)(77) to quantify cI mRNA copy-number statistics in lysogenic cells (FIGURE 4C). The measured histograms followed a negative binomial distribution, consistent with the notion of transcription bursts following Poissonian statistics (75, 82). The parameters of this distribution allowed us to estimate the burst frequency r. We then measured the spontaneous switching rate from the lysogenic state, S (97). This was done by measuring the rate of appearance of free phages in a culture of exponentially growing lysogenic cells(59).

We thus had the ability to relate promoter activity and lysogen stability. Such a measurement, however, only gave us a single data point. To create a “stability curve” we needed to tune system parameters—promoter activity and the resulting lysogen stability. This was done by using a series of phage mutants: the temperature-sensitive allele cI857, in which the efficiency of the repressor decreases as temperature is increased (47, 48, 51); as well as 18 additional mutants modified in either the P_RM or cI sequence (66, 97). When examining the relation between lysogen stability S and the P_RM burst frequency R in the set of lysogens, we found that the data was consistent with the theoretical prediction, S ≈ exp(−R)(FIGURE 4 D).

At first glance, it may seem surprising that such an over-simplified model was able to capture the behavior of a real-life, naturally evolved system where the stability is believed to be an important phenotype (59). However, in line with this observation that many system parameters are “coarse-grained” to produce the stability phenotype, there is a body of work from the last decade, mainly from the Little lab (7–9, 59, 66, 67), pointing to the robust performance of the lambda lysogeny switch even when system parameters are genetically perturbed. Although only semi-quantitative in nature, these studies are consistent with the idea that an intricate genetic circuitry with fine-tuned parameters is not needed for obtaining a stable lysogenic state.

It is tempting to contemplate the possible relevance of our results concerning the stability of cellular state to higher systems, where the ability to maintain an inheritable memory of gene-expression state is key to cellular differentiation (45, 69). Admittedly, the maintenance of bacterial lysogeny does not exhibit the complexity of cell differentiation in higher eukaryotic systems, where a range of additional mechanisms play a role in cellular memory (18). Nevertheless, the fundamental feature of auto-regulation by the fate-determining protein appears central there too (28, 45, 57). Thus, investigating the stability of differentiated states in higher, and in particular multicellular, systems, is a promising direction for experimental investigation.

Forced induction: Switching dynamics

In contrast to the case of spontaneous induction discussed above, switching of the cellular state from lysogeny to lysis can also be achieved in a directed manner. Experimentally, forced induction is commonly achieved by one of two ways: (1) Using DNA-damaging agents, for example irradiating the cells with Ultra-violet (UV) light. When cellular DNA is damaged, the protease activity of RecA is turned on as part of the cell’s SOS response (58). This leads to degradation of CI proteins. (2) Using a temperature-sensitive allele of the lambda repressor (cI857) which becomes inactivated at high temperature (47, 48, 51). In both cases, the dynamical-systems picture is that the increased elimination rate of CI leads to a loss of the [CI]> 0 (lysogenic) steady state (see FIGURE 4B above).

Traditional biochemical assays demonstrated the expected decrease in cellular CI levels preceding cell lysis (12). However, population-averaged characterization of induction obscures the histories of individual cells—for example, the presence of temporal oscillations in the SOS response (36). The quantitative features of induction kinetics remain largely unexplored. One example of such feature is depicted in FIGURE 5A ((23); also see (54)). A culture of lysogens was irradiated with UV, and the fraction of cells induced (switched to lysis) was measured as a function of UV amount. It was found that the UV dose-response can be closely approximated by a Hill function y(x) = x^h/(k^h + x^h) with a Hill coefficient of h = 4. Moreover, the same coefficient holds for phage strains with mutated cI genes (which otherwise exhibit a very different phenotype in terms of their spontaneous induction levels and the amount of UV required to induce the cells) as well as for different numbers of phage genomes in the lysogen. Thus, the power of 4 appears to be a universal feature of the switch.

FIGURE 5. Cell-state switching.

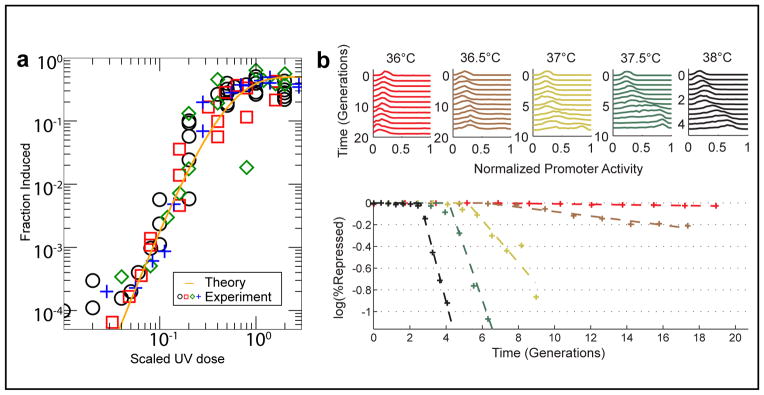
(A) The fraction of lysogens in a population that were induced, as a function of the amount of UV radiation. Experimental data (markers) is from wild type as well as different lambda mutants. Solid line is a fit to the theoretical expression using reliability theory (23), yielding a power law with an exponent of 4. Reprinted with permission from (23). Copyright (2009) by the American Physical Society.

(B) Single-cell measurements. The activity of P_RM and P_R was measured in individual cells using a two-color fluorescence reporter. Temperature was used to tune the state of the lysis/lysogeny circuit, and the population statistics of promoter activities was measured at different times after the temperature shift (above). When examining the fraction of switched cells as a function of time (below), one observes a delay period, in which the population remains fully lysogenic, followed by a temperature-dependent rate of switching to the Cro-dominated state. Adapted from (13).

A possible way to think about this result is to consider the lysogeny maintenance circuit as consisting of 4 redundant elements—the CI dimers bound at 4 operator sites (O_R1, O_R2, O_L1, O_L2)—and to assume that only the failure of all elements will lead to lysis. Using the formalism of reliability theory, one can write down the expected fraction of “failure” events as a function of the UV dose and arrive at the observed power law (FIGURE 5A). For more details see (23).

To go beyond this simple phenomenology and elucidate the kinetics of cell-state switching, the activity of P_RM has to be followed in individual cells during the induction process. If the standard picture is correct, then as the level of CI monotonically diminishes (a process that takes ~30–45 minutes in the case of UV induction (12)), P_RM is expected to react by “scanning” through a large range of its response curve in an attempt to counter the decreasing CI levels (FIGURE 4B above). In most cases this attempt will fail. Occasionally, however, CI production will succeed in overcoming elimination, leading to the reestablishment of lysogeny (“abortive induction” (78)). In any case, forced induction thus offers a possible window into the shape of P_RM autoregulatory curve which lies at the heart of the lysogeny maintenance system.

To examine the process of forced induction at single-cell resolution, we recently characterized the induction kinetics using a 2-color fluorescent reporter, which allows us to simultaneously examine the activity of both P_RM (maintaining lysogeny) and P_R (initiating lysis) in individual cells (13). Promoter activities were followed over time, under a range of “induction strengths” (again using the temperature-sensitive allele cI857) (FIGURE 5B). Our results indicate that the fraction of induced cells over time exhibits a biphasic behavior: there is first a delay (of up to a few generations), in which all cells remain in the lysogenic state. This is followed a constant flux of cells into the de-repressed (Cro dominated) state. During the delay period there are already changes in gene activity; however, these changes are still insufficient to tilt the individual cells from lysogeny to lysis. It will be interesting to examine whether this behavior can be explained using a simple stochastic model of the underlying gene circuitry.

SUMMARY

Despite heroic efforts to illuminate cellular decision-making in higher systems (see e.g. (14, 43, 76, 87)), I still believe that important insights can be gained by attacking the same processes in their simplest instantiation. In this review I used the system comprised of E. coli and bacteriophage lambda to make that case. We are obviously still very far from achieving the desired quantitative narrative for the viral life cycle. However, as described above, the quantitative experimental study of the system has already yielded new insights regarding the way randomly moving viruses find their target on the cell surface; the way cell-fate decisions are made at a level finer than that of the whole cell; the way bursty gene activity affects the stability of cellular state; and more.

At the same time, before applying the principles learned here to higher organisms, we must beware: As physicists studying living systems, we are always in jeopardy of over-assuming universality. Against that ever present temptation, one has to keep in mind the distinction between Occam’s razor and Occam’s rug¹: The former, of course, is the guiding rule for physicists, who will always choose the simplest, most universal explanation for an observed phenomenon. The principle of Occam’s rug, on the other hand, states the following: When studying a living system, a simple elegant narrative often implies that too much of the data was swept under the rug. In other words, always be wary of claims of simplicity and universality in biology.

Summary points.

• The life cycle of bacteriophage lambda serves as a paradigm for decision-making in living systems.

• Quantitative, high-resolution experimental investigation of the lambda system has already yielded new insights, for example:

• Receptors on the cell surface guide the infecting phage through its target-finding process.

• Following infection, the decision between alternative fates is first made at the level of individual phages.

• Stability of the lysogenic (dormant) cellular state is determined by the frequency of activity bursts from the fate-determining gene.

Acronyms

MOI

multiplicity of infection

Glossary

Bacteriophage(short: phage)

A virus that infects bacterial cells

Lysis

The death of a bacterial cell following phage infection

Lysogeny

The condition of a bacterial cell following phage infection, in which the phage does not kill the cell but instead lies dormant. The dormant intracellular phage is called a prophage

Induction

A switch from lysogeny to lysis; can occur spontaneously or as a result of an external signal

LamB

A receptor protein on the surface of E. coli, which triggers the injection of phage lambda DNA into the cell

MOI (multiplicity of infection)

The number of phages simultaneously infecting a single bacterial cell

Differentiation

The process by which a cell acquires a unique gene-expression state and maintains it for a long time