Quantifying Immune Response to Influenza Virus Infection via Multivariate Nonlinear ODE Models with Partially Observed State Variables and Time-Varying Parameters

Summary

Influenza A virus (IAV) infection continues to be a global health threat, as evidenced by the outbreak of the novel A/California/7/2009 IAV strain. Previous flu vaccines have proven less effective than hoped for emerging IAV strains, indicating a more thorough understanding of immune responses to primary infection is needed. One issue is the difficulty in directly measuring many key parameters and variables of the immune response. To address these issues, we considered a comprehensive workflow for statistical inference for ordinary differential question (ODE) models with partially observed variables and time-varying parameters, including identifiability analysis, two-stage and NLS estimation, and model selection etc‥ In particular, we proposed a novel one-step method to verify parameter identifiability and formulate estimating equations simultaneously. Thus, the pseudo-LS method can now deal with general ODE models with partially observed state variables for the first time. Using this workflow, we verified the relative significance of various immune factors to virus control, including target epithelial cells, cytotoxic T-lymphocyte (CD8+) cells and IAV specific antibodies (IgG and IgM). Factors other than cytotoxic T-lymphocyte (CTL) killing contributed the most to the loss of infected epithelial cells, though the effects of CTL are still significant. IgM antibody was found to be the major contributor to neutralization of free infectious viral particles. Also, the maximum viral load, which correlates well with mortality, was found to depend more on viral replication rates than infectivity. In contrast to current hypotheses, the results obtained via our methods suggest that IgM antibody and viral replication rates may be worth of further explorations in vaccine development.

1. Introduction

New influenza virus strains arise annually, through antigenic drift or antigenic shift, and large-scale pandemics result in significant morbidity and mortality. In addition, the unpredictable emergence of novel strains, such as the recent A/California/7/2009 H1N1 pandemic influenza, highlights the need to better understand the kinetics of the immune response to influenza infection. Unfortunately, experimental methods for understanding human responses to influenza vaccine or infection are hindered by our inability to sample immune cells from major compartments where the immune response is actually occurring. We can only sample peripheral blood mononuclear cells and their subsets. A second issue, even for in vivo murine models of influenza virus infection and response, is that many of the parameters we would like to understand (infection rates, viral clearance rates due to antibody, CD8 T cell killing rates for infected respiratory epithelial cells, etc.) are not directly measureable. Such a detailed quantitative understanding of the viral and cellular immune parameters in an effective influenza infection or vaccine immune response would be highly desirable for a better virus control.

This work was motivated by experimental measurements of the anti-influenza immune response. Both animal models and human studies which make use of peripheral blood mononuclear cell (PBMC) sampling have long been used to study the immune response to influenza infection (Baer et al., 2010; Falsey et al., 2009; Halliley et al., 2010). Animal models have some advantages over human studies, including high frequency sampling of multiple tissues (Miao et al., 2010) and the ability to block or deplete individual immune response elements such as the CD8 effector and B cell mediated antibody responses (Teijaro et al., 2010; Zeng et al., 2009). Studies at the level of cellular kinetics, including division, differentiation, migration, and infection, are critical for understanding the organismal response to IAV infection (Baccam et al., 2006; Lee et al., 2009; Miao et al., 2010). However, even for the animal models, the number of measurable variables in cell kinetics studies is limited by the cost and the availability of assays. Also, it is a common scenario in experimental studies that some variables of great interest cannot be measured directly (called latent variables). Fortunately, mathematical models coupled with novel statistical approaches could help to overcome some of these difficulties.

Several unresolved scientific questions regarding the immune response to influenza infection are very amenable to an approach of ordinary differential equation modeling coupled with parameter estimation from detailed time-course experimental data, and motivated this article. One such question is the relative contributions of the innate and adaptive immune responses to a primary influenza infection (Miao et al., 2010), and a second important question which is difficult to solve by standard experimental and modeling approaches is the relative contribution of the innate (IgM) and adaptive (IgG) antibody response to the clearance of IAV.

Mathematical models, and specifically ordinary differential equation (ODE) models, have long been used to investigate viral dynamics and immune responses (Nowak and May, 2000), including influenza virus related problems (Baccam et al., 2006; Beauchemin, Samuel and Tuszynski, 2005; Bocharov and Romanyukha, 1994; Hancioglu, Swigon and Clermont, 2007). In this study, we focus on modeling of the immune responses in the lung because lung is the primary site of influenza infection and clearing IAV from the lung compartment is necessary for the survival of the infected host. We first describe a model of primary IAV infection in the lung compartment that is a multivariate nonlinear ODE model with partially observed state variables. To perform reliable statistical inference for such a model, we used a workflow incorporating multiple techniques, including identifiability analysis, parameter estimation and model selection criteria (Liang, Miao and Wu, 2010; Miao et al., 2009; Wu et al., 2008; Xue, Miao and Wu, 2010). Specifically, several methods for parameter estimation in ODE models have been developed previously, including the nonlinear least squares method (Bard, 1974; Li, Osborne and Pravan, 2005; Xue et al., 2010), the smoothing-based techniques (Brunel, 2008; Chen and Wu, 2008a; Liang and Wu, 2008; Varah, 1982; Wu, Xue and Kumar, 2011), the principal differential analysis (PDA) and the generalized profiling procedure (Ramsay et al., 2007) and the Bayesian approaches (Donnet and Samson, 2007; Huang, Liu and Wu, 2006; Putter et al., 2002). Among these methods, the smoothing-based approaches have the advantage of being conceptually simple, computationally efficient, and easy to implement. The multistage smoothing-based approach coupled with the nonlinear least squares method has been recently applied to a nonlinear HIV dynamic model for parameter estimation (Liang et al., 2010). However, the existing smoothing-based approaches require that all of the state variables are directly measured, which is a condition difficult to satisfy in practice, and especially with studies of human IAV infection. Here we propose a novel solution to this problem for multivariate nonlinear ODE models, achieved by combining identifiability analysis techniques with smoothing-based approaches. To our knowledge, this is the first use of the smoothing-based pseudo-LS method to handle ODE models with partially observed state variables.

The remainder of the paper is organized as follows. In Section 2, the ODE models with both constant and time-varying parameters are presented to describe the immune response to IAV infection in the lung. In Section 3 we perform the identifiability analysis and propose two estimation methods: one approach is the generalized estimating equation method and the other is the nonlinear least squares estimation approach. We also derive the theoretical properties of the estimation methods and present the estimation results in this section. In Section 4, we explore alternative models using a model selection approach, and based on the refined model structure, we investigate the characteristics of hypothesized new influenza strains and explore potential vaccine targets via model predictions. Finally, Section 5 discusses the insights gained from the statistical and modeling approaches concerning the innate and adaptive immune responses to IAV infection, as well as the broader application of the statistical methods to other biologic systems. The limitations of the proposed methods are also discussed.

2. Mathematical Models for Influenza Infection

The immune response to IAV infection in the lung compartment can be described by the following differential equation models (Miao et al., 2010):

$$\{\begin{array}{l}\frac{d}{dt}{E}_p={\rho }_E{E}_p-{\beta }_{\alpha }{E}_{P}V\\ \frac{d}{dt}{E}_p^{*}={\beta }_{\alpha }{E}_{P}V-k_E{E}_P^{*}{T}_E(t)-{\delta }_{E^{*}}{E}_p^{*}\\ \frac{d}{dt}V={\pi }_{\alpha }{E}_P^{*}-k_{VG}V{A}_G(t)-k_{VM}V{A}_M(t)-c_{V}V\end{array},$$ (1)

where E_p denotes the number of target epithelial cells per lung that are vulnerable to IAV infection, $E_p^{*}$ the number of infected epithelial cells per lung, V the viral titer (EID₅₀/ml), T_E the number of effector CD8+ T cells per lung, A_G the concentration of IAV-specific serum IgG (pg/ml), A_M the concentration of IAV-specific serum IgM (pg/ml), and (ρ_E, β_α, k_E, δ_E*, π_α, k_VG, k_VM, c_V) are model parameters. More specifically, ρ_E is the net growth rate of infectable target epithelial cells, β_α the infection rate of target epithelial cells per unit of infectious virus titer, k_E the killing rate of infected epithelial cells due to effector CD8+ T cells, δ_E* the death rate of infected epithelial cells due to factors other than CTL killing (e.g., innate immunity or apoptosis), π_α the virus production rate per infected cell, k_VG the virus neutralization rate due to IgG only, k_VM the virus neutralization rate due to IgM only, and c_V the virus clearance rate due to kinetics other than antibodies IgG and IgM. In this model, we assume that epithelial cells comprise the majority of the target cells in the lung. Also, the contributions of innate immune cytokines and NK cell lysis are included in parameters c_V and δ_E*, and thus are not explicitly distinguished in this study. In addition, we make the assumption that the antibody levels are proportional to the actual virus-control mechanisms.

Finally, notice that the overall virus clearance rate consists of the three terms in the last equation of Model (1): c_V + k_VGA_G (t) + k_VM A_M (t), which is time varying. If we introduce a time-varying parameter η(t) =c_V + k_VGA_G (t) + k_VMA_M (t), the last equation in Model (1) becomes

$$\frac{d}{dt}V={\pi }_{\alpha }{E}_P^{*}-\eta (t)V.$$ (2)

This model will be used to determine the nonparametric form of virus clearance rate and then to verify the relative contributions of IgG and IgM to the infectious virus neutralization.

3. Parameter Estimation Procedure

Here we describe the parameter estimation workflow for ordinary differential equation models with partially-observed variables and time-varying parameters. We then present the estimation results of the example models and data.

3.1. Structural Identifiability Analysis

It is necessary to study parameter identifiability of ODE models before developing or applying statistical methods to estimate model parameters from experimental data; otherwise, including unidentifiable unknown parameters in a model is likely to result in biased estimates and thus misleading conclusions. In the previous section, we have proposed the immune response model (1), in which the CD8+ T cell counts in lung and the serum IgG and IgM antibody concentrations were treated as known covariates. However, among the three state variables E_p, $E_p^{*}$ and V, only the viral titer V could be measured in our experiments. For this reason, it is necessary to perform identifiability analysis for the proposed ODE models with only V measured.

A variety of structural identifiability analysis techniques have been proposed (Miao et al., 2011). Particularly, the differential algebra (Ljung and Glad, 1994; Ritt, 1950) and the implicit function theorem approach (Xia and Moog, 2003) have been developed for general nonlinear ODE models to eliminate latent variables from which we can obtain the expressions consisting of only given system inputs, measured system outputs and unknown parameters. More interestingly, these expressions can also be used to formulate the estimating equations for the smoothing-based approaches in the next section.

In this study, we use the implicit function theorem method (Wu et al., 2008; Xia and Moog, 2003) to evaluate the identifiability. The approach is to eliminate all latent variables from an ODE model and construct a function of measured variables and unknown parameters that is equal to zero. Starting with Model (1) and recalling that only the viral titer (V) is experimentally measured, we can eliminate E_p and $E_P^{*}$ from the model to obtain

$$V‴=(V″+\mathbb{Z})({\rho }_E-{\beta }_{\alpha }V+V\prime V^{-1})-\mathbb{Z}\prime ,$$ (3)

where

$$\mathbb{Z}=(k_E{T}_E+{\delta }_{E^{*}})(V\prime +c_{V}V+k_{VG}V{A}_G+k_{VM}V{A}_M)+(c_V+k_{VG}{A}_G+k_{VM}{A}_M)V\prime +(k_{VG}{A}_G^{\prime }+k_{VM}{A}_M^{\prime })V,$$

V′, V″ and V‴ are the first-, second-, and third-order derivatives of V(t) with respect to time t, and ℤ′, $A_G^{\prime }\text{and}{A}_M^{\prime }$ are the first-order derivatives of ℤ, A_G and A_M with respect to time t, respectively. Note that none of the initial conditions such as E(0) shows up in Eq. (3) so their identifiability cannot be analyzed using the structural identifiability analysis techniques alone, but later we will find out that E(0) is not distinguishable from π_α in Section 3.3. More importantly, from Eq. (3), it is immediately seen that parameter π_α vanishes and is therefore unidentifiable. To verify the identifiability of the remaining parameters θ = (ρ_E, β_α, k_E, δ_E*, c_V, k_VG, k_VM), we define the identifiability function based on Eq. (3),

$$𝔽=V‴-(V″+\mathbb{Z})({\rho }_E-{\beta }_{\alpha }V+V\prime V^{-1})+\mathbb{Z}\prime \equiv 0.$$ (4)

According to the implicit function theorem (Wu et al., 2008; Xia and Moog, 2003), the identifiability problem reduces to evaluating whether the following identifiability matrix 𝕄 is of full rank,

$${𝕄}_{kl}=\frac{\partial 𝔽(t_k)}{\partial {\theta }_l},k,l=1,2,\dots ,p,$$ (5)

where p = 7 is the number of unknown parameters, t_k are time points selected within the time range of interest (e.g., days 0~14 after IAV infection) such that t_k ≠ t_l and V(t_k) ≠ V(t_l) if k ≠ l. Substituting the nominal parameter values in literatures (Baccam et al., 2006) into 𝕄, it can be easily verified that 𝕄 is of full rank and thus all parameters in θ are locally identifiable in theory. In addition, since the unidentifiable parameter π_α does not appear in the identification function (4), it should not affect the estimates of other parameters even if we assign an arbitrary positive value to π_α (Miao et al., 2010). However, this does not suggest π_α is not important; actually, models (1) and (2) will not fit the data without the π_α term as the virus production by infected epithelial cells is biologically important.

3.2. Estimation Method

In this section, we describe the estimating equation approach for parameter estimation in nonlinear ODE models with latent variables in detail, and the same procedure can be applied to time-varying parameter estimation after one approximates the time-varying parameters using, e.g., splines (Chen and Wu, 2008b; Xue et al., 2010).

The basic idea is to directly employ the identifiability function as the estimating equation, which can be obtained from the theoretical identifiability analysis described in the previous section. To illustrate this approach, we formulate the estimating equation based on Eq. (4). First, we estimate the functions V(t) (t ∈ [a,b]) and its derivatives, V′(t), V″(t) and V‴(t), using the penalized spline method (Claeskens, Krivobokova and Opsomer, 2009; Li and Ruppert, 2008; Ruppert, Wand and Carroll, 2003). Let {Y(t_i):i = 1,…,n} denote the observed data at time points t₁,…,t_n, then we use the measurement model Y(t_i) = V(t_i) + ε_i for i = 1,…,n, where {ε_i : i = 1,…,n} are independent measurement errors with a mean zero and a finite variance σ². Now we approximate V(t) by $V(t)\approx \sum _{j=-k}^d{\xi }_j{b}_{j,k+1}(t)$, where ξ = {ξ_−k,…,ξ_d}^T is the unknown coefficient vector to be estimated from the data, and B_k+1(t) = {b_−k,k+1(t),…,b_d,k+1(t)}^T is the B-spline basis function vector of degree k (or order k + 1) at the sequence of knots a = τ_−k = τ_−k+1 = … = τ₋₁ = τ₀ < τ₁ < … < τ_d < τ_d+1 = τ_d+2 = … τ_d+k+1 = b on [a,b]. Define Z = {B_k+1(t₁),…B_k+1(t_n)}^T, Y = {Y(t₁),…,Y(t_n)}^T and let $D=\underset{a}{\overset{b}{\int }}{B}_{k+1}^{"}(t){[B_{k+1}^{"}(t)]}^{T}dt$. The penalized spline estimator V̂ of V can be obtained by minimizing

$${(Y-Z\xi )}^T(Y-Z\xi )+\lambda {\xi }^{T}D\xi ,$$ (6)

where the smoothing parameter λ can be determined using the generalized cross validation (GCV) method (Craven and Wahba, 1979). Then V̂ can be obtained in the following form

$$\widehat{V}(t)=B_{k+1}^T(t){(Z^{T}Z+\lambda D)}^{-1}{Z}^{T}Y.$$

The estimates of the first three order derivatives of V can also be obtained as

$$\frac{{\partial }^i}{\partial t^i}\widehat{V}(t)={[B_{k+1}^{(i)}(t)]}^T{(Z^{T}Z+\lambda D)}^{-1}{Z}^{T}Y,\text{for}i=1,2,3.$$

Finally, the estimating equation can be obtained by simply substituting V̂, V̂′, V̂″, and V̂‴ into Eq. (4). That is,

$$\widehat{𝔽}(t)=\widehat{V}‴-[\widehat{V}″+\mathbb{Z}(\widehat{V},\widehat{V}\prime )]({\rho }_E-{\beta }_{\alpha }\widehat{V}+\widehat{V}\prime {\widehat{V}}^{-1})+\mathbb{Z}\prime (\widehat{V},\widehat{V}\prime ).$$ (7)

Estimators of (ρ_E, β_α, k_E, δ_E*, c_V, k_VG, k_VM) can be obtained by minimizing $\sum _{i=1}^{n}w(t_i){[\widehat{𝔽}(t_i)]}^2$, where w(t) is a weight function. Similar to Wu et al. (2011), this weight function is required to achieve the desirable asymptotic properties for the estimator under some technical assumptions (see Supplementary Materials).

Note that the estimating equation approach described above extends the two-stage pseudo-LS estimation method (Brunel, 2008; Chen and Wu, 2008a; Liang and Wu, 2008; Varah, 1982) to be capable of dealing with general nonlinear ODE models with partially observed state variables. The asymptotic theories of the two-stage pseudo-LS estimator are also extended from first-order ODE models to higher-order ODE models in this study (see Supplementary Materials). However, it should be mentioned that the proposed estimating equation method is also a smoothing-based approach. In previous studies such as Liang et al. (2010), extensive simulation studies have shown that the approximation errors in the smoothing-based methods can be large even for the first order derivative. In our example, the third order derivatives need to be approximated by basis spline so the approximation error could be even larger. To deal with such a problem, Ramsay and Silverman (2005) addressed that the choice of the smoothing penalty is critical to the performance of the smoothing-based estimators. In this study, we used the recommended GCV approach in Ramsay and Silverman (2005) to choose the smoothing penalty. Another issues associated with the smoothing-based methods is the choice of the order of derivatives to penalize on. Ramsay and Silverman (2005) suggested to penalize the derivative two orders higher than the highest derivative one wants to estimate. In our case, we are therefore supposed to penalize the fifth-order derivative since V‴ needs to be estimated. However, note that cubic splines are widely used in practice partially because higher order splines (or polynomials) are likely to introduce artificial oscillations called Runge’s effect (Runge, 1901). To avoid such a problem, we also used cubic splines in this study. Unfortunately, the 4^th- and 5^th-order derivatives of cubic splines are simply zero, which leaves us nothing to penalize on. We thus still penalized the second order derivative in this study.

In short, the estimating equation method is computational efficiency, less accurate, and very useful in practice because the search of the accurate parameter estimates for nonlinear ODE models is difficult and time-consuming, especially when no information on initial parameter values is available. Thus, the estimating-equation based estimate is usually used as a rough initial estimate to help with narrowing down the search range for the more accurate nonlinear least squares (NLS) estimate (Liang et al., 2010; Xue et al., 2010).

3.3. Model Fitting and Estimation Results

In this study, we collected time course data of CD8+ T cells, viral titers and serum antibodies (IgG and IgM) in response to a primary A/X31 influenza infection in mice. A total of 340 inbred strains of C57BL/6 mice in 3 cohorts were intranasally infected with 0.03 ml of 0.96 × 10⁵ H3N2 A/Hong Kong/X31 (X31) influenza virus as previously described (Miao et al., 2010). Note that 11 samples were excluded from the analysis due to technical problems such as immunofluorescent staining problems or other measurement failures. Viral titers were measured from the lung samples using the hemagglutination (HA) assay and the number of effector CD8+ T cells were measured from lymphocytes isolated and analyzed using flow cytometry as previously described (Miao et al., 2010). Anti-X31 IgG and IgM titers were measured in serum by ELISA. CD8+ cell counts, and IgG and IgM antibody concentrations (corresponding to T_E(t), A_G(t) and A_M(t) in model (1), respectively) were treated as covariates measured with error since these covariates are merely input variables to models (1) and (2). We used a nonparametric smoothing approach to deal with the measurement error in covariates in the ODE model as suggested in (Liang and Wu, 2008).

Models (1) and (2) were fitted to log₁₀ transformed viral titer data. Therefore, the measurement model is given as follows

$${\text{log}}_{10}Y(t_i)={\text{log}}_{10}V(t_i)+\epsilon (t_i),i=1,2,\dots ,n$$

where ε(t_i) are i.i.d. measurement errors following a distribution with a mean zero and a common variance σ². In this study, the smoothing-based approach was first employed to quickly obtain initial parameter estimates; then the more accurate nonlinear least squares (NLS) method was employed to refine the parameter estimates.

The initial number of infected epithelial cells was assumed to be zero $(E_P^{*}(0)=0)$, the initial viral titer was directly determined from the first few data points in log₁₀ scale (excluding the viral titer measurement at t = 0 due to the delay of virus spreading) via a linear regression (V(0) ≈ 1473 EID₅₀/ml), and E_p(0) was treated as an unknown parameter to be estimated. In addition, the data of T_E(t), A_G(t) and A_M(t) (that is, the CD8+ T cell counts, and the anti-X31 IgG and IgM titers, respectively) were smoothed using the R routine smooth.spline and the smoothed curves were substituted into the model (Liang and Wu, 2008). Also, the hybrid optimization algorithm, which combines the differential evolution algorithm (Storn and Price, 1997) and sequential quadratic programming method (Ye, 1987), was employed to locate the global minimum of the nonlinear least squares objective function (Liang et al., 2010). Finally, the 95% confidence intervals of parameter estimates were calculated. The Fisher-information matrix (FIM) approach can be used to obtain confidence intervals; unfortunately, this method is found numerically unstable due to the calculation of derivatives and the FIM becomes singular for our examples in Eqns (1) and (2). Therefore, we considered the weighted bootstrap method (Barbe and Bertail, 1995) based on 500 runs. Briefly, the weight bootstrap method is a non-parametric approach, in which the weights (W_i, i = 1,2,…,n) are i.i.d positive random numbers drawn from a distribution (e.g., exponential) with mean one (E(W) = 1) and variance one (Var(W) = 1).

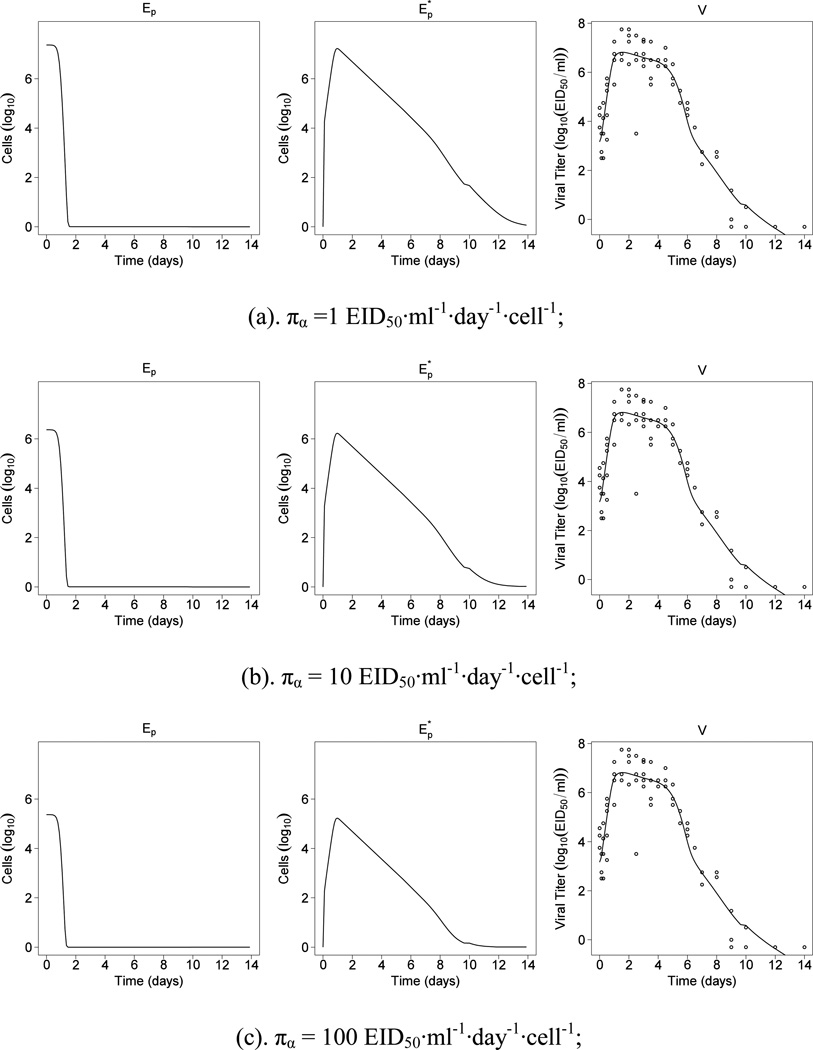
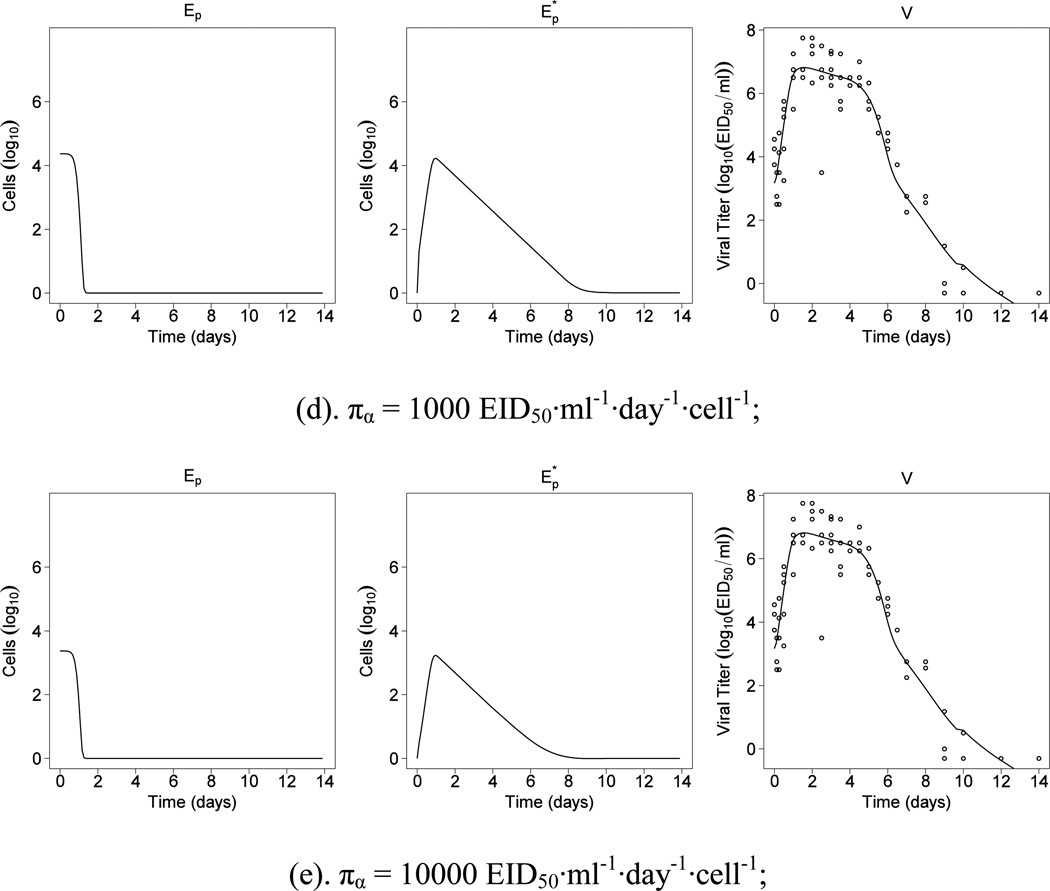
The model fitting results are summarized in Tables 1. For different values of π_α from 1 to 10000, the parameter estimates of (β_α, k_E, δ_E, k_VM) are the same as indicated in Tables 1. This observation should not be interpreted as meaning that “virus production rate does not alter the immune response.” Instead, it suggests that this single unidentifiable parameter’s value has no effect on the estimates of the remaining model parameters. Also, as suggested in Table 1, π_α is strongly and negatively correlated with E_p(0). That is, the increase in π_α is completely compensated by the decrease in E_p(0), which is not discovered by the structural identifiability analysis in Section 3.1. It will be ideal if the structural identifiability analysis techniques can also take the initial conditions such as E_p(0) into consideration. Unfortunately, among the four approaches for structural identifiability analysis in Miao et al. (2011), none of them can achieve this because general nonlinear ODE models usually do not have a closed-form solution. Even though, our structural identifiability analysis result is valid because one can clearly tell from Table 1 that, the values of π_α do not affect the estimates of all other parameters except for E_p(0). The indistinguishability between π_α and E_p(0) is later revealed by our numerical analysis results in Table 1, and this technique is often referred as the practical identifiability analysis (Miao et al., 2011). The structural and practical identifiability analyses together complete the identifiability analysis cycle.

Table 1.

Estimation results with 95% bootstrap confidence intervals for parameters in ODE model (1).

πα EID50· ml−1· day−1·cell−1	EP(0) cells per lung	ρE day−1	βα ml· EID50−1·day−1	kE cell−1 day−1	δE* day−1	cV day−1	kvG ml/ (pg·day)	kvM ml/ (pg·day)
1	2.3E+07 (6.1E+06, 1.0E+09)	9.9E-04 (4.5E-06, 1.0E+00)	5.1E-06 (8.5E-07, 1.8E-05)	1.4E-05 (3.7E-10, 4.9E-05)	1.2E+00 (7.5E-01, 1.6E+00)	3.1E-05 (1.6E-06, 5.2E-01)	1.7E-08 (4.4E-09, 7.0E-06)	7.8E-02 (5.2E-02, 8.1E+00)
10	2.4E+06 (6.3E+05, 1.0E+08)	8.8E-04 (6.6E-06, 1.0E+00)	5.1E-06 (8.9E-07, 1.8E-05)	1.4E-05 (2.0E-10, 5.0E-05)	1.2E+00 (7.5E-01, 1.6E+00)	8.2E-06 (2.4E-06, 5.3E-01)	3.7E-08 (4.3E-09, 7.2E-06)	7.8E-02 (5.0E-02, 7.9E+00)
100	2.4E+05 (6.4E+04, 10E+06)	8.6E-04 (4.8E-06, 1.00E+00)	5.1E-06 (9.1E-07, 1.7E-05)	1.4E-05 (1.1E-10, 5.0E-05)	1.2E+00 (7.4E-01, 1.6E+00)	5.5E-06 (2.2E-06, 5.3E-01)	4.5E-08 (4.7E-09, 8.1E-06)	7.8E-02 (5.1E-02, 8.1E+00)
1000	2.3E+04 (6.1E+03, 1.0E+06)	9.2E-04 (4.0E-06, 1.0E+00)	5.1E-06 (8.9E-07, 1.8E-05)	1.4E-05 (2.4E-10, 4.9E-05)	1.2E+00 (7.5E-01, 1.6E+00)	5.2E-06 (1.7E-06, 5.3E-01)	2.6E-08 (6.2E-09, 8.4E-06)	7.8E-02 (5.1E-02, 8.2E+00)
10000	2.4E+03 (6.1E+02, 1.0E+05)	9.4E-04 (8.1E-06, 1.0E+00)	5.1E-06 (1.0E-06, 1.8E-05)	1.4E-05 (1.6E-10, 4.9E-05)	1.2E+00 (7.8E-01, 1.6E+00)	1.3E-05 (2.4E-06, 5.2E-01)	3.9E-08 (3.2E-09, 7.8E-06)	7.8E-02 (5.1E-02, 8.2E+00)

Also, we note that the estimates of (ρ_E, c_V, k_VG) in Table 1 vary even notably although they should stay the same for different values of π_α according to the identifiability analysis result. A reasonable explanation for this observation is that, when fitting model to experimental data, statistically or practically insignificant parameters are difficult to be accurately determined due to data noise. This explanation is supported by the model selection results in Section 4.1, which suggest (ρ_E, c_V, k_VG) are all negligible. For convenience, the fitted curves were plotted in Figure 1. From Figure 1, we can see that the target cells, E_p, is depleted to nearly zero around day 1.5. Note that E_p in our models is defined as the number of “infectable” target epithelial cells instead of total target cells. The depletion of infectable epithelial cells could be due to either virus infection or innate immune processes rendering cells resistant to IAV infection, such as the antiviral effects of Type I interferon (IFN) or other innate immune responses (Handel, Longini and Antia, 2010; Saenz et al., 2010).

Figure 1.

Results from fitting model (1) to the viral titer data for different virus production rate.

Table 1 shows that the net growth rate (ρ_E) of uninfected epithelial cells is of the magnitude 10⁻⁴, which is statistically significant but practically negligible. The infection rate (β_α) of the target cells is 5.1×10⁻⁶ ml·EID₅₀⁻¹·day⁻¹. The killing rate (k_E) of infected epithelial cells due to CD8+ effector cells is 1.4×10⁻⁵ cell⁻¹·day⁻¹, and the disappearance rate (δ_E*) of infected epithelial cells due to kinetics other than CTL killing is 1.2 day⁻¹. The virus neutralization rate (k_VM) by serum IgM is 0.078 ml/(pg·day), which is orders of magnitude larger than the rate (k_VG) by serum IgG (~10⁻⁸ ml/(pg·day)) and the rate (c_V) due to other kinetics (~ 10⁻⁵ day⁻¹). The average half-life of infected epithelial cells is ~0.5 days and the average half-life of free infectious viral particles is ~0.1 days or 2.4 hours. Our parameter estimates using the statistical methods described correlate well with published literature. For example, (Baccam et al., 2006) investigated the kinetics of influenza A virus infection in human subjects during the first week of infection. In their study, the half-life of infected target cells was estimated to be from 0.05 to 0.3 days, which is in a similar magnitude of our estimate of 0.5 days. The half-life of free infectious virus particles was estimated to be from 0.05 to 0.3 days in (Baccam et al., 2006), which covers our estimate of 0.1 day. We will discuss more biological implications of our findings at length in Section 5.

4. Model Selection and Prediction

After parameter estimation, it is usually necessary to screen out the practically insignificant parameters so a refined and robust model structure can be obtained. Model predictions based on the selected model structure can provide us reliable new insights into the biology.

4.1. Parameter Selection

In this section, we describe the use of model selection criteria to evaluate alternative models and identify and rank the most important factors in immune responses to IAV infection in lung. Also, a time-varying parameter representing the overall virus neutralization effects will be estimated to verify the relative contributions of IgG and IgM to virus neutralization.

As suggested in (Burnham and Anderson, 2004), AICc, a variation of AIC with a bias correction term for a small sample size, is recommended for model selection

$$\text{AICc}=-2\text{ln}L+\frac{2np}{n-p-1},$$

where L is the likelihood function, p the number of unknown parameters, and n the sample size.

Applying the AICc criterion to the proposed influenza models, we evaluated various hypotheses of interest: 1) the net growth of target cells is negligible during the early immune response (ρ_E = 0); 2) the loss of infected epithelial cells is mainly due to both innate immunity and CTL killing (k_E ≠ 0, δ_E* ≠ 0); and 3) anti-influenza IgM antibodies are the major factor in virus neutralization (c_V = 0, k_VG = 0, k_VM ≠ 0). Some model selection results are summarized in Table 2. The full model has an AICc score −33.2 and the sub-model with ρ_E = 0 has a smaller AICc score −34.2, which suggests that the net growth of uninfected epithelial cells is negligible during the time window (days 0~14) of this study. This conclusion is also consistent with other experimental observations. For example, in (Rawlins and Hogan, 2008), it is reported an average half-life of ciliated epithelial cells in lung is as long as 17 months. Finally, the AICc score for the sub-model with k_E = 0 and δ_E* = 0 is 137, which suggests that the constant death rate presumably due to innate immunity and the adaptive immune response of CTL killing of infected epithelial cells are important.

Table 2.

Model selection results using AICc for π_α = 100 EID₅₀·ml⁻¹·day⁻¹·cell⁻¹ (see also Table 3 in (Miao et al., 2010)).

Model	RSS	AICc
Full model	49.4	−33.2
ρE=0	49.4	−34.2
kE=0, δE*=0	360	137
cv=0, kvG=0	49.4	−36.2
cv=0, kvG=0, kvM =0	484	159
ρE=0, cv=0, kvG=0	49.4	−39.2

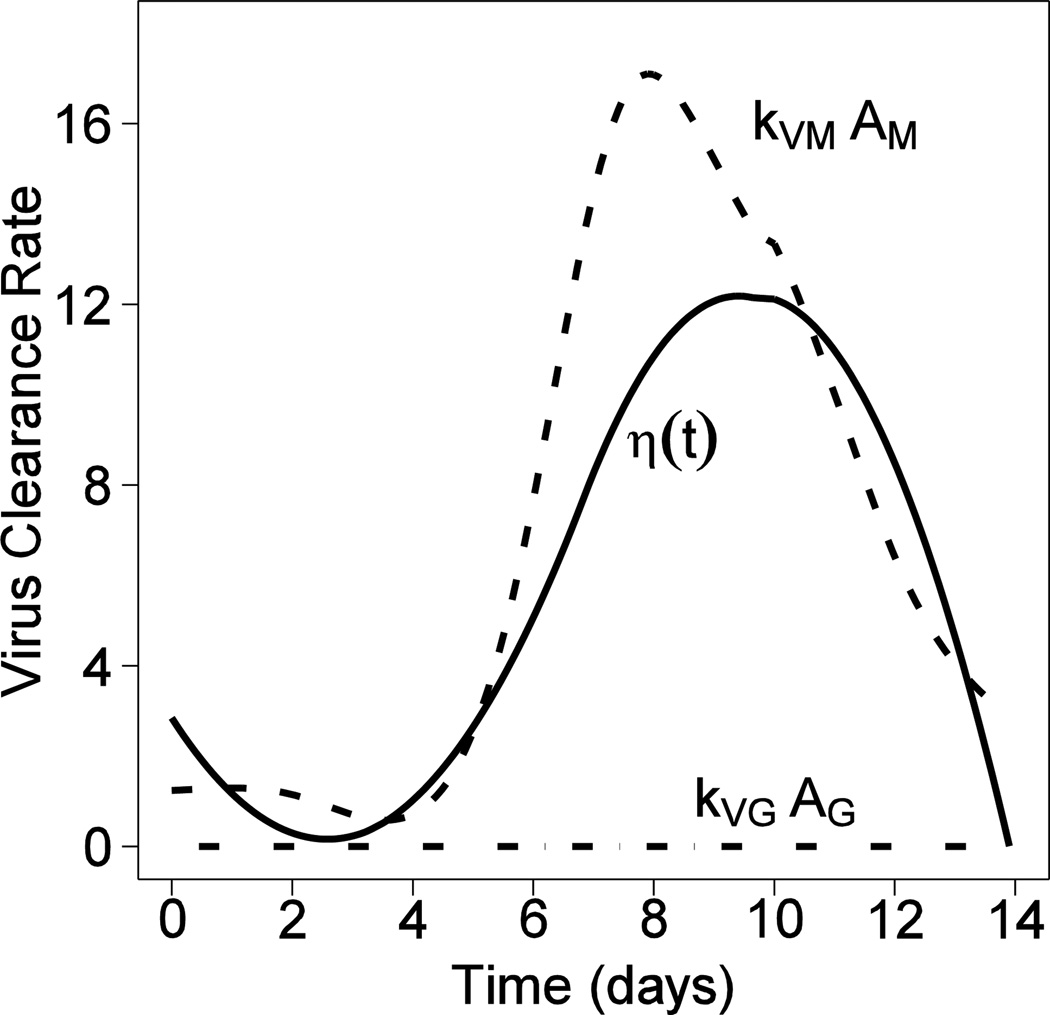
It is also of interest to assess the relative contributions of IgG and IgM to virus clearance. In contrast to the current paradigm, we found that the estimated effect of IgM on virus neutralization is much greater than that of IgG (Table 1). Two approaches were employed to verify the importance of antibody IgM over IgG during the primary influenza infection. First, we calculated the AICc score for the sub-model with c_V = 0 and k_VG = 0 to be −36.2, which is 9% smaller than the AICc score of the full model. Second, we employed the proposed estimation method described in Section 3.2 to estimate the time-varying parameter in model (2). For more details about the time-varying parameter estimation, the reader is referred to (Liang et al., 2010; Xue et al., 2010). The estimated η(t) was plotted and compared to the estimated k_VMA_M(t) and k_VGA_G(t) in Fig. 2. We observe that both the pattern and magnitude of k_VMA_M(t) is close to η(t); however, such pattern is not observed in k_VGA_G(t) and the magnitude of k_VGA_G(t) is very small compared with either η(t) or k_VMA_M(t). Therefore, it is not surprising that the estimated effect of IgM is prominent when both IgM and IgG are considered in the model. Biologically, one might argue that what should actually be measured in the experiment is the amount of IAV irrevocably bound to IgM or IgG within the lung itself. However, this is technically challenging for a variety of reasons, including the rapid clearance of antibody-virus complexes and the difficulty of extracting all of these complexes from solid tissue. Thus, IgG and IgM measurements in our dataset are from the peripheral blood, instead of the lung tissue space. The rise and fall of IgM reflect both the clearance of IgM-IAV complexes and the normal immune process of class switching of B cells in the germinal center to IgG antibody production, depleting the pool of IgM secreting cells. For these reasons, further experimental evidence is needed to verify the importance of the IgM effect on virus neutralization during a primary influenza infection.

Figure 2.

Comparison of the patterns of the estimated time-varying parameter η(t), k_VMA_M(t) and k_VGA_G(t) for π_α = 100 EID₅₀·ml⁻¹·day⁻¹·cell⁻¹.

4.2. Model Prediction

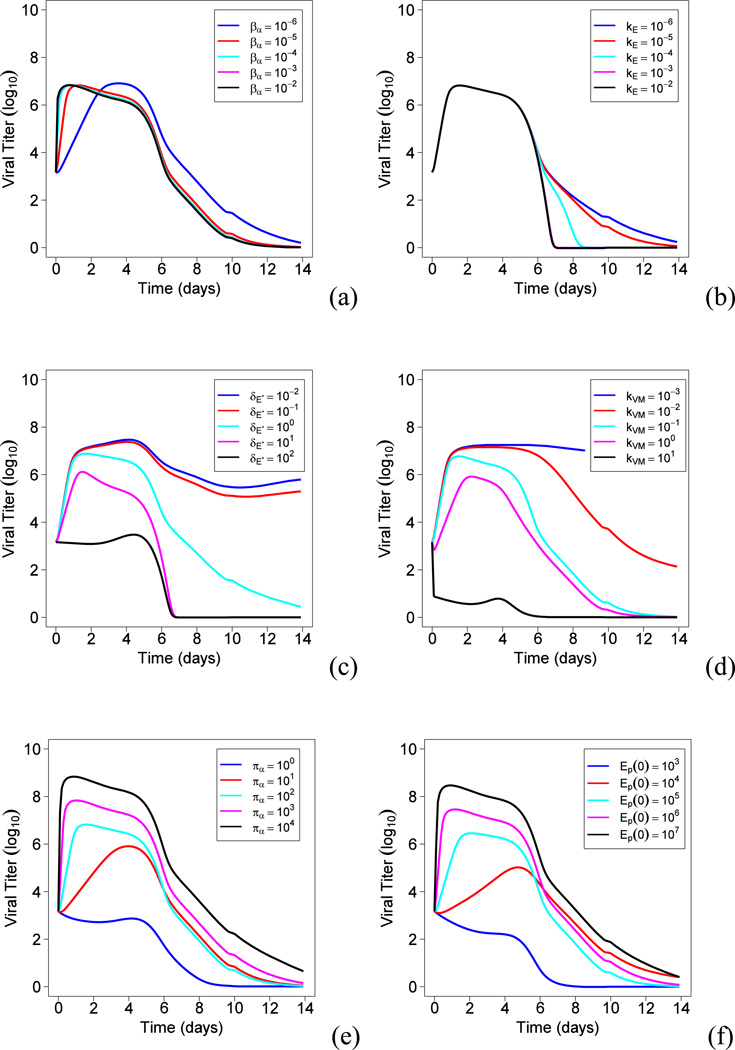
Characteristics of different influenza viral strains can be very different from each other (e.g., more than 10 fold difference in key kinetic parameters like the production rate), it is therefore interesting and important to predict the possible outcomes that a new viral strain can result in within a host. Correspondingly, we can manipulate different immune response parameters by a 10-fold change in value and examine the impacts on the peak viral load V_max. During the early immune response to a primary IAV infection, one key concern is the magnitude of the peak viral load V_max in lung, which strongly correlates with mortality of IAV infection. The prediction results based on Model (1) and the parameter estimates mentioned in Section 3.3 are reported in Fig. 3.

Figure 3.

The effects of different parameters on the peak viral load. (a) The effect of β_α ; (b) The effect of k_E ; (c) The effect of δ_E* ; (d) The effect of k_VM ; (e) The effect of π_α ; (f) The effect of E_p(0).

We first examine the effects of the infection rate (β_α) on V_max. As suggested in Fig. 3(a), when the infection rate increases from 10⁻⁶ to 10⁻² ml·EID₅₀⁻¹·day⁻¹, V_max remains nearly the same but its occurrence time shifts closer to day 0. This result is consistent with the fact that the number of target epithelial cells is limited and thus a higher infection rate will result in an earlier exhaustion of the infectable target cell pool. Also, the total number of viral particles produced after infection is proportional to the total number of infected cells. Thus, given all target cells are infected as predicted in Fig. 1, V_max remains the same for different infection rates.

Second, we examined the effects of the CTL killing rate (k_E) on V_max, as shown in Fig. 3(b). Since the number of antigen-specific CD8+ T cells becomes detectable only after day 5 after infection, it is not surprising that the increase in k_E has no effects on V_max but does help to reduce the viral load down to zero more rapidly during the adaptive immune response phase (days 5~14) in a primary IAV infection.

Third, we examined the effects of the death rate (δ_E*) of infected cells due to factors other than CTL killing on V_max. Note that δ_E* is a constant loss/death rate of infected epithelial cells presumably due to the innate immune response, which is not antigen-specific but takes effects at the very beginning of IAV infection. Thus, V_max is expected to decrease if the innate immunity is more efficient at killing infected cells. Furthermore, as suggested in Fig. 3(c), if δ_E* becomes as large as 10² day⁻¹, viral replication is directly suppressed and no viral titer peak can be observed. Similarly, the effect of the viral neutralization rate (k_VM) by antibody IgM follows the same pattern as shown in Fig 3(d). When the neutralization rate k_VM becomes as large as 10 ml/(pg.day), the virus is also directly suppressed and no viral load peak is observed.

Next, as suggested in Fig. 3(e), if the virus production rate (π_α) increases from 10⁰ to 10⁴ EID₅₀·ml⁻¹·day⁻¹·cell⁻¹ with all other parameter values and E_p(0) held constant, the magnitude of V_max increases from 10³ to 10⁸ EID₅₀. Recall that the increase of infection rate has nearly no effect on V_max (Fig. 3(a)). This suggests that a viral strain with a high production rate and a low infection rate could result in a higher mortality rate than a viral strain with a high infection rate and a low production rate.

Finally, we examined the effects of limited target cells, E_p(0), on virus control by increasing the initial number of target epithelial cells from 10³ to 10⁷ cells per lung. As shown by Fig. 3(f), when E_p(0) is as small as 10³ cells per lung, IAV infection is not sustainable. However, as E_p(0) increases from 10⁴ to 10⁷ cells per lung, the magnitude of peak viral titer increases from 10⁵ to 10⁸ EID₅₀/ml, which confirms the target-limit theory during influenza infection. Note that here the target cells are influenza-infectable epithelial cells in the lung, instead of all epithelial cells.

5. Discussion and Conclusion

Mathematical models, especially using ODEs, have become a standard and powerful tool for investigating infectious diseases. It is of great interest to develop and apply efficient and reliable estimation methods to such models to determine biologically important parameters and thus gain new insights into the mechanisms of infection and viral immunity. In particular, our modeling results clarify several important scientific issues in the immune response to IAV infection.

One significant prediction of the model is that, when the viral infection rate increases, the time of peak viral load (V_max) occurs earlier in the infection, but the peak viral load does not change significantly. This could occur if a new pandemic influenza strain emerges in a population that lacks any cross-reactive CD8+ or antibody based immunity. As the peak viral load has a high correlation with death, this strongly suggests that any therapy, such as anti-viral medications or therapies that block viral entry into epithelial cells, must be given very early during infection to reduce the viral load. The modeling approach we described, in combination with specific information about viral infection kinetics, could be used to examine new therapeutic approaches in silico prior to clinical trials.

A second finding relates to the importance of IgM in IAV neutralization during the antibody response in a primary infection. The predominant view of the antibody response to influenza has been that the rapid rise in high affinity anti-IAV IgG is responsible for the majority of viral clearance in a primary infection, where the host lacks pre-existing B cell immunity from prior vaccination or infection (Baumgarth et al., 1999; Kopf, Brombacher and Bachmann, 2002). However, our model predicts a predominance of IgM antibody in clearing a primary influenza infection. The use of the identifiability analysis and the AIC model selection criteria allowed us to verify this prediction. Interestingly, murine experiments suggest that two different B cell types produce IgM with different kinetics: B-1 B cells which produce natural (innate) anti-influenza IgM antibodies that do not increase with infection, and B-2 B cells which produce high levels of anti-influenza IgM induced by infection. Mice deficient in either or both of these B cell types have significantly increased death rates in a primary infection model (Baumgarth et al., 2000). Thus, our modeling approach has allowed us to put forward the alternate hypothesis that IAV specific IgM antibodies are the predominant mode of antibody-mediated IAV clearance in a primary infection.

Although this study is based on mouse data, the results are also useful to better understand human IAV infection and vaccine development. Specifically, a primary difficulty in quantitatively modeling human immune responses is that many parameters of the human immune response against pathogens cannot be measured for technical or ethical reasons. A strategy to address this issue is to monitor the immune responses to influenza infection and vaccination in mouse experiments, where multiple immune compartments can be sampled. Basic parameter estimates in the mouse can be compared to the human estimates. When human data cannot be obtained, murine estimates can be appropriately scaled to human conditions if the various physical and chemical differences between mouse and human immune systems (Mestas and Hughes, 2004) can be taken into consideration. Fortunately, this is becoming doable. For example, it has been found for some given parameters, the functions appear to be reasonably uniform across a broad range of animal species (Boxenbaum, 1982; Mcmahon and JT, 1983; Schmidt-Nielsen, 1996). In particular, the principles described in the pioneer work of Wiegel and Perelson (2004) can be adopted to link our results to human studies.

In this article, we proposed two estimation methods for use with general nonlinear ODE models that have partially observed state variables and time-varying parameters. Specifically, the identifiability-based estimating equation approach is proposed to efficiently locate parameter ranges and initial estimates, and the nonlinear least squares method equipped with the hybrid optimization algorithm is proposed to refine the estimates and reliably locate the global solution. The identifiability-based estimation approach, significantly and for the first time, overcomes the difficulty of requiring measurements of all state variables in existing smoothing-based approaches (Brunel, 2008; Chen and Wu, 2008a; Liang and Wu, 2008; Varah, 1982). The combined use of these methods has significant advantages over the existing nonlinear least squares or smoothing-based approaches in the sense of both efficiency and accuracy of parameter estimation (Liang et al., 2010).

In summary, we have integrated a set of methodologies such as identifiability analysis, parameter estimation methods and model selection techniques for differential equation models to explore a complex biological problem such as the influenza viral dynamics. Notice that since it is not possible to include all biological details in one model or explore all possible model structures in one article for a complicated problem like influenza infection, we have focused on the two model structures here after exploring many alternatives. We believe that the proposed two models can represent our current best knowledge on immune responses with a focus on adaptive immune responses to primary influenza infection. However, we have to ignore many detailed elements of immune responses such as the interferon (IFN) effects and other innate immune responses since we do not have experimental data for these components. Thus, we must use caution to interpret our biological findings and conclusions, which depend on the assumptions of our model structure. Some potential extensions of the proposed ODE models for influenza virus dynamics include state-space models or stochastic differential equations for which the Bayesian or likelihood-based approaches (Andrieu, Doucet and Holenstein, 2010; Ionides, Bretó and King, 2006) can be used for inference.