What Data to Co-register for Computing Atlases

Abstract

We argue that registration should be thought of as a means to an end, and not as a goal by itself. In particular, we consider the problem of predicting the locations of hidden labels of a test image using observable features, given a training set with both the hidden labels and observable features. For example, the hidden labels could be segmentation labels or activation regions in fMRI, while the observable features could be sulcal geometry or MR intensity.

We analyze a probabilistic framework for computing an optimal atlas, and the subsequent registration of a new subject using only the observable features to optimize the hidden label alignment to the training set. We compare two approaches for co-registering training images for the atlas construction: the traditional approach of only using observable features and a novel approach of only using hidden labels. We argue that the alternative approach is superior particularly when the relationship between the hidden labels and observable features is complex and unknown.

As an application, we consider the task of registering cortical folds to optimize Brodmann area localization. We show that the alignment of the Brodmann areas improves by up to 25% when using the alternative atlas compared with the traditional atlas. To the best of our knowledge, these are the most accurate Brodmann area localization results (achieved via cortical fold registration) reported to date.

1. Introduction

This paper explores the general problem of optimal atlas construction with the aim of predicting the locations of hidden labels in a test image using observable features assuming a training set is available. The terms “labels” and “features” are used in a general sense. For example, the hidden labels could be segmentation labels, activation regions in fMRI or Brodmann areas, while the observable features could be cortical folds or voxel intensities. Furthermore, the roles of hidden labels and observable features are problem specific. For example, one could ask the question of localizing cortical folds based on fMRI observations.

The traditional approach to atlas construction employs image registration algorithms that maximize the similarity between image features to bring training subjects into an image-matched coordinate frame. The goal is to make the images look as similar as possible, most of the time ignoring label information. This approach assumes that correspondence across all training and test subjects can and should be achieved using these observable features. Once the training subjects are in correspondence, regressors (statistical or otherwise) relating the observable features and hidden labels are computed to summarize the population, which can later be used to infer unobserved labels in a test image.

Alternatively, we propose computation of an atlas by co-registering the hidden labels in the training set. This yields a different alignment, particularly if the labels and features are not strongly correlated. For example, the observable features could be cortical folds (visible in in-vivo MRI) and unseen labels could be cytoarchitectural structures (not visible in in-vivo MRI). Consequently, statistics computed in this alternative label-matched coordinate frame differ from those of the traditional atlas and the resulting registration of a test image will therefore also be different.

The following toy example illustrates the differences between the two approaches. Figures 1(a,d) show two training images, where the red and blue boxes represent observable image features and the black box is an unobservable label. The black hidden label is completely predicted by the blue observable feature, i.e., it is always to the right of the blue feature. In both images, the red feature is the dominant observable image feature and is not predictive of the black label. Allowing for only translations, the image-matching approach aligns the red feature since it dominates the blue feature. In contrast, the label-matching approach aligns the black label, with the blue feature aligned as a result. Figures 1(b,e) show the mean image in the image-matched and label-matched reference frames respectively. Figures 1(c,f) show the variance image in the image-matched and label-matched reference frames respectively. The aligned features and labels have zero variance (empty boxes). In particular, the blue feature has zero variance in the label-matched frame, implying that low variance features are predictive of the labels. When we register an unlabeled image using only the red and blue features, the hidden label will be aligned with only one training image in the image-matched frame. In contrast, the hidden label will be aligned to the labels of both images in the label-matched frame.

Figure 1.

Toy Example (see text for detailed explanations). (a,d): Training Images. Black rectangle represents a hidden label. Blue and red boxes are observable features. The red box is much bigger than the blue box. Allowing for only translations, after co-registration of training images: (b,e): mean and variance images in the image-matched frame. (c,f): mean and variance images in the label-matched frame. Empty boxes denote zero variance.

In practice, there might not exist features that completely predict the hidden labels. However, the constellation of low variance predictive features in the label-matched coordinate frame could conceivably improve the alignment of the hidden labels. In this paper, we show that the alternative label-matched atlas strategy yields significantly improved alignment of the Brodmann areas between the test and training images compared with a traditional image-matched atlas.

2. Background

2.1. Registration and Atlas Construction

Registration aims to bring images into the same frame of reference allowing for meaningful comparisons. To register a population of images, one can register a new subject to all subjects in the database [9, 19]. A more efficient method is to summarize the population with a representative. Rather than picking an arbitrary subject as a representative, some methods have focused on determining the most unbiased atlas [10, 14, 18] or multiple atlases [16] from a group of subjects. This usually involves the registration of the subjects into an image-matched coordinate frame, followed by atlas statistics computation. Zollei et al. [24] avoid picking a particular representative altogether in the co-registration of the training images. However, the final reference frame is still an image-matched coordinate frame.

A question then arises on how well the features should be aligned due to the tradeoff between image fidelity and warp regularization. Twining et al. [20] optimizes this tradeoff by finding the least complex atlas that explains the image features of the population. This is useful if the goal is a model to explain these observable features.

However, registration to an atlas is often only an intermediate step before further computation such as shape analysis. In segmentation, the conventional paradigm warps a new subject to the image-matched coordinate frame of the training set. The segmentation labels of the training subjects are then used to infer those of the subject. In joint registration-segmentation [15], the hidden labels and warps of a new subject are inferred simultaneously with respect to the atlas. However, most studies on atlas-based joint registration-segmentation are inconsistent due to the use of segmentation labels in the registration of a new subject but not in the co-registration of the training images.

An exception is the joint registration-parcellation of cortical surfaces [22] that provides a consistent scheme of utilizing segmentation labels in the registration of both test and training images. Van Leemput [12] finds the least complex atlas that explains the manual labels of a training set, dual to Twining’s work [20]. While Van Leemput did not show any verification of his atlas, our results in this paper seem to suggest his atlas might be useful for segmentation.

A fundamental modeling assumption in almost all the atlas construction literature is the choice of the image-matched coordinate frame. This works well when the goal is feature alignment or when the observable features define or strongly correlate with the hidden labels (true for many applications). However, if the hidden labels and observable features have weak or complex correlations, then learning the correlations should lead to improved results.

2.2. Brodmann Areas

The application we consider is the parcellation of the human cerebral cortex into Brodmann areas [4]. The cytoarchitectonic properties defining the Brodmann areas are mostly visible only in histology and more recently exvivo MRI [3]. Unfortunately, much of the cytoarchitectonics cannot be observed with current in-vivo imaging. Yet, today, most studies report their functional findings with respect to Brodmann areas, usually achieved by visual comparison of cortical folds with Brodmann’s original drawings without estimates of confidence. More recently, probabilistic Brodmann area maps created in the Talairach and Colin27 normalized space via combined histology and MRI [6, 17, 23] promise a more principled approach.

Despite the widespread practice of using macro-anatomy such as cortical folds to estimate and report Brodmann areas in individual brains, little is known about their relationship. In fact, studies have shown that even prominent Brodmann areas, e.g., V1 (BA17) and V2 (BA18), have significantly variable Talairach coordinates across subjects [1]. Yet, it is not clear whether the widely reported inaccuracy in Brodmann area localization reflects the true variability of the underlying architectonic areas with respect to macro-anatomical cortical folds or is due to the poor quality of inter-subject alignment.

In this paper, we employ a non-linear surface-based registration algorithm to co-register the labels in the training images into a label-matched coordinate frame by converting the label images into signed distance maps [13]. The resulting atlas consists of the mean and variance images of cortical geometry computed in this label-matched coordinate frame. The same algorithm is used to register a new subject’s cortical geometry to the atlas, assigning more importance to low variance atlas regions which are more predictive of Brodmann area locations via natural weighting of the variance. These low variance regions are not necessarily close to the Brodmann areas.

Our approach is similar to methods that segment regions of low or no contrast, based on predictive information from other regions that can be more easily segmented [11, 21]. However, most of these automatic methods employ expert knowledge about the domain to determine these “predictors”. In contrast, we discover these predictors automatically and use them to drive the registration of a new subject.

In the next section, we discuss two modeling approaches for atlas construction and the alignment of a new subject. In sections 4.1 and 4.2, we instantiate the model with respect to a data-set that contains Brodmann labels obtained via histology and mapped to the corresponding MRI volume [17, 23]. We present experimental results in section 4.3.

3. Theory: Registration & Atlas Computation

Let $L_1^N=\{L_1,\cdots ,L_N\}$ and $Y_1^N=\{Y_1,\cdots ,Y_N\}$ denote the hidden labels and observable features given in a training set of N images respectively. Let Y_N+1 be the observation of a new subject.

We denote $R_1^N=\{R_1,\cdots ,R_N\}$ and R_N+1 to be the registration parameters of the training set and new subject respectively. Let Φ be the atlas parameters that we aim to learn from the training set that model the hidden labels and/or observable features in the normalized reference frame. For example, Φ can model the spatial distribution of different brain structures L and/or the MR intensity distribution Y of a particular tissue type L.

We will follow the common approach of estimating the unknowns Φ, $R_1^N$ and R_N+1 sequentially. We begin with the maximum a-posteriori (MAP) formulation to estimate the atlas parameters Φ and registration parameters $R_1^N$:

$$({\mathrm{\Phi }}^{*},R_1^{N*})=\underset{\mathrm{\Phi },R_1^N}{\text{arg max}}p(\mathrm{\Phi },R_1^N|L_1^N,Y_1^N)$$ (1)

Assuming a uniform prior on Φ, we obtain the following Maximum Likelihood (ML) atlas objective function:

$$({\mathrm{\Phi }}^{*},R_1^{N*})=\underset{\mathrm{\Phi },R_1^N}{\text{arg max}}p(R_1^N,L_1^N,Y_1^N|\mathrm{\Phi })$$ (2)

Given the estimated atlas parameters Φ*, we can then estimate the registration of a new subject R_N+1 via:

$$R_{N+1}^{*}=\underset{R_{N+1}}{\text{arg max}}p(Y_{N+1},R_{N+1}|{\mathrm{\Phi }}^{*})$$ (3)

Such a sequential estimation process is not optimal but can be shown to be a reasonable approximation of the much more computationally expensive MAP problem:

$$({\mathrm{\Phi }}^{*},R_1^{N+1*})=\underset{\mathrm{\Phi },R_1^{N+1}}{\text{arg max}}p(\mathrm{\Phi },R_1^{N+1}|Y_1^{N+1},L_1^N)$$ (4)

We now concentrate on the atlas term (eq. 2) by rewriting it as:

$$p(R_1^N,L_1^N,Y_1^N|\mathrm{\Phi })=p(R_1^N|\mathrm{\Phi })p(L_1^N,Y_1^N|\mathrm{\Phi },R_1^N)$$ (5)

The first term $p(R_1^N|\mathrm{\Phi })$ can be thought of as the prior or regularization on the registration parameters. The crux of this paper lies in the second term, which is the data-fidelity function:

$$p(L_1^N,Y_1^N|\mathrm{\Phi },R_1^N)=p(Y_1^N|{\mathrm{\Phi }}_Y,R_1^N)p(L_1^N|{\mathrm{\Phi }}_{L|Y},Y_1^N,R_1^N)$$ (6)

$$=p(L_1^N|{\mathrm{\Phi }}_L,R_1^N)p(Y_1^N|{\mathrm{\Phi }}_{Y|L},L_1^N,R_1^N)$$ (7)

where Φ = Φ_Y ⋃ Φ_L|Y = Φ_L ⋃ Φ_Y|L. Φ_Y and Φ_L are the parameters that model only Y and only L respectively. For example, Φ_L can model the spatial distribution of different brain structures L. Φ_Y|L model the observations Y given the labels L. For example, Φ_Y|L can model the MR intensity distribution Y of a particular tissue type L. Similarly, Φ_L|Y model the labels L given observations Y.

Consider the following two approaches of modeling the data-fidelity function:

1. Traditionally (for example [7]), the atlas parameters Φ_Y and $R_1^N$ are estimated by optimizing the first term $p(Y_1^N|{\mathrm{\Phi }}_Y,R_1^N)$ of eq. (6) with the regularization p(R|Φ). This can be done in a coordinate-ascent manner by alternating steps of optimizing the registration parameters $R_1^N$ and optimizing the atlas parameters Φ_Y. The optimal $R_1^{N*}$ for the first term are then used to estimate Φ_L|Y in the second term $p(L_1^N|{\mathrm{\Phi }}_{L|Y},Y,R_1^{N*})$.

   Given a new subject, ${\mathrm{\Phi }}_Y^{*}$ are used to register the subject to the atlas space via maximizing $p(Y_{N+1},R_{N+1}|{\mathrm{\Phi }}_Y^{*})$. This can be followed by the use of ${\mathrm{\Phi }}_{L|Y}^{*}$ for segmentation.

   Depending on the relationship between the labels and features, Φ_L|Y might be complex. In this work, we will focus only on the registration part, i.e., ignore the design and estimation of Φ_L|Y.

   In effect, this approach co-registers the images to an image-matched coordinate frame and learns the parameters Φ that model the observations and labels in this common space.

2. Alternatively, we propose to estimate Φ_L and $R_1^N$ by optimizing the first term $p(L_1^N|{\mathrm{\Phi }}_L,R_1^N)$ of eq. (7) with the regularization p(R|Φ). Like before, this can be done in a coordinate-ascent manner. The optimal $R_1^{N*}$ for the first term are then used to estimate Φ_Y|L in the second term $p(Y_1^N|{\mathrm{\Phi }}_{Y|L},L_1^N,R_1^{N*})$.

   Once again, Φ_Y|L might be complex depending on the relationship between the labels and observations. In this work, we will ignore the design and estimation of Φ_Y|L.

   However, we do need to estimate Φ_Y because given a new subject, we would like to register it to the atlas space by optimizing $p(Y_{N+1},R_{N+1}|{\mathrm{\Phi }}_Y^{*})$. Φ_Y can be estimated by optimizing $p(Y_1^N|{\mathrm{\Phi }}_Y,R_1^{N*})$ where $R_1^{N*}$ are found from co-registering the labels.

   In effect, this method co-registers the training images using their labels to a label-matched coordinate frame, and learns the parameters Φ that model the observations and labels in this common space.

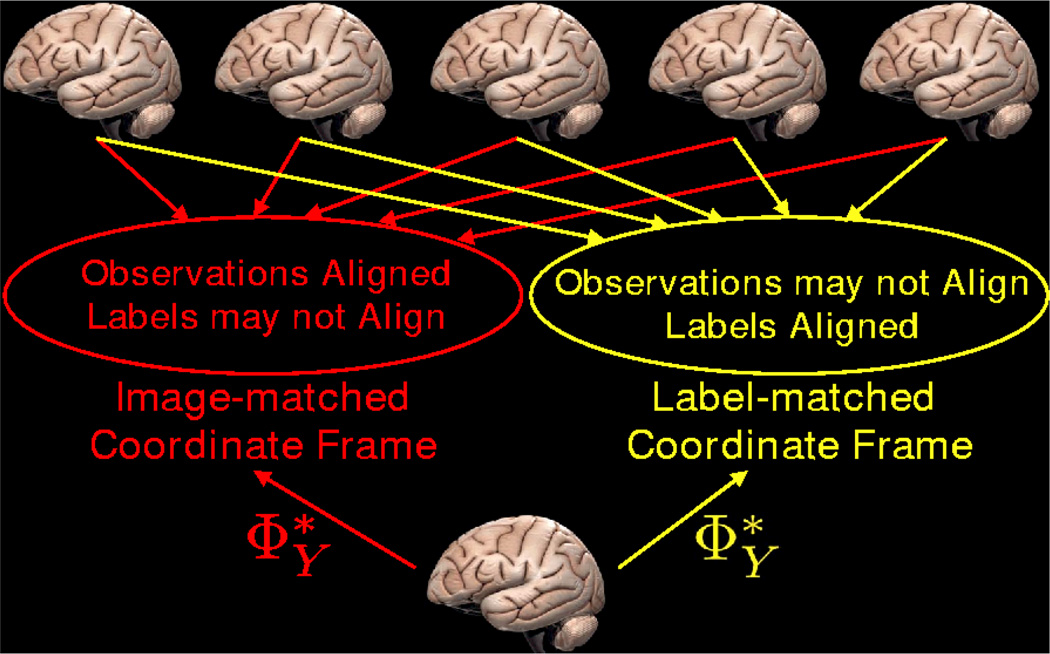
In summary, the difference between the two models is that the model parameters are learned in different spaces, as illustrated in Figure 2. In particular, in the image-matched coordinate frame, the observations of the training set are matched and thus have low variance, while in the label-matched coordinate frame, the observations might not be well-aligned, and will in general have a higher variance. On the other hand, in the label-matched coordinate frame, the labels are matched, while in the image-matched coordinate frame this may not be the case.

Figure 2.

Comparison of methods: In approach 1, images are aligned into the image-matched coordinate frame where observations are matched. In approach 2, images are aligned into the label-matched coordinate frame where labels are matched. ${\mathrm{\Phi }}_Y^{*}$ describe the statistics of observations in the coordinate frame. Therefore, a new image registered using ${\mathrm{\Phi }}_Y^{*}$ will be brought into the coordinate frame in which Φ_Y were learned.

Since the model parameters Φ_Y are learned in a particular common space, ${\mathrm{\Phi }}_Y^{*}$ describe the statistics of observations in that coordinate frame. Therefore given a new subject, optimizing $p(Y_{N+1},R_{N+1}|{\mathrm{\Phi }}_Y^{*})$, involves finding the registration R_N+1 that warps the new subject into that particular common space in which Φ_Y were learned. If Φ_Y were learned in the label-matched coordinate frame, then the new image would be brought into a space where labels are well-aligned.

More concretely, in the label-matched coordinate frame, observable features with low variance arise when aligning the labels also align them, suggesting that these low-variance features are predictive of the labels. A possible strategy of summarizing the label-matched coordinate frame with Φ_Y is to weigh the importance of the features inversely proportional to their variance. This is accomplished in section 4.

As previously discussed, approach 1 is traditional in segmentation. Most segmentation problems deal with regions strongly related to the observations. This is supported by the fact that manual delineation is usually performed by an expert, directly on the image data. As a result, aligning the observable features (e.g., MR intensity) also aligns the hidden labels (e.g., white and gray matter) and vice versa. Thus the image-matched and label-matched reference frames are similar and in practice, we expect both methods to perform comparably in such problems.

On the other hand, in applications where the relationship between the observed features and underlying labels is complex or weak, e.g., cortical geometry vs. Brodmann areas (Figure 3), the two methods will yield different results. In such cases, as demonstrated with the toy example in the introduction, we expect approach 2 to yield better alignment of the hidden labels.

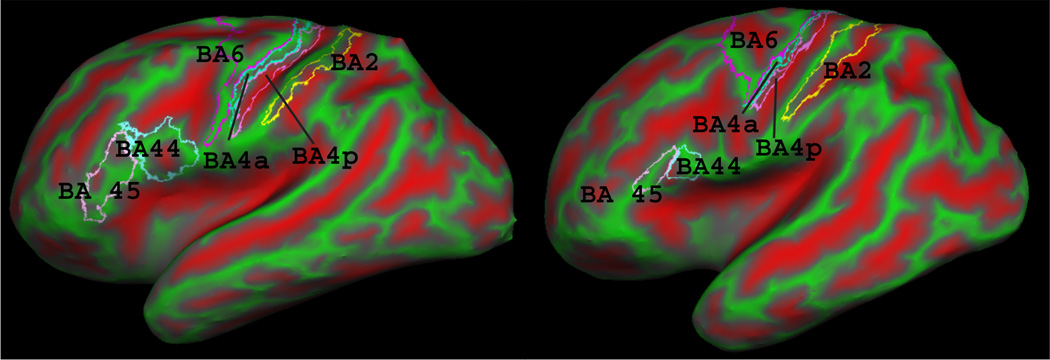
Figure 3.

Brodmann areas 2, 4a, 4p, 6, 44 and 45 on two subjects’ inflated cortical surfaces. Red and green represent sulci and gyri, respectively. Notice the variability of BA44 and BA45 with respect to the underlying folding pattern.

4. Experiments

We now demonstrate the utility of our approach on a data set that contains Brodmann labels mapped to the corresponding MRI volume. 10 human brains were analyzed histologically postmortem using the techniques described in [17, 23]. The histological sections were aligned to postmortem MR with nonlinear warps to build a 3D histological volume. These volumes were segmented to separate white matter from other tissue classes, and the segmentation was used to generate topologically correct and geometrically accurate surface representations of the cerebral cortex using a freely available suite of tools (http://surfer.nmr.mgh.harvard.edu/fswiki) [5]. The 8 manually labeled Brodmann area maps (areas 2, 4a, 4p, 6, 44, 45, 17 and 18) were sampled onto the surface representations of each hemisphere, and errors in this sampling were manually corrected (e.g. when a label was erroneously assigned to both banks of a sulcus). A morphological close was then performed on each label to remove small holes. 6 of the 8 Brodmann areas on the resulting cortical representations for two subjects are shown in Figure 3. Finally, the left and right hemispheres of each subject were mapped onto a spherical coordinate system [8].

4.1. Atlas Computation

We construct the atlas in the label-matched coordinate frame by co-registering the training images to align the identified Brodmann areas. Following a commonly used approach of extending local features to image-wide descriptors, we convert each Brodmann area in each image to its signed distance representation [13].

This yields an I-dimensional distance image D_n for each subject n, where I is the total number of Brodmann areas. We use the signed distance image D_n as a proxy for aligning the Brodmann areas. In our application, the number of available Broadman areas is I = 8 and the number of subjects is N = 10.

Each subject also has a J-dimensional observation image Y_n. In our application, J = 3, where the observations are “sulcal depth” and the mean curvature of the cortical surface before and after partial inflation [8]. We note that the mean curvature of the partially inflated surface serve as a large-scale feature for avoiding local optima.

To bring the subjects into the label-matched coordinate frame, we repeatedly register each of the N distance maps {D_n} to the current atlas defined by the mean and variance of the distance maps. In particular, at iteration k, we maximize $p(L_n|{\mathrm{\Phi }}_Y^{(k-1)*},R_n^k)\triangleq p(D_n|{\mathrm{\Phi }}_Y^{(k-1)*},R_n^k)$ for each subject n.

Assuming independent Gaussians both spatially and across Brodmann areas for the I distance maps that make up D_n, we get the equivalent maximization (after taking log) problem:

$$\underset{R_n}{\text{arg max}}\text{log}p(R_n)-\frac{1}{2}\sum _{i=1}^I\sum _{\overrightarrow{x}}\frac{{(D_{ni}(\overrightarrow{x}(R_n^k))-M_i^{k-1}(\overrightarrow{x}))}^2}{V_i^{k-1}(\overrightarrow{x})}$$

where x⃗ denotes vertex location. D_ni denotes the signed distance image of the ith label in subject n. $M_i^{k-1}(\overrightarrow{x})=\frac{1}{N}{\sum }_n{D}_{ni}(\overrightarrow{x}(R_n^{(k-1)*}))$ is the mean distance map for Brodmann area i after iteration k − 1 and $V_i^{k-1}(\overrightarrow{x})=\frac{1}{N}{\sum }_n{(D_{ni}(\overrightarrow{x}(R_n^{(k-1)*}))-M_i^{k-1}(\overrightarrow{x}))}^2$ is the variance of the distance map for Brodmann area i after iteration k − 1.

Similar to [7], we define the regularization p(R|Φ) ≜ p(R) to be:

$$\text{log}p(R)=\text{log}F(R)-S\left[\sum _u\sum _{\upsilon \in N_u}{\left(\frac{d_{u\upsilon }^R-d_{u\upsilon }^0}{d_{u\upsilon }^0}\right)}^2\right]$$ (8)

where $R_{u\upsilon }^R$ is the distance between vertices u and υ under registration R, $d_{u\upsilon }^0$ is the original distance and N_u denotes a neighborhood of υ. Our regularization penalizes metric distortion weighted by a scalar S which reflects the amount of smoothness of the final warp. Function F(·) ensures invertibility and is zero if the warp introduces folds in the surface and one otherwise. R is optimized by warping each vertex individually. In this work, S is set to 1. Exploration of the parameter S is a topic of future research.

Once the co-registration is completed, we compute the atlas parameter ${\mathrm{\Phi }}_Y^{*}$ using $R_n^{*}$. Let Y_nj denote the scalar image corresponding to the j-th observation in subject n. ${\mathrm{\Phi }}_Y^{*}$ consists of two images: the observation mean image

$$M_j^A(\overrightarrow{x})=\frac{1}{N}\sum _n{Y}_{nj}(\overrightarrow{x}(R_n^{*})),$$

and the observation variance image

$$V_j^A(\overrightarrow{x})=\frac{1}{N}\sum _n{(Y_{nj}(\overrightarrow{x}(R_n^{*}))-M_j^A(\overrightarrow{x}))}^2.$$

For the computation of the image-matched coordinate frame atlas, we repeat the construction discussed above but replacing the distance map D_n with Y_n. The construction is then essentially the same as FreeSurfer [7].

4.2. Registration of a New Brain

The registrations of an unlabeled brain Y_N+1 to both the image-matched and label-matched atlases are performed by optimizing $p(Y_{N+1},R_{N+1}|{\mathrm{\Phi }}_Y^{*})$. Consistently with the procedure used for atlas construction, we estimate the registration parameters R_N+1 for the new image by optimizing

$$-\frac{1}{2}\sum _{j=1}^J\sum _{\overrightarrow{x}}\frac{{(Y_{N+1,j}(\overrightarrow{x}(R_{N+1}))-M_j^A(\overrightarrow{x}))}^2}{V_j^A(\overrightarrow{x})}$$ (9)

with the same regularization as (8). This assumes a Gaussian model with independence across space and the observable image features. A more general model could replace the individual variances $V_j^A$ with a covariance matrix. Note the role of the variances reflect the intuition that in the label-matched coordinate frame, low variance features are more predictive of the labels and are given more weight.

4.3. Results

We quantify the alignment quality of a corresponding Brodmann area of a given pair of registered labeled maps with the modified Hausdorff distance (MHD). To compute the asymmetrical MHD H_1→2 between a “corresponding label of subject 1 and subject 2 in subject 2’s native space”, for each boundary point of the label in subject 1, the shortest distance to the boundary of the label in subject 2 is found. We repeat by computing all shortest distances from the label boundary in subject 2 to the label boundary in subject 1. H_1→2 is then the average of all shortest distances. The asymmetry in the above process comes from the computation of distances along the cortical surface (native space) of subject 2 rather than some average surface in atlas space. This prevents the possibility of obtaining artificially good results because the images are squeezed together in atlas space. Unlike overlap measures, such as the Dice coefficient, MHD provides the measure in mm of the uncertainty of localization, and is invariant to the size of an area.

For our benchmark, we compute an “image-matched 10” atlas (IM10) from the 10 ex-vivo brains using the FreeSurfer algorithm (see section 4.1). Since the 10 ex-vivo brains are already co-registered to construct the atlas, the brains are already in correspondence and we compute the MHD between the Brodmann areas of each pair of ex-vivo brains resulting in 90 (instead of 45 because of the asymmetry) comparisons per structure.

As a second benchmark, we compute an “image-matched 40” atlas (IM40) from a set of 40 in-vivo brains. In this case, we register each of the 10 ex-vivo brains to IM40 via eq. (9) and compute the MHD between the Brodmann areas of each pair of ex-vivo brains resulting in 90 comparisons per structure.

Finally, we compute a leave-one-out “label-matched 9” atlas (LM9) for each of the 10 ex-vivo brains, i.e. the 10 brains minus the test subject. We use the leave-one-out procedure so as to exclude the Brodmann areas of the test subject from the atlas construction. We then register the test subject to the corresponding LM9 atlas according to equation (9) and compute the MHD between the Brodmann areas of the test subject and the 9 brains in the atlas. Once again, we get 90 comparisons per structure.

For each Brodmann area, we want to test whether the 90 MHD measurements from LM9 are statistically significantly smaller than those of IM10 or IM40. Yet, the comparisons are not independent, nor is there really a one-to-one correspondence between the measurements. We therefore perform a permutation test, where we pool all the measurements into a group of 180 measurements. We then repeatedly split the 180 measurements into 2 equally sized groups and computed the difference in means between the groups, building an empirical distribution of the difference in means under the null hypothesis. For each structure, we perform a million random permutations. Under the null hypothesis that the means of the 2 groups are the same, such a test is valid despite the unknown correlations.

Table 1 lists the average MHD’s for the three atlases and eight Brodmann areas, along with the p-values for LM9 vs. IM10 and LM9 v. IM40. We see that, in general, the IM40 atlas yields a significantly better alignment than the IM10 atlas. From our experience, this is because IM40 contains many more subjects and thus yields better estimates for the atlas parameters. The label-matched LM9 atlas, however, achieves the best alignment for all Brodmann areas. The alignment error is up to 25% less than that of IM40 with statistical significance (p < 0.01) in 12 out of 16 regions (all, except BA44 in the left hemisphere, BA4p, BA6 and BA44 in the right hemisphere). Figure 5 provides a more detailed comparison between the results of the two best atlases: LM9 and IM40. Figure 4 shows the Brodmann areas with statistically significant improvement on the cortical surface.

Table 1.

Average alignment errors in mm for the three atlases. Best alignment for each Brodmann area is in bold. The last two rows of each table contain a statistical comparison (permutation test p-value) between the label-matched atlas LM9 and the image-matched atlases IM10 and IM40. The p-values that do not reach significance are shown in italic.

Left Hemisphere
	V1	BA4a	BA4p	BA2	V2	BA6	BA44	BA45
IM10	3.83	4.38	3.77	6.28	4.64	7.01	7.41	6.81
IM40	2.89	3.81	3.60	5.62	4.25	7.06	7.57	6.92
LM9	2.34	2.86	3.00	4.63	3.31	5.87	6.92	4.63
P-values
IM10 v. LM9	10−6	10−6	10−6	10−6	10−6	10−6	1.2 × 10−1	10−6
IM40 v. LM9	10−6	10−6	3.8×10−5	3.5×10−5	10−6	1.2×10−4	6.7 × 10−2	10−6
Right Hemisphere
	V1	BA4a	BA4p	BA2	V2	BA6	BA44	BA45
IM10	3.85	3.76	3.11	5.92	3.97	6.50	11.54	9.88
IM40	2.70	3.58	2.92	5.66	3.58	6.34	10.49	9.20
LM9	2.39	3.07	2.89	4.73	3.05	5.90	9.72	7.40
P-values
IM10 v. LM9	10−6	10−6	2.8 × 10−2	10−6	10−6	3.8 × 10−2	6.6 × 10−3	3 × 10−4
IM40 v. LM9	8.7−4	2.1×10−4	4.0 × 10−1	8.6×10−5	10−6	8.9 × 10−2	1.3 × 10−1	4.2−3

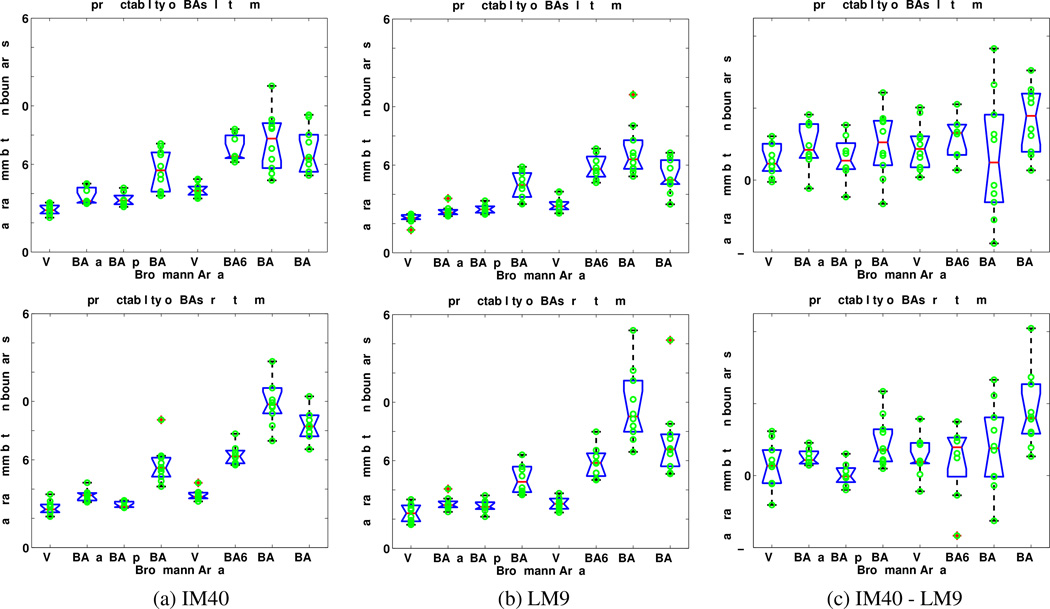
Figure 5.

Box plots of the modified Hausdorff distances for 8 Brodmann areas for the image-matched atlas IM40 and the label-matched atlas LM9. (Top row) Left Hemispheres. (Bottom row) Right Hemispheres. (a) IM40. (b) LM9. (c) Difference between the alignment errors of IM40 and LM9. Positive values indicate that LM9 yields better results. Blue boxes indicate lower and upper quartiles, red lines are medians. Dotted lines extend 1.5 times the inter-quartile spacing. Data points outside of the lines are considered outliers.

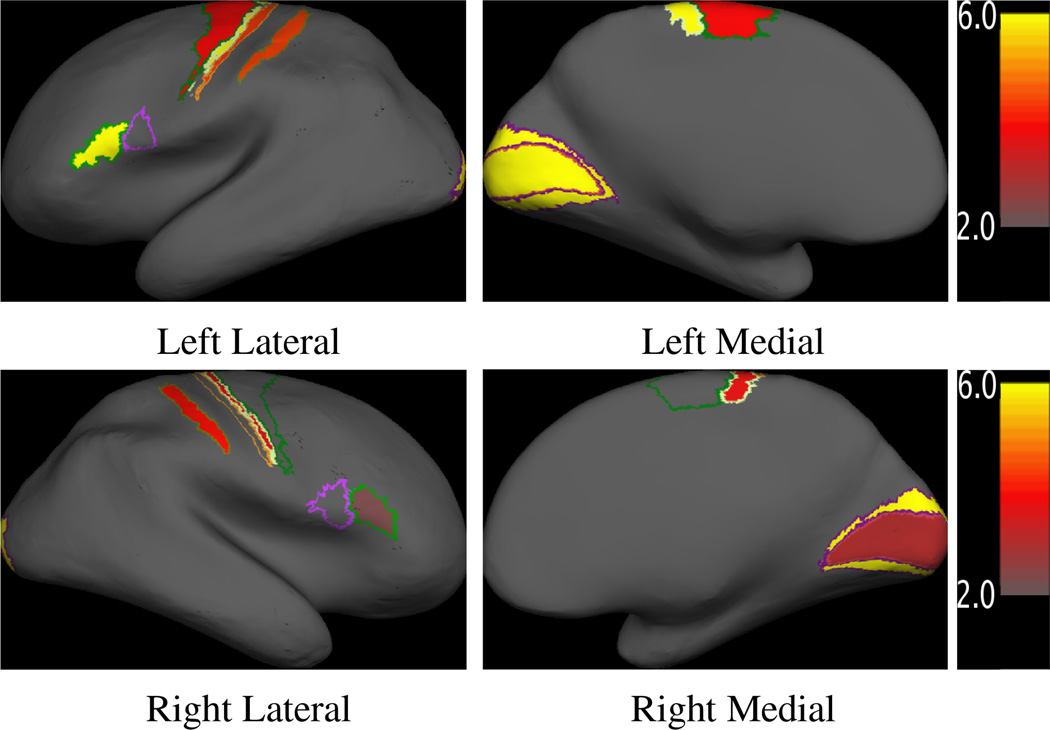
Figure 4.

Maps of p-values of the difference in alignment quality between the label-matched atlas LM9 and image-matched atlas IM40. The p-values are plotted in minus log-scale so that large values correspond to being more significant. Only statistically significant regions are shown in color.

5. Conclusion

In this paper, we argue that the goal should drive the computation of an atlas. In particular, we investigate an approach that co-registers hidden labels in a training data set to compute a probabilistic atlas based on observable features. The purpose of the atlas is to localize unobserved labels in a new data set. The atlas construction process automatically discovers important observable features since low-variance observable features are more predictive of the hidden labels. Given a new subject, the registration algorithm gives more importance to the low-variance regions via natural weighting of the variance.

We show that a registration algorithm that nonlinearly registers observable folding patterns of a brain with a label-matched atlas can achieve surprisingly high accuracy in the localization of a set of cytoarchitectonic Brodmann areas. In particular, alignment errors for V 1, BA4a, BA4p and V 2 of both hemispheres are less than 3.5mm. The remaining areas are more variable, but still exhibit significantly improved overall predictability relative to the more standard 12 degree of freedom volumetric alignment. In particular, Broca’s area (left hemisphere BA44 and BA45) has a surprisingly low estimation error compared with previously reported results [2]. The results we present are, to our knowledge, the best of their kind and may have important implications in the study of the relationship between the macroanatomical and cytoarchitectonic organization of the brain.

Future work involves the discovery of more Brodmann predictive macro-anatomical features and the understanding from a neuro-scientific perspective why some folds are more predictive than others of Brodmann area location.