From Spatial Regularization to Anatomical Priors in fMRI Analysis

Abstract

In this paper, we study Markov Random Fields as spatial smoothing priors in fMRI detection. Relatively high noise in fMRI images presents a serious challenge for the detection algorithms, creating a need for spatial regularization of the signal. Gaussian smoothing, traditionally employed to boost the signal-to-noise ratio, often removes small activation regions. Recently, the use of Markov priors has been suggested as an alternative regularization approach. In this work, we investigate fast approximate inference algorithms for using MRFs in fMRI detection, propose a novel way to incorporate anatomical information into the detection framework, validate the methods through ROC analysis on simulated data and demonstrate their application in a real fMRI study.

1 Introduction

Functional magnetic resonance imaging (fMRI) provides a non-invasive dynamic method for studying brain activation by capturing the change in the blood oxygenation level. Most fMRI detection algorithms operate by comparing the time course of each voxel with the experimental protocol, labelling the voxels whose time courses correlate significantly with the protocol as “active”. The commonly used general linear model (GLM) [9] further assumes that the fMRI signal possesses linear characteristics with respect to the stimulus and that the temporal noise is white. Application of GLM to an fMRI time series results in the so-called statistical parametric map (SPM), which is often thresholded to produce a binary map of active areas. However, because of a low signal-to-noise ratio (SNR), the binary maps typically contain many small false positive islands.

A common approach to reducing such false detections employs a Gaussian filter to smooth the fMRI signal prior to applying the GLM detector. Unfortunately, Gaussian smoothing, though intended to combat low SNR, leads to overly smoothed SPMs and a loss of detail in the resulting binary activation maps. A number of alternative approaches have explicitly incorporated spatial and temporal correlations into the estimation procedure. Examples include autoregressive spatio-temporal models [4, 24], Markov Random Fields (MRFs) [5, 8, 7], Bayesian models inferring hidden psychological states [15], adaptive thresholding methods that adjust statistical significance of active regions according to their size, based on the Gaussian Random Field theory [10]. In this paper, we focus on MRFs for modeling spatial coherency, study their performance and develop several increasingly rich spatial prior models. Following the formulation in [5], we assume that, given the activation state of each voxel, the time courses of different voxels are conditionally independent and can be reduced to a sufficient statistic. This work therefore concentrates on spatial regularization of the activation maps. Temporal regularization models can be easily incorporated into our framework by changing the activation statistic.

For MRFs with binary states, exact solution can be obtained in polynomial time. An fMRI detection algorithm based on the GLM statistic and the binary activation states was demonstrated in [5]. However, if one wants to go beyond binary states (e.g., treating positively and negatively activated voxels differently), the problem of estimating the optimal activation states becomes intractable and approximation algorithms must be used. Prior work in MRF-based fMRI detection employed simulated annealing [8, 21] and the iterated conditional mode algorithm [22]. We adopt the Mean Field solver, introduced in statistical physics [18], which has been widely used for image segmentation [16, 17, 20, 25]. In our experiments with binary MRFs, the Mean Field algorithm produced results comparable to those of the exact solver while reducing computation time by one to two orders of magnitude¹.

We further refine the activation priors by incorporating anatomical information. Similarly to segmentation, where a probabilistic atlas serves as a spatially varying prior on the tissue types, the anatomical information can provide a prior on the activation map. Intuitively speaking, we want the prior to reflect the fact that activation is much more likely to occur in gray matter than in white matter, and not at all in cerebrospinal fluid (CSF) or bone. In addition, the spatial coherency of activation is strong within each tissue and not across tissue boundaries. In this model, the hidden nodes encode both the tissue type and the activation state. Segmentation provides an additional, potentially noisy, observation at each node. We derive the detection algorithm for this model and evaluate it on simulated and real data, achieving high detection accuracy with significantly shorter time courses compared to the standard GLM detector.

Anatomical scans have certainly been used in fMRI analysis and visualization before. Hartvig [14] used the anatomical information in his marked point process spatial prior. Moreover, in some systems (e.g., BrainVoyager [1]), the subject’s anatomical image is transformed into a standard coordinate frame (such as Talairach) and the functional activation map is displayed on the surface that corresponds to the cortical sheet in that coordinate frame. Other systems (e.g., FSL [2]) rely on sophisticated segmentation algorithms to extract a topologically correct representation of the cortical surface from the anatomical scan [6]. Performing Gaussian smoothing on the surface eliminates irrelevant voxels from the weighted average for the cortical locations. In contrast, our approach does not require a surface extraction algorithm, but instead utilizes anatomical information to inject the anatomically based coherency bias into the detection algorithm while performing the computation directly on the volumetric data. The inspiration for this work comes from the success enjoyed by MRFs in providing spatial smoothing priors for image segmentation [16, 17, 20, 25].

In the next section, we briefly outline how the GLM detector can be augmented with an MRF prior closely following the derivation presented in [5], review the Mean Field algorithm, and present the empirical evaluation of the detector on simulated data. In Section 3, we extend the Markov priors to incorporate the anatomical information and show the empirical evaluation of this new, refined model. Section 4 illustrates the proposed detectors on a real fMRI data set.

2 Markov Priors for Activation Maps

Background

An fMRI scan contains a time course $y_i∊{\mathbb{ℝ}}^T$ for each voxel i (i = 1, …, N), where T is the number of time samples and N is the number of voxels in the scan. GLM models the fMRI signal as a linear combination of the protocol-dependent component B, and the protocol-independent component A, such as cardiopulmonary factors. The presence of the protocol-dependent signal indicates that the corresponding voxel is active due to the stimulus. Let H₁ be the hypothesis that a voxel is active and H₀ be the null hypothesis. Under GLM,

$$H_0:y_i=A{\alpha }_i+{∊}_i{H}_1:y_i=A{\alpha }_i+B{\beta }_i+{∊}_i$$

for i = 1, …, N. For white temporal noise, ${∊}_i~N(0,{\sigma }_i^{2}I)$. Least squares estimates of the activation response β_i and the protocol-independent factors α_i are found through a linear regression on the design matrix C = [A B]:

$$\left[{\widehat{\alpha }}_i{\widehat{\beta }}_i\right]={\left(C^{T}C\right)}^{-1}{C}^T{y}_i,$$ (1)

and the corresponding F-statistic is given by $F_i={\widehat{\beta }}_i^T{\widehat{\Sigma }}_{{\beta }_i}^{-1}{\widehat{\beta }}_i∕N_{\beta }$, where N_β is the number of the regression coefficients in β_i and ${\widehat{\Sigma }}_{{\beta }_i}$ is their estimated covariance.

Let random variable X = [X₁, …, X_N] represent an activation configuration of all voxels in the volume, and x = [x₁, …, x_N] be one possible configuration i.e., the activation map. In the case of binary hypothesis testing, the random variable X_i, which represents the activation state of voxel i, is also binary. Given an fMRI scan [y₁, …, y_N], the GLM estimate of the activation map x^∗ is obtained by thresholding the statistic value F_i for all voxels in the volume at a certain user-specified level.

It can be shown that the maximum log-likelihood ratio

$$z_i=\log \frac{{\max }_{{\alpha }_i,{\beta }_i,{\sigma }_i^2}p({\mathit{y}}_i\mid H_1)}{{\max }_{{\alpha }_i,{\sigma }_i^2}p({\mathit{y}}_i\mid H_0)}=\log \frac{{\max }_{{\alpha }_i,{\beta }_i,{\sigma }_i^2}N({\mathit{y}}_i;B{\beta }_i+A{\alpha }_i+{\sigma }_i^{2}I)}{{\max }_{{\alpha }_i,{\sigma }_i^2}N({\mathit{y}}_i;A{\alpha }_i,{\sigma }_i^{2}I)}$$ (2)

is a monotonic function of the F statistic (see [5] for a detailed derivation). We can therefore consider z_i as an alternative statistic indicative of the activation state of voxel i. We will use this fact in the derivations of the MRF-based detection. If a different model of fMRI activation is proposed, it can be easily incorporated into our algorithm by formulating the corresponding maximum log-likelihood ratio and using it in place of z_i.

Markov Priors

A Markov prior on the activation configuration X, $P_{\mathit{X}}\left(x\right)=\frac{1}{\lambda }{\prod }_{<i,j>}{\Psi }_{ij}(x_i,x_j){\prod }_i{\Psi }_i\left(x_i\right)$, is defined in terms of the singleton potentials Ψ_i(x_i) that provide bias over state values x_i for voxel i, and the pairwise potentials Ψ_ij (x_i, x_j) (often referred to as the compatibility matrices) that evaluate the compatibility of voxel i being in state x_i and voxel j being in state x_j for each pair < i, j > of neighboring voxels. λ is a normalization constant, also called the partition function. Given the activation statistic values z, we seek the maximum a posteriori (MAP) estimate of the activation configuration:

$$\begin{array}{cc}\hfill x^{\ast }& =\arg \underset{x}{\max }{P}_{\mathit{X}\mid \mathit{Z}}(x\mid z)=\arg \underset{x}{\max }{P}_{\mathit{X},\mathit{Z}}(x,z)=\arg \underset{x}{\max }{P}_{\mathit{X}}\left(x\right)P_{\mathit{Z}\mid \mathit{X}}(z\mid x)\hfill \\ \hfill & =\arg \underset{x}{\max }\frac{1}{\lambda }\prod _{<i,j>}{\Psi }_{ij}(x_i,x_j)\prod _i{\Psi }_i\left(x_i\right)P_{Z_i\mid X_i}(z_i\mid x_i)\hfill \end{array}$$ (3)

The last equality is based on the assumption that the observations at different voxels are independent given the activation state of each voxel, and the likelihood over the volume can therefore be written as a product of the individual likelihood terms for each voxel. Fig. 1 depicts the corresponding graphical model, using a two-dimensional grid for illustration purposes only. The estimation is performed fully in 3D in all experiment reported here. We assume a spatially stationary generative model, i.e., $P_{Z_i\mid X_i}$, Ψ_i and Ψ_ij are identical for all voxels in the volume. The observations (the fMRI signal, and in Section 3, the anatomical information) move the MAP estimate away from the spatially stationary configurations.

Fig. 1.

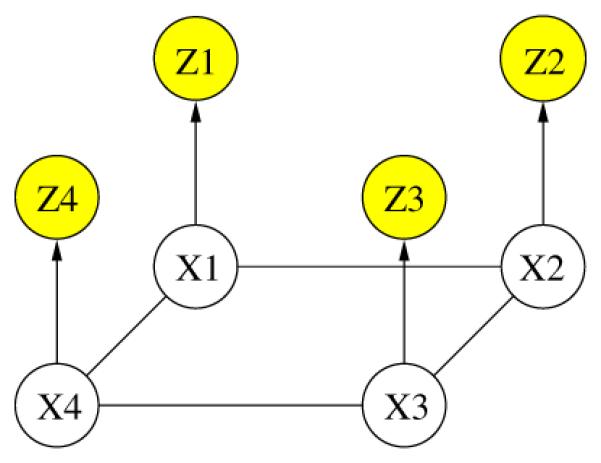
Graphical model for P_{X ,Z}

Direct search for the optimal activation configuration is intractable in general. However, a polynomial-time algorithm for exact MAP estimation exists for binary MRFs [13], based on a reduction to the Minimum-Cut-Maximum-Flow problem. We refer to this exact solver as Min-Max throughout this paper. Min-Max is still computationally intensive when applied to the volumetric data: in our experiments, it took 1-3 hours, depending on the pairwise potential settings and the initial threshold applied to the GLM statistic. On the other hand, the Mean Field approximation for MRFs is fast (ten to hundred times faster than Min-Max on the 3D grids we consider in this paper) and reasonably accurate, as our results in the remainder of this section indicate.

Mean Field Solution

The Mean Field algorithm approximates P_{X |Z} (x|z) by a product distribution $Q\left(x\right)={\prod }_i{b}_i\left(x_i\right)$ through minimization of the KL-Divergence between the two distributions:

$$D(Q\Vert P_{\mathit{X}\mid \mathit{Z}})=\sum _{x}Q\left(x\right)\log \left(Q\left(x\right)\right)-\sum _{x}Q\left(x\right)\log \left(P_{\mathit{X}\mid \mathit{Z}}(x\mid z)\right)$$ (4)

b_i(x_i) denotes the probability of voxel i being in state x_i (often called the belief), therefore ${\sum }_{x_i=1}^M{b}_i\left(x_i\right)=1$, where M is the number of possible states of X_i. The KL-Divergence measures how closely Q approximates P_X|Z; it is non-negative and is equal to zero only for Q = P_X|Z. It is easy to see that the minimum of D(·) is achieved for the same state configuration x that minimizes the so called free energy, $F_{MF}=D(Q\Vert P_{\mathit{x}\mid z})=\log \left(P_{\mathit{z}}\left(z\right)\right)-\log \left(\lambda \right)$, since the last two terms of the latter function are independent of x. Substituting the product form for Q, we obtain,

$$\begin{array}{cc}\hfill F_{MF}\left(\mathit{b}\right)& =-\sum _i\sum _{j\in N\left(i\right)}\sum _{x_i=1}^M\sum _{x_j=1}^M{b}_i\left(x_i\right)b_j\left(x_j\right)\log \left({\Psi }_{ij}(x_i,x_j)\right)\hfill \\ \hfill & +\sum _i\sum _{x_i=1}^M{b}_i\left(x_i\right)[\log \left(b_i\left(x_i\right)\right)-\log \left(P_{Z_i\mid X_i}(z_i\mid x_i){\Psi }_i\left(x_i\right)\right)]\hfill \end{array}$$ (5)

Setting $\partial F_{MF}\left(\mathit{b}\right)∕\partial b_i=0$ under the constrains ${\sum }_{x_i=1}^M{b}_i\left(x_i\right)=1\forall i$ yields the following iterative update rule:

$$b_i^{t+1}\left(x_i\right)\leftarrow \gamma P_{Z_i\mid X_i}(z_i\mid x_i){\Psi }_i\left(x_i\right)e^{{\Sigma }_{j\in N\left(i\right)}{\Sigma }_{x_j=1}^M{b}_j^t\left(x_j\right)\log {\Psi }_{ij}(x_i,x_j)}$$ (6)

The normalization constant γ ensures the solution is a valid probability distribution. N (i) is the set of voxel i’s neighbors. In each iteration of the Mean Field algorithm, the voxel’s belief is updated according to the linear combination of its neighbors’ beliefs in the previous iteration. The probability model (i.e., $P_{Z_i\mid X_i}$, Ψ_i and Ψ_ij) determines the exact form of the update rule. Each voxel is assigned the state value with the highest belief at the end of the procedure (for binary MRFs, the voxel is set active if b_i(1) > b_i(0)).

Estimating Model Parameters

The potential functions Ψ_i, and Ψ_ij and the observation likelihood $P_{Z_i\mid X_i}$ must correspond to our notions of the appropriate bias toward desired solutions. In this work, we follow a common practice of setting the potential functions (same for all voxels) to the corresponding marginal probability distributions estimated from data: Ψ_i(x_i) is set to the expected percentage of voxels in state x_i, Ψ_ij (x_i, x_j) is set to the joint frequency of the states x_i and x_j, and $P_{Z_i\mid X_i}$ is approximated by a smoother version of a class-conditional histogram. Other forms of potential functions have also been explored [7, 11, 12].

Lack of training data or ground truth necessary for estimating the marginal frequencies is a more serious problem. Unlike the segmentation application, where manual segmentations by experts can be used to construct priors on the frequencies and co-occurrences of tissue types, in most fMRI experiments even the experts cannot provide such information. Model parameters in the currently used detectors are either set using researcher’s intuition on the underlying activation properties (e.g., the threshold in GLM or the kernel width in Gaussian smoothing) or estimated from the input images (e.g., the noise variance in GLM). We take a similar approach of first running the GLM detector without smoothing and using the resulting SPM at a user-chosen threshold to estimate the probability model. To study the sensitivity of the method to the parameter settings, we ran experiments where the values of the singleton potentials and the compatibility matrices varied substantially (0.1 to 2 times the estimated frequencies). The variability in the detection accuracy (3-7%) was within the variability across different data sets as reported below.

Empirical Evaluation

To quantitatively evaluate the performance of the method, we generated realistic phantom data by applying EM segmentation [19] to an anatomical MRI scan and placing activation areas of variable size (average diameter of 15mm) randomly in the gray matter. We then downsampled the scan to an fMRI resolution. The gray matter voxels represent 10% of the total number of voxels in the volume, and the active voxels represent about 10% of the gray matter voxels in these images. We then created simulated fMRI scans based on a fixed parametric hemodynamic response function, an event-related protocol, and varying levels of noise. We used the estimated SNR, $\widehat{\mathrm{SNR}}=-10{\log }_{10}(\mid B\widehat{\beta }{\mid }^2)∕{\widehat{\sigma }}^2$, to determine a realistic level of the simulated noise as the true SNR is unaccessible for real fMRI scans. Since the signal and the noise overlap in some frequency bands, part of the noise energy is assigned to the estimated signal during detection. The estimated SNR is therefore an optimistic approximation of the true SNR, which can still be used as a monotonic upper bound of the true SNR. In our real fMRI studies, the estimated SNR is about −5dB. Here, we illustrate the results for two levels of true SNR, −6dB and −9dB, which correspond to estimated SNR of −4.3dB and −6.2dB respectively.

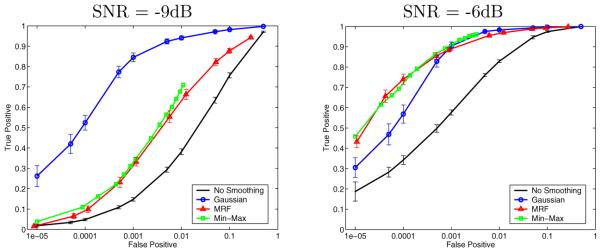
In all experiments, we used the same GLM detector based on a 10-bin non-parametric hemodynamic response function. To create a baseline for comparison, we ran the GLM detector with and without Gaussian smoothing. To evaluate the Markov priors, we ran GLM coupled with the exact Min-Max solver and with the approximate Mean Field solver on the same raw images. Fig. 2 shows the ROC curves created for the four methods by varying the threshold applied to the GLM statistic. Due to the large number of voxels in the volume and the relatively small number of active voxels, only very low false positive rates are of interest (we focus on the false positive rates below 0.1%, which corresponds to about 10% of the total number of the active voxels, or approximately 250 voxels). The error bars indicate the standard deviation of the true detection rate over 15 different, independently created and processed, data sets. The Min-Max ROC curve does not have the error bars, as the estimation takes too long (1 to 3 hours for a single run). Moreover, the Min-Max ROC curve is incomplete because extreme threshold values cause it to run even longer (we stopped the runs after 3 hours).

Fig. 2.

ROC curves for different smoothing techniques, at two noise levels. False positive rate is shown on the log scale

The Mean Field detection accuracy is very close to the exact Min-Max solution, providing a reasonable approximation to the exact solution that also takes much less time to compute (most Mean Field runs finished in a few minutes). The Min-Max accuracy is sometimes lower than the Mean Field accuracy, which appears to contradict the optimality of Min-Max. However, we note that both algorithms solve a particular estimation problem that does not necessarily describe the ground truth precisely but rather approximates it using a Markov model. Thus, the lowest energy state under this model might not be the best detector in practice. It is still reassuring to see that the approximate solver performs as well as the exact algorithm. It also suggests that more realistic spatial priors could further improve the detection accuracy.

As expected, the accuracy of all methods improves with increasing SNR. At high noise levels (low SNR), Gaussian smoothing outperforms MRFs. As the simplest smoothing technique, Gaussian smoothing is more robust to noise. We also believe that our current way of constructing the likelihood term in the MRF model over-emphasizes the data evidence over the prior. We are investigating ways to compensate for this in the estimation of the model. As the SNR increases, MRFs provide better regularization of the activation state (for example, at SNR=−6dB, at the false positive rate of 0.01%, the MRF outperforms the Gaussian smoothing by about 15% in true detection accuracy; at 70% true detection, the MRF approximately halves the false detections compared to the Gaussian smoothing). With the improving scanning technology, we believe MRFs will become even more helpful in reducing spurious false detection islands.

3 Anatomical Priors for Spatial Regularization

The general nature of the Mean Field algorithm allows straightforward extension of the probabilistic model in the previous section to include the tissue type for each voxel. We define V = [V₁, …, V_N] to be the tissue types of all voxels, and W = [W₁, …, W_N] the tissue type observations, such as a result of an automatic segmentation procedure. W_i’s are noisy observations due to imperfect registration between the fMRI image and the anatomical scan, the mismatch in their resolution and the noise in the segmentation itself. Now each voxel has two hidden attributes: the activation state X_i and the tissue type V_i. We combine these attributes into a single hidden node U_i, as illustrated in Fig. 3. For example, for a binary activation states (active or not active) and three tissue types (gray matter, white matter, or other), U_i has six possible states. Similarly to the derivations in the previous section, the MAP estimate in this case is as follows:

Fig. 3.

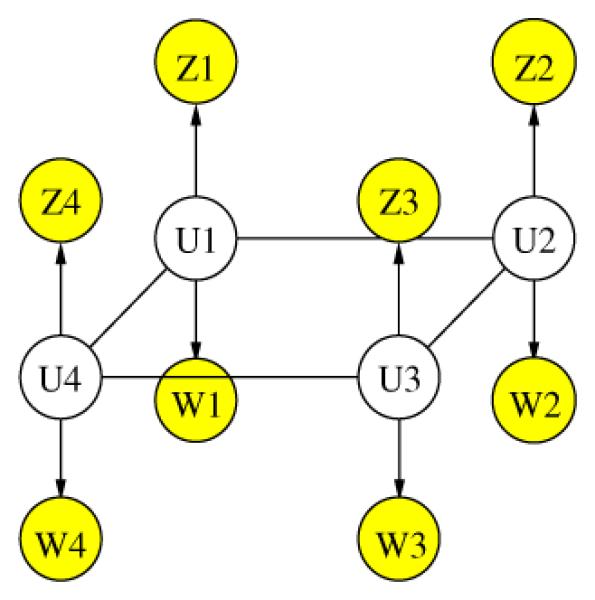
Graphical model for P_{U ,Z ,W}

$$\begin{array}{cc}\hfill {\mathit{u}}^{\ast }& =\arg \underset{u}{\max }{P}_{\mathit{U}\mid \mathit{Z},\mathit{W}}(u\mid z,w)=\arg \underset{u}{\max }{P}_{\mathit{U}}\left(\mathit{u}\right)P_{\mathit{Z}\mid \mathit{U}}(z\mid u)P_{\mathit{W}\mid \mathit{U}}(w\mid u)\hfill \\ \hfill & =\arg \underset{u}{\max }\frac{1}{\lambda }\prod _{<i,j>}{\Psi }_{ij}(u_i,u_j)\prod _i{\Psi }_i\left(u_i\right)P_{Z_i\mid U_i}(z_i\mid u_i)P_{W_i\mid U_i}(w_i\mid u_i)\hfill \end{array}$$ (7)

We assume that the segmentation W and the fMRI observation Z are conditionally independent given the state of the voxel since they are obtained from two different images. Similarly to the previous section, we derive the iterative update step in the estimation procedure:

$$b_i^{t+1}\left(u_i\right)\leftarrow \gamma P_{W_i\mid U_i}{P}_{Z_i\mid U_i}(z_i\mid u_i){\Psi }_i\left(u_i\right)e^{{\Sigma }_{j\in N\left(i\right)}{\Sigma }_{u_j=1}^M{b}_j^t\left(u_j\right)\log {\Psi }_{ij}(u_i,u_j)}$$ (8)

This update rule is similar to Eq. (6), with the exception of the extra likelihood term $P_{W_i\mid U_i}(w_i\mid u_i)$ for the tissue type observation. The compatibility matrix Ψ_ij (x_i, x_j) is M × M , where M is the number of states in U_i.

Empirical Evaluation

We used the same phantom data sets described earlier to evaluate the performance of the anatomically-guided detectors. The basic GLM with anatomical prior suppresses activations outside of the gray matter using segmentation as a guidance (“soft” masking could also account for misregistration and errors in segmentation). To incorporate the anatomical information into the Gaussian filter, we adjust the weights of the filter based on the tissue types of the voxel’s neighbors: when evaluating the filter at voxel i, we assign higher weights to the neighbors sharing the same segmentation results as voxel i. Fig. 4 illustrates the ROC analysis for the three regularization methods investigated in the previous section (solid lines) and their anatomically-based variants (dashed lines). We omit the Min-Max solver for the MRF model, as it cannot handle multi-valued states.

Fig. 4.

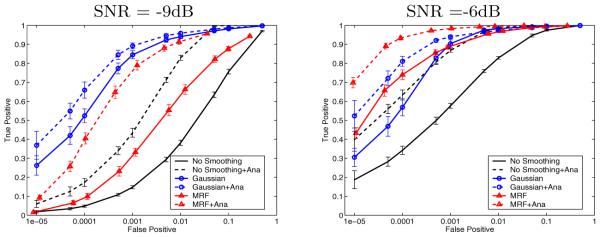
ROC curves for different smoothing techniques augmented with the anatomical information, at two noise levels. False positive rate is shown on the log scale

In addition to the trends observed before, we note that the anatomical information significantly boosts the performance of all detectors at all noise levels. At high noise levels (SNR = −9dB) and false positive rates between 0.01% and 0.1%, all methods gain at least 10% in true detection rate when using the anatomical information. The MRF model benefits more than the Gaussian smoothing, but its detection accuracy is still lower. At the lower noise level (SNR = −6dB), the basic GLM detector augmented with anatomical information approaches the performance of the Gaussian smoothing. At 0.01% false positive rate, the anatomically-guided MRF outperforms the anatomically-guided Gaussian smoothing by about 15% in true detection rate, achieving over 90% detection accuracy. The large boost experienced by the basic GLM when augmented with anatomical information is easy to understand: since false detections occur relatively uniformly throughout the volume, masking the gray matter improves the performance substantially.

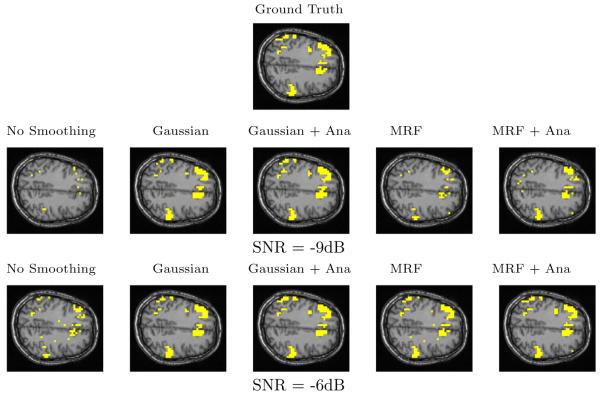
In addition to the quantitative analysis presented above, we find it useful to visually inspect the resulting activation maps. Fig. 5 illustrates the detection results by showing one axial slice of the estimated activation map. The top image shows the phantom activation areas that were placed in the volume and used to generate the simulated fMRI scan. The middle and the bottom rows show the same slice in the reconstructed volume at two different noise levels. All the reconstructions were performed at 0.05% false positive rate. In other words, each image in Fig. 5 shows one slice in the reconstructed volume that corresponds to a point on the ROC curve of the respective detector at 0.05% false positive rate.

Fig. 5.

One slice from estimated activation maps for the same ground truth at 0.05% false positive rate. True and false detections are shown in yellow. The on-line version shows true and false detections in different colors

The basic GLM produces a fragmented activation map that contains a number of false detection islands at high SNR and shows very little of the original activation at low SNR. Given either of these maps, the users would have troubles inferring the true activation areas and disambiguating them from spurious false detections. The Gaussian smoothing leads to a reasonable estimate of the ground truth. Gaussian smoothing tends to make the detections “spherical”, which may change the shape of the detected activations. The smoothing effectively over-estimates the extent of the regions. Consequently, many false positive voxels in the Gaussian smoothing occur at the boundaries of the activation regions. Imposing anatomical information reduces this over-smoothing effect for some of the areas. At low SNR (-9dB), the MRF model fills in many of the active pixels that were missed by the GLM, but as we saw before, it does not produce as accurate result as Gaussian smoothing. At higher SNR (-6dB), MRF produces a relatively accurate result. Not all of the scatter activation islands are removed through regularization, but the activation map looks more similar to the ground truth. The activation map is further improved when the anatomical information is incorporated into the model.

4 Real fMRI Experiment

In real fMRI experiments, the ground truth is unavailable, and ROC analysis is not possible. Instead, we visually compare the resulting activation maps produced by different detectors to evaluate their performance on reduced-length time courses. This effectively evaluates the ability of each method to reconstruct the true activation areas with less evidence on the strength of the signal.

In this fMRI study [23], the original scans were obtained during an auditory “two-back” word experiment. Each experiment consisted of five rest epochs and four task epochs, each epoch 30 seconds long. In the rest condition, the subjects were instructed to concentrate on the noise of the scanner and lie still. In the task condition, the subjects were presented with a series of pre-recorded single-digit numbers, one number every three seconds. The subjects were asked to tap their index finger to the thumb when hearing a number that was the same as the one spoken two numbers before. The experiment was repeated ten times for each subject. The anatomical images were acquired on a 1.5 Tesla GE signa clinical MR scanner (T1-weighted SPGR, 256×256, 124 slices, 1.5mm slice thickness). The EPI images were acquired on the same scanner (axial, TR/TE=2500/50msec, FA90, 64×64, 24 slices, 6mm slice thickness, no gap). The original study contains nine subjects, but for the purposes of voxel-by-voxel comparison of the detectors, we present the results for one subject across all detectors. The estimated SNR when averaging over all voxels in the brain was −4.7dB (−2.3dB when averaging voxels in selected ROIs relevant to the task).

Fig. 6a shows one axial slice in the reconstructed activation map using GLM without any spatial smoothing on the full-length fMRI signal (all 9 epochs). The ground truth for this scan is unknown, but we can use this map as a visual reference when evaluating the performance of the detectors on the time course of reduced length. For example, Fig. 6b shows the result of applying the same GLM detector to the first 5 epochs of the time course. This map is more fragmented due to loss in SNR from reducing the length of the signal. The other four images illustrate the results of applying GLM with the Gaussian smoothing and the MRF priors, as well as their anatomically augmented versions. Although Gaussian smoothing removes most of the single voxel activation islands, its activation map (Fig. 6c) is an overestimate compared with Fig. 6a. Anatomical weighting slightly reduces the overestimate in the Gaussian smoothing. MRF regularization (Fig. 6e,f) yields reconstruction results that are close to the activation map estimated from the full-length signal, but do not look overly smoothed. This highlights the potential benefit of using the Markov priors in fMRI detection. Similarly to the Gaussian smoothing, the MRF model benefits from using anatomical information to remove spurious activations.

Fig. 6.

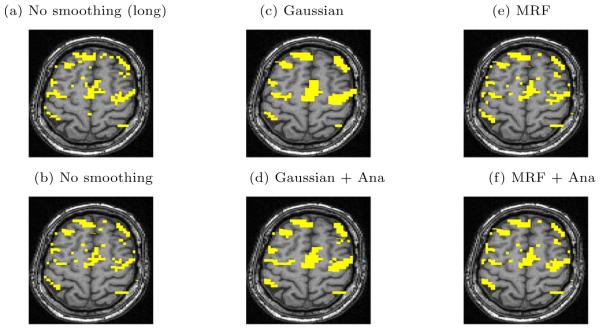
Real fMRI study. One slice in the estimated activation map. (a) No spatial smoothing, using the entire time course. (b)-(f) Estimation based on the first five epochs of the time course using different spatial smoothing methods

5 Discussion and Conclusions

Our experiments confirm the importance of spatial regularization in reducing fragmentation of the activation maps. This paper investigates two improvements in spatial modelling for fMRI detection: Markov priors and anatomical bias. An MRF provides a spatial prior that refines the structure of the resulting activation map over the Gaussian smoothing, as demonstrated by our experiments on phantom and real data. In this work, we explored fast approximate solvers in application to MRF-based fMRI detection and showed that they provide reasonably accurate approximations to the exact solution while taking substantially less time to evaluate. We also note that since the Markov model itself is an approximation of the real geometry of the activation regions, we should not dwell on the small differences in the activation maps introduced by the approximate solvers but rather focus on their performance relative to the ground truth.

A separate insight of this paper is that we can use anatomical information to bias the fMRI detector. Gaussian smoothing can be straightforwardly augmented with the anatomical prior by rescaling the coefficients of the smoothing kernel. Moreover, we derived an algorithm for anatomically-guided MRF estimation. One of the problems that should be investigated in the future is the partial voluming effects. The anatomical information comes at much higher resolution than the fMRI signals. Right now, we downsample the anatomical scan to match the resolution of the functional scan. A better solution would be to use the high-resolution anatomical scans to resolve the activation in the functional voxels that are on the boundary of the gray matter, leading to a “super-resolution” detector.

We evaluated the methods on phantom data by performing ROC analysis and on real data by studying their ability to recover activation from significantly shorter time courses. While in high noise settings the Gaussian smoothing outperformed other methods, as the SNR in the images increased, the Markov priors offered a substantial improvement in the detection accuracy. Using this smoothing prior enabled us to shorten fMRI scan length by half while retaining the detection power comparable with the full-length fMRI scan. We expect a similar effect to occur with respect to the spatial resolution when we extend the method to utilize the anatomical information at the original scan resolution. As the quality of the scanning equipment improves, the sophisticated spatial models, such as MRFs, will become even more important in recovering the details of the activation regions.