A High-resolution Atlas and Statistical Model of the Vocal Tract from Structural MRI

Abstract

Magnetic resonance imaging (MRI) is an essential tool in the study of muscle anatomy and functional activity in the tongue. Objective assessment of similarities and differences in tongue structure and function has been performed using unnormalized data, but this is biased by the differences in size, shape, and orientation of the structures. To remedy this, we propose a methodology to build a 3D vocal tract atlas based on structural MRI volumes from twenty normal subjects. We first constructed high-resolution volumes from three orthogonal stacks. We then removed extraneous data so that all 3D volumes contained the same anatomy. We used an unbiased diffeomorphic groupwise registration using a cross-correlation similarity metric. Principal component analysis was applied to the deformation fields to create a statistical model from the atlas. Various evaluations and applications were carried out to show the behaviour and utility of the atlas.

1. Introduction

The vocal tract is a complex system that consists of both movable and immovable structures, coordinating numerous functions. It is involved in critical human functions such as breathing, eating, and speaking. The movable structures such as the lips, jaw, tongue, and velum are the primary articulators during speech production. In particular, the human tongue forms remarkably complex shapes. It is a muscular hydrostat [1] with three orthogonal fibre directions and extensive fibre inter-digitations. Any bundle of fibres may contain multiple muscles, including intrinsic and extrinsic muscles, categorized by their function. The understanding of tongue muscle structure and function is essential for the diagnosis and treatment of disease and for the scientific studies of the vocal tract itself. To date, however, frustratingly little is known regarding the relationship between tongue structure and function. This is partly because the complex anatomy of the tongue poses challenges to spatially distinguishing each muscle and characterizing muscle interaction and function [2].

Imaging of the human vocal tract and tongue with magnetic resonance imaging (MRI) has played an essential role in interpreting muscle anatomy and function. MRI is a noninvasive imaging technique which can capture high spatial resolution images (high-resolution MRI), muscle fibre directions (diffusion tensor MRI), and tissue point motion (tagged MRI), leading to functional information about the vocal tract [3–5]. MRI provides quantities that capture features of vocal tract structure and function including surface shapes [6] and the deformation of the internal tongue musculature [4, 5]. MRI-based imaging continues to be a crucial tool for vocal tract research.

Although MRI has played an important role in vocal tract imaging, there are several limiting factors in its use in vocal tract analysis. First, the size and shape of the vocal tract including the tongue and muscles vary from one subject to another as illustrated in Fig. 1. As a result, objective assessment of similarities and differences in tongue structure and function has been performed using unnormalized data; this process, however, is biased by differences in size, shape, and orientation of the structures. Second, there exists no comprehensive framework to assess variability of the vocal tract’s hard and soft tissue structures. Both of these limitations can be addressed by using an atlas, which provides a normalized space in which all subjects from a target population can be mapped and compared. This in turn facilitates quantitative comparisons of anatomical features [7] including their statistical variation [8].

Figure 1.

Examples of high-resolution MR images acquired at rest position. Each subject has different vocal tract proportions. The white rectangle shows the vocal tract area.

Atlases constructed from populations of subject images are widely used computational tools, playing important roles in the diagnosis and treatment of diseases, segmentation and labelling for surgical planning, and provision of a common coordinate space for comparing subjects of all types [9, 10]. Brain atlases, in particular, have been used as references for normalization of groups of individuals, spatial maps for brain delineation, and characterization of tissue distribution [11]. To the best of our knowledge, however, currently there is no atlas constructed from a population of images for the study of vocal tract structure and function.

In this work, we constructed a vocal tract atlas and statistical model using structural MRI. Together, the atlas and the statistical model provide an average description of human vocal tract architecture along with its variability within the training population. The atlas building method is a multi-step procedure as illustrated in Fig. 2. First, twenty normal subjects were imaged using three orthogonal image stacks (i.e., axial, coronal, and sagittal) (Fig. 2A). Second, for each subject a single high-resolution volume was generated via a super-resolution volume reconstruction technique (Fig. 2B) [12]. Third, we processed each volume to remove extraneous image data and bound the vocal tract in order for each stack to have the same anatomical structures (Fig. 2B). Fourth, we applied a state-of-the-art groupwise registration technique to construct an average atlas image volume together with its anatomical correspondences to each subject (Fig. 2C). Manual segmentation of the tongue and a variety of muscle structures was then carried out in the atlas (Fig. 2C). Finally, we performed principal component analysis (PCA) on the deformation fields resulting from atlas building, which yields a statistical model comprising principal modes of the sample covariance on the deformation fields (Figs. 2D and 2E). In this work, we use the term atlas to refer to the average of the warped volumes in the common space. The statistical model refers to the PCA analysis on deformation fields and other quantities computed in the atlas space.

Figure 2.

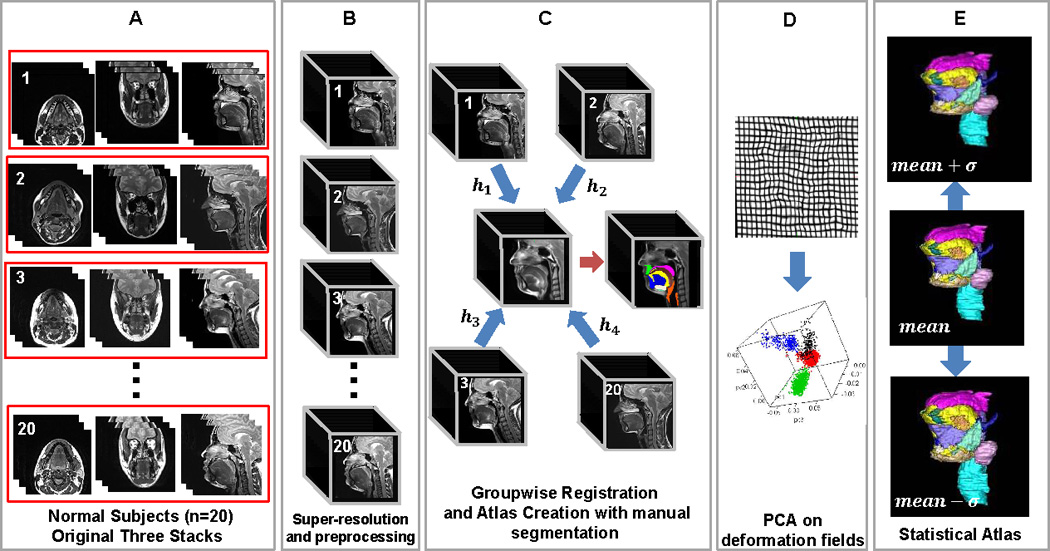
Overview of the atlas construction method.

The remainder of this paper is structured as follows. The atlas building method for the vocal tract is presented in Sec. 2. In Sec. 3, we describe experiments for quantitative and qualitative validations of the atlas using tongue and muscle segmentations. Results and discussion are presented in Secs. 4 and 5, respectively. Finally, the conclusion is given in Sec. 6.

2. Methods and Materials

2.1. Subjects and Data Acquisition

Twenty high-resolution MR datasets were used. All MRI scanning was performed on a Siemens 3.0 T Tim Trio system (Siemens Healthcare Inc., Malvern, PA) with a 12-channel head and a 4-channel neck coil using a segmented gradient echo sequence. In addition, a T2-weighted Turbo Spin Echo sequence with echo train length of 12 and TE/TR of 62ms/2500ms was used. The field-of-view (FOV) of each image was 240 mm×240 mm and was sampled at 256×256 pixels. Each dataset contains a sagittal, coronal, and axial stack of images encompassing the tongue and surrounding structures. The image size for the high-resolution MRI is 256×256×z (where z ranges from 10 to 24) with 0.94 mm×0.94 mm in-plane resolution and 3 mm slice thickness. The datasets were acquired at a rest position and the subjects were required to remain still from 1.5 to 3 minutes for each orientation. Table 1 summarizes the characteristics of the twenty healthy subjects.

Table 1.

Characteristics of the 20 healthy subjects (M: male, F: Female)

Subject	Age	Gender	Weight (lb)	Subject	Age	Gender	Weight (lb)
1	23	M	155	11	21	F	126
2	31	F	150	12	25	M	150
3	24	F	100	13	22	M	130
4	57	F	170	14	43	M	180
5	43	F	217	15	26	M	240
6	35	M	210	16	42	F	180
7	45	F	180	17	52	M	156
8	27	F	180	18	39	M	210
9	22	F	160	19	50	F	260
10	44	M	155	20	27	M	175

2.2. Construction of the Atlas and Statistical Models

2.2.1. Super-resolution Volume Reconstruction

It is desirable to start atlas creation from a high-resolution, isotropic 3D MR image volume. However, it was not possible to acquire such a volume directly because the image acquisition time would be longer than most subjects can refrain from swallowing. Therefore, we acquired three separate orthogonal image stacks—axial, sagittal, and coronal—and combined them using a maximum a posteriori-Markov random field (MAP-MRF) super-resolution technique [12]. The resulting volume has an improved signal-to-noise ratio (SNR) and an isotropic spatial resolution (0.94 mm × 0.94 mm × 0.94 mm); and because it uses edge-preserving regularization, the resulting volumes have clearer anatomical details than the source images themselves. A detailed description of the algorithm is found in [12].

2.2.2. Preprocessing

Once super-resolution volumes were generated for each subject, we performed several preprocessing steps prior to atlas construction. These steps include: 1) removing the MRI wraparound artefact, 2) spatially bounding the volumes so that each volume has the same anatomical features, and 3) intensity bias correction to reduce the impact of the intensity inhomogeneities [13]. These steps improve the registration performance in atlas construction (see Figs. 2A vs. 2B).

2.2.1. Groupwise Registration and Atlas Construction

Aligning and combining image data from a group of individuals into a common space allows us to build a model of average vocal tract anatomy, to obtain a volume with increased SNR, and to investigate similarities and differences across subjects [10]. The atlas building procedure involves a groupwise affine registration as an initial transformation followed by a groupwise deformable registration using the Symmetric Normalization (SyN) algorithm [13] to further register the image volumes. We obtained the final atlas by averaging all the registered volumes.

We made use of an unbiased groupwise registration using the SyN algorithm with a cross-correlation (CC) similarity metric [10, 13]. This method has been demonstrated to be among the most accurate intensity-based normalization methods [14]. Let ${\{I_i\}}_{i=1}^N$ be a group of N subject volumes (N=20 in this work) to be registered using the SyN algorithm and I_R be the atlas that is sought. The objective of the atlas construction is to find I_R that minimizes

$${\sum }_{i=1}^{N}E(I_R,I_i),$$

where E is an energy between the atlas and each image. The energy is evaluated by first finding a diffeomorphic registration between the two images and then evaluating a cost criterion based on the integrated CC metric and the two velocity fields describing the symmetric diffeomorphism.

The CC metric is evaluated locally at each spatial position x and is given by [15]

$$CC(I_R,I_i,x)=\frac{{\sum }_j((I_R(x_j)-{\mu }_{I_R}(x)){(I_i(x_j)-{\mu }_{I_i}(x))}^2}{{\sum }_j{(I_R(x_j)-{\mu }_{I_R}(x))}^2{\sum }_j{(I_i(x_j)-{\mu }_{I_i}(x))}^2},$$

where the local means μ_IR(x) and μ_Ii(x) are computed in a 5×5×5 square volume around x and the summations are also carried out over the same local volume. The use of a CC metric is particularly important to cope with the inter-subject image intensity inhomogeneity. Next, two optimal diffeomorphic transformations ${\phi }_{1i}^{*}$ and ${\phi }_{2i}^{*}$ for each image I_i are computed by minimizing the following functional:

$$E(I_R,I_i,{\phi }_{1i},{\phi }_{2i})={\sum }_{\mathrm{\Omega }}CC\left[I_R\right({\phi }_{1i}(x,\frac{1}{2})),I({\phi }_{2i}(x,\frac{1}{2})),x]+{\int }_0^{\frac{1}{2}}{\Vert v_{1i}(x,t)\Vert }_L^{2}dt+{\int }_0^{\frac{1}{2}}{\Vert v_{2i}(x,t)\Vert }_L^{2}dt,\text{subject to}\frac{\partial {\phi }_{k_i}(x,t)}{\partial t}=v_{ki}({\phi }_{ki}(x,t),t),k=1,2.$$

The velocity fields v_1i(x, t) and v_2i(x, t) are associated with the diffeomorphic transformations as described in [15]. The pairwise energy function is then defined as $E(I_R,I_i)=E(I_R,I_i,{\phi }_{1i}^{*},{\phi }_{2i}^{*})$. The algorithm iterates between finding a new atlas image I_R and finding optimal diffeomorphisms ${\phi }_{1i}^{*}$ and ${\phi }_{2i}^{*}$ until convergence to a minimum total energy is achieved.

2.2.3. Manual Tongue and Muscle Segmentation

For purposes of validation, a manual segmentation of the tongue surface was performed on each of the twenty subjects and the atlas (the “average” image volume) by one expert observer. With an in-house software based on Lee et al. [16], initial tongue segmentations were obtained and these segmentations were then refined manually using ITK-SNAP software [17]. This approach reduces segmentation time significantly and helps the observer to delineate the tongue regions consistently. These manual segmentations serve as ground truths to validate the mappings used for the atlas building.

In addition, a variety of vocal tract structures (16 in total) in the atlas were manually segmented, including (1) the hyoid bone, (2) the palate and maxillary bone, (3) the mandibular bone, (4) the tongue, (5) the larynx, (6) the soft palate and hard palate mucosa, (7) the geniohyoid muscle, (8) the genioglossus muscle, (9) the hyoglossus muscle, (10) the digastric muscle, (11) the mylohyoid muscle, (12) the styloglossus muscle, (13) the inferior longitudinal muscle, (14) the superior longitudinal muscle, (15) the sublingual gland, and (16) the submandibular gland (see Figs. 3, 4, and 5). These manual segmentations allow construction of the statistical shape model so that it includes these additional muscles and structures in addition to the tongue surface.

Figure 3.

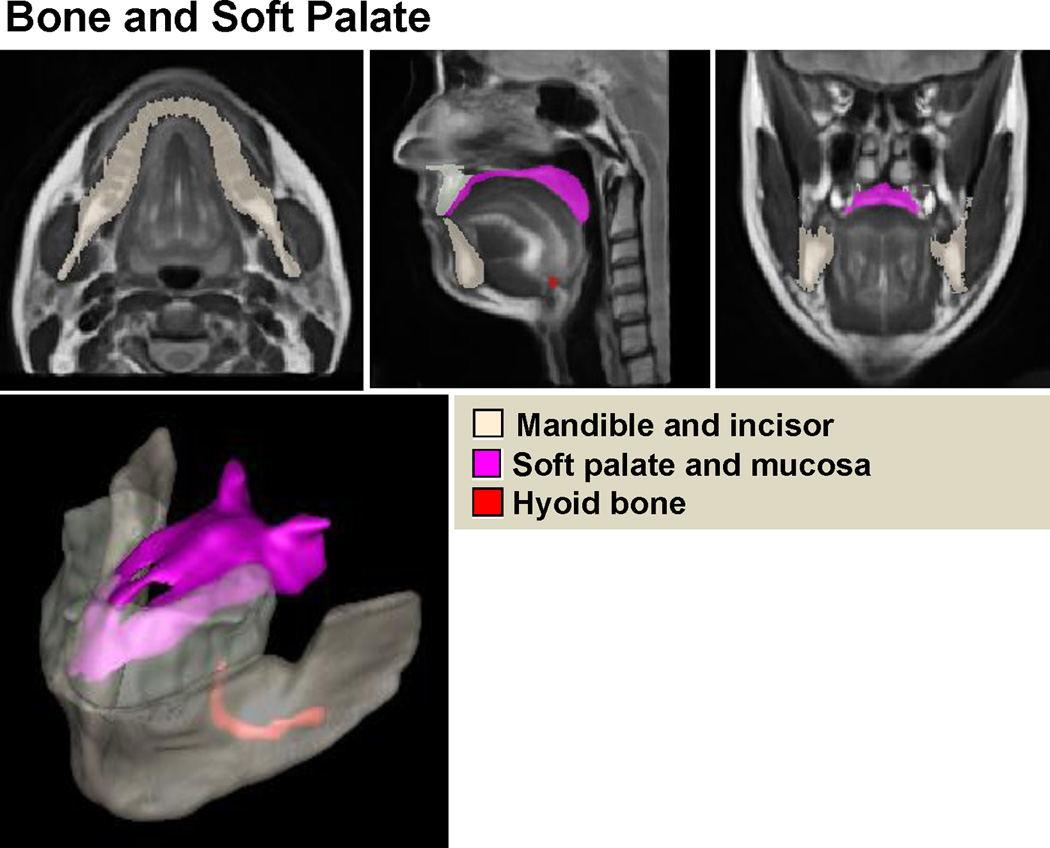
High-resolution vocal tract atlas overlaid with manual segmentation of bone and soft palate. The atlas allows definition of the standard bone and soft palate structures.

Figure 4.

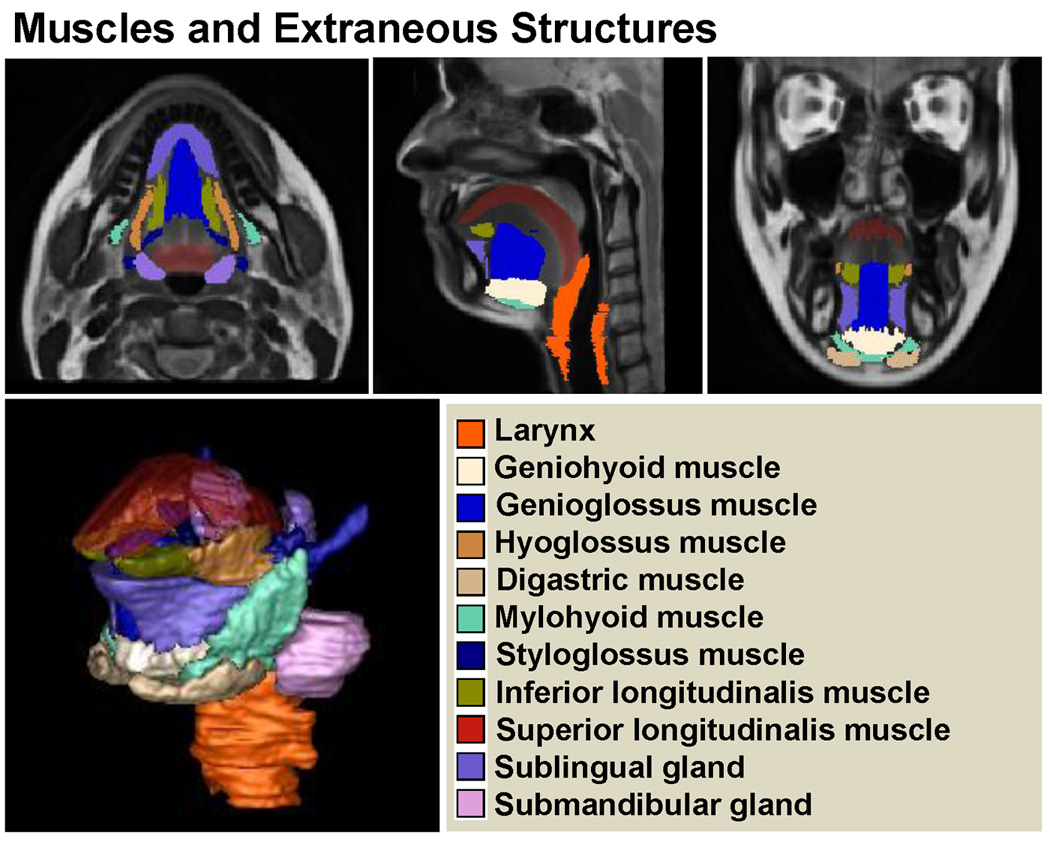
High-resolution vocal tract atlas overlaid with manual segmentation of muscles and extraneous structures. The atlas allows definition of the standard muscular structures.

Figure 5.

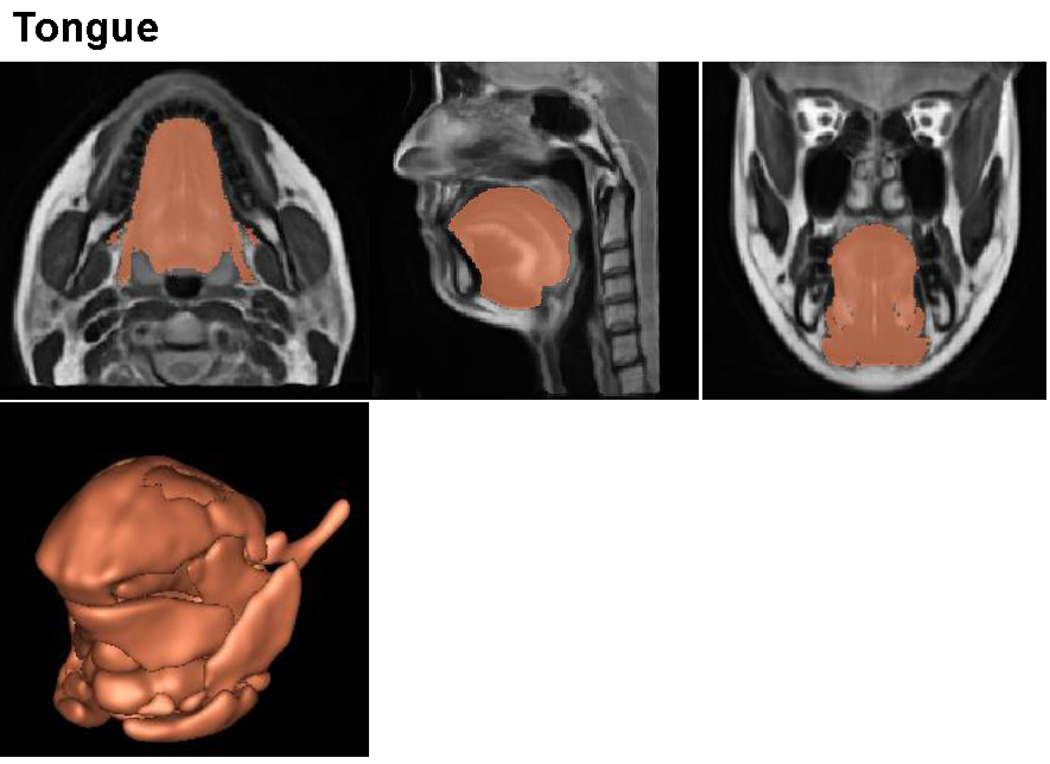
High-resolution vocal tract atlas overlaid with manual segmentation of the tongue. The atlas allows definition of the standard tongue.

2.2.4. Statistical Models Using PCA

In this section, we describe a PCA method to create the statistical models in atlas space. PCA is used to analyze the variability of the entire volume (see Fig. 6 below) as well as shape variability of the segmented structures within the volume (see Fig. 7 below). We apply PCA to the deformation fields required to map individual anatomies to the atlas, which provides second-order statistics by finding the principal modes of the sample covariance on the deformation fields. The PCA used here is a global PCA for the entire anatomy, which is different from multi-object statistical models such as in [18–21]. Let us first denote the deformation fields, {h₁, h₂, …, h_N}, N = 20, defined by the mappings from an individual anatomy to the atlas. In this work, we are particularly interested in two deformations. They are Deformation I, which is a global transformation that represents the homogeneous plus local volume changes achieved by removing the rigid transformations from the cascade of the affine transformation and local deformations (SyN), and Deformation II, which represents the local deformations provided by SyN only. The average deformation field at every point is then given by

$$m_h=\frac{1}{N}{\sum }_{i=1}^N{h}_i,$$

where N=20. The sample covariance of the deformation fields is constructed by

$$C=\frac{1}{N}{\sum }_{i=1}^N(h_i-m_h){(h_i-m_h)}^T,$$

where the mean offset map, h_i−m_h, is a column vector.

Figure 6.

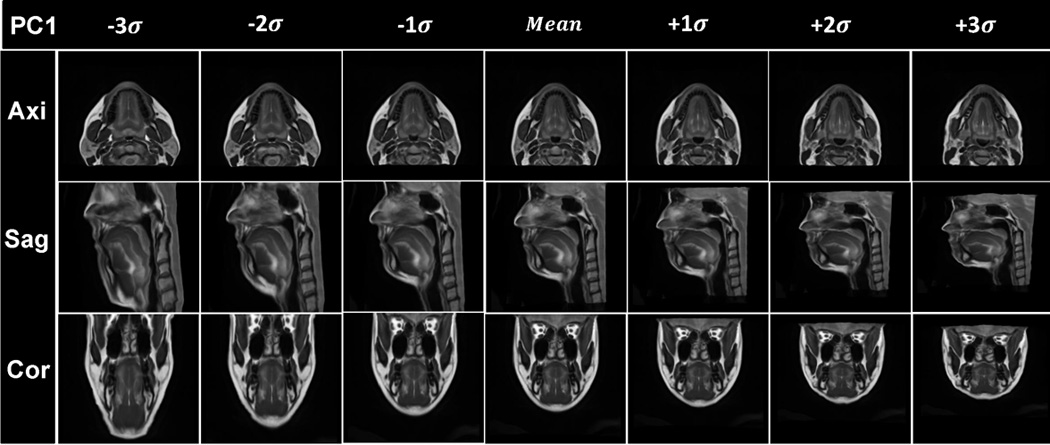
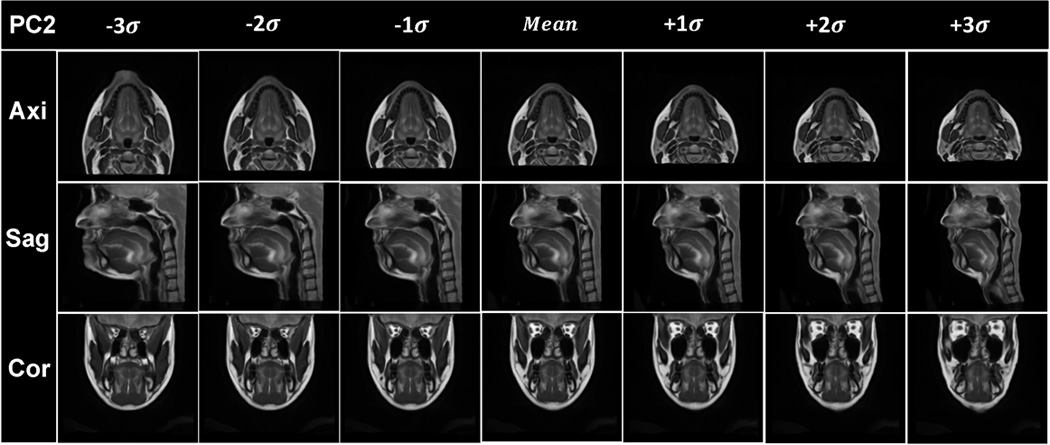
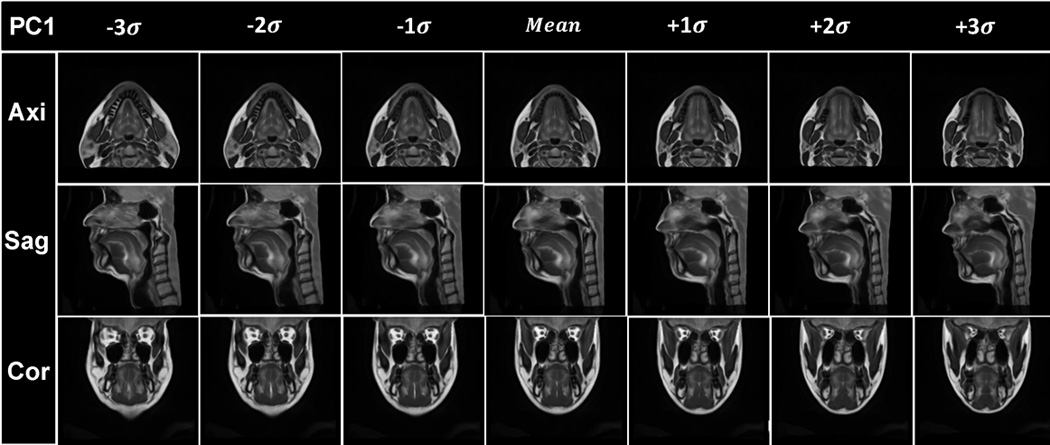
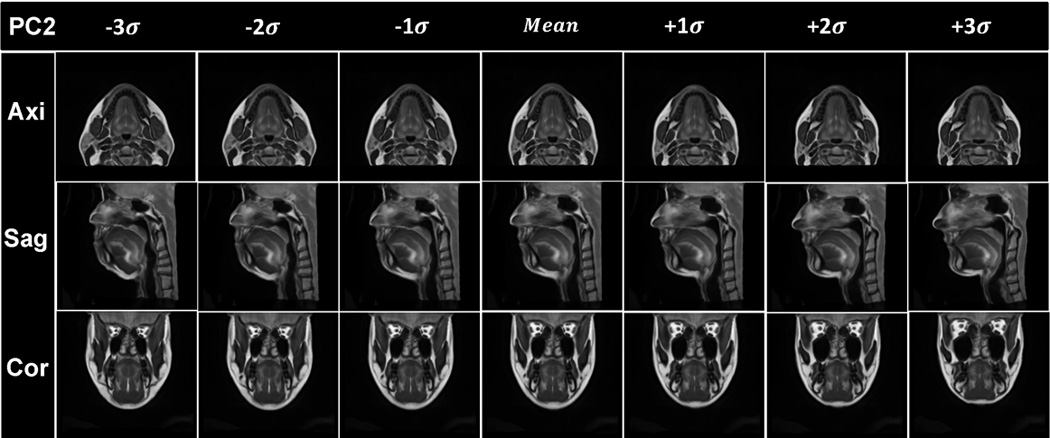
Visualization of the results of PCA analysis. The vocal tract atlas was warped by the first two PC’s using Deformations I and II. (a) PC1 of Deformation I shows variance in vertical length changes. (b) Atlas warping by PC2 of Deformation I shows variance in AP width. (c) Atlas warping by PC1 of Deformation II shows variance in the LR width. (d) Atlas warping by PC2 of Deformation II represents vertical differences in the posterior oral cavity. Deformation I represents the homogeneous plus local volume changes by removing the rigid transformations from the cascade of the affine transformation and local deformations (SyN) and Deformation II represents the local deformations only (SyN).

Figure 7.

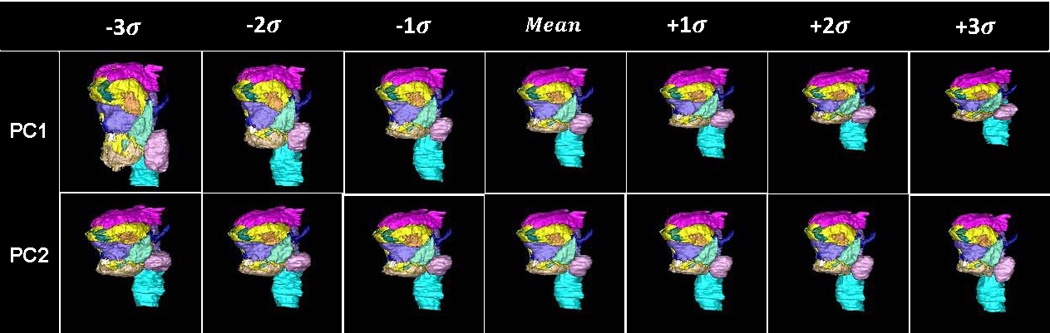
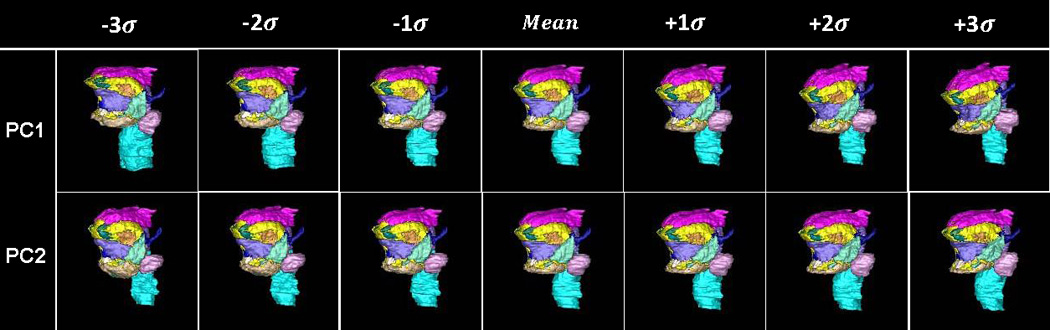
The surface renderings of segmented structures of the vocal tract atlas. (a) The surface of the substructures of the vocal tract atlas was warped by PC1 and PC2 of Deformation I, respectively. (b) The surface of the substructures of the vocal tract atlas was warped by the PC1 and PC2 of Deformation II, respectively.

Using singular value decomposition, the covariance matrix is decomposed into the set of orthogonal modes of variation and a diagonal matrix of corresponding singular values. The principal components (PC) of variation are the eigenvectors e_i of the covariance matrix C, and a deformation field h can be approximated using the first k eigenvectors e_i corresponding to the largest eigenvalues λ_i by

$$h=m_h+{\sum }_{i=1}^k{\omega }_i{e}_i,$$

where ω_i ∈ ℝ are weights for the different PCs. The instances of the atlas and segmented structures can then be computed by projection onto the PCs as given by

$$V_S\cong V(m_h+{\sum }_{i=1}^k{\omega }_i{e}_i)\text{and}{M}_S\cong M(m_h+{\sum }_{i=1}^k{\omega }_i{e}_i),$$

where V and M denote the atlas and the segmented structures in the atlas space and V_S and M_S represent the volume and shapes with different modes of variation. The mean shape, the PCs, and the associated eigenvalues compose the statistical model.

3. Evaluations and Applications

In this section, we describe a series of experiments to assess the vocal tract atlas and statistical models both qualitatively and quantitatively and to demonstrate potential applications of the atlas. The experiments include PCA analysis on the deformation fields, segmentation of the tongue using transformations used in building the atlas, and deformation-based voxel analysis.

3.1. PCA analysis

PCA’s are computed on two deformations (Deformations I and II) of the data to assess the contribution of homogeneous and local deformations. We create statistical models of the volume and shapes of different muscles using the two deformations and describe the effect of the PCs computed using each deformation.

3.2. Segmentation of the Tongue Surface Using the Atlas

We perform leave-one-out experiments using twenty-one subjects by creating twenty-one atlases, each made up of twenty subjects. We then use an atlas-based segmentation to delineate the tongue of each excluded subject in all twenty-one experiments. We use the same registration method used in our atlas building, which includes an affine registration, followed by a deformable registration using the SyN algorithm with the CC similarity measure. Two measurements are used to gauge the accuracy of the segmentation results. The first measurement is the dice similarity coefficient (DSC) defined as

$$\mathrm{D}\mathrm{S}\mathrm{C}=\frac{2|A_S\cap A_g|}{\left|A_S\right|+\left|A_g\right|},$$

where A_S and A_g are the areas enclosed by the segmented contour registered to the excluded subject and the manual segmentation in the excluded subject, respectively. The second measurement is the intraclass correlation coefficient (ICC) [22, 23], demonstrating the reliability of the volume measurements obtained from different methods. The mean and standard deviation of the measurements are computed to evaluate the variation of the segmentation results. In our study, statistical significance is evaluated using a paired t-test (p<0.05).

3.3. Deformation-based Voxel Analysis

The deformation fields (e.g., Deformations I and II) obtained in atlas construction carry information about global differences in the local volume when the Jacobian of the deformation field is applied. In addition, the deformation fields reveal the degree and location where the tongue volume varies during the atlas building. In this analysis, we derive the volume changes using Deformations I and II. We first compute the Jacobian of Deformation I to characterize volume changes that indicate anatomical changes. In order to observe volume changes in each muscle, a mask obtained from the muscle segmentation is used to restrict the muscle region in the atlas space. The Jacobian of the deformation field at each voxel is defined as follows:

$$J(\mathrm{x})=\left(\begin{array}{ccc}\frac{\partial h_x(\mathrm{x})}{\partial x}\hfill & \frac{\partial h_x(\mathrm{x})}{\partial y}\hfill & \frac{\partial h_x(\mathrm{x})}{\partial z}\hfill \\ \frac{\partial h_y(\mathrm{x})}{\partial x}\hfill & \frac{\partial h_y(\mathrm{x})}{\partial y}\hfill & \frac{\partial h_y(\mathrm{x})}{\partial z}\hfill \\ \frac{\partial h_z(\mathrm{x})}{\partial x}\hfill & \frac{\partial h_z(\mathrm{x})}{\partial y}\hfill & \frac{\partial h_z(\mathrm{x})}{\partial z}\hfill \end{array}\right)$$

The Jacobian determinant is then computed to calculate the volume changes at each voxel. The volume changes [24] in each muscle is given by

$$\text{Volume Ratio}=\frac{{\int }_{\Omega }|J(\mathrm{x})|M(\mathrm{x})dx}{{\int }_{\Omega }|M(\mathrm{x})|dx},$$

where |J(x)| denotes the Jacobian determinant and M(x):Ω ⊂ ℝ³ → (0,1) denotes the segmented mask region defined in the atlas space Ω.

4. Results

The computations were performed on a Dell R415 server running Fedora Linux 14, the system has 12 processors with a clock speed of 2.73GHz and 47.25GB of RAM. The computation time to create the atlas was 196 hours. The final vocal tract atlas and manual tongue and muscle segmentations are illustrated in Figs. 3, 4, and 5. The vocal tract atlas allows us to define the standard anatomy. The bone structure and palate are shown in Fig. 3, various muscles and other structures are shown in Fig. 4, and the tongue is shown in Fig. 5, respectively.

4.1. PCA Analysis

Figs. 6(a) and 6(b) show the statistical volume atlas using PC1 and PC2 of Deformation I, respectively. PC1 and PC2 appear to provide horizontal and vertical stretch and represent 63% and 19% of the statistical variability, respectively. This indicates that the greatest transformation between subjects is affine (i.e., global stretching, shearing, and scaling), accounting for 82% of the variance.

Figs. 6(c) and 6(d) show the statistical volume atlas using PC1 and PC2, respectively, of Deformation II. PC1 appears to represent local changes in the distribution of tissue in the lower half of the face and tongue so that positive PC1 shows a thin face from left-to-right and front-to-back and is elongated vertically, whereas negative PC1 shows a wide face front-to-back and left-to-right and is shortened vertically. These local effects account for 31% of the variance. In particular, for PC2, the most salient effect is the change from a very sloped chin (see images in Fig. 6(d), column −3σ) to a more horizontal chin (see images in Fig. 6(d), column +3σ).

Figs. 7(a) and 7(b) depict the 3D statistical shape atlas using PC1 and PC2 of Deformations I and II, respectively, applied to the segmented structures in the atlas. The shape changes are the same as those shown in Fig. 6, but here one can better appreciate the 3D characteristics of the shape changes and also observe a differentiation of effects on separate parts of the anatomy. Table 2 lists the variances accounting for each PC of Deformations I and II.

Table 2.

PC loadings for each deformation

PC	Deformation I	Deformation II
PC1	63%	21%
PC2	19%	11%
PC3	7%	9%
PC4	5%	8%
PC5	1%	7%

4.2. Segmentation of the Tongue Surface Using the Atlas

In this section, we describe the results of tongue segmentation using an atlas-based segmentation. Fig. 8 depicts an example of manual segmentation of the tongue (first row) and the segmentation obtained using the atlas-based segmentation (second row). Fig. 9 shows an example of the tongue volume comparison between the atlas-based segmentation and manual segmentation. The mean values of the tongue volume calculated from twenty-one subjects by using the atlas-based segmentation and manual segmentation of the subject were 118.1±30.9 ml and 120.9±29.3 ml, respectively. There was excellent correlation between the two measurements (r=0.9, p=0.23), with a best-fit linear relationship of y=1.0207x. The ICC was found to be 0.85.

Figure 8.

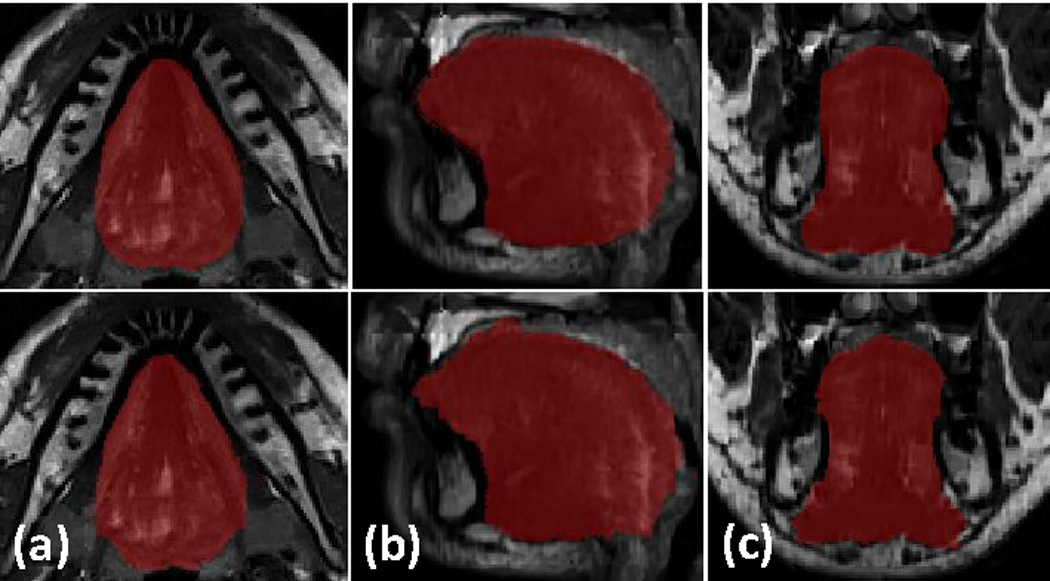
The first row shows one resulting volume from super-resolution volume reconstruction overlaid with a tongue manual segmentation. The second row shows segmentation using the atlas and the inverse mapping. Axial, sagittal, and coronal directions are shown in (a), (b), and (c), respectively. The DSC is 0.938 in this case.

Figure 9.

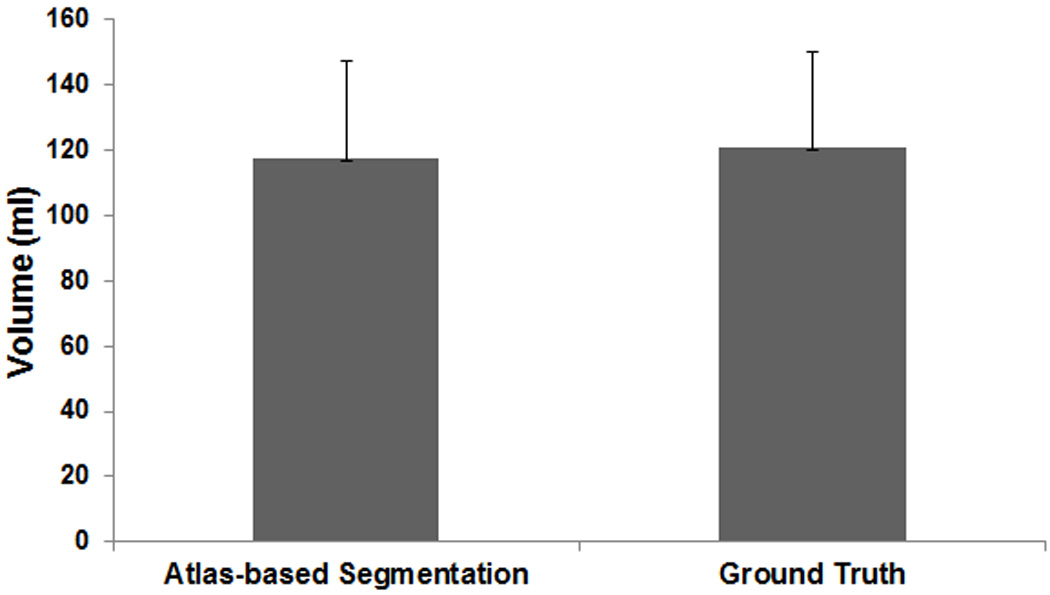
A plot of average volume of the original tongue region and segmentation by using the atlas and the inverse mapping.

A Bland-Altman analysis for manual segmentation and segmentation using the atlas is shown in Fig. 10; this indicates a satisfactory result with only one outlier. A plot of all DSC results is provided in Fig. 11. Across all twenty-one atlases, the mean and standard deviation of the DSC is 0.91 and 0.03, respectively. We found that two subjects had low DSCs (0.83 and 0.84) and their heads were quite rotated backward and forward. Rigid body registration, followed by deformable registration improved the dice coefficient to 0.84 and 0.86, respectively. The above results show that the atlas-based segmentation of the whole tongue from the atlas to the individuals accurately characterizes the geometry and volume provided by manual delineation.

Figure 10.

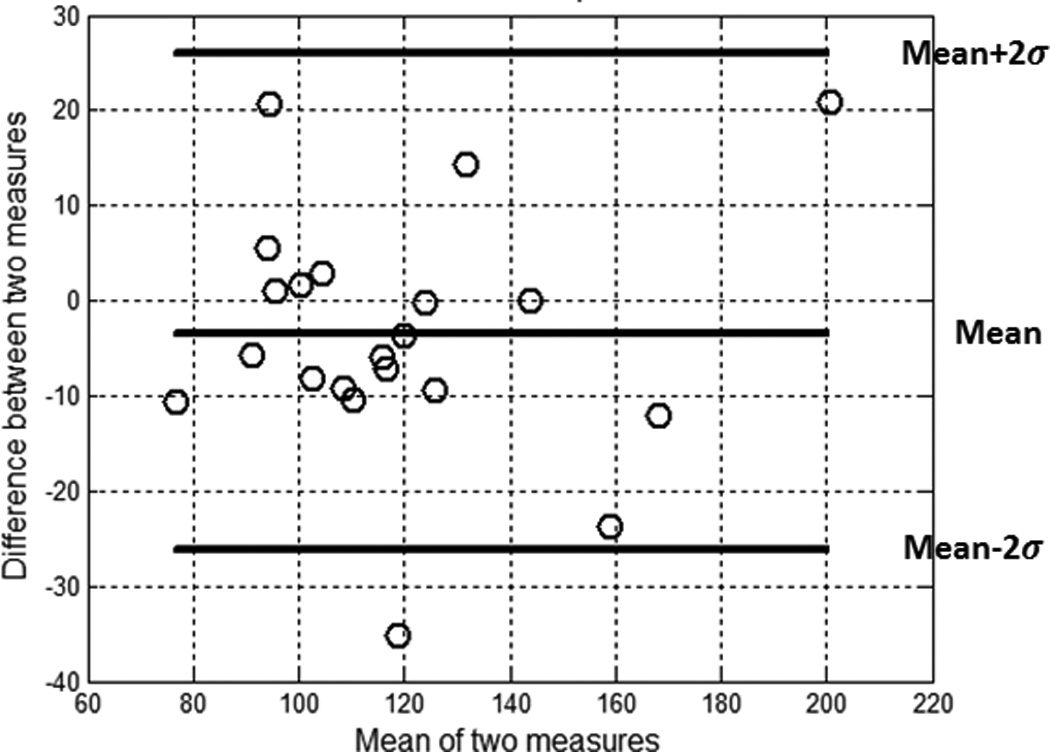
The Bland-Altman plot characterizing agreement between manual segmentation and segmentation using atlas.

Figure 11.

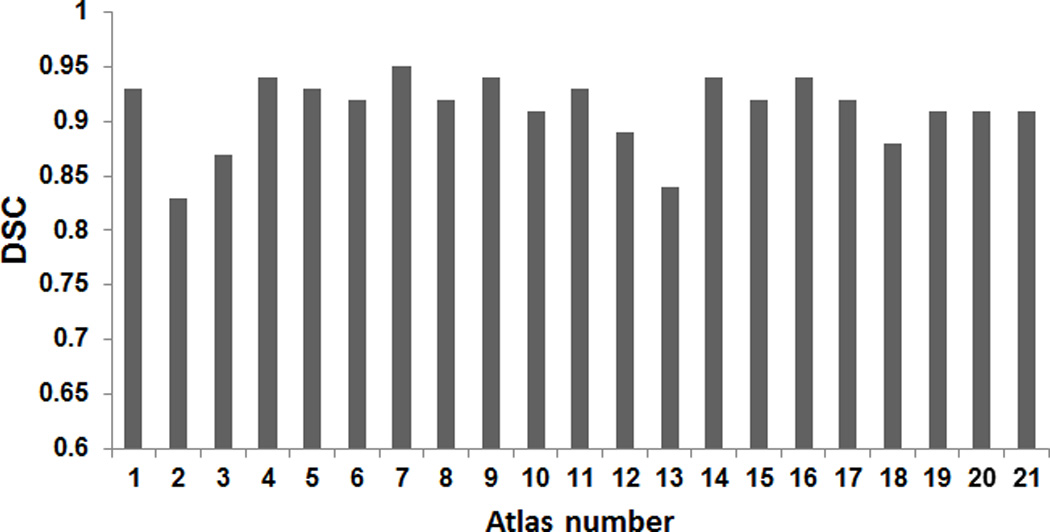
The dice similarity coefficient for all subjects used in the atlas building. The mean and standard deviation is 0.92±0.05.

4.3. Deformation-based Voxel Analysis

We present here a deformation-based voxel analysis including the Jacobian map and volume ratio using the Jacobian determinant. The 16 manually segmented structures shown in Figs. 3, 4, and 5 identify the regions of interest in the tongue and vocal tract. By analysing the Jacobian map derived from the deformation fields used in atlas-building or a pair-wise registration between the atlas and a subject, one can observe the volume and anatomical differences of each muscle. Fig. 12 shows an example of the log Jacobian map of Deformation I of the whole tongue in one subject. The red and blue colors indicate tissue expansion and shrinkage, respectively, relative to the atlas. Figs. 13(a) and 13(b) illustrate the statistics of the volume ratio for each muscle between the twenty subjects and the atlas using Deformations I and II, respectively. The mean and standard deviation of the volume ratios for the combination of the muscle volumes in the whole tongue using Deformations I and II is 1.0±0.2 and 1.0±0.1, respectively. The volume ratios for each of the 16 structures varied more, indicating that the distribution of muscle volume is not uniform across subjects.

Figure 12.

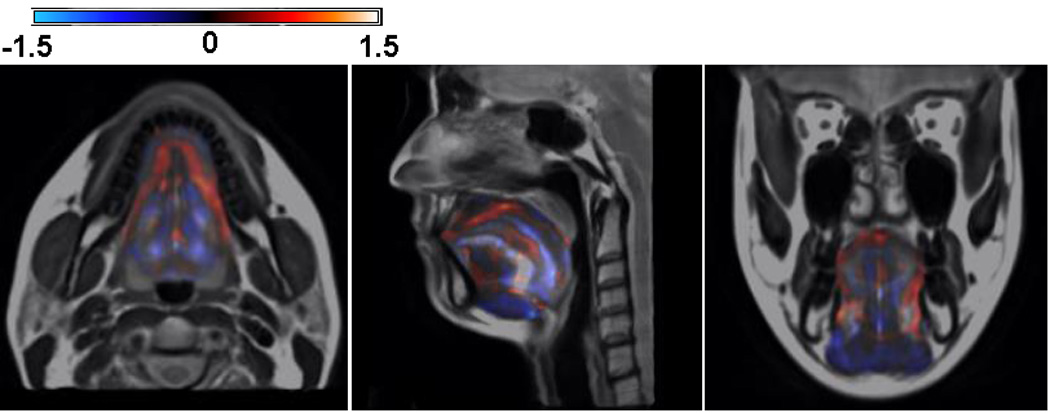
Illustration of the log Jacobian map of Deformation I. The blue shows the tissue expansion and the red indicates the volume shrinkage relative to the atlas. It is clearly shown that log Jacobian map exhibits the volume and anatomical changes of each muscle during the atlas building.

Figure 13.

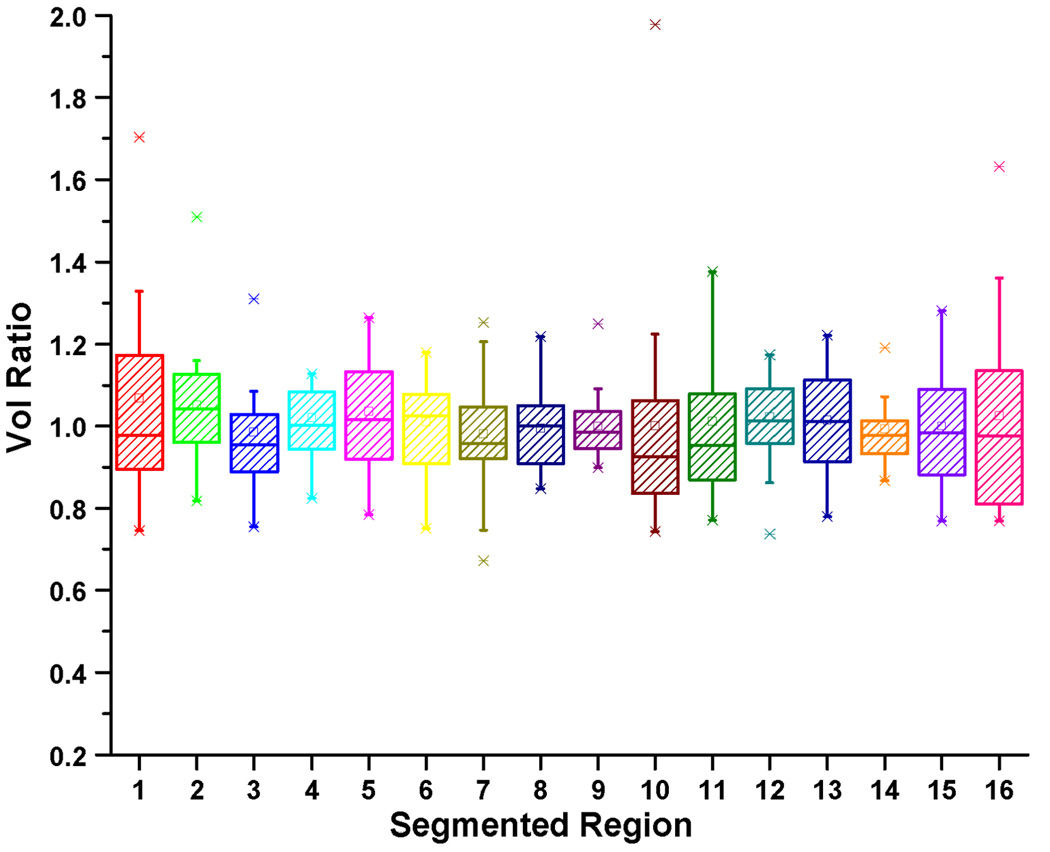
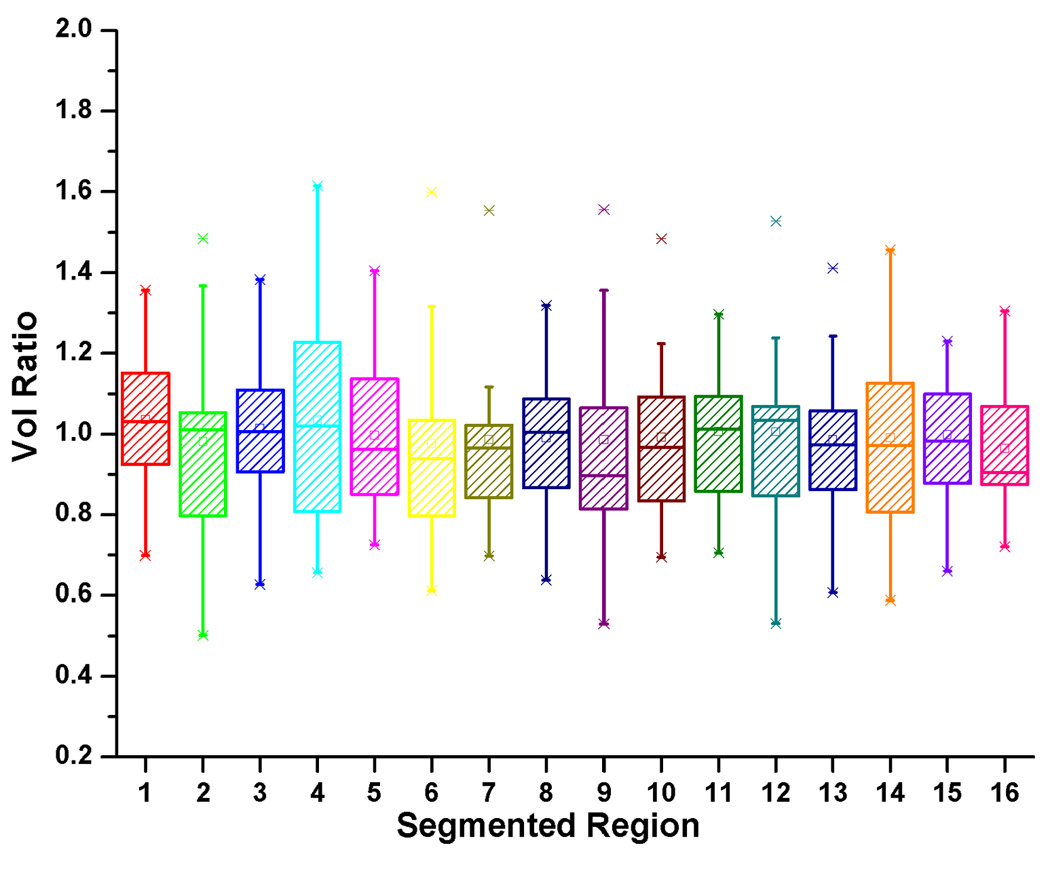
The box-and-whisker diagram for the volume ratio in each muscle using (a) Deformation I and (b) Deformation II. Please note that the combined volume ratio was preserved across subjects.

5. Discussion

An anatomical vocal tract atlas was created using a symmetric and diffeomorphic groupwise registration from the super-resolution volumes of twenty subjects. PCA was used to construct statistical models for the whole volume and for the segmented vocal tract structures.

There are several important characteristics and potential uses of this vocal tract atlas. First, the atlas represents an average, not a specific subject, and therefore any use of it is not biased by a specific individual's anatomical features. Second, the entire volume and all the segmented structures are normalized at the same time, saving computation time in this and future atlases. Third, information from the atlas can be incorporated into the segmentation or registration process as statistical prior information. Fourth, the atlas allows the capture of anatomical variability by providing a coordinate space for motion analyses using PCA or cluster analysis of velocity fields as in [25]. In addition, statistical analyses can be applied to individual structures or the entire volume.

The transformations needed to deform subjects to the atlas were analysed by PCA. Affine transformation is adequate when the difference between images involves global rotation, scaling, and shearing. Deformable registration is used to capture the local shearing or scaling as shown in Figs. 6(c) and 6(d). In the present study, Deformation I was sufficient to capture the most of the variance between subjects as these are all normal adults. However, when creating atlases or transforming other populations into this atlas, such as patients with structural malformations or children, then the local deformation may yield a larger percentage of variance.

For different reasons, the literature indicates the lack of consensus on how to measure volume differences across subjects. For example, there has been some literature questioning the relative sizes of muscles volume and relative sizes of muscles consistent across subjects with different total muscle volumes [26]. In their work, these questions were addressed by measuring muscle volumes in healthy subjects from MRI. In the present work, however, deformation fields were used to measure volume differences of muscles and extraneous structures relative to the atlas.

We see a few directions for improvement in the present work. First, we will characterize the muscle interaction and function using both muscle segmentation and motion information obtained from the speech data. Second, we will compare muscle volume differences from (1) the atlas results, (2) those results transformed back into subject’s space, and (3) unnormalized results to further determine the quality of the atlas results.

Following from analogous work in the brain [27, 28], we anticipate several applications of the atlas to the analysis of tongue image data. The atlas may be used to register functional data from different subjects to a common anatomical space, thereby allowing group-level inferences [29]. Individual differences in tongue and muscle structures as assessed by different imaging modalities, such as diffusion tensor imaging, could be related to normal variations of behaviour or one of many disease states. Thus far, it has been difficult to accurately characterize the relationship between structure (i.e., anatomy) and function (i.e., speech) due to the varied sizes and shapes of the tongue and its muscles. With future studies, this atlas has the potential to accurately inform how the interactions among different muscles impact overall speech production, opening a new window for the investigation of dynamic speech production and speech disorders.

6. Conclusion

In this work, we presented a vocal tract atlas construction method and statistical models of vocal tract variation from twenty normal subjects. Super-resolution volumes were constructed and unbiased groupwise registration was used to create the atlas and symmetric and diffeomorphic deformation fields from the atlas to the subjects. Principal component analysis applied to the deformation fields provided a statistical model of anatomic variation. PC1 and PC2 of Deformations I and II accounted for 82% and 33% of the variance, respectively. The single atlas-based segmentation of the whole tongue from the atlas to the individuals yielded accurate characterization of the geometry and volume (the mean of DSC was 0.9). This vocal tract provides an integrative framework in which individual subjects can be mapped and compared, thus opening new vistas for structural and functional studies of the vocal tract.