Hierarchical Factor Models for Large Spatially Misaligned Data: A Low-Rank Predictive Process Approach

Summary

This article deals with jointly modeling a large number of geographically referenced outcomes observed over a very large number of locations. We seek to capture associations among the variables as well as the strength of spatial association for each variable. In addition, we reckon with the common setting where not all the variables have been observed over all locations, which leads to spatial misalignment. Dimension reduction is needed in two aspects: (i) the length of the vector of outcomes, and (ii) the very large number of spatial locations. Latent variable (factor) models are usually used to address the former, although low-rank spatial processes offer a rich and flexible modeling option for dealing with a large number of locations. We merge these two ideas to propose a class of hierarchical low-rank spatial factor models. Our framework pursues stochastic selection of the latent factors without resorting to complex computational strategies (such as reversible jump algorithms) by utilizing certain identifiability characterizations for the spatial factor model. A Markov chain Monte Carlo algorithm is developed for estimation that also deals with the spatial misalignment problem. We recover the full posterior distribution of the missing values (along with model parameters) in a Bayesian predictive framework. Various additional modeling and implementation issues are discussed as well. We illustrate our methodology with simulation experiments and an environmental data set involving air pollutants in California.

1. Introduction

With enhanced capabilities in collecting, storing, and accessing geographically referenced data sets, spatial analysts today frequently encounter data comprising a large number of variables across a very large number of locations. In several instances, inference focuses upon three major aspects: (i) estimate associations among the variables, (ii) estimate the strength of spatial association for each variable, and (iii) predict the outcomes at arbitrary locations.

Modeling multiple geographically referenced outcomes proceeds from two different premises. One approach (Royle and Berliner, 1999; Gelfand et al., 2004) considers a conditional regression-like approach where the marginal distribution of the first outcome is specified, followed by the conditional distribution of the second outcome given the first, and so on. This approach is more suitable when there is a natural “ordering” of the outcomes suggesting the sequence for constructing the conditional distributions.

Settings that lack such information prefer joint modeling for the set of outcomes to avoid the explosion in models emerging from alternate ordering schemes. Conditional inference can subsequently proceed from the joint distribution by conditioning on the relevant variables. The challenge in the joint modeling approach is to specify valid multivariate spatial processes using matrix-valued, cross-covariance functions ([e.g., Ch. 7]; Banerjee, Carlin, and Gelfand 2004). Gelfand et al. (2004) offer a detailed comparison of both approaches for multivariate spatial data. Here we focus upon the joint modeling approach.

The linear model of coregionalization (LMC) proposed by Matheron (1982) is among the most general models for multivariate spatial data analysis. Here, the spatial behavior of the outcomes is assumed to arise from a linear combination of the independent latent processes operating at different spatial scales (Chilés and Delfiner, 1999). The idea resembles latent factor analysis (FA) models for multivariate data analysis (e.g., Anderson, 2003) except that in the LMC the number of latent processes is usually taken to be the same as the number of outcomes. Then, an m × m covariance matrix has to be estimated for each spatial scale (see, e.g., Lark and Papritz, 2003; Castrignanó et al., 2005; Zhang, 2007; Finley et al., 2008), where m is the number of outcomes. When m is large (e.g., m ≥ 5 and 300 spatial locations), obtaining such estimates is expensive. Schmidt and Gelfand (2003) and Gelfand et al. (2004) associate only an m × m triangular matrix with the latent processes. However, high dimensional outcomes are still computationally prohibitive for these models.

When the number of independent latent processes in an LMC is taken to be fewer than the number of outcomes (e.g., Zhang, 2007), we obtain a spatial factor model. Wang and Wall (2003) studied multivariate indicators of cancer risk in Minnesota using one spatial factor. Liu, Wall, and Hodges (2005) deployed multiple factors with each underlying factor explaining its own unique set of observed/measured variables. Christensen and Amemiya (2002) developed semiparametric latent variable (shift-factor) models for rectangular grids. Hogan and Tchernis (2004) fitted a one-factor spatial model and compared the results using different forms of spatial dependence through the single factor. Minozzo and Fruttini (2004) applied log-linear spatial FA to geo-referenced frequency counts adopting the classical proportional covariance model to the latent factors.

Our current work is similar to the aforementioned articles in its use of independent latent spatial processes as underlying factors. However, we propose three methodological innovations within this framework. First, we use a multivariate low-rank spatial process to achieve dimension reduction over space. Critically, we need to work with irregularly spaced locations that do not necessarily lie on a grid, nor can they be easily projected onto the same. Although there are several choices here, we deploy the multivariate Gaussian predictive process (Banerjee et al., 2008, 2010). The method is closely related to kernel-convolutions, splines and low-rank kriging, (see, e.g., Wikle and Cressie, 1999; Kamman and Wand, 2003; Ver Hoef et al., 2004; Paciorek, 2007; Cressie and Johannesson, 2008), all of which attempt to facilitate computation through lower dimensional process representations. The predictive process can be applied to any spatial correlation function and maintain the richness of desired hierarchical spatial modeling specifications using a set of locations (or knots).

Second, we do not fix the number of factors but model it stochastically. We do so differently from some existing approaches. For example, Lopes and West (2004) addressed this problem by constructing proposals using the results of a preliminary Markov chain Monte Carlo (MCMC) run under each model. Such an approach has high computational demands, becoming infeasible as the sample size and potential number of factors increase. Dunson (2006) introduced a model averaging method for FA, but the construction of factor selection is inconvenient for spatial models. Chen and Dunson (2003) proposed a Bayesian random effect selection method which is similar to what we propose but, instead of selecting random variables, we choose the underlying latent processes that capture spatial dependence. We avoid complex computational strategies such as reversible jump algorithms and build our adaptive models by utilizing some key identifiability results, hitherto largely unaddressed, to construct hierarchical models.

Third, we reckon with spatial misalignment in the context of spatial FA. Misalignment occurs frequently in spatial data when not all variables have been observed across all locations. Put differently, the sets of observed locations for the different outcomes are not identical (either because they are missing or have been collected by different monitoring sets). Assuming that all covariates are available at a location, we want to estimate the functional relationship between the covariates and the outcomes at that location—even if all the outcomes have not been observed there. We also seek to predict the outcomes at any arbitrary location in the domain, thereby estimating the response surfaces for each outcome.

Our motivating application pertains to ambient air quality assessment in California. The deleterious impact of air pollution upon health and quality of life is widely recognized as a major environmental issue (e.g., Dominici et al., 2006). Spatial interpolation of air pollutants plays a crucial role in assessing and monitoring ambient air quality and modeling multiple pollutants can capture associations within and across different locations, which can enhance predictive performance. Our data set includes five commonly encountered pollutants observed over 300 monitoring stations across California and is spatially misaligned in the aforementined manner. Estimating fully specified joint models for such data will be exorbitant, which is why multivariate spatial modeling has rarely been undertaken in such frameworks.

The remainder of this article is organized as follows. Section 2 describes the features of the LMC and discusses the model construction, identifiability issues, stochastic selection, and prior specification. Section 3 outlines the proposed class of low-rank adaptive spatial factor models, how we handle misaligned data, and carry out inference. Section 4 illustrates the analysis for two simulated data sets and one air quality monitoring data. Finally, Section 5 concludes the paper with a summary and an eye toward future work.

2. Model Construction

2.1 LMC Model Structure and Specification

LMC consists of decomposing the set of original second-order random stationary outcomes into a set of reciprocally orthogonal regionalized factors. Suppose, for a study region D ⊆ ℝ^d, an m × 1 process Z(s) = (Z₁(s), …, Z_m (s))′ is a second-order stationary process. Then, for all s, h ∈ ℝ^d and i, j = 1, …, m, we have E[Z_i (s)] = μ_i and cov{Z_i (s), Z_j (s + h)} = C_ij (h). The matrix-valued function C(h) = {C_ij (h)} is called the multivariate cross-covariance. Generally for i ≠ j, a change in the order of the variables or a change in the sign of the separation vector h changes the values of the cross-covariances. If both the sequence and the sign are changed, we would have the same value C_ij (h) = C_{j i} (−h), which implies C(h) = C(−h)′. C(h) must also be a positive definite function. That is, for any finite set of spatial locations s₁, …, s_n ∈ D and any vectors a_i ∈ ℝ^m, i = 1, …, n, $\text{var}\{{\sum }_i^n{\mathbf{a}}_i^{\prime }\mathbf{Z}({\mathbf{s}}_i)\}={\sum }_{i,j}^n{\mathbf{a}}_i^{\prime }\mathbf{C}({\mathbf{s}}_i-{\mathbf{s}}_j){\mathbf{a}}_j\ge 0$. Specifying a valid cross-covariance function is less straightforward because of this constraint, but several spectral and constructive approaches (Ver Hoef and Barry, 1998; Chilés and Delfiner, 1999) have been proposed and used in multivariate spatial analysis.

A straightforward cross-covariance is the so-called intrinsic specification, C(h) = ρ(h)T, where T is an m × m positive definite matrix and ρ(h) is a univariate correlation function. The limitation here is that each Z_i (s) has the same spatial parameters, so each outcome would have the same strength in spatial association over the domain. An extension (Wackernagel, 2003) specifies $\mathbf{C}(\mathbf{h})={\sum }_{k=1}^r{\rho }_k(\mathbf{h};{\mathit{\varphi }}_k){\mathbf{T}}_k$, where for each k, T_k is a rank-one positive semidefinite matrix and ρ_k (h; ϕ_k) is a correlation function that depends upon additional parameters ϕ_k. Here, r is the total number of different spatial correlation functions in the multivariate cross-covariance.

The spectral decomposition yields ${\mathbf{T}}_k={\xi }_k{\mathbf{u}}_k{\mathbf{u}}_k^{\prime }$, where u_k is the normalized (i.e., ‖u_k‖ = 1) eigenvector of T_k corresponding to the only positive eigenvalue ξ_k of T_k. Because T_k is symmetric with rank one, all its other eigenvalues are zero. This implies that there is an m × 1 vector, ${\mathit{\lambda }}_k=\sqrt{{\xi }_k}{\mathbf{u}}_k$, which is the square root of T_k such that ${\mathit{\lambda }}_k{\mathit{\lambda }}_k^{\prime }={\mathbf{T}}_k$. Although ‖u_k‖ = 1, it still has two possible directions. To build a one-to-one transformation between T_k and λ_k, we need to impose some further constraints on λ_k by, for instance, restricting the first element of λ_k to be positive.

Let w_k (s), k = 1, …, r, be independently distributed univariate Gaussian processes, each with unit variance and a parametric correlation function. We write w_k (s) ~ GP(0, ρ_k (·; ϕ_k)) with var{w_k (s)} = 1, cov{w_k (s), w_k (t)} = ρ_k (s, t; ϕ_k), and cov{w_k (s), w_l (t)} = 0 whenever k ≠ l for all s and t (even when s = t). Here ρ_k (·; ϕ_k) is a correlation function associated with w_k (s), and ϕ_k includes the spatial decay and smoothness parameters. We can easily see that the multivariate cross-covariance function for the process w_k (s)λ_k is ρ_k (h; ϕ_k)T_k and hence, for ${\sum }_{k=1}^r{w}_k(\mathbf{s}){\mathit{\lambda }}_k$, the function is ${\sum }_{k=1}^r{\rho }_k(\mathbf{h};{\mathit{\varphi }}_k){\mathbf{T}}_k$.

We often assume that the mean of the outcomes arises linearly in the predictors so that the mean of the jth outcome Y_j (s) is modeled as x_j (s)′ β_j, where x_ij (s) is a p_j × 1 vector of predictors, assumed to be known at location s, and β_j is the corresponding p_j × 1 vector of slopes. Let Y(s) be the m × 1 vector of outcomes with jth element Y_j (s) and let X(s)′ be an m × p block diagonal matrix, where $p={\sum }_{j=1}^m{p}_j$ and the jth diagonal block is given by x_j(s)′ and $\mathit{\beta }=({\mathit{\beta }}_1^{\prime },{\mathit{\beta }}_2^{\prime },\dots ,{\mathit{\beta }}_m^{\prime })\prime$ is a p × 1 vector of slopes. Then, the spatial factor model is

$$\mathbf{Y}(\mathbf{s})=\mathbf{X}(\mathbf{s})\prime \mathit{\beta }+\sum _{k=1}^r{w}_k(\mathbf{s}){\mathit{\lambda }}_k+\mathit{\epsilon }(\mathbf{s})=\mathbf{X}(\mathbf{s})\prime \mathit{\beta }+\mathbf{\Lambda }\mathbf{w}(\mathbf{s})+\mathit{\epsilon }(\mathbf{s}),$$ (1)

where Λ = (λ₁, …, λ_r) is a m × r matrix with kth column λ_k, w(s) = (w₁(s), …, w_r (s))′, and ε(s) is an m × 1 vector of measurement errors distributed as N (0, Ψ). The measurement error variance Ψ can be any m × m positive definite matrix but is usually assumed diagonal with elements ${\psi }_j^2$ for j = 1, …, m along the diagonal.

2.2 Identifiability in Spatial Factor Model

Model (1) is similar to FA models with the factor-loading matrix Λ and latent factor w(s), except that w(s) is now a multivariate stochastic process positing spatial dependence. As is well known (see, e.g., Anderson, 2003), orthogonal FA models must be further constrained to ensure identifiability. A widely used approach is to fix certain elements of Λ to constant values, usually to zeroes, such as restricting Λ to be an upper or lower triangular matrix with strictly positive diagonal elements (Lopes and West, 1999).

In LMCs, (see, e.g., Schmidt and Gelfand, 2003; Gelfand et al., 2004; Finley et al., 2008), a lower triangular Λ with positive diagonal elements identifies the covariances among the outcomes within a location because C(0) = ΛΛ′. But what we really seek to model is C(h). Finding proper identifiability constraints on Λ is equivalent to finding transformations that retain the statistical properties of the model.

Let P be an r × r orthogonal matrix, so that P′P = PP′ = I_r. The random effect term in (1) can be written as Λw(s) = ΛPP′w(s) = Λ̄ w̄(s), where Λ̄ = ΛP and w̄(s) = P′w(s). For nonspatial or traditional FA, the elements of w(s) are uncorrelated and the model is invariant to any orthogonal transformation because w(s) and w̄(s) have identical cross-covariances and ΛΛ′ = Λ̄Λ̄′. One can, therefore, obtain an infinite number of equivalent matrices of factor loadings by simply applying orthogonal transformations.

Matters are subtly different when w(s) is a spatial process. The cross-covariance matrix cov{w(s), w(t)} = Γ(s, t; ϕ), is now diagonal (and not an identity matrix as in traditional FA) with the kth diagonal element ρ_k (s, t; ϕ_k). Orthogonal transformations can, therefore, alter the distribution of w̄(s). To be precise, now cov{w̄(s), w̄(t)} = P′Γ(s, t; ϕ)P, which is neither necessarily diagonal nor equal to Γ(s, t; ϕ). Therefore, spatial factor models are not necessarily invariant to any orthogonal transformation.

Our primary motivation for using a Λ without any pre-specified 0 element is stochastic modeling for the number of factors (see Section 2.3). Such a model would automatically identify the latent spatial processes and, hence, the corresponding columns of Λ that are retained in (1). Specifying Λ to be lower triangular is now problematic because it is unlikely that such a structure will be retained throughout the stochastic selection process. On the other hand, using a Λ that is identifiable but that does not restrict certain elements to be zero will avoid such awkwardness.

In fact, we argue (see Web Appendix A for details) that only two groups of orthogonal transformations lead to nonidentifiability in spatial factor models. The first transformation P satisfies P′Γ(s, t; ϕ)P = Γ(s, t; ϕ). Such a P must be diagonal with 1’s and −1’s only. It is a special reflector (i.e., P² = I) and is obtained as a product of elementary reflectors of the form $\mathbf{I}-2{\mathbf{e}}_i{\mathbf{e}}_i^{\prime }$, where e_i is the ith Euclidean standard coordinate vector. The orthogonal matrix P alters the sign of the columns in Λ. To identify Λ (or have a one-to-one relationship between Λ and ΛΛ′), we need to specify one element in each column of Λ as positive or negative. Without losing generality, we could set the first row of Λ to be positive.

Permutation matrices constitute the second group of orthogonal transformations that lead to nonidentifiability in spatial factor models. A permutation matrix switches the elements of w(s) and the corresponding columns of Λ simultaneously, so the distributions of Λ̄w̄(s) and Λw(s) are the same. To address such identifiability issues, we impose some constraints on ρ_k (h; ϕ_k), more specifically on ϕ_k (Zhang, 2007). For simplicity, we consider the exponential correlation function ρ_k (h; ϕ_k) = exp(−ϕ_k ‖h‖), which has a spatial decay parameter ϕ_k as the only unknown parameter. We require the range parameter ϕ_k, k = 1, …, r, to be ordered as ϕ₁ < ϕ₂ ⋯ < ϕ_r or ϕ₁ > ϕ₂ ⋯ > ϕ_r. Simulation studies (see Sections 4.1 and 4.2) reveal that without this constraint, parameter estimation becomes problematic.

2.3 Adaptive Bayesian Factor Model

Determining the number of spatial factors (r) is challenging because of the lack of rigorous theoretical results that hint at the data’s ability to inform about r. Generally, previous work Webster, Atteias, and Duboiss (1994) employing the LMC assumes r < m is fixed. The choice of the number of spatial processes and their respective scales is a critical point in geostatistical models. In the applications of LMC to multivariate spatial analysis (see, e.g., Webster et al., 1994; Castrignanó et al., 2005; Buttafuoco et al., 2010), the spatial correlation functions ρ_k (h; ϕ_k), the parameters ϕ_k, and r are obtained from empirical estimates of the auto- and cross-variograms before any modeling. This approach ignores the uncertainty in the estimates of the spatial parameters and may yield dubious inference.

We adapt earlier work by Kuo and Mallick (1998) and Chen and Dunson (2003) to propose an approach for selecting spatial processes corresponding to different spatial scales using a Bayesian hierarchical model. Indicator variables δ = {δ₁, …, δ_r}, where each δ_k is supported at two points 1 and 0, are introduced in model (1) to yield:

$$\mathbf{Y}(\mathbf{s})=\mathbf{X}(\mathbf{s})\prime \mathit{\beta }+\sum _{k=1}^r{\delta }_k{w}_k(\mathbf{s}){\mathit{\lambda }}_k+\mathit{\epsilon }(\mathbf{s}).$$ (2)

When δ_k = 1, we include the kth spatial random process w_k (s) and the corresponding λ_k in the model. Otherwise, we omit the kth spatial scale. This yields 2^r submodels. We call (2) the adaptive Bayesian factor model, in which the unknown parameters are estimated together with which factors will be retained.

2.4 Prior Specification

We place a multivariate normal prior on the slope parameter β with mean μ_β and variance Σ_β. Often, a flat prior ${\mathbf{\Sigma }}_{\mathit{\beta }}^{-1}=\mathbf{O}$ is used. Each diagonal element of Ψ is assigned an Inverse Gamma (IG) distribution. With ${\psi }_i^2~\mathrm{I}\mathrm{G}(a,b)$, the prior for Ψ becomes $\pi (\mathbf{\Psi }|a,b)\propto {\prod }_{i=1}^m{({\psi }_i^2)}^{-a-1}\text{exp}\{-b/{\psi }_i^2\}$ with hyperparameters a and b. A customary choice is to use a = 2, which suggests a distribution with infinite variance and a mean of b (often gleaned from a semivariogram).

For simplicity, we assume independent priors for δ and Λ (Kuo and Mallick, 1998). The indicator variables δ_k, k = 1, …, r, are taken a priori to be independent, with p(δ_k = 1 | ω) = ω. We regard ω as unknown and assume that it has a uniform prior on (0, 1). Imposing constraints on Λ, only requires a minor modification in the derivation of the full conditional distribution. Here, we take independent priors such as ${\mathrm{\Lambda }}_{jk}~N(0,c_0^2)$. The first row of Λ is restricted to be positive, that is, ${\mathrm{\Lambda }}_{1k}~N(0,c_0^2)I({\mathrm{\Lambda }}_{1k}>0)$ for k = 1, …, r, where I(·) is the indicator function. Berger and Pericchi (2001) suggest caution in the use of such priors in generic hierarchical models because the outcome of the model selection process can be quite sensitive to their vagueness. However, this seems to be less of an issue in dynamic factor models once the loading matrix is made identifiable (Lopes and West, 2004), where-upon inference and model selection were robust to the prior specifications. Similar results are obtained in random effect selection models (Chen and Dunson, 2003; Cai and Dunson, 2006). In our current context, restricting the first row of Λ to be positive, hence assigning a truncated normal to each element of the first row of Λ, ensures robust model selection and related inference to $c_0^2$.

One also needs to assign priors on $\mathit{\varphi }={\{{\mathit{\varphi }}_k\}}_{k=1}^r$. The prior for ϕ depends upon the choice of correlation functions. Quite remarkably, the spatial process parameters are not consistently estimable and the effect of the prior does not disappear with increasing amounts of data (Zhang, 2004). Hence, prior information becomes an even more delicate issue. Typically, we set prior distributions for the range parameters relative to the size of their domains. In this article, an exponential correlation function is used and the prior for the range parameter is specified on a support with upper and lower limits denoted as ϕ_u = −log(0.01)/d_min and ϕ_l = −log(0.05)/d_max, where d_min and d_max are the minimum and maximum distances across all the locations (Wang and Wall, 2003). Because of identifiability issues discussed in Section 2.2, we construct a joint distribution for the ϕ_k’s to ensure ordering. In particular, we set

$$\pi (\mathit{\varphi })=\pi ({\varphi }_1)\pi ({\varphi }_2|{\varphi }_1)\cdots \pi ({\varphi }_k|{\varphi }_{k-1},\dots ,{\varphi }_1)\cdots \pi ({\varphi }_r|{\varphi }_{r-1},\dots ,{\varphi }_1),$$

where π(ϕ₁) is a uniform density with support (ϕ_l, ϕ_u) and subsequently, for k = 2, 3, …, r,

$$\pi ({\varphi }_k|{\varphi }_{k-1},\dots ,{\varphi }_1)\propto \text{exp}\{-\frac{c_k}{{\varphi }_k-{\varphi }_{k-1}}\}$$ (3)

$$I({\varphi }_u>{\varphi }_k>{\varphi }_{k-1}).$$

Here the hyperparameters c_k > 0 controls the shape of the distribution and the separation of the ϕ_k’s. In all our subsequent analyses, we fix c_k = 2k as a reasonable choice that delivers robust inference. For any finite domain this prior is proper (i.e., integrable). To offer some additional insight, let ϕ_k − ϕ_k−1 ∈ (0, hc_k) and h = 4. Numerical integration yields p(ϕ_k − ϕ_k−1 < c_k /2 | ϕ_k−1) < 0.01. This implies that ϕ_k is unlikely to appear in (ϕ_k−1, ϕ_k−1 + c_k /2) unless there is a strong mode from the likelihood. So (3) could efficiently separate the ϕ_k’s. On the other hand, $\frac{p(3c_k\le {\varphi }_k-{\varphi }_{k-1}<4c_k|{\varphi }_{k-1})}{p(2c_k\le {\varphi }_k-{\varphi }_{k-1}<3c_k|{\varphi }_{k-1})}=1.1$, which indicates that π(ϕ_k | ϕ_k−1) becomes informative when ϕ_k−1 and ϕ_k are away from each other.

An alternative specification is π(ϕ) ∝ I (ϕ_l < ϕ₁) I (ϕ₁ < ϕ₂) ⋯ I (ϕ_r < ϕ_u). This is somewhat simpler than (3), but encounters problems in practical implementation. Here, the posteriors for ϕ_k and ϕ_{k +1}, although they theoretically obey ϕ_k < ϕ_{k +1}, can become very close to each other. In that case, one of the two latent processes becomes redundant, yet stochastic factor selection keeps both processes. The specification in (3) avoids this situation.

3. Predictive Process Factor Models

Although FA is a powerful tool for summarizing multivariate outcomes and conducting dimension reduction on the number of outcomes, the spatial FA is prohibitive with a large number of locations. A popular model-based approach for dimension reduction over space uses low- or fixed-rank representations for w(s). Their likelihood resembles linear-mixed models and can be estimated using standard algorithms with some minor adaptations.

Here we consider one such representation that projects the spatially associated latent factors w(s) onto a lower-dimensional subspace determined by a partial realization of the process w(s) over a manageable set of locations called “knots.” Unlike several other low-rank methods, the predictive process does not introduce additional parameters or kernels. Also, some approaches require empirical estimates of the data’s covariance structure. This may be challenging here as the variability in the “data” is assumed to be a sum of unobserved factors. Therefore, we cannot use variograms on the data to isolate empirical estimates of its spatial covariance structure from that of the individual factors.

3.1 Model Construction

A Gaussian predictive process (see, e.g., Banerjee et al., 2008; Finley et al., 2009; Banerjee et al., 2010) uses a set of fixed “knots” ${𝒮}^{*}=\{{\mathbf{s}}_1^{*},\dots ,{\mathbf{s}}_{n^{*}}^{*}\}$, n* ≤ n which are usually fixed and may, but need not, form a subset of the observed locations 𝒮 = {s₁, …, s_n}. The Gaussian process defined in Section 2.1 implies that ${\mathbf{w}}_k^{*}=(w_k({\mathbf{s}}_1^{*}),\dots ,w_k({\mathbf{s}}_{n^{*}}^{*}))\prime$ follows $N_{n^{*}}(\mathbf{0},{\mathbf{D}}_k^{*}({\mathit{\varphi }}_k))$, where ${\mathbf{D}}_k^{*}({\mathit{\varphi }}_k)$ is the n* × n* covariance matrix whose (i, j)th element is ${\rho }_k({\mathbf{s}}_i^{*},{\mathbf{s}}_j^{*};{\mathit{\varphi }}_k)$. The spatial interpolation or “kriging” function at a site s₀ is given by ${\tilde{w}}_k({\mathbf{s}}_0)=\mathrm{E}[w_k({\mathbf{s}}_0)|{\mathbf{w}}_k^{*}]={\mathbf{d}}_k({\mathbf{s}}_0;{\mathit{\varphi }}_k)\prime {\mathbf{D}}_k^{*}{({\mathit{\varphi }}_k)}^{-1}{\mathbf{w}}_k^{*}$, where d_k (s₀; ϕ_k) is an n* × 1 vector whose ith element is ${\rho }_k({\mathbf{s}}_0,{\mathbf{s}}_i^{*};{\mathit{\varphi }}_k)$. This defines the predictive process w̃_k (s) ~ GP(0, ρ̃_k (·; ϕ_k)) derived from the parent process w_k (s), where ${\tilde{\rho }}_k({\mathbf{s}}_i,{\mathbf{s}}_j;{\mathit{\varphi }}_k)={\mathbf{d}}_k({\mathbf{s}}_i;{\mathit{\varphi }}_k)\prime {\mathbf{D}}_k^{*}{({\mathit{\varphi }}_k)}^{-1}{\mathbf{d}}_k({\mathbf{s}}_j;{\mathit{\varphi }}_k)$.

The predictive process underestimates the variance of the parent process w_k (s₀) at any location s₀ because var{w_k (s₀)} − var{w̃_k (s₀)} = var{w_k (s₀) − w̃_k (s₀)} ≥ 0. The veracity of this is an immediate consequence of the definition of w̃_k (s) as a conditional expectation. This means that the estimated Ψ from the predictive process model roughly captures the same amount of variability as the estimated Ψ + Λ(I_r − E[Γ̃(s₀)])Λ′ from (1), where Γ̃(s₀) is an r × r diagonal matrix with kth diagonal element ρ̃_k (s₀, s₀; ϕ_k).

Defining $f_k(\mathbf{s})|{\tilde{w}}_k(\mathbf{s})~N({\tilde{w}}_k(\mathbf{s}),{\sigma }_{f_k}^2(\mathbf{s}))$, where ${\sigma }_{f_k}^2(\mathbf{s})=1-{\tilde{\rho }}_k(\mathbf{s},\mathbf{s},{\mathit{\varphi }}_k)$, we easily obtain var{f_k (s)} = var{w_k (s)} = 1, as desired. Replace w(s) with f(s) = (f₁(s), …, f_r (s))′ in (2) and define f_k = (f_k (s₁), …, f_k (s_n))′, F = (f₁, …, f_r) and ${\mathbf{w}}^{*}=(\mathbf{w}({\mathbf{s}}_1^{*})\prime ,\dots ,\mathbf{w}({\mathbf{s}}_{n^{*}}^{*})\prime )\prime$. This yields the posterior distribution p(F, w*, β, Ψ, ϕ, Λ, δ, ω |Y) proportional to

$$\pi (\omega )\times \pi (\mathit{\varphi })\times \prod _{k=1}^r\mathit{\text{Ber}}({\delta }_k|\omega )\times N_m({\mathit{\lambda }}_k|\mathbf{0},c_0^2{\mathbf{I}}_m)\times \mathbf{I}({\mathbf{\Lambda }}_{1k}>0)\times N_p(\mathit{\beta }|{\mathit{\mu }}_{\mathit{\beta }},{\mathbf{\Sigma }}_{\mathit{\beta }})\times \prod _{j=1}^{m}IG({\psi }_j^2|a,b)\times \prod _{k=1}^r{N}_n\times ({\mathbf{f}}_k|{\mathbf{D}}_k({\mathit{\varphi }}_k){\mathbf{D}}_k^{*}{({\mathit{\varphi }}_k)}^{-1}{\mathbf{w}}_k^{*},{\mathbf{\Sigma }}_{{\mathbf{f}}_k}({\mathit{\varphi }}_k))\times \prod _{k=1}^r{N}_{n^{*}}({\mathbf{w}}_k^{*}|\mathbf{0},{\mathbf{D}}_k^{*}({\mathit{\varphi }}_k))\times \prod _{i=1}^n{N}_m\times (\mathbf{Y}({\mathbf{s}}_i)|\mathbf{X}({\mathbf{s}}_i)\prime \mathit{\beta }+\sum _{k=1}^r{\delta }_k{f}_k({\mathbf{s}}_i){\mathit{\lambda }}_k,\mathbf{\Psi }),$$ (4)

where D_k (ϕ_k) = (d_k (s₁), …, d_k (s_n))′ and Σ_fk is an n × n diagonal matrix with ith diagonal element ${\sigma }_{f_k}^2({\mathbf{s}}_i)$. π(ω) is uniformly distributed on (0, 1) and π(ϕ) is defined in (3). Estimation of (4) proceeds using MCMC sampling (see Web Appendix B for details).

We offer some remarks on knot selection. With evenly distributed locations, knots on a uniform grid (see, e.g., Diggle and Lophaven, 2006) may suffice. With irregular locations, space-covering designs (e.g., Royle and Nychka, 1998) yield a more representative set. In general, different knots selection methods still produce robust results in predictive process models (see, e.g., Finley et al., 2009; Banerjee et al., 2010). And the modified predictive process model f_k (s) is even less sensitive than w̃_k (s) to such choices. Here, we use the K-means clustering algorithm (Hartigan and Wong, 1979) to arrive at a set of knots.

3.2 Handling Missing Observations

Missing outcomes arise frequently in many environmental applications. The outcomes may be missing for a variety of unintended reasons: nonresponse, equipment failure, lack of collection, and so on. Bayesian analysis often proceeds from data augmentation (Tanner, 1993) or multiple imputation (Rubin, 1976) to handle the incomplete data problem. Both methods impute the missing values within a Gibbs step and then use the complete data set. Instead, here we condition on the latent factors, which simplifies the MCMC algorithm and reduces the computational burden. Conditional on the latent factor f(s), the outcomes are independent of each other, which yields a likelihood depending only upon observed data. The missing values can, then, be recovered from the posterior predictive distribution.

Let Y(s) be the m × 1 vector of measured and unmeasured outcomes at site s. Suppose the measured and unmeasured elements of Y(s) have indices i₁, …, i_ds and i_ds+1, …, i_m, respectively, where d_s is the number of observed outcomes at s. Let v_j, j = 1, …, m, be an m × 1 vector whose jth element is 1 and the rest are all 0. We can then construct matrices R₁(s)_ds×m and R₂(s)_(m−ds)×m, which can extract the observed and unobserved elements when multiplied by Y(s). More precisely, R₁(s) = (v_i1, …, v_ids)′ and R₂(s) = (v_ids+1, …, v_im)′.

Observe that Y_o (s) = R₁(s)Y(s) and Y_u (s) = R₂(s)Y(s) consist of the observed and unobserved elements, respectively. Multiplying both sides of model (2) by R₁(s) reveals that the likelihood p(Y_o (s) | f(s), γ, β, Λ, Ψ) follows a multivariate normal distribution with variance R₁(s)ΨR₁(s)′ and mean ${\mathbf{R}}_1(\mathbf{s})[\mathbf{X}(\mathbf{s})\prime \mathit{\beta }+{\sum }_{k=1}^r{\delta }_k{f}_k(\mathbf{s}){\mathit{\lambda }}_k]$. Note that R₁(s)ΨR₁(s)′ is a d_s × d_s diagonal matrix with lth diagonal element ${\psi }_{i_l}^2$ for l = 1, …, d_S. This ensures that R₁(s)ΨR₁(s)′ is a valid covariance matrix, and so is R₂(s)ΨR₂(s)′ for similar reasons. See Web Appendix B for implementation details.

3.3 Prediction and Predictive Model Comparison

Spatial analysis for data sets with missing values customarily entail three types of inference: (i) recover missing values, (ii) predict outcome Y(t) = (Y₁(t), …, Y_m (t))′ at any arbitrary location t, and (iii) generate replicates for the observed data for use in model assessment and selection (Gelfand and Ghosh, 1998).

To recover the missing values, we use composition sampling to draw Y_u from p(Y_u|Y_o), where Y_o = (Y_o (s₁)′, …, Y_o (s_n)′)′ and Y_u = (Y_u (s₁)′, …, Y_u (s_n)′)′. Note that

$$p({\mathbf{Y}}_u|{\mathbf{Y}}_o)=\int \prod _{i=1}^{n}p({\mathbf{Y}}_u({\mathbf{s}}_i)|\mathbf{f}({\mathbf{s}}_i),\mathit{\theta })p(\mathbf{F},\mathit{\theta }|{\mathbf{Y}}_o)\mathrm{d}\mathbf{F}\mathrm{d}\mathit{\theta }=\int \prod _{i=1}^{n}N({\mathbf{Y}}_u({\mathbf{s}}_i)|{\mathbf{R}}_2({\mathbf{s}}_i)[\mathbf{X}({\mathbf{s}}_i)\prime \mathit{\beta }+\tilde{\mathbf{\Lambda }}\mathbf{f}({\mathbf{s}}_i)],\times {\mathbf{R}}_2({\mathbf{s}}_i)\mathbf{\Psi }{\mathbf{R}}_2({\mathbf{s}}_i)\prime )p(\mathbf{F},\mathit{\theta }|{\mathbf{Y}}_o)\mathrm{d}\mathbf{F}\mathrm{d}\mathit{\theta },$$

where Λ̃ = (δ₁λ₁, …, δ_rλ_r). Using the samples {F^(l), θ^(l)} from p(F, θ |Y_o), the missing value at s is recovered by drawing ${\mathbf{Y}}_u^{(l)}(\mathbf{s})$ for each, l = 1, …, L, from an (m − d_s) × 1 multivariate normal distribution with mean R₂(s)[X(s)′ β^(l) + Λ̃^(l) f^(l) (s)] and variance R₂(s)Ψ^(l)R₂(s)′.

Prediction of the outcomes at unsampled or ungauged sites is often a major study objective. Using notations defined earlier, we have

$$p(\mathbf{Y}(\mathbf{t})|{\mathbf{Y}}_o)=\int p(\mathbf{Y}(\mathbf{t})|\mathbf{f}(\mathbf{t}),\mathit{\theta })p(\mathbf{f}(\mathbf{t})|\mathbf{F},\mathit{\varphi },{\mathbf{Y}}_o)\times p(\mathbf{F},\mathit{\theta }|{\mathbf{Y}}_o)\mathrm{d}\mathbf{F}\mathrm{d}\mathit{\theta }\mathrm{d}\mathbf{f}(\mathbf{t})=\int N(\mathbf{Y}(\mathbf{t})|\mathbf{X}(\mathbf{t})\prime \mathit{\beta }+\tilde{\mathbf{\Lambda }}\mathbf{f}(\mathbf{t}),\mathbf{\Psi })\prod _{k=1}^r\times N(f_k(\mathbf{t})|{\mu }_{f_k(\mathbf{t})|{\mathbf{f}}_k},{\sigma }_{f_k(\mathbf{t})|{\mathbf{f}}_k}^2)\times p(\mathbf{F},\mathit{\theta }|{\mathbf{Y}}_o)\mathrm{d}\mathbf{F}\mathrm{d}\mathit{\theta }\mathrm{d}\mathbf{f}(\mathbf{t}),$$

where ${\sigma }_{f_k(\mathbf{t})|{\mathbf{f}}_k}^2=1-{\mathbf{d}}_k(\mathbf{t};{\mathit{\varphi }}_k)\prime {\mathbf{D}}_k^{*}{({\mathit{\varphi }}_k)}^{-1}{\mathbf{D}}_k({\mathit{\varphi }}_k)\prime {\mathbf{G}}_k{({\mathit{\varphi }}_k)}^{-1}{\mathbf{D}}_k({\mathit{\varphi }}_k){\mathbf{D}}_k^{*}{({\mathit{\varphi }}_k)}^{-1}{\mathbf{d}}_k(\mathbf{t};{\mathit{\varphi }}_k)$ and ${\mu }_{f_k(\mathbf{t})|{\mathbf{f}}_k}={\mathbf{d}}_k(\mathbf{t};{\mathit{\varphi }}_k)\prime {\mathbf{D}}_k^{*}{({\mathit{\varphi }}_k)}^{-1}{\mathbf{D}}_k({\mathit{\varphi }}_k)\prime {\mathbf{G}}_k{({\mathit{\varphi }}_k)}^{-1}{\mathbf{f}}_k$. Here, G_k (ϕ_k) is the variance of f_k, which equals ${\mathbf{D}}_k({\mathit{\varphi }}_k){\mathbf{D}}_k^{*}{({\mathit{\varphi }}_k)}^{-1}{\mathbf{D}}_k({\mathit{\varphi }}_k)\prime +{\mathbf{\Sigma }}_{{\mathbf{f}}_k}$. For prediction, we would first sample f_k (t)^(l) from $N(f_k(\mathbf{t})|{\mu }_{f_k(\mathbf{t})|{\mathbf{f}}_k},{\sigma }_{f_k(\mathbf{t})|{\mathbf{f}}_k}^2)$ using posterior samples ${\mathbf{f}}_k^{(l)}$ and ${\mathit{\varphi }}_k^{(l)}$. Then, Y(t)^(l) is drawn from an m ×1 multivariate normal distribution with mean X(t)′β^(l) + Λ̃^(l) f(t)^(l) and variance Ψ^(l).

Finally we turn to generating replicated observations for Y_o. This is easily achieved by first sampling from p(w*, θ |Y_o). The replicate ${\mathbf{Y}}_o^{\mathit{\text{rep}}}{(\mathbf{s})}^{(l)}$ is generated from a d_s × 1 multivariate normal distribution with mean R₁(s)[X(s)′β^(l) + Λ̃^(l) w̃^(l)(s)] and variance R₁(s)[Ψ^(l) + Λ̃^(l) Σ_f(s) (ϕ^(l))Λ̃^(l)′]R₁(s)′, where Σ_f(s) is a diagonal matrix with kth diagonal element ${\sigma }_{f_k}^2(\mathbf{s})$. Then ${\mu }_i^{\mathit{\text{rep}}}=\mathrm{E}[Y_{oi}^{\mathit{\text{rep}}}|{\mathbf{Y}}_o]$ and ${\sigma }_i^{2\mathit{\text{rep}}}=\text{var}\{Y_{oi}^{\mathit{\text{rep}}}|{\mathbf{Y}}_o\}$ can be calculated respectively, where i indexes the observed data. Gelfand and Ghosh (1998) present a posterior predictive criterion that balances goodness-of-fit and predictive variance under a squared error loss function. This assigns a score to each model that is the sum of two terms, P and G, where $G={\sum }_i{({\mu }_i^{\mathit{\text{rep}}}-Y_{oi})}^2$ is an error sum of squares and represents goodness-of-fit, whereas $P={\sum }_i{\sigma }_i^{2\mathit{\text{rep}}}$ represents predictive variance and acts as a penalty term. Therefore, complexity is penalized and a parsimonious choice with lower D = G + P indicates preferred models.

4. Illustrations

We executed our adaptive spatial factor models using the R programming language. The most demanding model (12 × 1 vector of outcomes across 1, 000 locations) took approximately 48 hours to deliver its entire inferential output from 20, 000 MCMC iterations, including 4, 000 samples for burn-in, on a 3.10-GHz Intel i5–2400 processor with 4.0 Gbytes of RAM. The statistics of Gelman and Rubin (1992) was used to assess chain convergence alongside visual inspection of the trace plots and empirical autocorrelation functions.

4.1 Simulation Study One

The objective of this simulation study is to explore different specifications for Λ and demonstrate model identifiability. Adaptive factor modeling and predictive processes are not employed here. The data generating model uses a 2 × 2 factor loading matrix Λ and a spatial range parameter ϕ whose first element is smaller than the second. A synthetic data set comprising 250 locations within a [0, 50] × [0, 50] square was generated from (1) with r = m = 2. An isotropic exponential correlation function, ρ_k (s − t; ϕ_k) = exp(−ϕ_k ‖s − t‖) for k = 1, 2, was used to produce a spatially dependent bivariate random field. The bivariate outcomes, Y(s), were simulated with the following parameters:

$$\mathit{\beta }=\left(\begin{array}{c}\hfill 5\\ \hfill 10\end{array}\right),\mathbf{\Lambda }=\left(\begin{array}{cc}\hfill 3& \hfill 1\hfill \\ \hfill -2& \hfill 2\hfill \end{array}\right),\mathbf{\Psi }=\left(\begin{array}{cc}\hfill 2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 5\hfill \end{array}\right),\text{and}\mathit{\varphi }=\left(\begin{array}{c}\hfill 0.1\hfill \\ \hfill 0.6\hfill \end{array}\right),$$

where β is the mean vector for Y(s) and $\mathbf{C}(\mathbf{0})=\mathbf{\Lambda }\mathbf{\Lambda }\prime =(\begin{array}{cc}\hfill 10& \hfill -4\\ \hfill -4& \hfill 8\end{array})$. Note the strong negative cross-correlation between the two spatial processes. Also, the correlation decays six times faster in the second process than in the first, yielding spatial ranges −log(0.05)/ϕ₁ ≈ 30 and −log(0.05)/ϕ₂ ≈ 5 units for the first and second process, respectively.

Three models are estimated and compared. The first restricts Λ to be lower-triangular, as in the LMC setting, but does not order the ϕ_i’s a priori. The other two models use factor loadings with positive elements in the first row of Λ and use the prior in (3) for ϕ. One of these two models assumes ϕ₁ < ϕ₂, reflecting the true ordering, although the other reverses the inequality and results in a misspecified model a priori. However, because the factor loadings are now identifiable, the estimated Λ contains permuted columns according to the order of the ϕ_i’s. This is attractive in practice—one need not ascertain the correct ordering of the range parameters a priori. We arrange them in the same order as the true values although presenting estimates in Table 1.

Table 1.

Posterior percentiles (50%, 2.5%, and 97.5%) estimated for the parameters in different model specifications

True parameter	Lower triangular setting	General factor loadings
		Increasing ϕk	Decreasing ϕk
β1 = 5	4.77 (1.22, 7.49)	5.00 (3.29, 6.98)	5.58 (3.77, 7.85)
β2 = 10	10.38 (8.65, 12.73)	10.15 (8.38, 11.60)	9.68 (7.73, 11.16)
C(0)1,1 = 10	8.59, (4.76, 15.08)	10.82 (6.53, 18.54)	10.65 (6.23, 17.66)
C(0)2,1 = −4	−5.64 (−9.99, −2.93)	−5.34 (−10.84, −1.82)	−5.11 (−9.88, −1.67)
C(0)2,2 = 8	12.17 (6.76, 17.54)	12.99 (7.15, 19.43)	12.83 (7.15, 18.42)
Ψ1 = 2	3.65 (2.61, 4.88)	2.30 (1.19, 3.66)	2.35 (1.15, 3.55)
Ψ2 = 5	3.27 (0.97, 8.38)	3.33 (1.06, 7.99)	3.21 (0.99, 7.99)
ϕ1 = 0.1	0.06 (0.05, 0.12)	0.07 (0.05, 0.13)	0.07 (0.05, 0.14)
ϕ2 = 0.6	0.95 (0.25, 2.15)	1.17 (0.52, 2.58)	1.15 (0.49, 2.44)
Λ1,1 = 3	2.93 (2.18, 3.88)	3.11 (2.32, 4.15)	3.07 (2.31, 4.06)
Λ1,2 = −2	−1.93, (−2.80, −1.17)	−2.53 (−3.42, −1.79)	−2.48 (−3.33, −1.68)
Λ2,1 = 1	Fixed at 0	1.02 (0.56, 1.68)	1.01 (0.55, 1.78)
Λ2,2 = 2	2.89, (1.84, 3.47)	2.57 (1.33, 3.22)	2.60 (1.34, 3.23)

In the first model Λ₂₁ = 0, ϕ_i’s are assigned uniform priors over (ϕ_l, ϕ_u) without any further restrictions. Priors for the two other models are assigned as discussed in Section 2.4 with hyperparameters μ_β = 0, ${\mathbf{\Sigma }}_{\mathit{\beta }}^{-1}=\mathbf{O},c_0^2=10$, ϕ_l = 0.047, ϕ_u = 25, a = 2, and b = 5. Posterior inferences for the latter two models are consistent. This indicates the importance of ordering constraints; without them, the posterior distributions for ϕ and Λ can produce multiple modes as the MCMC chain could jump between the possible specifications (Lopes and West, 2004). The parameter Λ₂₁ (boldface in Table 1), which was set as 0 in the lower triangular setting, is significantly different from 0 in both the models using general factor loadings. Thus, we can capture the underlying cross-covariance structure without restricting the loading matrix, but by imposing an ordering on the spatial decay parameters. In addition, our proposed models have a lower posterior predictive model comparison score (D = 14, 202) than the lower triangular setting (D = 14, 941). This, again, demonstrates a preference for using general factor loadings.

4.2 Simulation Study Two

Now we demonstrate the adaptive spatial factor model using a simulated data set with missing values. We generated 1, 000 locations in a [0, 30] × [0, 30] square. At each location, we simulated a 12 × 1 vector of outcomes, Y(s), from (1) with three factors and outcome-specific intercepts as the only regressors. Each spatial process, w_k (s), was generated from an isotropic exponential correlation function. The parameters are defined as:

$$\mathit{\mu }=\{9,5,-7,-4,-15,7,-5,-6,13,-1,0,-9\},$$

$$\mathit{\varphi }=\{0.1,0.8,1.5\},$$

$$\mathbf{\Psi }=\text{diag}\{0.75,1.31,1.37,1.21,1.44,1.49,1.47,1.48,0.50,1.37,0.65,1.18\},$$

$$\mathbf{\Lambda }\prime =\left(\begin{array}{cccccccccccc}\hfill 2.2\hfill & \hfill -2.6\hfill & \hfill 1.8\hfill & \hfill 0.4\hfill & \hfill -2.8\hfill & \hfill -1.1\hfill & \hfill -3.0\hfill & \hfill -1.0\hfill & \hfill 1.9\hfill & \hfill -2.0\hfill & \hfill 1.4\hfill & \hfill 1.7\hfill \\ \hfill 1.6\hfill & \hfill -1.4\hfill & \hfill 2.1\hfill & \hfill 2.6\hfill & \hfill -2.6\hfill & \hfill -2.4\hfill & \hfill 2.9\hfill & \hfill -1.2\hfill & \hfill -0.1\hfill & \hfill 2.8\hfill & \hfill -1.4\hfill & \hfill -2.8\hfill \\ \hfill 2.0\hfill & \hfill 0.9\hfill & \hfill 2.8\hfill & \hfill -0.8\hfill & \hfill 2.7\hfill & \hfill -1.7\hfill & \hfill -2.9\hfill & \hfill 0.9\hfill & \hfill 0.1\hfill & \hfill -2.9\hfill & \hfill -2.2\hfill & \hfill 3.0\hfill \end{array}\right).$$

After the data was generated, we allowed a quarter of the locations to retain all the outcomes, although randomly omitting 2/3 of the outcomes from the remaining locations. This produced a data set with approximately 50% missingness.

We applied the Gibbs sampling algorithm described in Section 3 for estimation. For the predictive process, we selected 200 knots using a K-means clustering algorithm (Hartigan and Wong, 1979). The maximum number of latent factors, r, was taken to be 5. For comparison, we also fit spatial factor models using a fixed number of latent factors for the same data set. The prior distributions resemble those in Section 4.1, except that now ϕ_l = 0.07 and ϕ_u = 310 to better reflect the domain. Also, for the adaptive model we used independent Bernoulli priors for δ with p(δ_k = 1| ω) = ω, k = 1, …, r and ω ~ U(0, 1).

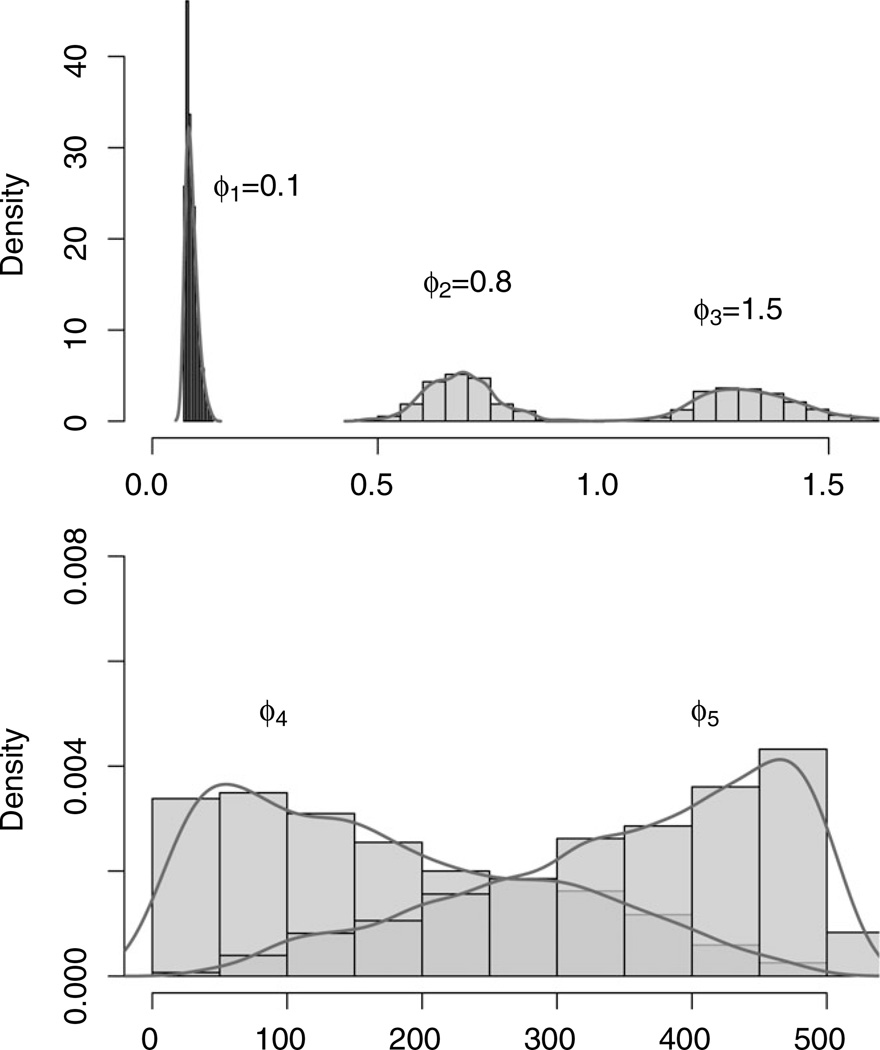
Stochastic selection produced the final model with three latent factors based upon the highest posterior probabilities. Figure 1 illustrates the posterior distributions for ϕ. The spatial parameters in the active processes are ϕ₁, ϕ₂, ϕ₃ (corresponding to δ_k = 1) and their posteriors are well identified. The true values are all included in the central 95% credible intervals. The posteriors for ϕ₄ and ϕ₅ only reflect prior information. The wide range of their posteriors suggest that there is very little posterior learning and the MCMC sampler is sampling from the prior. The marginal posterior density for ω reveals substantial posterior learning. The credible intervals of β and Ψ contain the true values, as does most of the elements of Λ, suggesting sound estimative performance.

Figure 1.

Histograms of the posterior distributions for ϕ.

Spatial factor models with fixed number of latent factors equaling 1, 2, 4, and 5 are also fitted. The posterior predictive criterion discussed in Section 3.3 is presented for model assessment and the scores are compared in Table 2. The adaptive spatial factor model with D = 99740 (boldface in Table 2) seems to be the winner here. There is overwhelming evidence that the regression model with random processes f₁(s), f₂(s), and f₃(s) is optimal. This, pleasantly, agrees with the true specification.

Table 2.

Simulation study two: Model comparison criteria

	Number of factors
Criterion	r = 1	r = 2	Adaptive factor	r = 4	r = 5
G	69567	53893	45982	46011	46036
P	71698	60173	53758	53880	53939
D	141265	114066	99740	99891	99975

4.3 Air Monitor Value Data

Our current application involves data compiled from the Environmental Protection Agency across 316 air monitors in California involving five pollutants: carbon monoxide (CO), nitrogen dioxide (NO₂), ozone (O₃), particulate matter with diameter < 2.5 micrometers (PM2.5), and particulate matter with diameter < 10 micrometers (PM10). Concentrations (ppm) measured by monitoring equipments are used for CO, NO₂, and O₃ and (µg/m³) for PM2.5 and PM10. Here we use the annual average of the monitor values recorded in 2008. All the variables were standardized to mean 0 and variance 1.

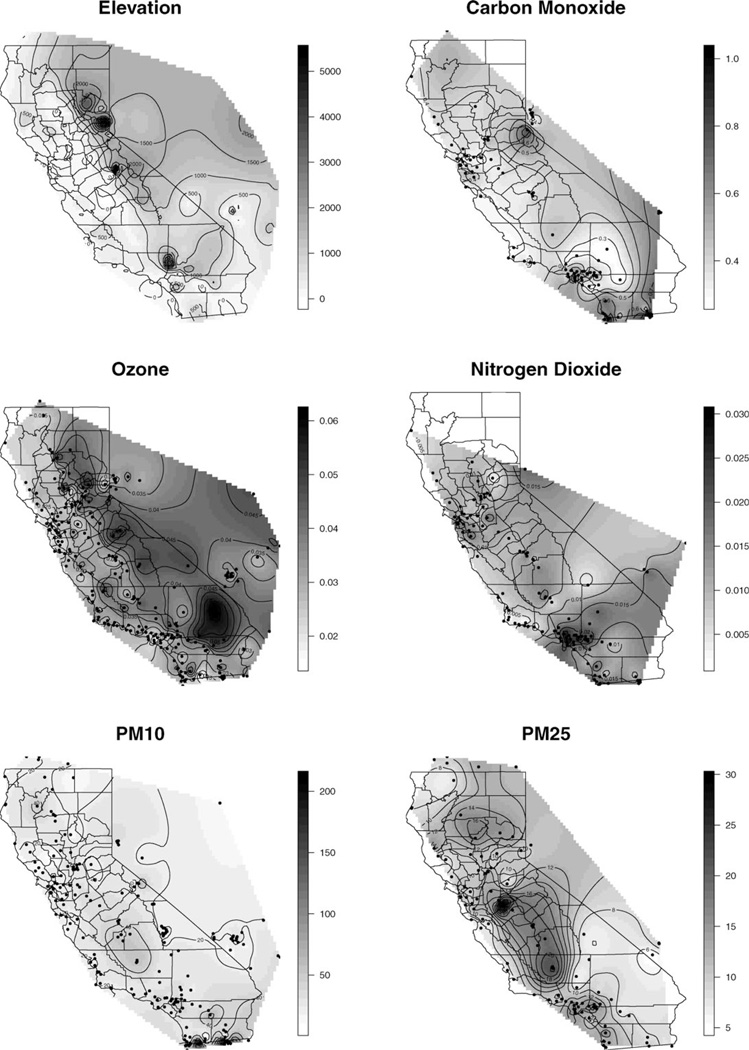
For the modeling, each pollutant is assigned its own intercept term. Elevation (in kilometers) is the only predictor and is depicted as a contoured image in the top-left panel of Figure 2. The instruments only monitor some of the five pollutants at most of the sites, so the data set has about 53% of observations missing. The longitude and latitude of the monitors are transformed to Easting and Northing in kilometer units. For the predictive process, 50 knots were selected using a K-means clustering algorithm. Interpolation for the air pollutants and the locations of monitor sites (·) appear in Figure 2.

Figure 2.

Interpolation of air pollutants measured on monitor sites across California.

Visually, the air pollutants exhibit spatially varying concentrations as well as the associations among them at a given location. We seek to model both kinds of dependence. It is not clear whether it is appropriate to assume a single factor underlying the different air pollutants or if additional factors need to be introduced. To address this question, we repeated the approach described in Section 3 using the exact model (4). The priors are the same as in Section 4.2 except for ϕ, which has distribution (3) with ϕ_l = 0.002 and ϕ_u = 136.

The model is implemented in the same manner as in Section 4.2. The maximum possible number of factors r is taken to be 3. We decide to use 4,000 iterations for a burn-in period, and then a further 16,000 iterations for posterior inference.

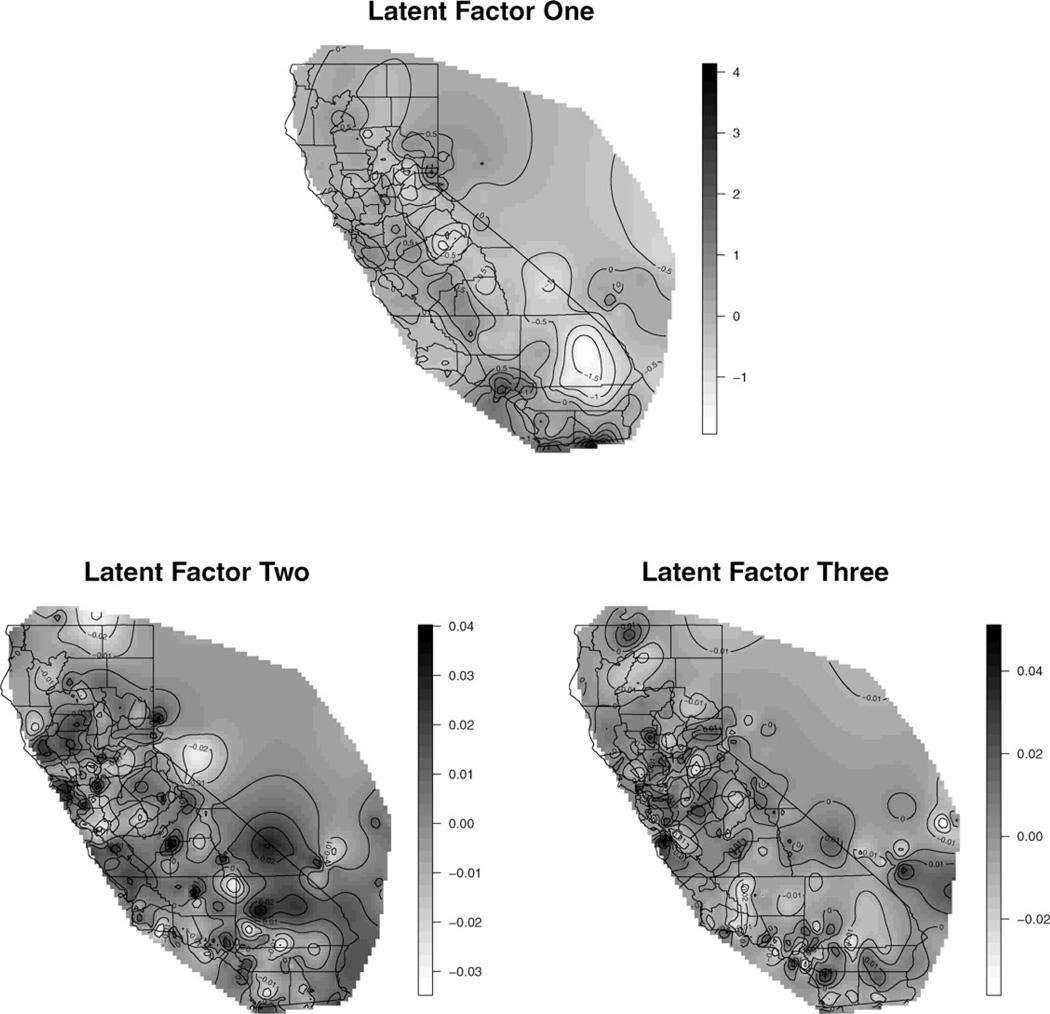
The probability assigned to the model with one latent factor is 1, suggesting that one factor is sufficient. The interpolation of the latent spatial processes are displayed in Figure 3. The panel at the top depicts the only active process (δ₁ = 1), which presents some characteristics for the spatial concentrations of the air pollutants. The panels at the bottom do not show significant association with the data and only demonstrate the prior information. For each air pollutant Y_j (s), the percentage of the variance explained by the spatial factor f_k (s), is simply ${\delta }_k{\mathrm{\Lambda }}_{jk}^2/({\sum }_{k=1}^r{\delta }_k{\mathrm{\Lambda }}_{jk}^2+{\psi }_j^2)$, j = 1, …, 5. Overall, about 50% of the variation is explained by the first latent factor—NO₂ and CO are more closely related to this latent factor, although PM2.5 is weakly explained.

Figure 3.

Interpolation of latent spatial factors across California.

Table 3 presents the posterior inferences of β, Ψ, ϕ, Λ, and the correlation ρ = {ρ_i,j}, i, j = 1, …, 5, j > i, among air pollutants, which is estimated from the variance estimator ΛΛ′ + Ψ. Only CO and NO₂ reveal significant (negative) intercept coefficients. The slope parameters seem to suggest that elevation has a significant impact only upon Ozone among the five pollutants. The posterior inference for ϕ₁ has median 0.018, which corresponds to the effective range (i.e., the distance at which the correlation drops to 0.05) roughly 160 kilometers. The posterior inferences for ϕ₂ and ϕ₃ indicate weak spatial dependence. So we only present the first column of Λ and omit the rest in Table 3. The Λ_j1’s reflect the influence of the common factor on the corresponding outcome variables. Because the residual variances, ${\psi }_j^2’\mathrm{s}$, differ across j, the Λ_j1’s measure covariances on different scales and cannot be directly compared to assess strength of association between outcomes. The parameters ${\psi }_1^2,\dots ,{\psi }_5^2$ can be interpreted as independent measurement error variances. The covariances of the outcomes collected within one set are ${\mathit{\lambda }}_1{\mathit{\lambda }}_1^{\prime }+\mathbf{\Psi }$, where λ₁ = (Λ₁₁, …, Λ₅₁)′. The corresponding correlations among the outcomes are also presented in Table 3.

Table 3.

The posterior credible intervals estimated for the parameters in air pollutants data set. The subscripts 1–5 in β, Ψ, ρ, and the row index of λ₁ refer to CO, NO₂, O₃, PM10, and PM25, respectively. Subscripts on ϕ refer to the three spatial range parameters

Parameter	50% (2.5%, 97.5%)	Parameter	50% (2.5%, 97.5%)	Parameter	50% (2.5%, 97.5%)
β1,0	−0.76 (− 1.37, −0.29)	Λ11	0.85, (0.58, 1.39)	ρ1,2	0.60 (0.44, 0.80)
β2,0	−0.61 (− 1.23, −0.14)	Λ21	0.88 (0.64, 1.47)	ρ1,3	−0.45 (− 0.70, −0.27)
β3,0	0.04 (− 0.24, 0.41)	Λ31	−0.57 (− 0.98, −0.36)	ρ1,4	0.50 (0.33, 0.68)
β4,0	−0.30 (− 0.69, 0.05)	Λ41	0.68, (0.49, 1.02)	ρ1,5	0.39 (0.19, 0.64)
β5,0	−0.27 (− 0.72, 0.07)	Λ51	0.55 (0.27, 1.00)	ρ2,3	−0.48 (− 0.73, −0.28)
β1,E lev	−0.02 (− 0.50, 0.45)	${\psi }_1^2$	0.52 (0.35, 0.77)	ρ2,4	0.52, (0.37, 0.70)
β2,E lev	0.33 (− 0.24, 0.91)	${\psi }_2^2$	0.44 (0.30, 0.63)	ρ2,5	0.41 (0.20, 0.66)
β3,E lev	0.40 (0.21, 0.58)	${\psi }_3^2$	0.59 (0.44, 0.79)	ρ3,4	−0.39 (− 0.60, −0.23)
β4,E lev	0.02 (− 0.28, 0.33)	${\psi }_4^2$	0.63 (0.45, 0.85)	ρ3,5	−0.30 (− 0.55, −0.14)
β5,E lev	−0.12 (− 0.43, 0.16)	${\psi }_5^2$	0.86 (0.62, 1.19)	ρ4,5	0.33 (0.15, 0.55)
ϕ1	0.018 (0.004, 0.039)
ϕ2	43(5.1, 110)
ϕ3	101(33, 136)

5. Summary

We have addressed the problem of modeling large multivariate spatial data, where dimension reduction is sought both in the number of outcomes and in the number of spatial locations. The former is achieved with fewer number of factors, although the latter is achieved using a knot-based predictive process. Model-based strategies (Guhaniyogi et al., 2011) exist for choosing knots but recent findings, including our own explorations here, suggests that simple space-covering or clustering algorithms usually deliver robust inference. Our adaptive model lets the number of factors be stochastic and allows the data to drive the inference.

One can use either the predictive process w̃_k (s) or its “modification” f_k (s) in the adaptive spatial factor models but f_k (s) adapts better to the data and, hence, is less sensitive to the knots. Although the substantive inference is quite robust to both these processes, some subtle differences are seen in the estimation algorithm with regard to transition among models. This is related to the strength of the spatial random field and is explained in Web Appendix C.

Given the widespread use of R as a statistical language, we presented computational benchmarks on R running on fairly standard architectures. In multivariate spatial analysis, “large” refers to the size of m × n, where m is the number of outcomes and n is the number of locations. With R running on standard architectures, mn > 1, 000 is usually deemed exorbitant without dimension reduction. Substantial computational gains accrue from using lower-level languages (C/C++) on shared memory systems.

Alternative approaches for modeling large spatial data sets include an SPDE/GMRF approach proposed by Lindgren, Rue, and Lindström (2011) that uses explicit Markov representations of the Matérn covariance family using a class of stochastic partial differential equations. Rather than MCMC, they use a faster Integrated Nested Laplace Approximation algorithm for Bayesian inference. Another approach, termed covariance tapering (Furrer, Genton, and Nychka 2006), relies upon compactly supported correlation functions to produce sparse covariance matrices containing only a moderate number of nonzero elements. How effective these alternative approaches will be with dynamic spatial factor models is yet to be ascertained.

Space-time or dynamic factor modeling using low-rank processes can also be envisioned. Misalignment can now occur both over space and over time to yield data matrices that are highly irregular. Our formulation can, nevertheless, be easily adapted to such settings. Also, although we attended only to point-referenced data here, adaptive space-time factor models could be used for multivariate regionally aggregated data (Jin, Banerjee, and Carlin 2007) as well. Here, usually the number of regions is not onerous, so dimension reduction is relevant over the number of outcomes (FA) and time (a temporal predictive process).