Abstract
Objective
Computational models of calcium (Ca2+) signaling have been constructed for several cell types. There are, however, no such models for retinal pigment epithelium (RPE). Our aim was to construct a Ca2+ signaling model for RPE based on our experimental data of mechanically induced Ca2+ wave in the in vitro model of RPE, the ARPE-19 monolayer.
Methods
We combined six essential Ca2+ signaling components into a model: stretch-sensitive Ca2+ channels (SSCCs), P2Y2 receptors, IP3 receptors, ryanodine receptors, Ca2+ pumps, and gap junctions. The cells in our epithelial model are connected to each other to enable transport of signaling molecules. Parameterization was done by tuning the above model components so that the simulated Ca2+ waves reproduced our control experimental data and data where gap junctions were blocked.
Results
Our model was able to explain Ca2+ signaling in ARPE-19 cells, and the basic mechanism was found to be as follows: 1) Cells near the stimulus site are likely to conduct Ca2+ through plasma membrane SSCCs and gap junctions conduct the Ca2+ and IP3 between cells further away. 2) Most likely the stimulated cell secretes ligand to the extracellular space where the ligand diffusion mediates the Ca2+ signal so that the ligand concentration decreases with distance. 3) The phosphorylation of the IP3 receptor defines the cell’s sensitivity to the extracellular ligand attenuating the Ca2+ signal in the distance.
Conclusions
The developed model was able to simulate an array of experimental data including drug effects. Furthermore, our simulations predict that suramin may interfere ligand binding on P2Y2 receptors or accelerate P2Y2 receptor phosphorylation, which may partially be the reason for Ca2+ wave attenuation by suramin. Being the first RPE Ca2+ signaling model created based on experimental data on ARPE-19 cell line, the model offers a platform for further modeling of native RPE functions.
Introduction
Epithelial tissue covers and lines all internal and external body surfaces. These cell layers have multiple functions depending on their location, and many of these functions are controlled by Ca2+ activity[1]. Retinal pigment epithelium (RPE), a monolayer of pigmented polarized cells, is crucial for the maintenance of visual functions. Located in the back of the eye between photoreceptors and choriocapillaries, RPE forms a vital part of the blood-retinal barrier (BRB)[2]. The physiology of RPE is tightly coupled with the activity of the various ion channels, such as Ca2+ channels that are associated with several important RPE functions including transepithelial transport of ions and water, dark adaption of photoreceptor activity, phagocytosis, secretion, and differentiation[3]. In RPE, as well as in other epithelia, local deformation of the cell membrane initiates a significant Ca2+ wave [4–6]. Such deformation of the cell membrane can occur in clinically important pathological conditions such as retinal tear resulting from complications after photodynamic therapy[7], intravitreal bevacizumab injection[8], or intravitreal pegaptanib injection[9]. Intercellular Ca2+ signaling is also linked to the initial stages of wound repair: excessive mechanical stimulation causes cell death and thus initiates Ca2+ waves that create Ca2+ gradients which play an important role in cell migration[1]. In addition, Ca2+ waves also regulate the local transepithelial ion transport to maintain the spatial ion gradients across the epithelium[1]. We recently demonstrated in RPE that an easily induced and repeatable Ca2+ wave could be produced by mechanical stimulation[5]. This provides an experimental way to study Ca2+ activity in the epithelial monolayer.
In silico models of various cellular processes are becoming an increasingly important part of biological research, including drug discovery and toxicology studies. The importance of this was recently emphasized in a review of cardiotoxicity testing [10]. Computational models of Ca2+ signaling, specifically, have been developed for many cell types including pancreatic and parotid acinar cells[11], astrocytes[12], and hepatocytes[13]. Epithelial Ca2+ signaling, however, differs from other cell types because the epithelium forms a highly polarized cell monolayer that comprises organized apical and basal cell membranes. The epithelial cells are tightly connected with tight junctions and gap junctions between the cells[14]. At present, there are only a few epithelial Ca2+ signaling models available, for example for the urothelial monolayer[15] and for the airway epithelium[16]. RPE has many unique functions compared to other epithelia as it supports the complex processes of vision. Indeed, in the treatment of many eye diseases, RPE is either the drug target or it hinders drug penetration and provides a barrier between most of the eye and the blood stream. Hence, computational models of the functions of RPE, including Ca2+ dynamics, are well warranted.
The aim of this study, therefore, is to provide a deeper understanding of the study of Ca2+ activity by introducing a detailed computational model of RPE Ca2+ dynamics. The computational model described in this paper is based on our experimental data on a mechanically induced Ca2+ wave in ARPE-19 cells, a commercial immortalized human RPE cell line that is widely used to assess RPE cell functions in vitro [17–19], regardless of its limitations in cellular morphology, organization and function [20].
The computational model is mostly based on the experimental data of Abu Khamidakh et al. 2013[5]. In addition, the model comprises our new unpublished α-glycyrrhetinic acid (GA)-suramin-treated data. We constructed the model by combining previously published cell Ca2+ dynamics model components of P2Y2 receptors [21], inositol 1,4,5-trisphosphate (IP3) receptors [22], ryanodine receptors [23], Ca2+ pumps and gap junctions to a new model component of mechanical stretch. Furthermore, we connected the epithelial cells to each other in the model to enable the diffusion of the molecules and propagation of the stretch. We developed the model based on two experimental data sets: the GA-treated data, where gap junctions (GJs) were blocked by α-glycyrrhetinic acid and untreated control data, where GJs define the connections between the cells. The varying conditions the cells are exposed to due to the mechanical stimulation were modeled by defining three location-specific variables: stretch, extracellular ligand concentration, and IP3 receptor phosphorylation rate. In addition, we validated the model by simulating the combined blocking effect of GJs and P2 receptors by GA and suramin. This way, we obtained the first RPE Ca2+ signaling model, and we could reveal a deeper understanding of Ca2+ activity.
Materials and Methods
Experimental data
In this study, the experimental data of Abu Khamidakh et al. 2013[5] was complemented with new experimental data. Passage numbers for confluent cultures of human RPE immortalized cells (ARPE-19 cell line [ATCC Manassas, VA, U.S.A.]) were p. 23, 24, 30 for GA-treated dataset, p. 23, 24, 28, 30 for control data set and p. 29, 30, 31 for GA-suramin-treated data set. These ARPE-19 cultures were used for Ca2+ imaging, by loading them with the Ca2+-sensitive dye fura-2-acetoxymethyl ester. Single cell mechanical stimulation, membrane perforation of one cell, was induced with a glass micropipette. The intracellular Ca2+ concentration transient travelled over the ARPE-19 monolayer starting from the mechanically stimulated (MS) cell, and spreading to the neighboring (NB) cells (Fig 1). The NB cells immediately surrounding the MS cell were defined as the first NB cell layer (NB layer 1 = NB1); cells immediately surrounding the first layer were defined as the second NB layer (NB layer 2 = NB2) and so on. The ratio of the emitted fluorescence intensities resulting from excitation at 340 and 380 nm (F340/F380) was determined for each cell after background correction. Normalized fluorescence (NF), which reflects the changes in intracellular Ca2+ concentration, was then obtained by dividing the fluorescence value by the mean fluorescence value before the mechanical stimulation.[5] The experimental work produced data in NF units. The computational model, however, is presented in absolute calcium concentrations. Due to the lack of absolute reference we consider the model predictions only relative.
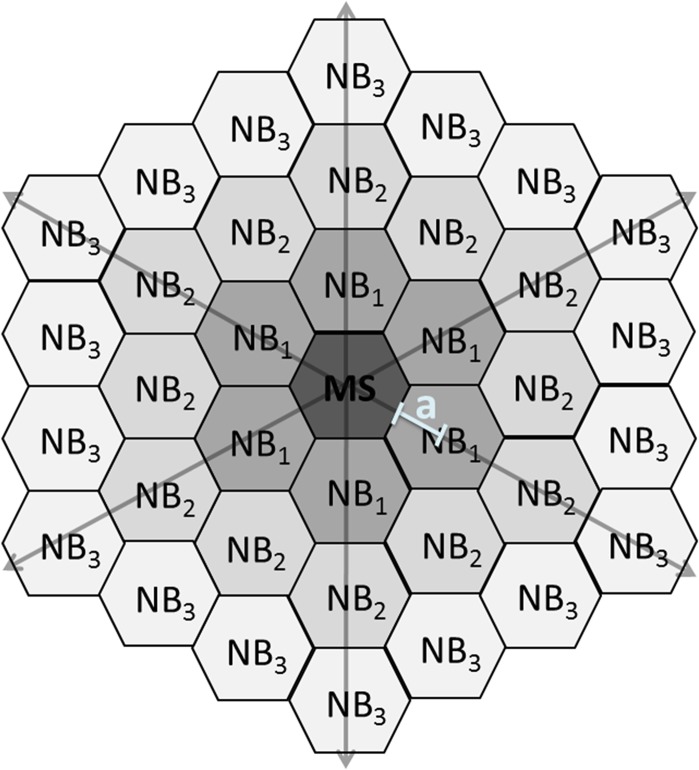
Fig 1. Numbering of the cell layers.
Schematic representation of the location of the mechanically stimulated (MS) cell with respect to the neighboring (NB) cell layers: NB1 is the first layer which is in direct contact with the MS cell; NB2 is the second layer which is in direct contact with NB1, and so forth. White line segment marks an apothem (a) of a hexagon.
Three data sets were simulated with the model. Firstly, in the GA-treated data set the gap junctions (GJs) were blocked by α-glycyrrhetinic acid (GA) (Sigma-Aldrich, St. Louis, MO, USA). Secondly, the model was verified with an untreated control data set that was based on the previous model—only the GJ model component was added. Thirdly, the model was applied to predict a combined blocking effect of GA and P2 receptor blocker suramin (Sigma-Aldrich) with GA-suramin-treated data set. Each data set was averaged from at least three separate experiments.
The experiments with GA-suramin-treated ARPE-19 cells were not included in the original paper of Abu Khamidakh et al. 2013[5]. The experimental details concerning the ARPE-19 cells as well as the experimental solutions, infrastructure, and protocols are presented in[5] with the following exception: the cells were incubated in a solution containing 30μM GA (incubation time 30 min) and 50μM suramin (incubation time 25 min) prior to mechanical stimulation. To receive representative data for each NB layer, the raw data was averaged so that the NF graphs were aligned by the starting time of mechanical stimulation, and the mean values were calculated for each NB with a one-second sampling rate. This was previously done for the control data set[5], but the averaging was performed also here for the GA-treated and GA-suramin-treated data sets.
Indirect immunofluorescence staining
ARPE-19 cells (p. 24, 27, 44, three cover slips from each passage) were cultured on glass coverslips for two days. For immunofluorescence staining, the samples were washed three times with PBS and fixed for 15 min with 4% paraformaldehyde (pH 7.4; Sigma-Aldrich) at room temperature (RT). After three subsequent washes with PBS, the samples were permeabilizing by a 15 min incubation in 0.1% Triton X-100 in PBS (Sigma-Aldrich) at RT. This was followed again by three PBS washes, after which the samples were incubated with 3% bovine serum albumin (BSA; Sigma-Aldrich) at RT for 1 h. Primary antibody Zonula Occludens (ZO-1) 1:100 (33–9100, Life Technologies) was diluted in 3% BSA PBS and incubated for 1 h at RT. Samples were then washed four times with PBS, and followed by 1h incubation at RT with secondary antibody donkey anti-mouse Alexa Fluor 568 (A10037, Life Technologies) diluted 1:400 in 3% BSA in PBS. The washes with PBS were repeated again and nuclei were stained with 4′, 6′ diamidino-2-phenylidole (DAPI) included in the mounting medium (P36935, Life Technologies).
Confocal microscopy and image processing
Zeiss LSM780 LSCM on inverted Zeiss Cell Observer microscope (Zeiss, Jena, Germany) with Plan-Apochromat 63x/1.4 oil immersion objective was used for confocal microscopy. Voxel size was set to x = y = 66nm and z = 200nm, pixel stacks were set to 1024x1024, and approximately 50–80 slices were acquired with line average of 2. DAPI and Alexa-568 were excited with 405nm and 561nm lasers and detected with emission windows of 410–495nm and 570–642nm, respectively. The images saved in czi format were processed with ImageJ (Rasband, W.S., ImageJ, U. S. National Institutes of Health, Bethesda, Maryland, USA, http://imagej.nih.gov/ij/, 1997–2014.) and assembled using Adobe Photoshop CS6 (Adobe Systems, San Jose, USA).
Construction of the model
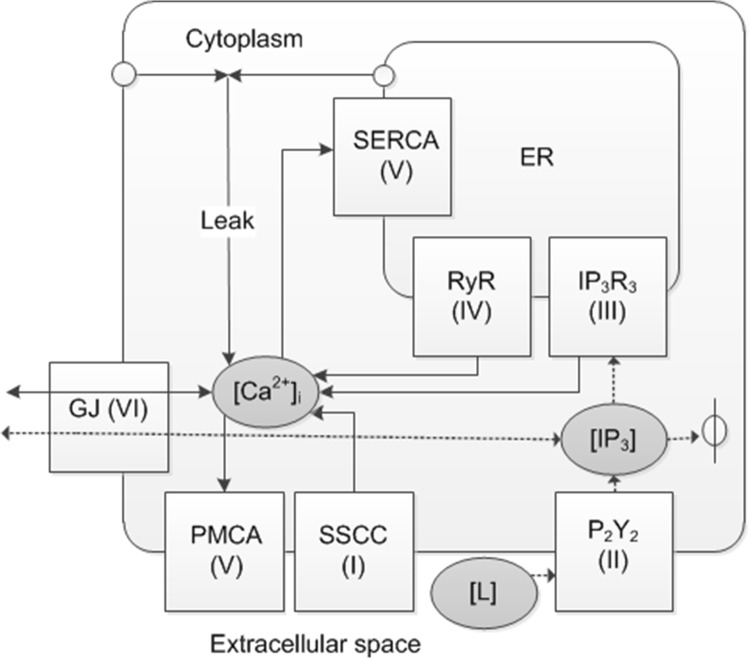
The Ca2+ model was constructed by combining six subcellular model components that included the stretch component designed in this study and the P2Y2 receptor models of Lemon et al. 2003[21], the IP3 receptor type 3 (IP3R3) of LeBeau et al. 1999[22], and the ryanodine receptor (RyR) of Keizer & Levine 1996[23]. The GJ model component connected the neighboring cells. These model components with corresponding numbering and their rationale, hypothesized Ca2+ wave propagation mechanisms as well as model equations (see chapter Detailed model equations) that were used for the NB layers and data sets are summarized in Table 1. The basis for the mathematical implementation is presented in Fig 2 as a schematic model.
Table 1. Model design.
| Mechanism | Number | Component | Rationale | Equations | NB layer | Data set |
|---|---|---|---|---|---|---|
| Mechanical stimulus applied to MS cell may stretch ARPE-19 cells near the site of stimulation [5] resulting in the opening of SSCCs that conduct Ca2+ from the extracellular space to the cytoplasm. It is shown that ARPE-19 cells can secrete ligand to the extracellular space as a response to stimuli [38]. | I | Stretch-sensitive Ca2+ channel (SSCC) | Cultured rat RPE expresses SSCCs on plasma membrane [4,53]. In ARPE-19 [Ca2+]i wave was seen in NB1-NB4 layers even when the ER was depleted[5], indicating a Ca2+ influx mechanism independent of the ER, possibly the SSCCs. | 7–9 a | 1–4 | GA-treated, Control, GA-suramin-treated |
| The ligand, likely ATP or UTP [3,30,38,54], interacts with G-protein coupled purinergic receptor type P2Y2 on the cell membrane leading to the production of inositol 1,4,5-trisphosphate (IP3) to the cytoplasm in a ligand concentration dependent manner. | II | Purinergic P2Y2 receptor (P2Y2) | The presence of P2Y2 receptors has been shown in cultured human RPE[30], bovine and human fetal RPE as well as in Long-Evans rats[55] | 10–16 b | 1–10 | GA-treated, Control, GA-suramin-treated e |
| IP3 diffuses across the cytoplasm to the endoplasmic reticulum (ER), where it interacts with IP3R3 resulting in a release of Ca2+ from the ER[22]. | III | IP3 receptor type 3 (IP3R3) | Currently there is no direct evidence about the subtype of IP3R expressed in ARPE-19. Hence, the data from other epithelia [56], [57], and[58] and an epithelial model [16] was utilized to choose the subtype 3 (IP3R3). | 17–21 c | 1–10 | GA-treated, Control, GA-suramin-treated |
| As the cytoplasmic Ca2+ concentration increases, RyRs become activated releasing more Ca2+ to the cytoplasm from the ER[23]. | IV | Ryanodine receptor (RyR) | RyRs, locating on the membrane of ER participate in Ca2+ signaling in rat RPE[4], and ARPE-19[51]. | 22–24 d | 1–10 | GA-treated, Control, GA-suramin-treated |
| The cytoplasmic Ca2+ concentration is decreased by the pumping activities of SERCA and PMCA. IP3 is degraded in the cytoplasm. Ca2+ leak currents maintain the cytoplasmic Ca2+ baseline level. | V | Sarco/endoplasmic reticulum ATPase (SERCA), plasma membrane Ca2+ ATPase (PMCA), Leak | The presence of SERCA has been shown by blocking it to deplete the ER from Ca2+ in ARPE-19 cells[5] and rat RPE[53]. PMCA has been identified on the plasma membrane of cultured human RPE[59]. | 25 | 1–10 | GA-treated, Control, GA-suramin-treated |
| GJs form intercellular connections between neighboring cells allowing diffusion of Ca2+ and IP3 between the NB layers. | VI | Gap junction (GJ) | GJs form intercellular connections in ARPE-19[5], and rat RPE[4,60] enabling Ca2+ wave to spread over the monolayer. | 26–28 | 1–10 | Control |
Fig 2. Schematic diagram of the Ca2+ signaling model.
Solid arrows represent Ca2+ fluxes and dashed arrows IP3 dynamics. Roman numerals denote the model components I-VI. Abbreviations: [Ca2+]i = cytoplasmic Ca2+ concentration, [L] = extracellular ligand concentration, [IP3] = cytoplasmic IP3 concentration, SSCC = stretch-sensitive Ca2+ channel, P2Y2 = purinergic receptor type P2Y2, IP3R3 = IP3 receptor type 3, RyR = ryanodine receptor, SERCA = sarco/endoplasmic reticulum Ca2+ ATPase, PMCA = plasma membrane Ca2+ ATPase, Leak = combinatory Ca2+ leak from the extracellular space and the endoplasmic reticulum (ER), GJ = gap junction, ϕ = degradation.
Parameters and parameterization
The model parameters are represented in Table 2 and the parameters specific for each NB layer in Table 3. Most of the parameters were adopted from the models of Lemon et al. 2003[21], LeBeau et al. 1999[22], and Keizer & Levine 1996[23]. Typically, the volumes of ARPE-19 cells[5,24,25] and RPE cells[26,27] are variable. The cell width was approximated to be 14μm from the corner-to-corner of a hexagon and the height was 12μm[5].The cytoplasmic volume was approximated to be about 70% of the total cell volume[28]. Thus, a cytoplasmic volume (v) of 1.07 10–15 m3 was used in the simulations. The initial values, the values at time of mechanical stimulation, were taken mostly from the model of Lemon et al. 2003[21]. The initial value 0.12μM for intracellular Ca2+ concentration ([Ca2+]i) is an arbitrary value approximating the baseline Ca2+ concentration determined from GA-treated data set for NB5-NB10 layers using Matlab SimBiology Toolbox.
Table 2. Constant parameters and initial conditions.
| Parameter | Description | Value | Reference |
|---|---|---|---|
| I Stretch-sensitive Ca 2+ channels (SSCCs) | |||
| kSSCC | Maximal SSCC flux rate | 1.025 μM s-1 | fitted |
| kf | SSCC forward rate constant | 0.1382 s-1 | fitted |
| kb | SSCC backward rate constant | 0.04027 s-1 | fitted |
| kθ | Stretch-relaxation parameter | 0.08105 s-1 | fitted |
| II Metabotropic receptor P 2 Y 2 | |||
| L0 | Bolus extracellular ligand concentration at x = 0μm | 1310 μM | fitted |
| DATP | Diffusion coefficient of A | 236 μm2 s-1 | [61] |
| [RT] | Total number of P2Y2 receptors | 2∙104 | [62] |
| K1 | Unphosphorylated receptor dissociation constant | 5 μM | [21] |
| K2 | Phosphorylated receptor dissociation constant | 100 μM | [21] |
| kr | Receptor recycling rate | 1.75∙10–4 s-1 | [21] |
| kp | Receptor phosphorylation rate | 0.03 s-1 | [21] |
| ke | Receptor endocytosis rate | 6∙10–3 s-1 | [21] |
| ξ | Fraction of mobile receptors | 0.85 | [21] |
| [GT] | Total number of G-protein molecules | 1∙105 | [63] |
| kdeg | IP3 degradation rate | 1.25 s-1 | [64] |
| ka | G-protein activation rate | 0.017 s-1 | [21] |
| kd | G-protein deactivation rate | 0.15 s-1 | [21] |
| [(PIP2)T] | Total number of PIP2 molecules | 5.0∙104 | [21] |
| rr | PIP2 replenishment rate | 0.015 s-1 | [21] |
| δ | G-protein intrinsic activity parameter | 1.238∙10–3 | [21] |
| K3 | Dissociation constant for Ca2+ binding to PLC | 0.4 μM | [21] |
| α | Effective signal gain parameter | 2.781∙10–5 s-1 | [21] |
| Na | Avogadro's constant | 6.02252∙1023 | |
| v | Volume of the cytoplasmic space | 1.07∙10–15 m3 | see text |
| III IP 3 receptor type 3 (IP 3 R 3 ) | |||
| α1 | Maximum rate of k1 | 40 μM s-1 | [22] |
| β1 | [Ca2+]i for half-maximal k1 | 0.8 μM | [22] |
| k-1 | Rate of O to S transition | 0.88 s-1 | [22] |
| k2 | Rate of O to I1 transition | 0.5 s-1 | [22] |
| k3 | Rate of I1 to S transition | 0.5 s-1 | [22] |
| β4 | [IP3] for half-maximal k4 | 0.01 μM | [22] |
| k5 | Rate of I2 to S transition | 0.02 s-1 | [22] |
| Maximum IP3R3 flux rate | 155.8 μM s-1 | fitted | |
| IV Ryanodine receptor (RyR) | |||
| Ka | Keizer & Levine dissociation constant | 0.37224 μM | [23] |
| Kb | Keizer & Levine dissociation constant | 0.63601 μM | [23] |
| Kc | Keizer & Levine dissociation constant | 0.05714 μM | [23] |
| kRyR | Maximum RyR flux rate | 16.04 μM s-1 | fitted |
| V Ca 2+ pumps and leak current | |||
| VPump | Maximal pump rate | 5.341 μM s-1 | fitted |
| KPump | [Ca2+]i for half-maximal VPump | 0.5030 μM | fitted |
| JLeak | Ca2+ leak current | 0.1450 μM s-1 | fitted |
| VI Gap junctions (GJ) | |||
| Diffusion coefficient of Ca2+ through GJs | 512.7 μm2 s-1 | fitted | |
| Diffusion coefficient of IP3 through GJs | 913.9 μm2 s-1 | fitted | |
| Ca2+ input to NB1 | -0.003320 μM s-1 | fitted | |
| IP3 input to NB1 | 0.5771 μM s-1 | fitted | |
| Ca2+ output from NB10 | 0 μM s-1 | see text | |
| IP3 output from NB10 | 0 μM s-1 | see text | |
| Initial conditions (time 0s) | |||
| [RS] | Total number of unphosphorylated surface receptors | 17000 | [21] |
| [RS p] | Total number of phosphorylated surface receptors | 0 | [21] |
| [G] | Basal number of G-protein molecules | 14 | [21] |
| [IP3] | Basal IP3 concentration | 0.01 μM | [21] |
| [PIP2] | Basal number of PIP2 molecules | 49997 | [21] |
| [Ca2+]i | Basal cytoplasmic Ca2+ concentration | 0.12 μM | see text |
Table 3. Location-dependent parameters with respect to the MS cell.
| Parameter | Description | Equation | Range |
|---|---|---|---|
| x | Distance from the MS cell centre | 1 | From 12.12 μm (NB1) to 121.24 μm (NB10) |
| θ | Stretch | 2 (exponential decay) | From 0.096 (NB1) to 1.014 10–6 (NB10) |
| L | Extracellular ligand concentration | 3 (exponential decay) | From 26.14 μM (NB1) to 2.61 μM (NB10) |
| α4 | IP3R3 phosphorylation rate | 4 (exponential rise) | From 0.0413 s-1 (NB1) to 0.1548 s-1 (NB10) |
| 5 (exponential rise) | From 0.0333 (NB1) to 0.1503 (NB10) | ||
| Ca2+ flux through GJs | 26 | From 0.049 μM s-1 (NB1→NB2) to 1.8 10–6 μM s-1 (NB9→NB10) | |
| IP3 flux through GJs | 27 | From 0.407 μM s-1 (NB1→NB2) to 0.022 μM s-1 (NB9→NB10) | |
| A | Area of the cell membranes connecting NB layers | 28 | From 1512 μm2 (NB1) to 10584 μm2 (NB10) |
The rest of the parameters were fitted with Matlab SimBiology Parameter Fit Task: First, the parameter values, excluding SSCC and GJ model components, were fitted with GA-treated data set in NB5 layer. This layer has in general the largest Ca2+ response from those NB layers that do not experience any stretch due to mechanical stimulation, according to our assumption. Secondly, the SSCC model component parameters, excluding the location-specific stretch (θ) parameter (see below), were fitted with the same GA-treated data set in NB1 layer that is assumed to have the largest stretch. These values were then used in all simulations for all data sets and NB layers. For the control data set with gap junctions, all other parameters were kept unchanged but the GJ related diffusion parameters, , , and , were fitted using NB1 layer. As a boundary condition we assumed that there is no outflow of IP3 and Ca2+ outside the epithelium, thus and were assigned to be zero.
Location-dependent parameters
Three parameters were assumed to vary according to the location of the cell with respect to the MS cell: stretch (θ) activating the stretch-sensitive Ca2+ channels (SSCCs), the extracellular ligand concentration ([L])[6,16,29,30], and the phosphorylation rate of IP3R3 (α4)[22]. Ca2+ concentration was modeled separately in each NB layer. The distance (x) defines the distance of the NB layer from the MS cell centre that was calculated using the idealized hexacon RPE cell architecture (Fig 1) as
| (1) |
where a is an apothem of the hexagon, 6 is the number of corners in the hexagon, s = 7μm is the length of the hexagon side and n = 1, 2, 3…10 according to the NB layer numbering.
The stretch component was present in cell layers NB1-NB4. Stretch (θ) was parameterized in the GA-treated data set separately for each NB layer. The obtained parameters resulted in an exponentially decaying function corresponding to the decay of an amplitude envelope of a damped wave in a membrane [31]. This function was then used for modeling the stretch
| (2) |
where x is the distance from the MS cell (R2 = 0.9878).
Ligand diffusion in the extracellular space is modelled according to thin film solution to Fick’s diffusion law [32] as follows describing the ligand concentration (L) as a function of time (t)
| (3) |
where L0 is the initial bolus ligand concentration above the MS cell (at x = 0), DATP is the diffusion coefficient for ATP, and x describes the NB layer distance from the central MS cell.
IP3R3 phosphorylation rate (α4) used in Eq 21 was fitted separately for each NB layer in GA-treated and control data sets, which resulted in shallowly rising exponential functions with respect to the distance of the cell from the MS cell (x). The equation for GA-treated data set (R2 = 0.9740) is
| (4) |
and for control data set (R2 = 0.9798)
| (5) |
Similarly to θ and L, these functions were then used in simulations instead of values from separate fits.
Model simulations
The parameters were fitted with Matlab SimBiology (R2012a, The MathWorks, Natick, MA) to the experimental data using Parameter Fit task, where the maximum iterations was 100. The solver type was ode45 (Dormand-Prince) and the error model was constant error model. The time step in the simulations was set to ∆t = 0.1 seconds.
Sensitivity analysis
Sensitivity analysis was performed to evaluate the uncertainty of selected parameters that were fitted in this study (parameters , kRyR, VPump, KPump, JLeak, , , and from Table 2) or behaved as location-specific parameters (parameters θ, L and α4 from Table 3). Values of these parameters were changed -25%, -10%, 0%, +10% and +25% in the model including all the model components I-VI for the control data set. The influence of these parameter were studied for NB layers NB1, NB5 and NB10 concentrating on the following features of the Ca2+ wave: peak amplitude, time to peak, Ca2+ wave width at half maximum, and Ca2+ concentration at the end of the Ca2+ wave (at 90 seconds’ time point).
Model prediction of drug effect: suramin
With the model, we investigated the mechanism by which suramin influences the Ca2+ waves in ARPE-19 cells. First, we compared the peak amplitude, time to peak, Ca2+ wave width at half maximum, and Ca2+ concentration in the end of the Ca2+ wave at 90 seconds’ time point between two experimental data sets: GA-treated and GA-suramin-treated data sets. Second, we made sensitivity analysis about the behaviour of P2Y2 receptor regulation parameters (K1, K2, kr, kp, ke, ξ), since suramin is a known unspecific antagonist of P2 receptors. Suramin has also been suggested to disrupt the coupling between the receptor in the cell membrane and the G-protein by blocking the association of the G-protein α and βγ subunits[33]. Hence, the G-protein cascade parameters ka, kd and δ were also evaluated. The sensitivity analysis was done in the model for GA-treated data set (including model components I-V) in NB1, NB5 and NB10 layers. The parameter values were changed in the model by -25% and +25% in order to compare the effects of parameter modifications to the observed differences in the experimental data between GA-treated and GA-suramin-treated data sets. All other parameters were kept unchanged. Third, based on the results of this approach, the model was fitted to the GA-suramin-treated data set by refitting those P2Y2 receptor and G-protein cascade parameters that were observed to change the Ca2+ curve similarly to the differences seen in the experimental data between GA-treated and GA-suramin-treated data sets. This was done with Matlab SimBiology Parameter Fit task for each NB layer.
Detailed model equations
Time dependent changes in intracellular Ca2+ concentration [Ca2+]i are presented in the model as a combination of Ca2+ fluxes
| (6) |
where the subscripts indicate the source of the flux: stretch-sensitive Ca2+ channels (JSSCC), inositol 1,4,5-trisphosphate (IP3) receptor type 3 (), and ryanodine receptor (JRyR). JPump combines the Ca2+ pumping functions of sarco/endoplasmic reticulum ATPase (SERCA) and the plasma membrane Ca2+ ATPase (PMCA). Leak Ca2+ current (JLeak) describes the total leakage from the extracellular space and the endoplasmic reticulum (ER) to the cytoplasm. is the Ca2+ flux through gap junctions.
I Stretch-sensitive Ca2+ channels (SSCCs)
Stretch-sensitive Ca2+ channels (SSCCs) on the cell membrane are activated, when exposed to mechanical stimulation. Their closure is caused either by relaxation in the mechanical force or by their adaption to that mechanical force[34]. The SSCC model is described with Eqs 7–9. In this study, a model for SSCCs was developed according to the kinetic diagram shown in Fig 3, where CSSCC describes the proportion of the channels in the closed state. OSSCC is the proportion of SSCCs in the open state defined as
| (7) |
where kf is the forward rate constant and kb is the backward rate constant. Ca2+ flux via SSCCs (JSSCC) is expressed as
| (8) |
where kSSCC is the maximum Ca2+ flux rate via SSCCs. Parameter θ is dimensionless, and describes the quantity of stretch induced at the time of mechanical stimulation, which then decreases with time
| (9) |
according to a stretch-relaxation parameter kθ.
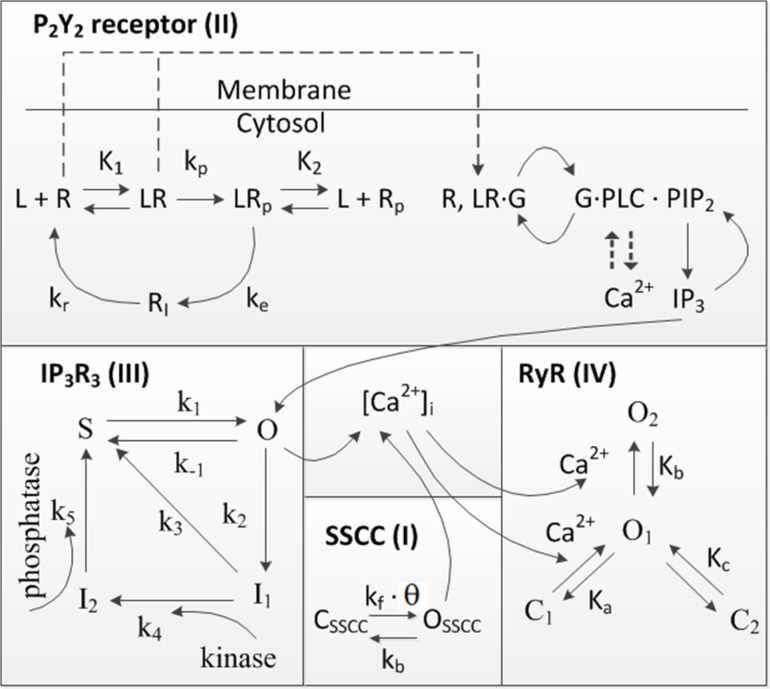
Fig 3. Kinetic diagram.
Kinetics of the model component I (SSCC) were combined with the kinetics of model components II-IV from the original models of the P2Y2 receptor[21], IP3R3[22], and RyR[23].
II Purinergic receptor P2Y2
The agonist-induced activation of the second messenger system, here P2Y2, is represented by Eqs 10–16[21].The kinetic diagram for the P2Y2 receptor is presented in Fig 3. Some of the ligand-bound P2Y2 receptors on the cell surface are phosphorylated irreversibly at rate kp, which causes desensitization of the receptors. Phosphorylated receptors are internalized at a rate ke, and these internalized receptors are then dephosphorylated and recycled back to the surface at rate kr. G-proteins can only be activated by the unphosphorylated P2Y2 receptors [RS] defined by
| (10) |
where [RT] denotes the total number of surface receptors, K1 is the dissociation constant for unphosphorylated receptors, and [L] is the extracellular ligand concentration. The total number of phosphorylated surface receptors is
| (11) |
where K2 is the dissociation constant for phosphorylated receptors. The binding of the ligand to the G-protein coupled receptor P2Y2 results in a cascade of events leading to the activation of enzyme phospholipase C (PLC). This enzyme then hydrolyses the phosphatidylinositol 4,5-bisphosphate (PIP2) to IP3. The activation rate (ka) of the G-protein is proportional to two ratios: the ratio of the activities of the ligand unbound and bound receptor species (δ), and the ratio of the number of ligand bound receptors and the total number of receptors (pr). Denoting the deactivation of G-protein to occur at a deactivation rate of kd, the equations for the amount of Gα∙GTP labeled as [G] as well as for the ratio pr can be expressed as
| (12) |
and
| (13) |
Equation for the concentration of IP3 is
| (14) |
where kdeg is the degradation rate of IP3 and is the IP3 flux through gap junctions. The rate coefficient for PIP2 hydrolysis (rh) includes the effective signal gain parameter (α) and the dissociation constant for Ca2+ binding to PLC (K3) that can be expressed as
| (15) |
Replenishment of PIP2 is required for IP3 production to be maintained over sustained periods of agonist stimulation. The equation for the number of PIP2 molecules [PIP2] is
| (16) |
where rr represents the PIP2 replenishment rate and [(PIP2)T] the total number of PIP2 molecules.[21]
III IP3 receptor type 3 (IP3R3)
The IP3 receptor type 3 (IP3R3) function is represented by the Eqs 17–21[22]. The kinetic diagram for IP3R3 is shown in Fig 3. The IP3-induced release of Ca2+ from the ER through IP3R3 () is
| (17) |
where is the maximum rate of Ca2+ release, and IP3R3 comprises four subunits that all must be in the open state (O) for the receptor to conduct. The steady-state proportion of open receptors (O) is
| (18) |
Where ϕ function controls the sensitivity of IP3R3 to [IP3], and it can be expressed as
| (19) |
with rate coefficients k-1, k2, k3, and k5 being constants. Coefficient k1 describes a rate for IP3R3 transition from shut state (S) to open state (O)
| (20) |
where constant α1 is the maximum rate of S to O transition, and β1 is the [Ca2+]i at which the rate is half of its maximum. Coefficient k4 expresses the rate for IP3R3 from the first inactivated state (I1) to the second inactivated state (I2). It can be expressed as
| (21) |
where the I1 to I2 transition is agonist specific and involves a phosphorylation of IP3R3 by kinase activity. This is defined by parameter α4 that denotes the maximum rate of I1 to I2 transition, while β4 denotes the value of [IP3] at which the rate is half maximal.[22]
IV Ryanodine receptor (RyR)
The ryanodine receptor (RyR) dynamics were modeled by Keizer & Levine 1996[23] with Eqs 22–24. In Fig 3 the kinetic diagram for RyR is illustrated. The Ca2+ release from the ER through RyR (JRyR) is defined by the maximum RyR flux rate (kRyR) multiplied by the open probability (PRyR) as
| (22) |
where
| (23) |
and where w ∞ is the RyR sensitivity function
| (24) |
and Ka, Kb, and Kc are dissociation constants. [23]
V Sarco/endoplasmic reticulum Ca2+ ATPase (SERCA) and plasma membrane Ca2+ ATPase (PMCA)
JPump combines the pumping functions of sarco/endoplasmic reticulum Ca2+ ATPase (SERCA) and plasma membrane Ca2+ ATPase (PMCA)
| (25) |
where VPump indicates the maximum flux rate of the pumps and KPump states the [Ca2+]i for half-maximal pumping rate.
VI Gap junctions (GJs)
Gap junctions (GJs) and the Ca2+ flux via GJs () are modeled as
| (26) |
where n is the number of the NB layer. The NB layer n receives Ca2+ from the previous NB layer n − 1 and delivers Ca2+ to the next NB layer n + 1 according to the concentration gradient. Similarly, IP3 flux through GJs () is modelled as
| (27) |
where n is the number of the NB layer. is the diffusion coefficient for Ca2+ and is the diffusion coefficient for IP3. These diffusion coefficients do not take into account the open probability, regulation, or density of the GJs as they describe the actual movement of Ca2+ and IP3 from one NB layer to the next NB layer. As an exception to other NB layers, the fluxes from MS cell to NB1 layer are modelled by parameters and for Ca2+ and IP3, respectively. Similarly, the fluxes from NB10 layer to distant cell layers are modelled with parameters and .
Parameter A describes the area of the cell membranes connecting the neighbouring NB layers in the monolayer. The value for A is received by multiplying the area of one hexagon side, that is the length of the hexagon side (l = 7μm) times the height of the cell (h = 12μm), by the number of hexagon edges between the two NB layers as
| (28) |
where n is the number of the NB layer (n = 1, 2, 3….10). Each NB layer has six cells with three connecting sides and (n-1) 6 cells with two connecting sides (see Fig 1). In other words, the area (A) increases with distance from the central MS cell.
Results
Polarization of the ARPE-19 monolayer
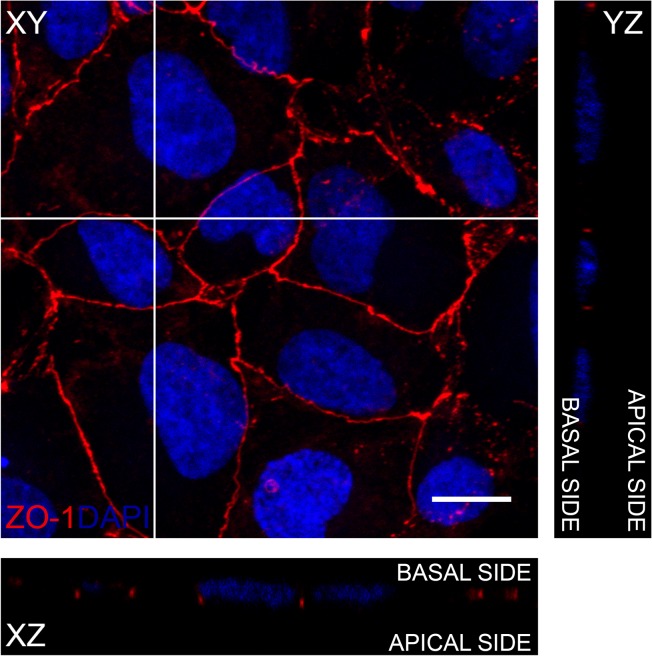
Polarization of the ARPE-19 monolayer was demonstrated by immunolabeling the tight junctions in the monolayer. Confocal microscopy image (Fig 4) shows that within 2 days the ARPE-19 cells have formed a monolayer where ZO-1 is localised continuously in the junctions of the cells, forming a homogeneous network. This can be taken as an indication of the polarization of the epithelial cell culture [35].
Fig 4. Polarization of the ARPE-19 monolayer.
Z-projections (XZ and YZ) from apical side to basal side and maximum intensity projection of the XY plane in the ARPE-19 monolayer represent the localization of Zonula Occludens (ZO-1, red) in the confocal micrograph after immunofluorescence labeling with the nuclear label 4’,6-diamidino-2-phenylindole (DAPI, blue). Scale bar is 10μm.
Ca2+ signal propagation mechanisms
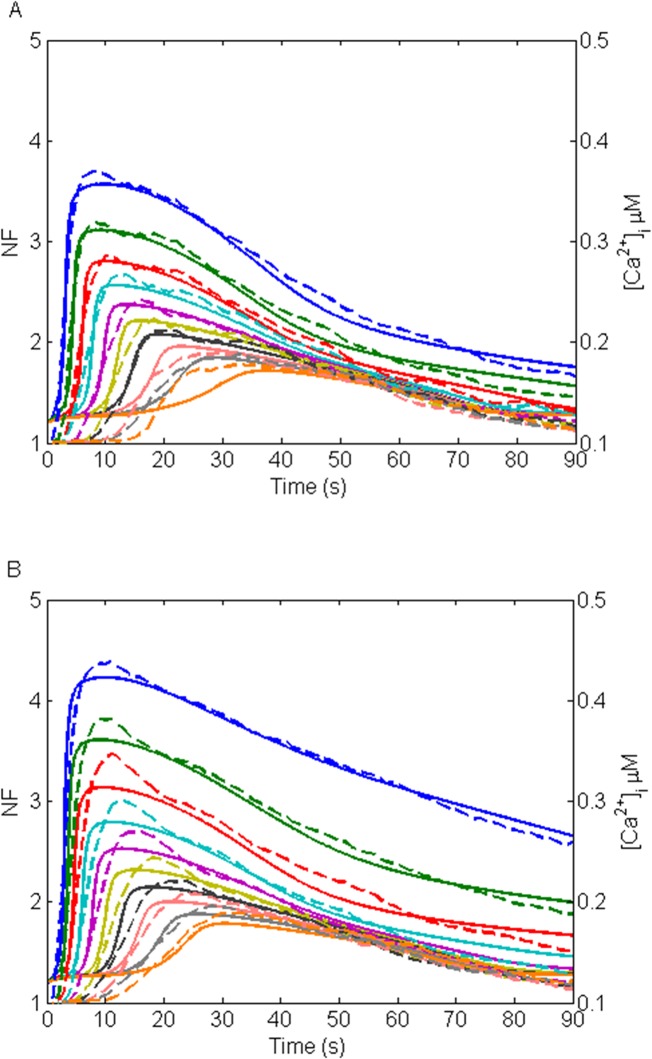
The fittings of the model to the experimental data in the NB1-NB10 layers are illustrated in Fig 5A for the GA-treated data set and in Fig 5B for the control data set. The model simulations managed to catch very well the features of the experimental data in both data sets. In GA-treated data set (Fig 5A), the simulations closely followed the data in peak amplitude, time to peak, Ca2+ wave width at half maximum and end Ca2+ concentration in NB1-NB9 layers. In NB10 layer, however, time to peak was longer in the simulation results than in the data. In the control data set (Fig 5B), the Ca2+ wave features differed slightly between the model and the data, but overall the curve shape of the model followed the data reasonably well. R2 values describing the goodness of fit are presented in Table 4. In GA-treated data set and control data set R2 values were higher than 0.8 in NB1-NB9 and lower than 0.8 in NB10. Hence, 90% of the fits in GA-treated data set and control data set resulted in R2 > 0.8.
Fig 5. Fittings of the model to the experimental data.
(A) GA-treated, and (B) control data sets with dashed lines representing the data in dimensionless NF units and solid lines representing the model simulations with arbitrary units representing [Ca2+]i in μM concentrations. The uppermost curve pair (blue) represents NB1, the second uppermost NB2 (green), followed by NB3 (red), NB4 (light blue), NB5 (purple), NB6 (yellow), NB7 (black), NB8 (light red), NB9 (grey), and NB10 (orange).
Table 4. R2 values indicating the goodness of fit between the model and the data.
| Data set | NB1 | NB2 | NB3 | NB4 | NB5 | NB6 | NB7 | NB8 | NB9 | NB10 |
|---|---|---|---|---|---|---|---|---|---|---|
| GA-treated | 0.9839 | 0.9815 | 0.9811 | 0.9651 | 0.9716 | 0.9627 | 0.9677 | 0.9326 | 0.8837 | 0.4561 |
| Control | 0.9665 | 0.9613 | 0.9454 | 0.9653 | 0.9686 | 0.9558 | 0.9508 | 0.9419 | 0.9108 | 0.6259 |
| GA-suramin-treated | 0.8633 | 0.8543 | 0.9344 | 0.9323 | 0.9414 | 0.9156 | 0.9253 | 0.7812 | 0.6110 | 0.2297 |
R2 values are listed separately for each data set and NB layer.
The model includes the model components of SSCCs, P2Y2 receptors, IP3R3s, RyRs, Ca2+ pumps and GJs, and the parameters were either obtained from previous studies or defined in this study for ARPE-19. The basic fit was done in GA-treated data set for NB5, but the SSCC model component was fitted in NB1 (Table 2). Three location-specific parameters were defined in this study: stretch (θ), extracellular ligand concentration (L) and phosphorylation rate of IP3R3 (α4) (Table 3). The stretch (θ) and extracellular ligand concentration (L) decayed exponentially from NB1 towards the distant NB cell layers. The IP3R3 phosphorylation rate regulated by the kinase activity (α4) increased following a shallow exponential, almost linear function, from NB1 to NB10. The corresponding values of α4 with the distance were lower in the control data set (Eq 5) than in the GA-treated data set (Eq 4) indicating a possible role of IP3 receptor phosphorylation rate as a regulator of Ca2+ signaling. The GJ model component was parameterized in control data set for NB1. GJs mediated the Ca2+ signal by allowing the diffusion of Ca2+ and IP3 between adjacent cell layers so that the fluxes of these species decreased with distance from the MS cell due to the increasing area of the cell membranes connecting the NB layers (Table 3).
The resulting model of mechanical stimulus induced Ca2+ dynamics is: 1) Cells near the stimulus site conduct Ca2+ through plasma membrane SSCCs, and gap junctions conduct the Ca2+ and IP3 between cells further away from stimulated cell. 2) The MS cell secretes one or several types of ligand to the extracellular space where the ligand diffusion mediates the Ca2+ signal so that the ligand concentration decreases with distance. 3) The phosphorylation of the IP3 receptor defines the cell’s sensitivity to the extracellular ligand attenuating the Ca2+ signal in the distance.
Results of the sensitivity analysis
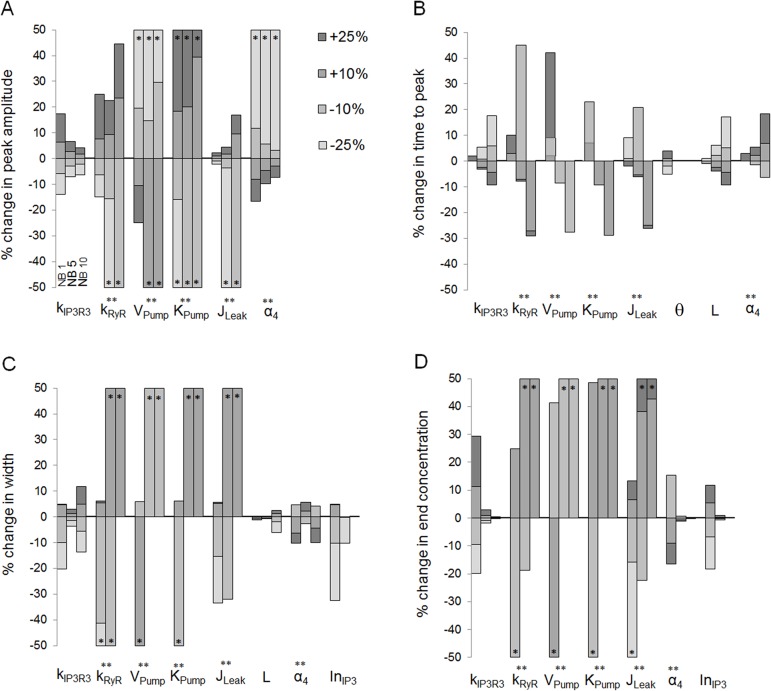
The sensitivity of the four Ca2+ wave features described in Materials and Methods was studied for a set of parameters that were fitted in this study for NB1, NB5 and NB10 layers (Fig 6). From the location-dependent parameters, θ, L and α4, Ca2+ wave features were most sensitive to modifications in α4 and the least sensitive to modifications in θ. Overall, decreasing the stretch parameter (θ) resulted in faster Ca2+ waves in NB1 (Fig 6B). Increasing the extracellular ligand concentration (L) in turn decreased the time to peak (Fig 6B) and increased the Ca2+ wave width at half maximum (Fig 6C). The effects of the changes in IP3 receptor phosphorylation rate (α4) on Ca2+ wave features were complex: with decreasing α4 Ca2+ wave peak amplitude increased (Fig 6A), time to peak decreased (Fig 6B), the Ca2+ wave width at half maximum increased or decreased depending on the NB layer (Fig 6C), and the end concentration increased (Fig 6D). The Ca2+ wave features were insensitive to gap junction related parameters , and so that the tested modifications in their values resulted in less than 5% change in the features from the original conditions. Thus, they are not illustrated in Fig 6. However, increasing IP3 input to NB1 via GJs () increased the Ca2+ wave width at half maximum (Fig 6C) and end concentration (Fig 6D), and the sensitivity was significantly higher in NB1 layer than in the more distant NB layers. In general, the sensitivity of the model to the changes in tested parameters depended on the NB layer and thus on the distance to the MS cell. Few parameters, however, were independent of the location (parameters , kRyR, VPump, KPump, JLeak), but changes in their values affected significantly the investigated Ca2+ wave features.
Fig 6. Sensitivity analysis of the model parameters.
Percentage changes in Ca2+ wave (A) peak amplitude, (B) time to peak, (C) Ca2+ wave width at half maximum, and (D) end Ca2+ concentration at 90 seconds’ time point due to changes in model parameters , kRyR, VPump, KPump, JLeak, θ, L, α4, , , , and as marked in the x-axis. The analysis was carried out in NB layers NB1, NB5 and NB10 as denoted in (A) for parameter . The amount of modification (-25%, -10%, +10% or +25%) is shown in the grayscale of the histogram. The histogram bar is marked with asterisk (*) if the change was greater than 50%, and with double asterisk (**) if parameter modification did not result typical Ca2+ waveform. Regarding each Ca2+ wave feature, the parameter is illustrated only if the change was more than 5%.
Possible suramin effect on attenuation of Ca2+ waves
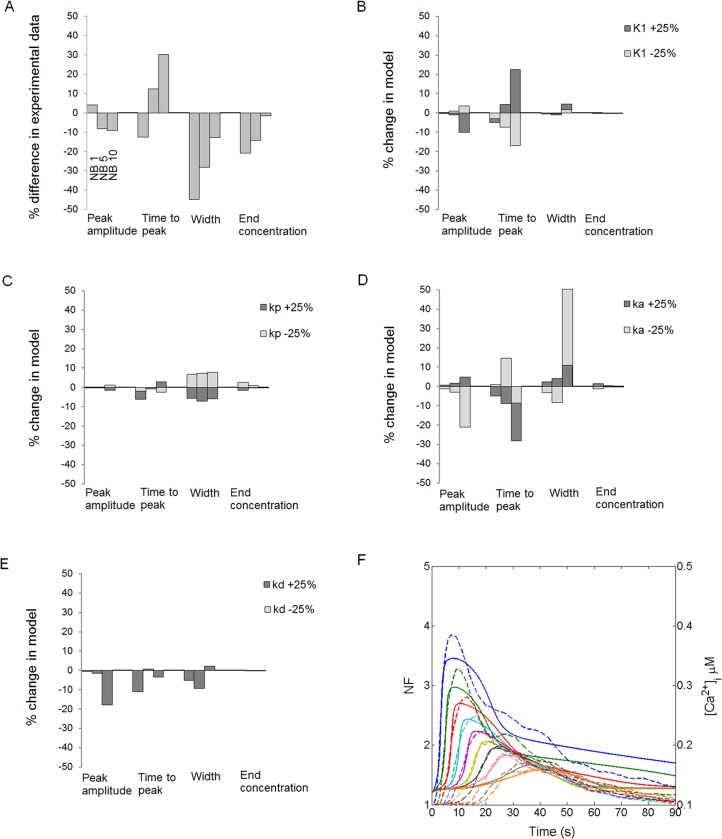
Similarly to the general sensitivity analysis, the four Ca2+ wave features were compared between the experimental GA-treated and GA-suramin-treated data sets as well in NB1, NB5 and NB10 layers (Fig 7A). In the GA-suramin-treated data set, differences in peak amplitude were less than 10% compared to the GA-treated data set. However, time to peak decreased for NB1 and increased for NB5 and NB10 layers in the GA-suramin-treated data set. Furthermore, in this data set the Ca2+ wave width at half maximum and the end Ca2+ concentration were lower than in the GA-treated data set.
Fig 7. Suramin effects on Ca2+ wave.
(A) Comparison of the peak amplitude, time to peak, Ca2+ wave width at half maximum, and end Ca2+ concentration at 90 seconds’ time point in cell layers NB1, NB5 and NB10 between the experimental GA-treated and GA-suramin-treated data sets. The deviations of each Ca2+ wave feature in GA-suramin-treated data set from GA-treated data set are expressed as percentages. (B) Unphosphorylated P2Y2 receptor dissociation constant (K1), (C) P2Y2 receptor phosphorylation rate (kp), (D) G-protein activation rate (ka), and (E) G-protein deactivation rate (kd) were changed in the model for GA-treated data set either -25% or +25%, as denoted in the grayscale of the histogram, and the percentage change in each Ca2+ wave feature is illustrated. (F) Fitting of the model to the GA-suramin-treated data set. Dashed lines represent the data in dimensionless NF units, whereas solid lines represent the model simulations with arbitrary units representing [Ca2+]i in μM concentrations. The uppermost curve pair (blue) represents NB1, the second uppermost NB2 (green), followed by NB3 (red), NB4 (light blue), NB5 (purple), NB6 (yellow), NB7 (black), NB8 (light red), NB9 (grey), and NB10 (orange).
Since suramin is a known P2 receptor blocker, we studied the sensitivity of the model to P2Y2 receptor parameters for the GA-treated data set (including model components I-V) by changing their values by ±25%. Similarly, G-protein cascade parameters were studied as well to consider the possible effect of suramin to disrupt the coupling between the receptor in the cell membrane and the G-protein. Our aim was to investigate the degree to which the observed differences in the Ca2+ wave features between GA-treated and GA-suramin-treated data sets could be accounted for by the changes in these parameters. The sensitivity analysis revealed that the modifications in P2Y2 unphosphorylated receptor dissociation constant (K1) and P2Y2 receptor phosphorylation rate (kp) indeed induced changes that were similar to the experimental observations (see Fig 7A): increase in K1 modified the time to peak (Fig 7B) and increase in kp narrowed the Ca2+ wave width at half maximum (Fig 7C). This would indicate disrupted ligand binding to the receptor or a higher phosphorylation rate of P2Y2 receptors as well as a faster desensitization of the receptors after ligand binding. P2Y2 receptor parameters K2, kr, ke, ξ, on the contrary, had a negligible influence on Ca2+ wave behaviour: the modifications of these parameters by ±25% resulted only in less than 3% change on Ca2+ wave features, as was the case also for G-protein cascade parameter δ. G-protein cascade parameters G-protein activation rate (ka) (Fig 7D) and G-protein deactivation rate (kd) (Fig 7E) had diverse effects on the Ca2+ wave features: for example decreasing ka and increasing kd narrowed the Ca2+ wave width at half maximum in NB1 and NB5, but widened it in NB10. Thus, their behaviour did not follow the observations from the experimental data and therefore these factors were not considered to be responsible for the effects of suramin on the Ca2+ wave.
Fig 7F illustrates the fit of the model to the GA-suramin-treated data set after refitting the model parameters K1 and kp. The values of these parameters ranged as follows: K1 values decreased from 8.83μM in NB1 to 5.15μM in NB10 and kp values decreased from 0.19s-1 in NB1 to 0.05s-1 in NB10. Overall, the values of K1 and kp were higher in the GA-suramin-treated data set than in the GA-treated data set. The simulated curves seem to fit well to the experimental data, except in NB1 layer at the end of the Ca2+ wave. In GA-suramin-treated data set, R2 values were higher than 0.8 in NB1-NB7 and lower than 0.8 in NB8-NB10 (Table 4). 70% of the fits in GA-suramin-treated data set resulted in R2 > 0.8 indicating that the model explains only partially the combined effect of GA and suramin on Ca2+ waves especially in the distant NB layers.
Discussion
The ARPE-19 cell line is an important biological model of human RPE despite its certain limitations [20]. This paper presents the first computational RPE model of Ca2+ signaling using the experimental data measured from the ARPE-19 monolayer after mechanical stimulation. We aimed to create a model that combines the most important Ca2+ signaling mechanisms in ARPE-19 cells so that the model can be used later in the development of more complicated RPE and epithelial models. Furthermore, the model was used to simulate and explain the Ca2+ signaling of epithelia, especially RPE, taking into account the following factors: 1) cells are on the monolayer; 2) they are connected to each other by GJs permeating Ca2+ and IP3, and 3) the cells are most probably experiencing different stretching and chemical conditions depending on their distance from the mechanical stimulation site. To the best of our knowledge, this is the first time as Ca2+ signaling model has been implemented for the ARPE-19 monolayer. The model uses a set of location specific parameters including stretch, extracellular ligand concentration, and IP3R3 phosphorylation rate as well as the Ca2+ and IP3 fluxes through GJs.
The identity of the extracellular ligand
The airway epithelium secretes the signal carriers ATP or UTP to the extracellular space in response to mechanical stimulation[16,36]. The connection of these ligands to Ca2+ signaling as extracellular signal mediators has been mathematically modeled[16]. It is likely that a similar function can be linked to ARPE-19 or RPE, where the ligand interacts with the cell membrane P2Y2 receptors. In our model, the ligand carried the signal in the extracellular space from the MS cell towards the distant NB cell layers after mechanical stimulation. According to our model, the extracellular ligand concentration decreased exponentially from NB1 towards NB10. We suggest, based on our modeling results, that the MS cell secretes ligand to the extracellular space. Epithelial cells such as ARPE-19 have been shown to secrete ATP under different stimuli[37,38]. On the other hand, the ligand degradation by ectonucleotidase activity[39] decrease the ligand concentration. The model predicts that the magnitude of the extracellular ligand concentration partly defines the nature of the cell response: higher and faster Ca2+ waves were observed with higher ligand concentrations. The ligand concentration was derived from diffusion equation, and the obtained exponential decay function fitted well to the experimental data. Experimental studies show that the Ca2+ wave peak amplitude value increases with increased ligand concentration in cultured human RPE[30] and in human airway epithelium[6]. Also, in the mathematical model of Warren et al. 2010[16], it was observed that the time to peak for human airway epithelium decreased as the ligand concentration increased. These observations are in good agreement with our model.
The role of IP3 receptor phosphorylation rate
The phosphorylation of the IP3 receptor represents an important regulatory mechanism for Ca2+ release[40–42]. It has been shown that the production of cyclic AMP (cAMP) through the activation of the adenylyl cyclase pathway leads to the activation of protein kinase A that phosphorylates IP3 receptors[43].
Our simulation results show that the maximal phosphorylation rate of IP3R3 (α4) followed a shallow exponential, almost linear, increase from NB1 to NB10 in all three data sets. The parameter α4 has previously been modeled as agonist specific only [22]. It is of note, however, that in addition to ATP or UTP and their interaction with P2Y2 receptors, also other types of ligand-receptor interactions may occur. One plausible explanation could be that MS cell secretes different types of ligands, because its cell membrane was broken in mechanical stimulation. This would further lead to complex biological interactions at the cellular level, which is seen as a chance of this parameter with cell location.
The need to model α4 separately for the GA-treated data set and the control data set may be related to the functioning of the GJs, especially to their ability to alter ligand secretion in different cell types. Previous studies show that GJs participate in the regulation of the release of signaling molecules to the extracellular medium [44]. In astrocytes, as an example, GJs have been proposed to regulate the release of glutamate[45], an excitatory neurotransmitter and an important regulator of astrocyte Ca2+ oscillations[46].
Overall, α4 parameter may reflect a number of ligands and cell mechanisms not modelled in this nor other epithelial Ca2+ models. The low α4 values near the MS cell enable higher and faster Ca2+ waves at corresponding ligand concentrations compared to the distal cell layers, where higher levels of kinase activity attenuate and slow down the signal. This aligns well with the literature. In RPE, the addition of 8-Br-cAMP counteracted the elevation of [Ca2+]i induced by connective tissue growth factor (CTGF)[47], and the cell migration inhibitor adrenomedullin increased intracellular cAMP and decreased [Ca2+]i[48]. The effect of the adenylyl cyclase pathway on IP3R kinetics has been ignored in most of the previously published Ca2+ models e.g.[16,21,29], possibly because the kinase activity may not have been activated in those cell types or experimental conditions.
Gap junctions in Ca2+ wave propagation
GJs connect the adjacent cells together and allow the diffusion of signaling molecules between them. The diffusion through GJs has previously been modeled, for example, in airway epithelium[16]. In our model, GJs carried the Ca2+ signaling molecules between the NB layers based on the Ca2+ and IP3 concentration gradients, and permeated Ca2+ and IP3 selectively. As expected, NB layers near the MS cell were more sensitive to IP3 input than the distant NB layers, and this was seen especially in the end Ca2+ concentration at 90 seconds’ time point.
Possible Ca2+ wave attenuation mechanisms of suramin
In the GA-suramin-treated data set, the experimental data was reproduced in our model by increasing the unposphorylated receptor dissociation constant, which likely reflects disrupted ligand binding, and by increasing the phosphorylation rate of the P2Y2 receptors to enhance their desensitization. This may indicate that suramin targets on P2Y2 receptors as an unspecific P2 receptor antagonist attenuating the Ca2+ wave. This intriguing model hypothesis driven from the model results needs to be confirmed experimentally. It is worth noting, however, that suramin has also been considered to disrupt the coupling between the receptor in the cell membrane and the G-protein by blocking the association of the G-protein α and βγ subunits[33]. In our model, modifications in G-protein cascade parameters influenced the peak amplitude, time to peak and Ca2+ wave width at half maximum. Despite the observed diversity in their effects between the NB layers, it is possible that suramin targets the G-protein cascade as well, by acting as an attenuator of the Ca2+ wave.
Limitations of the model
Our work presents a computational model of epithelial Ca2+ signaling based on experimental work on the ARPE-19 cell line. This cell line is used extensively as a model of RPE, although it differs from it to some extent. The limitations of ARPE-19 compared to native human RPE arise, for example, from cell organization and metabolism[20]. Importantly for our study, ARPE-19 cell line in our experimental setup lacked pigmentation which resulted in a lack of the large Ca2+ stores, melanosomes, and needs to be taken into account when expanding our model to describe native RPE. In addition, we confirmed the polarity of the ARPE-19 monolayer with confocal microscopy. Trans-epithelial resistance (TER) that is a general measure of epithelial integrity was not measured due to technical challenges to perform the measurements on glass cover slips with our present equipment [49]. Nevertheless, the computational model created in this study describes the most important components of epithelial and ARPE-19 Ca2+ activity. Thus it provides a good basis to address the native RPE in the future, even though it, being based on an in vitro model of RPE, needs to be considered only as a model. To improve the model further, experimental data and model implementations on certain additional Ca2+ related mechanisms, such as P2X receptors[50], voltage-sensitive Ca2+ channels[51] and Na+/Ca2+ exchangers[52] would be well warranted. Finally, it is worth noting that the experimental work of Abu Khamidakh et al. 2013[5] did not produce absolute Ca2+ concentrations, and therefore our model also features only relative Ca2+ activity.
Conclusions
A full mathematical understanding of RPE and epithelial Ca2+ signaling would allow one to simulate cellular Ca2+ responses under several physiological, pathological, and experimental conditions. Our present model represents significant progress towards this goal since it is able to reproduce the experimental data from an RPE type epithelium, ARPE-19 cell line, in different conditions, simulate several epithelial Ca2+ signaling mechanisms, and predict drug responses in the epithelia. Our future work will include further development of the model especially focusing on the role of the voltage sensitive Ca2+ channels in the RPE.
Data Availability
All relevant data are within the paper.
Funding Statement
This study was financially supported by the Academy of Finland (grant numbers 252225, 260375, 218050 and 137801), TEKES- the finnish funding agency for innovation (Human Spare Part Project), and Doctoral Programme of the President of the Tampere University of Technology. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Sanderson MJ, Charles AC, Boitano S, Dirksen ER. Mechanisms and function of intercellular calcium signaling. Mol Cell Endocrinol. 1994;98: 173–187. [DOI] [PubMed] [Google Scholar]
- 2. Konari K, Sawada N, Zhong Y, Isomura H, Nakagawa T, Mori M. Development of the blood-retinal barrier in vitro: Formation of tight junctions as revealed by occludin and ZO-1 correlates with the barrier function of chick retinal pigment epithelial cells. Exp Eye Res. 1995;61: 99–108. [DOI] [PubMed] [Google Scholar]
- 3. Wimmers S, Karl MO, Strauss O. Ion channels in the RPE. Prog Retin Eye Res. 2007;26: 263–301. [DOI] [PubMed] [Google Scholar]
- 4. Himpens B, Stalmans P, Gomez P, Malfait M, Vereecke J. Intra- and intercellular Ca2+ signaling in retinal pigment epithelial cells during mechanical stimulation. The FASEB Journal. 1999;13: 63–68. [DOI] [PubMed] [Google Scholar]
- 5. Abu Khamidakh AE, Juuti-Uusitalo K, Larsson K, Skottman H, Hyttinen J. Intercellular Ca2+ wave propagation in human retinal pigment epithelium cells induced by mechanical stimulation. Exp Eye Res. 2013;108: 129–139. 10.1016/j.exer.2013.01.009 [DOI] [PubMed] [Google Scholar]
- 6. Hansen M, Boitano S, Dirksen ER, Sanderson MJ. Intercellular calcium signaling induced by extracellular adenosine 5′-triphosphate and mechanical stimulation in airway epithelial cells. Journal of Cell Science. 1993;106: 995–1004. [DOI] [PubMed] [Google Scholar]
- 7. Gelisken F, Inhoffen W, Partsch M, Schneider U, Kreissig I. Retinal pigment epithelial tear after photodynamic therapy for choroidal neovascularization. Am J Ophthalmol. 2001;131: 518–520. [DOI] [PubMed] [Google Scholar]
- 8. Garg S, Brod R, Kim D, Lane RG, Maguire J, Fischer D. Retinal pigment epithelial tears after intravitreal bevacizumab injection for exudative age-related macular degeneration. Clin Experiment Ophthalmol. 2008;36: 252–256. 10.1111/j.1442-9071.2008.01710.x [DOI] [PubMed] [Google Scholar]
- 9. Singh RP, Sears JE. Retinal pigment epithelial tears after pegaptanib injection for exudative age-related macular degeneration. Am J Ophthalmol. 2006;142: 160–162. [DOI] [PubMed] [Google Scholar]
- 10. Rae Shi K. Revolution dawning in cardiotoxicity testing. Nature Reviews Drug Discovery. 2013;12: 565–567. 10.1038/nrd4083 [DOI] [PubMed] [Google Scholar]
- 11. Sneyd J, Tsaneva-Atanasova K, Bruce JIE, Straub SV, Giovannucci DR, Yule DI. A model of calcium waves in pancreatic and parotid acinar cells. Biophys J. 2003;85: 1392–1405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Höfer T, Venance L, Giaume C. Control and plasticity of intercellular calcium waves in astrocytes: A modeling approach. The Journal of Neuroscience. 2002;22: 4850–4859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Wu D, Jia Y, Zhan X, Yang L, Liu Q. Effects of gap junction to Ca2+ and to IP3 on the synchronization of intercellular calcium oscillations in hepatocytes. Biophys Chem. 2005;113: 145–154. [DOI] [PubMed] [Google Scholar]
- 14. Rizzolo LJ. Development and role of tight junctions in the retinal pigment epithelium. Int Rev Cytol. 2007;258: 195–234. [DOI] [PubMed] [Google Scholar]
- 15. Appleby PA, Shabir S, Southgate J, Walker D. Cell-type-specific modelling of intracellular calcium signalling: A urothelial cell model. Journal of The Royal Society Interface. 2013;10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Warren NJ, Tawhai MH, Crampin EJ. Mathematical modelling of calcium wave propagation in mammalian airway epithelium: Evidence for regenerative ATP release. Experimental Physiology. 2010;95: 232–249. 10.1113/expphysiol.2009.049585 [DOI] [PubMed] [Google Scholar]
- 17. Dunn KC, Marmorstein AD, Bonilha VL, Rodriguez-Boulan E, Giordano F, Hjelmeland LM. Use of the ARPE-19 cell line as a model of RPE polarity: Basolateral secretion of FGF5. Investigative Ophthalmology & Visual Science. 1998;39: 2744–2749. [PubMed] [Google Scholar]
- 18. Glotin A, Debacq-Chainiaux F, Brossas J, Faussat A, Tréton J, Zubielewicz A, et al. Prematurely senescent ARPE-19 cells display features of age-related macular degeneration. Free Radical Biology and Medicine. 2008;44: 1348–1361. 10.1016/j.freeradbiomed.2007.12.023 [DOI] [PubMed] [Google Scholar]
- 19. Yamamoto A, Akanuma S, Tachikawa M, Hosoya K. Involvement of LAT1 and LAT2 in the high- and low-affinity transport of L-leucine in human retinal pigment epithelial cells (ARPE-19 cells). J Pharm Sci. 2010;99: 2475–2482. 10.1002/jps.21991 [DOI] [PubMed] [Google Scholar]
- 20. Ablonczy Z, Dahrouj M, Tang PH, Liu Y, Sambamurti K, Marmorstein AD, et al. Human retinal pigment epithelium cells as functional models for the RPE in vivo. Investigative Ophthalmology & Visual Science. 2011;52: 8614–8620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Lemon G, Gibson WG, Bennett MR. Metabotropic receptor activation, desensitization and sequestration—I: Modelling calcium and inositol 1,4,5-trisphosphate dynamics following receptor activation. J Theor Biol. 2003;223: 93–111. [DOI] [PubMed] [Google Scholar]
- 22. LeBeau AP, Yule DI, Groblewski GE, Sneyd J. Agonist-dependent phosphorylation of the inositol 1,4,5-trisphosphate receptor. The Journal of General Physiology. 1999;113: 851–872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Keizer J, Levine L. Ryanodine receptor adaptation and Ca2+(-)induced Ca2+ release-dependent Ca2+ oscillations. Biophys J. 1996;71: 3477–3487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Ahmado A, Carr A, Vugler AA, Semo M, Gias C, Lawrence JM, et al. Induction of differentiation by pyruvate and DMEM in the human retinal pigment epithelium cell line ARPE-19. Investigative Ophthalmology & Visual Science. 2011;52: 7148–7159. [DOI] [PubMed] [Google Scholar]
- 25. Dunn KC, Aotaki-Keen AE, Putkey FR, Hjelmeland LM. ARPE-19, a human retinal pigment epithelial cell line with differentiated properties. Exp Eye Res. 1996;62: 155–170. [DOI] [PubMed] [Google Scholar]
- 26. Peng S, Rahner C, Rizzolo LJ. Apical and basal regulation of the permeability of the retinal pigment epithelium. Investigative Ophthalmology & Visual Science. 2003;44: 808–817. [DOI] [PubMed] [Google Scholar]
- 27. Ross MH, Romrell LJ, Kaye GI. Histology a text and atlas Baltimore: Lippincott Williams & Wilkins; 1995. [Google Scholar]
- 28. Feeney-Burns L, Hilderbrand ES, Eldridge S. Aging human RPE: Morphometric analysis of macular, equatorial, and peripheral cells. Investigative Ophthalmology & Visual Science. 1984;25: 195–200. [PubMed] [Google Scholar]
- 29. Wang J, Huang X, Huang W. A quantitative kinetic model for ATP-induced intracellular oscillations. J Theor Biol. 2007;245: 510–519. [DOI] [PubMed] [Google Scholar]
- 30. Sullivan DM, Erb L, Anglade E, Weisman GA, Turner JT, Csaky KG. Identification and characterization of P2Y2 nucleotide receptors in human retinal pigment epithelial cells. J Neurosci Res. 1997;49: 43–52. [DOI] [PubMed] [Google Scholar]
- 31. Giancoli DC. Physics for scientists and engineers with modern physics (3rd edition): Prentice Hall; 2000. [Google Scholar]
- 32. Fall CP, Marland ES, Wager JM, Tyson JJ. Computational cell biology New York: Springer; 2002. [Google Scholar]
- 33. Chung W, Kermode JC. Suramin disrupts receptor-G protein coupling by blocking association of G protein α and βγ subunits. Journal of Pharmacology and Experimental Therapeutics. 2005;313: 191–198. [DOI] [PubMed] [Google Scholar]
- 34. Hamill OP. Twenty odd years of stretch-sensitive channels. Pflugers Arch—Eur J Physiol. 2006;453: 333–351. [DOI] [PubMed] [Google Scholar]
- 35. Luo Y, Zhuo Y, Fukuhara M, Rizzolo LJ. Effects of culture conditions on heterogeneity and the apical junctional complex of the ARPE-19 cell line. Investigative Ophthalmology & Visual Science. 2006;47: 3644–3655. [DOI] [PubMed] [Google Scholar]
- 36. Homolya L, Steinberg TH, Boucher RC. Cell to cell communication in response to mechanical stress via bilateral release of atp and utp in polarized epithelia. The Journal of Cell Biology. 2000;150: 1349–1360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Reigada D, Mitchell CH. Release of ATP from retinal pigment epithelial cells involves both CFTR and vesicular transport. American Journal of Physiology—Cell Physiology. 2005;288: C132–C140. [DOI] [PubMed] [Google Scholar]
- 38. Mitchell CH. Release of ATP by a human retinal pigment epithelial cell line: Potential for autocrine stimulation through subretinal space. The Journal of Physiology. 2001;534: 193–202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Reigada D, Lu W, Zhang X, Friedman C, Pendrak K, McGlinn A, et al. Degradation of extracellular ATP by the retinal pigment epithelium. American Journal of Physiology—Cell Physiology. 2005;289: C617–C624. [DOI] [PubMed] [Google Scholar]
- 40. Chaloux B, Caron AZ, Guillemette G. Protein kinase A increases the binding affinity and the Ca2+ release activity of the inositol 1,4,5-trisphosphate receptor type 3 in RINm5F cells. Biology of the Cell. 2007;99: 379–388. [DOI] [PubMed] [Google Scholar]
- 41. Betzenhauser MJ, Fike JL, Wagner LE, Yule DI. Protein kinase A increases type-2 inositol 1,4,5-trisphosphate receptor activity by phosphorylation of serine 937. Journal of Biological Chemistry. 2009;284: 25116–25125. 10.1074/jbc.M109.010132 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Caron AZ, Chaloux B, Arguin G, Guillemette G. Protein kinase C decreases the apparent affinity of the inositol 1,4,5-trisphosphate receptor type 3 in RINm5F cells. Cell Calcium. 2007;42: 323–331. [DOI] [PubMed] [Google Scholar]
- 43. Wojcikiewicz RJH, Luo SG. Phosphorylation of inositol 1,4,5-trisphosphate receptors by cAMP-dependent protein kinase. Journal of Biological Chemistry. 1998;273: 5670–5677. [DOI] [PubMed] [Google Scholar]
- 44. Nielsen MS, Nygaard Axelsen L, Sorgen PL, Verma V, Delmar M, Holstein-Rathlou N. Gap junctions. 2012;July;2(3): 1981–2035. 10.1002/cphy.c110051 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Ye Z, Wyeth M, Baltan-Tekkok S, Ransom B. Functional hemichannels in astrocytes: A novel mechanism of glutamate release. J Neurosci. 2003;May 1;23(9): 3588–3596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. De Pittà M, Goldberg M, Volman V, Berry H, Ben-Jacob E. Glutamate regulation of calcium and IP3 oscillating and pulsating dynamics in astrocytes. J Biol Phys. 2009;35(4): 383–411. 10.1007/s10867-009-9155-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Guo C, Wang Y, Hu D, Han Q, Wang J, Hou X, et al. Modulation of migration and Ca2+ signaling in retinal pigment epithelium cells by recombinant human CTGF. Current Eye Research. 2009;34:10: 852–862. 10.3109/02713680903128935 [DOI] [PubMed] [Google Scholar]
- 48. Huang W, Wang L, Yuan M, Ma J, Hui Y. Adrenomedullin affects two signal transduction pathways and the migration in retinal pigment epithelial cells. Investigative Ophthalmology & Visual Science. 2004;45: 1507–1513. [DOI] [PubMed] [Google Scholar]
- 49. Savolainen V, Juuti-Uusitalo K, Onnela N, Vaajasaari H, Narkilahti S, Suuronen R, et al. Impedance spectroscopy in monitoring the maturation of stem cell-derived retinal pigment epithelium. Annals of Biomedical Engineering. 2011;39: 3055–3069. 10.1007/s10439-011-0387-1 [DOI] [PubMed] [Google Scholar]
- 50. Yang D, Elner SG, Clark AJ, Hughes BA, Petty HR, Elner VM. Activation of P2X receptors induces apoptosis in human retinal pigment epithelium. Investigative Ophthalmology & Visual Science. 2011;52: 1522–1530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Wimmers S, Halsband C, Seyler S, Milenkovic V, Strauss O. Voltage-dependent Ca2+ channels, not ryanodine receptors, activate Ca2+-dependent BK potassium channels in human retinal pigment epithelial cells. Mol Vis. 2008;14: 2340–2348. [PMC free article] [PubMed] [Google Scholar]
- 52. Loeffler KU, Mangini NJ. Immunohistochemical localization of na+/Ca2+ exchanger in human retina and retinal pigment epithelium. Graefe's Arch Clin Exp Ophthalmol. 1998;236: 929–933. [DOI] [PubMed] [Google Scholar]
- 53. Stalmans P, Himpens B. A decreased Ca2+-wave propagation is found among cultured RPE cells from dystrophic RCS rats. Investigative Ophthalmology & Visual Science. 1998;39: 1493–1502. [PubMed] [Google Scholar]
- 54. Peterson WM, Meggyesy C, Yu K, Miller SS. Extracellular ATP activates calcium signaling, ion, and fluid transport in retinal pigment epithelium. The Journal of Neuroscience. 1997;17: 2324–2337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Maminishkis A, Jalickee S, Blaug SA, Rymer J, Yerxa BR, Peterson WM, et al. The P2Y2 receptor agonist INS37217 stimulates RPE fluid transport in vitro and retinal reattachment in rat. Investigative Ophthalmology & Visual Science. 2002;43: 3555–3566. [PubMed] [Google Scholar]
- 56. Siefjediers A, Hardt M, Prinz G, Diener M. Characterization of inositol 1,4,5-trisphosphate (IP3) receptor subtypes at rat colonic epithelium. Cell Calcium. 2007;41: 303–315. [DOI] [PubMed] [Google Scholar]
- 57. Maranto AR. Primary structure, ligand binding, and localization of the human type 3 inositol 1,4,5-trisphosphate receptor expressed in intestinal epithelium. Journal of Biological Chemistry. 1994;269: 1222–1230. [PubMed] [Google Scholar]
- 58. Sugiyama T, Yamamoto-Hino M, Wasano K, Mikoshiba K, Hasegawa M. Subtype-specific expression patterns of inositol 1,4,5-trisphosphate receptors in rat airway epithelial cells. Journal of Histochemistry & Cytochemistry. 1996;44: 1237–1242. [DOI] [PubMed] [Google Scholar]
- 59. Kennedy BG, Mangini NJ. Plasma membrane calcium-ATPase in cultured human retinal pigment epithelium. Exp Eye Res. 1996;63: 547–556. [DOI] [PubMed] [Google Scholar]
- 60. Stalmans P, Himpens B. Confocal imaging of Ca2+ signaling in cultured rat retinal pigment epithelial cells during mechanical and pharmacologic stimulation. Investigative Ophthalmology & Visual Science. 1997;38: 176–187. [PubMed] [Google Scholar]
- 61. Shen J, Gimbrone MA Jr, Luscinskas FW, Dewey CF Jr. Regulation of adenine nucleotide concentration at endothelium-fluid interface by viscous shear flow. Biophys J. 1993;64: 1323–1330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62. Garrad RC, Otero MA, Erb L, Theiss PM, Clarke LL, Gonzalez FA, et al. Structural basis of agonist-induced desensitization and sequestration of the P2Y2 nucleotide receptor. Journal of Biological Chemistry. 1998;273: 29437–29444. [DOI] [PubMed] [Google Scholar]
- 63. Mahama PA, Linderman JJ. A monte carlo study of the dynamics of G-protein activation. Biophys J. 1994;67: 1345–1357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64. Fink CC, Slepchenko B, Loew LM. Determination of time-dependent inositol-1,4,5-trisphosphate concentrations during calcium release in a smooth muscle cell. Biophys J. 1999;77: 617–628. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All relevant data are within the paper.