Abstract
Purpose
to investigate the relationship between hemodynamic conditions created immediately after flow diversion and subsequent occlusion of experimental aneurysms in rabbits.
Methods
The hemodynamic environment before and after flow diversion treatment of elastase induced aneurysms in 20 rabbits was modeled using image-based computational fluid dynamics. Local aneurysm occlusion was quantified using a voxelization technique on 3D images acquired 8 weeks after treatment. Global and local voxel-by-voxel hemodynamic variables were used to statistically compare aneurysm regions that later thrombosed to regions that remained patent.
Results
Six aneurysms remained patent at 8 weeks while 14 were completely or nearly completely occluded. Patent aneurysms had statistically larger neck sizes (p=0.0015) and smaller mean transit times (p=0.02). The velocity, vorticity and shear rate were about 2.8 times (p<0.0001) larger in patent regions, i.e. had larger “flow activity”, than regions that progressed to occlusion. Statistical models based on local hemodynamic variables were capable of predicting local occlusion with good precision (84% accuracy), especially away from the neck (92–94%). Predictions near the neck were poorer (73% accuracy).
Conclusion
These results suggests that the dominant healing mechanism of occlusion within the aneurysm dome are related to slow flow induced thrombosis while near the neck other processes could be at play simultaneously.
Keywords: cerebral aneurysm, flow diversion, hemodynamics, thrombosis
Introduction
Despite the increased use of flow diverting (FD) devices for treating intracranial aneurysms, the exact effects and processes responsible for the evolution of the aneurysm and ultimate outcome of these procedures are poorly understood [1–4]. Intra-saccular thrombosis and endothelial cell growth across the aneurysm neck have been observed after FD and have been proposed as the main mechanisms driving the healing process [5–7]. However, the interaction, dominance, relative importance, and time precedence of these processes are not well understood. Knowledge of these mechanisms is important to facilitate the development of future devices and therapies.
The purpose of this study was to investigate the relationship between the hemodynamic conditions created immediately after deployment of FD devices and the subsequent aneurysm occlusion in a rabbit model of saccular aneurysms.
Methods
Animal models and imaging
A total of 23 elastase-induced aneurysms were created in New Zealand white rabbits, following the approach described in [8]. Four weeks after their creation the aneurysms were treated with a FD device (Pipeline Embolization Device, Covidien). Two days before treatment, the subjects were pre-medicated with aspirin (10 mg/kg PO) and clopidogrel (10 mg/kg PO), and continued for one month after treatment. Immediately prior to treatment, 3D rotational angiography (3DRA) images were acquired, and velocities in the surrounding vessels were measured with Doppler ultrasound (DUS). Six animals were sacrificed before 1 week after treatment, all others after 8 weeks. Immediately prior to sacrifice 3DRA imaging was repeated. Some of the rabbits employed in this study were used as part of another investigation, where we analyzed the mechanism of the endothelialization after flow diverter implantation. This manuscript is entirely unrelated to the previous study.
Hemodynamics modeling
Subject-specific CFD models were constructed from pre-treatment 3DRA images [9]. Unstructured grids were generated with a resolution of 0.2 mm. Models of the FD devices used to treat the aneurysms were created and virtually deployed within the reconstructed vascular models [10]. Blood flows were modeled by solving the unsteady 3D incompressible Navier-Stokes equations [11]. Physiologic flow conditions were derived from the DUS velocity measurements and imposed as boundary conditions in the computational models. Wall compliance was not included in the model. Blood density was set to ρ=1.0 g/cm3 and blood viscosity to μ=0.04 Poise. The governing equations were numerically solved using an efficient finite element solver with a time-step of 0.01 sec [12]. After deployment of the FD device, the mesh was adaptively refined to resolve the stent wires and a new CFD simulation was performed using immersed grids [13, 14].
Occlusion modeling
Regions of the aneurysm that remained open or patent and regions that were occluded at the time of sacrifice were identified by constructing a second vascular model from the 3DRA image acquired prior to sacrifice. The pre-treatment model and this pre-mortem or follow-up model were manually aligned using rigid registration. A new grid was generated filling the volume of the follow-up model. The aneurysm neck was interactively delineated on the pre-treatment model by connecting selected points along the path of minimum geodesic distance [15]. The aneurysm orifice defined by the delineated neck was triangulated, and grid points on each side of this surface were labeled as belonging to the aneurysm or the vessel [15]. The bounding box of the aneurysm was found and voxelized with isotropic voxels of the same resolution of the 3DRA images. Mesh points in the aneurysm region were then labeled as open or occluded depending on whether they were inside or outside the aligned follow-up model. The methodology is illustrated in Figure 1.
Figure 1.
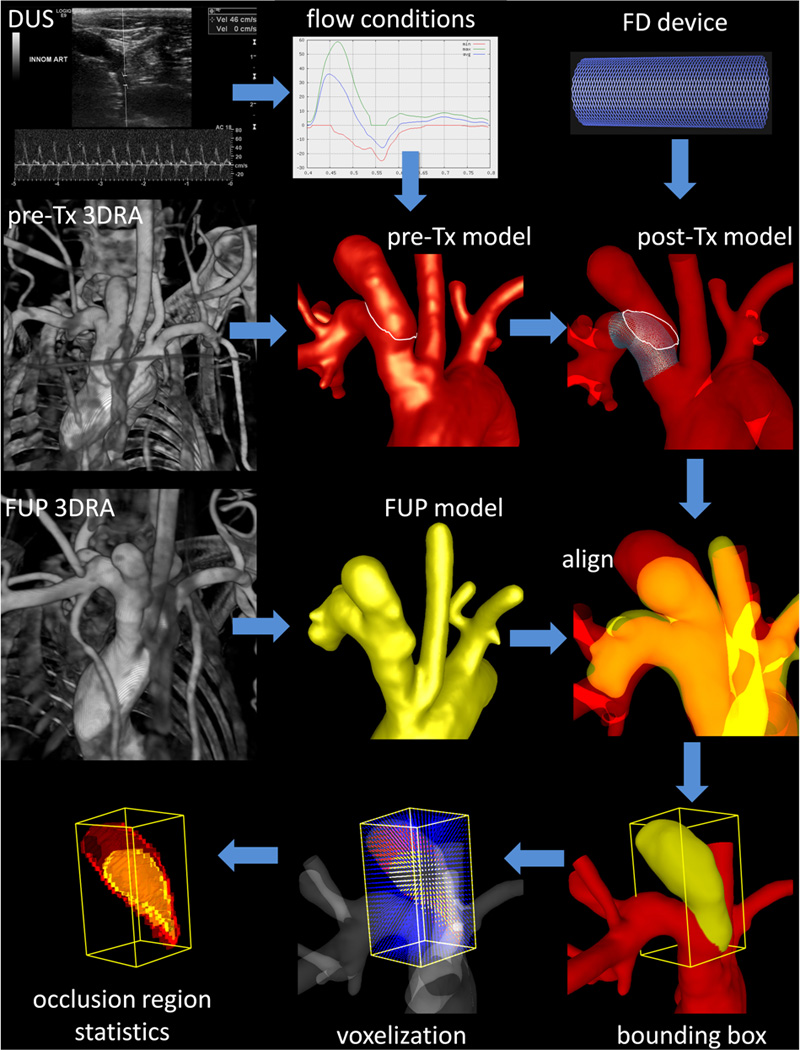
Imaging, modeling and data analysis.
Global (per aneurysm) data analysis
The degree of aneurysm occlusion at the time of sacrifice was quantified by the percent of occluded voxels identified as described above. Aneurysms were then classified into two groups: a) “patent group”: less than 80% of the voxels occluded at follow-up, b) “occluded group”: more than 80% of the voxels occluded at follow-up. This 80% threshold was chosen because aneurysms with more than 80% occlusion of their volume looked almost completely closed on DSA images with perhaps a small “bump” in the parent artery, i.e. they did not exhibit remnant necks of persistent filling of the sac.
Using the 3D meshes, geometrical variables including volume, maximum size, neck area and maximum neck size were calculated for each aneurysm. Similarly, of the following hemodynamic quantities were calculated over the aneurysm region and averaged over the cardiac cycle: mean aneurysm inflow rate <Q>mean aneurysm velocity <v>mean aneurysm wall shear stress <τ>and mean aneurysm shear rate <γ̇>. These quantities were computed before and after treatment. Additionally, a new variable denoted “mean aneurysm transit time” (MATT) was defined as:
where V is the aneurysm volume, A is the neck area and <v> is the mean aneurysm velocity. The rationale is that this variable, which has units of time, should:
increase with the aneurysm volume, i.e. it takes longer to traverse a large aneurysm;
decrease with the neck area, i.e. larger neck implies more chances of getting out of the aneurysm, while smaller neck implies more chances of staying within the aneurysm and recirculate;
decrease with the blood velocity, i.e. slower velocities imply longer transit times.
The values of geometric and hemodynamic variables were then averaged over the patent and occluded groups. Cases belonging to the incompletely occluded group sacrificed before one week after treatment (between brackets in the tables) were excluded from the statistical analysis. The Wilcoxon non-parametric test was used to test if the means were statistically different between the occluded and patent groups.
Local (voxel-by-voxel) data analysis
Velocity (v), vorticity (ω) and shear rate (γ̇) were calculated on the CFD mesh and interpolated and averaged over each aneurysm voxel. The mean values of these quantities over open or occluded voxels of each aneurysm were calculated and compared.
Predictive statistical models of regional occlusion were then constructed. Two classes or outcomes were defined: i) occluded voxels (+1), and ii) open voxels (−1). Seven attributes or features were considered: 1) <v>pre, 2) <ω>pre, 3) <γ̇>pre, 4) <v>post, 5) <ω>post, 6) <γ̇>post, and 7) d=path distance to the neck. These values were calculated for each voxel from the pre-treatment and post-treatment CFD simulations. A logistic regression model [16] was trained using a ‘Leave One Out’ methodology. Specifically, it was trained with all open and occluded voxels from all aneurysms except one. The aneurysm left out was then used to test the accuracy of the model. The probabilities of each voxel of this aneurysm of belonging to each class were and the voxel was “predicted” to belong to the class of the highest probability. The accuracy of the prediction was calculated by counting the number of correctly and incorrectly classified voxels. The process was repeated by leaving each aneurysm out at a time, and the total predictive accuracy of the model was computed.
Next, the voxels of each aneurysm were divided into three groups according to their distance to the aneurysm neck. Denoting by d the distance from a voxel to the neck and dmax the maximum distance from any voxel to the neck, voxels were assigned to the following three groups: a) dome if d/dmax>2/3, b) body if 1/3≤d/dmax≤2/3, and c) neck if d/dmax<1/3. The predictive statistical analysis described above using the logistic regression model was repeated for voxels in each of these three regions. The corresponding predictive accuracies were calculated and compared.
Finally, the predictive power of the following statistical models typically employed in machine learning studies were computed and compared [17]: a) logistic regression, b) neural network, and c) support vector machine. Each of these models was trained with data from all aneurysms except one and tested on the one left out. The process was repeated by leaving each aneurysm out in turn. The total predictive accuracy of each model was computed and compared.
Results
Hemodynamics
Flow visualizations revealed that velocities within the aneurysm are substantially reduced after treatment, that flow structures may change and in particular become smoother and simpler (i.e. less swirling), and that the location of the inflow stream may shift from the distal part of the neck to the proximal part. To illustrate these observations, two examples are presented in Figure 2, corresponding to incomplete and complete occlusions. The placement of FD devices thus causes both quantitative and qualitative changes in the hemodynamic environment within the aneurysm.
Figure 2.
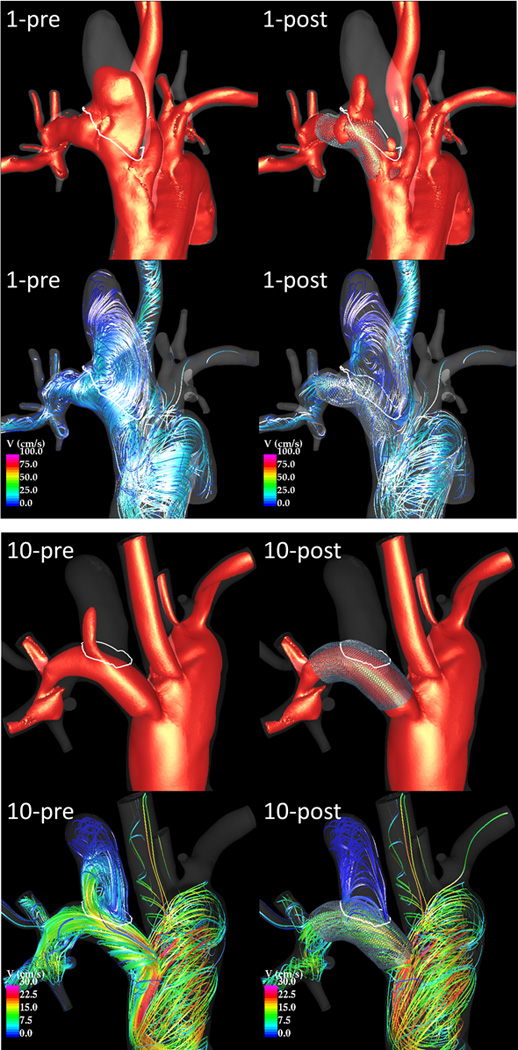
Visualization of peak systole flow structures pre and post-treatment in an incompletely occluded aneurysm (case 1 – top) and in a completely occluded aneurysm (case 10 – bottom). Each panel shows 20 cm/s velocity iso-surfaces (top) and flow streamlines (bottom) before (left) and after (right) treatment.
Global (per aneurysm) characteristics
Geometrical characteristics of the aneurysms, the parent arteries and the FD devices are presented in Table 1. Aneurysms have been ordered by percent occlusion, and aneurysms in the patent group have been highlighted. The aneurysm volume was not statistically different between the open and occluded aneurysm groups. The neck area (p=0.0006), maximum neck size (p=0.0015), and maximum aneurysm size (p=0.02) were significantly larger in the patent than in the occluded groups.
Table 1.
Aneurysm occlusion, geometry and device data.
| case | aneurysm occlusion (%) |
PPA diameter (mm) |
DPA diameter (mm) |
device size (mm×mm) |
aneurysm volume (cm3) |
aneurysm size (cm) |
neck size (cm) |
neck area (cm2) |
|---|---|---|---|---|---|---|---|---|
| 1 | 7% | 3.23 | 3.18 | 3.75×10 | 0.36 | 1.90 | 0.93 | 0.45 |
| 2 | 19% | 3.28 | 2.66 | 4.5×12 | 0.17 | 1.13 | 0.86 | 0.48 |
| 3 | 31% | 2.96 | 3.94 | 3.75×10 | 0.13 | 1.20 | 0.79 | 0.34 |
| 4 | 41% | 3.72 | 3.54 | 3.75×12 | 0.06 | 1.17 | 0.65 | 0.27 |
| [5] | 46% | 3.47 | 3.11 | 3.50×12 | 0.12 | 1.31 | 0.60 | 0.22 |
| [6] | 73% | 3.19 | 3.40 | 3.25×10 | 0.08 | 0.74 | 0.53 | 0.14 |
| 7 | 75% | 3.41 | 3.89 | 4.75×10 | 0.19 | 1.43 | 0.61 | 0.30 |
| [8] | 76% | 3.11 | 3.34 | 3.50×12 | 0.13 | 1.20 | 0.57 | 0.22 |
| 9 | 77% | 2.86 | 3.79 | 4.75×10 | 0.03 | 1.49 | 0.64 | 0.31 |
| [10] | 82% | 3.26 | 3.02 | 3.50×10 | 0.08 | 0.94 | 0.47 | 0.14 |
| 11 | 84% | 3.97 | 4.18 | 4.00×10 | 0.20 | 1.33 | 0.61 | 0.25 |
| [12] | 90% | 3.44 | 3.11 | 3.50×10 | 0.12 | 1.20 | 0.42 | 0.12 |
| 13 | 91% | 3.07 | 3.58 | 3.50×12 | 0.32 | 1.42 | 0.70 | 0.34 |
| 14 | 91% | 3.95 | 4.24 | 4.00×10 | 0.08 | 1.01 | 0.53 | 0.09 |
| 15 | 94% | 3.10 | 3.03 | 4.75×12 | 0.25 | 1.42 | 0.65 | 0.28 |
| 16 | 98% | 3.57 | 3.57 | 4.25×10 | 0.06 | 0.91 | 0.34 | 0.07 |
| [17] | 100% | 3.25 | 3.48 | 4.75×10 | 0.15 | 1.17 | 0.60 | 0.25 |
| 18 | 100% | 3.82 | 3.25 | 3.50×10 | 0.01 | 0.39 | 0.24 | 0.04 |
| 19 | 100% | 3.70 | 2.50 | 4.25×10 | 0.03 | 0.62 | 0.30 | 0.07 |
| 20 | 100% | 4.24 | 3.96 | 4.75×10 | 0.03 | 0.59 | 0.41 | 0.12 |
| 21 | 100% | 3.79 | 3.43 | 4.75×12 | 0.12 | 1.09 | 0.56 | 0.19 |
| 22 | 100% | 3.65 | 2.89 | 4.00×10 | 0.02 | 0.53 | 0.31 | 0.05 |
| 23 | 100% | 3.53 | 3.79 | 3.50×12 | 0.07 | 0.74 | 0.63 | 0.17 |
| average over patent group | 0.16 | 1.39 | 0.75 | 0.36 | ||||
| average over occluded group | 0.11 | 0.96 | 0.49 | 0.16 | ||||
| ratio (patent / occluded) | 1.41 | 1.44 | 1.54 | 2.25 | ||||
| p-value | 0.2655 | 0.0200* | 0.0015* | 0.0006* | ||||
| AUC | 0.51 | 0.67 | 0.70 | 0.73 | ||||
Statistically significant differences (p<0.05) are marked with a
Cases between [] were sacrificed before one week and not included in the analysis.
Results from the global hemodynamics analysis are presented in Table 2. Only the mean inflow rate and mean aneurysm transit time were significantly different between the patent and occluded groups. The inflow rate before (p=0.0015) and after treatment (p=0.0305) were about 2.8 times larger in the patent group. The mean aneurysm transit time after treatment (p=0.02) was about 3 times larger in occluded aneurysms than in patent aneurysms. The mean post-treatment shear rate achieved marginal significance (p=0.0757) and was about 1.6 times larger in the patent group. All other quantities were not statistically different between the open and occluded groups.
Table 2.
Aneurysm occlusion and hemodynamic data.
| case | occlusion (%) |
<Q> (ml/s) | <v> (cm/s) | <τ> (dyne/cm2) | <γ̇> (1/s) | MATT (s) |
||||
|---|---|---|---|---|---|---|---|---|---|---|
| pre | post | pre | post | pre | post | pre | post | |||
| 1 | 7% | 3.75 | 2.29 | 2.00 | 0.96 | 1.78 | 0.93 | 24.90 | 11.80 | 0.84 |
| 2 | 19% | 4.24 | 1.76 | 0.28 | 0.13 | 1.42 | 0.81 | 20.00 | 9.86 | 2.58 |
| 3 | 31% | 2.83 | 0.37 | 1.44 | 0.20 | 1.16 | 0.36 | 23.79 | 3.22 | 1.83 |
| 4 | 41% | 2.03 | 0.51 | 0.92 | 0.18 | 1.55 | 0.42 | 19.79 | 3.85 | 1.39 |
| [5] | 46% | 4.49 | 1.2 | 1.39 | 0.25 | 1.82 | 0.42 | 24.09 | 4.43 | 2.23 |
| [6] | 73% | 6.37 | 2.03 | 1.56 | 0.25 | 2.11 | 0.51 | 26.20 | 5.65 | 2.30 |
| 7 | 75% | 3.75 | 2.29 | 2.81 | 0.49 | 3.50 | 0.82 | 41.43 | 7.34 | 1.28 |
| [8] | 76% | 4.24 | 1.76 | 1.94 | 0.26 | 2.48 | 0.35 | 31.83 | 4.17 | 2.26 |
| 9 | 77% | 2.83 | 0.37 | 1.55 | 0.48 | 1.52 | 0.74 | 20.53 | 6.87 | 0.25 |
| [10] | 82% | 1.16 | 0.19 | 1.00 | 0.14 | 1.49 | 0.38 | 19.16 | 2.92 | 3.95 |
| 11 | 84% | 2.31 | 0.54 | 1.37 | 0.22 | 1.69 | 0.54 | 19.88 | 4.12 | 3.62 |
| [12] | 90% | 0.45 | 0.2 | 1.02 | 0.12 | 1.51 | 0.33 | 19.11 | 2.61 | 7.57 |
| 13 | 91% | 2.9 | 1.33 | 1.45 | 0.35 | 1.23 | 0.38 | 16.96 | 4.36 | 2.72 |
| 14 | 91% | 1.77 | 0.57 | 0.94 | 0.20 | 1.16 | 0.42 | 18.12 | 4.73 | 4.47 |
| 15 | 94% | 4.23 | 1.87 | 2.53 | 0.37 | 2.39 | 0.64 | 33.82 | 6.73 | 2.36 |
| 16 | 98% | 0.7 | 0.11 | 1.01 | 0.14 | 1.59 | 0.47 | 21.46 | 3.80 | 5.71 |
| [17] | 100% | 0.11 | 0.02 | 1.49 | 0.48 | 1.60 | 0.57 | 21.38 | 7.06 | 1.22 |
| 18 | 100% | 1.82 | 0.75 | 0.43 | 0.06 | 0.91 | 0.28 | 13.44 | 2.31 | 5.01 |
| 19 | 100% | 0.37 | 0.06 | 0.20 | 0.04 | 0.44 | 0.16 | 5.53 | 1.30 | 10.43 |
| 20 | 100% | 0.55 | 0.37 | 1.45 | 0.56 | 2.06 | 1.03 | 27.30 | 11.23 | 0.54 |
| 21 | 100% | 1.22 | 0.57 | 1.44 | 0.20 | 1.87 | 0.37 | 24.02 | 3.44 | 3.24 |
| 22 | 100% | 0.39 | 0.11 | 0.46 | 0.08 | 1.07 | 0.37 | 14.56 | 3.14 | 3.98 |
| 23 | 100% | 1.76 | 0.28 | 1.39 | 0.32 | 1.92 | 0.66 | 23.58 | 5.50 | 1.26 |
| mean patent | 3.95 | 1.36 | 1.50 | 0.41 | 1.82 | 0.68 | 25.08 | 7.16 | 1.36 | |
| mean occluded | 1.41 | 0.49 | 1.15 | 0.24 | 1.50 | 0.48 | 19.89 | 4.52 | 4.01 | |
| ratio | 2.80 | 2.73 | 1.30 | 1.72 | 1.21 | 1.21 | 1.26 | 1.58 | (2.94)−1 | |
| p-value | 0.0015* | 0.0305* | 0.3429 | 0.2074 | 0.6501 | 0.1093 | 0.1528 | 0.0757† | 0.0200* | |
| AUC | 0.67 | 0.54 | 0.51 | 0.51 | 0.43 | 0.56 | 0.53 | 0.58 | 0.12 | |
Statistically significant differences (p<0.05) are marked with a
Cases between [] were sacrificed before one week and not included in the analysis.
In order to assess the possibility of predicting whether the aneurysm will be completely occluded at follow-up or not, a receiving operating curve (ROC) analysis was performed. The area under the curve (AUC) was calculated for each geometric and hemodynamic variable (listed in Table 1 and Table 2). The best predictor was the neck area and size, with an accuracy of about 70–73%. However, our sample included a small number of aneurysms and it is likely that this accuracy could be improved with larger samples.
Regional (voxel-by-voxel) characteristics
Results from the local hemodynamics analysis are presented in Figure 3. This figure shows the mean value of post-treatment hemodynamics variables (velocity, vorticity and shear rate) averaged over the open (red) and occluded (green) voxels of each aneurysm. Aneurysms in the x-axis are ordered by percent occlusion. It can be seen that open voxels have larger post-treatment velocity, vorticity and shear rate than occluded voxels. These differences are less pronounced in aneurysms that had large patent regions (towards the left of Figure 3). The differences seem to increase with the percent of occluded voxels (to the right of Figure 3). Ratios of post-treatment hemodynamic variables in open voxels over occluded voxels are presented in Table 3 for aneurysms that were not completely occluded. These results indicate that velocity, vorticity and shear rate are on average larger by a factor of about 2.6 in open regions than in occluded regions. The ratios, however, are larger in aneurysms that were nearly completely occluded than in incompletely occluded ones. The p-values indicate that these differences are statistically significant.
Figure 3.
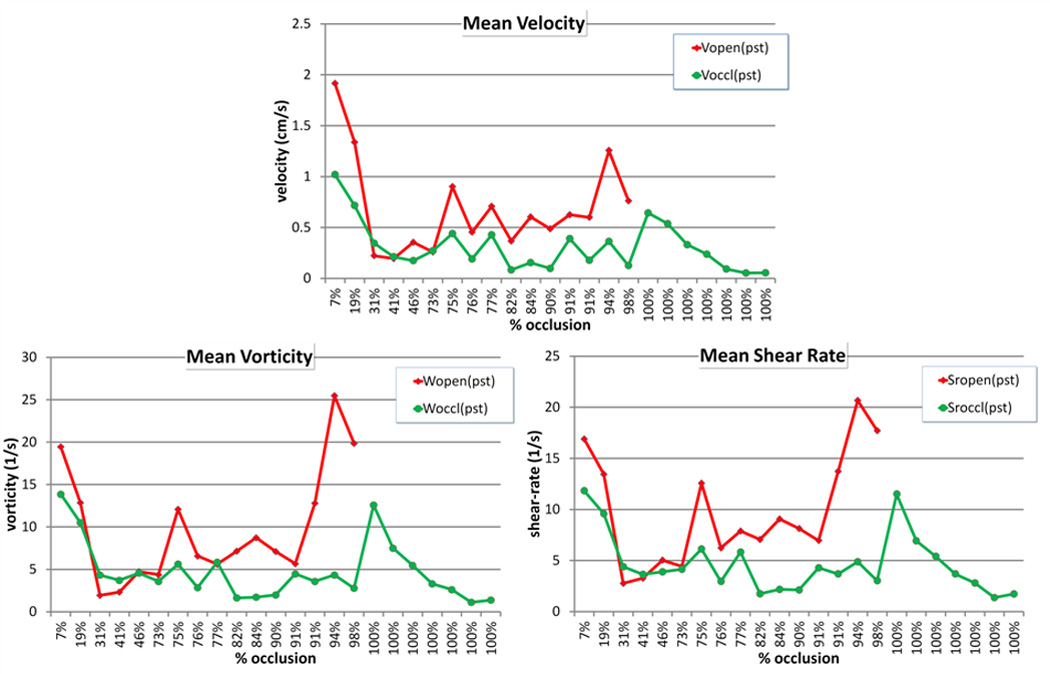
Post-treatment hemodynamic variables averaged over open and occluded regions.
Table 3.
Ratio of mean post-treatment hemodynamic variables in open over occluded regions.
| case | Ratio(v) | Ratio(ω) | Ratio(<γ̇>) |
|---|---|---|---|
| 1 | 1.88 | 1.40 | 1.43 |
| 2 | 1.87 | 1.22 | 1.40 |
| 3 | 0.64 | 0.45 | 0.63 |
| 4 | 0.92 | 0.62 | 0.89 |
| [5] | 2.03 | 1.04 | 1.29 |
| [6] | 0.95 | 1.22 | 1.07 |
| 7 | 2.05 | 2.15 | 2.05 |
| [8] | 2.38 | 2.31 | 2.11 |
| 9 | 1.66 | 0.96 | 1.35 |
| [10] | 4.42 | 4.38 | 4.04 |
| 11 | 3.90 | 5.06 | 4.16 |
| [12] | 4.96 | 3.56 | 3.83 |
| 13 | 1.61 | 1.27 | 1.63 |
| 14 | 3.38 | 3.58 | 3.72 |
| 15 | 3.46 | 5.87 | 4.24 |
| 16 | 6.06 | 7.15 | 5.86 |
| mean | 2.64 | 2.64 | 2.48 |
| mean open | 1.60 | 1.26 | 1.36 |
| mean occluded | 3.97 | 4.41 | 3.93 |
| p-value | 0.0139* | 0.0046* | 0.0023* |
Statistically significant differences (p<0.05) are marked with a
Cases sacrificed before one week after treatment are indicated between [] and not included in the statistical analysis.
Predictive models
Table 4 presents the accuracy and number of correctly predicted voxels over the total number of voxels for logistic regression models created for the entire aneurysm (sac), the dome, the body, and the neck regions. In addition, a range of accuracy values is provided for each region. These ranges were computed by calculating the accuracy of all possible combinations of the 7 features used to build the models (255 models for each region). It can be seen that overall the logistic regression model is capable of predicting which voxels will be occluded with very good accuracy, and that voxels near the dome are more easily predicted than voxels near the neck.
Table 4.
Accuracy of logistic regression models of local occlusion.
| region | accuracy | correct/total | range (%) |
|---|---|---|---|
| sac | 84 % | 28054 / 33254 | [82.6, 84.5] |
| dome | 94 % | 9649 / 10299 | [92.7, 94.0] |
| body | 92 % | 12232 / 13274 | [91.5, 92.4] |
| neck | 73 % | 11060 / 15050 | [71.8, 73.9] |
A comparison of different statistical classifiers typically used in machine learning is presented in Table 5. Overall, all statistical models had similar accuracies. The best performance was obtained with the neural network. The cases that were most difficult to predict were the ones with patent regions that were about 60% to 70% of the aneurysm volume. The predictive accuracy for aneurysms that were about 30% to 46% occluded ranged from about 40% to 50% (data not shown).
Table 5.
Accuracy of different statistical models of local occlusion.
| model | accuracy | RMS error |
|---|---|---|
| logistic regression | 86% | 0.32 |
| neural network | 90% | 0.27 |
| support vector machine | 85% | 0.38 |
Discussion
Flow diverters cause a significant disruption of the aneurysm inflow stream which induces both qualitative and quantitative changes in the hemodynamic environment within the aneurysm. Aneurysms completely or almost completely occluded after treatment had statistically smaller necks than aneurysms that remained patent. They also had larger mean aneurysm transit times (related to the aneurysm residence time). Immediately after FD implantation, the local velocity, vorticity (speed of rotation or swirling of fluid elements) and shear rate (rate of deformation of fluid elements) were all statistically smaller in regions later observed to occlude than in regions that remained patent. Statistical models based on local hemodynamic conditions were able to predict local occlusion with a very good accuracy. For a given aneurysm, regions close to the neck were more difficult to predict than regions that were close to the aneurysm dome.
The mechanism of intra-saccular thrombosis and subsequent aneurysm occlusion is intimately related to the hemodynamic environment created after treatment. This environment depends mainly on the geometry of the aneurysm and parent artery and on the hemodynamic effects of the FD device. Aneurysm morphology, in particular the location of the orifice on the parent artery and the neck size determine the inflow stream into the aneurysm. The characteristics of the FD device in turn determine the disruption of this inflow stream and subsequent recirculation within the aneurysm sac. Thus, associations between both geometric and hemodynamic variables with outcome are expected. However, in this series, all aneurysms were created at the same location and were treated with similar FD devices. Thus it is not surprising that the best predictor of complete occlusion was the neck size. Further studies with larger samples are needed to better understand the relationships between geometry, hemodynamics and outcomes.
Previous studies have largely focused on the changes of hemodynamic quantities from pre- to post-treatment. Pereira et al. [18] used dynamic DSA images to estimate the mean aneurysm velocity (MAFA: mean aneurysm flow amplitude) before and after FD treatment in a pilot clinical study (n=21), and found that at a later follow up exam aneurysms that were completely occluded (n=18) had larger reductions of the MAFA than aneurysms still patent (n=3). Zhang et al. [19] used CFD porous media to model the flow in two stented aneurysms, one remained patent and the other completely occluded. They reported larger reduction of aneurysm inflow velocity in the occluded than in the patent aneurysm. Huang et a. [20] analyzed the flow dynamics in 14 rabbit aneurysm models treated with FDs. They used micro CT images of harvested arteries with the FD to create a model of the stent and place it in CFD models, and found larger reductions in aneurysm inflow and larger increases of relative residence time in occluded aneurysms (n=10) than in patent aneurysms (n=4), although these differences did not reach statistical significance. They also observed changes in the location of the inflow stream, from the distal part of the neck to a more central/proximal position. In our study, we used CFD models with subject specific flow conditions and FD models that reproduce the geometrical characteristics of the implanted devices, and compared global and local hemodynamic quantities in both occluded and patent aneurysms as well as between occluded and patent regions of each aneurysm. Our study focused on hemodynamic conditions created immediately after treatment rather than on changes from pre- to post-treatment.
The results of our study suggest that global hemodynamic conditions may not be sufficient to understand or predict aneurysm occlusion following flow diversion treatment. They also suggest that thrombosis induced by the local hemodynamic conditions seems to be the main driver of aneurysm occlusion at the dome and body of the aneurysm, while other mechanisms such as endothelial tissue growth may be important near the neck. It is also possible that the thrombosis starts at the dome and progresses towards the neck, altering the intra-aneurysmal hemodynamic environment and inducing thrombus formation near the neck at a later time followed by endothelialization. The regional analysis described in this work provides local information that could potentially be used to establish thresholds for thrombosis initiation and develop quantitative predictive models of local aneurysm occlusion.
The current study has a number of limitations that should be considered when interpreting the results. Unlike human cerebral arteries, flow reversals were observed in the parent arteries of our animal models. This could affect the values of the time averaged hemodynamic quantities investigated. Alignment of follow-up and pre-treatment vascular models was done manually. This could result in inaccuracies of the quantification of the patent and occluded regions of the aneurysm. Our analysis did not distinguish between voxels that were close to the wall or near the middle of the aneurysm, which may have different hemodynamic environments. Likewise, the changes in the hemodynamic environment as the aneurysm progressively thromboses were not taken into account, only the hemodynamic conditions immediately post-treatment were studied. More refined models incorporating thrombus formation and proximity to the wall should be considered in future studies. The virtual deployment, the estimation of flow conditions from Doppler ultrasound images, as well as the many assumptions and approximations made during the CFD modeling process may affect the hemodynamic results. However, previous studies have indicated that these models were able to reproduce in vivo velocity measurements and observed flow characteristics [21]. Finally, the number of animal models included in the study is limited. Studies with larger number of subjects are needed to confirm the trends observed in this work and to achieve stronger statistical significance.
Despite these limitations, this study confirms that local hemodynamic conditions created immediately after FD implantation play an important role in determining whether different regions of the aneurysm will thrombose and occlude or remain patent. The next set of studies should focus on the connection between hemodynamic conditions and biologic processes responsible not only for thrombosis and aneurysm occlusion but also for endothelial tissue growth and parent artery reconstruction.
Conclusions
Aneurysms completely occluded at follow-up had statistically smaller necks and larger mean transit times than aneurysms that remained patent. Post-treatment velocity, vorticity and shear rate were significantly larger in regions that remained patent, i.e. had larger “flow activity”, than in regions that occluded. Machine learning models based on local hemodynamic variables were capable of predicting local occlusion with good precision, especially away from the neck. This suggests that the dominant healing mechanism at the dome and body of the aneurysm are related to flow induced thrombosis while near the neck other processes such as flow modulated endothelialization may also play a fundamental role.
Acknowledgements
This work was supported by NIH grant NS076491. We thank Covidien Inc. for generously providing flow diverters.
References
- 1.Lylyk P, Miranda C, Ceratto R, Ferrario A, Scrivano E, Luna H, Berez A, Tran Q, Nelson PK, Fiorella D. Curative endovascular reconstruction of cerebral aneurysms with the pipeline embolization device: the Buenos Aires experience. Neurosurgery. 2009;64(4):632–642. doi: 10.1227/01.NEU.0000339109.98070.65. [DOI] [PubMed] [Google Scholar]
- 2.Nelson PK, Lylyk P, Szikora I, Wetzel SG, Wanke I, Fiorella D. The pipeline embolization device for the intracranial treatment of aneurysms trial. AJNR Am J Neuroradiol. 2011;32(1):34–40. doi: 10.3174/ajnr.A2421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Seong J, Wakhloo AK, Lieber BB. In Vitro Evaluation of Flow Divertors in an Elastase-Induced Saccular Aneurysm Model in Rabbit. Journal of Biomechanical Engineering. 2007;129(6):863–872. doi: 10.1115/1.2800787. [DOI] [PubMed] [Google Scholar]
- 4.Kulcsar Z, Houdart E, Bonafe A, G P, Millar J, Goddard AJ, Renowden S, Gal G, Torowski B, Mitchell K, Gray F, Rodriguesz M, van den Berg R, Gruber A, Desal H, Wanke I, Rüfenacht DA. Intra-aneurysmal thrombosis as a possible cause of delayed aneurysm rupture after flow-diversion treatment. AJNR American Journal of Neuroradiology. 2011;32(1):20–25. doi: 10.3174/ajnr.A2370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kallmes DF, Ding YH, Dai D, Kadirvel R, Lewis DA, Cloft HJ. A new endoluminal, flow disrupting device for treatment of saccular aneurysms. Stroke. 2007;38(8):2346–2352. doi: 10.1161/STROKEAHA.106.479576. [DOI] [PubMed] [Google Scholar]
- 6.Kallmes DF, Ding YH, Dai D, Kadirvel R, Lewis DA, Cloft HJ. A second-generation, endoluminal, flow-disrupting device for treatment of saccular aneurysms. AJNR Am J Neuroradiol. 2009;30(6):1153–1158. doi: 10.3174/ajnr.A1530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Szikora I, Berentei Z, Kulcsar Z, Marosfoi M, Vajda ZS, Lee W, Berez A, Nelson PK. Treatment of Intracranial Aneurysms by Functional Reconstruction of the Parent Artery: The Budapest Experience with the Pipeline Embolization Device. AJNR American Journal of Neuroradiology. 2010;31(6):1139–1147. doi: 10.3174/ajnr.A2023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Altes TA, Cloft HJ, Short JG, DeGast A, Do HM, Helm GA, Kallmes DF. 1999 ARRS Executive Council Award. Creation of saccular aneurysms in the rabbit: a model suitable for testing endovascular devices. American Roentgen Ray Society. American Journal of Roentgenology. 2000;174(2):349–354. doi: 10.2214/ajr.174.2.1740349. [DOI] [PubMed] [Google Scholar]
- 9.Cebral JR, Castro MA, Appanaboyina S, Putman CM, Millan D, Frangi AF. Efficient pipeline for image-based patient-specific analysis of cerebral aneurysm hemodynamics: Technique and sensitivity. IEEE Transactions in Medical Imaging. 2005;24(1):457–467. doi: 10.1109/tmi.2005.844159. [DOI] [PubMed] [Google Scholar]
- 10.Mut F, Cebral JR. Effects of Flow-Diverting Device Oversizing on Hemodynamics Alteration in Cerebral Aneurysms. AJNR Am J Neuroradiol. 2012;33(10):2010–2016. doi: 10.3174/ajnr.A3080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kundu PK, Cohen IM. Fluid mechanics. New York: Academic Press (Elsevier); 2004. [Google Scholar]
- 12.Mut F, Aubry R, Löhner R, Cebral JR. Fast numerical solutions in patient-specific simulations of arterial models. IJNMBE Int J Num Meth Biomed Eng. 2010;26(1):73–85. doi: 10.1002/cnm.1235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Appanaboyina S, Mut F, Löhner R, Putman CM, Cebral JR. Computational Fluid Dynamics of Stented Intracranial Aneurysms using Adaptive Embedded Unstructured Grids. International Journal for Numerical Methods in Fluids. 2008;57:457–493. [Google Scholar]
- 14.Appanaboyina S, Mut F, Löhner R, Putman CM, Cebral JR. Simulation of intracranial aneurysm stenting: techniques and challenges. Computer Methods in Applied Mechanics and Engineering. 2009;198(45–46):3567–3582. [Google Scholar]
- 15.Mut F, Löhner R, Chien A, Tateshima S, Viñuela F, Putman CM, Cebral JR. Computational hemodynamics framework for the analysis of cerebral aneurysms. Int J Num Meth Biomed Eng. 2011;27(6):822–839. doi: 10.1002/cnm.1424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Fan RE, Chang KW, Hsieh CJ, Wang XR, Lin CJ. LIBLINEAR: a library for large linear classification. Journal of Machine Learning Research. 2008;9:1871–1874. [Google Scholar]
- 17.Hall M, Frank E, Holmes G, Pfahringer B, Reutemann P, Witten IH. The WEKA data mining software: an update. SIGKDD Explorations. 2009;11(1) [Google Scholar]
- 18.Pereira VM, Bonnefous O, Ouared R, Brina O, Stawiaski J, Aerts H, Ruijters D, Narata AP, Bijlenga P, Schaller K, Lovblad KO. A DSA-Based Method Using Contrast-Motion Estimation for the Assessment of the Intra-Aneurysmal Flow Changes Induced by Flow-Diverter Stents. AJNR Am J Neuroradiol. 2013;34(3):805–815. doi: 10.3174/ajnr.A3322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Zhang Y, Chong W, Qian Y. Investigation of intracranial aneurysm hemodynamics following flow diverter stent treatment. Med Eng Phys. 2013;35(5):608–615. doi: 10.1016/j.medengphy.2012.07.005. [DOI] [PubMed] [Google Scholar]
- 20.Huang Q, Xu J, Cheng J, Wang S, Wang K, Liu JM. Hemodynamic Changes by Flow Diverters in Rabbit Aneurysm Models: A Computational Fluid Dynamic Study Based on Micro-Computed Tomography Reconstruction. Stroke. 2013 doi: 10.1161/STROKEAHA.113.001202. [DOI] [PubMed] [Google Scholar]
- 21.Cebral JR, Mut F, Raschi M, Kadirvel R, Kallmes DF. Flow diversion in rabbit aneurysm models. ASME Summer Bioengineering Conference; 2013; Sunriver, OR. [Google Scholar]


